Numerical Simulation of the Tip Leakage Vortex Characteristics in a Semi-Open Centrifugal Pump
Abstract
:1. Introduction
2. Computational Model and Method
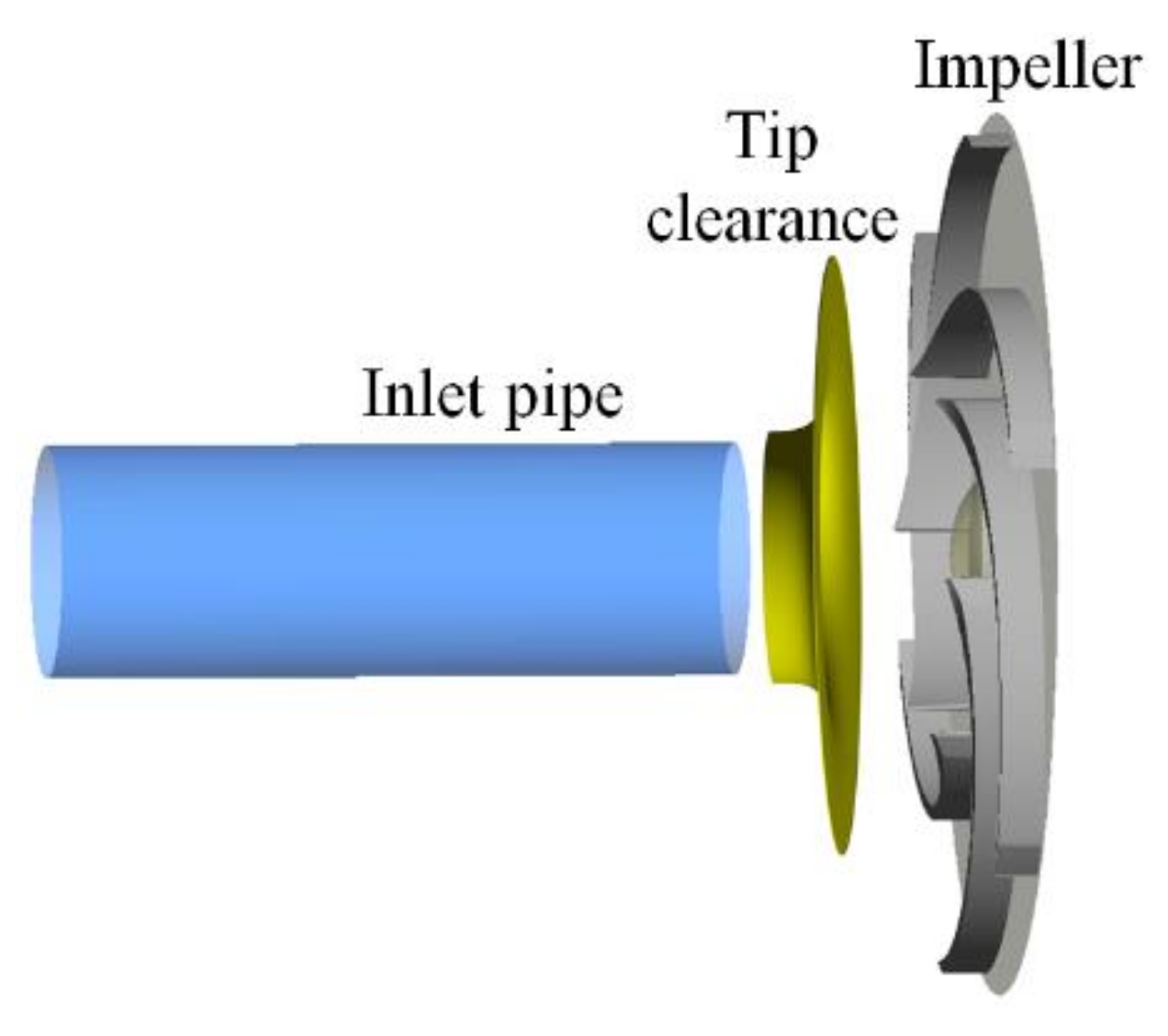
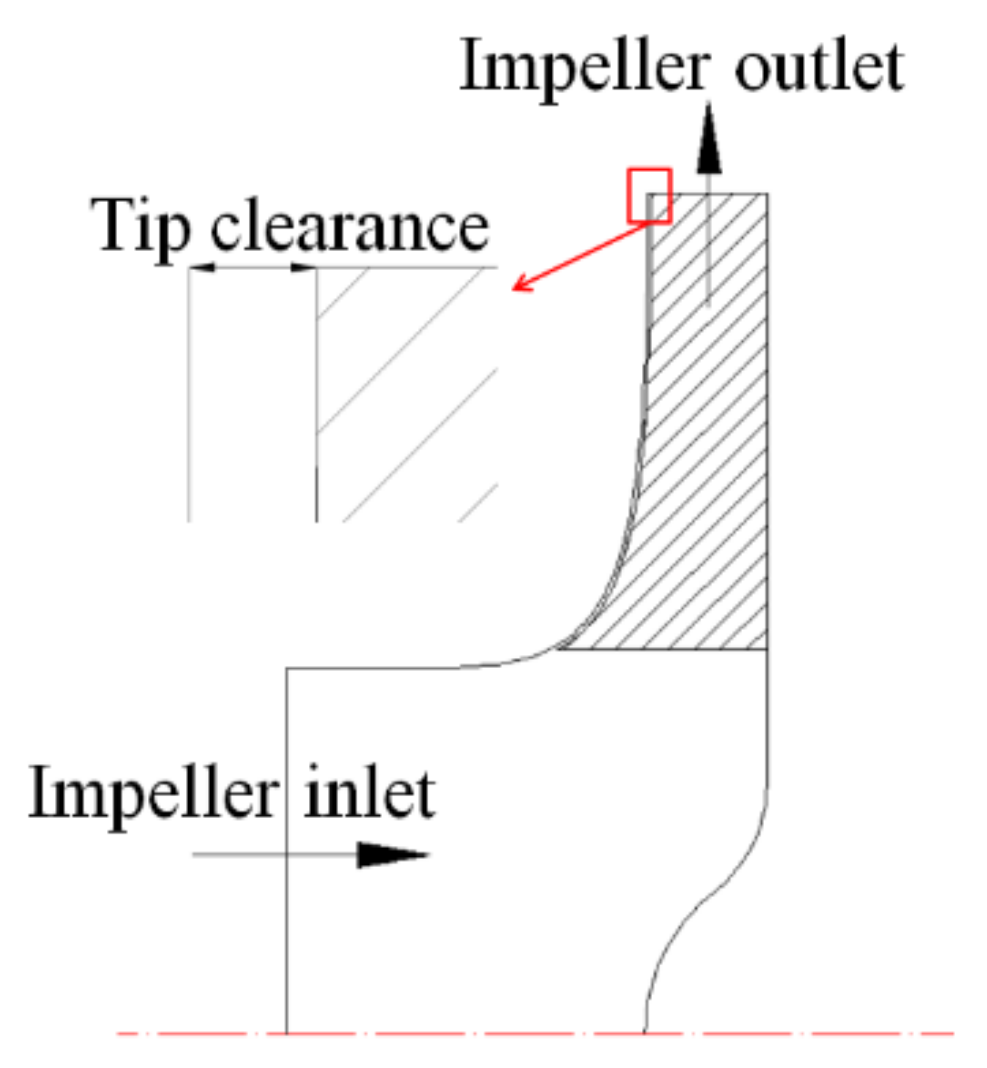
2.1. Physical Model of the Pump
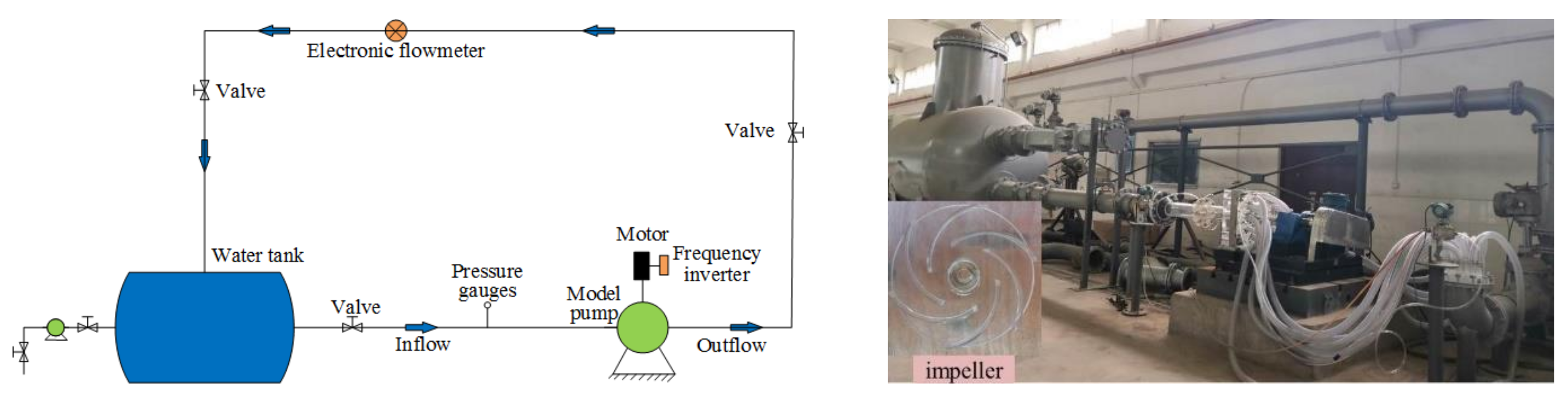
2.2. Test Rig
2.3. Numerical Method
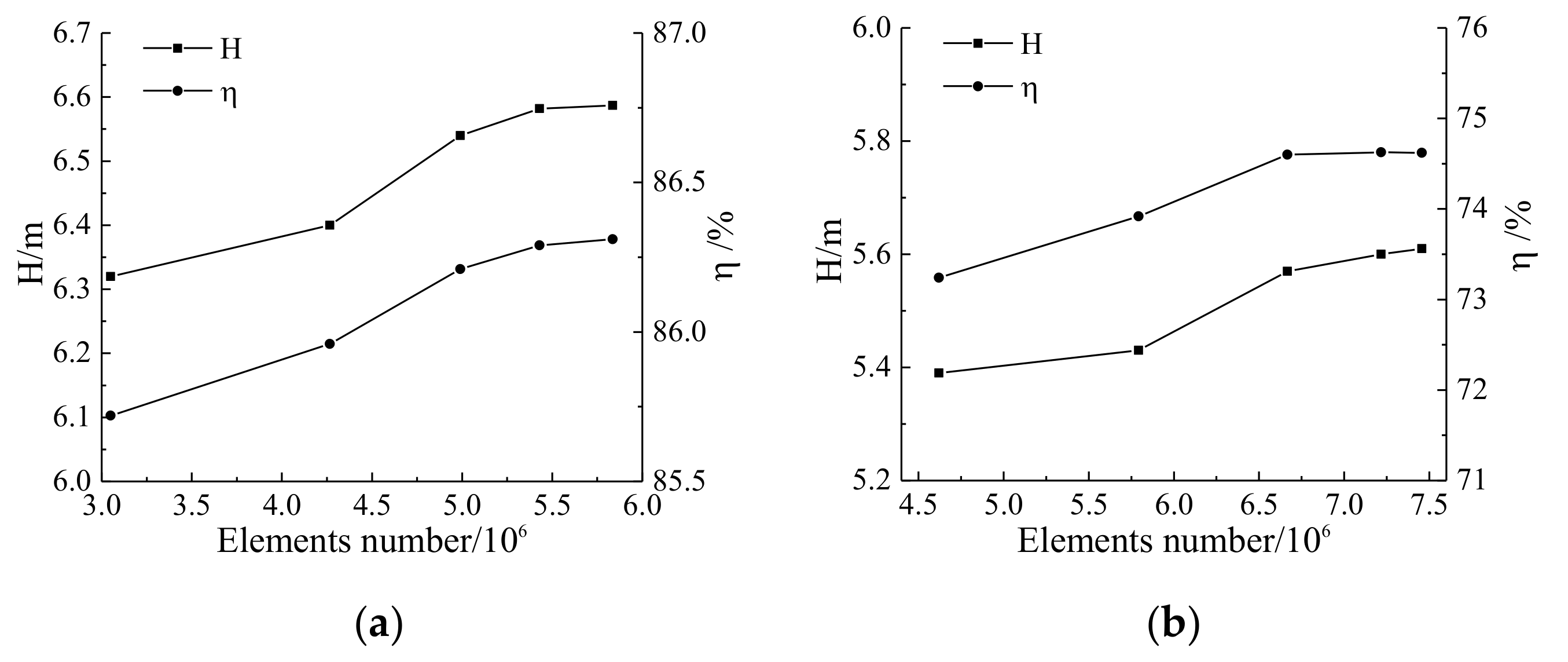
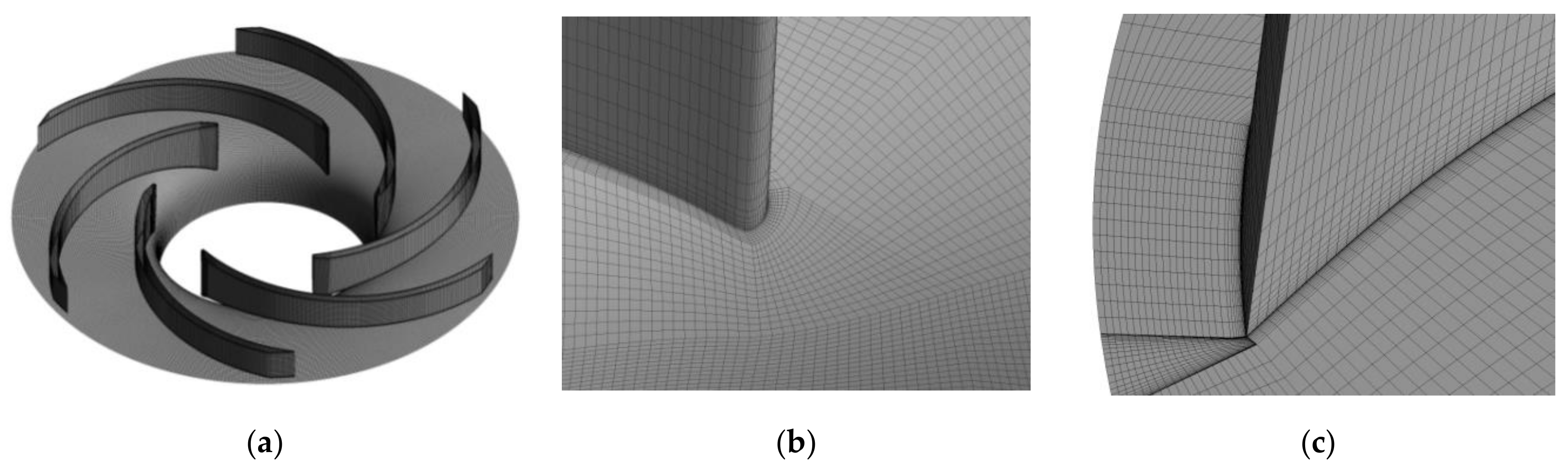
2.4. Grid Production
3. Results and Discussions
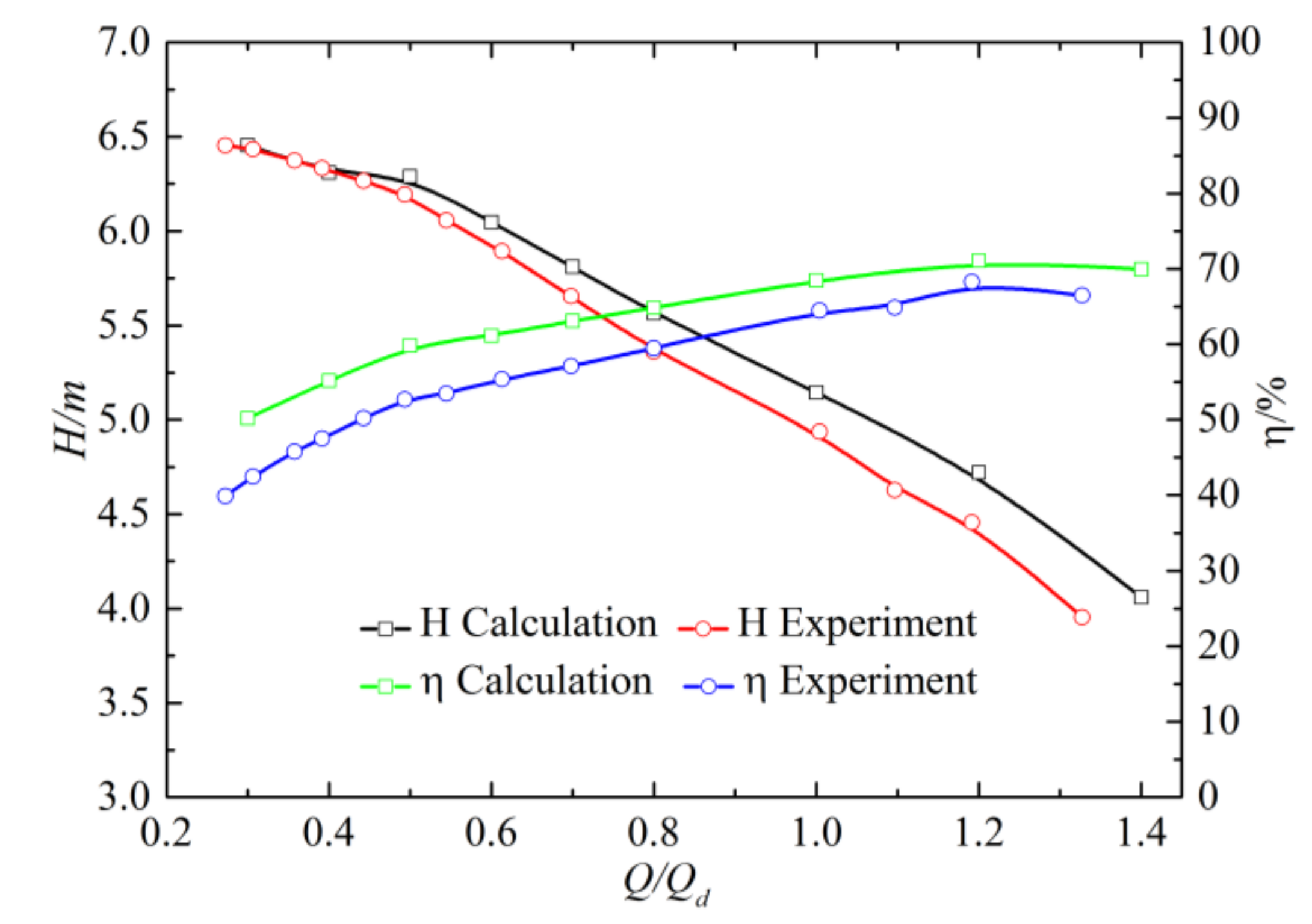
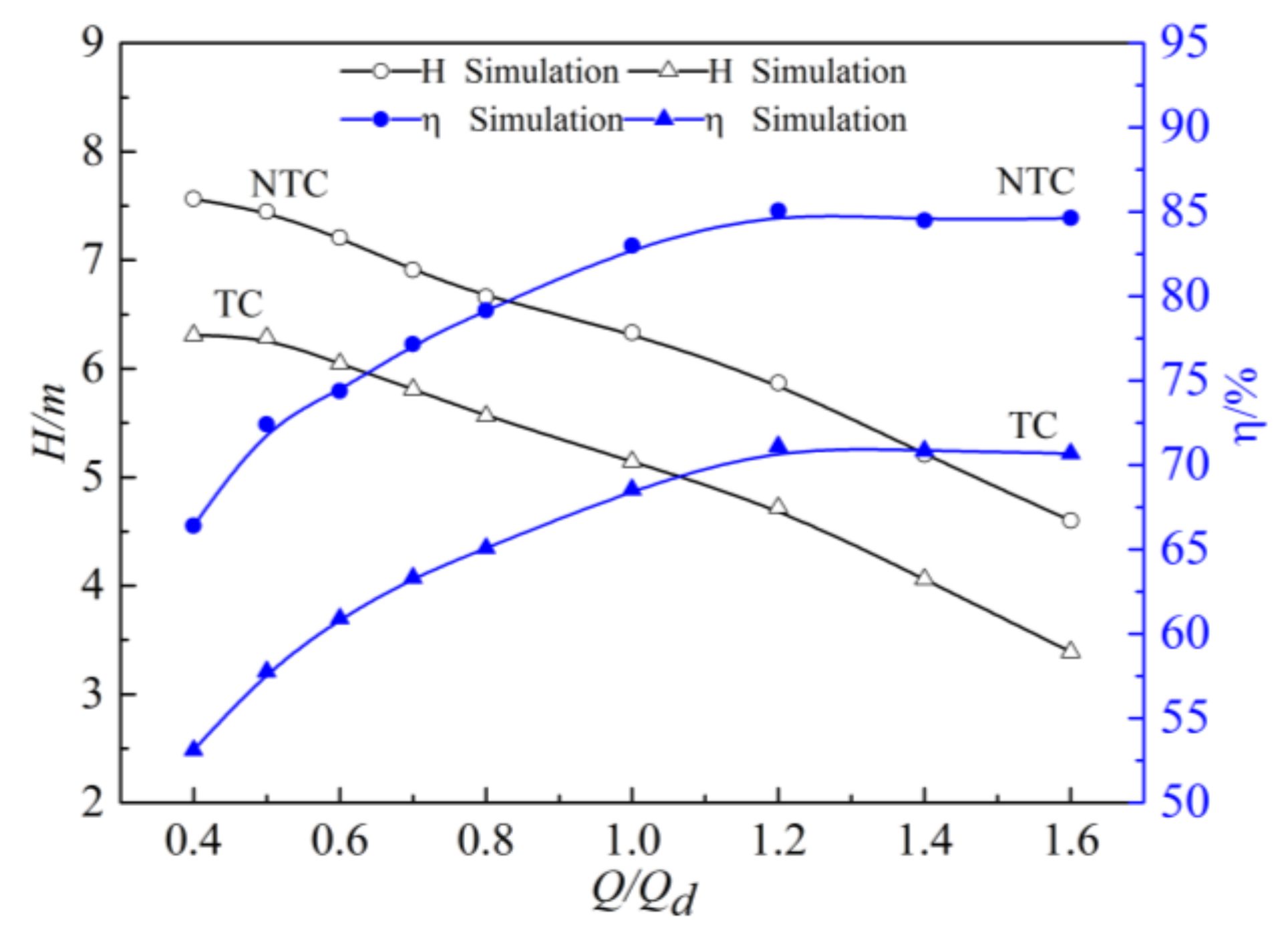
3.1. Numerical Results Validation
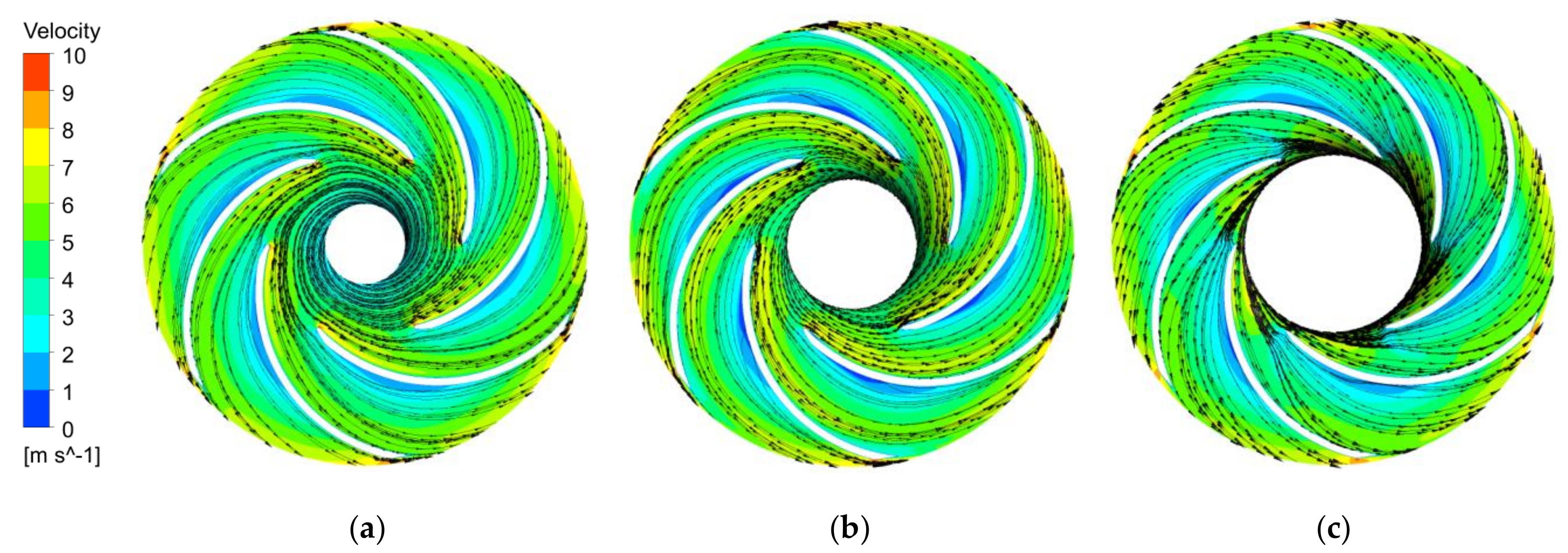
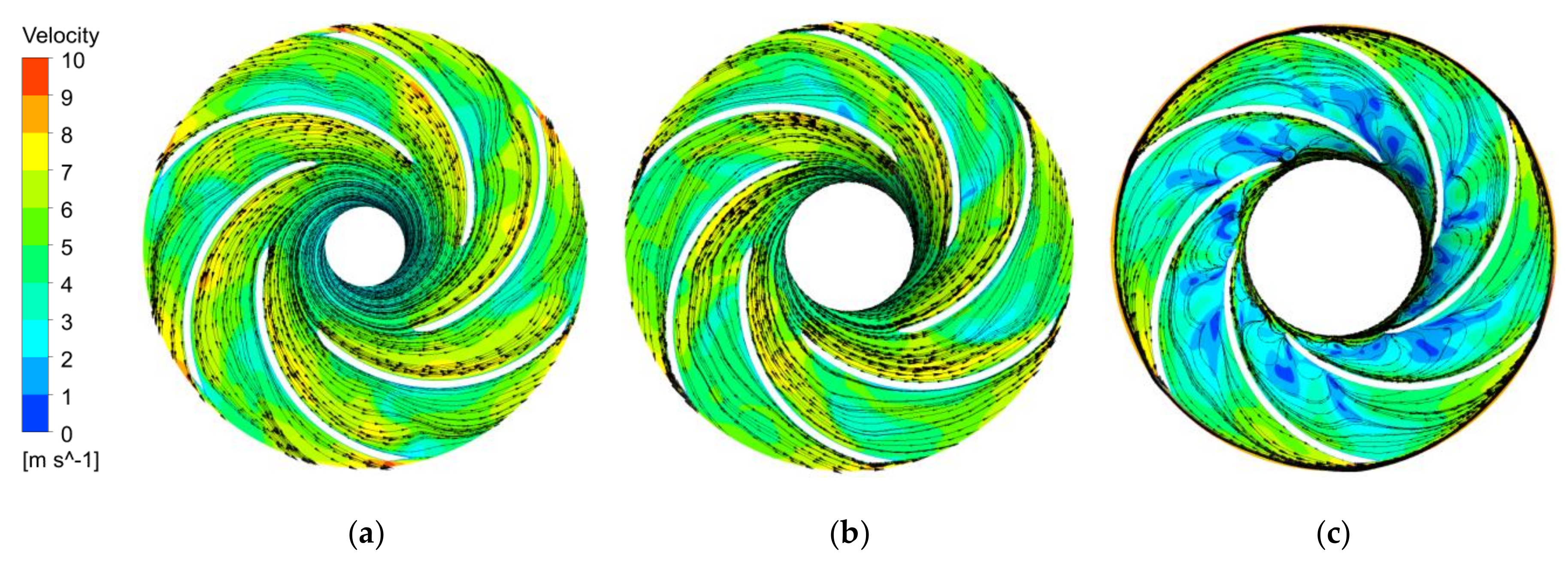
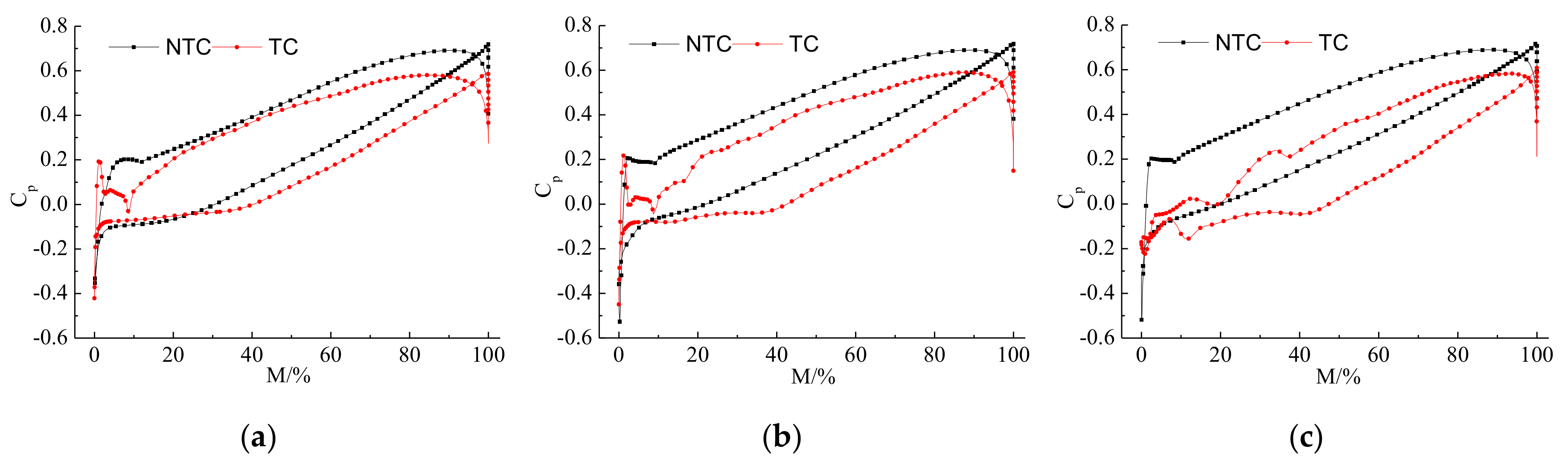
3.2. Internal Flow Field
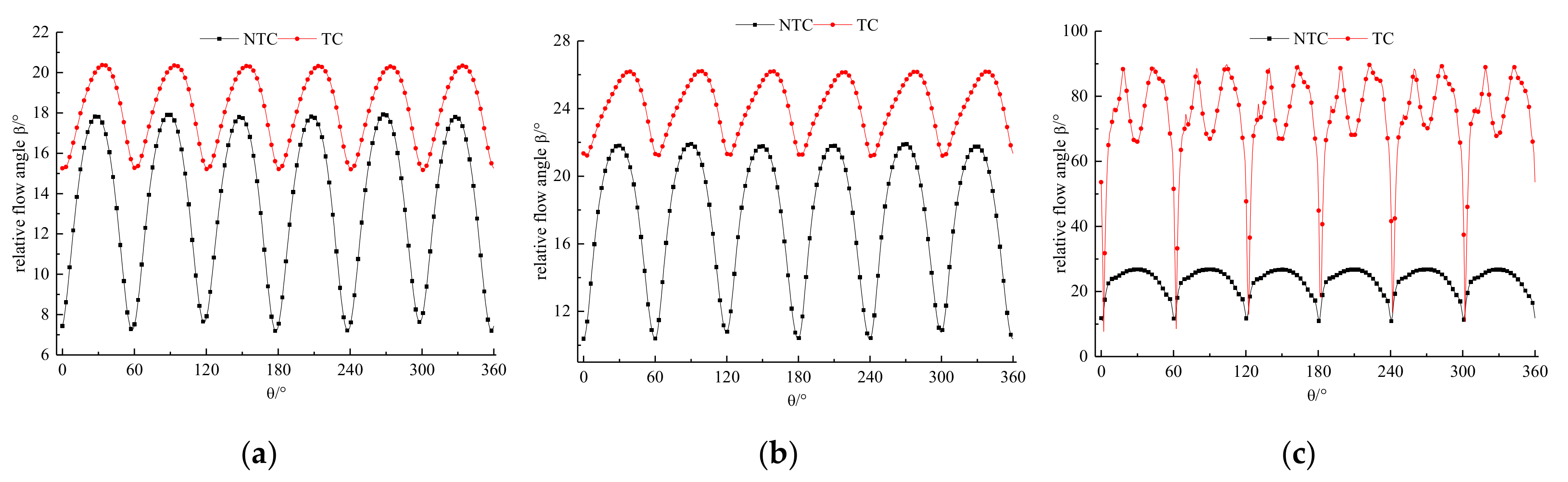
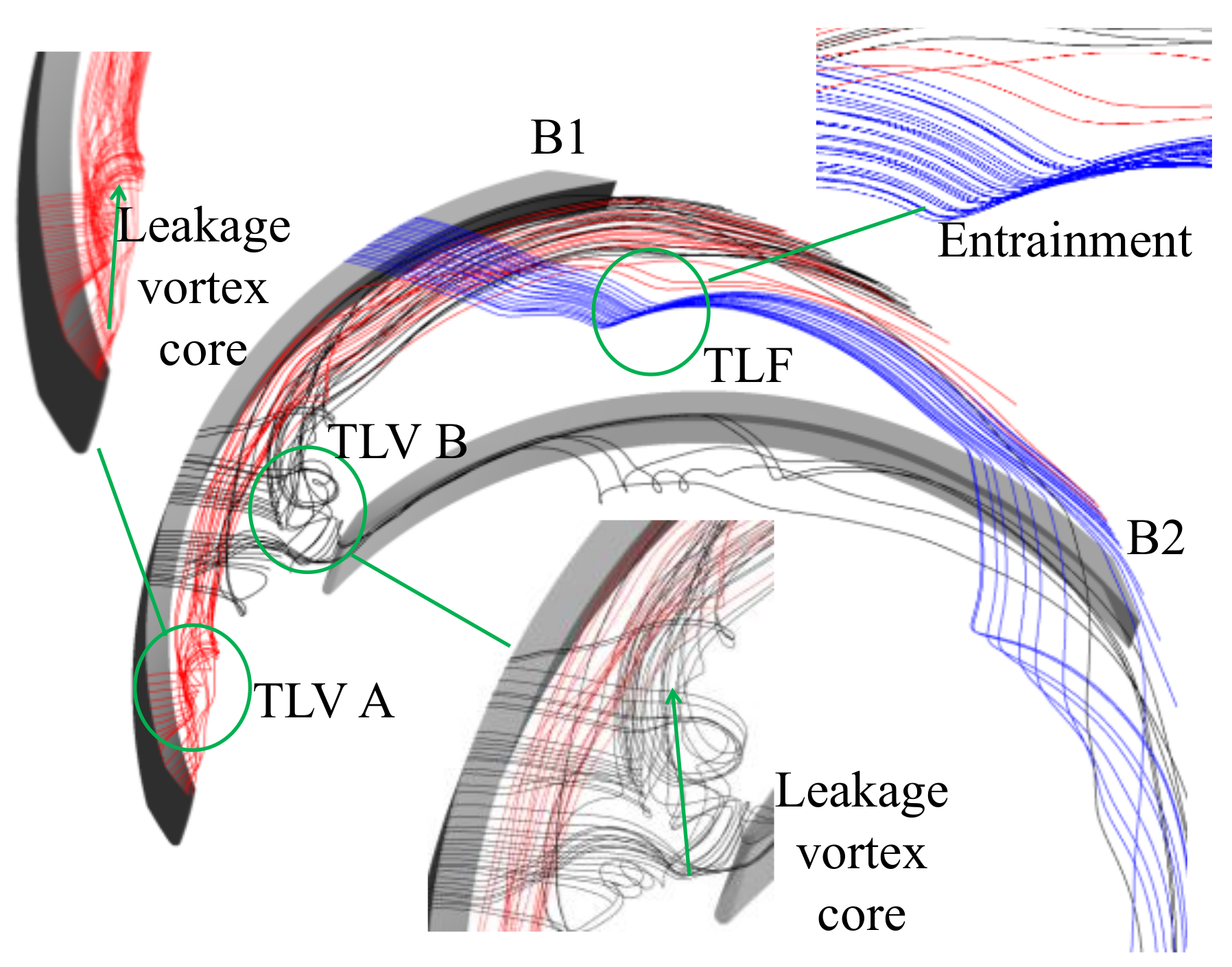
3.3. Structure of the Tip Leakage Vortex
3.4. Vortex Analysis of Tip Leakage Vortex
4. Conclusions
- (1)
- The numerical data and experiment results agreed well. Leakage vortex formed in the tip clearance led to a decrease in head and efficiency, which, respectively, decreased by 18.7% and 14.4% under the design condition. This decline became increasingly serious with the flow rate. The large negative attack angle at the blade inlet was formed and led to the appearance of the low-speed region. The static pressure distribution law near the leading edge was changed, and the static pressure coefficient of the blade was reduced.
- (2)
- The structure of tip leakage vortex in the impeller mainly comprised TLV A formed at the leading edge, TLV B formed at the middle of the blade, and the tip leakage flow near the trailing edge. TLV A broke at approximately 35% M. The core region of TLV B extended to the leading edge of the adjacent blade. Most of the fluid was blocked by the wall; thus, fluid moved in the opposite direction and broke at approximately 60% M. The passage vortex was generated due to the deterioration of the flow field by tip leakage vortex. The entrainment effect was formed between the tip leakage flow and mainstream, and the secondary leakage flow emerged at the trailing edge of the adjacent blade.
- (3)
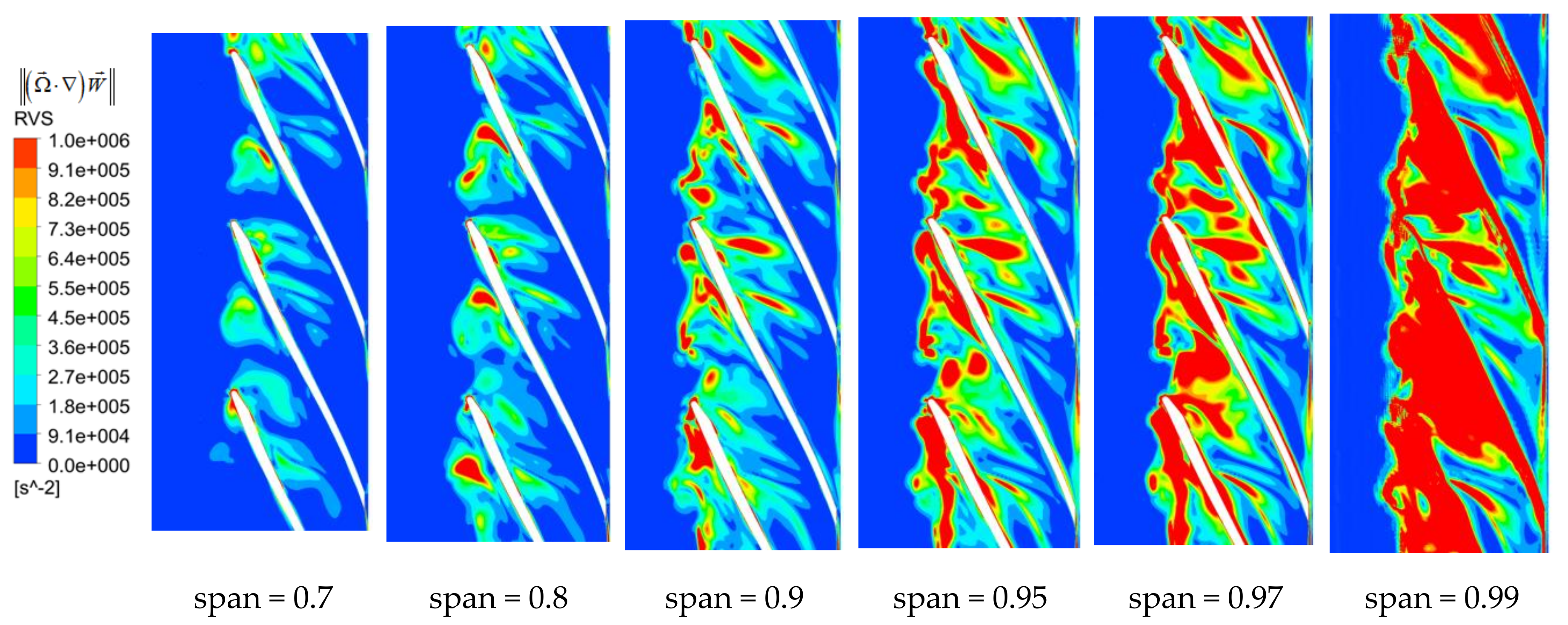
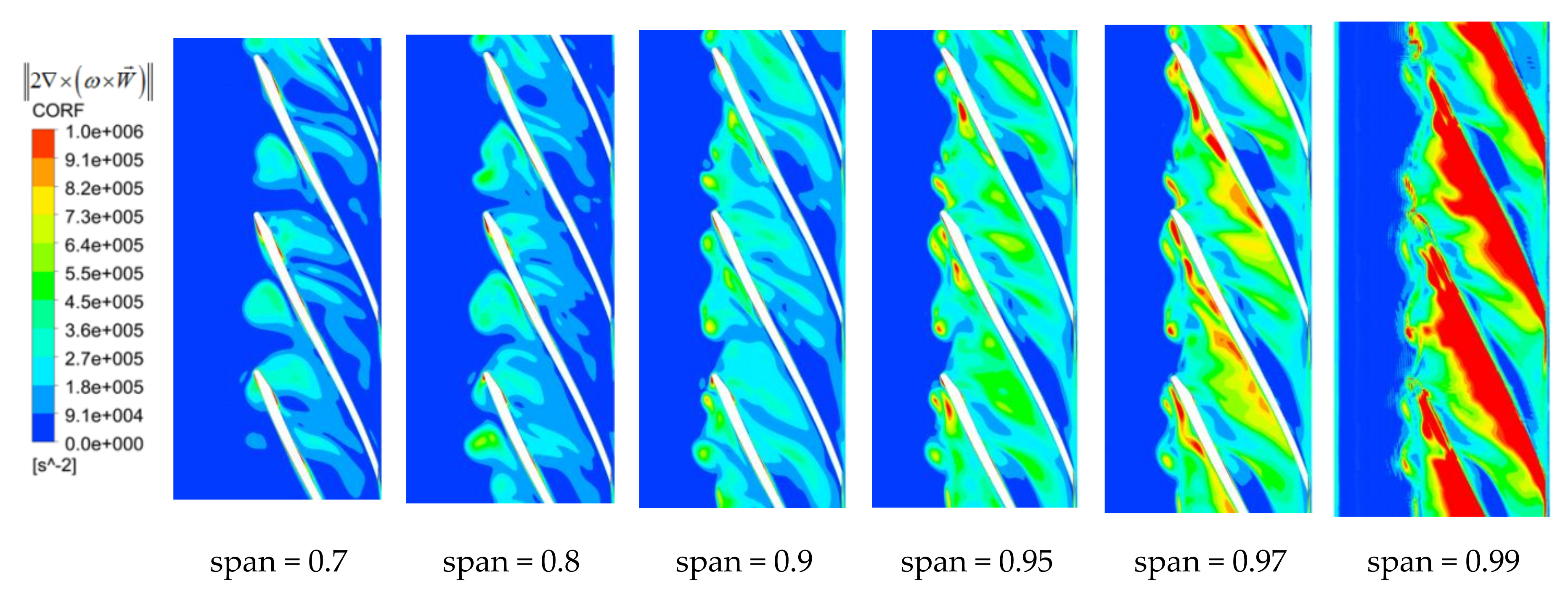
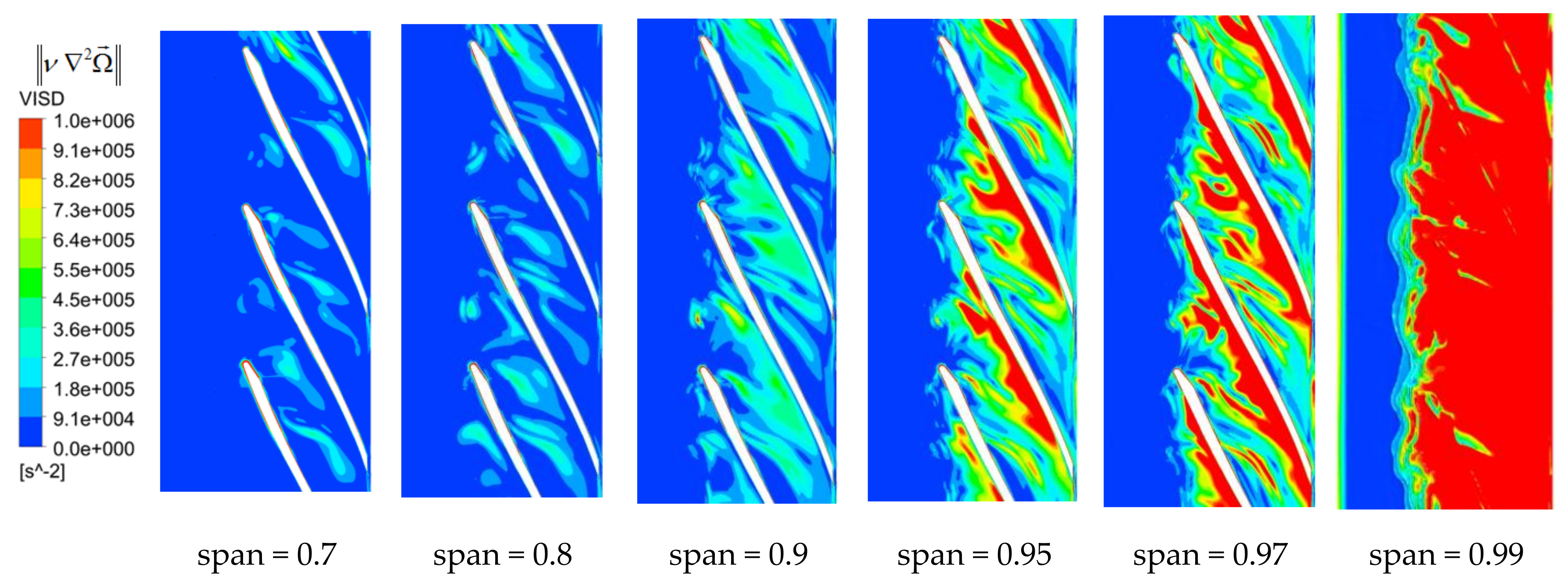
- The relative vorticity transport equation was adapted to analyze the movement mechanism of the tip leakage flow. High RVS was the main reason for the formation and development of tip leakage vortex. CORF could reflect changes in vorticity due to tip leakage flow. The relative motion with different velocities was formed between micro-jet and rotating impeller and fixed shroud, so VISD became vorticity source. All terms decreased with the blade span.
- (4)
- The change of the structure, trajectory, and breakdown position of the tip leakage vortex would affect the performance and stability of the semi-open centrifugal pump. This provided a reference for the design of the high-performance semi-open centrifugal pump and provided ideas for the research and development of efficient and stable flow control technology. We would study the influence mechanism of other parameters, such as the strength and initial position of tip leakage vortex on the centrifugal pump, and work on reducing and restraining the effect of tip leakage vortex by flow control technology in our future research.
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, P.F.; Yuan, S.Q.; Huang, L.Y. Research Status and Development Trend of Low Specific Speed Centrifugal Pump. Pump Technol. 2004, 1, 20–24. [Google Scholar]
- Yang, J.L.; Lai, H.X.; Yu, X.H.; Tu, X.D. Numerical simulation of internal flow field of an unshrounded centrifugal impeller in a low specific speed pump. J. Eng. Thermophys. 2013, 34, 262–265. [Google Scholar]
- Boitel, G.; Fedala, D.; Myon, N. Tip clearance effects on loads and performances of semi-open impeller centrifugal pumps at different specific speeds. IOP Earth Environ. Sci. 2016, 49, 032013. [Google Scholar] [CrossRef]
- Michael, M.; Bernd, W.; Thévenin, D. Effect of tip clearance gap and inducer on the transport of two-phase air-water flows by centrifugal pumps. Exp. Therm. Fluid Sci. 2018, 99, 487–509. [Google Scholar]
- Zhang, D.S.; Shao, P.P.; Shi, W.D. Numerical simulation of Tip Leakage Vortex Hydrodynamics Characteristics in Axial Flow Pump. Trans. Chin. Soc. Agric. Eng. 2014, 45, 70–75. [Google Scholar]
- Zhang, H.; Chen, B.; Wang, B.Q.; Shi, C.B.; Shen, D.W. Influence of tip clearance on internal pressure fluctuation of screw centrifugal pump. Trans. Chin. Soc. Agric. Eng. 2017, 33, 84–89. [Google Scholar]
- Liu, Y.; Tan, L. Spatial-temporal evolution of tip leakage vortex in a mixed flow pump with tip clearance. J. Fluid Eng. 2019, 141, 081302. [Google Scholar] [CrossRef]
- Kaneko, M.; Tsujita, H. Numerical investigation of influence of tip leakage flow on secondary flow in transonic centrifugal compressor at design condition. J. Therm. Sci. 2015, 24, 117–122. [Google Scholar] [CrossRef]
- Robert, K.; Schwarz, P.; Wilkosz, B. Experimental and Numerical Investigation of Tip Clearance and Bleed Effects in a Centrifugal Compressor Stage with Pipe Diffuser. J. Turbo 2012, 135, 011005. [Google Scholar]
- Zhao, H.J.; Xi, G.; Duan, Y.F.; Wang, Z.H. Experimental study of tip clearance effects on performance and flow field of a centrifugal conprossor. J. Eng. Thermophys. 2018, 39, 1453–1459. [Google Scholar]
- Jia, X.C.; Wang, Z.M.; Cai, R.X. The Numerical Study of Tip Clearance Effects on Acrodynamic Performance in Turbomachines. J. Eng. Thermophys. 2001, 22, 431–434. [Google Scholar]
- Gao, L.M.; Xi, G.; Wang, S.J. Influence of Tip Clearance on the Flow Field and Aerodynamic Performance of the Centrifugal Impeller. Chin. J. Aeronaut. 2002, 3, 139–144. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, L.; Hao, Y. Energy performance and flow patterns of a mixed flow pump with different tip clearance sizes. Adv. Mech. Eng. 2017, 10, 191. [Google Scholar] [CrossRef]
- Bing, H.; Cao, S.L.; He, C.L. Experimental study of the effect of blade tip clearance and blade angle error on the performance of mixed-flow pump. Sci. Chin. Technol. Sci. 2013, 56, 293–298. [Google Scholar] [CrossRef]
- Zhang, W.W.; Yu, Z.Y.; Zhu, B.S.; Yang, C. Study of Tip Clearance Effects on Performances and Flow Field of a Low Specific Speed Mixed-flow Pump. J. Mech. Eng. 2017, 53, 182–189. [Google Scholar] [CrossRef]
- Jia, X.Q.; Cui, B.L.; Zhang, Y.L.; Zhu, Z.C. Study on Internal Flow and External Performance of a Semi-open Impeller Centrifugal Pump with Different Tip Clearances. Int. J. Turbo Jet Engines 2015, 32, 1–12. [Google Scholar] [CrossRef]
- Farid, A.A.; Abdalla, H.M.; Abou, E.A. Effect of semi-open impeller side clearance on the centrifugal pump performance using CFD. Aerosp. Sci. Technol. 2015, 47, 247–255. [Google Scholar]
- Zhao, X.R.; Xiao, Y.X.; Wang, Z.W. Numerical analysis of non-axisymmetric flow characteristic for a pump-turbine impeller at pump off-design condition. Renew. Energy 2017, 115, 1075–1085. [Google Scholar]
- Li, J.W.; Zhang, Y.N.; Liu, K.H. Numerical simulation of hydraulic force on the impeller of the reversible pump turbine in generating mode. J. Hydrodyn. 2017, 29, 603–609. [Google Scholar] [CrossRef]
- Zhou, K.; Zhou, C. Unsteady effects of vortex interaction on tip leakage vortex breakdown and its loss mechanism. Aerosp. Sci. Technol. 2018, 82, 363–371. [Google Scholar] [CrossRef]
- Antonio, P.; Antonio, L. Effect of working conditions and diffuser setting angle on pressure fluctuation within a cetrifugal pump. Int. J. Heat Fluids Flow 2019, 75, 44–60. [Google Scholar]
- Gao, Y.Q.; Chu, W.L.; Zhang, H.G. The Influence of the Tip Clearance to a Low-speed Centrifugal Impeller Performance and the Flow Field Analysis of the Neat trailing edge. Mach. Des. Manuf. 2013, 9, 107–109. [Google Scholar]
- Li, Y.B.; Hu, P.L.; Li, R.N. Numerical Analysis for Effects of Different Blade Tip Clearance on Performance in Mixed-flow Pump. Trans. Chin. Soc. Agric. Eng. 2014, 30, 86–93. [Google Scholar]
- Xu, Y.; Tan, L.; Liu, Y. Pressure fluctuation and flow pattern of a mixed flow pump with different blade tip clearances under cavitation condition. Adv. Mech. Eng. 2017, 9, 1687814017696227. [Google Scholar] [CrossRef]
- Li, X.; Yuan, S.; Pan, Z. Dynamic Characteristics of Rotating Stall in Mixed Flow Pump. J. Appl. Math. 2013, 10, 4819–4828. [Google Scholar] [CrossRef]
- Lu, J.L.; Guo, L.; Wang, L.K.; Wang, W.; Guo, P.C.; Luo, X.Q. Research on the Unsteady Flow of Tip Clearance in Semi-open Impeller Centrifugal Pump. Trans. Chin. Soc. Agric. Eng. 2019, 50, 163–172. [Google Scholar]
- Iwakiri, K.; Furukawa, M.; Ibaraki, S.; Tomita, I. Unsteady and three-dimensional flow phenomena in a transonic centrifugal compressor impeller at rotating stall. In Proceedings of the ASME Turbo Expo 2009: Power for Land, Sea, and Air, Orlando, FL, USA, 8–12 June 2009; pp. 1611–1622. [Google Scholar]
- Zhao, H.J.; Wang, Z.H.; Xi, G. Unsteady flow structures in the tip region for a centrifugal compressor impeller before rotating stall. Sci. China Technol. Sci. 2017, 06, 122–132. [Google Scholar] [CrossRef]
- Zhang, H.Z.; Yang, C.; Yang, D.F.; Wang, W.L. Investigation on the Stall Inception Circumferential Position and Stall Process Behavior in a Centrifugal Compressor with Volute. J. Eng. Turb. Power. 2019, 141, 021030. [Google Scholar] [CrossRef]
- Buren, T.V.; Whalen, E.; Amitay, M. Eddies, stream and convergence zones in turbulent flows. Phys. Fluids 2015, 30, 512–516. [Google Scholar]
- Tristan, F. Dynamics of the Cavitation Processing Vortex Rope for Francis Turbines at Part Load Operating Conditions; EPFL: Lausanne, Switzerland, 2016. [Google Scholar]
- Anup, K.C.; Lee, Y.H.; Thapa, B. CFD study on prediction of vortex shedding in draft tube of Francis turbine and vortex control techniques. Renew. Energy 2016, 86, 1406–1421. [Google Scholar]
- Lu, J.L.; Wang, L.K.; Liao, W.L.; Zhao, Y.P.; Ji, Q.F. Entropy Production Analysis for Vortex Rope of a Turbine Model. J. Hydraul. Eng. ASCE 2019, 50, 233–241. [Google Scholar]
- Ji, B.; Luo, X.W. Numerical analysis of unsteady cavitating turbulent flow and shedding horse-shoe vortex structure around a twisted hydrofoil. Int. J. Multiphas. Flow 2013, 51, 33–43. [Google Scholar] [CrossRef]
- Huang, R.; Ji, B.; Luo, X.W. Numerical investigation of cavitation-vortex interaction in a mixed-flow waterjet pump. J. Mech. Sci. Technol. 2015, 29, 3707–3716. [Google Scholar] [CrossRef]
- Ji, B.; Luo, X.W.; Arndt, R.E.A. Numerical simulation of three dimensional cavitation shedding dynamics with special emphasis on cavitation-vortex interaction. Ocean Eng. 2014, 87, 64–77. [Google Scholar] [CrossRef]
- Liu, Y.B.; Tan, L. Tip clearance on pressure fluctuation intensity and vortex characteristic of a mixed flow pump as turbine at pump mode. Renew. Energy 2018, 129, 606–615. [Google Scholar] [CrossRef]

| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Impeller inlet diameter, D1 | 100 mm | Impeller outlet diameter, D2 | 232 mm |
| Impeller outlet width, b2 | 16 mm | Blade number, Z | 6 |
| Blade inlet angle, β1 | 16.6° | Blade outlet angle, β2 | 18.6° |
| Wrag angle, Φ | 99.4 | Blade thickness, T | 4 mm |
| Impeller radius of suction surface | 88 mm | Impeller radius of pressure surface | 92 mm |
| Tip Clearance/mm | Inlet Pipe/106 | Impeller/106 | Vaneless Diffuser/106 | Total/106 |
|---|---|---|---|---|
| 0 | 0.45 | 4.52 | 0.45 | 5.42 |
| 1 | 0.59 | 6.10 | 0.62 | 7.21 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Lu, J.; Liao, W.; Zhao, Y.; Wang, W. Numerical Simulation of the Tip Leakage Vortex Characteristics in a Semi-Open Centrifugal Pump. Appl. Sci. 2019, 9, 5244. https://doi.org/10.3390/app9235244
Wang L, Lu J, Liao W, Zhao Y, Wang W. Numerical Simulation of the Tip Leakage Vortex Characteristics in a Semi-Open Centrifugal Pump. Applied Sciences. 2019; 9(23):5244. https://doi.org/10.3390/app9235244
Chicago/Turabian StyleWang, Like, Jinling Lu, Weili Liao, Yaping Zhao, and Wei Wang. 2019. "Numerical Simulation of the Tip Leakage Vortex Characteristics in a Semi-Open Centrifugal Pump" Applied Sciences 9, no. 23: 5244. https://doi.org/10.3390/app9235244
APA StyleWang, L., Lu, J., Liao, W., Zhao, Y., & Wang, W. (2019). Numerical Simulation of the Tip Leakage Vortex Characteristics in a Semi-Open Centrifugal Pump. Applied Sciences, 9(23), 5244. https://doi.org/10.3390/app9235244






