Rates of High-Temperature Evaporation of Promising Fire-Extinguishing Liquid Droplets

Abstract

Differences in the rates of heating and evaporation of droplets with the component composition are important parameters of heat transfer processes and phase transformations. This paper presents the values of high-temperature (up to 600 °C) evaporation rates of droplets of promising fire-extinguishing compositions (water, bentonite suspension, bischofite solution, EA-5 solution, and foaming agent emulsion) at convective (in the air stream), conductive (on a heated surface), and radiation (in a muffle furnace) heating. A high-speed video recording system and tracking software algorithms are used. At identical initial sizes of droplets of fire-extinguishing suspensions, known as emulsions and solutions, the times of their complete evaporation are shown to differ 3.7 times when heating on the substrate, 1.25 times in the air flow, and 1.9 times in the muffle furnace. A general approximation expression is formulated, and the empirical constants are calculated to predict the evaporation rate of the droplets of extinguishing agents in a wide range of temperatures (up to 600 °C) and heat fluxes (up to 100 kW/m²), which are characteristic of forest fires. With the use of the experimental data obtained, it is possible to predict the completeness of evaporation of promising extinguishing liquids at different schemes of heat supply.

1. Introduction

Technologies of large-scale fire extinguishing are being developed toward simultaneous intensification of different mechanisms of localization and suppression of combustion and thermal decomposition [1]. These are reducing the temperature in the combustion and pyrolysis zone, displacing the oxidant from the combustion zone, and blocking the mixing of pyrolysis and combustion products with the oxidant. Experimental and theoretical studies [2,3,4] have shown that the largest influence on the characteristics of combustion suppression is exerted by an endothermic phase transition: evaporation of extinguishing compositions due to a high heat of vaporization (in particular, those based on water—about 2 MJ/kg). Comparing the influence of heat flux due to high heat capacity and energy of vaporization, the authors of Reference [4] justify that it is expedient to spray the compositions in the flame combustion zone. Introducing liquid in large monolithic volumes to this zone is not sufficient. In this case, the liquid volume variation has little effect on combustion characteristics of a fire bed. Therefore, it is important to intensify its evaporation. In recent years, quite a few experimental results have been published for the suppression of pyrolysis and combustion of substances and materials of different dispersion [5] and component composition [6] by aerosol flows. In the interpretations of such research results, it is often concluded that a reliable determination of the values of droplet evaporation rates is rather difficult. It is especially complex at high temperatures (from 300 to 1100 °C) and at an essentially inhomogeneous component composition, i.e., when using suspensions, emulsions, and solutions. For forest fires, the average temperature of the flame burning of tree crowns is 1100 °C [2,3,4]. At the tree base, the temperature can reach 200 to 500 °C [2,3,4]. Therefore, the most relevant range of studied temperatures of intensive evaporation of fire extinguishing agents is 200–1100 °C. At temperatures above 600 °C, inhomogeneous liquid droplets (especially water-containing emulsions and suspensions) are characterized by the effects of intensive dispersion (in puffing or micro-explosion modes) [7,8,9,10,11]. Therefore, it is difficult to assess the differences in their evaporation rates under such conditions. Thus, as the first approximation, it is advisable to study the evaporation characteristics of fire-extinguishing water-containing compositions in the temperature range up to 600 °C.

Papers [12,13] presented the determined rates (and, accordingly, the typical durations) of high-temperature heating and evaporation of water droplets at intensification of one of the three mechanisms of energy supply (conductive, convective, and radiation). Heating systems with substrate, air flow, and muffle furnace were used. With each of these systems, the total heat flux included components due to conductive, convective, and radiative heat transfer. When certain temperature values were reached, the pronounced dominance of one of them was recorded. Since droplet heating in the experiments [12,13] was essentially unsteady and was accompanied by intensive evaporation, the use of even miniature low-inertia thermocouples was complicated. Therefore, the non-contact optical method of Planar Laser Induced Fluorescence (PLIF) was used [12,13]. Three stands were developed for heating water droplets on a substrate (conductive mechanism) in a muffle furnace (radiation) and in a heated air flow (convective). Heat flux densities corresponded to promising high-temperature gas-vapor-droplet technologies in the field of fire and thermal purification of liquids from non-regulatory impurities, and corresponding to polydisperse fire extinguished with rational water consumption, etc. In such applications, operating temperatures are usually above 500 °C and sometimes exceed 1000 °C. The initial dimensions (radii) of water droplets ranged from 1 to 2 mm [12,13]. A high-speed (up to 10⁵ frames per second) video recording system was used to determine the times of complete evaporation of water droplets (their existence). Quantitative differences in the heating rates (the ratio of heating to complete evaporation times) of water droplets on the three stands used were established using the PLIF method. The maximum temperature values of droplet heating at different mechanisms of energy supply were determined. The criterion dependences relating the main characteristics of formation of the temperature field of the evaporating water droplet to the heating conditions were obtained. The prospects of application of research results and development of the created experimental approach were highlighted. However, in References [12,13], the experimental data are given only for water droplets. In the case of inhomogeneous component compositions of droplets, the PLIF method will show a significant error in registering their temperature (due to the influence of additives on the optical properties of a drop with a fluorophore dye for the implementation of PLIF measurements). Therefore, the most rational method is to study the evaporation rates of inhomogeneous extinguishing agents using high-speed video recording, i.e., the rate of reduction of droplet size during heating [14]. In recent years, a lot of promising water additives has been developed for effective extinguishing and localization of forest fires. Among them, there is a typical group of powders and liquid additives [15,16,17,18,19,20]: bentonite, bischofite, foaming agent, and extinguishing agent EA-5. With their application of aqueous solutions, suspensions and emulsions are prepared. The rates of heating and evaporation of water droplets with the addition of such promising fire-extinguishing impurities have not been established yet. Since their rheological and thermophysical properties significantly differ from water, noticeable discrepancies in the rates of heating and evaporation are also foreseeable. Furthermore, these experimental data will serve to predict the rates of heating and evaporation not only of fire extinguishing agents, but also of various suspensions, emulsions, and solutions, in which the evaporation has been actively studied in recent years.

The approach based on a significant decrease in the temperature of liquid droplets due to endothermic phase transformations is used in many technological processes, especially in microelectronics [21], chemical industry [22], spray cooling [22,23], spray combustion [24], and more. Aqueous salt solutions are used in heat pumps, which are widely applied in the energy sector [25]. Therefore, the results of experimental studies of heating and evaporation of droplets of suspensions, solutions, and emulsions are important for developing not only firefighting but other technologies as well. As a result, in the well-known research works, the ranges of heating temperatures and concentrations of components of suspensions, solutions, and emulsions are very wide. For example, some of the studies provided data for evaporation of a drop of sulfur-purified wastewater (electrolyte) with different concentrations of solute, obtained by suspending it on a glass fiber in a heated chamber at varying ambient temperatures (90–170 °C) [26]. The radius of the droplet during evaporation was recorded. When a drop of distilled water evaporated, the temperature was measured (a thermocouple junction was placed in the drop). A mathematical model was developed to take into account the influence of concentration of the water activity and density changes. The solution concentration in the experiment was significantly higher than that obtained in the simulation. The theoretical results obtained for the case of homogeneous concentration illustrated a higher evaporation rate at the end of the droplet lifetime. The change in droplet density was shown to be a more important and dominant factor, which affects the evaporation rate of the electrolyte solution droplet. It was found that the evaporation and crystallization affect the surface of the droplet, which limits the diffusion of the solute. This effect maintains a high concentration of solute near the free surface of the droplet. These regularities explain the differences in the results for radius changes in water without impurities and solutions.

The paper [27] presented the results of studies of evaporation of droplets (radius ≈ 10 mm) on the substrates of extrusion polystyrene, plexiglass, and stainless steel at 24 °C and a relative humidity of 30%. It was assumed that the transport of water vapor and trapped air mainly moves upward due to the low molar mass of the water vapor. Simulation results using finite plane sources and semi-infinite solids served to estimate the droplet temperature and evaporation rate. The main dependence of the evaporation on the substrate material and droplet sizes was established. It was shown that, in the experiments, there was natural convection, which provides evaporation rates significantly exceeding the rates of diffusion into stagnant air.

The effect of the thermocouple junction on the characteristics of the evaporation of a droplet of a binary solution of n-Dodecane and n-Hexadecane has been experimentally and theoretically investigated. The corresponding droplets with an initial diameter of 900 μm were placed on the thermocouple junction or on the end of the quartz fiber to record the values of the integral evaporation characteristics [24]. At low ambient temperatures (200 °C), the conductivity of the fiber mainly affects the early evaporation stage. At a high temperature (500 °C), it affects the entire evaporation process. The influence of the fiber diameter on droplet evaporation has also been investigated. The evaporation rate of droplets is shown to vary nonlinearly with an increasing fiber diameter.

Features of heating and internal convective flows were theoretically studied to estimate the mobility of droplets on a hydrophobic surface [28]. Temperature and velocity fields of intra-droplet convection were modeled against the background of experimental conditions. The acceleration of the liquid inside the droplet was predicted for droplets of different sizes. The results of theoretical studies of convection were compared with measurements of particle velocities recorded by the Particle Image Velocimetry (PIV) method. Adhesion, inertia, and shear forces were determined for the case of droplet slip on a hydrophobic surface. It was found that the calculated velocities were in good agreement with the PIV data. Two vortices were formed in the droplet with circulating flows, rotating in opposite directions due to the interaction of Marangoni flows and buoyancy. The Bond number was found to be less unified (in particular, in the range of 0.03–0.2) for all droplet sizes (15–100 μL). This indicated that the Marangoni flow dominated over the buoyancy flow within the drop. The inertia force of the droplet became greater than the adhesion and shear forces of the liquid when heating. Hence, the droplet slid onto a hydrophobic surface, which was also observed in the experiments. The values of the Nusselt and Bond numbers increased with the growth of the droplet volume and reached maxima of 151 and 0.2 at a droplet size of 100 μL.

Evaporation of water and ethanol droplets was experimentally studied in the paper [22]. The results of studies of the evaporation rate of droplets suspended on a thermocouple under the influence of laser radiation and without it were presented. Laser excitation was shown to lead to a significant temperature increase in the droplets. The evaporation rate turned out to be higher than without laser excitation. As the frequency and intensity of the laser increased, the evaporation rate and the temperature increased as well. Explosive evaporation occurred at a higher power and at a higher frequency of the laser for water droplets and ethanol. However, this phenomenon is much more significant for water than for ethanol. Thus, the results of Reference [22] similar to References [7,8,9,10,11] show that a comparative analysis of the rates of heating and evaporation of liquid droplets with different component compositions is possible in a limited temperature range. When some threshold values of the latter are exceeded, the droplets are intensively transformed and dispersed. It is difficult to record the rates of change in droplet size, surface position, temperature fields, convection rates, and concentrations. According to the results of studies [7,8,9,10,11] of promising water-containing emulsions, solutions, and suspensions, the preferred temperature ranges from 100 °C to 600 °C.

The purpose of this work is to determine the rates of high-temperature evaporation of the group of promising extinguishing agents under different schemes of heat supply with a view of formulating a general approximation expression and calculating the empirical constants that allow reliable predictions for the values of the evaporation rate of droplets of fire-extinguishing compositions in wide ranges of temperature and heat fluxes, specific to the conditions of localization and extinguishing of large-scale forest fires.

2. Materials

In the experiments, the droplets of the studied liquids of the required volume were formed with the help of a multi-channel dispenser Finnpipette Novus. The step of volume variation was 0.1 µL. In accordance with recommendations formulated on the basis of experimental results of References [7,8,9,10,11], the initial volume of droplets was chosen as V_d ≈ 10 µL (corresponding to the radius R_d ≈ 0.84 mm). The choice of volume and, accordingly, the size of the drop was conditioned by the possibility to place the drop on the substrate and holders in the flow and muffle furnace (the drop did not break off from the latter). It was also possible to record the rate of reduction of its size due to heating and evaporation.

Water without impurities, foaming agent emulsion, bentonite suspension, bischofite solution, and Extinguishing Agent-5 (EA-5) solution were used as the studied liquids in the experiments. All solutions, suspensions, and emulsions were prepared by stirring for 10 minutes using an ultrasonic bath Sapphire 2.8. This approach minimized the effects of stratification and the heterogeneity of concentration of components in the container from which liquids were taken by the Finnpipette Novus dispenser.

Table 1. Properties of components and prepared solutions, suspensions, and emulsions.

Composition	Typical Mass Concentrations of Water Admixtures at Extinguishing	Properties of Admixtures and Prepared Extinguishing Compositions	Regulatory Documents
Water	-	Density 998.2 kg/m3 Surface tension 72.7 × 10−3 N/m Dynamic viscosity 1.004 × 10−3 Pa∙s Temperature diffusivity 14.3 × 10−6 m2/s Heat capacity 4.183 kJ/(kg∙K) Thermal conductivity 0.599 W/(m∙K)	-
Foaming agent emulsion	1–10%	Kinematic viscosity of the concentrate at 20 °C is not above 40 mm2/s, Material density up to 20 °C is 1002–1187 kg/m3. Properties of 10% solution [19]: Dynamic viscosity 0.12 Pa∙s Surface tension 17.3 × 10−3 N/m Temperature diffusivity 12.9 × 10−6 m2/s Heat capacity 3.995 kJ/(kg∙K) Thermal conductivity 0.595 W/(m∙K)	SS 50588-2012
Bentonite suspension	1–10%	The first group of fire-proof efficiency Melting point >1250 °C Properties of 10% solution [20]: Density 1100 kg/m3 Surface tension 68.5 × 10−3 N/m Dynamic viscosity 24.3 × 10−3 Pa∙s Temperature diffusivity 5.44 × 10−4 m2/s Heat capacity 3.83 kJ/(kg∙K) Thermal conductivity 0.704 W/(m∙K)	SS 16363, CCR-21-03-2003
Bischofite solution	5–10%	The first group of fire-proof efficiency Properties of 10% solution [21,22]: Thermal conductivity 0.58 W/(m∙K) Heat capacity 3.603 kJ/(kg∙K) Density 1081.49 kg/m3 Dynamic viscosity 1.015 × 10−3 Pa∙s Boiling point 151.05 °C Surface tension 75.8 × 10−3 N/m	SS7759-55, CCR-21-03-2003 Patent No. 2318012
EA-5 solution	5–15%	The first group of fire-proof efficiency Properties of 10% solution: Density 1099.1 kg/m3 Surface tension 45 × 10−3 N/m Dynamic viscosity 1.112 × 10−3 Pa∙s Temperature diffusivity 12.9 × 10−6 m2/s Heat capacity 3.853 kJ/(kg∙K) Thermal conductivity 0.624 W/(m∙K)	Patent No. SU 1544450 A1 (TU 6-18-61-88)

shows typical ranges of variation in relative mass concentrations of water additives in forest fire suppression and localization. According to these ranges, it can be concluded that the maximum value of such concentrations for all types of impurities is generally 10%. In this regard, in this paper, we used compositions with maximum concentrations, in particular: 10% foaming agent emulsion, 10% bentonite suspension, 10% bischofite solution, and 10% EA-5 solution.

Table 1 presents regulatory documents, which determine requirements for the extinguishing agents using these water additives.

The thermophysical and rheological characteristics of the latter and the prepared compositions were generally determined using the known techniques. In particular, the thermophysical properties of all additives were defined by preparing solid pellets. The system DLF-1200 TA Instruments was used to provide measurements at temperatures in the thermostat of up to 1773 °C. Its principle of operation is based on evaluating the propagation velocity of the heat pulse in the sample. Errors of temperature diffusivity coefficients were ±2.3%, for heat capacity were ±4%, and were ±5% for thermal conductivity. For water, the coefficients of thermal conductivity, heat capacity, and temperature diffusivity were taken in accordance with the reference data. The values of thermophysical characteristics of solutions, suspensions, and emulsions were calculated under the assumption of their additivity, taking into account the fractions of components. Surface tension, density, and viscosity were determined for each prepared solution, emulsion, and suspension. The viscosity of the compositions was studied using Brookfield DV3T LV viscometer at room temperature of the liquid (within the range of 20–23 °C). To measure the viscosity of liquids, the standard set of viscometer included four spindles. The rotation velocity of the spindles ranged from 10–250 rpm. The measurement error of the unit in accordance with ASTM D445 was ±1%. The surface tension was measured using the Kruss K6 tensiometer by the ring method (du Nouy method) at a temperature of 20 °C. The device was calibrated by measuring the surface tension of bi-distilled water (correction factor = 0.995). The density of the prepared extinguishing agents was determined by a measuring tank with a volume of 0.1 L and electronic scales. The calculation error was no larger than 5%.

It should be noted that water additives used in the present work allow for obtaining fire-extinguishing compositions with significantly different mechanisms of impact on the fire bed. Therefore, the conditions of interaction with the flame and the heated surface of the decomposing material may also differ. Therefore, it is advisable to identify several key features of foaming agent emulsions, solutions of bischofite and EA-5, and bentonite suspension with combustion beds on the basis of the analysis of References [15,16,17,18,19,20]. In particular, emulsions of foaming agents are intended for extinguishing fires of classes A and B using fresh or sea water. They are used to produce foam of low, medium, and high multiplicity, as well as wetting agent solutions. They are produced in the form of concentrates for obtaining 1%, 3%, and 6% aqueous solutions (and other concentrations, if requested). The foaming agent of S type (green) can be used as a wetting agent for extinguishing solid materials with a working concentration of 2% to 10%. Foaming agents such as AFFF (blue) and AFFF/AR (red) are designed to extinguish fires of organic solvents, alcohols, esters, acids, water-soluble combustible and flammable liquids, wet samples of solid bulk materials, and forest litter. The composition of the foaming agent includes an additional polymer substance to isolate the foam layer from organic solvents. Considering the suspension of bentonite, it is necessary to note two important factors. The first is that a protective insulating layer is created on the surface, and the second is the retainment of water for a very long time. Bischofite solutions have hygroscopicity, and moistened combustible materials are in a wet state for a long time. This property can be used for fire protection of wood, fibrous materials, and creation of protective lines at suppression of forest fires. The solution not only has a fire-extinguishing effect, but adsorbs combustible material. When applying the bischofite solution to the wood surface, the formation of a protective coke layer is accelerated. The fire-extinguishing and fire-retaining compositions of long-term action include solutions of EA-5 (Russia), which is based on: urea 31–32 wt. %, sulfanol 2–3 wt. %, acid dye 0.5–1 wt. %, ammonium chloride 13–15 wt. %, and diammonium phosphate. Well-known foreign analogues are: U.S. Pat. No. 27,503 of 17 September 1970, British Pat. No. 1,242, 290 of 11 August 1971, Romanian Patent 51,226 of 17 August 1968. EA-5 solutions not only suppress the flaming phase of combustion, but also affect the material in a state of intense pyrolysis (in the phase of smoldering) and are used when laying the fire protective lines. Certification trials and tests (according to the regulatory documents specified in Table 1) have shown that the forest fuel materials treated by this solution do not burn for several days.

3. Experimental Setup and Methods

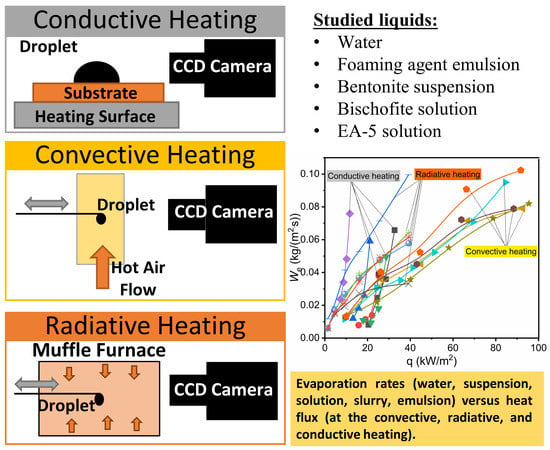
In experiments, three schemes of heating of a drop of a fire-extinguishing liquid were applied: on a heated surface (it is traditionally called conductive), in a gas stream (convective), and in a muffle furnace (radiation) (Figure 1). Each of them meets the conditions [29,30,31] of real fires especially during heating on the surface of the burning material or fire-resisting walling, during motion in gas or steam-gas flow (a mixture of flue gases, air, and vapors), and when reaching the front of the flame burning.

When calculating values of heat fluxes (q_cond, q_conv, q_rad), the following expressions were used [12]: q_conv = α·(T_a − T_s), W/m²; q_cond = λ_d·(T_sub − T_s)/R_d, W/m², q_rad = ε_d·σ·(T_a⁴ − T_s⁴) + ε_a·σ·T_a⁴, W/m² (the approach based on the assumption that droplets are opaque grey spheres [31]), α = Nu·λ_a/(2R_d), W/(m²·K), Nu = (2 + 0.57·Re^1/2·Pr^1/3)/(1 + B_f)^0.7 (for forced convection), Nu = 0.675·Ra^0.058 (for free convection), Re = 2R_d·U_a/ν_a, Ra = Pr·Gr, Gr = (g·β_a·d³·(T_a − T_s))/(ν_a·T_a)², Pr = ν_a·ρ_a·C_a/λ_a, ε_d = 0.9, ε_a = 0.1, σ = 5.68·10⁻⁸, W/(m²·K⁴). When calculating forced convection, it was assumed that there was no spatial gradient along a droplet’s surface, and recirculation inside the droplets was not taken into account [31]. In Reference [30], radiation heat was calculated using the expression q_rad = πd²·σ·ε·(T_a⁴ − T_s⁴) at ε_d = 0.95 and equal to absorptivity. It has been found that it is accurate when compared to other tedious procedures. The result shows that the equation can predict q_rad to within 4% [30]. The Nu expression for forced convection takes into account the evaporation of droplets Nu = (2 + 0.57·Re^1/2·Pr^1/3)/(1 + B_f)^0.7 [31], B_f = [C_a·(T_a − T_s)/L]·(1 − |q_d|/|q_c| + |q_R|/|q_c|)—mass transfer number (|q_d| is the rate at which heat is spent on raising the temperature of a liquid droplet, |q_c| and |q_R| are the heat rates supplied to droplets by convection and radiation, respectively, and L—latent heat of vaporization per unit mass). The performed calculations have shown that taking into account the parameter B_f, heat fluxes q_conv will decrease by 2%–15% at a temperature growth from 100 to 600 °C. Values of thermophysical parameters of air λ_a, ν_a, ρ_a, and C_a were chosen according to data from Reference [29] by taking into account their dependence on temperature. When calculating values of q_cond, the registered radius of the contact spot was taken as R_d, i.e., taking into account the factor of significantly different conditions of the spread of droplets of the studied compositions on the substrate. Accordingly, the q_cond values for the studied compositions (especially when comparing the foaming agent emulsion and EA-5 solution with other liquids) differed significantly at identical heating temperatures. The choice of expressions for the calculation of Nu numbers was made in the analysis of the main conclusions [30,32,33,34,35,36].

Similar to generalization of experimental results in the study [12], possible heat losses are not taken into account in this work when calculating the values of specific heat fluxes. Analysis and refinement of heat loss data for the three used heating schemes represent an independent and rather large-scale study that may be performed in the future using specialized equipment [37] or mathematical modeling [38,39,40] by the example of one of the extinguishing agents. In this paper, one of the significant factors is the differences in the rates of heating and evaporation of droplets of typical extinguishing agents. Since heat losses occur in all experiments, and identical heating conditions are observed for different compositions, these estimates can be performed in the first approximation without taking into account heat losses.

3.1. Heating on the Substrate

For the realization of conductive heat transfer (Figure 1a), the heating plate PL-01 is used (the operating temperature range of the heating surface is 40–400 °C, and the accuracy of temperature setting is ±1 °C). A polished copper substrate (with thickness of 4 mm and diameter of 50 mm) is placed in the center of the plate, heated to a predetermined temperature (depending on the experiment, the temperature varies from 70 to 100 °C). After the temperature on the substrate surface reaches the set value, a drop of liquid with a volume of V_d ≈ 10 µL is placed on it with the help of a dispenser. Evaporation of the droplet lying on the substrate is observed using a high-speed video camera with shooting frequency of up to 6·10⁵ frames per second and the maximum shooting resolution of 1280 × 1280 pixels. To determine the substrate temperature, an infrared thermometer is used (Testo 835-H1, with a 4-point laser designator and temperature measurement accuracy of ± 0.5% of the measured value). Typical video frames obtained in the experiments are shown in Figure 2.

It should be noted that the gas space above the substrate was open, i.e., the drop on the substrate was not covered with any cap. Therefore, we can conclude on the conditions of natural air convection over the substrate surface in the vicinity of the droplet. Using a low-inertia thermocouple, additional measurements were performed. They have shown that the air temperature near the droplet surface is 4–8 °C above the initial temperature in the experiment. At that time, the substrate temperature ranged from 50 to 100 °C. Therefore, we have taken into account the droplet heating from the substrate.

The performed video recording has revealed significant differences in the velocities and other characteristics of the droplet speed among the studied compositions on the substrate. The studies are carried out on an experimental setup similar to References [41,42] using the shadow method. A drop with a given volume is placed on a polished copper substrate using a high-precision single-channel electronic dispenser Finnpipette Novus. Then, using the shadow method, droplets are photographed. The contact angle (θ), diameter (d), height (h), and drop area (S) are determined from the shadow image using the drop profile processing methods (

Table 2. Geometric characteristics of a sessile drop of the fire extinguishing agent on the used substrate.

Parameters	Water	Bentonite Suspension	Bischofite Solution	EA-5 Solution	Foaming Agent Emulsion
θ, °	91.3	88.5	78.3	53.6	22.6
d, mm	3.41	3.45	3.78	4.74	8.16
h, mm	1.63	1.58	1.45	1.01	0.36
S, mm2	17.81	17.51	18.16	21.21	52.30

).

The relative error of the methods for determining these parameters when processing photographic images does not exceed 5% [42]. Typical shadow images of droplets of the studied extinguishing agents are presented in Figure 3.

3.2. Heating in the Air Stream

The scheme of droplet heating is similar to the one used in experiments of Reference [43]. The study of evaporation of single liquid droplets during their motion through a high-temperature gas medium employs a stand (Figure 1b) with the main elements: a high-speed video camera with a shooting frequency of up to 10⁵ frames per second and a maximum shooting resolution of 1280 × 1280 pixels, a measuring complex consisting of a high-speed analog input Board of the “National Instruments 9219” type with a sampling rate of 100 points/s, and a synchronizing processor with signal discretization not exceeding 10 Ns, supporting external and internal launch modes.

To generate a heated air flow (Figure 1b) with controlled parameters (temperature T_a and velocity U_a), we used the unit consisting of an industrial heater Leister LE 5000 HT (temperature range of 20–1000 °C), a fan Leister ROBUST (flow rate of 0.5–5 m/s), and a hollow transparent cylinder (with outer diameter of 0.1 m and wall thickness of 2 mm) of quartz glass (with maximum permissible temperature of about 1800 °C). The temperature was monitored using the controller Leister CSS (with temperature error of ±1 °C). The air velocity was changed using the frequency Converter LEISTER FC 550.

Using a dispenser, a drop of liquid was placed on the holder (with a tip diameter of 0.25 mm). The latter was moved into the channel with heated air using an automated coordinate mechanism. The optimal rate of introduction (about 0.1 m/s) was determined empirically to eliminate the conditions of the drop break from the holder. Droplets were introduced into a muffle furnace in a similar way (p. 3.3). Typical video frames obtained during experiments with droplets of extinguishing agents in the air stream are shown in Figure 4.

3.3. Heating in a Muffle Furnace

Radiative heat transfer was realized on the third stand (Figure 1c). The experiments were carried out using a Nabertherm tube furnace (maximum temperature of 1100 °C and chamber volume of 0.004 m³). Controlling and setting the required heating temperature T_a were performed using an integrated controller and an S type thermocouple (platinum-rhodium–platinum, maximum operating temperature of 1150 °C, thermal inertia index of no more than 5 s, and the limit of permissible deviations of ±1 °C). A drop of liquid, similar to p 3.2., was fixed on the holder and introduced into the chamber to its center to provide the required heating conditions. Typical frames of the droplet evaporation registration in the muffle are shown in Figure 5.

3.4. Determining the Rates of Heating and Evaporation of Liquids

In accordance with the main conclusions [12], the expressions W_h = T_d/t_h and W_e = ρ_d·R_d/t_d were used to calculate the rates of heating and evaporation of liquid droplets under the assumption of their sphericity, i.e., a uniform decrease in the droplet size over all three coordinates during the heating time. Thus, in contrast with the experiments of Reference [12], only the average values of the evaporation rate were calculated in this paper by taking into account the total lifetime t_d. In Reference [43], the instantaneous values of droplet evaporation rate were also calculated using the expression W_e = ρ_d·ΔR_d/Δt_d. With this approach, it was possible to calculate the rate of liquid evaporation during any time interval Δt_d.

In determining the drop warming rate, temperature T_d was recorded in different sections of the droplet. For this purpose, a low-inertia thermocouple and a specialized software package were used. The latter allowed moving the junction during heating and evaporation behind the moving surface of the droplet (similar to Reference [12]). Values of T_d on the droplet surface were used to estimate W_h. A junction of a low-inertia chromel-aluminum thermocouple (measured temperature range of 0–1200 °C and systematic error of ±1.5 °C) was advanced to the droplet surface. The module of “National Instruments 9213” with registration frequency of 2 Hz was used for temperature registration. A drop with a miniature thermocouple junction approaching its surface was introduced into the high-temperature gas region. The temperature field of the droplet T_d(R_d,t) was changed by varying the air temperature T_a.

It should be noted that the values of W_h were determined only in experiments with droplet heating in the air flow. This is because the registration of W_h values in experiments with a muffle furnace is characterized by large measurement errors due to radiative heating of the junction. In experiments with the substrate, the calculation of W_h requires information about the surface temperature T_d of the droplet near the solid wall surface. Such measurements are extremely difficult to carry out reliably. In addition, on transverse and longitudinal cross-sections, the values of T_d for the droplets of the studied compositions differ significantly due to different conditions and characteristics of droplets spread on the substrate. Therefore, only in the case of a drop placed in the air flow, it is possible to measure and to average the temperature of its surface in different sections relative to the incoming gas flow.

4. Results and Discussion

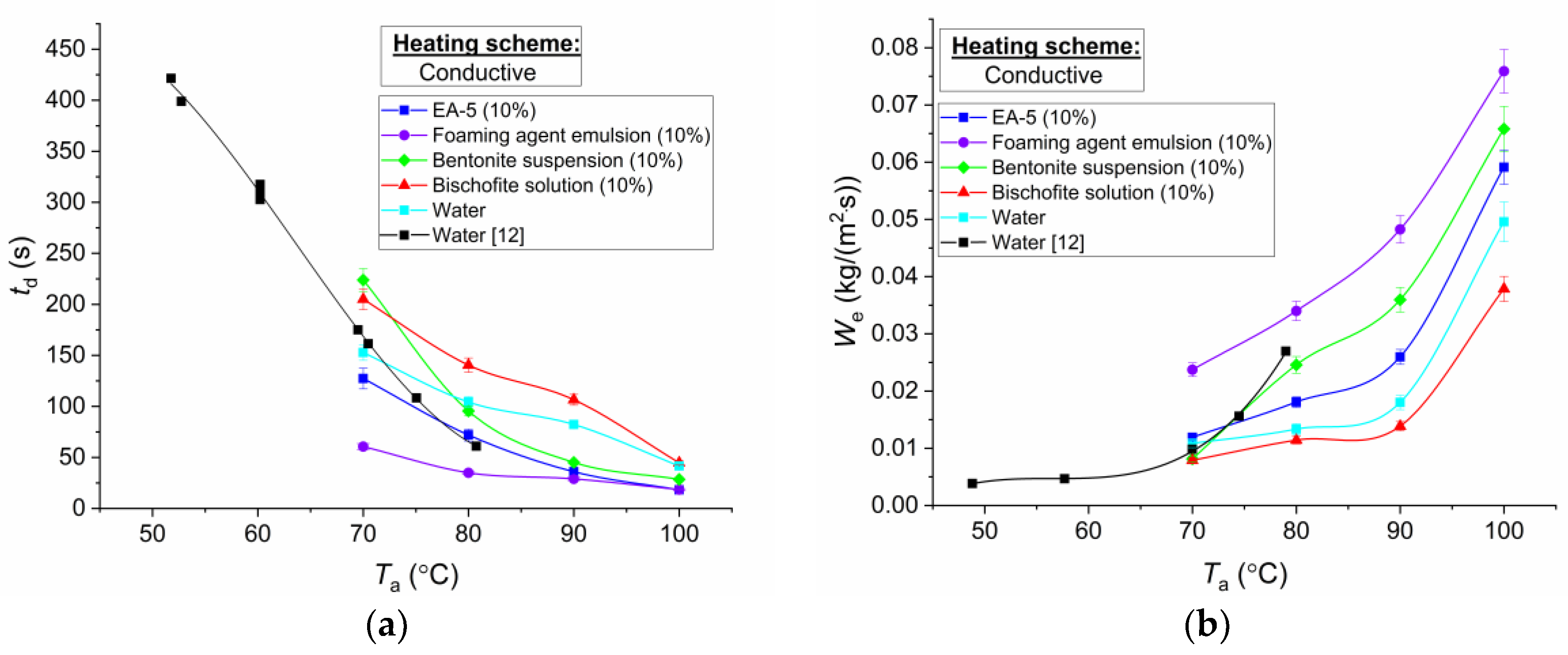
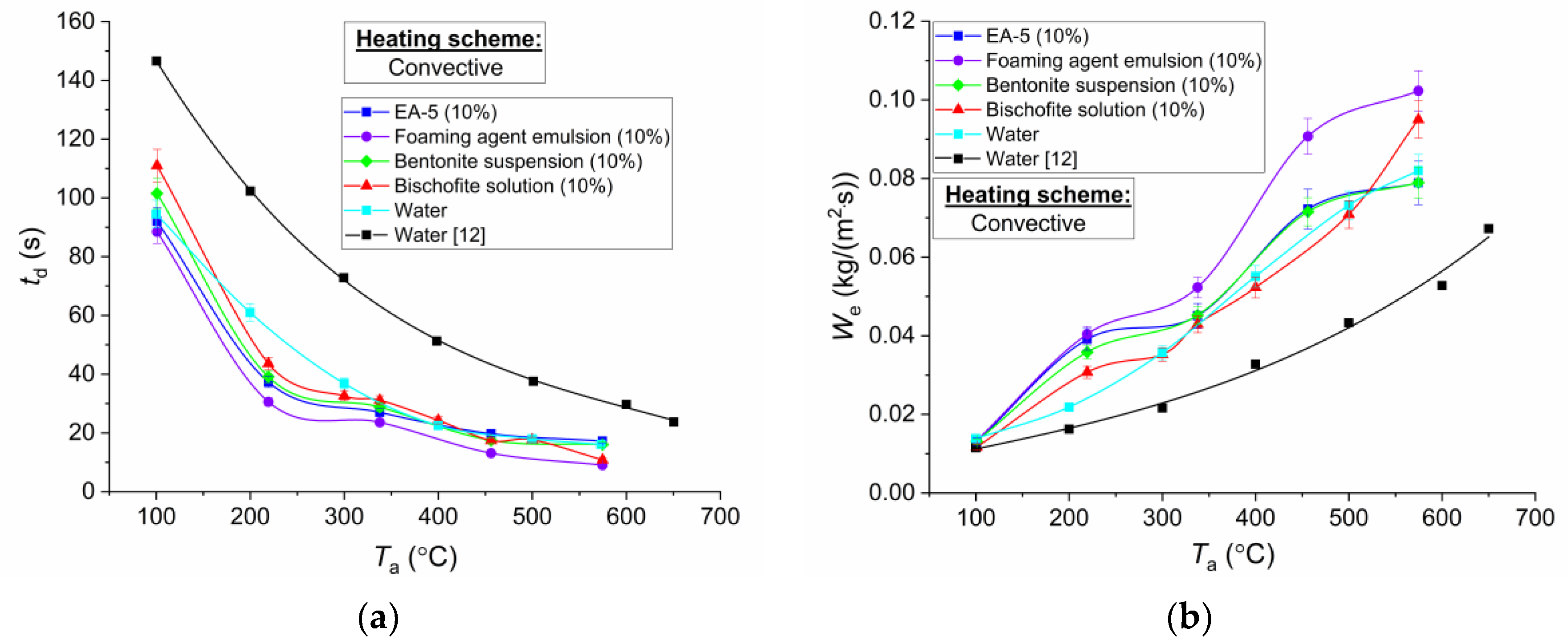
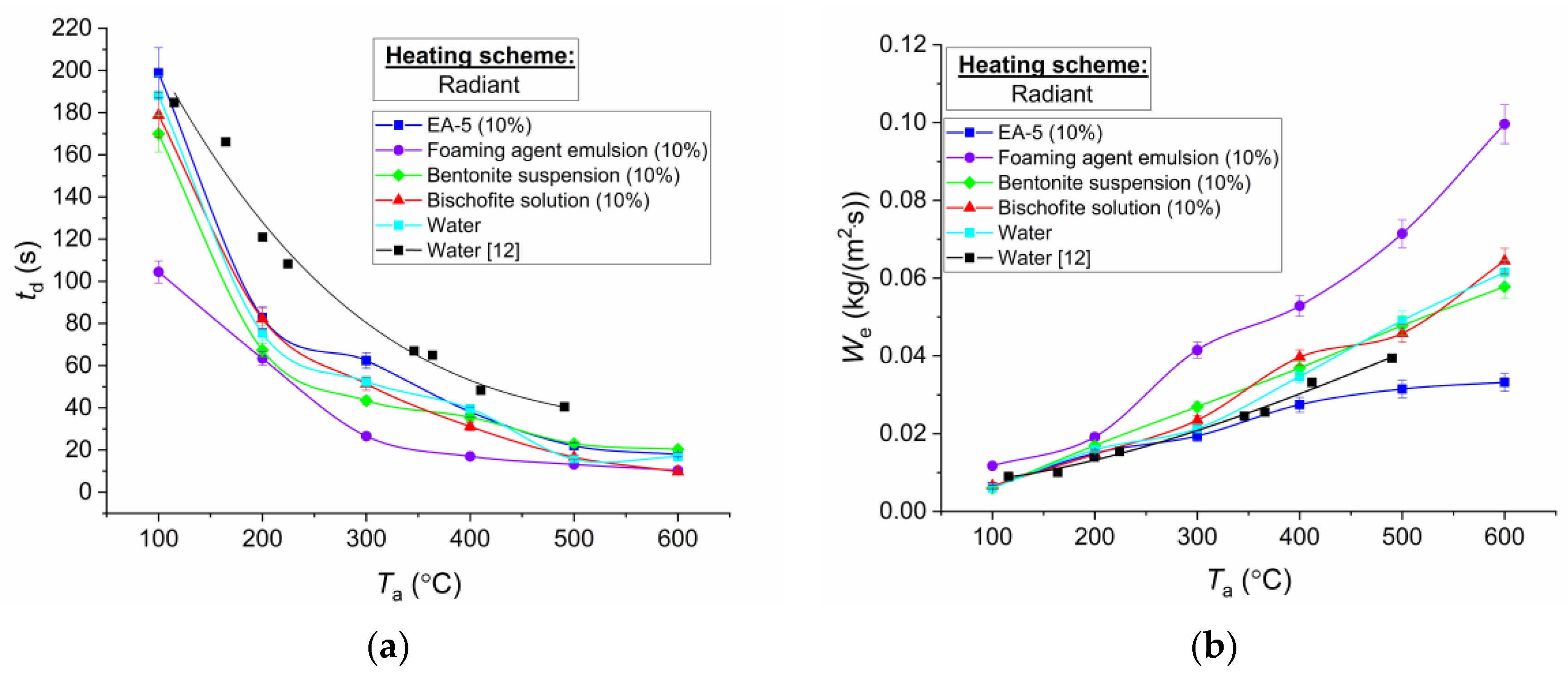
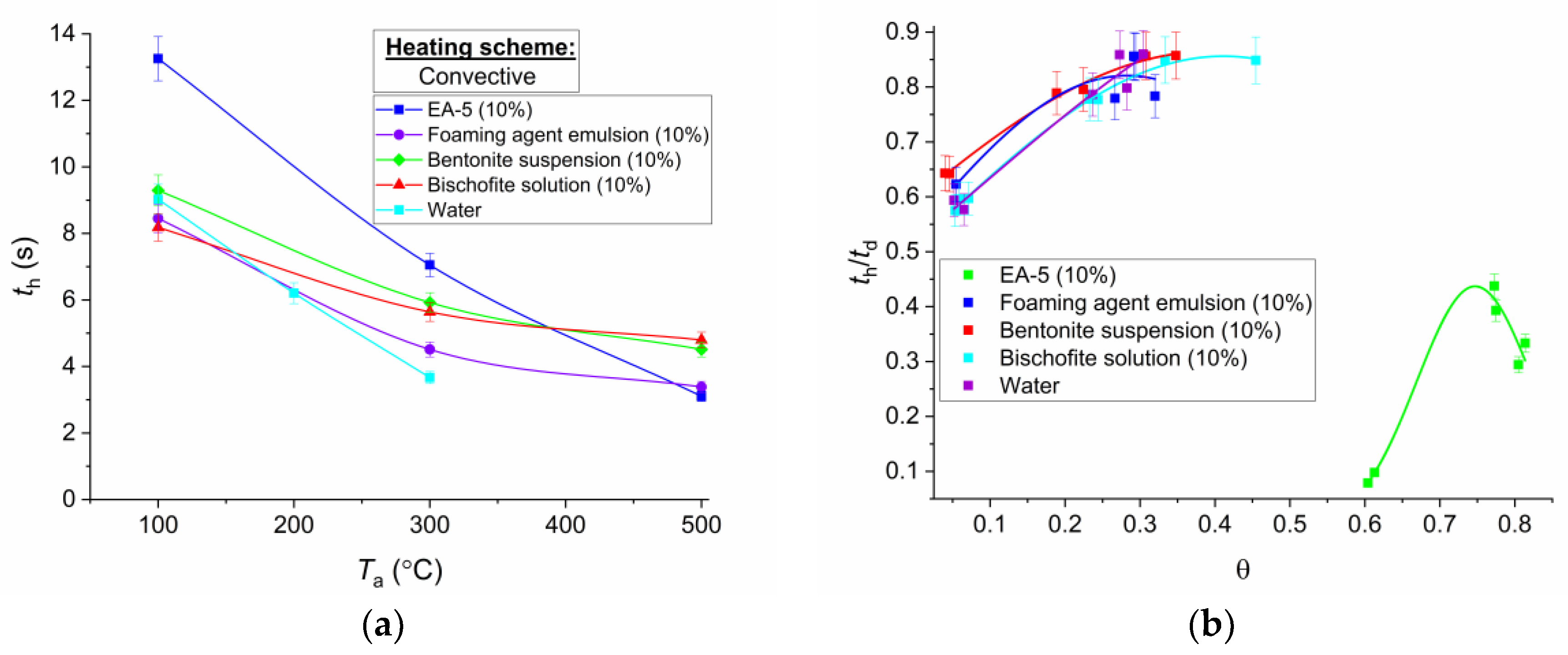
Figure 6, Figure 7 and Figure 8 show the registered times of full evaporation of droplets of the investigated compositions under heating temperature variation at three schemes of energy supply. The values of the evaporation rates W_e calculated using the recorded times t_d are also presented. Nonlinear (described by power polynomials and exponential expressions) dependences of t_d and W_e on T_a have been established for all compositions. They agree well with the results of experiments for water given in Reference [43]. When heating on a substrate and in a muffle furnace, the differences between the experimental values of W_e for water and the data of Reference [12] generally correspond to the confidence intervals of the experiments. The greatest dispersion of values of evaporation rates of water droplets was registered when heating in an air stream (Figure 7). This is because, in the placement of droplets of the studied compositions on the holder in this work, the contact area was approximately 15% to 17% larger than in the experiments of Reference [12] (estimates were made by using the method from Reference [43]). Accordingly, the times of complete evaporation of droplets in the experiments of Reference [12] were higher and the evaporation rates were lower, as can be seen in Figure 7. The increase in this area was due to a small rounding of the end of the holder. The need to modify the tip was caused by different rheological characteristics of the droplets, in contrast to Reference [12]. When using a tip similar to Reference [12], droplets of foaming agent emulsion and EA-5 solution were separated from its surface, while being moved by the coordinate mechanism, or spread almost completely. Therefore, it was difficult to register the rates of reduction of the drop radii and, accordingly, the evaporation rates. The difference in area of the droplet contact with the holder from Reference [12] led to a difference in the shape and, accordingly, the average size in the conditions of the air flow. This was because the incoming air flow pressed the drop to the holder. Therefore, these features should be taken into account when comparing the data, previously obtained in Reference [12] for water and, in this research, in the scheme with heating in the air flow (Figure 7). In experiments with the muffle furnace, this factor was weak. The differences between the results of this work and the data of Reference [12] were insignificant (Figure 8) and within the random errors of the registration of varied and controlled parameters.

The experiments for all heating schemes and studied compositions have resulted in registering the general form of dependence t_d(T_a) and dependence W_e(T_a) (Figure 6, Figure 7 and Figure 8). In particular, the maximum values of total evaporation times (and accordingly, the minimum values of evaporation rates) corresponded to water and salt solutions. The maximum values of evaporation rates have been registered in experiments with foaming agent emulsion and EA-5 solution. The bentonite suspension was characterized by average rates of vaporization relative to the emulsion, solutions, and water without impurities. These patterns can be explained by the influence of a group of properties and effects manifested in the experiments. Since different synergetic effects were registered depending on the studied heating scheme, it is advisable to comment on differences in the curves in Figure 6, Figure 7 and Figure 8 for each of these schemes separately.

Figure 6 demonstrates the results of experiments when placing droplets of the studied compositions on a heated substrate. Several significant results may be distinguished.

(i) The evaporation rates of the saline solution are lower than those of water and other studied extinguishing agents. The higher the heating temperature, the greater the difference in evaporation rates is. Even with the addition of 5–10% bischofite, the differences in evaporation rates can reach 20% to 25%. This is due to the influence of a group of factors registered in the experiments. In particular, when a drop of bischofite salt solution (MgCl₂∙6H₂O+additives) evaporated, a thin crystalline film was formed. Over time, it covered almost the entire drop. Accordingly, the evaporation area decreased. Meanwhile, with an increase in concentration of aqueous solutions of salts, the heat of vaporization is known to grow. Therefore, the amount of energy required for complete evaporation increases. It is also advisable to take into account that the surface tension of the salt solution is higher than that of water. This reduces the area of the droplet contact with the heated substrate at spreading. Therefore, the evaporation times of the bischofite salt solution are at maximal rates (Figure 6).

(ii) Minimum lifetimes and maximum evaporation rates were recorded in experiments with droplets of foaming agent emulsions. This is mainly due to significantly (several times) lower surface tension of the foaming agent emulsion compared to other studied compositions. Therefore, the contact angle for emulsion droplets was 22.6°. As a result, the greatest area of interaction with the substrate and, accordingly, the maximum evaporation rates were achieved. For the EA-5 solution, the surface tension values were higher than for the emulsion, but, in comparison with water, bentonite suspension, and salt solution, this parameter was significantly (almost 2 times) lower. As a consequence, the contact angles and the time of complete evaporation were close to the same characteristics of the emulsion of the foaming agent.

(iii) When comparing the times of complete evaporation of water and bentonite suspension, smaller values of W_e can be noted for the latter. This is due to the influence of several mechanisms. The main one is associated with greater thermal conductivity and density, lower heat capacity, and, accordingly, greater temperature diffusivity of the suspension. By the results of video recording, it is also possible to note the pattern of agglomeration of bentonite powder particles in different parts of the droplet. This increased the surface area of water evaporation, since the area of the contact boundary with the heated particles deposited on the substrate surface increased. At the same time, for experiments with suspension droplets on the substrate, the maximum fluctuations of the total evaporation times and the rates of phase transformations were registered. This was due to an important pattern, established in the analysis of video frames. Solid particles in the drop during its evaporation agglomerated chaotically, holding (closing) different volumes of water in-between. The symmetry of the suspension droplet on the substrate was often violated due to these effects. Hence, several larger fluctuations, compared to experiments with other compositions, were observed when averaging the results of radius calculations. In the case of adding 10% bentonite powder to water droplets, the effects of swelling, which are characteristic of moistened bentonite, did not manifest. However, this additive is a natural mineral of clay nature with a high binding capacity, which leads to absorption. This can also explain rather intense water retention between the particles of bentonite powder.

(iv) When the heating temperature increased, the average times of complete evaporation of droplets of the studied compositions became comparable. This was because a buffer steam zone was formed between the droplet and the substrate when the substrate heating temperature increased to the boiling point of water, which is the main component of the studied droplets. It reduced the heat flux due to significantly lower thermal conductivity and temperature diffusivity of vapors compared to the liquid and solid wall. Accordingly, the differences in the lifetimes of the studied droplets decreased.

The previously mentioned fluctuations of t_d and W_e, as functions of T_a, were even more significant in experiments with a dominant convective heat exchange (Figure 7). This was due to the fact that the air flow incident to droplets led to the transformation of their surface and more significant deviations from the spherical shape (closer to ellipsoidal). In general, the established trends of the curves placement relative to each other are similar to Figure 6 (the maximum values of evaporation rates correspond to the emulsion and the solution with reduced surface tension, minimum salt solution, and water without impurities). However, the deviations of t_d and W_e are much smaller since the influence of the droplet spreading factor was somewhat weakened when using holders and blowing by the air flow, compared to the substrate. A more significant portion of energy was supplied from the free surface of the drop. Therefore, the thermophysical properties of liquid compositions played an important role. The higher the thermal conductivity, the faster the droplets warmed up to higher temperatures. As a consequence, the rate of evaporation increased.

Another important factor leading to high rates of heating and evaporation of droplets of foaming agent emulsions is a significant decrease in viscosity when heating. In the case of convective heating, this factor is particularly significant. It is associated with the fact that the rates of intra-drip convection depend on the geometric (size), thermal (temperature), and aerodynamic (flow velocity) factors [44]. Analysis of data from Table 1 shows that the viscosity reduction factor during heating is the most significant for foaming agent emulsions. Therefore, in conditions of identical droplet sizes and velocities of the incoming air flow, high rates of intra-droplet convection for emulsions can be concluded. In experiments with water droplets [44], the intensification of convection was shown to lead to an increase in the temperature of the droplet and in evaporation rates. Therefore, this factor contributed to an additional increase in the evaporation rate in the case of foaming agent emulsions.

The main difference of liquid droplets in experiments with heating in a muffle furnace from the results of studies using the scheme with the air flow (Figure 7) and the substrate (Figure 6) is the low values of evaporation rates of droplets of EA-5 solution. In the schemes with heating in the air flow and on the substrate, the evaporation rates of droplets of this composition were close to the values of the same parameter for the foaming agent emulsion. The key difference between the evaporation conditions at heating in a muffle furnace was that a drop of solution thickened and got covered with a crystalline film. When heated in the air stream and on the substrate, the formation of such a film was not recorded. Most likely, this is due to a significant transformation of the surface of the droplet and layers (because of intra-drop convection) due to the incoming air flow in the case of convective heating and interaction with the substrate. The formation of this film is associated with the properties of the EA-5 solution including creating a thermal insulation layer for burning structures. Therefore, this film acts as a buffer zone between the external gas medium and the internal liquid layers. The film reduces the evaporation rate. The higher the heating temperature, the greater the difference of W_e is. Therefore, it can be concluded that, for intensive evaporation of EA-5, it is expedient to increase the dynamics of transformation of the surface of droplets and layers. In this case, evaporation rates can be even higher than those of suspensions, salt solutions, and water without impurities, as shown in the substrate and air flow schemes. The key feature of the application of the EA-5 solution is the formation of a buffer steam zone between the envelope, material, or substance, and the heating source. In addition to the above film, the formation of a vapor layer was observed on the videograms with conductive heating. The temperature diffusivity of vapors is an order of magnitude lower than that of liquids and solid materials. Therefore, the heat flux was significantly reduced after the passage of radiation through the vapor layer.

In the analysis of Figure 8, it can be concluded that the most significant differences in the times of complete evaporation and vaporization rates are characteristic of the foaming agent emulsion compared to other studied component compositions. However, these differences are significant at low heating temperatures (up to 100 °C). The higher the heating temperature is, the smaller the difference in total evaporation times is. This result characterizes the fact that the rates of radiation heating of most extinguishing agents are close. However, due to different areas of the droplet contact with the holder and different areas of its free surface (the dynamics of droplet spreading is different, as mentioned above), the values of evaporation rates also differed even with an increasing temperature (Figure 8). If the key parameters of radiation heat transfer are taken into account, the determinant should be the emissivity of droplets of extinguishing agents. Therefore, the values of the heat fluxes to the surface of the studied droplets are comparable.

When generalizing the experimental data obtained for each of the dependent factors in Figure 6, Figure 7 and Figure 8, approximation expressions are formulated to most closely describe the experimental data. A similar work has been carried out to determine the approximation expressions for the dependence of the evaporation rates on the heating temperature. A general form of the approximation expression has been obtained for the evaporation rate dependence on the heating temperature by taking into account the scheme of heat supply to the drop: W_e = a·T² + b·T + c.

Table 3. The values of empirical constants for the expression W_e = a·T² + b·T + c.

Liquid	In Muffle Furnace				In Air Flow				On the Substrate
	a	b	c	R2	a	b	c	R2	a	b	c	R2
EA-5 (10%)	−1 × 10−7	1 × 10−4	−6 × 10−3	0.919	−9 × 10−8	2 × 10−4	−5.1 × 10−3	0.977	1 × 10−4	−15.9 × 10−3	0.6164	0.918
Foaming agent (10%)	4 × 10−8	1 × 10−4	−2.5 × 10−3	0.832	−2 × 10−8	2 × 10−4	−7.2 × 10−3	0.973	4 × 10−5	−5.7 × 10−3	0.2083	0.997
Bentonite (10%)	−1 × 10−9	1 × 10−4	−4.2 × 10−3	0.999	−7 × 10−8	2 × 10−4	−4.8 × 10−3	0.977	3 × 10−5	−3.9 × 10−3	0.1151	0.987
Bischofite (10%)	8 × 10−8	5 × 10−5	1.1 × 10−3	0.966	2 × 10−7	4 × 10−5	8.2 × 10−3	0.988	5 × 10−5	−7.8 × 10−3	0.3021	0.954
Water	3 × 10−8	8 × 10−5	−3.5 × 10−3	0.809	1 × 10−7	1 × 10−4	−1.4 × 10−3	0.936	8 × 10−5	−12.8 × 10−3	0.5032	0.992

shows the values of empirical constants and the approximation confidence value (R²).

In all cases, it was possible to most closely describe the dependence of the evaporation rates of liquids on the heating temperature using a polynomial of the second degree. This allows concluding that the determining influence on the evaporation rate is exerted not only by the heating temperature or the heat flux, but several more factors, i.e., at least two (otherwise, it would be possible to apply exponential and power functions or polynomials of the first order). We have attempted to describe an experimental dependence with approximation expressions based on exponential, power, and polynomial dependent factors. The best correspondence has been found when applying the polynomial of the second degree. If a polynomial of the third or fourth degree is applied, the approximation curves may be approached to the experimental values. However, these refinements will be insignificant in comparison with the use of the polynomial of the second degree. The analysis of the studied processes has shown that the key ones are: the contact area with the heating medium, the temperature of the medium, the heat flux, and the thermophysical and rheological characteristics of the liquid. In the first approximation, it was possible to use one general approximation expression and to compile a table with empirical constants. Furthermore, it is necessary to determine the relationship of the latter with the properties of liquids. Large-scale parametric synthesis accounting for each of the performed experiments will be necessary. On the received general approximation expression and a range of empirical constants, it is possible to draw a conclusion that such a synthesis is possible and expedient in the future.

Depending on the heating scheme at high temperatures, the values of full evaporation times and evaporation rates of the droplets of the studied liquids can both converge and differ significantly. This is due to the fact that, at high heating temperatures, the size of the droplets due to evaporation changes with large fluctuations. The reasons for such fluctuations mainly consist of the fact that high-temperature heating leads to local overheating and boiling of droplets, Leindenfrost effects, changes in the shape of droplets relative to a spherical shape, etc. The more components are in a droplet with significantly different thermophysical and rheological characteristics, the more noticeable these factors are. Under such conditions, experimental data in Figure 6, Figure 7, Figure 8 and Figure 9 should be taken as ranges of full evaporation times and rates of vaporization of typical fire-extinguishing compositions. The upper and lower curves in each of these figures illustrate the boundaries of the registered parameter regions. These areas are of primary interest for mathematical modeling and for predicting the values of evaporation rates of extinguishing agents in practice.

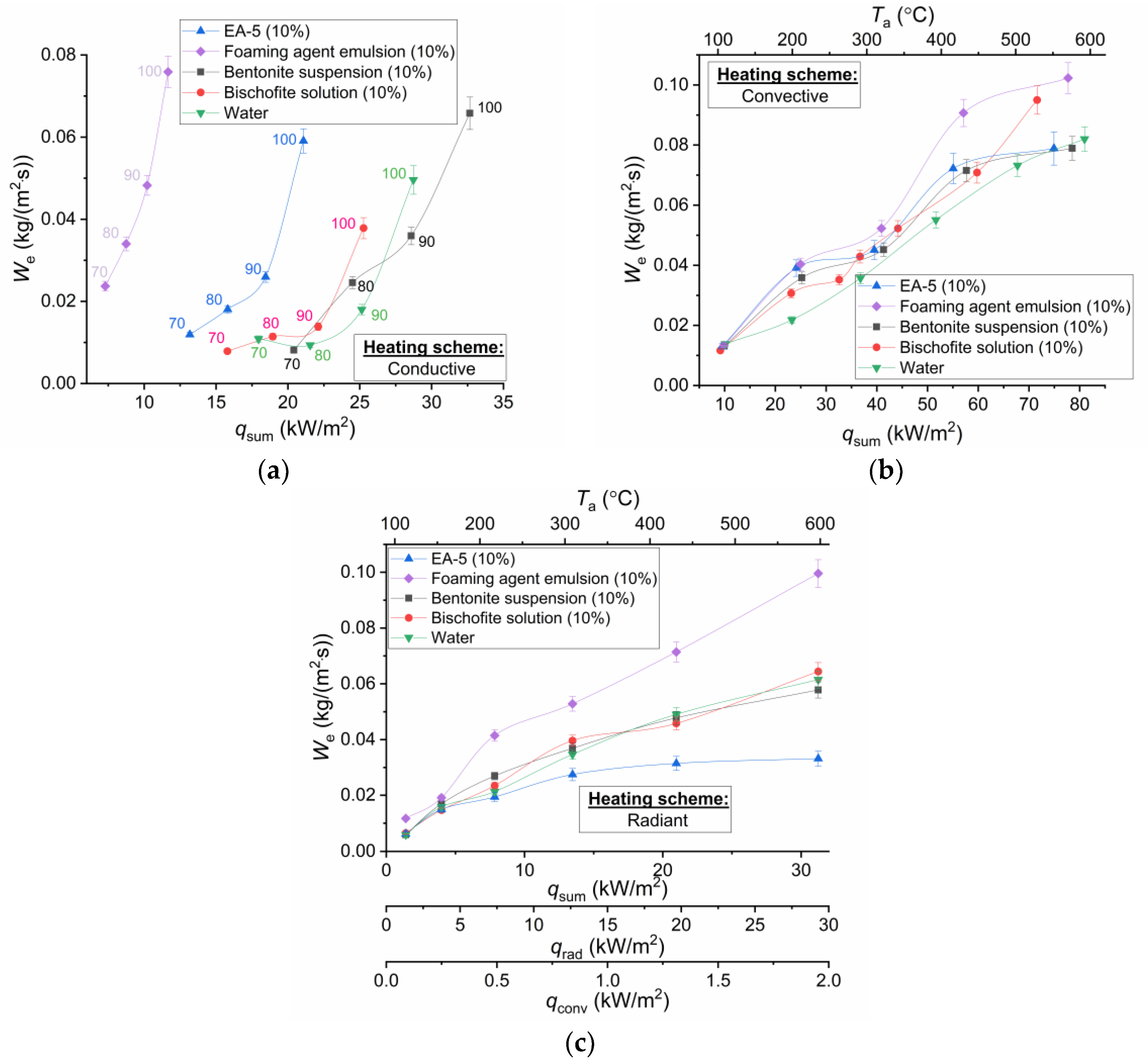
Figure 9 presents values of the calculated heat fluxes supplied to the studied droplets using three schemes of the heat supply. The total values of heat fluxes for the studied droplet heating schemes are presented along the abscissa axis: on the substrate q_sum = q_cond (Figure 9a), in the air stream q_sum = q_conv (Figure 9b), and in the muffle furnace q_sum = q_conv + q_rad (Figure 9c).

In the analysis of Figure 9, it may be noted that the highest values of evaporation rates recorded in experiments with convective air flow are due to the large values of the supplied heat flux to the surface of the droplet, if the three used schemes are compared at identical temperatures. Diffusion also plays an important role. In particular, in experiments with a substrate and a muffle furnace, a vapor buffer layer is formed on the surface of the droplet and restrains the growth of the evaporation rate due to a high concentration of vapors and small gradients of this parameter in the vicinity of the droplet surface. In the case of a scheme with an impinging air flow, the formed vapors are carried out of the droplet surface (as part of the vapor-gas mixture into its wake). Therefore, in a small near-surface layer, the concentration of vapors cannot be large, and the increase in the evaporation rate is not restrained, respectively. When comparing the values of evaporation rates calculated for the scheme with the substrate with other schemes of heat supply, it is worth noting the determining role of the droplet spreading factor, i.e., that the area of its contact for different compositions differed significantly. This significantly influenced the conditions of heat and mass transfer in the drop-substrate system.

The analysis of experimental results in Figure 9 shows that, at identical values of heat fluxes supplied to the heated surface of the droplets of the studied compositions, the heating conditions significantly affect the numerical values of the evaporation rates. It can be concluded that the non-identical conditions of supply to the droplet lying on the substrate in comparison with the droplet heating in the muffle furnace and the air flow lead to significantly lower evaporation rates (at the same heat fluxes). The latter is a consequence of less intense heating of droplets. Therefore, it may be concluded that the application of methods for determining the evaporation rates of droplets of any liquids (including suspensions, emulsions, and solutions) under conductive heating does not provide reliable characteristics of liquid droplet evaporation. If, in the conditions of convective heating, the experimental points of dependent factors of evaporation rates on the heat flux up to 50 kW/m² are located close enough (deviations do not go beyond the limits of confidence intervals), the numerical values of W_e for the compositions differ significantly in radiation heating. It is possible to make a reasonable conclusion that the foaming agent significantly intensifies the heating of the emulsion droplets, and the addition of EA-5 reduces the intensity of heating of the droplet of the aqueous solution. Dependent factors shown in Figure 9c imply that more strongly radiant heating of droplets, i.e., differences in the values of W_e in the scheme with an impinging air flow and a muffle furnace at identical q illustrate a significant absorption of radiation. The structure of droplets of the studied compositions differs significantly. Therefore, the characteristics of radiation transmission are also different. If the radiation was absorbed only in the near-surface layers, the evaporation rates of the droplets of all five liquid compositions would be very close.

During the experiments, the surface temperature of the droplets T_d was measured. Similar to the experiments with water droplets in the study [12], we have found out the tendency to a pronounced time interval during which the droplet warms up intensively. However, after its completion, the droplet temperature does not increase, i.e., it passes to a quasi-stationary state. Similar to the study [12], we can conclude that there are asymptotic values of T_d. For each of the heating temperatures T_a, the maximum values of droplet heating T_d differed such as in the experiments with water [12]. For example, in experiments with water at T_a of about 100 °C, the droplet warmed up to 40 °C. Differences in T_d registering from experiments of Reference [12] were about 2 °C, which is due to a slightly different layout of droplets on the holder and inertia of the measurement system. In Reference [12], a system based on the optical PLIF method was used, and the present work employed a low-inertia thermocouple. In this paper, it was not possible to apply the PLIF method for all the studied compositions since the luminosity of the fluorophores (dyes) Rhodamine B and Rhodamine 6G significantly depended on impurities in water.

In the comparative analysis of the time for warming up droplets of the studied compositions to some practically constant (asymptotic values) temperatures, it is possible to distinguish key features of the influence of thermophysical and rheological characteristics of liquids. In particular, Figure 10 and Figure 11 demonstrate the results of registration of the heating times (t_h) of droplets to almost constant values T_d and temperature drop ΔT_d (the difference between the final and initial value of T_d). It is clearly seen that the slowest heating was characteristic of droplets of EA-5 solution. This is due to the above highlighted property, associated with the formation of a thermal insulation buffer film. Therefore, the properties characteristic of EA-5 are simultaneous extinguishing capability and fire-protective ability, blocking the phase flaming combustion, and smoldering of combustible forest materials. Foaming agent emulsion and water without impurities warmed up faster. Bentonite suspension and bischofite salt solution warmed up a little longer, but to large asymptotic values of T_d.

When comparing the data of Figure 10 and Figure 11, the relation of maximum values of T_d and warm-up times t_h was observed for almost all compositions. The higher the T_d value was reached, the longer the heating took place, but the evaporation process was generally faster (i.e., the total evaporation times were smaller). Analyzing the features of the T_d changes for the EA-5 solution, we can note the maximum temperatures in contrast to other droplets, i.e., the droplets of this solution intensively accumulated the heat supplied. For other compositions, the T_d values were generally quite close to each other. The previously mentioned information explains the peculiarities of the formation of two buffer zones in the droplets of EA-5, which leads to the maintenance of the maximum temperature on the drop surface, and leads to significantly lesser energy passing into the deeper layers. As a consequence, heat accumulation occurred in the near-surface layer of EA-5 droplets (thus, the T_d values on the surface are maximum), unlike in other compositions.

The results of the studies have shown that the integral characteristics of the processes of heating and evaporation of fire extinguishing agent droplets significantly depend on a set of factors considered in this paper. In addition to the thermophysical characteristics, rheological characteristics are important, since the area of the droplet contact with the heating medium significantly changes the values of the heating times and, as a consequence, the rates of heating and evaporation of liquids. The most effective compositions, in terms of high rates of heating and evaporation, are a solution of EA-5 and emulsion foaming agent. Therefore, for maximum heat accumulation (due to heat capacity and heat of liquid vaporization) from the combustion zone in the case of extinguishing and localization of fires, it is advisable to apply these compositions. At identical values of heating temperature and heat fluxes, the rates of heating and evaporation of the latter may be higher by 15–25% in comparison with other fire-extinguishing compositions. Since the time of localization and extinguishing of fires matter, the corresponding acceleration of heating and evaporation of droplets may be important in the development of promising technologies for suppressing forest fuel combustion [45,46,47,48,49].

5. Conclusions

Experimental studies have shown that the lifetime (complete evaporation) of droplets of promising extinguishing agents (water without impurities, bentonite suspension, bischofite solution, EA-5 solution, and foaming agent emulsion) may differ when heating on the substrate 3.7 times (for example, at T ≈ 70 °C for bentonite suspension and foaming agent emulsion), in the air flow—1.25 times (at T ≈ 100 °C for foaming agent emulsion and bentonite suspension), and in the muffle furnace—1.9 times (at T ≈ 100 °C for EA-5 solution and foaming agent emulsion) at identical schemes and temperatures of the heating source. These results show that, in order to ensure the complete evaporation of droplets of such compositions in the zone of forest burning with different heat release, different discharge heights, and, accordingly, different warm-up and movement durations in the flame, the burning zones are required.

The range of evaporation rates of fire extinguishing agents was 0.00788–0.07589 kg/(m²·s) at a heating temperature of 70–100 °C (scheme with heating on the substrate). The maximum values of evaporation rates corresponded to the 10% foaming agent emulsion, and the minimum values corresponded to the 10% bischofite solution and water without impurities. In general, the range of changes in the registered values of evaporation rates of fire extinguishing agents was 0.006–0.02 kg/(m²·s) at heating temperatures of 70–600 °C.

When generalizing the results of experimental studies, the dependent factors of evaporation rates of promising fire-extinguishing compositions on the heating temperature for three schemes of heat supply have been established. These dependent factors in a general form are described by a single approximation expression W_e = a·T² + b·T + c. For each of the extinguishing agents, the values of empirical constants reliably predicting the evaporation characteristics were found.