Abstract
In non-cooperative multi-agent planning environments, it is essential to have a system that enables the agents’ strategic behavior. It is also important to consider all planning phases, i.e., goal allocation, strategic planning, and plan execution, in order to solve a complete problem. Currently, we have no evidence of the existence of any framework that brings together all these phases for non-cooperative multi-agent planning environments. In this work, an exhaustive study is made to identify existing approaches for the different phases as well as frameworks and different applicable techniques in each phase. Thus, an abstract framework that covers all the necessary phases to solve these types of problems is proposed. In addition, we provide a concrete instantiation of the abstract framework using different techniques to promote all the advantages that the framework can offer. A case study is also carried out to show an illustrative example of how to solve a non-cooperative multi-agent planning problem with the presented framework. This work aims to establish a base on which to implement all the necessary phases using the appropriate technologies in each of them and to solve complex problems in different domains of application for non-cooperative multi-agent planning settings.
1. Introduction
Traditionally, game theory research combined with Multi-Agent Planning (MAP) [1] tends to pay more attention to cooperative/coalitional approaches and strictly competitive approaches. In the first case, a set of agents come together in coalition to achieve a goal if it is beneficial to them [2,3]. In the case of strictly competitive problems, which are represented by zero-sum games in game theory, the agents have completely antagonistic objectives since one agent’s profit is directly proportional to the losses of the others. This case applied to multi-agent planning is known as adversarial MAP [4,5]. However, there is a field between the two mentioned that includes non-cooperative approaches but in a non-strictly competitive setting that is, the so-called general-sum games, in which the profit of one agent does not have to imply a loss in the others (Chapter 3 of [6]). Hence, agents seek to satisfy their private interests but not at the cost of hurting others as in zero-sum games.
The problems of non-cooperative multi-agent planning in a non-strictly competitive setting, which we will simply refer to as non-cooperative MAP, collect a considerable set of real-world problems that need to be studied. For example, traffic flow regulation, where all agents want a smooth driving avoiding collisions, but also congestion appears because of the use of the same road, which may decrease agents’ utility. Other similar examples are the management of self-interested urban fleets or open fleets of delivery services.
Therefore, considering the importance of non-cooperative MAP problems, in this work, we make an exhaustive study of the related works, first contextualizing the different branches of multi-agent planning with both altruistic and self-interested agents (game theory). With this study, we want to identify the different phases that can comprise the complete resolution of non-cooperative MAP problems as well as the proposals and techniques used for their resolution.
Furthermore, given the lack of frameworks that combine all these phases in the same context of non-cooperative MAP, in this paper, we propose an abstract framework that incorporates the phases we consider as a crucial part of a system of this type, which are: goal allocation to distribute the goals among the agents if necessary; strategic planning given the self-interested nature of the planning agents; execution to test the plans adopted by the agents in the previous phase; and reuse of the data to allow the agents to learn from previously solved problems. Our final goal is to provide an abstract framework that serves as a basis for a complete implementation of the framework for the automatic resolution of problems.
Finally, in this work, we also propose a concrete instantiation of the abstract framework and a case study with what we intend to give a specific vision of how this framework could be used taking the best advantage of it in each one of the phases.
This paper is structured as follows. Section 2 makes an exhaustive study of the related work of multi-agent planning and game-theoretic approaches, establishing a hierarchy to classify non-cooperative MAP, and including a discussion about the absence of abstract frameworks to solve these kinds of problems. In Section 3, the abstract framework for non-cooperative MAP proposed in this work is presented. Section 4 contains a detailed explanation of the framework phases with the particular techniques that we propose for our instantiation. A case study to illustrate how the abstract framework can be applied to non-cooperative MAP problems is presented in Section 5. Finally, Section 6 draws the conclusions and future work of this paper.
2. Related Work
Over the last few years, there has been rather intensive research in Multi-Agent Planning (MAP) [1] and also in game-theoretic approaches [7]. However, there is a lack of proposals that tackle non-strictly competitive MAP tasks. The assumptions adopted in MAP concerning the nature of the participating agents give rise to a great variety of MAP paradigms that range from altruistic planning, which assumes that agents are fully cooperative and do not have a strategic behavior or private interests, to adversarial MAP, where agents are self-interested and competitive.
Figure 1 shows a hierarchy of MAP, where the left branch depicts approaches that feature altruistic agents, and the right branch presents the research areas that deal with self-interested agents.
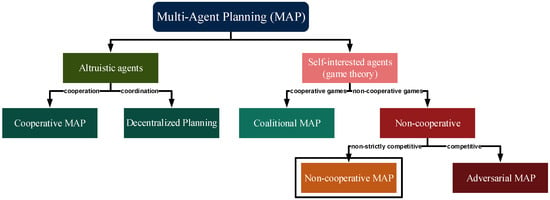
Figure 1.
Multi-agent planning hierarchy.
The left branch of Figure 1 comprises the MAP approaches that feature agents without private interests. This type of MAP is characterized by altruistic entities that do not follow a strategic behavior. We distinguish two main branches of non-strategic planning agents which are focused on cooperation (cooperative MAP) to solve a common task [8], or coordination (decentralized planning) of the agents’ local plans to achieve their goals in a global context [9]. However, agents are non-strategic and there is no need of a game-theoretic mechanism since the common objective is to satisfy a global utility function.
The research lines that feature self-interested planning agents are represented in the right branch of Figure 1. We consider two main branches within these lines. On the one hand, when planning agents are willing to cooperate by forming groups to achieve their goals like in cooperative game theory, this is known as coalitional MAP. On the other hand, the non-cooperative approaches of the right branch of the game-theoretic MAP approaches are divided into strictly competitive and non-strictly competitive. In a competitive MAP setting, agents only focus on defeating other agents, which is known as adversarial MAP [10], and it is commonly represented in game theory as zero-sum games. Non-strictly competitive MAP approaches feature conflicting and complementary interests, which are typically represented in game theory as general-sum games [11,12].
There is a significant branch of game theory that considers cooperative agents which form coalitions if it benefits them, this is known as coalitional or cooperative game theory, and it is devoted to the analysis of how the agents work together by forming coalitions [13]. Cooperative game theory has been applied in planning scenarios to solve coalitional goal allocation problems. The Coalition-Planning Game (CoPG) proposal [2] extends STRIPS (Stanford Research Institute Problem Solver (STRIPS) language [14]) models of single-agent planning to a system of multiple self-interested agents that may need to cooperate in order to achieve their single associated subgoals but are assumed to do so only in order to increase their net benefit. The second approach of this work is the Auction-Planning Game (AuPG), where coalitions of agents compete for the achievement of a single goal which yields a monetary reward for the coalition. The profit is always distributed among the coalition agents. A later work in the line of CoPG was presented in [15]. In this case, the proposed approach solves the so-called “safe” CoPG, a subset of the CoPG where no agent can benefit from making another agent’s plan invalid. A single-agent planner based on the relaxed planning task Fast Forward heuristic [16] is used to solve the multi-agent problem. The system proposed in [17] couples coalition formation with planning by allocating the best possible team of robots for each task, thus reducing planning complexity. Authors in [18] presented a temporal reasoning mechanism for self-interested planning agents. In this work, agents’ behavior is modeled on the basis of the Belief-Desire-Intention (BDI) theoretical model of cooperation to compute joint plans with time constraints. The mechanism ensures temporal consistency of a cooperative plan and it has been tested in real-life scenarios. In some approaches such as the one presented in [19], there is cooperation among agents for path planning avoiding obstacles. Concretely, the authors use a cooperative game and a multi-agent Q-learning algorithm to find Nash equilibrium.
Non-cooperative game theory in a strictly competitive setting studies problems in which the self-interested agents have opposed goals. These games are known as zero-sum games [20,21]. Some popular examples are two-player board games, the matching pennies game [22,23], or Rochambeau (http://www.rpscontest.com/) (also known as Rock, Paper, Scissors), which provides a three-strategy generalization of the matching pennies game. In a planning setting, a strictly competitive game, named adversarial MAP, is interpreted as agents pursuing completely opposed goals, e.g., one agent has to achieve the goal g and another one has to achieve . Some adversarial MAP approaches focus on solving problems in non-deterministic and unpredictable scenarios [24]. In this work, authors present an architecture for adversarial planning in battle management that involves control of several semi-autonomous intelligent agents; the need to adjust plans dynamically according to developments during plan execution; and the need to consider the presence of an adversary in devising plans. The work in [25] presents universal adversarial MAP algorithms for non-deterministic finite domains. These algorithms extend the family of ordered binary decision diagrams and are applied to stochastic games. Another research line of adversarial MAP is devoted to board games or general video games. Authors in [26] propose a planning framework that uses strategy simulation to achieve Nash equilibrium solutions. This framework is applied to army deployment problems in real-time strategy settings in order to improve strategic behavior of agents in modern video games. The works in [27,28] present an adversarial Hierarchical Task Network (HTN) [29,30] planning framework for goal-directed game playing. Particularly, this approach is only applied to solve the well-known game of Go (http://www.usgo.org/way-go). Similarly to alpha-beta pruning [31], the work in [4] proposes a forward-chaining approach to adversarial MAP based on the AND/OR* algorithm, which is guided by a heuristic evaluation function inspired by the relaxed planning graph used in the calculation of the Fast Forward heuristic [16]. This approach is only applicable to two-player games. In summary, in strictly competitive scenarios, agents have opposed goals, they seek to harm each other and only care about decisions that benefit them.
Non-Cooperative MAP
Agents in a non-strictly competitive setting do not seek to harm each other, but, since they have complementary and contrary interests, their purpose is to apply a collaborative strategy and conflict resolution process that aims to accommodate all participants (win–win strategy). Additionally, they do not form coalitions with the purpose of building their plans. There are several types of problems in non-cooperative MAP. In some problems, agents have to solve a MAP task and goal allocation is applied to distribute the goals of the task while retaining the agents’ private interests. Other problems feature multiple individual planning tasks. In this case, agents are assumed to independently work on their own part of the planning problem, and then their plans have to be coordinated with others. Similar settings focus on determining the amount of goals each agent can solve for its own planning task (soft goals), depending on the interactions with others, through non-cooperative games.
Non-cooperative MAP settings have been used for goal allocation [32]. Agents have to obtain an optimal solution to a MAP task, which means they have a common interest, while satisfying their private incentives. The objective is to determine the goals of the MAP task that will be solved by each agent, while guaranteeing an optimal solution that maximizes the sum of the agents’ utilities, i.e., utilitarian social welfare. Hence, when an agent is bidding for a goal, a payment is applied to reflect the impact of each agent’s participation on the other agents. This problem is solved with the Vickrey–Clarke–Groves (VCG) mechanism [33,34,35]. Other approaches use similar auction mechanisms to distribute goals among agents [36]. In this work, agents bid for the goals to solve and the MAP task is tackled with single-agent plan repair systems. The paper in [37] also presents an incentive-based approach called the Utilitarian Distributed Constraint Satisfaction Problems (UDisCSP), an extension of the DisCSP which uses utility-based agents that receive rewards for finding a solution at the cost of losing privacy.
MAP with self-interested agents is commonly regarded as a coordination problem in which several agents interact. Some approaches apply pre-planning coordination and decompose a global task into individual sub-tasks that agents can solve independently [38]. The underlying goal is to find a minimal set of precedence constraints that guarantees autonomous planning. The complexity of pre-planning coordination yields the problems intractable; however, reasonable solutions can be obtained by adding some additional constraints [39], or using approximation algorithms [38]. The work in [40] presents an application for ridesharing aimed at finding routes that travelers can share in order to save costs. The solution proposed by this work ensures that each individual is better off taking the shared ride rather than traveling alone.
In some MAP environments with multiple individual planning tasks, the aim is to determine the goals that each agent solves (soft goals) depending on the negative interactions with other agents. In [41], the authors propose a STRIPS model that calculates a solution plan by doing the inverse of the problem (the initial states of the agents are translated to soft goals, and the original goal of each agent to its initial state). This model represents the conflicts between the actions of the agents’ plans through a payoff matrix and finds an equilibrium for the whole problem goals or a part of them.
In [42], a preliminary formalization of equilibrium in multi-agent planning is introduced. MAP solutions are classified according to the agents’ possibility of reaching their goals and the paths of execution (combinations of local plans). However, this work has not been completely developed or empirically tested. Similarly, the work in [43] extends the classical planning model to multi-agent scenarios where agents perform online planning. Each agent wants to achieve its goals, but since planning is interleaved with execution, the feasibility of its actions is uncertain. Hence, agents decide which action to apply at each time step through a non-cooperative game. A “satisfaction profile” is defined to determine the possibilities that an agent has to achieve its goals when applying each action.
Non-cooperative MAP tasks can be seen as the coordination of the agents’ plans to come up with an executable joint plan. Agents have both cooperative interests (all agents want their plans fit together so as to ensure they are executable) as well as contradictory interests (every agent wants the execution of its plan to prevail over the others’ in case of conflict). Since agents are self-interested, stable (equilibrium) solution joint plans must be guaranteed so that no agent will deviate from the solution. We can distinguish different views to tackle non-cooperative MAP tasks aimed at synthesizing stable joint plans.
Best-Response Planning (BRP) [44] is an approach specifically devoted to solving the so-called congestion games [45], where the simultaneous use of a resource by multiple agents increases its cost. BRP is also applied to some planning domains for self-interested agents where convergence to equilibrium solutions is not guaranteed. In BRP, an initial conflict-free joint plan is calculated with the DisCSP cooperative planner [46]. Then, best-response dynamics, an iterative process in which each agent proposes its best plan considering the other agents plans, are applied in order to improve the initial solution. BRP is able to synthesize stable joint plans, where all agents achieve their goals, with remarkable performance in the presented experimental results with planning domains adapted to self-interested agents.
Agents in [47] have a limited set of precomputed plans that solve their planning tasks, and the MAP task of synthesizing a stable joint plan is solved with a two-game approach. One game determines the plan that each agent will use by computing an equilibrium. Each joint plan is scheduled through a second game where agents avoid planning conflicts by delaying the execution of their actions. Particularly, this game computes equilibrium solutions that are also Pareto Optimal (PO) [48] and fair, thus satisfying agents as much as possible. This is a significant novelty in the non-cooperative MAP literature.
A more recent work [49] models non-cooperative MAP as a general-sum game in which interactions such as conflicts and congestion are reflected in the agents’ utility. A tax is imposed to agents involved in conflicts to guarantee convergence using better-response planning. This approach is applied to a real-world transportation scenario that involves self-interested electric autonomous vehicles.
3. Abstract Framework
Although there has been significant research on non-cooperative MAP, there is a lack of a general system that contemplates the different phases in the resolution of this type of problems while considering different implementations of each of the phases. In general, we identify the following phases to be considered for an abstract framework: goal allocation, strategic planning, execution of the plans, and results storage for the reuse of plans or situations.
The assignment of goals is a crucial phase when there is a set of tasks to be carried out that must be distributed among the agents. Since the agents are self-interested, each one has his own preferences to solve goals that can bring him more or less benefit. Therefore, since there is this disparity and collision between the interests of the agents, the system must be provided with a mechanism that regulates the strategic behavior of the self-interested agents. This phase is only necessary when the goals are not pre-assigned, depending on the nature of the problem to be solved.
In a context with self-interested planning agents, it is necessary to consider a system in which strategic behavior is allowed when proposing individual plans in a shared environment. Therefore, it is necessary to provide the system with a mechanism that guarantees that an equilibrium is reached from which no agent deviates to ensure a satisfactory execution of the plans.
In many non-cooperative MAP works, the execution part is obviated. While this fact is not an impediment in many approaches, in other cases, it can be a problem since it does not allow for proving that the system works as expected. Therefore, in order to have a complete framework, it is necessary to have the execution part of the agents’ plans once an equilibrium has been reached, either executing the plans in a simulator or in a real environment. This ensures that the agreed solution works, and if it fails, the system can be fed back so that it does not happen again.
In systems where the same type of problems are periodically addressed, storing past information can improve both performance and quality by using this experience to alleviate the burden on planning and even avoid past failures. It is therefore advisable to use a storage system that allows agents to learn individually. A suitable alternative is Case-Based Planning (CBP) [50,51], as we propose in this framework, although other alternatives can be considered.
To the best of our knowledge, there is not any proposal of an abstract framework that accounts for a complete process within the phases explained above to solve non-cooperative MAP problems in a non-strictly competitive setting. Therefore, the aim of this work is to propose an abstract framework for strategic multi-agent planning using case-based planning.
It is important to note that there are framework proposals in classical planning that take into account most phases of a complete planning problem, such as planning, execution, monitoring, and learning [52,53,54]. More recent works [55,56] offer a system that considers both decentralised multi-agent planning and execution stages, mainly focused on run-time planning (i.e., online planning). Nevertheless, all these approaches do not consider non-cooperative MAP tasks and therefore are out of the scope of this work.
The abstract framework we propose in this work has different phases to solve non-cooperative MAP problems in a non-strictly competitive setting. Considering that the agents are self-interested, it is necessary to provide the framework with a goal allocation mechanism and also with a strategic planning system to obtain plans in equilibrium, thus allowing their strategic behavior. In addition, the execution phase of these plans is also included, as well as the results storage in order to feedback the system, allowing learning in the agents. These four phases of the abstract framework, depicted in the diagram of Figure 2, are summarized below:

Figure 2.
General diagram of the abstract framework.
- Goal allocation: This is the initial phase of the whole process. The goals to solve are distributed among the agents depending on the utility that report to each agent, that is, the preferences of the agents. This phase can be performed using different techniques such as auction protocols, or equivalent game-theoretic methods. This phase can be considered optional if the problem goals have a pre-established distribution among agents.
- Strategic planning: Each agent, by arbitrary turns, plans using its own CBP system or planner in order to come up with a plan that achieves all of its goals . This is done using the well-known game-theoretic technique best response [6] [Chapter 3], in which each agent iteratively best respond to the strategies of the other agents in its turn since a convergence point is reached, which is by definition a pure Nash equilibrium [57].
- Execution of the plans: The solution obtained in the previous phase in which each agent has its own plan is executed in a simulator that recreates a real scenario or, if possible, the solution is executed in the real world.
- Results storing: The results from the execution of the agents’ plans are gathered in order to improve the knowledge of the agents to generate better plans in the future. This updates their case bases (if a CBP is used) or their storage systems, which means they learn from experience.
4. Instantiated Framework
In this section, we explain in detail each of the phases that comprise the abstract framework and also the particular instantiation for each of the phases. However, the proposed instantiation belongs to our particular interpretation of the abstract framework. This implies that we leave open the use of different systems for each one of the phases, while our proposal is a suggestion that tries to take advantage of each one of the particularities of the phases with the objective of improving the global quality of the system.
A diagram representing our instantiated framework is depicted in Figure 3. Concretely, we propose the use of auction protocols for the goal allocation phase; best-response dynamics, with a CBP system for each agent, for the strategic planning phase; a simulator for the execution phase; and the corresponding stages of the CBP for the results storage phase.
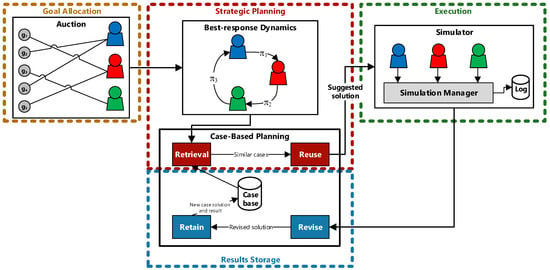
Figure 3.
Diagram of the instantiated framework.
4.1. Goal Allocation
In this paper, we assume goal allocation as the distribution of a set of goals among the different agents of the system. Depending on the type of problems, it might not be necessary to carry out this phase if there was already a previous distribution of the goals among the agents for any reason. However, when there is no pre-established distribution, and considering that the agents are self-interested, it is necessary to provide the system with a mechanism that allows goal allocation in a strategic way, that is, taking into account the preferences of the agents and their possible utility. We propose to use auctions or similar game-theoretic models for the goal allocation process.
An auction is a mechanism by which a set of goods is distributed to the highest bidder. There is a line of research in economics devoted to auction theory where the way in which people act in auctions and the properties of auctions are studied [58,59]. Auctions are regulated by a set of rules, and auction theorists seek to improve the efficiency of auctions as well as to promote optimal and equilibrium bidding strategies.
The goal allocation in the framework can be done with some system inspired by that of the works [32,36]. In both works, auction mechanisms are used to distribute the goals among the agents but trying to satisfy their private interests. However, we would have to consider a modification with respect to the work of [32] since it uses the sum of the utilities of the agents, that is, the utilitarian social welfare, whereas, in our framework of non-cooperative MAP, we do not seek to satisfy a global measure, but individual, which would be more similar to an equilibrium. Another interesting work that could inspire the goal allocation needed in our framework is the one presented in [60], which uses consensus-based auction algorithms for task allocation of autonomous vehicles fleets. However, an adaptation would be also needed since that work is intended to be applied in task allocation, which is slightly different from our target of goal allocation.
In the instantiation that we propose for the abstract framework, whose diagram is depicted in Figure 3, the goal allocation phase is performed with an auction in which the agents bid for each of the goals to solve until having all goals allocated. Then, the strategic planning phase can start.
4.2. Strategic Planning
Since the agents of the proposed framework are self-interested and, given the nature of non-cooperative MAP problems, it is necessary to provide the system with a game-theoretic mechanism for the analysis of the different situations of conflict of interest between the agents. Therefore, in this framework, we intend to promote strategic planning.
Although the abstract nature of this framework allows the use of any game theory technique that the user deems appropriate, we propose, by default, to use best-response dynamics. The agents, in turns, propose the plan they intend to execute, taking into account the plans of the other agents so as not to incur in conflicts or congestion by the concurrent use of a resource that prevent them from executing the plan or that cause them a decrease in the, a priori, expected utility [45]. The main advantage of this mechanism is that it corresponds to the natural way of dealing with problems by a group of parties who do not fully agree. Another advantage of best-response dynamics is that there is a guarantee that a solution will converge at some point, and that this solution will be a pure Nash equilibrium (PNE) [57]. Thus, none of the agents will deviate from such an equilibrium solution during execution as this would potentially imply a reduction of their own utility and that of others. This is guaranteed if the problem is formulated as a potential game since any finite potential game [61] will converge with best-response dynamics to a PNE regardless of the cost functions (e.g., they do not need to be monotonic).
Additionally, it is possible to use better-response dynamics instead of best-response dynamics since it is not necessary that agents best respond at every step. This means that better-response dynamics converge to a PNE in a finite number of steps as long as agents deviate to a better response Chapter 6 in [6]. Moreover, a better-response strategy can be implemented by an agent by randomly sampling another plan until one is found with a lower cost than the current plan’s and hence, it does not require that the agent knows the cost of every plan in its search space [62]. The possibility of using better-response dynamics offers the alternative of having a planning system that does not necessarily come up with the best plan in each situation, since it is enough to propose a plan that improves the current one (if such plan exists). Therefore, every potential game has at least one outcome that is a PNE, and better-response (or best-response) dynamics always converges to a PNE in any finite potential game Chapter 6 in [6], Chapter 19 in [7].
The best(better)-response dynamics process consists of the following steps:
- An arbitrary order is established among the agents to submit their proposals in turns.
- Each agent i in his own turn proposes the best plan that he can (or that improves the previous one if it is better-response dynamics) depending on the plans that are currently proposed by the other agents (if there are any). If the agent had already proposed a plan and this is the best one he can propose in the current situation, he would not propose any new plan.
- The previous step is repeated until in a complete iteration none of the agents proposes a new plan. When this situation arises, the process of best(better)-response dynamics has converged to a solution, which is the combination of the plans of the agents that they have currently proposed. As we have already mentioned, this solution is guaranteed to be a PNE.
In the diagram depicted in Figure 3, best(better)-response dynamics are represented inside the strategic planning phase, which is performed after the goal allocation phase. In addition, each agent in the best(better)-response dynamics uses its own CBP, concretely the retrieval and reuse stages, to come up with plans that solve their goals in the current situation of the best-response dynamics.
Regarding the planning system of the abstract framework, we propose to use Case-Based Planning. However, any planner could be used. It is important to note each agent must be provided with its own planning system, as can be deducted from how best-response dynamics works.
Case-Based Planning (CBP) [50,51] is based directly on the well-known Case-Based Reasoning (CBR) [63,64]. In general, a CBR system acts as a case base created from experience. In this way, when a new problem has to be solved, a problem with similar characteristics that was already solved in the past in the case base is looked for, and thus the same solution that worked previously is applied. The previous solution may be applied directly or may need some adjustments for the current situation. Finally, a new case is created or the existing case is updated with the results obtained from the application of the solution, whether the result was positive or negative.
A CBP system is a specialization of a CBR system. The particularity of a CBP system is that the cases, in general, are descriptions of the state of the planning world (initial state and final state) and the solutions are the plans applied to reach the final or goal state [50]. CBP is defined as “the idea of planning as remembering” [51].
The advantages of a CBP system over the use of a planner are remarkable. On the one hand, solutions to previous problems can be reused efficiently. On the other hand, storing the generated knowledge keeps the agent up to date. These advantages result in improved performance by avoiding planning to get a previously used plan, especially in an environment where similar problems can be repeated. In addition, the system can be learning or varying its knowledge depending on how the environment evolves both over time and also influenced by other agents.
As in CBR, the main stages of CBP are:
- retrieve: given a description of the problem (initial state) a case with a similar description is searched in the case base using a similarity algorithm and establishing a minimum coincidence threshold. Matching cases according to these criteria are extracted in order to be used to solve the current problem.
- reuse: in this step, the necessary modifications are made to the solution (plan) of the chosen case so that it is applicable to the current situation (initial state).
- revise: this stage consists of revising the solution to check its validity.
- retain: a new case is added to the case base with the problem solved in this iteration, or an existing case is updated with the solution used in this occasion.
In this framework, CBP stages take place at different phases of the framework. On the one hand, the retrieve and reuse stages are used during the best-response process when the CBP system is asked for a plan that suits current requirements. On the other hand, the revise and retain stages are performed after execution phase, i.e., during the results storage phase. All these processes and information flow are represented in Figure 3, where the best-response dynamics process is connected to each of the CBP systems of the agents. Then, the solution that proposes each agent through its CBP system after the best-response dynamics process converged is sent to be executed in the simulator.
4.3. Execution of the Plans
The execution of the plans is an important part in some contexts of automated planning and scheduling research. The execution consists of carrying out the actions of the plan in the specified instants of time or schedule, either in the real environment or in a simulated environment [52].
The execution in a real environment is the ideal case of the planning since it allows for corroborating that the computed plans are applicable to the real world. Therefore, whenever possible, it is advisable to execute the plans in the real environment and hence the results collected and the learning derived from these data can lead to much more positive feedback to ultimately improve the planning process.
While a real environment allows execution to be tested in the real world, making results more reliable, execution in a simulated environment provides other advantages. On the one hand, preparing and executing different problems can be less costly in both time and resources, so many more tests can be performed. On the other hand, collecting data in a simulated environment can be simpler and more effective than in many real environments. Then, all of this leads to cost savings in the application of different execution tests.
The ideal situation to take a significant advantage of a simulator would be to launch many problems and thus the case bases of the agents can be populated with many experiences. Then, all this knowledge could be applied to the real environment, yielding very positive results from the beginning. Therefore, the simulator could be considered a training before running the system in the real environment. This will avoid the well-known problem named cold start, which represents the issues derived from starting a system without enough data in the case bases of the agents.
In the case of the framework that we propose, whether the execution is in a real environment or in a simulated environment, the crucial part is the collection of data from that execution. With this data, the whole system can be improved since the agents can learn individually whether their plans have worked as they expected or not. If a CBP system is used, the feedback is done in the retain stage, and CBP’s own mechanisms (inherited from CBR systems) manage the learning by creating new cases or updating some of the existing ones in both positive and negative results. For other planning proposals that do not include a CBP system in the proposed framework, learning is subject to the type of planning mechanism used and its possibilities for including learning.
Our proposal in the instantiated framework depicted in Figure 3 is the use of a simulator for the execution phase. As we mentioned above, it is a simple way to be able to run a set of problems easily and getting a large collection of results that the agents can learn from.
4.4. Results Storage
A crucial part of the framework is the results storage as it allows individual agents to keep track of what has happened in past problems. Since the framework is designed to solve a set of problems, it offers the above-mentioned advantages of reusing past solutions that can improve both the quality of the plans and the efficiency of the system. In addition, this also implies that agents learn and modify their knowledge, thus evolving at the same time as their environment.
The results storage can be done in different ways; however, it is necessary to have a system in which such data can be easily reused by the agents to be really helpful.
As mentioned before, a CBP system provides such advantages since it stores data from previous iterations so that it can be easily reused in the future. The stages of the CBP system that act in this phase of the framework are revise and retain. The revise stage is in charge of checking that the solution applied has worked as expected. On the other hand, the retain stage is in charge of saving the data by creating a new case or modifying an existing one, whether the result was positive or not.
Therefore, we could consider that, in our instantiation of the framework, there is a cycle or dependency relation between the strategic planning phase and the results storage phase since the CBP system acts in both cases using its different stages. This relation can be seen in Figure 3, where the stages revise and retain of the CBP system of each agent belong to the results storage phase and collect the results from the simulation, while the retrieve and reuse stages of the CBP system of each agent belong to the strategic planning phase of the framework.
5. Case Study
In this section, we present a case study in which the abstract framework introduced in this work with a specific instantiation is applied. Particularly, this case study shows each of the phases of the framework using a specific technology or system.
This case study consists of a logistical problem in which a series of trucks must carry packages from the point of origin of each package to its corresponding destination. Trucks represent self-interested agents with the particularity that they all belong to the same company, which implies that they have common interests because they do not seek to hurt others, but receive a reward depending on the packages delivered, which is understood as contrary interests. Thus, the nature of the problem determines that it is necessary to use a non-cooperative MAP system in a non-strictly competitive setting, since the profit of one agent does not necessarily imply a loss in the other agents, but all have their private interests.
The problem to be solved in this case study consists of three trucks that are self-interested agents that we will call A, B, and C, respectively. These trucks must deliver three packages, taking them from their place of origin to their corresponding destination. Figure 4 shows the distribution of the truck agents and packages in a representation of a city map. Concretely, a square represents the package origin position and a dotted circle represents the destination of the package. The lines in different colors represent the possible routes to deliver the packages. Therefore, the goals for which the agents compete in this case are the packages, since completing a goal gives them a reward, while movements without cargo only incur costs but not profits. In this way, agents will try to minimize movements without cargo, while trying to solve as many goals as they can. In this case study, we also take into account the congestion caused by using the same road at the same instant of time. Note that we make a simplification of this to have an illustrative example, as only two trucks should not cause congestion in the general case. In addition, in more complex problems where the use of petrol stations or electric vehicle charging stations is included, other types of congestion could appear due to concurrent use. However, in this case study, we want a simple example to show how the framework works with a prototypical problem.
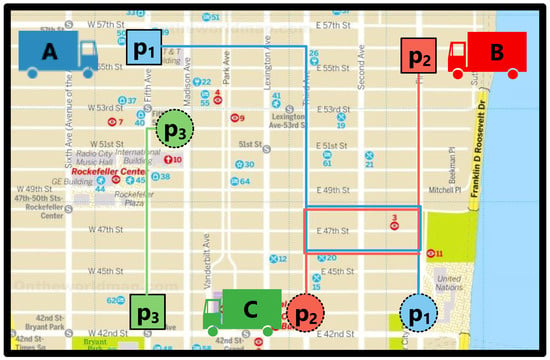
Figure 4.
Case study example.
5.1. Goal Allocation
First, goal allocation is performed through an auction system. In this way, truck agents can bid for the goals they are most interested in based mainly on the distance of origin of the package and the current position of the truck. We assume that the payment or reward they receive for packages is proportional to the distance between the origin and destination of the package, so we can consider that there are no particular or superior incentives for specific packages. In other words, all packages are worth the same depending on the route to be taken to deliver it. This implies that the agents will prioritize the packages that are closest to them and those that come to them in passing with other deliveries.
The goal allocation problem is similar to what is traditionally called resource allocation. Thus, the Bertsekas auction algorithm [65,66] can be used to solve the goal allocation in our framework. This algorithm can be used when there are n agents and m goals to assign (with ). Each goal can be assigned to an agent with a certain cost and the main objective of the process is to minimize the total cost of the global assignment. The idea of this algorithm is that agents bid for their preferred goal (the least expensive) and the value of that bid is the difference between the best cost and the second best cost (for this agent). In addition, each goal has a price (which starts at 0), and, if there are several agents who want the same goal, it increases in price. A goal is assigned to an agent if the agent’s bid is the highest. This process is repeated until all goals are assigned.
Based on the representation of Figure 4 of this case study, we assume that the costs of each of the agents associated with the delivery of each of the packages are those shown in Table 1. Therefore, it is easy to assume the allocation that will be made considering the costs. It should be noted that these costs are proportional to the distance between the agent and the point of origin of the package, as well as the distance to take the package from its origin to its destination. Once the Bertsekas auction algorithm has been applied (for simplicity’s sake, we obviate its application), agent A would be assigned the package , agent B the package , and package would be assigned to agent C.

Table 1.
Costs of each agent to deliver each package .
5.2. Strategic Planning
The strategic planning phase involves two systems. On the one hand, we use best-response dynamics to manage the strategic behavior of the agents, allowing them to make their proposals until a convergence point is reached, which is by definition a Nash equilibrium. On the other hand, each agent is provided with a CBP system that allows him to obtain plans to solve the problem based on past experiences. In the following, we explain how both systems are used in this case study.
An arbitrary order is chosen among the truck agents. Let’s assume the order is A, B, and C, for simplicity. Then, each truck agent, in turns, proposes, by retrieving a plan from its case base, the best plan to solve his goals considering the plans of the other agents (if any). This means that the plan of an agent can affect another if there is any congestion that may decrease the expected utility because the cost of the simultaneous use of a road is increased (i.e., fuel/battery consumption increases and/or travel time increases). The best-response dynamics process takes place as follows:
- Agent A retrieves the case/plan that best matches with the problem to solve with a similarity of . The past case match with the current problem of delivering package since the origin and destination are almost the same with a slight deviation. Since there is no agent who has proposed his plan yet, there is no interaction, so, for agent A, this extracted plan is his best option.
- Agent B also retrieves the best plan/case to solve his goal with a similarity degree of . However, this plan introduces a congestion with the current plan of agent A for the simultaneous use of a road (see the rectangle area of blue and red lines in Figure 4 where the paths of both trucks can overlap). Although agent B is causing a congestion that reduces the expected utility to both agent A and agent B, plan still has more utility than the next alternative in his case base because it has a longer path at a higher cost. Thus, from a rational point of view, agent B prefers in congestion rather than another lower utility alternative that avoids congestion like .
- Agent C retrieves the best plan of his case base to solve his goal of delivering package with a similarity of . Since agent C does not have any interaction with the other agents, he can apply his plan with the expected utility, while also not affecting the utility of other agents.
- Agent A analyzes its current proposed plan which is affected by a congestion with agent B for the simultaneous use of a road. Using his CBP system is able to retrieve another case/plan with a similarity of to the current problem to solve, which is lower than the similarity of (). However, the similarity only refers to how similar one case is to another, but does not take into account how another agent’s plan may affect it (i.e., congestion interactions). Therefore, although the new case with a similarity of may have a lower utility a priori, it is actually higher than the utility of the previous plan , since, in that case, this utility is affected by the congestion and ends up being lower. Thus, agent A changes his proposed plan from to , with a slightly higher utility, which is in this moment his best response.
- Agent B analyzes his current plan and realizes that the congestion that existed with agent A has disappeared because agent A has changed his plan. Thus, the utility of has increased slightly with respect to the previous iteration. This implies that he still has his best plan and does not want to change it for another, which means that he is in best response.
- Agent C is already in best response since he previously proposed his best plan and he has no interactions with the other agents. Hence, he does not change his proposal.
- Agent A cannot generate a better plan than he already has, so we can say he is satisfied with the current one, which means he is in best response. Therefore, since none of the agents has changed their plan during an entire iteration, the best response process can be considered completed since a convergence point has been reached. At this point, the solution formed by the agents’ plans is a Nash equilibrium.
5.3. Execution of the Plans
For the execution phase of the framework, a simulator like the one proposed in [67] would be used. The solution of the previous phase, which is a Nash equilibrium, consists of a plan per agent to be executed. The main objective of this phase is to check the viability of previously agreed plans in a realistic environment, in this case a simulator.
In this case study, we assume the results of the execution of the plans in the simulator in order to provide the reader with an illustrative example of what could happen during this phase.
From the perspective of each agent, there are two main scenarios resulting from the simulation. On the one hand, it may happen that the execution of the plan is done as planned, without incidents, which means that the agent would receive the expected utility. This is the ideal scenario and would endorse the application of the plan for the solved problem. On the other hand, it may happen that the execution of the plan fails and the goal cannot be reached, or that the final utility is less than expected due to factors that have not been considered. In this situation, the simulator cannot provide any alternative (unless a replanning mechanism in execution is applied) and must simply provide as much information as possible to understand and reflect the execution failure so that it can be incorporated into the corresponding case of the case base.
5.4. Results Storage
This phase is intimately linked to the previous phase as the results of the execution, both positive and negative, should be reflected in the case bases of the agents in order to learn from experience.
For each agent of the problem, in the case that the result of the execution is positive and everything has occurred as expected in the plan, the case base would be updated by modifying the case used to add some indicator of the success rate of the case or some slight modification of it (some action that may have changed, which, depending on how the cases were defined, this change may imply a new case). This would occur in the stages revise and retain of the CBP system, the revise stage where the applied case is analyzed with its possible modifications, and the retain stage where all this information is stored in the case.
On the other hand, if the result of the execution is negative, that is, there has occurred some inconvenience by which either the final utility has been less than expected or directly the plan has not been able to finish, this result would also be stored in the same way as the previous one. Thus, this failure would be noted in the case and, if possible, the reason for the failure, to prevent it from being used in the future.
Finally, depending on the CBP system that is used and if it allows the generation of new plans (perhaps by combining it with a planner), it could happen that the plan used in execution was not yet in the case base. Therefore, this plan would become a new case and would be introduced in the case base for later use.
It should be noted that the use of this system is designed for a large set of problems that are solved continuously or sequentially. Therefore, depending on the execution phase with a simulator (or the real world in its case), any failure in the execution of the plans does not imply anything wrong, as long as it can represent a change in the conditions of the environment that would end up being reflected in the base cases of the agents. Thus, the case bases of the agents’ CBP systems would evolve together with the environment to reflect the current situation. This is an advantage to be exploited over the proposed system when using CBP.
6. Conclusions
In this paper, we presented an abstract framework for solving non-cooperative MAP problems in a non-strictly competitive setting. These types of problems represent a large number of real-life situations that are not yet addressed from the point of view of the non-cooperative MAP. Among the problems of this type are the strategic regulation of traffic, the management of self-interested urban fleets, open fleets of delivery services, among others.
An exhaustive study of non-cooperative MAP works was carried out to identify the different phases that we considered crucial to solve non-cooperative MAP problems. Hence, in the absence of any abstract framework that includes the goal allocation, strategic planning, execution and results storage phases, we made our proposal with the intention of filling this gap.
In addition, a specific instantiation of this framework was also proposed in which a type of system or paradigm is suggested for each phase of the framework. Therefore, the suggested instantiation is the one we consider the most suitable to take advantage of all the benefits that the framework can offer. Nevertheless, it is important to note that any user of the abstract framework is able to use alternative systems or mechanisms in the different phases.
The main advantages of the proposed framework are as follows. On the one hand, all phases are available together in a complete non-cooperative MAP problem solving system. On the other hand, with this proposal, a gap is filled attending to the need of the research community for the complete resolution of non-cooperative MAP problems in a non-strictly competitive setting. In addition, the implementation of this framework can be done using the techniques or technologies described in this paper that are currently available.
Finally, a case study has been presented that provides an example of solving a complete problem typical of non-cooperative MAP in a logistical context. This case study illustrates the feasibility of implementing the proposed abstract framework as well as its value for solving this type of problems.
As a future work, we plan to implement some of the proposed phases in an initial approach and, subsequently, we will be able to have a complete implementation of the entire framework, given the complexity of each of the phases and their combination.
Author Contributions
Conceptualization, J.J.; Formal analysis, J.J.; Investigation, J.J.; Methodology, J.B.; Project administration, V.J.; Supervision, J.B., V.B. and V.J.; Writing—original draft, J.J.; Writing—review and editing, J.J., J.B., V.B. and V.J.
Funding
This work was partially funded by MINECO/FEDER RTI2018-095390-B-C31 project of the Spanish government. Jaume Jordán and Vicent Botti are funded by Universitat Politècnica de València (UPV) PAID-06-18 project. Jaume Jordán is also funded by grant APOSTD/2018/010 of Generalitat Valenciana Fondo Social Europeo.
Conflicts of Interest
The authors declare no conflict of interest. The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Weerdt, M.D.; Clement, B. Introduction to Planning in Multiagent Systems. Multiagent Grid Syst. 2009, 5, 345–355. [Google Scholar] [CrossRef]
- Brafman, R.I.; Domshlak, C.; Engel, Y.; Tennenholtz, M. Planning Games. In Proceedings of the 21st International Joint Conference on Artificial Intelligence (IJCAI), Pasadena, CA, USA, 11–17 July 2009; pp. 73–78. [Google Scholar]
- Dunne, P.E.; Kraus, S.; Manisterski, E.; Wooldridge, M. Solving Coalitional Resource Games. Artif. Intell. 2010, 174, 20–50. [Google Scholar] [CrossRef]
- Bercher, P.; Mattmüller, R. A Planning Graph Heuristic for Forward-Chaining Adversarial Planning. In Proceedings of the European Conference on Artificial Intelligence, Patras, Greece, 21–25 July 2008; Volume 8, pp. 921–922. [Google Scholar]
- Cote, E.M.D.; Chapman, A.; Sykulski, A.M.; Jennings, N. Automated Planning in Repeated Adversarial Games. In Proceedings of the Proceedings of the 26th Conference on Uncertainty in Artificial Intelligence (UAI 2010), Catalina Island, CA, USA, 8–11 July 2010; pp. 376–383. [Google Scholar]
- Shoham, Y.; Leyton-Brown, K. Multiagent Systems: Algorithmic, Game-Theoretic, and Logical Foundations; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Nisan, N.; Roughgarden, T.; Tardos, E.; Vazirani, V. Algorithmic Game Theory; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Torreño, A.; Onaindia, E.; Komenda, A.; Štolba, M. Cooperative multi-agent planning: A survey. ACM Comput. Surv. (CSUR) 2018, 50, 84. [Google Scholar] [CrossRef]
- Amato, C.; Konidaris, G.; Cruz, G.; Maynor, C.A.; How, J.P.; Kaelbling, L.P. Planning for decentralized control of multiple robots under uncertainty. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 1241–1248. [Google Scholar]
- Ontanón, S.; Buro, M. Adversarial hierarchical-task network planning for complex real-time games. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar]
- Myerson, R.B. Game Theory; Harvard University Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Osborne, M.J.; Rubinstein, A. A Course in Game Theory; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Brandenburger, A. Cooperative Game Theory; Teaching Materials at New York University; New York University: New York, NY, USA, 2007. [Google Scholar]
- Fikes, R.; Nilsson, N. STRIPS: A New Approach to the Application of Theorem Proving to Problem Solving. Artif. Intell. 1971, 2, 189–208. [Google Scholar] [CrossRef]
- Crosby, M.; Rovatsos, M. Heuristic Multiagent Planning With Self-Interested Agents. In Proceedings of the 10th International Conference on Autonomous Agents and Multiagent Systems (AAMAS), Taipei, Taiwan, 2–6 May 2011; Volume 1–3, pp. 1213–1214. [Google Scholar]
- Hoffmann, J.; Nebel, B. The FF Planning System: Fast Planning Generation Through Heuristic Search. J. Artif. Intell. Res. 2001, 14, 253–302. [Google Scholar] [CrossRef]
- Dukeman, A.; Adams, J.A. Hybrid mission planning with coalition formation. Auton. Agents-Multi-Agent Syst. 2017, 31, 1424–1466. [Google Scholar] [CrossRef]
- Hadad, M.; Kraus, S.; Hartman, I.B.A.; Rosenfeld, A. Group Planning With Time Constraints. Ann. Math. Artif. Intell. 2013, 69, 243–291. [Google Scholar] [CrossRef]
- Guo, Y.; Pan, Q.; Sun, Q.; Zhao, C.; Wang, D.; Feng, M. Cooperative Game-based Multi-Agent Path Planning with Obstacle Avoidance. In Proceedings of the IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; pp. 1385–1390. [Google Scholar] [CrossRef]
- Von Neumann, J. Zur Theorie Der Gesellschaftsspiele. Math. Ann. 1928, 100, 295–320. [Google Scholar] [CrossRef]
- Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Mookherjee, D.; Sopher, B. Learning Behavior in an Experimental Matching Pennies Game. Games Econ. Behav. 1994, 7, 62–91. [Google Scholar] [CrossRef]
- Ochs, J. Games With Unique, Mixed Strategy Equilibria: An Experimental Study. Games Econ. Behav. 1995, 10, 202–217. [Google Scholar] [CrossRef]
- Applegate, C.; Elsaesser, C.; Sanborn, J. An Architecture for Adversarial Planning. IEEE Trans. Syst. Man Cybern. 1990, 20, 186–194. [Google Scholar] [CrossRef]
- Jensen, R.M.; Veloso, M.M.; Bowling, M.H. OBDD-Based Optimistic and Strong Cyclic Adversarial Planning. In Proceedings of the 6th European Conference on Planning, Toledo, Spain, 12–14 September 2001; pp. 265–276. [Google Scholar]
- Sailer, F.; Buro, M.; Lanctot, M. Adversarial Planning Through Strategy Simulation. In Proceedings of the 2007 IEEE Symposium on Computational Intelligence and Games, Honolulu, HI, USA, 1–5 April 2007; pp. 80–87. [Google Scholar] [CrossRef]
- Willmott, S.; Richardson, J.; Bundy, A.; Levine, J. An Adversarial Planning Approach to Go. In Proceedings of the International Conference on Computers and Games; Van Den Herik, H.J., Iida, H., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 93–112. [Google Scholar]
- Willmott, S.; Richardson, J.; Bundy, A.; Levine, J. Applying Adversarial Planning Techniques to Go. Theor. Comput. Sci. 2001, 252, 45–82. [Google Scholar] [CrossRef]
- Erol, K.; Hendler, J.; Nau, D.S. HTN Planning: Complexity and Expressivity; AAAI: Menlo Park, CA, USA, 1994; Volume 94, pp. 1123–1128. [Google Scholar]
- Nau, D.S.; Au, T.C.; Ilghami, O.; Kuter, U.; Murdock, J.W.; Wu, D.; Yaman, F. SHOP2: An HTN planning system. J. Artif. Intell. Res. 2003, 20, 379–404. [Google Scholar] [CrossRef]
- Knuth, D.E.; Moore, R.W. An Analysis of Alpha-Beta Pruning. Artif. Intell. 1975, 6, 293–326. [Google Scholar] [CrossRef]
- Nissim, R.; Brafman, R.I. Cost-Optimal Planning by Self-Interested Agents. In Proceedings of the 27th AAAI Conference on Artificial Intelligence, Bellevue, WA, USA, 14–18 July 2013; pp. 732–738. [Google Scholar]
- Vickrey, W. Counterspeculation, Auctions, and Competitive Sealed Tenders. J. Financ. 1961, 16, 8–37. [Google Scholar] [CrossRef]
- Clarke, E.H. Multipart Pricing of Public Goods. Public Choice 1971, 11, 17–33. [Google Scholar] [CrossRef]
- Groves, T. Incentives in Teams. Econometrica 1973, 41, 617–631. [Google Scholar] [CrossRef]
- Van Der Krogt, R.; De Weerdt, M. Self-Interested Planning Agents Using Plan Repair. In Proceedings of the ICAPS 2005 Workshop on Multiagent Planning and Scheduling, Monterey, CA, USA, 6–10 June 2005; pp. 36–44. [Google Scholar]
- Savaux, J.; Vion, J.; Piechowiak, S.; Mandiau, R.; Matsui, T.; Hirayama, K.; Yokoo, M.; Elmane, S.; Silaghi, M. DisCSPs with Privacy Recast as Planning Problems for Self-Interested Agents. In Proceedings of the IEEE/WIC/ACM International Conference on Web Intelligence (WI), Omaha, NE, USA, 13–16 October 2016; pp. 359–366. [Google Scholar] [CrossRef]
- Buzing, P.; Mors, A.T.; Valk, J.; Witteveen, C. Coordinating Self-Interested Planning Agents. Auton. Agents-Multi-Agent Syst. 2006, 12, 199–218. [Google Scholar] [CrossRef]
- Mors, A.T.; Witteveen, C. Coordinating Non Cooperative Planning Agents: Complexity Results. In Proceedings of the IEEE/WIC/ACM International Conference on Intelligent Agent Technology, Compiegne, France, 19–22 September 2005; pp. 407–413. [Google Scholar] [CrossRef]
- Hrnčíř, J.; Rovatsos, M.; Jakob, M. Ridesharing on Timetabled Transport Services: A Multiagent Planning Approach. J. Intell. Transp. Syst. 2015, 19, 89–105. [Google Scholar] [CrossRef]
- Galuszka, A.; Swierniak, A. Planning in Multi-Agent Environment Using Strips Representation and Non-Cooperative Equilibrium Strategy. J. Intell. Robot. Syst. 2010, 58, 239–251. [Google Scholar] [CrossRef]
- Bowling, M.H.; Jensen, R.M.; Veloso, M.M. A Formalization of Equilibria for Multiagent Planning. In Proceedings of the 18th International Joint Conference on Artificial Intelligence (IJCAI), Acapulco, Mexico, 9–15 August 2003; pp. 1460–1462. [Google Scholar]
- Larbi, R.B.; Konieczny, S.; Marquis, P. Extending Classical Planning to the Multi-Agent Case: A Game-Theoretic Approach. In Proceedings of the 9th European Conference Symbolic and Quantitative Approaches to Reasoning with Uncertainty, ECSQARU, Hammamet, Tunisia, 31 October–2 November 2007; pp. 731–742. [Google Scholar]
- Jonsson, A.; Rovatsos, M. Scaling Up Multiagent Planning: A Best-Response Approach. In Proceedings of the 21st International Conference on Automated Planning and Scheduling (ICAPS), Freiburg, Germany, 11–16 June 2011. [Google Scholar]
- Rosenthal, R.W. A class of games possessing pure-strategy Nash equilibria. Int. J. Game Theory 1973, 2, 65–67. [Google Scholar] [CrossRef]
- Nissim, R.; Brafman, R.I.; Domshlak, C. A General, Fully Distributed Multi-Agent Planning Algorithm. In Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems, Toronto, ON, Canada, 10–14 May 2010; pp. 1323–1330. [Google Scholar]
- Jordán, J.; Onaindía, E. Game-theoretic Approach for Non-Cooperative Planning. In Proceedings of the 29th AAAI Conference on Artificial Intelligence (AAAI-15), Austin, TX, USA, 25–30 January 2015; pp. 1357–1363. [Google Scholar]
- Arrow, K.J. Social Choice and Individual Values; Number 12; Yale University Press: New Haven, CT, USA, 1963. [Google Scholar]
- Jordán, J.; Torreño, A.; de Weerdt, M.; Onaindia, E. A better-response strategy for self-interested planning agents. Appl. Intell. 2018, 48, 1020–1040. [Google Scholar] [CrossRef]
- Veloso, M.; Muñoz-Avila, H.; Bergmann, R. Case-based planning: Selected methods and systems. AI Commun. 1996, 9, 128–137. [Google Scholar]
- Hammond, K.J. Case-Based Planning: Viewing Planning as a Memory Task; Elsevier: Amstelredam, The Netherlands, 2012. [Google Scholar]
- Ambros-Ingerson, J.A.; Steel, S. Integrating Planning, Execution and Monitoring; AAAI: Menlo Park, CA, USA, 1988; Volume 88, pp. 21–26. [Google Scholar]
- Sycara, K.; Pannu, A.S. The RETSINA multiagent system: Towards integrating planning, execution, and information gathering. In Proceedings of the Second International Conference on Autonomous Agents, Minneapolis, MN, USA, 10–13 May 1998. [Google Scholar]
- Haigh, K.Z.; Veloso, M.M. Planning, Execution and Learning in a Robotic Agent. In Proceedings of the Fourth International Conference on Artificial Intelligence Planning Systems, Pittsburgh, PA, USA, 7–10 June 1998; pp. 120–127. [Google Scholar]
- Cardoso, R.C.; Bordini, R.H. Decentralised Planning for Multi-Agent Programming Platforms. In Proceedings of the 18th International Conference on Autonomous Agents and MultiAgent Systems (AAMAS ’19), Montreal, QC, Canada, 13–17 May 2019; International Foundation for Autonomous Agents and Multiagent Systems: Richland, SC, USA, 2019; pp. 799–807. [Google Scholar]
- Cardoso, R.C.; Bordini, R.H. A distributed online multi-agent planning system. In Proceedings of the Workshop on Distributed and Mutiltiagent Planning (ICAPS), London, UK, 13–14 June 2016; pp. 15–23. [Google Scholar]
- Voorneveld, M.; Borm, P.; Van Megen, F.; Tijs, S.; Facchini, G. Congestion Games and Potentials Reconsidered. Int. Game Theory Rev. 1999, 01, 283–299. [Google Scholar] [CrossRef]
- Klemperer, P. Auctions: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2004. [Google Scholar]
- Krishna, V. Auction Theory; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Choi, H.; Brunet, L.; How, J.P. Consensus-Based Decentralized Auctions for Robust Task Allocation. IEEE Trans. Robot. 2009, 25, 912–926. [Google Scholar] [CrossRef]
- Monderer, D.; Shapley, L.S. Potential games. Games Econ. Behav. 1996, 14, 124–143. [Google Scholar] [CrossRef]
- Friedman, J.W.; Mezzetti, C. Learning in Games by Random Sampling. J. Econ. Theory 2001, 98, 55–84. [Google Scholar] [CrossRef]
- Aamodt, A.; Plaza, E. Case-based reasoning: Foundational issues, methodological variations, and system approaches. AI Commun. 1994, 7, 39–59. [Google Scholar]
- Kolodner, J. Case-Based Reasoning; Morgan Kaufmann: Burlington, MA, USA, 2014. [Google Scholar]
- Bertsekas, D.P. The auction algorithm: A distributed relaxation method for the assignment problem. Ann. Oper. Res. 1988, 14, 105–123. [Google Scholar] [CrossRef]
- Bertsekas, D.P.; Castanon, D.A. The auction algorithm for the transportation problem. Ann. Oper. Res. 1989, 20, 67–96. [Google Scholar] [CrossRef]
- Palanca, J.; Terrasa, A.; Carrascosa, C.; Julián, V. SimFleet: A New Transport Fleet Simulator Based on MAS. In Proceedings of the International Conference on Practical Applications of Agents and Multi-Agent Systems; Springer: Cham, Switzerland, 2019; pp. 257–264. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).