Tempo and Metrical Analysis by Tracking Multiple Metrical Levels Using Autocorrelation
Abstract
1. Introduction
2. Related Work
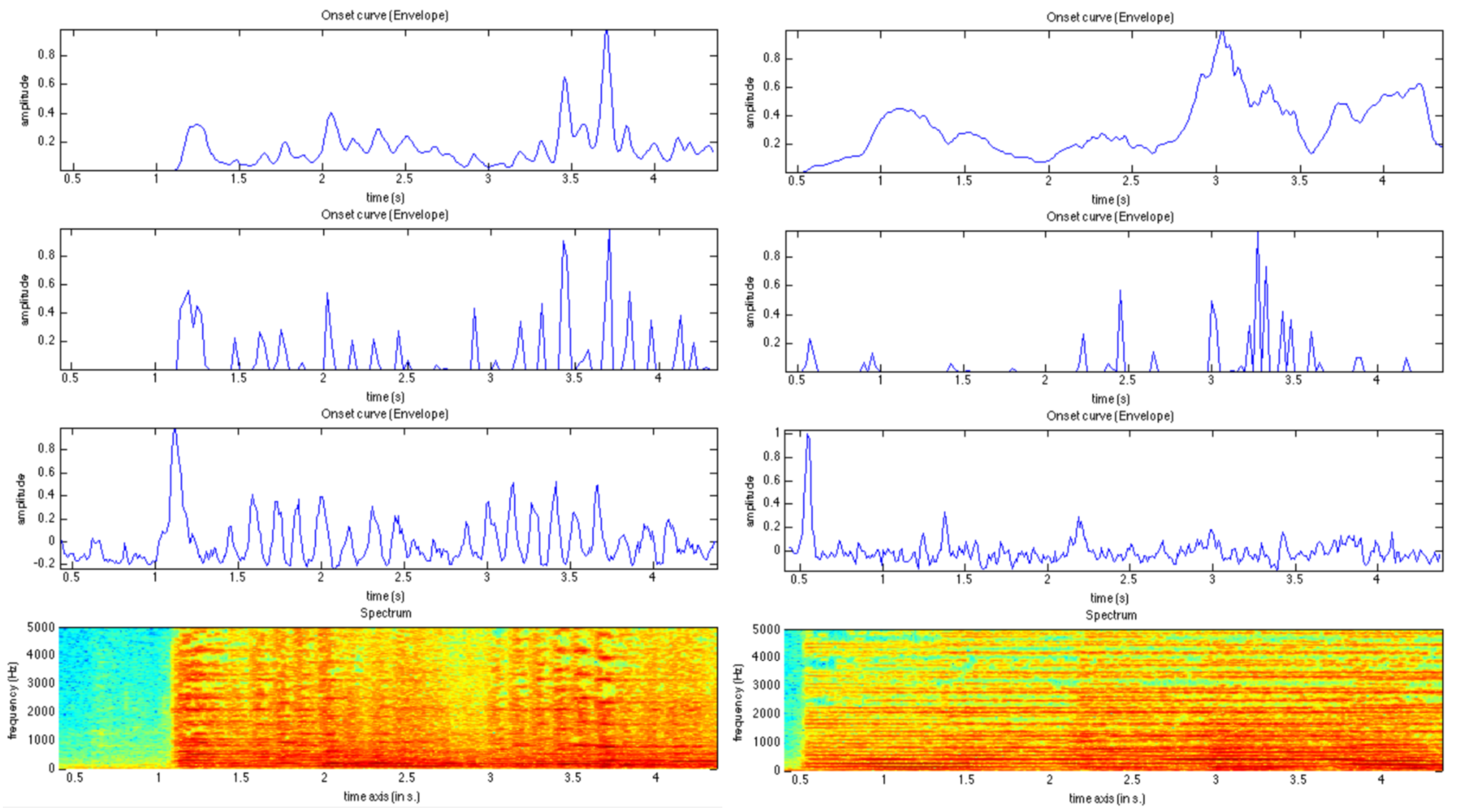
2.1. Accentuation Curve
2.1.1. Classical Methods
2.1.2. Localized Methods
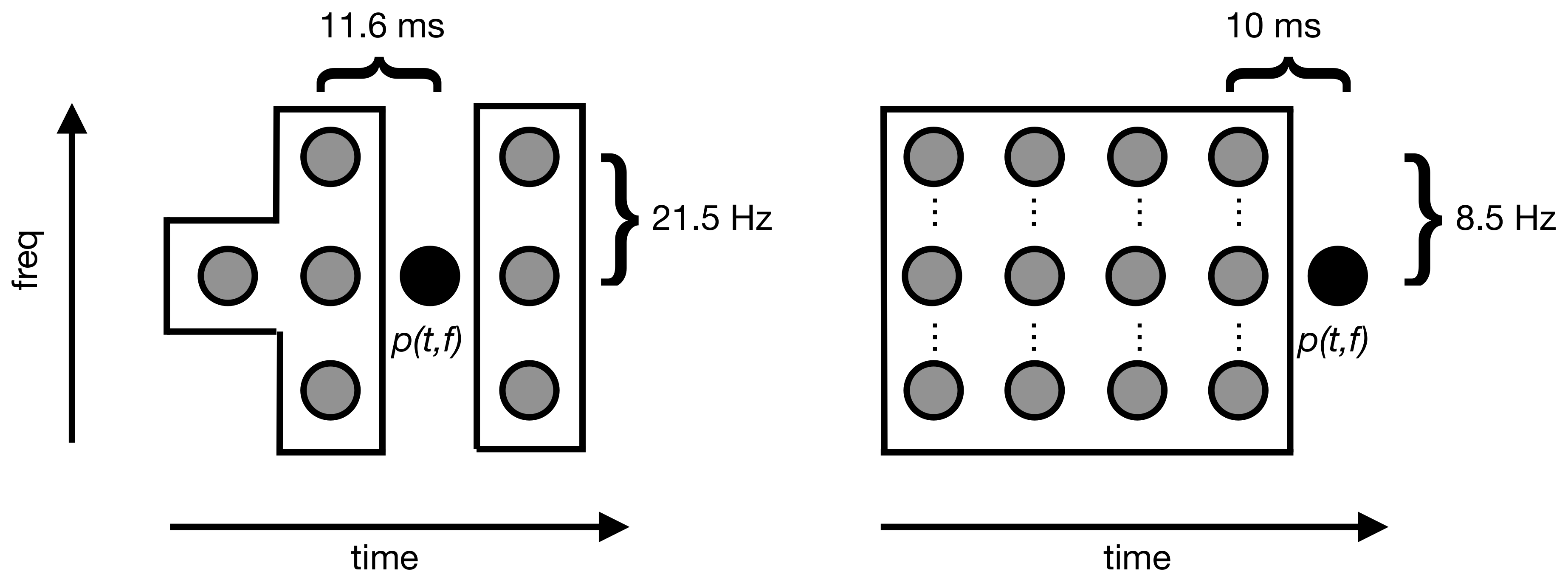
- The power of the spectral component at frequency f and time t, denoted , is higher than the power around the previous time frame at similar frequency:where is defined as follows:We propose to call this time-frequency region associated with contextual background at time t and frequency f. This is illustrated in Figure 3.
- The power at next time frame and similar frequency is higher than the power in the contextual background:where is given by the following definition:
2.2. Periodicity Analysis
2.3. Metrical Structure
- The tactus is considered to be the most prominent level, also referred as the foot-tapping rate or the beat. The tempo is often identified with the tactus level.
- The tatum—for “temporal atom”—is considered to be the fastest subdivision of the metrical hierarchy, such that all other metrical levels (in particular tactus and bar) are multiples of that tatum.
- The bar level or other metrical levels considered to be related to change of chords, melodic or rhythmic patterns, etc.
2.4. Deep-Learning Approaches
3. Proposed Method
- a tracking of the metrical grid featuring a large range of possible periodicities (Section 3.3). Instead of considering a fix and small number of pre-defined metrical levels, we propose to track a larger range of periodicity layers in parallel.
- a selection of core metrical levels, leading to a metrical structure, which enables the estimation of meter and tempo (Section 3.4).
3.1. Accentuation Curve
3.2. Periodicity Analysis
3.3. Tracking the Metrical Grid
3.3.1. Principles
- We first select a large set of periodicities inherent to the metrical structure, resulting in what we propose to call a metrical grid, where individual periodicities are called layers.
- We select, among those metrical layers, core metrical levels, where longer periods are multiple of shorter periods. Each other layers of the metrical grid is a multiple or submultiple of one metrical level. One metrical level is selected as the most prevalent, for the determination of tempo.
- theoretically, the temporal series of periods related to metrical layer i knowing the global tempo given by ;
- practically, the temporal series of lags effectively measured at peaks locations in the autocorrelation function.
3.3.2. Procedure
- For all the slower metrical layers i, we find those that have a theoretical period that is in integer ratio with the peak lag t:where is set to 0.02 if no other stronger peak in the current time frame n has been identified with the metrical grid, and else to 0.1 in the other case.If we find several of those slower periods in integer ratio, we select the fastest one, unless we find a slower one with a ratio defined in Equation (14) that would be closer to 0.
- Similarly, for all the faster metrical layers, i we find those that have a theoretical pulse lag that is in integer ratio with the peak lag:
- If we have found both a slower and a faster period, we select the one with stronger periodicity score.
- This metrical layer, of index , will be used as reference onto which the new discovered metrical layer is based. The new metrical index is defined as:
3.4. Metrical Structure
4. Experiments
4.1. Evaluation Campaigns Using Music with Constant Tempo
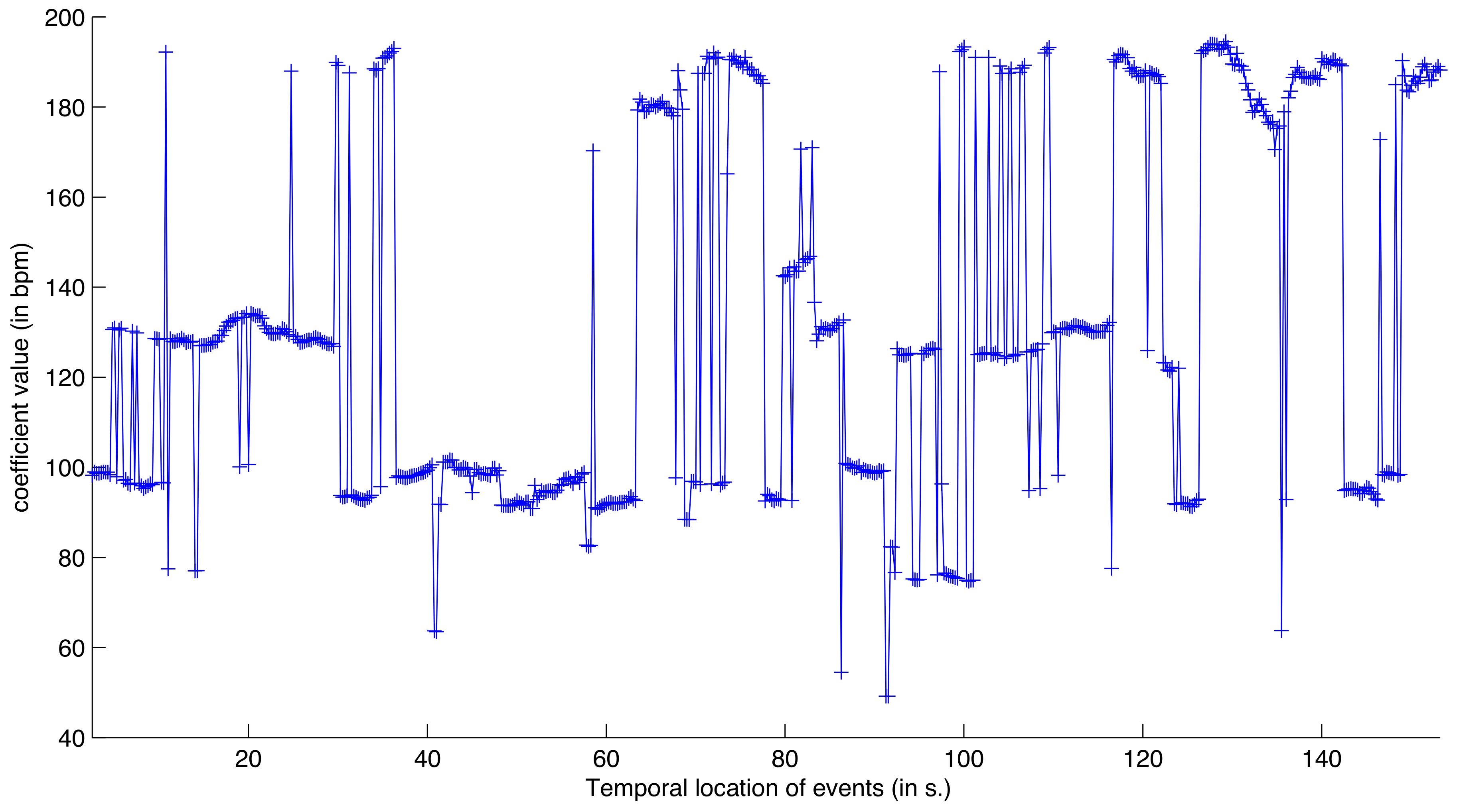
4.2. Assessment on Music with Variable Tempo
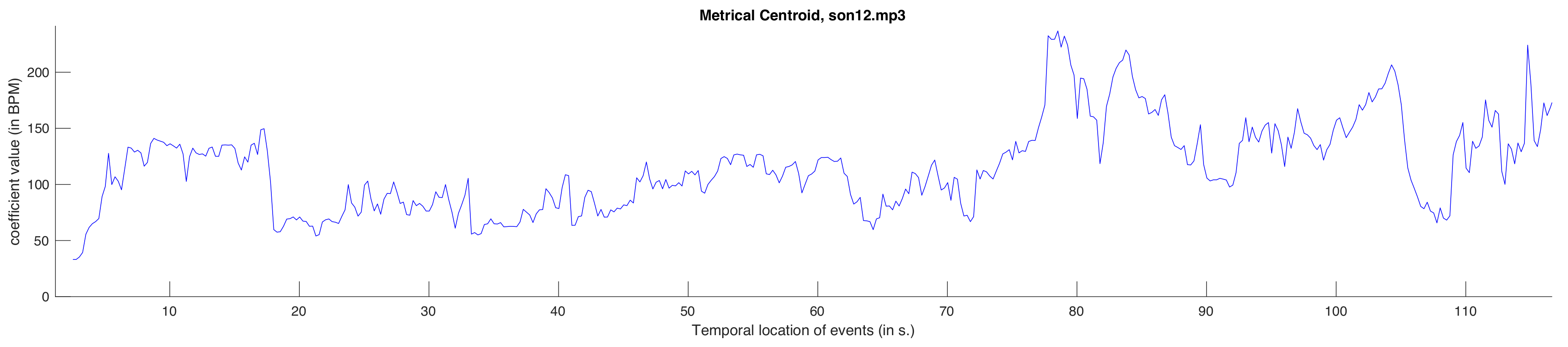
5. Metrical Description
6. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Böck, S.; Krebs, F.; Widmer, G. Accurate tempo estimation based on recurrent neural networks and resonating comb filters. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Malaga, Spain, 26–30 October 2015. [Google Scholar]
- Schreiber, H.; Müller, M. A single-step approach to musical tempo estimation using a convolutional neural network. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Paris, France, 23–27 September 2018. [Google Scholar]
- Lartillot, O.; Cereghetti, D.; Eliard, K.; Trost, W.J.; Rappaz, M.A.; Grandjean, D. Estimating tempo and metrical features by tracking the whole metrical hierarchy. In Proceedings of the 3rd International Conference on Music and Emotion, Jyväskylä, Finland, 11–15 June 2013. [Google Scholar]
- Lartillot, O.; Grandjean, D. Tempo and metrical analysis by tracking multiple metrical levels using autocorrelation. In Proceedings of the 16th Sound & Music Computing Conference, Malaga, Spain, 28–31 May 2019. [Google Scholar]
- MIREX 2018: Audio Tempo Estimation. 2018. Available online: https://www.music-ir.org/mirex/wiki/2018:Audio_Tempo_Estimation (accessed on 25 November 2019).
- Klapuri, A.P.; Eronen, A.J.; Astola, J.T. Analysis of the meter of acoustic musical signals. IEEE Trans. Audio Speech Lang. Process. 2006, 11, 803–816. [Google Scholar] [CrossRef]
- Alonso, M.; David, B.; Richard, G. Tempo and beat estimation of musical signals. In Proceedings of the International Conference on Music Information Retrieval, Barcelona, Spain, 10–14 October 2004. [Google Scholar]
- Bello, J.P.; Duxbury, C.; Davies, M.; Sandler, M. On the use of phase and energy for musical onset detection in complex domain. IEEE Sig. Proc. Lett. 2004, 11, 553–556. [Google Scholar] [CrossRef]
- Goto, M.; Muraoka, Y. Music understanding at the beat level—Real-time beat tracking for audio signals. In Proceedings of the IJCAI- 95 Workshop on Computational Auditory Scene Analysis, Montreal, QC, Canada, 20 August 1995; pp. 68–75. [Google Scholar]
- De Cheveigné, A.; Kawahara, H. YIN, a fundamental frequency estimator for speech and music. J. Acoust. Soc. Am. 2002, 111, 1917–1930. [Google Scholar] [CrossRef] [PubMed]
- Scheirer, E.D. Tempo and beat analysis of acoustic musical signals. J. Acoust. Soc. Am. 1998, 103, 558–601. [Google Scholar] [CrossRef]
- Large, E.W.; Kolen, J.F. Resonance and the perception of musical meter. Connect. Sci. 1994, 6, 177–208. [Google Scholar] [CrossRef]
- Toiviainen, P.; Snyder, J.S. Tapping to Bach: Resonance-based modeling of pulse. Music Percept. 2003, 21, 43–80. [Google Scholar] [CrossRef]
- Noorden, L.V.; Moelants, D. Resonance in the perception of musical pulse. J. New Music. Res. 1999, 28, 43–66. [Google Scholar] [CrossRef]
- Downie, J.S. MIREX. 2019. Available online: https://www.music-ir.org/mirex/wiki/MIREX_HOME (accessed on 25 November 2019).
- MIREX 2013: Audio Tempo Estimation. 2013. Available online: https://www.music-ir.org/mirex/wiki/2013:Audio_Tempo_Estimation (accessed on 25 November 2019).
- Moelants, D.; McKinney, M. Tempo perception and musical content: What makes a piece slow, fast, or temporally ambiguous? In Proceedings of the International Conference on Music Perception and Cognition, Evanston, IL, USA, 3–7 August 2004.
- MIREX 2013: Audio Tempo Extraction-MIREX06 Dataset. 2013. Available online: https://nema.lis.illinois.edu/nema_out/mirex2013/results/ate/ (accessed on 25 November 2019).
- Wu, F.H.F.; Jang, J.S.R. A Tempo-Pair Estimator with Multivariate Regression. In Proceedings of the MIREX Audio Tempo Extraction, Malaga, Spain, 30 October 2015. [Google Scholar]
- Wu, F.H.F.; Jang, J.S.R. A Method Of The Component Selection For The Tempogram Selector In Tempo Estimation. In Proceedings of the MIREX Audio Tempo Extraction, Curitiba, Brazil, 8 November 2013. [Google Scholar]
- MIREX 2018: Audio Tempo Extraction-MIREX06 Dataset. 2018. Available online: https://nema.lis.illinois.edu/nema_out/mirex2018/results/ate/mck/ (accessed on 25 November 2019).
- Elowsson, A.; Friberg, A. Tempo Estimation by Modelling Perceptual Speed. In Proceedings of the MIREX Audio Tempo Extraction, Curitiba, Brazil, 8 November 2013. [Google Scholar]
- Gkiokas, A.; Katsouros, V.; Carayannis, G.; Stafylakis, T. Music Tempo Estimation and Beat Tracking by Applying Source Separation and Metrical Relations. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012. [Google Scholar]
- Quinton, E.; Harte, C.; Sandler, M. Audio Tempo Estimation Using Fusion on Time-Frequency Analyses and Metrical Structure. In Proceedings of the MIREX Audio Tempo Extraction, Taipei, Taiwan, 31 October 2014. [Google Scholar]
- Aylon, E.; Wack, N. Beat Detection Using PLP. In Proceedings of the MIREX Audio Tempo Extraction, Utrecht, Netherlands, 11 August 2010. [Google Scholar]
- Davies, M.E.P.; Plumbley, M.D. Context-Dependent Beat Tracking of Musical Audio. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 1009–1020. [Google Scholar] [CrossRef]
- Schuller, B.; Eyben, F.; Rigoll, G. Fast and robust meter and tempo recognition for the automatic discrimination of ballroom dance styles. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP), Honolulu, HI, USA, 15–20 April 2007. [Google Scholar]
- Wu, F.; Lee, T.; Jang, J.; Chang, K.; Lu, C.; Wang, W. A two-fold dynamic programming approach to beat tracking for audio music with time-varying tempo. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Miami, FL, USA, 24–28 October 2011. [Google Scholar]
- Peeters, G.; Flocon-Cholet, J. Perceptual tempo estimation using gmm regression. In Proceedings of the Second International ACM Workshop on Music Information Retrieval with user-Centered and Multimodal Strategies, Nara, Japan, 2 November 2012. [Google Scholar]
- Krebs, F.; Widmer, G. MIREX Audio Audio Tempo Estimation Evaluation: Tempokreb. In Proceedings of the MIREX Audio Tempo Extraction, Porto, Portugal, 12 October 2012. [Google Scholar]
- Zapata, J.; Gómez, E. Comparative Evaluation and Combination of Audio Tempo Estimation Approaches. In Proceedings of the Audio Engineering Society Conference, San Diego, CA, USA, 18–20 November 2011. [Google Scholar]
- Pauws, S. Tempo Extraction and Beat Tracking with Tempex and Beatex. In Proceedings of the MIREX Audio Tempo Extraction, Miami, FL, USA, 27 October 2011. [Google Scholar]
- Daniels, M.L. Tempo Estimation and Causal Beat Tracking Using Ensemble Learning. In Proceedings of the MIREX Audio Tempo Extraction, Taipei, Taiwan, 31 October 2014. [Google Scholar]
- Ellis, D.P.W. Beat Tracking with Dynamic Programming. In Proceedings of the MIREX Audio Tempo Extraction, Victoria, BC, Canada, 11 October 2006. [Google Scholar]
- Pikrakis, A.; Antonopoulos, I.; Theodoridis, S. Music Meter and Tempo Tracking from raw polyphonic audio. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Barcelona, Spain, 10–14 October 2004. [Google Scholar]
- Brossier, P.M. Automatic Annotation of Musical Audio for Interactive Applications. Ph.D. Thesis, Queen Mary University of London, London, UK, 2004. [Google Scholar]
- Tzanetakis, G. Marsyas Submissions To Mirex 2010. In Proceedings of the MIREX Audio Tempo Extraction, Utrecht, The Netherlands, 11 August 2010. [Google Scholar]
- Baume, C. Evaluation of acoustic features for music emotion recognition. In Proceedings of the 134th Audio Engineering Society Convention, Rome, Italy, 4–7 May 2013. [Google Scholar]
- Li, Z. EDM Tempo Estimation Submission for MIREX 2018. In Proceedings of the MIREX Audio Tempo Extraction, Paris, France, 27 September 2018. [Google Scholar]
- Giorgi, B.D.; Zanoni, M.; Sarti, A. Tempo Estimation Based on Multipath Tempo Tracking. In Proceedings of the MIREX Audio Tempo Extraction, Taipei, Taiwan, 31 October 2014. [Google Scholar]
- Lartillot, O.; Toiviainen, P. MIR in Matlab (II): A Toolbox for Musical Feature Extraction From Audio. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Vienna, Austria, 23–30 September 2007. [Google Scholar]
- Lartillot, O.; Toiviainen, P.; Saari, P.; Eerola, T. MIRtoolbox 1.7.2. 2019. Available online: https://www.jyu.fi/hytk/fi/laitokset/mutku/en/research/materials/mirtoolbox (accessed on 25 November 2019).


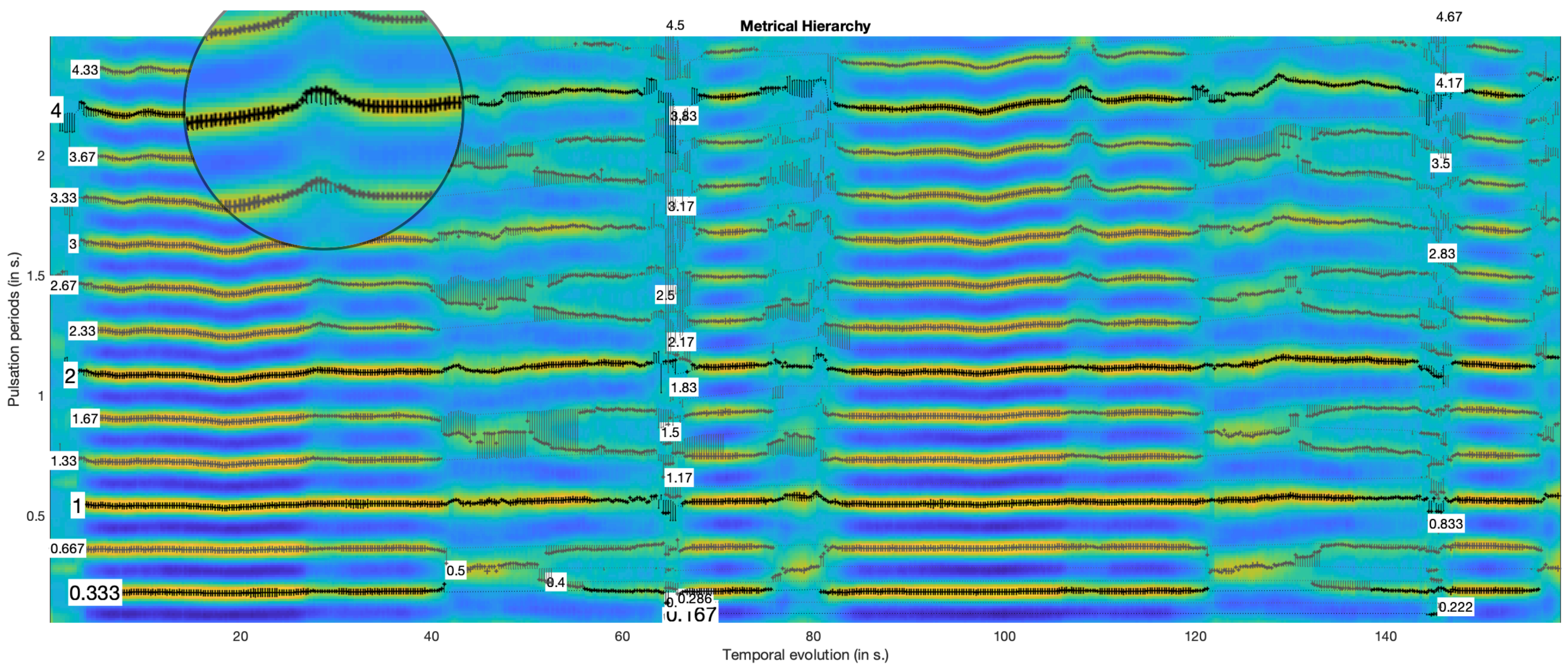
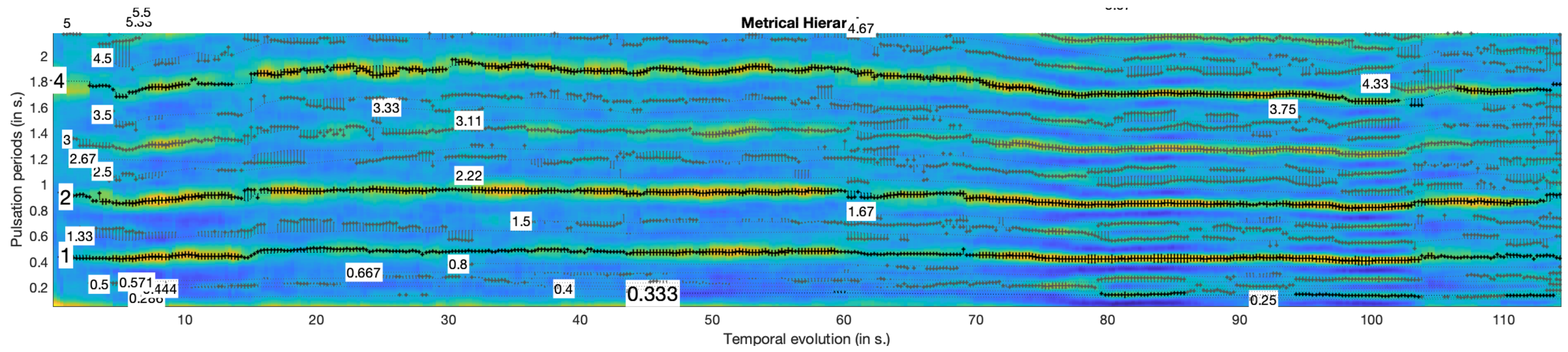
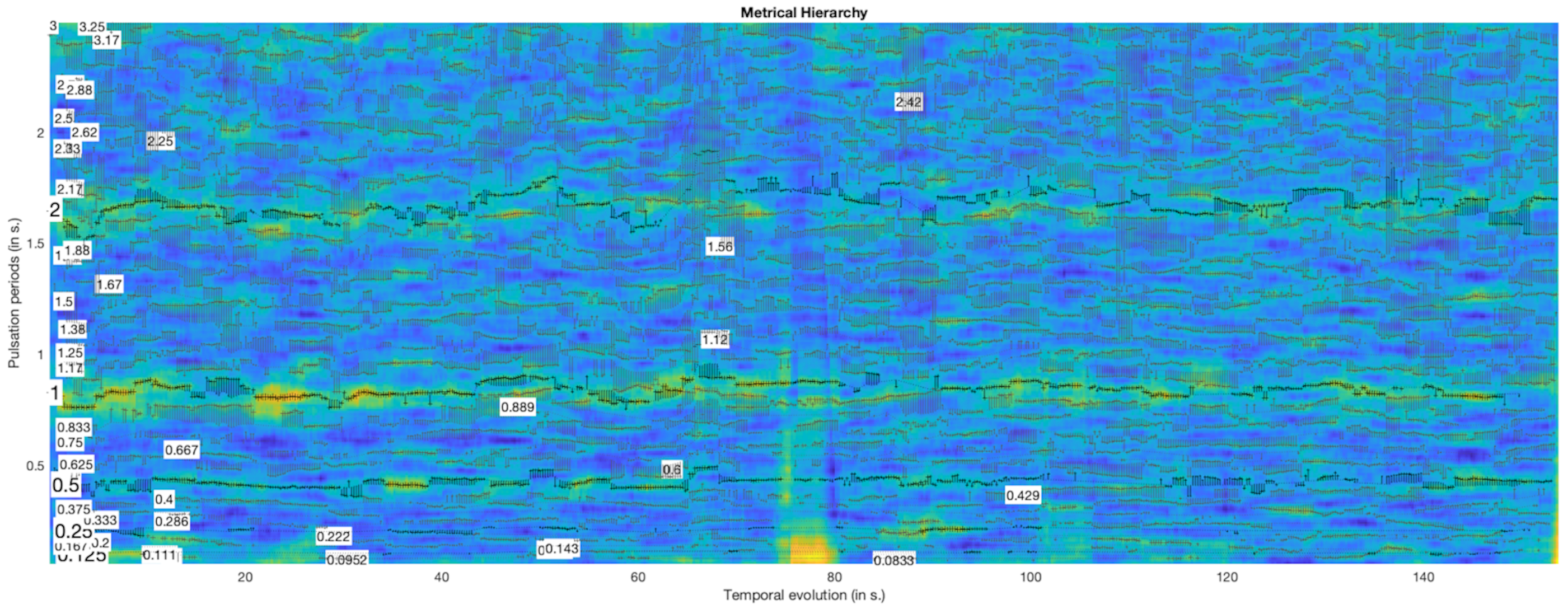
| Contestant | SB | HS | EF | FW | GK | OL | AK | QH | NW | DP | ES | TL | GP | FK | CD | ZG | AD | SP | MD | DE | AP | PB | GT | CB | ZL | BD |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Year (20xx) | 15 | 18 | 13 | 15 | 11 | 13 | 06 | 14 | 10 | 06 | 10 | 10 | 12 | 12 | 13 | 11 | 06 | 11 | 14 | 06 | 06 | 06 | 10 | 13 | 18 | 14 |
| Reference | [1] | [2] | [22] | [19] | [23] | [6] | [24] | [25] | [26] | [27] | [28] | [29] | [30] | [26] | [31] | [7] | [32] | [33] | [34] | [35] | [36] | [37] | [38] | [39] | [40] | |
| P-score | 0.90 | 0.88 | 0.86 | 0.83 | 0.83 | 0.82 | 0.81 | 0.80 | 0.79 | 0.78 | 0.77 | 0.76 | 0.75 | 0.75 | 0.74 | 0.73 | 0.72 | 0.71 | 0.69 | 0.67 | 0.67 | 0.63 | 0.62 | 0.61 | 0.60 | 0.54 |
| 1 tempo | 0.99 | 0.98 | 0.94 | 0.95 | 0.94 | 0.92 | 0.94 | 0.92 | 0.91 | 0.93 | 0.91 | 0.89 | 0.86 | 0.85 | 0.91 | 0.82 | 0.89 | 0.93 | 0.85 | 0.79 | 0.84 | 0.79 | 0.69 | 0.85 | 0.68 | 0.64 |
| both tempi | 0.69 | 0.66 | 0.69 | 0.57 | 0.62 | 0.57 | 0.61 | 0.56 | 0.50 | 0.46 | 0.55 | 0.48 | 0.61 | 0.62 | 0.55 | 0.57 | 0.46 | 0.39 | 0.47 | 0.43 | 0.48 | 0.51 | 0.51 | 0.26 | 0.46 | 0.38 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lartillot, O.; Grandjean, D. Tempo and Metrical Analysis by Tracking Multiple Metrical Levels Using Autocorrelation. Appl. Sci. 2019, 9, 5121. https://doi.org/10.3390/app9235121
Lartillot O, Grandjean D. Tempo and Metrical Analysis by Tracking Multiple Metrical Levels Using Autocorrelation. Applied Sciences. 2019; 9(23):5121. https://doi.org/10.3390/app9235121
Chicago/Turabian StyleLartillot, Olivier, and Didier Grandjean. 2019. "Tempo and Metrical Analysis by Tracking Multiple Metrical Levels Using Autocorrelation" Applied Sciences 9, no. 23: 5121. https://doi.org/10.3390/app9235121
APA StyleLartillot, O., & Grandjean, D. (2019). Tempo and Metrical Analysis by Tracking Multiple Metrical Levels Using Autocorrelation. Applied Sciences, 9(23), 5121. https://doi.org/10.3390/app9235121






