Gray Relational Analysis Optimization for Coalbed Methane Blocks in Complex Conditions Based on a Best Worst and Entropy Method
Abstract
1. Introduction
2. Establishment of an Evaluation Index System for CBM Development
2.1. Index System Construction
- (1)
- Reservoir depth. Reservoir depth controls the economic value and economic efficiency of CBM reservoirs, and this factor affects whether a reservoir has commercial developmental value. It has been known that, as the reservoir depth increases until critical depth, the gas content of CBM increases [20]. However, the permeability of the reservoir decreases continuously [21], which has a negative effect on the seepage and drainage pressure of the CBM well. As a result, the reservoir depth is a cost-type index in reservoir evaluation;
- (2)
- Gas content. Gas content is a key index that simultaneously determines the level of CBM resources abundance and controls the CBM enrichment and production [22]. Along with the increasing of the gas content, the critical desorption pressure and the effective desorption area increased. Therefore, the shorter gas breakthrough time resulted in enhanced gas production per well [23,24]. Obviously, the gas content serves as a profit-type index for reservoir evaluation;
- (3)
- Reservoir thickness. As the source rock and storage space of CBM, a thick enough reservoir thickness is a prerequisite for the enrichment, development, and production of CBM [25,26]. Theoretically, the thicker the reservoir, the more CBM will flow into the wellbore. That is to say, the thick coal seam can provide continuous and sufficient gas source for gas wells and ensure a longer production cycle and higher gas production [27]. Consequently, reservoir thickness is regarded as a profit-type index in the evaluation model;
- (4)
- Reservoir pressure gradient. The reservoir pressure gradient is the main driving force of water flow [28]. In CBM wells, gas is produced mainly by water pressure transmission and the effective drainage radius for reservoir presents a depressurization funnel trend. The greater reservoir pressure gradient resulting in the stronger force of the water flow, the greater the distance of the water pressure transfer, which is more favorable for gas production [29]. For this reason, the reservoir pressure gradient is a profit-type index for reservoir evaluation;
- (5)
- Ratio of critical desorption pressure to reservoir pressure (hereinafter referred to as “critical reservoir ratio”). The critical reservoir ratio represents the dynamic features of CBM desorption, diffusion, and seepage to the bottom of the well. Chen and Yang found that with the increase of the critical reservoir ratio, the gas saturation in the reservoir increased. Then the stronger methane power field made gas evolution under the same declining pressure more easily [30,31]. It was also found that a higher critical reservoir ratio shortened the time of CBM well drainage, which reduced the damage caused by effective stress on the permeability of reservoir during the drainage and depressurization stage, weakened the negative effect of fracturing fluid on critical desorption pressure of reservoir, and increased the aerodynamic force [3,32]. The critical reservoir ratio is considered to be a profit-type index for reservoir evaluation;
- (6)
- Permeability. The reservoir permeability represents the development degree of pores and fractures in coal seam and influences the degree of the gas flow in effective pores of the coal seam [23,33]. Permeability not only regulates the output efficiency of CBM but also affects the radius of the drainage and depressurization funnel in the CBM well [34]. Theory and practice have confirmed that permeability is one of the important reservoir indices for controlling CBM output [35,36]. As a result, permeability is the profit-type index of reservoir evaluation;
- (7)
- Reservoir temperature. Reservoir temperature is an important factor that influences CBM adsorption, desorption, and seepage [37]. As the temperature increased, the molecular energy, thermal activity, and desorption rate of CBM increased [38]. Especially at the later stage of stress unloading, the coalbed has been fully deformed under the influence of temperature [39]. At this time the molecules desorbed from the surface of the matrix are increasing, which will extend the gas production capacity of the CBM well. The reservoir temperature is regarded as a profit-type index in the evaluation model;
- (8)
- Young’s modulus. Young’s modulus represents the degree of deformation caused by stress, which can better reflect the stress-strain characteristics of rock [40]. Young’s modulus is positively correlated with crack height and negatively correlated with crack length and crack width. There are significant differences in the elastic modulus between coal seam and roof and floor rock, which makes the fractures induced by hydraulic fracturing in CBM wells different from conventional hydraulic fracturing. The larger the Young’s modulus difference, the larger the minimum horizontal principal stress difference between the layers, and the formed fractures are more easily controlled in the coal seam [41]. As a result, Young’s modulus is a cost-type index for reservoir evaluation.
2.2. Selection of CBM Development Block Indices
3. Determination of Evaluation Index Weights of CBM Development
3.1. Determination of Subjective Weight Based on BWM
- Step 1.
- Select the best criterion (aB) and the worst criterion (aW) among the eight indices, respectively permeability and reservoir temperature;
- Step 2.
- Determine the preference of the best criterion over all the other criteria using a number 1~9. The resulting Best-to-Others vector would be: .The results are shown in Table 2.
- Step 3.
- Determine the preference of all the criteria over the worst criterion using a number 1~9. The resulting Others-to-Worst vector would be: .The results are shown in Table 3.
- Step 4.
- The optimal weight for the criteria is the one where for each pair of and , and . For all j, we should find a solution where the maximum absolute differences and for all j is minimized. Considering the non-negativity and sum condition for the weights, the following problem has resulted:where aBj indicates the preference of the best criterion B over criterion j, ajW indicates the preference of the criterion j over the worst criterion W, and ξ is a constant.
3.2. Determination of Objective Weight Based on the Entropy Method
3.3. Determination of Combination Weights
4. Optimal Selection of CBM Development Blocks
4.1. Optimal Selection of GRA for CBM Blocks Based on Interval Value of the Evaluation Indices
4.2. Optimal Selection Results and Discussions
5. Conclusions
- (1)
- Within the examined CBM reservoirs, which are associated with complex conditions in China, eight resources and productivity characterization indices, namely, the reservoir depth, gas content, reservoir thickness, reservoir pressure gradient, critical reservoir ratio, permeability, reservoir temperature, and Young’s modulus, were selected as the main evaluation indices of development blocks;
- (2)
- The importance of an evaluation index was determined by the combination of the subjective experience of the experts, the objective deviation of the data through the BWM and the entropy method. The importance of the evaluation indices, ordered from high to low, is permeability, reservoir pressure gradient, gas content, reservoir thickness, reservoir depth, critical reservoir ratio, Young’s modulus, and reservoir temperature, and the weights are 0.5877, 0.2911, 0.0443, 0.0261, 0.0220, 0.0115, 0.0105, and 0.0067, respectively;
- (3)
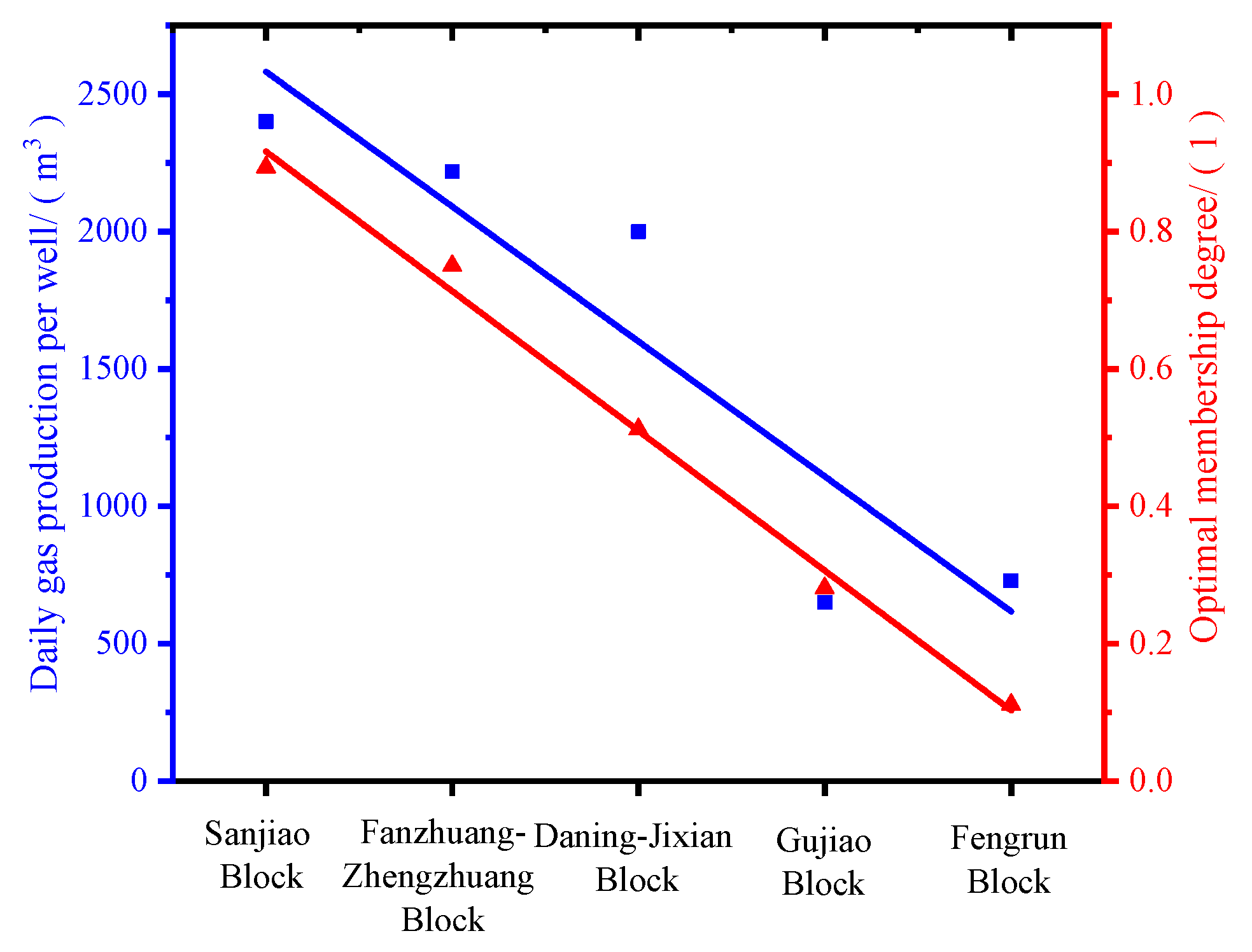
- Based on the gray system theory, a multi-index gray relational analysis optimization model was established, and the development potentials of CBM blocks in complex geological conditions with interval values were ranked. The ranking results, from most to least optimal, are Block 2 (Sanjiao block), Block 1 (Fanzhuang-Zhengzhuang block), Block 4 (Daning-Jixian block), Block 3 (Gujiao block), and Block 5 (Fengrun block). The optimum membership degrees are 0.8936, 0.7500, 0.5123, 0.2808, and 0.1112, respectively. The results of the evaluation are in accordance with the actual conditions. The multi-index gray relational analysis optimization model with interval numbers for evaluation indices has practicability and can be used for quantitative evaluation and optimization of CBM blocks under complex conditions. This model is suitable for the CBM blocks in the range of 547 km2~675 km2. When using this model, the index values must be representative and accurate.
Data Availability Statement
Author Contributions
Funding
Conflicts of Interest
References
- Ye, J.; Qin, Y.; Lin, D. Coalbed Methane Resources in China; China University of Mining Press: Xuzhou, China, 1998. [Google Scholar]
- Zhang, J.; Wang, H.; Zhao, Q. Geology of Coalbed Methane in China; Geological Publishing House: Beijing, China, 2000. [Google Scholar]
- Yao, J.; Yu, B.; Che, C.; Yang, H. Study of comprehensive evaluation of coalbed methane zone in China. Geoscience 2009, 23, 353–358. [Google Scholar]
- Li, G. Selection of the favorable coalbed methane (CBM) blocks in eastern Ordos Basin. Coal Geol. Explor. 2015, 43, 28–32. [Google Scholar]
- Deng, J. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar]
- Khan, M.; Han, K. An optimized network selection and handover triggering scheme for heterogeneous self-organized wireless networks. Math. Probl. Eng. 2014, 2, 1214–1225. [Google Scholar] [CrossRef]
- Kuo, Y.; Yang, T.; Huang, G. The use of grey relational analysis in solving multiple attribute decision-making problems. Comput. Ind. Eng. 2007, 55, 80–93. [Google Scholar] [CrossRef]
- Hamzacebi, C.; Pekkaya, M. Determining of stock investments with grey relational analysis. Expert Syst. Appl. 2011, 38, 9186–9195. [Google Scholar] [CrossRef]
- Arya, D.M.; Chaturvedi, V.; Vimal, J. Application of signal to noise ratio methodology for optimization of MIG welding process parameters. Int. J. Eng. Res. Appl. 2013, 3, 1904–1910. [Google Scholar]
- Kumar, P.N.; Rajadurai, A.; Muthuramalingam, T. Multi-response optimization on mechanical properties of silica fly ash filled polyester composites using taguchi-grey relational analysis. Silicon 2018, 10, 1723–1729. [Google Scholar] [CrossRef]
- Ahmadi, H.B.; Petrudi, S.H.H.; Wang, X.P. Integrating sustainability into supplier selection with analytical hierarchy process and improved greyrelational analysis: A case of telecom industry. Int. J. Adv. Manuf. Technol. 2017, 90, 2413–2427. [Google Scholar] [CrossRef]
- Lee, W.; Lin, Y. Evaluating and ranking energy performance of office buildings using Grey relational analysis. Energy 2011, 36, 2551–2556. [Google Scholar] [CrossRef]
- Akay, D.; Boran, F.E.; Yilmaz, M.; Atak, M. The evaluation of power plants investment alternatives with grey relational analysis approach for Turkey. Energy Source Part B 2012, 8, 35–43. [Google Scholar] [CrossRef]
- Aslan, N. Use of the grey analysis to determine optimal oil agglomeration with multiple performance characteristics. Fuel 2013, 109, 373–378. [Google Scholar] [CrossRef]
- Adem, A.; Mehmet, E.C.; İsmail, A.; Ramazan, Ç. Parametric optimization of energy and exergy analyses of a novel solar air heater with grey relational analysis. Appl. Therm. Eng. 2017, 122, 330–338. [Google Scholar]
- Tao, S.; Chen, S.; Pan, Z. Current status, challenges, and policy suggestions for coalbed methane industry development in China: A review. Energy Sci. Eng. 2019, 7, 1–16. [Google Scholar] [CrossRef]
- Tao, S.; Pan, Z.; Tang, S.; Chen, S. Current status and geological conditions for the applicability of CBM drilling technologies in China: A review. Int. J. Coal Geol. 2018, 202, 95–108. [Google Scholar] [CrossRef]
- Ayers, W.B. Coalbed gas systems, resources, and production and a review of contrasting cases from the San Juan and Powder River basins. AAPG Bull. 2002, 86, 1853–1890. [Google Scholar]
- Connell, L.D.; Lu, M.; Pan, Z.J. An analytical coal permeability model for tri-axial strain and stress conditions. Int. J Coal Geol. 2010, 84, 103–114. [Google Scholar] [CrossRef]
- Shen, J.; Qin, Y.; Fu, X.; Chen, G.; Chen, R. Properties of deep coalbed methane reservoir-forming conditions and critical Depth discussion. Nat. Gas Geosci. 2014, 25, 1470–1476. [Google Scholar]
- Mckee, C.R.; Bumb, A.C.; Koenig, R.A. Stress-dependent permeability and porosity of coal and other geologic formations. SPE Form. Eval. 1998, 3, 81–91. [Google Scholar] [CrossRef]
- Scott, A.R. Hydrogeologic factors affecting gas content distribution in coal beds. Int. J. Coal Geol. 2002, 50, 363–387. [Google Scholar] [CrossRef]
- Tao, S.; Tang, D.; Xu, H.; Gao, L.; Fang, Y. Factors controlling high-yield coalbed methane vertical wells in the Fanzhuang Block, Southern Qinshui Basin. Int. J. Coal Geol. 2014, 134–135, 38–45. [Google Scholar] [CrossRef]
- Lv, Y.; Tang, D.; Xu, H.; Luo, H. Production characteristics and the key factors in high-rank coalbed methane fields: A case study on the Fanzhuang Block, Southern Qinshui Basin, China. Int. J. Coal Geol. 2012, 96, 93–108. [Google Scholar] [CrossRef]
- Bustin, R.M.; Clarkson, C.R. Geological controls on coalbed methane reservoir capacity and gas content. Int. J. Coal Geol. 1998, 38, 3–26. [Google Scholar] [CrossRef]
- Pashin, J.C. Stratigraphy and structure of coalbed methane reservoirs in the United States: An overview. Int. J. Coal Geol. 1998, 35, 209–240. [Google Scholar] [CrossRef]
- Zhang, P.; Liu, Y.; Wang, Z.; Liu, N. Geological factors of production control of CBM well in south Qinshui Basin. Nat. Gas. Geosci. 2011, 22, 909–914. [Google Scholar]
- Morita, N.; Fuh, G.F. Parametric analysis of stress reduction in the cap rock above compacting reservoirs. SPE Drill. Completion. 2009, 24, 659–670. [Google Scholar] [CrossRef]
- Chen, M.; Chen, L.; Zhang, Q.; Wang, Z.; Yang, Y. Field pressure distribution of horizontal wells in low permeable stimulated reservoirs. J. Shenzhen Univ. Sci. Eng. 2016, 33, 401–408. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Y.; Yang, J.; Wang, X.; Chen, Y.; Zhao, Q. Influencing factors on coal-bed methane production of single well: A case of Fan zhuang Block in the south part of Qinshui Basin. Acta Pet. Sin. 2009, 30, 409–412. [Google Scholar]
- Yang, Y.; Tang, D.; Yang, Y.; Chen, L.; Tao, S. Influence on velocity sensitivity effect of coal reservoir to production law of pulverized coal and gas productivity. Coal Sci. Technol. 2015, 43, 96–99. [Google Scholar]
- Tao, S.; Wang, Y.; Tang, D.; Xu, H.; Lv, Y. Coal permeability damage caused by production pressure difference. Energy Sources. 2012, 34, 1801–1807. [Google Scholar] [CrossRef]
- Adeboye, O.O.; Bustin, R.M. Variation of gas flow properties in coal with probe gas, composition and fabric: Examples from western Canadian sedimentary basin. Int. J. Coal Geol. 2013, 108, 47–52. [Google Scholar] [CrossRef]
- Zou, M.; Wei, C.; Fu, X.; Bao, Y.; Cai, Z. Investigating reservoir pressure transmission for three types of coalbed methane reservoirs in the Qinshui Basin in Shan’xi Province, China. Pet. Geosci. 2013, 19, 375–383. [Google Scholar] [CrossRef]
- Durucan, S.; Edwards, J.S. The effects of stress and fracturing on permeability of coal. Min. Sci. Technol. 1986, 3, 205–216. [Google Scholar] [CrossRef]
- Hideki, M.; Kosuke, E.; Yasuhide, S.; Takeshi, K.; Norio, T.; Hideo, N. Characterization of hydraulic permeability and pore-size distribution of methane hydrate-bearing sediment using proton nuclear magnetic resonance measurement. Int. J. Offshore Polar. Eng. 2012, 22, 306–313. [Google Scholar]
- Winden, J.F.; Reichart, G.J.; McNamara, N.P.; Benthien, A.; Damsté, J.S.S. Temperature-induced increase in methane release from peat bogs: A mesocosm experiment. PLoS ONE 2012, 7, e39614. [Google Scholar] [CrossRef]
- White, C.M.; Smith, D.H.; Jones, K.L.; Goodman, A.L.; Jikich, S.A.; LaCount, R.B.; DuBose, S.B.; Ozdemir, E.; Morsi, B.I.; Schroeder, K.T. Sequestration of carbon dioxide in coal with enhanced coalbed methane recovery—A review. Energy Fuels 2005, 19, 659–724. [Google Scholar] [CrossRef]
- Skoczylas, N.; Dutka, B.; Sobczyk, J. Mechanical and gaseous properties of coal briquettes in terms of outburst risk. Fuel 2014, 134, 45–52. [Google Scholar] [CrossRef]
- Yaghoubi, A.A.; Zeinali, M. Determination of magnitude and orientation of the in-situ stress from borehole breakout and effect of pore pressure on borehole stability—Case study in Cheshmeh Khush oil field of Iran. J. Pet. Sci. Eng. 2009, 67, 116–126. [Google Scholar] [CrossRef]
- Blunschi, J.; Wang, J.; Ertekin, T. Hydraulic fracturing mechanisms in coal: A review. Int. J. Oil Gas Coal Technol. 2017, 14, 247–263. [Google Scholar] [CrossRef]
- Zhou, L. Study on Controlling Factors of CBM Reservoir in Fanzhuang-Zhengzhuang Block in Southern Qinshui Basin; Henan Polytechnic University: Jiaozuo, China, 2014. [Google Scholar]
- Tao, S.; Chen, S.; Tang, D.; Zhao, X.; Xu, H.; Li, S. Material composition, pore structure and adsorption capacity of low-rank coals around the first coalification jump: A case of eastern Junggar Basin, China. Fuel 2018, 211, 804–815. [Google Scholar] [CrossRef]
- Tao, S.; Wang, Y.; Tang, D.; Xu, H.; Lv, Y.M.; He, W.; Li, Y. Dynamic variation effects of coal permeability during the coalbed methane development process in the Qinshui Basin, China. Int. J. Coal Geol. 2012, 93, 16–22. [Google Scholar] [CrossRef]
- Tao, S. Dynamic Variation Effects of Coal Reservoir Permeability and the Response of Gas Productivity in Southern Qinshui Basin; China University of Geosciences: Beijing, China, 2011. [Google Scholar]
- Xue, G.; Liu, H.; Guo, J. A study on the occurrence law of coal seam gas in Shanxi. Adv. Ind. Civ. Eng. 2012, 594, 2244–2250. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiao, Y. Discussion on geological characteristics and occurrence law of coalbed methane in Sanjiao mining area, Hedong coalfield, Shanxi Province. Coal Geol. China 1996, 8, 66–70. [Google Scholar]
- Li, X.; Wang, P.; Li, J.; Tang, L.; Chen, C.; Meng, Q. New understanding of coal-bed methane exploration and development in Sanjiao area of Ordos Basin. J. Oil Gas Technol. 2011, 33, 39–42. [Google Scholar]
- Xia, P.; Zeng, F.; Song, X.; Meng, Y.; Li, K.; Wang, J.; Sun, B. Structural block division for further deep research in coalbed methane development in the Gujiao area, Xishan coalfield, North China. Arab. J. Geosci. 2016, 9, 713–730. [Google Scholar] [CrossRef]
- Xia, P.; Zeng, F.; Song, X. Parameters controlling high-yield coalbed methane vertical wells in the B3 area, Xishan coal field, Shanxi, China. Energy Explor. Exploit. 2016, 34, 711–734. [Google Scholar] [CrossRef]
- Han, B. Porosity, Permeability and Favorable Production Region of Coal Reservoirs in Gujiao Block, Xishan; China University of Mining and Technology: Xuzhou, China, 2015. [Google Scholar]
- Li, W.; Chen, G.; Sun, B.; Sun, F.; Zhao, Q. Geological controls of coalbed methane enrichment in Daning-Jixian area, southeastern Ordos Basin. Nat. Gas Geosci. 2011, 22, 352–360. [Google Scholar]
- Tian, W.; Tang, D.; Sun, B.; Ren, Y. Major controlling factors of coalbed methane enrichment in the southern Ningwu Basin. Nat. Gas Ind. 2010, 30, 22–25. [Google Scholar]
- Wang, X.; Jiang, W.; Gao, Y.; Zhao, Y. CBM exploration status and production test efficiency in Ningwu basin. Nat. Gas Ind. 2008, 28, 93–95. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Li, Y.; Tao, Z.; Qin, X.; Wang, X. Compination weight method for determing the index weight in geological disaster risk extenics evaluation. J. Harbin Inst. Technol. 2011, 43, 141–144. [Google Scholar]
- Deng, J. Gray System Basic Method, 2nd ed.; Huazhong University of Science and Technology Press: Wuhan, China, 2005. [Google Scholar]


| Category | Reservoir Depth/m | Gas Content /m3/t | Reservoir Thickness/m | Reservoir Pressure Gradient/MP/100 m | Critical Reservoir Ratio | Permeability /×10−3 µm2 | Reservoir Temperature/℃ | Young’s Modulus/MPa |
|---|---|---|---|---|---|---|---|---|
| Block 1 (Fanzhuang-Zhengzhuang block) | ||||||||
| Block 2 (Sanjiao block) | ||||||||
| Block 3 (Gujiao block) | ||||||||
| Block 4 (Daning-Jixian block) | ||||||||
| Block 5 (Fengrun block) |
| Criteria | Reservoir Depth | Gas Content | Reservoir Thickness | Reservoir Pressure Gradient | Critical Reservoir Ratio | Permeability | Reservoir Temperature | Young’s Modulus |
|---|---|---|---|---|---|---|---|---|
| Best criterion: Permeability | 6 | 3 | 5 | 2 | 8 | 1 | 9 | 7 |
| Criteria | Reservoir Depth | Gas Content | Reservoir Thickness | Reservoir Pressure Gradient | Critical Reservoir ratio | Permeability | Reservoir Temperature | Young’s Modulus |
|---|---|---|---|---|---|---|---|---|
| Best criterion: Reservoir temperature | 4 | 6 | 5 | 8 | 2 | 9 | 1 | 3 |
| Index | Reservoir Depth | Gas Content | Reservoir Thickness | Reservoir Pressure Gradient | Critical Reservoir ratio | Permeability | Reservoir Temperature | Young’s Modulus | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X | X | X | X | X | X | X | X | |||||||||
| Block 1 | 0.607 | 1.000 | 0.444 | 0.845 | 0.333 | 0.667 | 0.084 | 1.000 | 0.228 | 1.000 | 0.034 | 0.365 | 1.000 | 0.538 | 1.000 | 0.458 |
| Block 2 | 0.281 | 0.839 | 0.460 | 0.612 | 0.375 | 0.500 | 0.066 | 0.958 | 0.346 | 0.733 | 0.019 | 1.000 | 0.743 | 0.513 | 0.840 | 0.577 |
| Block 3 | 0.871 | 0.233 | 0.488 | 0.306 | 0.429 | 0.333 | 1.000 | 0.026 | 0.500 | 0.622 | 0.042 | 0.017 | 0.605 | 1.000 | 0.464 | 0.972 |
| Block 4 | 1.000 | 0.460 | 0.024 | 1.000 | 0.024 | 1.000 | 0.086 | 0.188 | 0.374 | 0.511 | 0.032 | 0.009 | 0.021 | 0.795 | 0.424 | 1.000 |
| Block 5 | 0.585 | 0.852 | 1.000 | 0.072 | 1.000 | 0.167 | 0.809 | 0.028 | 1.000 | 0.356 | 1.000 | 0.017 | 0.929 | 0.256 | 0.807 | 0.284 |
| Target Block | Block 1 | Block 2 | Block 3 | Block 4 | Block 5 |
|---|---|---|---|---|---|
| Optimal membership degree | 0.7500 | 0.8936 | 0.2808 | 0.5123 | 0.1112 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, G.; Kang, T.; Guo, J.; Zhang, R.; Li, L. Gray Relational Analysis Optimization for Coalbed Methane Blocks in Complex Conditions Based on a Best Worst and Entropy Method. Appl. Sci. 2019, 9, 5033. https://doi.org/10.3390/app9235033
Zhao G, Kang T, Guo J, Zhang R, Li L. Gray Relational Analysis Optimization for Coalbed Methane Blocks in Complex Conditions Based on a Best Worst and Entropy Method. Applied Sciences. 2019; 9(23):5033. https://doi.org/10.3390/app9235033
Chicago/Turabian StyleZhao, Guofei, Tianhe Kang, Junqing Guo, Runxu Zhang, and Ligong Li. 2019. "Gray Relational Analysis Optimization for Coalbed Methane Blocks in Complex Conditions Based on a Best Worst and Entropy Method" Applied Sciences 9, no. 23: 5033. https://doi.org/10.3390/app9235033
APA StyleZhao, G., Kang, T., Guo, J., Zhang, R., & Li, L. (2019). Gray Relational Analysis Optimization for Coalbed Methane Blocks in Complex Conditions Based on a Best Worst and Entropy Method. Applied Sciences, 9(23), 5033. https://doi.org/10.3390/app9235033






