Novel Generalized Three-Step Phase-Shifting Interferometry with a Slight-Tilt Reference

Featured Application

The method can be used in such areas as optical wave reconstruction, three dimensional microscopic imaging, and interference measurement.

Abstract

A convenient and powerful method is proposed and presented to find the unknown phase shifts in three-step generalized phase-shifting interferometry. A slight-tilt reference of 0.1 degrees is employed. As a result, the developed theory shows that the unknown phase shifts can be simply extracted by subtraction operations. Also, from the theory developed, the tilt angle of the tilt reference can also be calculated, which is important as it allows us to extract the object wave precisely. Numerical simulations and optical experiments were performed to demonstrate the validity and efficiency of the proposed method. The proposed slight-tilt reference allows the full and efficient use of the space-bandwidth product of the limited resolution of digital recording devices as compared to the situation in standard off-axis holography where typically several degrees for off-axis angle is employed.

1. Introduction

Phase-shifting interferometry (PSI) has been developing for decades and applied to many fields [1,2,3,4,5,6]. In the development of PSI techniques, there is a transition from the traditional fixed phase shifts to random unknown phase shifts [7,8]. In general, the phase shift of the reference beam introduced into the PSI is typically affected by environmental interference and phase shifter errors [9]. To further simplify the measurement procedures and avoid the negative effects of the environmental disturbances and phase shifter errors, Cai et al. have introduced generalized phase-shifting interferometry (GPSI), where the phase shifts are generally arbitrary, unequal and unknown values, but can be extracted from several interferograms [10,11]. Yoshikawa et al. later have developed GPSI by using statistical distribution of the diffracted wave and normalized holograms [12,13,14]. To achieve further convenience, non-iterative methods [11,15,16,17,18] begin to replace the iterative methods, which always need a long computation time, and sometimes it is difficult to make the extracted values convergent. However, complicated equations and tedious operations in these phase shift extraction processes give rise to some inconvenience in the application of GPSI.

In recent years, interference with a tilt reference [18,19] has been proposed in digital holography for monitoring purposes. In order to improve the convenience and stability of the phase-shift extracting algorithm further in three-step PSI, we propose a simpler and more reliable method to extract the unknown phase shifts with a slightly tilted reference beam during the recording process.

Three-step generalized phase-shifting interferometry (TGPSI) uses three interferograms to extract phase shifts and retrieve the original object wave. In GPSI research, TGPSI can retrieve the object wave stably by only three holograms without any additional measurements. In this paper, we propose the use of a slightly tilted reference so that the extraction of the phase shift can become simpler and more stable without iteration. We derive the theory behind the proposed method and carry out numerical simulations as well as optical experiments to verify our idea.

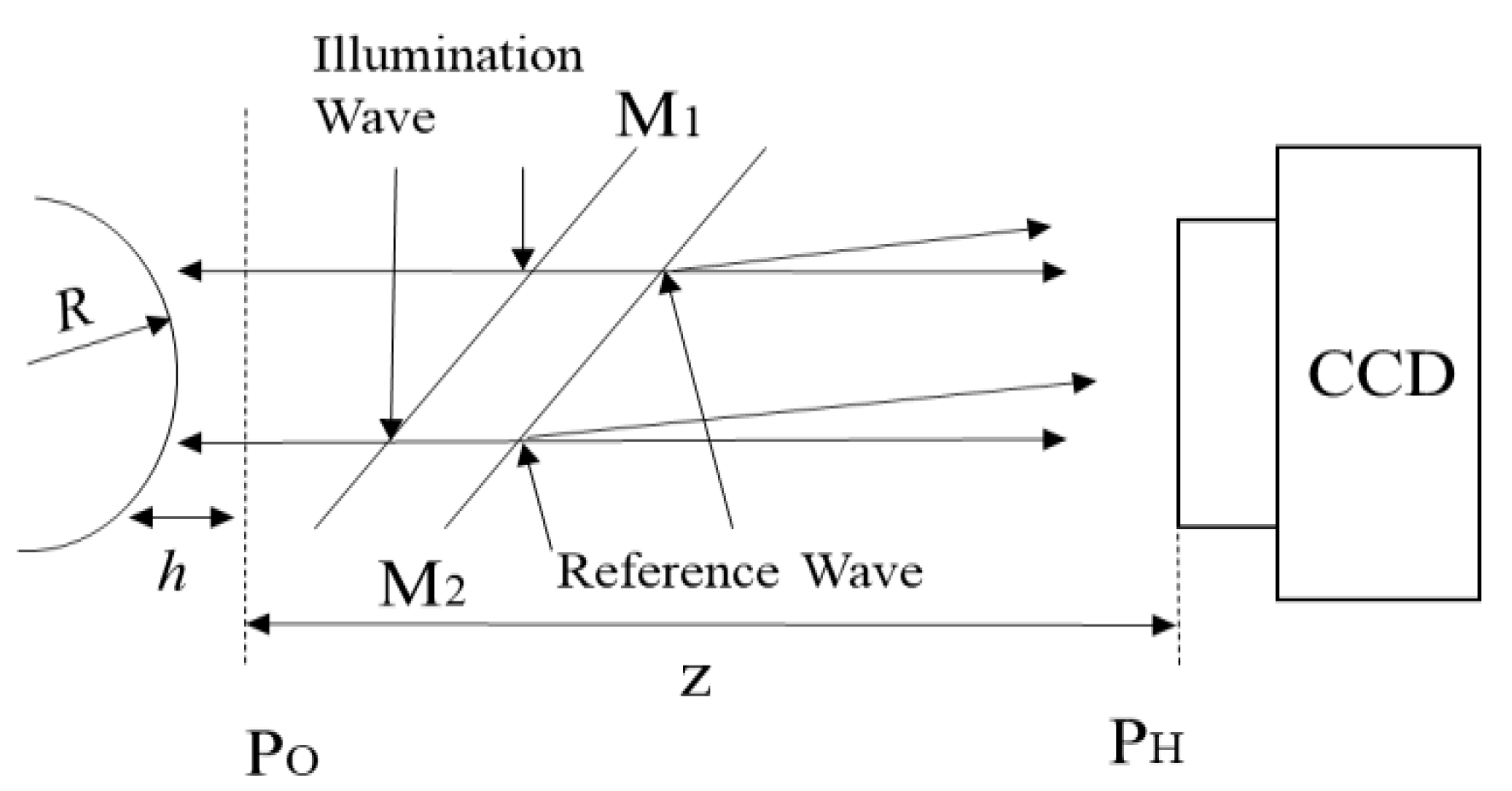
2. Basic Principle

In the TGPSI method, the complex amplitudes of object wave $\mathit{O}\left(x,y\right)$ and reference wave $\mathit{R}\left(x,y\right)$ on the recording plane ${\mathrm{P}}_{\mathrm{H}}$ can be written as

$$\mathit{O}\left(x,y\right)=A_o\left(x,y\right)\exp \left[-i{\phi }_o\left(x,y\right)\right],$$

(1)

$$\mathit{R}\left(x,y\right)=A_r\exp \left[-i{\phi }_r\left(x,y\right)\right],$$

(2)

where for brevity, we have assumed A_r to be constant. Obviously, in Equation (2) the phase of the tilt reference plane wave φ_r(x, y) is not a constant but a linear distribution on recording plane ${\mathrm{P}}_{\mathrm{H}}$ given by

$${\phi }_r\left(x,y\right)=\frac{2\pi }{\lambda }(x\cos {\theta }_x+y\cos {\theta }_y),$$

(3)

where $\lambda$ is the wavelength of the laser and ${\theta }_x$ and ${\theta }_y$ are the off-axis angles along the x and y directions. From Equations (1) and (2), the intensities for the three interferograms are described by

$$I_1=A_o^2+A_r^2+2A_o{A}_r\cos \left({\phi }_o-{\phi }_r\right),$$

(4)

$$I_2=A_o^2+A_r^2+2A_o{A}_r\cos \left({\phi }_o-{\phi }_r-\Delta {\phi }_r{}_1\right),$$

(5)

$$I_3=A_o^2+A_r^2+2A_o{A}_r\cos \left({\phi }_o-{\phi }_r-\Delta {\phi }_{r1}-\Delta {\phi }_{r2}\right),$$

(6)

where $\Delta {\phi }_r{}_1$ and $\Delta {\phi }_{r2}$ are unknown phase shifts that need to be determined. Subtracting Equations (5) and (6) from Equation (4) respectively, we have

$$I_2-I_1=4A_o{A}_r[\sin ({\phi }_o-{\phi }_r-\Delta {\phi }_{r1}/2)\sin \left(\Delta {\phi }_{r1}/2\right)],$$

(7)

$$I_3-I_1=4A_o{A}_r[\sin ({\phi }_o-{\phi }_r-\Delta {\phi }_{r1}/2-\Delta {\phi }_{r2}/2)\sin (\Delta {\phi }_{r1}/2+\Delta {\phi }_{r2}/2)].$$

(8)

From Equations (7) and (8), we derive the following expressions:

$$\begin{array}{l}{A}_o\sin ({\phi }_o-{\phi }_r)=\frac{1}{4A_r\sin (\Delta {\phi }_r{}_2/2)}\times \\ \left\{\frac{\sin (\Delta {\phi }_r{}_1/2)}{\sin [(\Delta {\phi }_r{}_1+\Delta {\phi }_r{}_2)/2]}(I_1-I_3)-\frac{\sin [(\Delta {\phi }_r{}_1+\Delta {\phi }_r{}_2)/2]}{\sin (\Delta {\phi }_r{}_1/2)}(I_1-I_2)\right\}\end{array},$$

(9)

$$\begin{array}{l}{A}_o\cos ({\phi }_o-{\phi }_r)=\frac{1}{4A_r\sin (\Delta {\phi }_r{}_2/2)}\times \\ \left\{\frac{\cos (\Delta {\phi }_r{}_1/2)}{\sin [(\Delta {\phi }_r{}_1+\Delta {\phi }_r{}_2)/2]}(I_1-I_3)-\frac{\cos [(\Delta {\phi }_r{}_1+\Delta {\phi }_r{}_2)/2]}{\sin (\Delta {\phi }_r{}_1/2)}(I_1-I_2)\right\}\end{array}$$

(10)

which are the imaginary and the real parts of the following complex amplitude:

$$\begin{array}{l}{\mathit{O}}_1\left(x,y\right)=A_o\exp \left[-i({\phi }_o-{\phi }_r)\right]\\ =A_o[\cos ({\phi }_o-{\phi }_r)-i\sin ({\phi }_o-{\phi }_r)]\end{array}$$

(11)

Substituting Equations (9) and (10) into (11), we have

$$\begin{array}{l}{\mathit{O}}_1=\frac{1}{4A_r\sin (\Delta {\phi }_r{}_2/2)}\times \\ \left\{\frac{\exp (i\Delta {\phi }_r{}_1/2)}{\sin [(\Delta {\phi }_r{}_1+\Delta {\phi }_r{}_2)/2]}(I_1-I_3)-\frac{\exp [i(\Delta {\phi }_r{}_1+\Delta {\phi }_r{}_2)/2]}{\sin (\Delta {\phi }_r{}_1/2)}(I_1-I_2)\right\}\end{array}.$$

(12)

Note that from Equation (11), we can see that this complex field is related to the original object wave $\mathit{O}$ (see Equation (1)) as follows:

$$\mathit{O}={\mathit{O}}_1\exp \left(-i{\phi }_r\right).$$

(13)

In order to extract $\mathit{O}$, we, therefore, need to know ${\mathit{O}}_1$ and ${\phi }_r$. Let us first concentrate on finding ${\mathit{O}}_1$. According to Equation (12), ${\mathit{O}}_1$ can be found with known intensities I₁, I₂, I₃ along with unknown, to be determined, phase shifts $\Delta {\phi }_r{}_1$ and $\Delta {\phi }_{r2}$.

It is known that the precise extraction of phase shifts $\Delta {\phi }_r{}_1$ and $\Delta {\phi }_{r2}$ is critical to the reconstruction of the object wave. In TGPSI, many time-consuming iterative algorithms are used to search for the actual values of the phase shift. We propose a powerful and reliable method to extract phase-shift values based on the theory developed so far. To this end, we first analyze the spectrum of the interferograms. Equations (4)–(6) can be rewritten as

$$I_1=A_o^2+A_r^2+A_o{A}_r\exp \left(-i{\phi }_o\right)\exp \left(i{\phi }_r\right)+A_o{A}_r\exp \left(i{\phi }_o\right)\exp \left(-i{\phi }_r\right),$$

(14)

$$\begin{array}{l}{I}_2=A_o^2+A_r^2+A_o{A}_r\exp \left(-i{\phi }_o\right)\exp \left(i{\phi }_r\right)\exp \left(i\Delta {\phi }_{r_1}\right)\\ +A_o{A}_r\exp \left(i{\phi }_o\right)\exp \left(-i{\phi }_r\right)\exp \left(-i\Delta {\phi }_{r1}\right)\end{array},$$

(15)

$$\begin{array}{l}{I}_3=A_o^2+A_r^2\\ +A_o{A}_r\exp \left(-i{\phi }_o\right)\exp \left(i{\phi }_r\right)\exp \left(i\Delta {\phi }_{r1}\right)\exp \left(i\Delta {\phi }_{r2}\right)\\ +A_o{A}_r\exp \left(i{\phi }_o\right)\exp \left(-i{\phi }_r\right)\exp \left(-i\Delta {\phi }_{r1}\right)\exp \left(-i\Delta {\phi }_{r2}\right)\end{array},$$

(16)

in order to obtain phase shifts $\Delta {\phi }_r{}_1$ and $\Delta {\phi }_{r2}$, Fourier transform (FT) operations on Equations (14)–(16) are needed, and they are

$$F_1\left(u,v\right)=F_A\left(u,v\right)+A_r^2\delta \left(u,v\right)+A_r\left[F_O\left(u+u_p,v+v_p\right)+F_O^{\ast }\left(-u+u_p,-v+v_p\right)\right],$$

(17)

$$\begin{array}{l}{F}_2\left(u,v\right)=F_A\left(u,v\right)+A_r^2\delta \left(u,v\right)+A_r{F}_O\left(u+u_p,v+v_p\right)\exp \left(i\Delta {\phi }_{r1}\right)\\ +A_r{F}_O^{\ast }\left(-u+u_p,-v+v_p\right)\exp \left(-i\Delta {\phi }_{r1}\right)\end{array},$$

(18)

$$\begin{array}{l}{F}_3\left(u,v\right)=F_A\left(u,v\right)+A_r^2\delta \left(u,v\right)\\ +A_r{F}_O\left(u+u_p,v+v_p\right)\exp \left(i\Delta {\phi }_{r1}\right)\exp \left(i\Delta {\phi }_{r2}\right)\\ +A_r{F}_O^{\ast }\left(-u+u_p,-v+v_p\right)\exp \left(-i\Delta {\phi }_{r1}\right)\exp \left(-i\Delta {\phi }_{r2}\right)\end{array},$$

(19)

where symbol ‘*’ presents the conjugate operation. F₁(u, v), F₂(u, v) and F₃(u, v) are the Fourier transforms of I₁, I₂ and I₃, respectively. The first term F_A(u, v) in the right side of Equations (17)–(19) is the spectrum of the object intensity, distributing in the central part of the spectrum plane. Because the reference intensities I_r is a constant, the second term of the three equations give a δ-function, showing a bright point at the origin (0, 0) on the spectrum plane. The last two terms in the right side of Equations (17)–(19) are the shifted spectra of the object wave and its conjugate, where F_O(u + u_p, v + v_p) is the Fourier transform of A_oexp(−iφ_o)exp(iφ_r) and F_O*(−u + up,−v + vp) is the Fourier transform of A_oexp(iφ_o)exp(−iφ_r). They are confined in two relatively small areas, but the centers are shifted to points (−u_p, −v_p) and (u_p, v_p) on the spectrum plane due to the tilt reference employed. In some cases of complicated object wave, points (−u_p, −v_p) and (u_p, v_p) may be difficult to locate as they are hidden within the spectra of F_O(u + u_p, v + v_p) or F_O*(−u + u_p, −v + v_p) due to the slight-tilt reference angle (fraction of a degree). However, we can perform interference of two plane waves as the spectrum of such interference contains δ-functions centered at (0,0), (−u_p, −v_p), and (u_p, v_p), which can be found easily. After (−u_p, −v_p), and (u_p, v_p) are determined, the spectrum at these points can be used to extract unknown phase shifts Δφ_r1 and Δφ_r2, to be explained below. Indeed, if we isolate the spectra at points (−u_p, −v_p) and (u_p, v_p) in the third term of Equations (17) and (18), we have $A_r{F}_O\left(u+u_p,v+v_p\right)$ and $A_r{F}_O\left(u+u_p,v+v_p\right)\exp \left(i\Delta {\phi }_{r1}\right)$, respectively $\Delta {\phi }_{r1}$ can be extracted by subtracting the argument of the above two terms and by evaluating at $u=-u_p$ and $v=-v_p$ to give:

$$\Delta {\phi }_{r1}=\arg [A_r{F}_O\left(0,0\right)\exp \left(i\Delta {\phi }_{r1}\right)]-\arg \left[A_r{F}_O\left(0,0\right)\right].$$

(20)

Alternatively, we can also use their conjugate terms, i.e., $A_r{F}_O^{\ast }\left(-u+u_p,-v+v_p\right)$ and $A_r{F}_O^{\ast }\left(-u+u_p,-v+v_p\right)\exp \left(-i\Delta {\phi }_{r1}\right)$. However, in this case, we need to evaluate the terms at $u=u_p$ and $v=v_p$ to give $\Delta {\phi }_{r1}=\arg \left[A_r{F}_O^{\ast }\left(0,0\right)\right]-\arg [A_r{F}_O^{\ast }\left(0,0\right)\exp \left(-i\Delta {\phi }_{r1}\right)]$.

Similarly, we extract $\Delta {\phi }_{r2}$ from the third terms of Equations (18) and (19). Again, we use $u=-u_p$ and $v=-v_p$, and we find

$$\Delta {\phi }_{r2}=\arg \left[A_r{F}_O\left(0,0\right)\exp \left(i\Delta {\phi }_{r1}\right)\exp \left(i\Delta {\phi }_{r2}\right)\right]-\left[\arg [A_r{F}_O\left(0,0\right)\exp \left(i\Delta {\phi }_{r1}\right)]\right],$$

(21)

where arg [ . ] in the above equations denotes taking the argument of a complex value in the square bracket. Equations (20) and (21) use only a simple subtraction operation to extract unknown phase shifts $\Delta {\phi }_{r1}$ and $\Delta {\phi }_{r2}$ without any iteration. This is the first contribution of using the proposed small-tilt reference.

Our next goal is to find object wave $\mathit{O}$. Now with $\Delta {\phi }_{r1}$ and $\Delta {\phi }_{r2}$ already extracted, we can calculate ${\mathit{O}}_1$ from Equation (12). $\mathit{O}$ and ${\mathit{O}}_1$ are related by Equation (13) through ${\phi }_r$ as follows:

$$\mathit{O}={\mathit{O}}_1\exp \left(i{\phi }_r\right)={\mathit{O}}_1\exp \left[i\frac{2\pi }{\lambda }\left(x\sin {\theta }_x+y\sin {\theta }_y\right)\right].$$

(22)

We can calculate off-axis angles ${\theta }_x$ and ${\theta }_y$ by the following relationships [1]

$$\sin {\theta }_x=\lambda \frac{u_p}{M{d}_x},\sin {\theta }_y=\lambda \frac{v_p}{N{d}_y},$$

(23)

where M and N are the total pixel numbers along the horizontal and vertical directions of the hologram. d_x and d_y are the corresponding pixel size in the two directions. Note that we have been using normalized spatial frequencies, u and v. Hence u_p and v_p are divided by the total length of the Charge-coupled Device (CCD) linear dimension, Md_x and Md_y. Since u_p and v_p have already been located, we can determine the off-axis angles. Once the angles are found, object wave $\mathit{O}$ is completely determined from Equation (22), and finally the complex amplitude of the original object can be calculated by performing backward Fresnel diffraction [1].

The whole process of the proposed new algorithm for finding the unknown phase shifts and object wave reconstruction can be summarized in the following steps:

Step 1: Set and determine the reference tilt angle before the test object is put in the optical path. Experimentally, we fix the tilt angle when dozens of fringes appear on the CCD from the interference of two plane waves. We label I₀ as the intensity pattern of the interference between the two plane waves. We then put in the object and record I₁, I₂ and I₃.

Step 2: Perform FT operations on the fringe pattern from the plane wave interference in Step 1 and search the brightest points on the spectral plane (not the point at the origin of the spectral plane) and locate the coordinates of the found points as (−u_p, −v_p) or (u_p,v_p). Perform FT operations on I₁, I₂ and I₃ and store the complex values of these two points. In most practical situations, (−u_p, −v_p) or (u_p, v_p) can also be found from the spectrum of either one of I₁, I₂ and I₃ without the need of two-plane wave interference.

Step 3: Calculate phase shift $\Delta {\phi }_{r1}$ and $\Delta {\phi }_{r2}$ by Equations (20) and (21) using the values stored in step 2.

Step 4: Reconstruct ${\mathit{O}}_1$ by Equation (12).

Step 5: Find the tilt angle by Equation (23) from the located coordinates of (−u_p, −v_p) or (u_p, v_p).

Step 6: Find $\mathit{O}$ by using Equation (22).

Step 7: Recover the original object image by backward Fresnel diffraction of $\mathit{O}$.

3. Computer Simulation and Optical Experiments

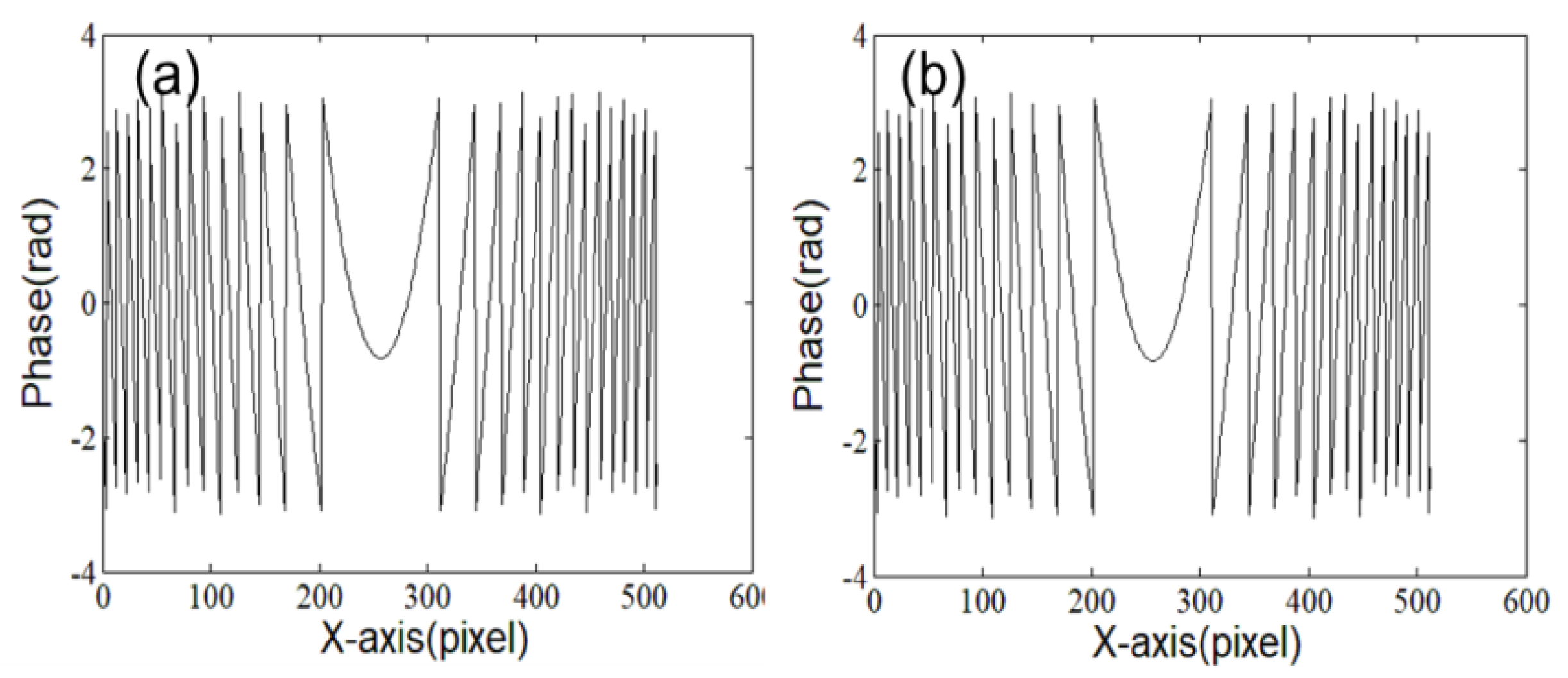
3.1. Computer Simulation

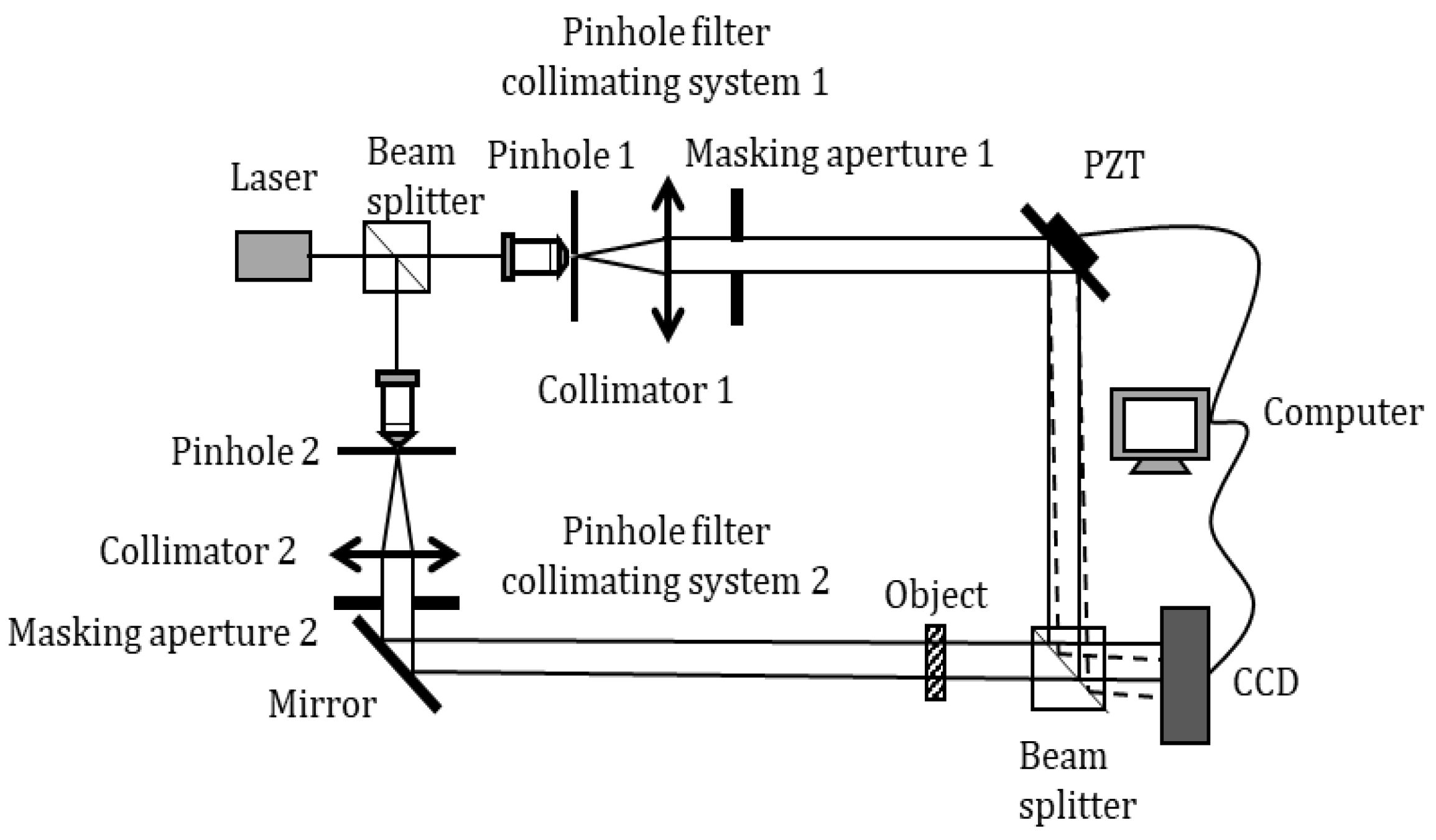
We have carried out a series of computer simulations to verify the effectiveness of the proposed method before any optical experiments. In these simulations, many elliptical surfaces with different parameters have been used as reflecting target objects. A plane wave of 532 nm illuminates these surfaces and is then reflected back onto the CCD in the recording setup illustrated in Figure 1.

In the simulation setup in Figure 1 [20], there were 512 × 512 pixels with 15 μm × 15 μm size on the CCD and the recording distance was set as z = 216.5 mm (all the parameters satisfy the sampling theory to avoid aliasing [1]). With the paraxial approximation of an elliptical wave, we set the phase distribution on the original object plane Po, which is tangential to the surface at the vertex, as 4πh(x,y)/λ, with h the surface depth determined by radius of curvature R. We used

$$h(x,y)=\frac{8x^2}{25R}+\frac{y^2}{2R}.$$

(24)

Accounting for the possible amplitude variation of an object wave, a Gaussian amplitude intensity distribution of the object wave in plane Po was introduced, decreasing gradually from the center of maximum 1 to the edge of minimum 0.7. Two-dimensional Fresnel diffraction makes the complex amplitude in plane Po give the object wave $\mathit{O}\left(x,y\right)$, in the recording plane P_H. Three different interferograms by two reference phase shifts are computer-generated. In this simulation we set two phase-shift values of 1 and 0.6 rad respectively, and we give only a few results with R = 2000 mm as example. The reference wave is a plane wave with a slight tilt angle along both the x-axis and the y-axis.

As for optical experimental procedures, in order to accurately determine the small tilt angle of the reference light, we introduce a plane wave as the object wave to obtain I₀. We control the tilt angle of the reference until there are dozens of fringes appearing on the CCD. We then obtain the corresponding spectrum to find (−u_p, −v_p) and (u_p, v_p).

Fast Fourier Transform (FFT) operations are carried out on the interferograms on the computer. Figure 2a shows the pattern of $I_0$ and its corresponding spectrum is shown in Figure 2d. The two delta functions are located at (−u_p, −v_p) and (u_p,v_p), which have been zoomed in for visual inspection. Figure 2b shows the pattern of $I_1$ and its corresponding spectrum is shown in Figure 2e. Note that the zero frequency has been suppressed for display purposes in Figure 2d,e. Figure 2c,f show the pattern of $I_2$ and $I_3$, respectively.

By searching the maximum value of the spectrum intensity from the FT of I₀, coordinates (−u_p, −v_p) and (u_p, v_p) are found to be (−45, 45) and (45, −45). Substituting u_p = 45, v_p = 45, λ = 0.532 μm, d_x = 15 μm, d_y = 15 μm and M = N = 512 into Equation (23), the reference wave angles in the x and y directions are found to be both approximately 0.18 degrees. After the spectrum coordinates (−u_p, −v_p) and (u_p, v_p) are found, the phase angle of the complex values of the spectra at pixel (−45, 45) or (45, −45) can be calculated and then the two phase shifts are extracted by subtraction operation using Equations (20) and (21).

The phase shifts, $\Delta {\phi }_{r1}$ and $\Delta {\phi }_{r2}$, calculated by our proposed method are 1.0002 rad and 0.6003 rad, respectively. The two phase shifts with errors of 0.0002 and 0.0003 rad are accurate enough in the non-iterative GPSI method. These phase shift errors come from the digital resolution on the FT spectral plane.

Using the three interferograms and the two extracted phase shifts, wavefront ${\mathit{O}}_1$ is retrieved through Equation (12) and then corrected by Equation (22) with the tilt angles of about θ_x = 0.18 degrees and θ_y = 0.18 degrees. Back Fresnel diffraction was carried out to obtain the object on the object plane.

Figure 3a,b shows the amplitude distributions for the original object wave and the reconstructed object wave. In the simulation setup, the intensity distribution was designed as a Gaussian function to simulate an object wave amplitude. That is to say, the object wave recorded has not only phase distribution but also amplitude variation. Although the amplitude of the original object wave is not uniform, the proposed method can recover it ideally, because there is almost no difference between Figure 3a,b. The phase of the original object wave and its reconstructed phase are shown in Figure 3c,d, respectively. It is difficult for us to find any difference between the two figures.

To inspect the phase distribution of the object wave quantitatively, the phase across the center of the zones are plotted in Figure 4. For comparison, the original phase and the reconstructed phase are shown in Figure 4a,b, respectively. Obviously Figure 4a,b are almost identical.

3.2. Optical Experiment

Optical experiments have also been carried out with the optical setup shown in Figure 5 with a 532 nm laser, and the target object is a USAF resolution target. The CCD installed has a recording chip with a resolution of 1392 by 1040 pixels, and the pixel size is 6.45 × 6.45 μm.

In our experiment, the phase shift is generated by a phase shifter. The results are illustrated in Figure 6. The three interferograms with unknown phase shifts are shown in Figure 6a–c. Figure 6d is the spectrum of Figure 6a, where the center part is enlarged and shown in the circle. We have used the spectrum of I₁ instead of I₀ to locate the coordinates (−u_p, −v_p) and (u_p, v_p) and they are found to be (−34, 0) and (34, 0). The reason is that there are two bright spots in the spectrum already. The enlarged portion of the spectrum clearly illustrates the two bright spots. Subsequently, the reference slight tilt angle can be calculated by Equation (23) and the result is about θ_x = 0.1 degree in the experiment. Phase shifts are calculated by using the brightest point at these locations on the three Fourier spectra of holograms I₁, I₂ and I₃. The phase shifts calculated using the proposed method are 0.5211 and 1.8018 rad. Figure 6e is the intensity distribution of the reconstructed image, and the reconstructing distance is 10.9 cm. Both the accuracy of the phase shift extraction and the quality of the reconstructed image are excellent.

4. Conclusions

We have proposed a method to extract unknown phase shifts in TGPSI with a slight-tilt reference. The major merit of the proposed method is that only two subtractions are used to calculate the unknown phase shifts. The technique is simple and yet powerful as no iteration is needed. It is convenient and accurate. The method needs only three interferograms to complete the phase shift extraction and wavefront reconstruction without iteration. Simulations and optical experiments have verified the feasibility and validity of the proposed method. It should be noted that this method works well when the zero-frequency component in the object spectrum is sufficiently large because the location of this spectrum is easy to find under such condition. For some extreme cases of complicated object waves, a slightly larger tilt angle is needed and the advantage of the efficient use of the space-bandwidth product is not obvious when this method is compared to the off-axis technique. This method is expected to be an attractive alternative for wide-ranging digital holography applications as it allows the full and efficient use of the space-bandwidth product of the limited resolution of digital recording devices because a slight tilt reference of 0.1 degrees is used.