Pull-Based Distributed Event-Triggered Circle Formation Control for Multi-Agent Systems with Directed Topologies

Abstract

This paper investigates a circle formation control problem for multi-agent systems with directed topologies via pull-based distributed event-triggered control principles. Firstly, for scenarios of continuous communication, a pull-based distributed event-triggered principle is proposed. It is proved that if the communication topology is irreducible and has a directed spanning tree, the event-triggered coupling continuous communication can lead multiple agents to form a desired circle formation. Then, the results are extended to discontinuous communication scenarios, where all the agents use a model of their neighborhoods to generate self-triggered instants without monitoring continuously, update the local controller here, and if necessary, local broadcast information based on the adopted control inputs to neighboring agents. In addition, Zeno behavior can be excluded during the whole process. Finally, numerical simulation results are given to demonstrate the effectiveness of the proposed circle formation control methods.

1. Introduction

In recent years, many studies have been performed on distributed multi-agent systems (MASs) [1,2,3,4,5]. Among which, data sharing is regarded as a general scheme in terms of distributed MASs problems [6,7]. In particular, communication costs play a crucial role in determining the number of messages send or receive by agents. Note that the commonly used continuous-time communication scheme was built on the assumption of sufficiently large communication bandwidth. However, from a practical point of view, it is not desirable. Concerning this problem, a discrete-time communication scheme was proposed based on periodic information exchange synchronously or asynchronously among agents [8]. Nevertheless, considering the increasing number of agents and the robustness requirements against internal uncertainties and external disturbances, it is unnecessary to exchange information and update the control actions for all agents simultaneously.

As a particular sampling strategy, event-triggered control is an alternative to periodic sample control methods [9,10,11,12,13]. The distinct character of event-triggered control is that to achieve the desired task with a certain level of performance, control actions update only when a specific event occurs, and as a result, the trade-offs are mitigated between communication, computation, and actuator effort. Currently, event-triggered control has been studied extensively in distributed MASs [14,15], centralized MASs [16,17], as well as in many other MASs’ cases. Moreover, event-triggered control has already been proven superior to the periodic sample control methods. It is also shown particularly useful in MASs’ applications, such as consensus problems [10,11], formation control [12,13], collision avoidance [18], and tracking control [19,20,21]. However, for event-triggered conditions in MASs [22,23], it still remains a challenge to exclude Zeno behavior, i.e., the system generates an infinite number of samplings over a finite time interval. Specifically, a sufficient condition to rule out Zeno behavior is to ensure that the event-triggered interval is strictly positive lower bounded [24,25].

Different from consensus-type algorithms coupling with event-triggered control, in this paper, the attention is paid to the circle formation control problem for MASs, aiming at guiding multiple agents to form and maintain a predetermined geometry. The work in [26] is regarded as the original work, in which the continuous-time control protocol was designed to address the distributed circle formation problem. In [12], protocols combined with state-dependent event-triggered was proposed to solve the circle formation problem for first-order MASs, the framework of which enables the event-triggered condition to rule out Zeno behavior automatically. In [27], encoder-decoder strategies were used to achieve circle formation asymptotically with a finite-level uniform quantization, where the quantizer is not saturated in bounded communication as the number of agents increases. Moreover, based on [27], in order to address the problem circle formation problem for MASs with a limitation of communication, [13] investigated an innovative algorithm that relies on the combination of quantitative communication techniques and event-triggered control.

In this paper, we mainly focus on the pull-based distributed event-triggered circle formation control for MASs over a class of weight-unbalanced digraphs. In our work, all agents, similar to the Pioneer 3-DX in [28], are equipped with a sensor to perceive the distances from themselves to the nearest neighbors in a counterclockwise direction and the counterparts in the clockwise direction. At event-triggered instants, one agent updates its controller when broadcasting its states to all its out-neighbors immediately. However, this does not indicate that the agent has to send a request to its in-neighbors at the event-triggered instance to ask for the state information. In order to distinguish it from event-triggered, this sort of feedback is called pull-based event-triggered. The critical advantage of the pull-based strategy is to avoid continuous transmission requests. It is worth noting that there are still challenges remains in the investigated problem, such as how to design the pull-based event-triggered condition to determine the pulling instants, and can the circle formation problem of MASs over such interactive topology be solvable under the designed control law and event-triggered condition.The main contributions of this paper are listed as follows: firstly, combined with a pull-based event-triggered scheme, an alternative algorithm is designed to solve the circle formation problem for MASs with directed topology, where each agent obtains the state information of its neighbors and the weight function does not need a priori knowledge of any other parameters. Secondly, under the scenarios of discontinuous communication, a model-based self-triggered strategy is proposed based on the pull-based methods to reduce the number of control actions and communication without a significant performance reduction. At last, the existence of such a bound is a stronger result than just prove the absence of Zeno behavior.

The remainder of this paper is organized as below. In Section 2, preliminary definitions, and the problem formulation are presented. A distributed pull-based event-triggered principle for MASs with directed topologies is designed in Section 3. Section 4 extend the pull-based event trigger method to the scenario of discontinuous communication to form a self-trigger circle formation control scheme. Simulation results are given in Section 5 before we conclude in Section 6.

2. Preliminaries and Problem Statement

In this section, we first introduce related notions and concepts used in this paper and then formulate a concerned circle formation problem for MASs.

2.1. Preliminaries

For a finite set $\mathcal{S}$, $\left|\mathcal{S}\right|$ denotes the number of its elements. For a vector or a matrix A, $\parallel A\parallel$ stands for its $\mathrm{Euclidean}$ norm, ${\parallel A\parallel }_{\infty }$ stands for its ∞-norm and $A^T$ is its transpose. ${\mathbf{1}}_N$ and ${\mathbf{0}}_N$ are the N dimension column vectors with all entries 1 and 0, respectively. The matrix $\mathrm{diag}\{a_1,a_2,\dots ,a_N\}$ denotes a diagonal matrix with diagonal entries $a_1,a_2,\dots ,a_N$. $\rho (.)$ denotes the spectral radius of matrix, and ${\rho }_2(.)$ stands for the minimum positive eigenvalue of matrix with positive eigenvalues.

For a directed graph $\mathcal{G}$, $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{A})$, where $\mathcal{V}=\{1,2,\dots ,N\}$ is a set of nodes, $\mathcal{E}=\mathcal{V}\times \mathcal{V}$ denotes a set edges, and $\mathcal{A}=\left[a_{ij}\right]\in {\mathbb{R}}^{N\times N}$ stands for a weighted adjacency matrix, in which $\mathbb{R}$ denotes a set of real numbers. In the directed graph $\mathcal{G}$, for all $i\in \mathcal{V}$, $(i,i)\notin \mathcal{E}$. Namely, for edge $(j,i)\in \mathcal{E}$, with an start of node j and an end of node i, agent i can get state information from agent j. To be specific, the edge $(i,j)$ links with the elements $a_{ij}$ of a weighted adjacency matrix $\mathcal{A}$, $a_{ij}>0$ if and only if $(i,j)\in \mathcal{E}$, otherwise $a_{ij}=0$. Although the opposite direction of transmission may not exist or have a different weight value $a_{ij}$. Given any two distinct nodes i and j, if there exists a directed path from j to i, the directed graph $\mathcal{G}$ is strongly connected.

Moreover, agent j is called an in- and out-neighbor of agent i. ${\mathcal{N}}_i^{in}=\{j\in \mathcal{V}|a_{ij}>0\}$ and ${\mathcal{N}}_i^{out}=\{j\in \mathcal{V}|a_{ji}<0\}$ are used to demonstrate the in- and out-neighbor set of agent i, respectively. Both the in- and out-degree of ith agent are denoted by $d_i^{in}={\sum }_{j=1}^N{a}_{ji}$, and $d_i^{out}={\sum }_{j=1}^N{a}_{ij}$, respectively. We define $\mathrm{Laplacian}$ matrix of $\mathcal{G}$ by $\mathcal{L}=\mathcal{D}-\mathcal{A}$, where $\mathcal{D}=\mathrm{diag}\{d_1^{out},d_2^{out},\dots ,d_N^{out}\}$. Accordingly, the eigenvalues of $\mathcal{L}$ can be listed in a descending order as ${\lambda }_N\ge \dots \ge {\lambda }_2\ge {\lambda }_1=0$, where ${\lambda }_N=\rho (\mathcal{L})$ denotes the spectral radius of $\mathcal{L}$.

The lemmas listed below are applied to facilitate the analysis in the following paper.

Lemma 1.

For any $x,y\in \mathbb{R}$ and $a>0$, the following properties are applied:

$$\begin{array}{cc}\hfill & 1.xy\le \frac{a}{2}{x}^2+\frac{1}{2a}{y}^2;\hfill \\ \hfill & 2.(x^2+y^2)\le {(x+y)}^2,ifxy\ge 0.\hfill \end{array}$$

(1)

Lemma 2

([29]). For a strong connected digraph $\mathcal{G}$, composed of a spanning tree, the vector $\xi ={[{\xi }_1,{\xi }_2,\dots ,{\xi }_N]}^T>0$ is the left eigenvector corresponding to zero eigenvalue of $\mathrm{Laplacian}$ matrix $\mathcal{L}$, that satisfies ${\sum }_{i=1}^N{\xi }_i=1$ and ${\xi }^T\mathcal{L}={\mathbf{0}}_N$. Furthermore, ${\mathcal{L}}^T\mathsf{\Theta }+\mathsf{\Theta }{\mathcal{L}}^T$ is semi-positive definite with all rows sum up to zeros and has zero eigenvalue with algebraic dimension one, where $\mathsf{\Theta }=\mathrm{diag}\{{\xi }_1,{\xi }_2,\dots ,{\xi }_N\}$.

2.2. Problem Formulation

Considering an MAS with N ($N\ge 2$) mobile agents, as shown in Figure 1, the agents are initially located on a predefined circle, and no pair of agents hold the same position at the same time. For simplicity, the agents are labeled counterclockwise and the position of agent i, $i\in (1,2,\dots N)$, is measured by angles $x_i(t)$. Typically, initial locations of all agents are set to satisfy:

$$0\le x_1(0)<\dots <x_i(0)<x_{i+1}(0)<\dots <x_N(0)<2\pi .$$

(2)

As we can see in this case, each agent only has two neighbors, i.e., in front of or behind itself. The following rules are given to denote two neighbors of the mobile agent i:

$${\mathcal{N}}_i=\{i^{+},i^{-}\},$$

(3)

where

$$i^{+}=\left\{\begin{array}{cc}i+1,\hfill & \mathrm{when}i=1,2,\dots ,N-1,\hfill \\ 1,\hfill & \mathrm{when}i=N,\hfill \end{array}\right.$$

and

$$i^{-}=\left\{\begin{array}{cc}i-1,\hfill & \mathrm{when}i=2,3,\dots ,N,\hfill \\ N,\hfill & \mathrm{when}i=1.\hfill \end{array}\right.$$

The dynamics of agents for circle formation control are described as:

$${\dot{x}}_i(t)=u_i(t),i\in \mathcal{V},$$

(4)

where $x_i\in \mathbb{R}$ stands for the scalar state of agent i, and $u_i\in \mathbb{R}$ denotes its control input.

At time t in counterclockwise, $y_i(t)\in \mathbb{R}$ are described as the angular distance from agent i to agent $i^{+}$ measured by agent i, which yields to:

$$y_i(t)=\left\{\begin{array}{cc}{x}_{i^{+}}(t)-x_i(t)+2\pi ,\hfill & \mathrm{when}i=N,\hfill \\ x_{i^{+}}(t)-x_i(t),\hfill & \mathrm{when}i=1,2,\dots ,N-1,\hfill \end{array}\right.$$

(5)

where $y(t)={[y_1(t),y_2(t),\dots ,y_N(t)]}^T\in {\mathbb{R}}^N$, and ${\sum }_{i=1}^N{y}_i(t)=2\pi$ always holds.

Then, we define:

$$d={[d_1,d_2,\dots ,d_i,\dots ,d_N]}^T$$

(6)

determines the desired circle formation for $\mathrm{MASs}$, where $d_i\in \mathbb{R}$ stands for the desired angular distance between agent i and agent $i^{+}$. A desired circle formation is $\mathrm{achievable}$ if and only if d satisfies $d_i>0$ and ${\sum }_{i=1}^N{d}_i=2\pi$, $i=1,2,\dots ,N$.

The definition of the circle formation problem for MASs is described as follows:

Definition 1.

(Circle Formation Problem) Given an admissible circle formation characterized by d, a distributed control law $u_i(t,y_i(t)),i=1,2,\dots ,N$ is designed such that the solution to system (4) converges to the equilibrium point $x^{*}$ under initial condition (2). Namely, $y^{*}=d$ is satisfied.

3. Pull Based Event-Triggered Strategy

A sampled-date based way-point control law was designed in [26], shown as:

$$\begin{array}{c}\hfill u_i(t)=\frac{d_{i^{-}}}{d_i+d_{i^{-}}}{y}_i(t)-\frac{d_i}{d_i+d_{i^{-}}}{y}_{i^{-}}(t),\end{array}$$

(7)

where $i=0,1,2,\dots ,N$.

It has been approved that the continuous updating control protocol (7) can drive all agents to their equilibrium point $x^{*}$, but typically costs unnecessary transmission energy and communication bandwidth. To address this problem, we propose a pull-based event-triggered strategy. Particularly, the controllers of agents only update at discrete event instants. Meanwhile, continuous communication between neighboring agents maintain. Let an increasing sequence ($t_0^i,t_1^i,\dots ,t_k^i,\dots$) denotes the event instants of agent i, such that $y_i(t_k^i)$ is the state of of agent i at the k-th event instants. It is noteworthy that since all agents are asynchronously triggered, each agent has its sequence of events.

Based on the event triggered control, a distributed circle formation control law for agent i is designed as:

$$\begin{array}{c}\hfill u_i(t)=\frac{d_{i^{-}}}{d_{i^{-}}+d_i}{y}_i(t_k^i)-\frac{d_i}{d_{i^{-}}+d_i}{y}_{i^{-}}(t_{k^{,}}^{i^{-}}),t\in [t_k^i,t_{k+1}^i),\end{array}$$

(8)

Control law (8) suggests that the controller of agent i updates at its own event sequence ($t_0^i,t_1^i,\dots ,t_k^i,\dots$) and transmits this renewed state $y_i(t_k^i)$ to all its out-neighbours at the same time. For simplicity, assume ${\widehat{y}}_i(t)=y_i(t_k^i)$, ${\widehat{\delta }}_i(t)={\widehat{y}}_i(t)/d_i$, consequently, control law (8) can be rewritten as:

$$\begin{array}{c}\hfill u_i(t)=\frac{d_i{d}_{i^{-}}}{d_{i^{-}}+d_i}({\widehat{\delta }}_i(t)-{\widehat{\delta }}_{i^{-}}(t)),t\in [t_k^i,t_{k+1}^i).\end{array}$$

(9)

Substituting (5) and (9) into (4), a closed-loop form of agent i can be rewritten by ${\delta }_i$ as:

$${\dot{\delta }}_i(t)=\sum _{j\in {\mathcal{N}}_i^{in}}\frac{d_j}{d_i+d_j}\left({\widehat{\delta }}_j(t)-{\widehat{\delta }}_i(t)\right),t\ge 0.$$

(10)

Define $e_i(t)={\widehat{\delta }}_i(t)-{\delta }_i(t)$, then a compact form of the system is derived as:

$$\begin{array}{c}\hfill \dot{\delta }(t)=-L_d^T(\delta (t)+e(t)),t\in [t_k^i,t_{k+1}^i)\end{array}$$

(11)

where $\delta (t)=[{\delta }_1(t),{\delta }_2(t), \dots ,{\delta }_N(t)]\in {\mathbb{R}}^N$, and $e(t)=[e_1(t),e_2(t), \dots ,e_N(t)]\in {\mathbb{R}}^N$, and

$$L_d=\left[\begin{array}{ccccc}\frac{d_2}{d_2+d_1}+\frac{d_N}{d_N+d_1}& -\frac{d_1}{d_2+d_1}& \dots & 0& -\frac{d_1}{d_N+d_1}\\ -\frac{d_2}{d_2+d_1}& \frac{d_3}{d_3+d_2}+\frac{d_1}{d_2+d_1}& \dots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& \dots & \frac{d_N}{d_N+d_{N-1}}+\frac{d_{N-2}}{d_{N-1}+d_{N-2}}& -\frac{d_{N-1}}{d_N+d_{N-1}}\\ -\frac{d_N}{d_N+d_1}& 0& \dots & -\frac{d_N}{d_N+d_{N-1}}& \frac{d_1}{d_N+d_1}+\frac{d_{N-1}}{d_N+d_{N-1}}\end{array}\right].$$

(12)

Define:

$$\begin{array}{c}\hfill \mathsf{\Lambda }=\frac{1}{2}(L_d\mathsf{\Theta }+\mathsf{\Theta }{L}_d^T),\end{array}$$

(13)

where according to Lemma 2, $\mathsf{\Lambda }$ is semi-positive definite. The eigenvalues of $\mathsf{\Lambda }$ can be arranged in an ascending order as $0={\gamma }_1\le {\gamma }_2\le \dots \le {\gamma }_N$.

Let

$$\begin{array}{c}\hfill \mathsf{\Psi }=\mathsf{\Theta }-\xi {\xi }^T.\end{array}$$

(14)

From (14), we can obtain that $\mathsf{\Psi }$ has a zero eigenvalue and its eigenvalues increasingly ordered as $0={\nu }_1\le {\nu }_2\le ...\le {\nu }_N$. We define the eigenvalues of $L_d{L}_d^T$ by $0={\omega }_1\le {\omega }_2\le ...\le {\omega }_N=\rho (L_d{L}_d^T)$. Hence, for an arbitrary vector $\delta (t)$, the following inequalities are applied:

$$\begin{array}{c}\hfill {\gamma }_2{\delta }^T(t)\delta (t)\le {\delta }^T(t)\mathsf{\Lambda }\delta (t),\end{array}$$

(15)

$$\begin{array}{c}\hfill {\delta }^T(t)\mathsf{\Psi }\mathsf{\Psi }\delta (t)\le {\nu }_N^2{\delta }^T(t)\delta (t).\end{array}$$

(16)

Combining (15) and (16), we have:

$$\begin{array}{c}\hfill \mathsf{\Lambda }\ge \frac{{\gamma }_2}{{\nu }_N^2}\mathsf{\Psi }\mathsf{\Psi },\end{array}$$

(17)

$$\begin{array}{c}\hfill L_d{L}_d^T\ge \frac{{\gamma }_2}{{\nu }_N^2}\mathsf{\Psi }\mathsf{\Psi }\end{array}$$

(18)

and

$$\begin{array}{c}\hfill \frac{{\gamma }_N}{{\omega }_2^2}{L}_d{L}_d^T\ge \mathsf{\Lambda }\ge \frac{{\gamma }_2}{\rho (L_d{L}_d^T)}{L}_d{L}_d^T\end{array}$$

(19)

For the designed system (4) and control law (9), the event-triggered circle formation control for the distributed MASs can be solved according to Theorem 1.

Theorem 1.

Given any admissible circle formations characterized by d and considering system (4) and the designed control law (9) over a directed graph $\mathcal{G}$ containing a spanning tree, the Circle Formation Problem can be solved when the event-trigger condition designs as:

$$\begin{array}{c}\hfill t_{k+1}^i=\underset{\tau >t_k^i}{max}\left\{\tau :\parallel \tilde{e}(t)\parallel \ge \frac{\parallel \tilde{\delta }(t)\parallel }{\sqrt{2a\phi (t)}}\right\},\end{array}$$

(20)

where $0<a<\frac{2{\gamma }_2}{{\nu }_N^2}$, ${\tilde{\delta }}_i(t)=-{\sum }_{j=1}^N{L}_d^T(i,j){\delta }_j(t)$, ${\tilde{e}}_i(t)={\tilde{\delta }}_i(t_k^i)-{\tilde{\delta }}_i(t)$, and the condition

$$\begin{array}{cc}\hfill & \phi (t)=(1-\frac{a{\nu }_N^2}{2{\gamma }_2})\frac{{\gamma }_2}{\rho (L_d{L}_d^T)}-\frac{{\omega }_2\varphi (t)}{{\nu }_N}>0,\hfill \\ \hfill & \varphi (t)\ge \dot{s}(t)/s(t)\hfill \end{array}$$

(21)

holds simultaneously, where $s(t)$ is the weight function. That is, ${lim}_{t\to \infty }y(t)=d$.

Proof. 

By Lemma 2, we get:

$$\begin{array}{c}\hfill \sum _{i=1}^N{\xi }_i{\delta }_i(t+1)=\sum _{i=1}^N{\xi }_i{\delta }_i(t)=\dots =\sum _{i=1}^N{\xi }_i{\delta }_i(0).\end{array}$$

Combining (8) and (13), all conditions lead to:

$$\underset{t\to \infty }{lim}{\delta }_i(t)=\underset{t\to \infty }{lim}{\delta }_j(t)=\sum _{i=1}^N{\xi }_i{\delta }_i(0)=c,$$

(22)

where $c\in \mathbb{R}$ is a constant.

Additionally, ${\sum }_{i=1}^N{y}_i=2\pi$, $\forall t\ge 0$ always satisfies, and ${\sum }_{i=1}^N{d}_i=2\pi$. Together with $y_i(t)=d_i{\delta }_i(t)$, we conclude that $c=1$. More precisely, ${lim}_{t\to \infty }y(t)=d.$

Therefore, the results indicate that the desired circle formation can be reached by all mobile agents.

Consider a $\mathrm{Lyapunov}$ function as:

$$\begin{array}{c}\hfill V(t)=\frac{1}{2}s(t)\sum _i^N{\xi }_i{({\delta }_i(t)-\overline{\delta }(t))}^2=\frac{1}{2}s(t){\delta }^T(t)\mathsf{\Psi }\delta (t),\end{array}$$

(23)

where $\mathsf{\Psi }$ is the same diagonal matrix as in (14), and $\overline{\delta }(t)={\sum }_{i=1}^N{\xi }_i{\delta }_i(t)$ is the weighted average of $\delta (t)$.

As a result, $V(t)\le 0$ and $V(t)=0$ if the Circle Formation Problem is solvable. Further, the derivative of the $\mathrm{Lyapunov}$ function (23) along of the trajectories of the system yields to:

$$\begin{array}{c}\hfill \dot{V}(t)=s(t)\sum _{i=1}^N{\xi }_i({\delta }_i(t)-\overline{\delta }(t))({\dot{\delta }}_i(t)-\dot{\overline{\delta }}(t))+\frac{1}{2}\dot{s}(t){\delta }^T(t)\mathsf{\Psi }\delta (t).\end{array}$$

(24)

Owing to ${\xi }^T{L}_d^T=0$, it leads to:

$$\begin{array}{cc}\hfill \dot{\overline{\delta }}(t)& =\sum _{i=1}^N{\xi }_i{\dot{\delta }}_i(t)=\sum _{i=1}^N{\xi }_i\sum _{j=1}^N{L}_d^T(i,j){\widehat{\delta }}_j(t)\hfill \\ \hfill & =\sum _{i=1}^N{\widehat{\delta }}_j(t)\sum _{j=1}^N{\xi }_i{L}_d^T(i,j)=0.\hfill \end{array}$$

(25)

For clarity, (24) can be divided into two parts, the former part of (24) is calculated by:

$$\begin{array}{cc}\hfill & s(t)\sum _{i=1}^N{\xi }_i({\delta }_i(t)-\overline{\delta }(t)){\dot{\delta }}_i(t)\hfill \\ \hfill & =-s(t)\sum _{i=1}^N{\xi }_i({\delta }_i(t)-\overline{\delta }(t))\sum _{j=1}^N{L}_d^T(i,j){\widehat{\delta }}_j(t)\hfill \\ \hfill & =s(t)\sum _{i=1}^N{\xi }_i({\delta }_i(t)-\overline{\delta }(t)){\tilde{\delta }}_i(t_k^i)\hfill \\ \hfill & =s(t)\sum _{i=1}^N{\xi }_i({\delta }_i(t)-\overline{\delta }(t))({\tilde{e}}_i(t)+{\tilde{\delta }}_i(t))\hfill \\ \hfill & =s(t)\sum _{i=1}^N{\xi }_i({\delta }_i(t)-\overline{\delta }(t)){\tilde{e}}_i(t)-s(t)\sum _{i=1}^N\sum _{j=1}^N{\xi }_i({\delta }_i(t)-\overline{\delta }(t))L_d^T(i,j){\delta }_j(t)\hfill \\ \hfill & =s(t){\delta }^T(t)\mathsf{\Psi }\tilde{e}(t)-s(t){\delta }^T(t)\mathsf{\Lambda }\delta (t).\hfill \end{array}$$

(26)

Together with Lemma 1 and (17), (26) is rewritten as:

$$\begin{array}{cc}\hfill & s(t)\frac{a}{2}{\delta }^T(t)\mathsf{\Psi }\mathsf{\Psi }\delta (t)+s(t)\frac{1}{2a}{\tilde{e}}^T(t)\tilde{e}(t)-s(t){\delta }^T(t)\mathsf{\Lambda }\delta (t)\hfill \\ \hfill & \le -s(t)(1-\frac{a{\nu }_N^2}{2{\gamma }_2}){\delta }^T(t)\mathsf{\Lambda }\delta (t)+s(t)\frac{1}{2a}{\tilde{e}}^T(t)\tilde{e}(t),\hfill \end{array}$$

(27)

where $0<a<\frac{2{\gamma }_2}{{\nu }_N^2}$.

By using (19), the former part of (24) is rearranged as:

$$\begin{array}{cc}\hfill & -s(t)(1-\frac{a{\nu }_N^2}{2{\gamma }_2})\frac{{\gamma }_2}{\rho (L_d{L}_d^T)}{\delta }^T(t)L_d{L}_d^T\delta (t)+s(t)\frac{1}{2a}{\tilde{e}}^T(t)\tilde{e}(t)\hfill \\ \hfill & \le -s(t)\left((1-\frac{a{\nu }_N^2}{2{\gamma }_2})\frac{{\gamma }_2}{\rho (L_d{L}_d^T)}{\tilde{\delta }}^T(t)\tilde{\delta }(t)+\frac{1}{2a}{\tilde{e}}^T(t)\tilde{e}(t)\right).\hfill \end{array}$$

(28)

Meanwhile, from (18), the latter part of (24) is written as:

$$\begin{array}{c}\hfill \frac{\dot{s}(t){\delta }^T(t)\mathsf{\Psi }\mathsf{\Psi }\delta (t)}{2\mathsf{\Psi }}\le \dot{s}(t)\frac{{\omega }_2}{{\nu }_N}{\tilde{\delta }}^T(t)\tilde{\delta }(t).\end{array}$$

(29)

Together with (28) and (29), (24) can be rearranged as:

$$\begin{array}{c}\hfill \dot{V}(t)\le -s(t)\left((1-\frac{a{\nu }_N^2}{2{\gamma }_2})\frac{{\gamma }_2}{\rho (L_d{L}_d^T)}{\tilde{\delta }}^T(t)\tilde{\delta }(t)-\frac{\dot{s}(t){\omega }_2}{s(t){\nu }_N}{\tilde{\delta }}^T(t)\tilde{\delta }(t)-\frac{1}{2a}{\tilde{e}}^T(t)\tilde{e}(t)\right).\end{array}$$

(30)

Enforcing the event condition in (20), we can immediately obtain that $\dot{V}(t)\le 0$ and $\dot{V}(t)=0$ if and only if the Circle Formation Problem is solvable. The proof is completed. □

As a particular case, we have the following results.

Corollary 1.

Given any admissible circle formation characterized by d, considering system (4) and the designed control law (9) over a directed graph $\mathcal{G}$ containing a spanning tree, the Circle Formation Problem is solvable when the event-trigger condition designs as:

$$\begin{array}{c}\hfill t_{k+1}^i=\underset{\tau >t_k^i}{max}\left\{\tau :\parallel \tilde{e}(t)\parallel \ge \frac{\parallel \tilde{\delta }(t)\parallel }{\sqrt{2a\phi }}\right\},\end{array}$$

(31)

where $0<a<\frac{2{\gamma }_2}{{\nu }_N^2}$, and the condition

$$\begin{array}{cc}\hfill & \phi =(1-\frac{a{\nu }_N^2}{2{\gamma }_2})\frac{{\gamma }_2}{\rho (L_d{L}_d^T)}-\frac{{\omega }_2\varphi }{{\nu }_N}>0,\hfill \\ \hfill & \varphi \ge \dot{s}(t)/s(t)\hfill \end{array}$$

(32)

holds simultaneously, where $s(t)=e^{\varphi t}$ is the weight function. That is, ${lim}_{t\to \infty }y(t)=d$.

To use the event-triggering strategy, the following two issues should be addressed. First, under the proposed policy in Theorem 1, there exists at least one agent i, where the event interval between $t_1^k$ and $t_1^{k+1}$ is strictly positive before the circle formation is achieved.

As a matter of fact, we have the assumption that there is no trigger event when $t>T$. Then, we have:

$$\begin{array}{c}\hfill {\dot{\delta }}_i(t)=\sum _{j=1}^N{L}_d^T(i,j){\delta }_j(T_{k^{,}(T)}^i),t>T,i=1,2, \dots ,N,\end{array}$$

(33)

which implies ${\delta }_i(t)-{\delta }_i(T)=(t-T){\sum }_{j=1}^N{L}_d^T(i,j){\delta }_j(T_{k^{,}(T)}^i)$.

From Theorem 1, we observe ${\delta }_i(t)-{\delta }_j(t)\to 0$. Thus, for all $i,j=1,2, \dots ,N$, we get:

$$\begin{array}{c}\hfill \sum _{j=1}^N{L}_d^T(i,j){\delta }_j(T_{k^{,}(T)}^i)=\sum _{i=1}^N{L}_d^T(j,i){\delta }_i(T_{k^{,}(T)}^j),\end{array}$$

(34)

$$\begin{array}{c}\hfill {\delta }_i(T)={\delta }_j(T).\end{array}$$

(35)

From (35), we can easily obtain that for all $t>T$ and $i,j=1,2, \dots ,N$, ${\delta }_i(t)={\delta }_j(t)$. Namely, there is no trigger time for all $t>T$ such that the circle formation is achieved at time T.

Second, in any finite interval $[t_1,t_2]$, there are only finite triggers. However, it is still an open question to prove that Zeno behavior can be avoided under Theorem 1.

To address this issue, we propose another triggering strategy as Theorem 2.

Theorem 2.

Given any admissible circle formation characterized by d, considering system (4) and the control law (9) over a directed graph $\mathcal{G}$ containing a spanning tree, the Circle Formation Problem is solvable when the event-trigger condition designs as:

$$\begin{array}{c}\hfill t_{k+1}^i=\underset{\tau >t_k^i}{max}\left\{\tau :\parallel \tilde{e}{(t)\parallel }^2\ge s^{-1}(t)\right\}\end{array}$$

(36)

where weight function $s(t)$ satisfies:

$$\left\{\begin{array}{c}s(t)>0,\dot{s}(t)>0,\frac{\dot{s}(t)}{s(t)}\le \varphi ,\hfill \\ \underset{t\to \infty }{lim}s(t)=+\infty ,\hfill \end{array}\right.$$

(37)

and the condition

$$\begin{array}{c}\hfill a+\varphi <\frac{2{\gamma }_2}{{\nu }_N}\end{array}$$

(38)

holds simultaneously, where $a>0$, $\varphi >0$ are positive real number. That is ${lim}_{t\to \infty }y(t)=d$. Moreover, system (9) does not have Zeno behavior under event-trigger condition (36).

Proof. 

From (24) and (26), the former part of time derivative of the Lyapunov function along the trajectory of system (11) is turned into:

$$\begin{array}{cc}\hfill & s(t)\sum _{i=1}^N{\xi }_i({\delta }_i(t)-\overline{\delta }(t))({\tilde{e}}_i(t)+{\tilde{\delta }}_i(t))\hfill \\ \hfill & =s(t)\sum _{i=1}^N{\xi }_i{\Delta }_i(t){\tilde{e}}_i(t)-s(t)\sum _{i=1}^N\sum _{j=1}^N{\xi }_i{\Delta }_i(t)L_d^T(i,j){\Delta }_j(t)\hfill \\ \hfill & \le s(t)(-\frac{{\gamma }_2}{{\nu }_N}+\frac{a}{2})\sum _{j=1}^N{\xi }_i{({\Delta }_i(t))}^2+s(t)\frac{1}{2a}\sum _{i=1}^N{\xi }_i{({\tilde{e}}_i(t))}^2,\hfill \end{array}$$

(39)

where ${\Delta }_i(t)={\delta }_i(t)-{\overline{\delta }}_i(t)$ and the last inequality is deduced from Lemma 1 and inequality (19).

By using (39) and (29), we can conclude:

$$\begin{array}{cc}\hfill \dot{V}(t)& \le 2s(t)(-\frac{{\gamma }_2}{{\nu }_N}+\frac{a}{2}+\frac{\dot{s}(t)}{2s(t)})V(t)+s(t)\frac{1}{2a}\sum _{i=1}^N{\xi }_i{({\tilde{e}}_i(t))}^2.\hfill \end{array}$$

(40)

To avoid $\mathrm{Zeno}$ behaviour, we further provide an estimate of the positive lower bound on the inter-event times. From conditions (36) and (40), it implies:

$$\begin{array}{cc}\hfill \dot{V}(t)& \le 2s(t)(-\frac{{\gamma }_2}{{\nu }_N}+\frac{a}{2}+\frac{\varphi }{2})V(t)+\frac{1}{2a}.\hfill \end{array}$$

(41)

where $s(t)V(t)$ are bounded, i.e., there exists $M>0$, such that $0<s(t)V(t)<M$ for all $t>0$.

Therefore, we have:

$$\begin{array}{c}\hfill V(t)<\frac{M}{s(t)}\end{array}$$

(42)

and

$$\parallel {\Delta }_i(t)\parallel \le \sqrt{\frac{2M{s}^{-1}(t)}{{\xi }_i}},i=1,2, \dots ,N.$$

(43)

Furthermore, for any $t\in [t_k^i,t_{k+1}^i]$, it yields to:

$$\parallel {\dot{\delta }}_i(t)\parallel =∥\sum _{j=1}^N{L}_d^T(i,j){\Delta }_j(t_k^i)∥\le 2L_d^T(i,i)\sqrt{\frac{2M{s}^{-1}(t_k^i)}{{min}_j{\xi }_j}}.$$

(44)

As a results, for any $t\in [t_k^i,t_{k+1}^i]$, we have:

$$\parallel {\dot{\tilde{e}}}_i{(t)\parallel }^2\le M_1{s}^{-1}(t_k^i),$$

(45)

where $M_1$ is a positive constant, which is related to the network topology.

From the above analysis, we have:

$$\begin{array}{c}\hfill M_1{s}^{-1}(t_k^i)(t_{k+1}^i-t_k^i)\ge {\parallel {\tilde{e}}_i(t_{k+1}^i)-{\tilde{e}}_i(t_k^i)\parallel }^2=s^{-1}(t_{k+1}^i).\end{array}$$

(46)

Combining (37), we get:

$$\begin{array}{c}\hfill 0<s(t_{k+1}^i)\le s(t_k^i)e^{\varphi (t_{k+1}^i-t_k^i)}.\end{array}$$

(47)

Then

$$\begin{array}{c}\hfill t_{k+1}^i-t_k^i\ge \frac{e^{-\varphi (t_{k+1}^i-t_k^i)}}{M_1}.\end{array}$$

(48)

Consequently, there is a constant c such that $t_{k+1}^i-t_k^i>c>0$, which indicates that Zeno behavior is excluded. □

Similar to Corollary 1, we have:

Corollary 2.

Given any admissible circle formations characterized by d, considering system (4) and control law (11) over a strongly connected weight-unbalanced digraph $\mathcal{G}$, the Circle Formation Problem is solvable when the event-trigger condition is designed as:

$$\begin{array}{c}\hfill t_{k+1}^i=\underset{\tau >t_k^i}{max}\left\{\tau :\parallel \tilde{e}{(t)\parallel }^2\ge e^{-\varphi t}\right\},\end{array}$$

(49)

and the condition

$$\begin{array}{c}\hfill a+\varphi <\frac{2{\gamma }_2}{{\nu }_N}\end{array}$$

(50)

holds simultaneously, where a, ϕ are positive real number. That is, ${lim}_{t\to \infty }y(t)=d$.

Additionally, system (11) does not have Zeno behavior under event-trigger condition (36).

4. Model Based Self-Triggered Strategy

In this section, in order to avoid continuous event detection communication between adjacent agents, we apply the pull-based event-triggered strategy proposed in Section 3 in the scenarios of discontinuous communication, i.e., self-triggered scheme. The self-triggered strategy indicates that the next triggering time $t_{k+1}^i$ can be predicted from using the information at the previous trigger time $t_k^i$.

The model is given as:

$$\begin{array}{c}\hfill {\delta }_i(t_{k+1}^i)={\delta }_i(t_k^i)+(t_{k+1}^i-t_k^i)\sum _{j=1}^N{L}_d^T(i,j){\delta }_j(t_{k^{\prime }}^i).\end{array}$$

(51)

Then, the state of agent i at $t\in [t_k^i,t_{k+1}^i]$ ($t_{k+1}^i$ to be determined) can be written as:

$$\begin{array}{c}\hfill {\delta }_i(t)={\delta }_i(t_k^i)+(t-t_k^i){\tilde{\delta }}_i(t_k^i),t\in [t_k^i,t_{k+1}^i].\end{array}$$

(52)

Since agent $j\in {\mathcal{N}}^{in}$ transmits trigger state to agent i whenever agent j triggers, at any given time instant t, agent i can obtain the estimation of agent j based on

$$\begin{array}{c}\hfill {\delta }_j(t)={\delta }_j(t_k^j)+(t-t_k^j){\tilde{\delta }}_j(t_k^j),\end{array}$$

(53)

until agent j triggers next. Then, from Theorem 2 we have Algorithm 1.

Algorithm 1: Self-triggered update

1: $\mathbf{loop}$  2:  Integrate the dynamical model ${\dot{x}}_i(t)=u_i(t)$ from the initial condition $x_j(0)$   for all the neighbouring agents $j\in {\mathcal{N}}^{in}$, while listening to possible transmission   from them;  3:  Substituting (52) and (53) into (36), the following maximizing problem   is solved to find out $t_{k+1}^i$:       $t_{k+1}^i={max}_{\tau >t_k^i}\left\{\tau :\parallel \tilde{e}{(t)\parallel }^2\ge s^{-1}(t)\right\}$;  4:  $\mathbf{if}$ any in-neighbors of agent i trigger at time $t\in [t_k^i,t_{k+1}^i]$, $\mathbf{then}$  5:   Agent i receives renewal information form its in-neighbors;  6:   Updating $\tau \leftarrow t$ and go to step (3);  7:  $\mathbf{end}$ $\mathbf{if}$  8:  $\mathbf{if}$ any of agent i’ in-neighbors do not trigger during $[\tau ,t_{k+1}^i]$, $\mathbf{then}$  9:   Agent i triggers at time $t_{k+1}^i\leftarrow \tau$;  10:   $\tilde{e}(t)\leftarrow 0$;  11:   Update the control input to the value $u_i(t)={\sum }_{j=1}^N{L}_d^T(i,j){\delta }_j(t_k^i)$,   and sends the renewed information to all its out-neighbors immediately  12:   $\mathbf{end}$ $\mathbf{if}$  13: $\mathbf{end}$ $\mathbf{loop}$

Consequently, the system (4) achieves the desired circle formation, and Zeno behavior can be ruled out.

We observe that Algorithm 1 could be regarded as an implementation of Theorem 2, which eliminates continuous communication between different states.

5. Simulation Results

Considering an MAS with six agents, the desired distances between each pair of adjacent agents are set to $d={\left[\frac{\pi }{8},\frac{\pi }{2},\frac{3\pi }{8},\frac{\pi }{2},\frac{\pi }{3},\frac{\pi }{6}\right]}^T$, which satisfy (6) and the initial values of the $\mathrm{MAS}$ are randomly generated to satisfy (2). In addition, the unique normalized positive left eigenvector of $L_d^T$ with respect to eigenvalue 0 is $\xi ={[0.0625,\mathrm{0.0.25},0.1875,0.25,0.1667,0.0833]}^T.$ In order to verify the effectiveness of the proposed strategy, the simulated event detection is implemented in the form of sampled data. Here, according to [26], the sampling period h in real-time control is set to $0.2s$. To ensure the condition (36) hold in real-time control, the permitted range $\sigma$ is set to $0.9$.

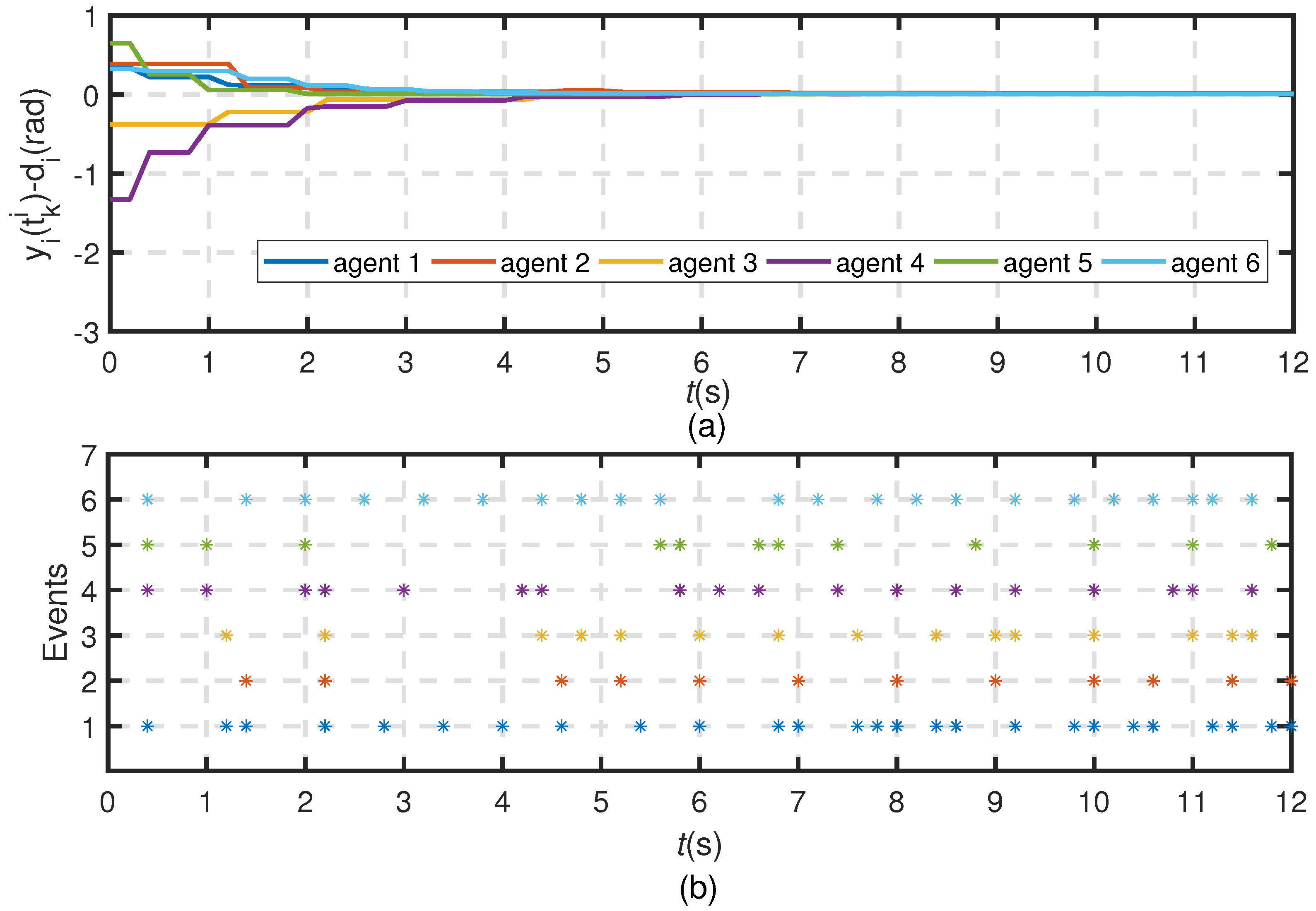
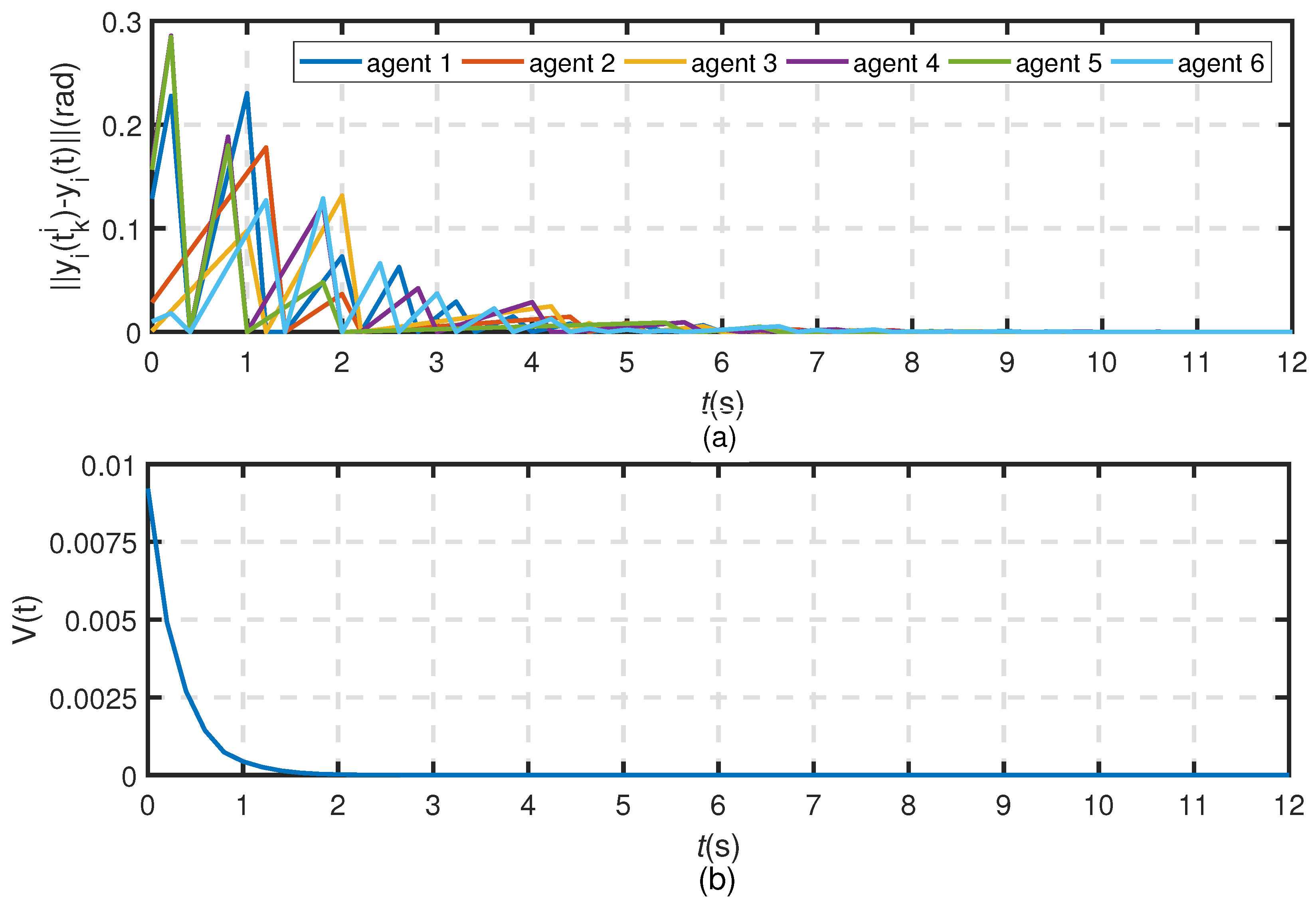
Simulation results are shown in Figure 2 and Figure 3. Figure 2a shows the evolution of the difference between the event-triggered angular distance and the expected counterpart, Figure 2b reveals each agent’s own event sequence. Figure 3 illustrates the fluttering of the measurement error $\parallel y_i(t_k^i)-y_i(t)\parallel$. The results indicate that the desired circle formation can be asymptotically achieved under the proposed control law. From Figure 2b, it can be seen that under the self-triggering algorithm in Theorem 2, $V(t)$ is exponential to 0, and the interevent times of each agent are strictly greater than some positive constants. Additionally, according to Figure 2, we calculate the average inter-event time overall mobile agents resulting to $h_{avg}=0.6724$. We conclude that the proposed method with an average sampling period of $h_{avg}$ has the advantages of reducing the number of control updates and communication frequencies.

6. Conclusions

In this paper, we proposed distributed event-triggered algorithms to address the circle formation control problem of MASs with directed topologies. We first proposed a pull-based event-triggered algorithm, where the graph is reducible with a spanning tree, and the event-triggered instant of each agent with continuous monitoring was provided by the inequality (20), which only depends on the states of in-neighbors of each agent. It has been proven that with guaranteeing a lower bound for the inter-event times between consecutive updates, Zeno behavior can be ruled out. The results were then extended to discontinuous monitoring, where all agents check for a triggered condition in order to compute its next event-triggered instant in advance. Finally, the effectiveness of the proposed methods is verified by numerical simulation.