Bayesian Proxy Modelling for Estimating Black Carbon Concentrations using White-Box and Black-Box Models
Abstract
1. Introduction
1.1. Motivation
1.2. Data-Driven Air Pollution Models
2. Case Study: Jordan Air Pollution Measurement Campaign
3. Methods: Bayesian Modelling
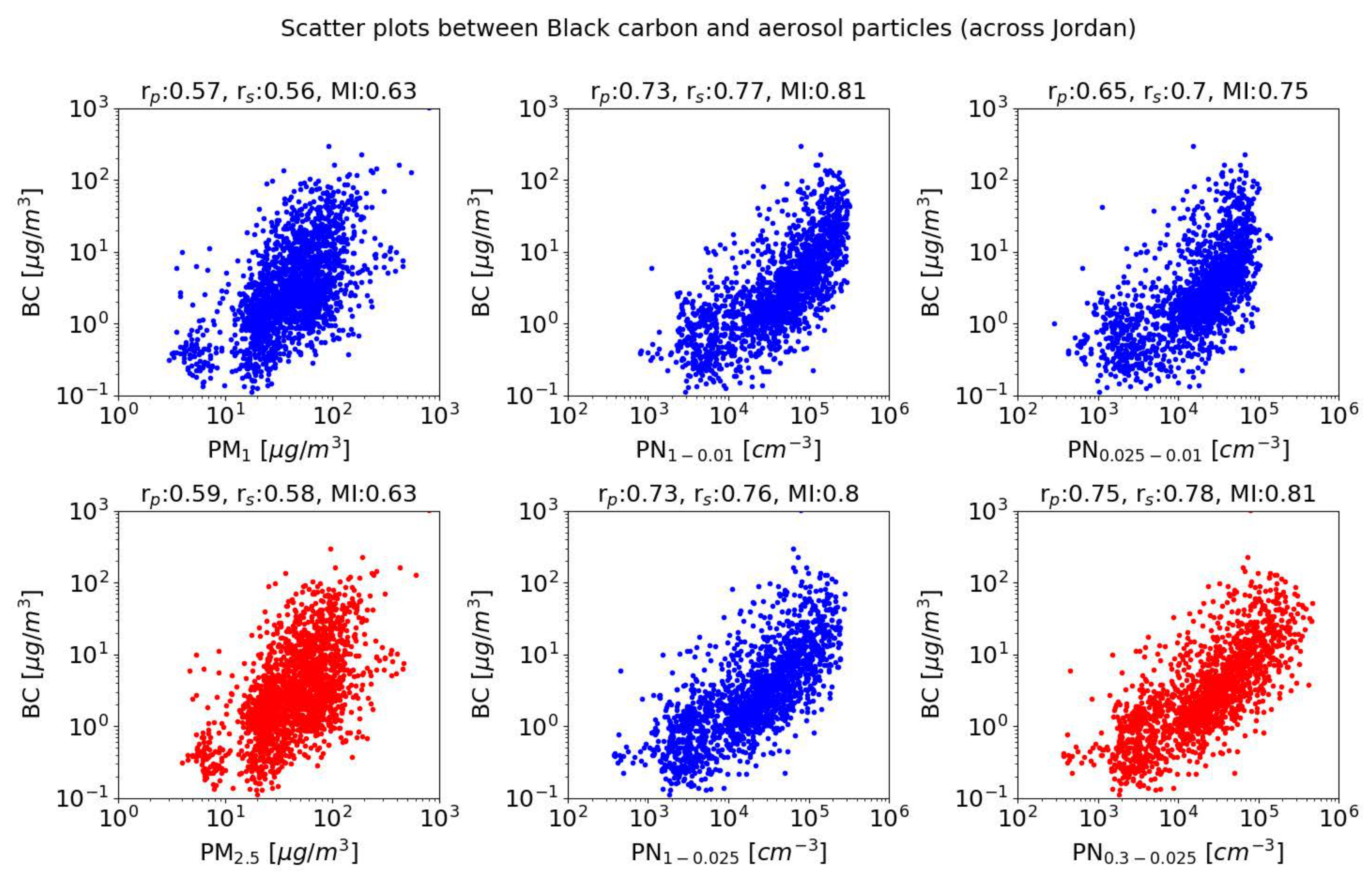
3.1. Features Analysis
3.2. Bayesian Model: White Box
3.2.1. Prior Distribution
3.2.2. Likelihood Function
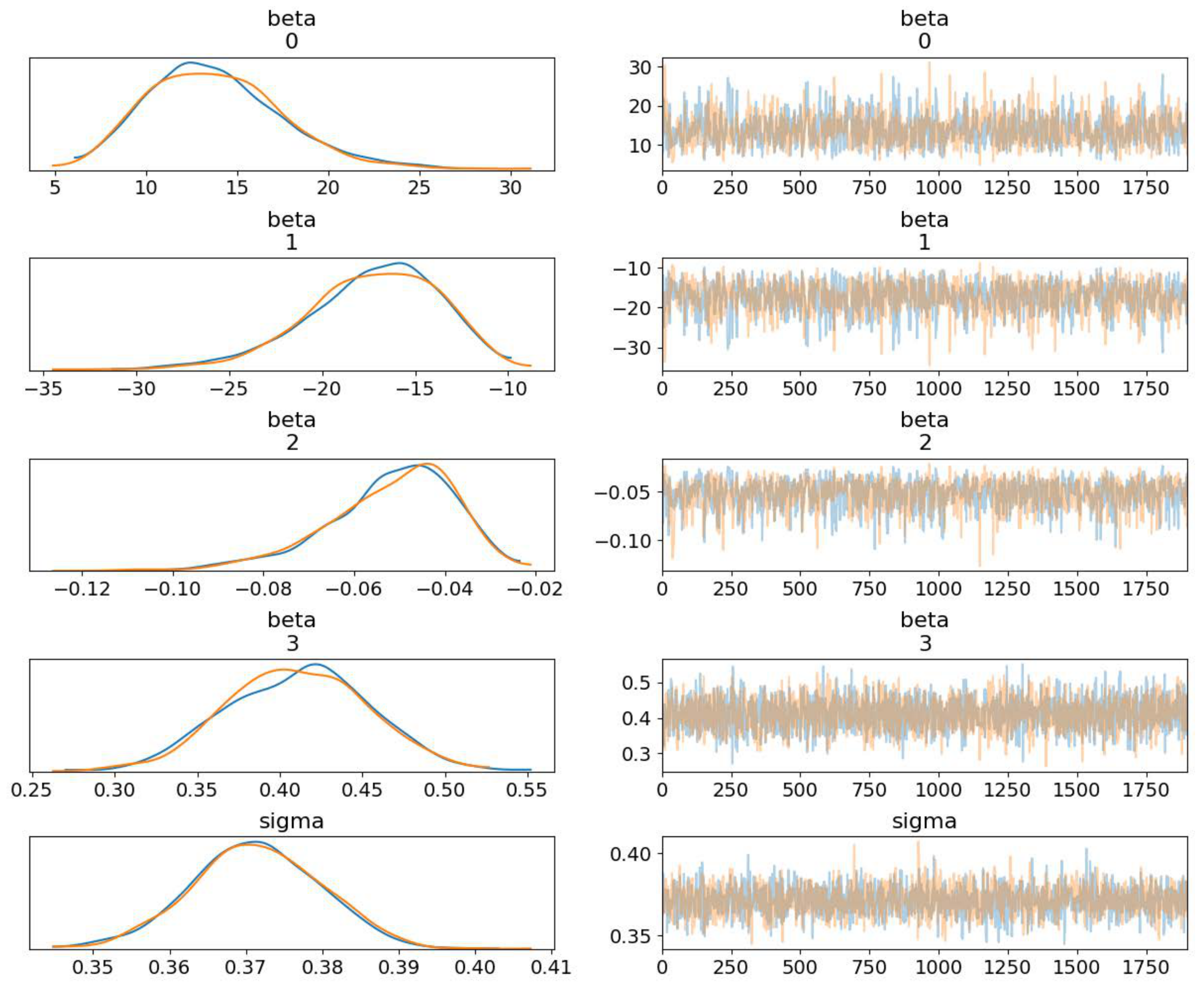
3.2.3. Posterior and Predictive Distributions
3.3. Bayesian Model: Black Box
4. Results
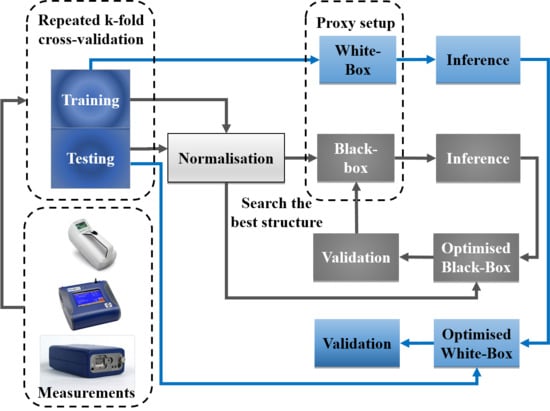
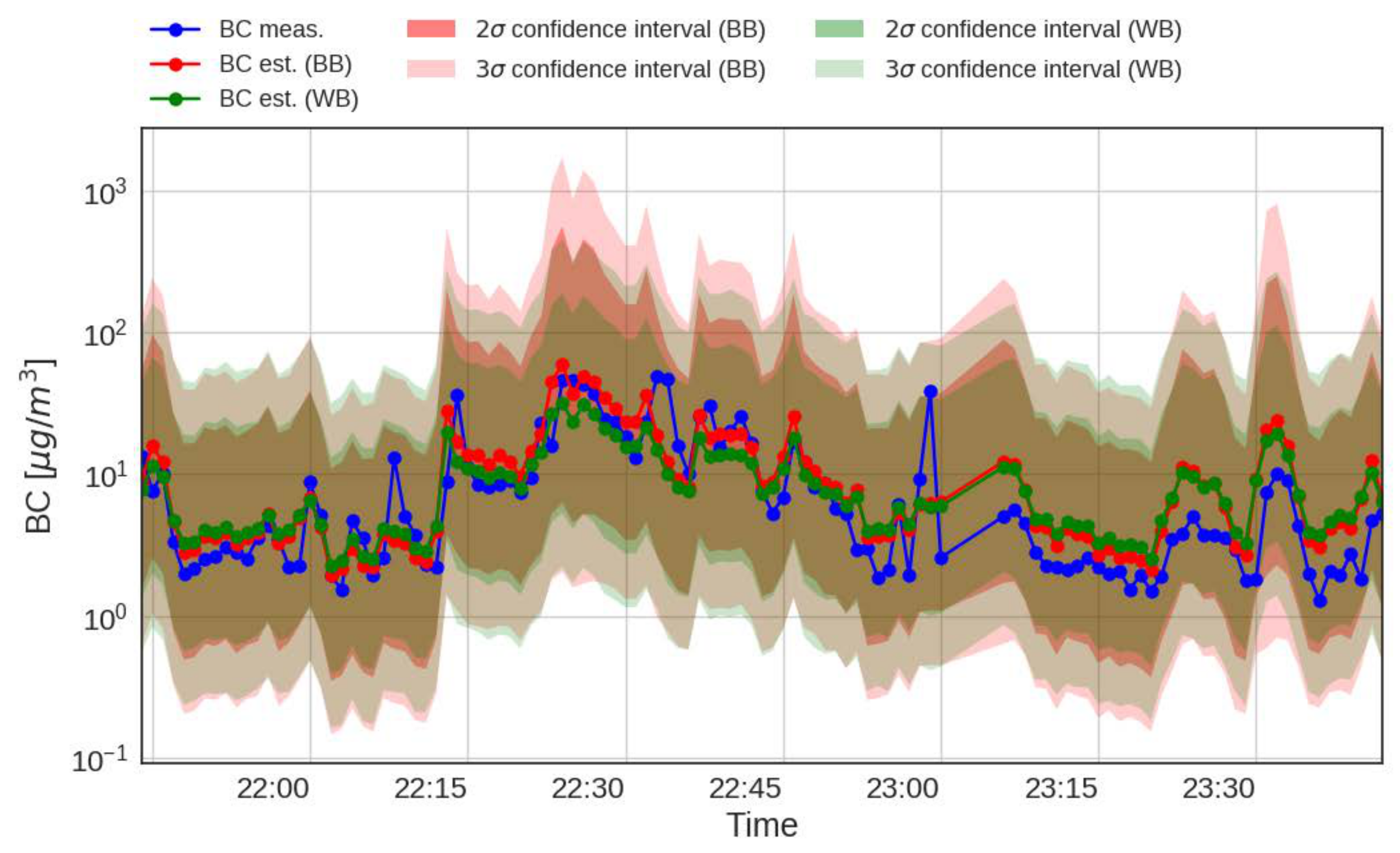
4.1. Modelling Process
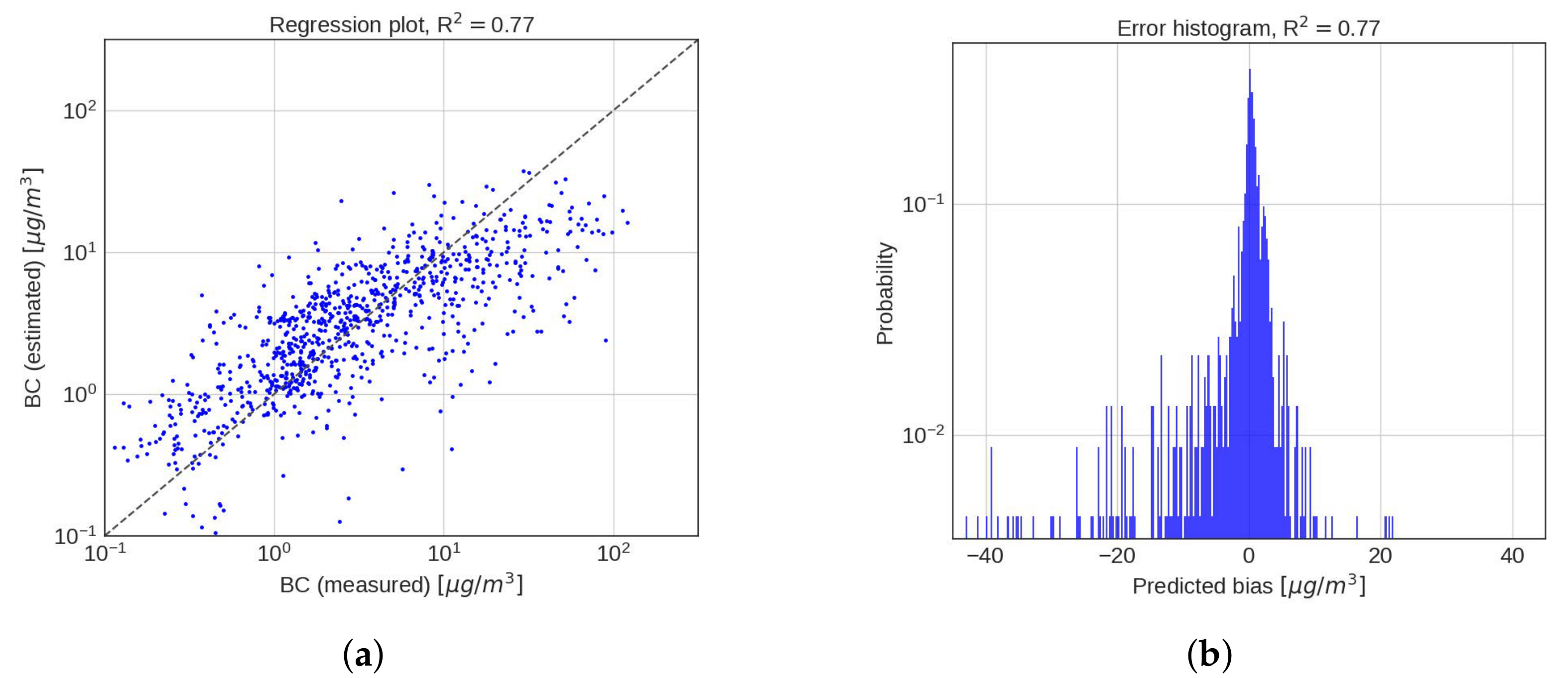
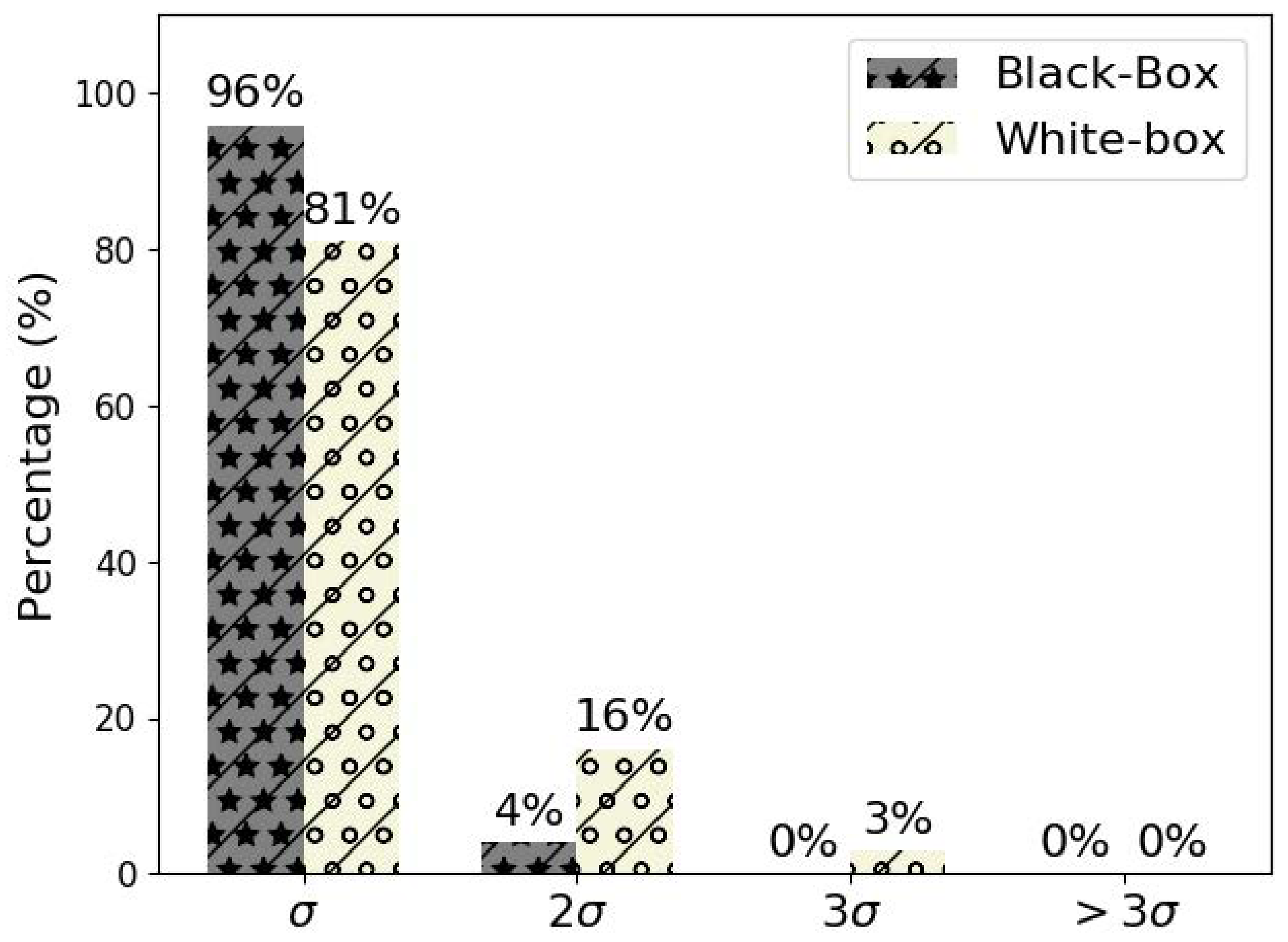
4.2. Performance Analysis
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ADVI | Automatic Differentiation to Variational Inference |
| AR | Auto Regressive |
| ARX | Auto Regressive eXogenous |
| BB | Black Box |
| BC | Black Carbon |
| BNN | Bayesian Neural Network |
| CO | Carbon Monoxide |
| MAE | Mean Absolute Error |
| MCMC | Markov Chain Monte Carlo |
| MENA | Middle East and North Africa |
| NO | Nitrogen Oxides |
| NUTS | No-U-Turn Sampler |
| O | Ozone |
| PM | Particulate Matter |
| PN | Particle Number |
| ReLU | Rectified Linear Unit |
| RMSE | Root Mean Squared Error |
| SO | Sulfur Dioxide |
| tanh | hyperbolic tangent function |
| UFP | Ultra-Fine Particle |
| WB | White Box |
| WHO | World Health Organization |
References
- WHO Global Ambient Air Quality Database. Available online: https://www.who.int/airpollution/data/en/ (accessed on 17 August 2019).
- Kumar, R.; Peuch, V.H.; Crawford, J.H.; Brasseur, G. Five Steps to Improve Air-Quality Forecasts. Nature 2018, 561, 27–29. [Google Scholar] [CrossRef] [PubMed]
- Guarnieri, M.; Balmes, J.R. Outdoor air pollution and asthma. Lancet 2014, 383, 1581–1592. [Google Scholar] [CrossRef]
- Fuzzi, S.; Baltensperger, U.; Carslaw, K.; Decesari, S.; Denier van der Gon, H.; Facchini, M.C.; Fowler, D.; Koren, I.; Langford, B.; Lohmann, U.; et al. Particulate matter, air quality and climate: lessons learned and future needs. Atmos. Chem. Phys. 2015, 15, 8217–8299. [Google Scholar] [CrossRef]
- Evans, K.A.; Halterman, J.S.; Hopke, P.K.; Fagnano, M.; Rich, D.Q. Increased ultrafine particles and carbon monoxide concentrations are associated with asthma exacerbation among urban children. Environ. Res. 2014, 129, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Reche, C.; Querol, X.; Alastuey, A.; Viana, M.; Pey, J.; Moreno, T.; Rodríguez, S.; González, Y.; Fernández-Camacho, R.; Rosa, J.; et al. New considerations for PM, Black Carbon and particle number concentration for air quality monitoring across different European cities. Atmos. Chem. Phys. 2011, 11, 6207–6227. [Google Scholar] [CrossRef]
- Singh, V.; Ravindra, K.; Sahu, L.; Sokhi, R. Trends of atmospheric black carbon concentration over the United Kingdom. Atmos. Environ. 2018, 178, 148–157. [Google Scholar] [CrossRef]
- Yang, F.; Tan, J.; Zhao, Q.; Du, Z.; He, K.; Ma, Y.; Duan, F.; Chen, G. Characteristics of PM 2.5 speciation in representative megacities and across China. Atmos. Chem. Phys. 2011, 11, 5207–5219. [Google Scholar] [CrossRef]
- Ding, A.; Huang, X.; Nie, W.; Sun, J.; Kerminen, V.M.; Petäjä, T.; Su, H.; Cheng, Y.; Yang, X.Q.; Wang, M.; et al. Enhanced haze pollution by black carbon in megacities in China. Geophys. Res. Lett. 2016, 43, 2873–2879. [Google Scholar] [CrossRef]
- Bond, T.C.; Doherty, S.J.; Fahey, D.; Forster, P.; Berntsen, T.; DeAngelo, B.; Flanner, M.; Ghan, S.; Kärcher, B.; Koch, D.; et al. Bounding the role of black carbon in the climate system: A scientific assessment. J. Geophys. Res. Atmos. 2013, 118, 5380–5552. [Google Scholar] [CrossRef]
- Ramanathan, V.; Ramana, M.V.; Roberts, G.; Kim, D.; Corrigan, C.; Chung, C.; Winker, D. Warming trends in Asia amplified by brown cloud solar absorption. Nature 2007, 448, 575. [Google Scholar] [CrossRef]
- Saide, P.; Spak, S.; Pierce, R.; Otkin, J.; Schaack, T.; Heidinger, A.; da Silva, A.; Kacenelenbogen, M.; Redemann, J.; Carmichael, G. Central American biomass burning smoke can increase tornado severity in the US. Geophys. Res. Lett. 2015, 42, 956–965. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, J.; Tao, S.; Ban-Weiss, G. Long-range transport of black carbon to the Pacific Ocean and its dependence on aging timescale. Atmos. Chem. Phys. 2015, 15, 11521–11535. [Google Scholar] [CrossRef]
- Petzold, A.; Ogren, J.A.; Fiebig, M.; Laj, P.; Li, S.M.; Baltensperger, U.; Holzer-Popp, T.; Kinne, S.; Pappalardo, G.; Sugimoto, N.; et al. Recommendations for reporting “black carbon” measurements. Atmos. Chem. Phys. 2013, 13, 8365–8379. [Google Scholar] [CrossRef]
- Sharma, S.; Leaitch, W.R.; Huang, L.; Veber, D.; Kolonjari, F.; Zhang, W.; Hanna, S.J.; Bertram, A.K.; Ogren, J.A. An evaluation of three methods for measuring black carbon in Alert, Canada. Atmos. Chem. Phys. 2017, 17, 15225–15243. [Google Scholar] [CrossRef]
- Junger, W.; De Leon, A.P. Imputation of missing data in time series for air pollutants. Atmos. Environ. 2015, 102, 96–104. [Google Scholar] [CrossRef]
- Mishra, D.; Goyal, P.; Upadhyay, A. Artificial intelligence based approach to forecast PM2. 5 during haze episodes: A case study of Delhi, India. Atmos. Environ. 2015, 102, 239–248. [Google Scholar] [CrossRef]
- Chang, M.E.; Cardelino, C. Application of the urban airshed model to forecasting next-day peak ozone concentrations in Atlanta, Georgia. J. Air Waste Manag. Assoc. 2000, 50, 2010–2024. [Google Scholar] [CrossRef]
- Mueller, S.F.; Mallard, J.W. Contributions of natural emissions to ozone and PM2. 5 as simulated by the community multiscale air quality (CMAQ) model. Environ. Sci. Technol. 2011, 45, 4817–4823. [Google Scholar] [CrossRef]
- Hanna, S.R.; Lu, Z.; Frey, H.C.; Wheeler, N.; Vukovich, J.; Arunachalam, S.; Fernau, M.; Hansen, D.A. Uncertainties in predicted ozone concentrations due to input uncertainties for the UAM-V photochemical grid model applied to the July 1995 OTAG domain. Atmos. Environ. 2001, 35, 891–903. [Google Scholar] [CrossRef]
- Borrego, C.; Monteiro, A.; Ferreira, J.; Miranda, A.; Costa, A.; Carvalho, A.; Lopes, M. Procedures for estimation of modelling uncertainty in air quality assessment. Environ. Int. 2008, 34, 613–620. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, H.; Palazoglu, A.; Singh, A.; Zhang, W.; Liu, S. Prediction of 24-hour-average PM2.5 concentrations using a hidden Markov model with different emission distributions in Northern California. Sci. Total Environ. 2013, 443, 93–103. [Google Scholar] [CrossRef] [PubMed]
- Jiang, P.; Dong, Q.; Li, P. A novel hybrid strategy for PM2.5 concentration analysis and prediction. J. Environ. Manag. 2017, 196, 443–457. [Google Scholar] [CrossRef] [PubMed]
- Cabaneros, S.M.S.; Calautit, J.K.; Hughes, B.R. A review of artificial neural network models for ambient air pollution prediction. Environ. Model. Softw. 2019, 119, 285–304. [Google Scholar] [CrossRef]
- Zhou, Y.; De, S.; Ewa, G.; Perera, C.; Moessner, K. Data-driven air quality characterization for urban environments: A case study. IEEE Access 2018, 6, 77996–78006. [Google Scholar] [CrossRef]
- Wang, R.; Tao, S.; Shen, H.; Wang, X.; Li, B.; Shen, G.; Wang, B.; Li, W.; Liu, X.; Huang, Y.; et al. Global emission of black carbon from motor vehicles from 1960 to 2006. Environ. Sci. Technol. 2012, 46, 1278–1284. [Google Scholar] [CrossRef]
- Liu, M.; Peng, X.; Meng, Z.; Zhou, T.; Long, L.; She, Q. Spatial characteristics and determinants of in-traffic black carbon in Shanghai, China: Combination of mobile monitoring and land use regression model. Sci. Total Environ. 2019, 658, 51–61. [Google Scholar] [CrossRef]
- Cooke, W.F.; Wilson, J.J. A global black carbon aerosol model. J. Geophys. Res. Atmos. 1996, 101, 19395–19409. [Google Scholar] [CrossRef]
- Yang, J.; Kang, S.; Ji, Z.; Chen, D. Modeling the origin of anthropogenic black carbon and its climatic effect over the Tibetan Plateau and surrounding regions. J. Geophys. Res. Atmos. 2018, 123, 671–692. [Google Scholar] [CrossRef]
- Boniardi, L.; Dons, E.; Campo, L.; Van Poppel, M.; Panis, L.I.; Fustinoni, S. Annual, seasonal, and morning rush hour Land Use Regression models for black carbon in a school catchment area of Milan, Italy. Environ. Res. 2019, 176, 108520. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, M.; Cheng, Y.; Geng, G.; Hong, C.; Li, H.; Li, X.; Tong, D.; Wu, N.; Zhang, X.; et al. Modeling the aging process of black carbon during atmospheric transport using a new approach: A case study in Beijing. Atmos. Chem. Phys. 2019, 19, 9663–9680. [Google Scholar] [CrossRef]
- Maciejewska, K.; Juda-Rezler, K.; Reizer, M.; Klejnowski, K. Modelling of black carbon statistical distribution and return periods of extreme concentrations. Environ. Model. Softw. 2015, 74, 212–226. [Google Scholar] [CrossRef]
- Isiugo, K.; Jandarov, R.; Cox, J.; Chillrud, S.; Grinshpun, S.A.; Hyttinen, M.; Yermakov, M.; Wang, J.; Ross, J.; Reponen, T. Predicting indoor concentrations of black carbon in residential environments. Atmos. Environ. 2019, 201, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Hussein, T.; Saleh, S.S.A.; dos Santos, V.N.; Abdullah, H.; Boor, B.E. Black Carbon and Particulate Matter Concentrations in Eastern Mediterranean Urban Conditions: An Assessment Based on Integrated Stationary and Mobile Observations. Atmosphere 2019, 10, 323. [Google Scholar] [CrossRef]
- Hussein, T.; Boor, B.E.; dos Santos, V.N.; Kangasluoma, J.; Petäjä, T.; Lihavainen, H. Mobile Aerosol Measurement in the Eastern Mediterranean—A Utilization of Portable Instruments. Aerosol Air Qual. Res. 2017, 17, 1775–1786. [Google Scholar] [CrossRef]
- Hussein, T.; Juwhari, H.; Al Kuisi, M.; Alkattan, H.; Lahlouh, B.; Al-Hunaiti, A. Accumulation and coarse mode aerosol concentrations and carbonaceous contents in the urban background atmosphere in Amman, Jordan. Arabian J. Geosci. 2018, 11, 617. [Google Scholar] [CrossRef]
- Cheng, Y.H.; Lin, M.H. Real-time performance of the microAeth® AE51 and the effects of aerosol loading on its measurement results at a traffic site. Aerosol Air Qual. Res. 2013, 13, 1853–1863. [Google Scholar] [CrossRef]
- Sohlberg, B. Grey box modelling for model predictive control of a heating process. J. Process Control 2003, 13, 225–238. [Google Scholar] [CrossRef]
- Hayashi, Y. The right direction needed to develop white-box deep learning in radiology, pathology, and ophthalmology: A short review. Front. Robot. AI 2019, 6, 24. [Google Scholar] [CrossRef]
- Yang, J.H.; Wright, S.N.; Hamblin, M.; McCloskey, D.; Alcantar, M.A.; Schrübbers, L.; Lopatkin, A.J.; Satish, S.; Nili, A.; Palsson, B.O.; et al. A White-Box Machine Learning Approach for Revealing Antibiotic Mechanisms of Action. Cell 2019, 177, 1649–1661. [Google Scholar] [CrossRef]
- Molnar, C.; Interpretable machine learning. In A Guide for Making Black Box Models Explainable; 2019. Available online: https://christophm.github.io/interpretable-ml-book/ (accessed on 19 November 2019).
- Lee Rodgers, J.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Croux, C.; Dehon, C. Influence functions of the Spearman and Kendall correlation measures. Stat. Methods Appl. 2010, 19, 497–515. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Haapasilta, V.; Relan, R.; Paasonen, P.; Kerminen, V.M.; Junninen, H.; Kulmala, M.; Foster, A.S. Exploring non-linear associations between atmospheric new-particle formation and ambient variables: A mutual information approach. Atmos. Chem. Phys. 2018, 18, 12699–12714. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Dada, L.; Alghamdi, M.A.; Al-Jeelani, H.; Lihavainen, H.; Hyvärinen, A.; Hussein, T. Mutual information input selector and probabilistic machine learning utilisation for air pollution proxies. Appl. Sci. 2019, 9, 4475. [Google Scholar] [CrossRef]
- IARC. IARC Monographs on the Evaluation of Carcinogenic Risks to Humans: Vol. 109, Outdoor Air Pollution; IARC: Lyon, France, 2015. [Google Scholar]
- Williams, R.; Duvall, R.; Kilaru, V.; Hagler, G.; Hassinger, L.; Benedict, K.; Rice, J.; Kaufman, A.; Judge, R.; Pierce, G.; et al. Deliberating performance targets workshop: Potential paths for emerging PM2. 5 and O3 air sensor progress. Atmos. Environ. X 2019, 2, 100031. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; Chapman and Hall/CRC: New York, NY, USA, 2013. [Google Scholar]
- Zaidan, M.A.; Harrison, R.F.; Mills, A.R.; Fleming, P.J. Bayesian hierarchical models for aerospace gas turbine engine prognostics. Expert Syst. Appl. 2015, 42, 539–553. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Rishi, R.; Mills, A.R.; Harrison, R.F. Prognostics of gas turbine engine: An integrated approach. Expert Syst. Appl. 2015, 42, 8472–8483. [Google Scholar] [CrossRef]
- Hoffman, M.D.; Gelman, A. The No-U-Turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014, 15, 1593–1623. [Google Scholar]
- Kucukelbir, A.; Tran, D.; Ranganath, R.; Gelman, A.; Blei, D.M. Automatic differentiation variational inference. J. Mach. Learn. Res. 2017, 18, 430–474. [Google Scholar]
- Turner, R.; Neal, B. How well does your sampler really work? arXiv 2017, arXiv:1712.06006. [Google Scholar]
- Pizzolato, M.; Yu, T.; Canales-Rodriguez, E.J.; Thiran, J.P. Robust T2 Relaxometry with Hamiltonian MCMC for Myelin Water Fraction Estimation. In Proceedings of the IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 8–11 April 2019. [Google Scholar]
- Salvatier, J.; Wiecki, T.V.; Fonnesbeck, C. Probabilistic programming in Python using PyMC3. PeerJ Comput. Sci. 2016, 2, e55. [Google Scholar] [CrossRef]
- Olden, J.D.; Jackson, D.A. Illuminating the “black box”: A randomization approach for understanding variable contributions in artificial neural networks. Ecol. Model. 2002, 154, 135–150. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Canova, F.F.; Laurson, L.; Foster, A.S. Mixture of clustered Bayesian neural networks for modeling friction processes at the nanoscale. J. Chem. Theory Comput. 2016, 13, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H.; De Jesus, O. Neural Network Design; PWS Publishing Company: Boston, MA, USA, 2014. [Google Scholar]
- Zaidan, M.A.; Mills, A.R.; Harrison, R.F.; Fleming, P.J. Gas turbine engine prognostics using Bayesian hierarchical models: A variational approach. Mech. Syst. Signal Process. 2016, 70, 120–140. [Google Scholar] [CrossRef]
- MacKay, D.J. A practical Bayesian framework for backpropagation networks. Neural Comput. 1992, 4, 448–472. [Google Scholar] [CrossRef]
- Neal, R. Bayesian Learning for Neural Networks. Ph.D. Thesis, Department of Computer Science, University of Toronto, Toronto, ON, Canada, 1995. [Google Scholar]
- Barber, D.; Bishop, C.M. Ensemble learning in Bayesian neural networks. Nato ASI Ser. F Comput. Syst. Sci. 1998, 168, 215–238. [Google Scholar]
- Paisley, J.; Blei, D.M.; Jordan, M.I. Variational Bayesian inference with stochastic search. In Proceedings of the International Conference on Machine Learning (ICML 2012), Edinburgh, UK, 26 June–1 July 2012. [Google Scholar]
- Hernández-Lobato, J.M.; Adams, R. Probabilistic backpropagation for scalable learning of bayesian neural networks. In Proceedings of the International Conference on Machine Learning (ICML 2015), Lille, France, 6–11 July 2015. [Google Scholar]
- Blundell, C.; Cornebise, J.; Kavukcuoglu, K.; Wierstra, D. Weight uncertainty in neural networks. In Proceedings of the International Conference on Machine Learning (ICML 2015), Lille, France, 6–11 July 2015. [Google Scholar]
- Kim, J.H. Estimating classification error rate: Repeated cross-validation, repeated hold-out and bootstrap. Comput. Stat. Data Anal. 2009, 53, 3735–3745. [Google Scholar] [CrossRef]
- Karlik, B.; Olgac, A.V. Performance analysis of various activation functions in generalized MLP architectures of neural networks. Int. J. Artif. Intell. Expert Syst. 2011, 1, 111–122. [Google Scholar]
- Taito Supercluster, CSC - IT Center for Science Ltd. Available online: https://research.csc.fi/taito-supercluster (accessed on 17 September 2019).
- Popoola, O.A.; Carruthers, D.; Lad, C.; Bright, V.B.; Mead, M.I.; Stettler, M.E.; Saffell, J.R.; Jones, R.L. Use of networks of low cost air quality sensors to quantify air quality in urban settings. Atmos. Environ. 2018, 194, 58–70. [Google Scholar] [CrossRef]
- Caubel, J.; Cados, T.; Kirchstetter, T. A new black carbon sensor for dense air quality monitoring networks. Sensors 2018, 18, 738. [Google Scholar] [CrossRef]
- Lagerspetz, E.; Motlagh, N.H.; Zaidan, M.A.; Fung, P.L.; Mineraud, J.; Varjonen, S.; Siekkinen, M.; Nurmi, P.; Matsumi, Y.; Tarkoma, S.; et al. Megasense: Feasibility of low-cost sensors for pollution hot-spot detection. In Proceedings of the 2019 IEEE 17th International Conference on Industrial Informatics (INDIN), Helsinki, Finland, 23–25 July 2019. [Google Scholar]
- Motlagh, N.H.; Zaidan, M.A.; Lagerspetz, E.; Varjonen, S.; Toivonen, J.; Mineraud, J.; Rebeiro-Hargrave, A.; Siekkinen, M.; Hussein, T.; Nurmi, P.; et al. Indoor air quality monitoring using infrastructure-based motion detectors. In Proceedings of the 2019 IEEE 17th International Conference on Industrial Informatics (INDIN), Helsinki, Finland, 23–25 July 2019. [Google Scholar]
- Morawska, L.; Thai, P.K.; Liu, X.; Asumadu-Sakyi, A.; Ayoko, G.; Bartonova, A.; Bedini, A.; Chai, F.; Christensen, B.; Dunbabin, M.; et al. Applications of low-cost sensing technologies for air quality monitoring and exposure assessment: How far have they gone? Environ. Int. 2018, 116, 286–299. [Google Scholar] [CrossRef] [PubMed]
- Zaidan, M.A.; Mills, A.R.; Harrison, R.F. Bayesian framework for aerospace gas turbine engine prognostics. In Proceedings of the 2013 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013; pp. 1–8. [Google Scholar]
- Nelles, O. Nonlinear System Identification: From Classical Approaches to Neural Networks and Fuzzy Models; Springer-Verlag: Berlin/Heidelberg, Germany; New York, NY, USA, 2013. [Google Scholar]
- Geman, S.; Bienenstock, E.; Doursat, R. Neural networks and the bias/variance dilemma. Neural Comput. 1992, 4, 1–58. [Google Scholar] [CrossRef]
- Ward-Caviness, C.K.; Nwanaji-Enwerem, J.C.; Wolf, K.; Wahl, S.; Colicino, E.; Trevisi, L.; Kloog, I.; Just, A.C.; Vokonas, P.; Cyrys, J.; et al. Long-term exposure to air pollution is associated with biological aging. Oncotarget 2016, 7, 74510. [Google Scholar] [CrossRef]
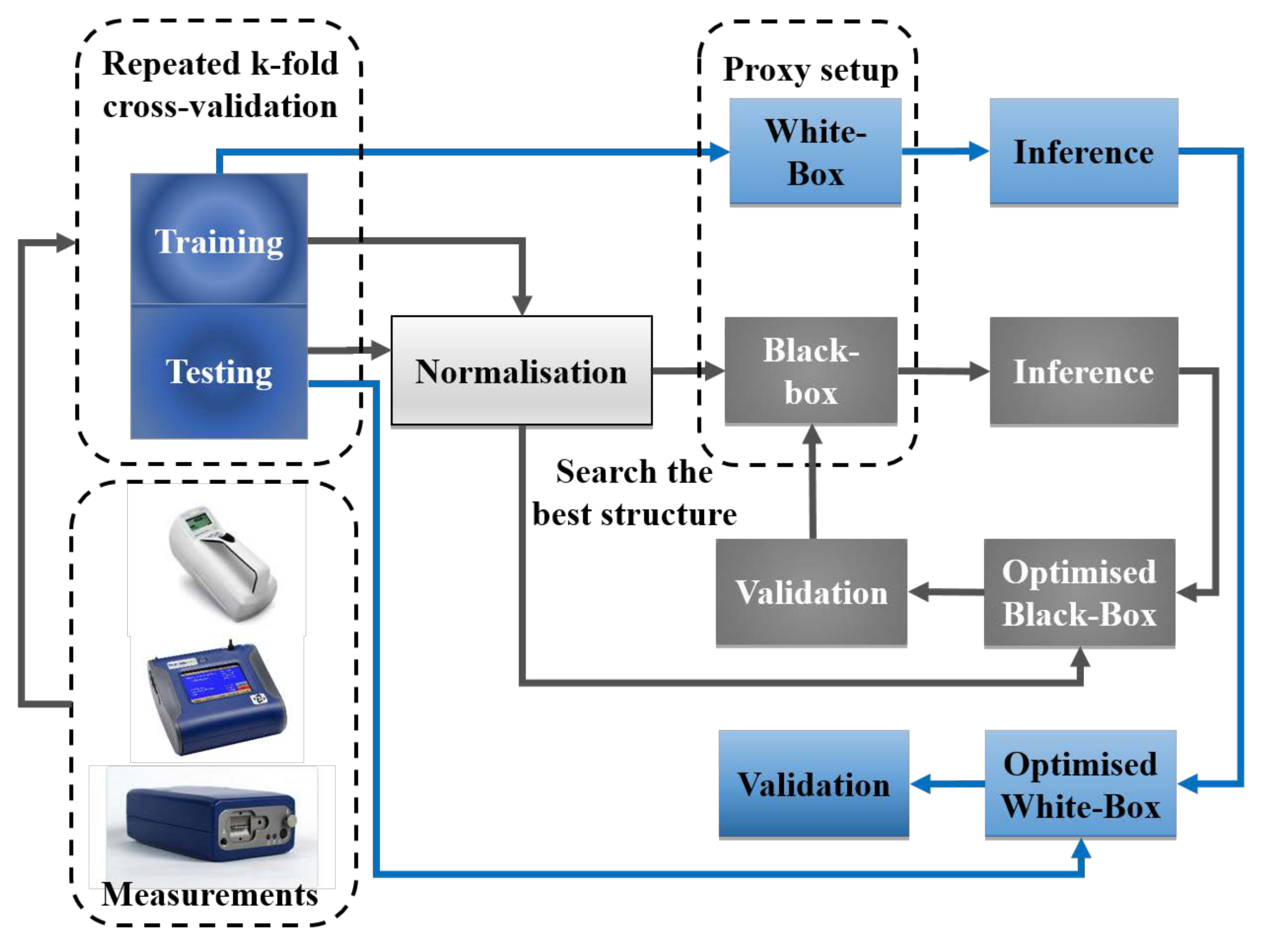
| Measured Variable | Instrument | Measurement Range | Maximum Concentration |
|---|---|---|---|
| Submicron particle number concentration (cm) | CPC 3007-2 (TSI Inc.) P-Trak 8525 (TSI Inc.) | 0.01 m–1 m 0.02 m–1 m | 4 × cm |
| Particle number size distribution (cm) | AeroTrak 9306-V2 (TSI Inc.) | 0.3 m–25 m (6 channels) | 210 cm |
| PM (g/m) | DustTrak DRX 8533 (TSI Inc.) | PM, PM, PM | 150 mg/m |
| Black carbon, BC (g/m) | microAeth AE51 aethalometer (AethLabs) | Fine fraction | 1 mg/m |
| Performance Metrics | Formulation |
|---|---|
| Mean Absolute Error | |
| Root Mean Squared Error | |
| Coefficient of Determination |
| Measurement Locations | MAE (g/m) | RMSE (g/m) | R | |||
|---|---|---|---|---|---|---|
| WB | BB | WB | BB | WB | BB | |
| Urban (Amman and Zarqa) | 1.834 | 1.777 | 2.111 | 2.061 | 0.76 | 0.77 |
| Jordan (including urban) | 1.945 | 1.893 | 2.414 | 2.358 | 0.77 | 0.78 |
| Proxy Usage Type | MAE (g/m) | RMSE (g/m) | R |
|---|---|---|---|
| Low-cost sensor use (one input) | 2.328 | 2.950 | 0.54 |
| “Real" instrument use (two inputs) | 1.945 | 2.414 | 0.77 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaidan, M.A.; Wraith, D.; Boor, B.E.; Hussein, T. Bayesian Proxy Modelling for Estimating Black Carbon Concentrations using White-Box and Black-Box Models. Appl. Sci. 2019, 9, 4976. https://doi.org/10.3390/app9224976
Zaidan MA, Wraith D, Boor BE, Hussein T. Bayesian Proxy Modelling for Estimating Black Carbon Concentrations using White-Box and Black-Box Models. Applied Sciences. 2019; 9(22):4976. https://doi.org/10.3390/app9224976
Chicago/Turabian StyleZaidan, Martha A., Darren Wraith, Brandon E. Boor, and Tareq Hussein. 2019. "Bayesian Proxy Modelling for Estimating Black Carbon Concentrations using White-Box and Black-Box Models" Applied Sciences 9, no. 22: 4976. https://doi.org/10.3390/app9224976
APA StyleZaidan, M. A., Wraith, D., Boor, B. E., & Hussein, T. (2019). Bayesian Proxy Modelling for Estimating Black Carbon Concentrations using White-Box and Black-Box Models. Applied Sciences, 9(22), 4976. https://doi.org/10.3390/app9224976