Saturation Based Nonlinear FOPD Motion Control Algorithm Design for Autonomous Underwater Vehicle
Abstract
:1. Introduction
2. Modelling of AUV
3. Fractional Calculus
Fractional-Order Derivative
4. Saturation Based Nonlinear FOPD Controller Design
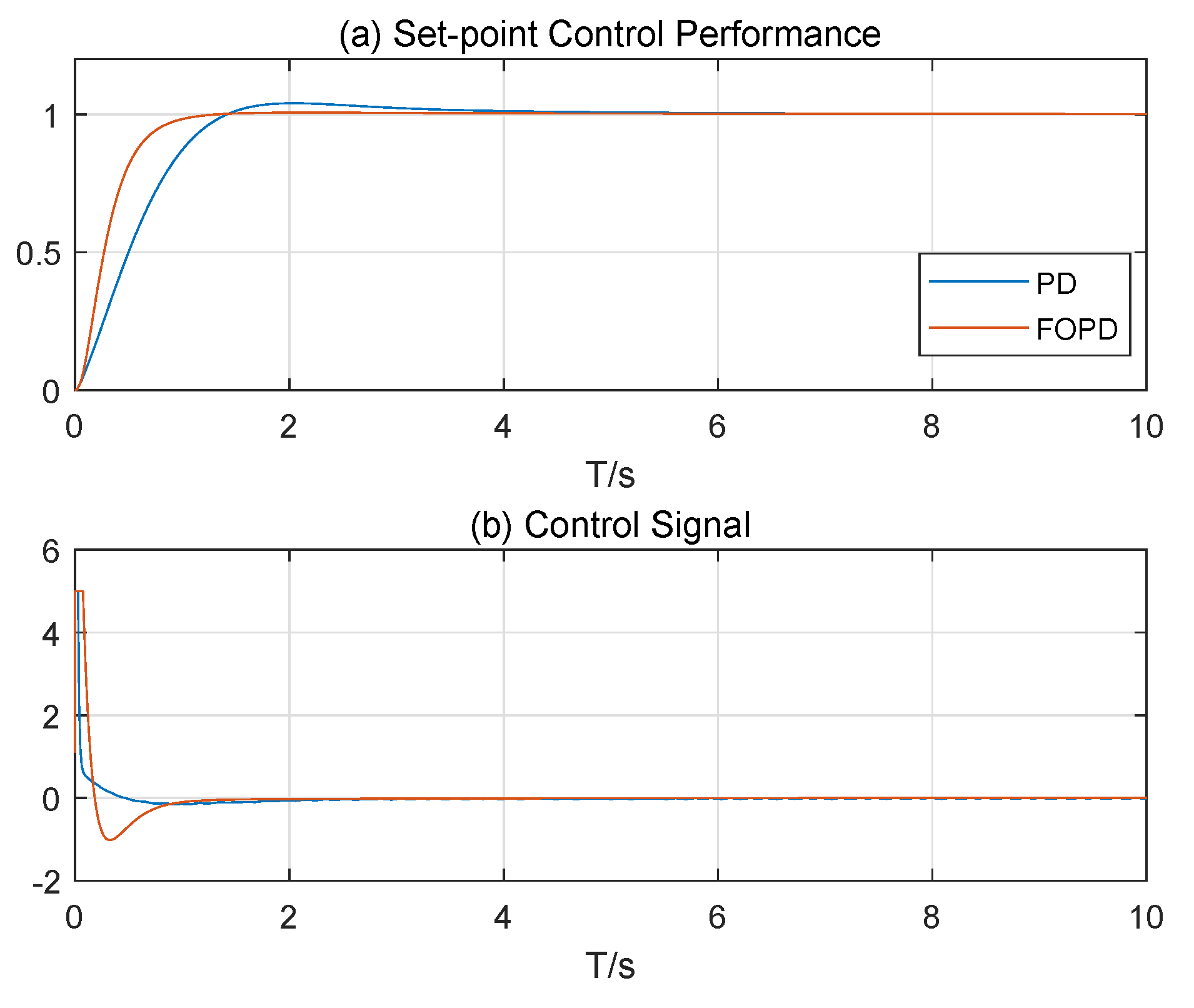
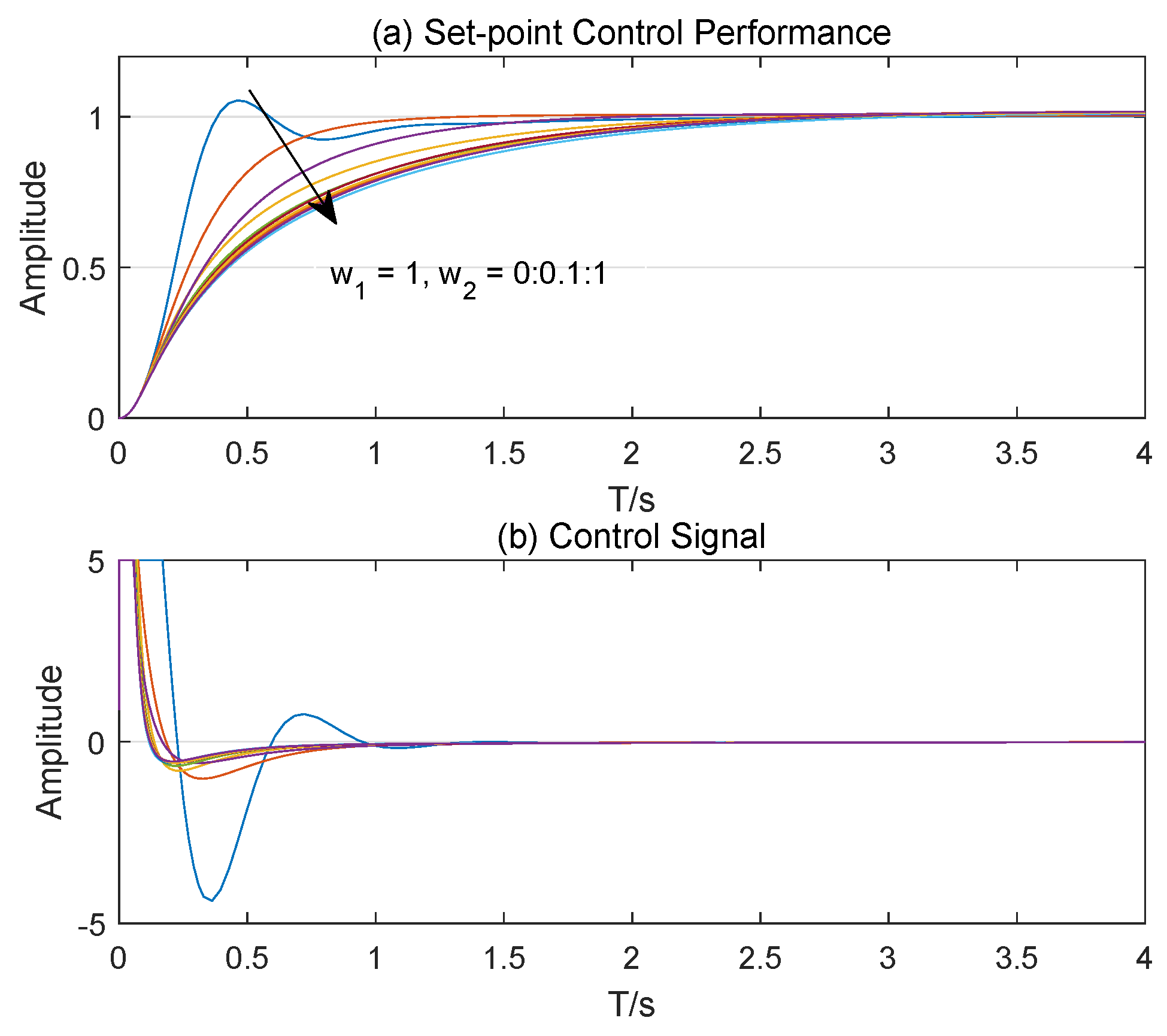
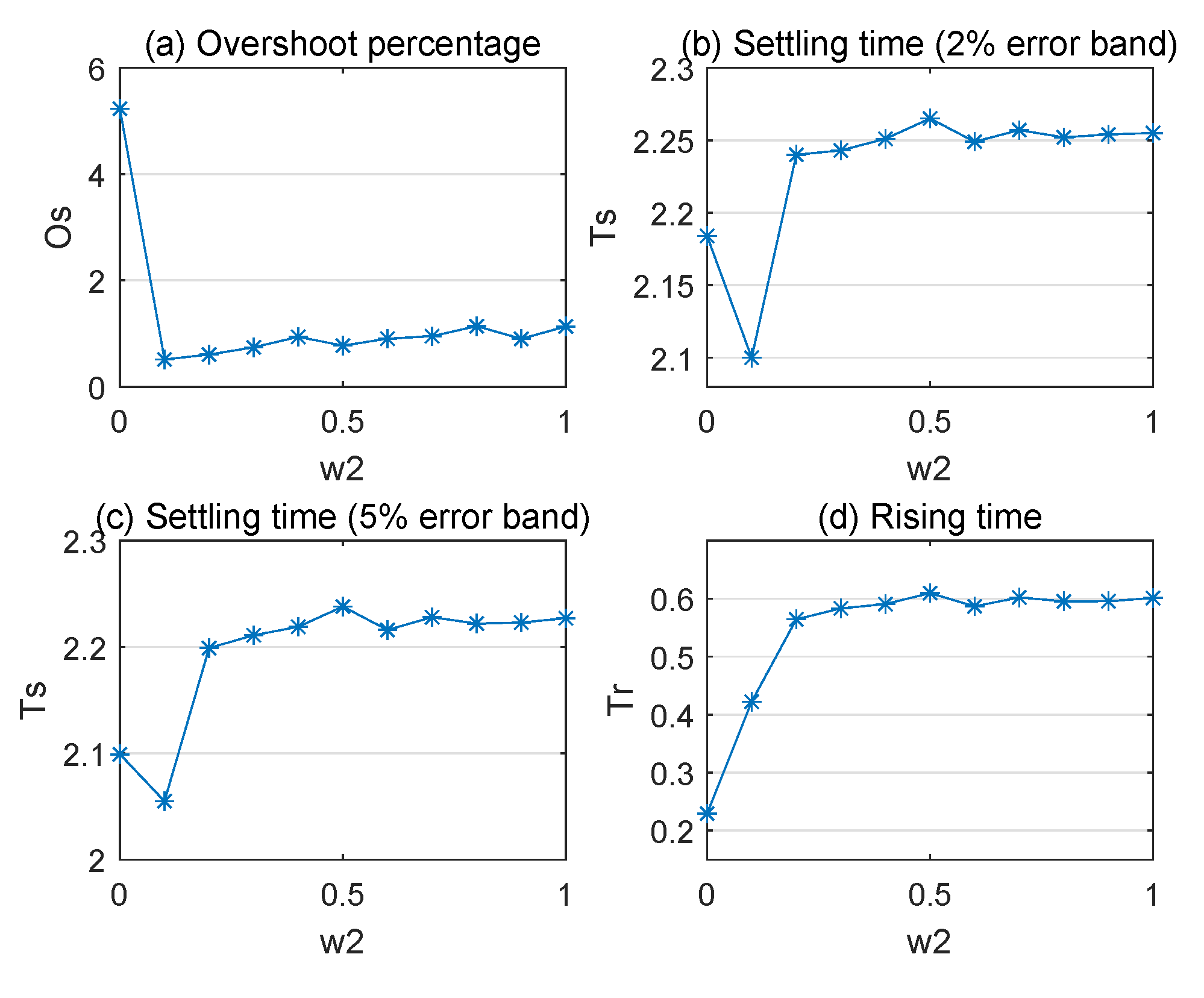
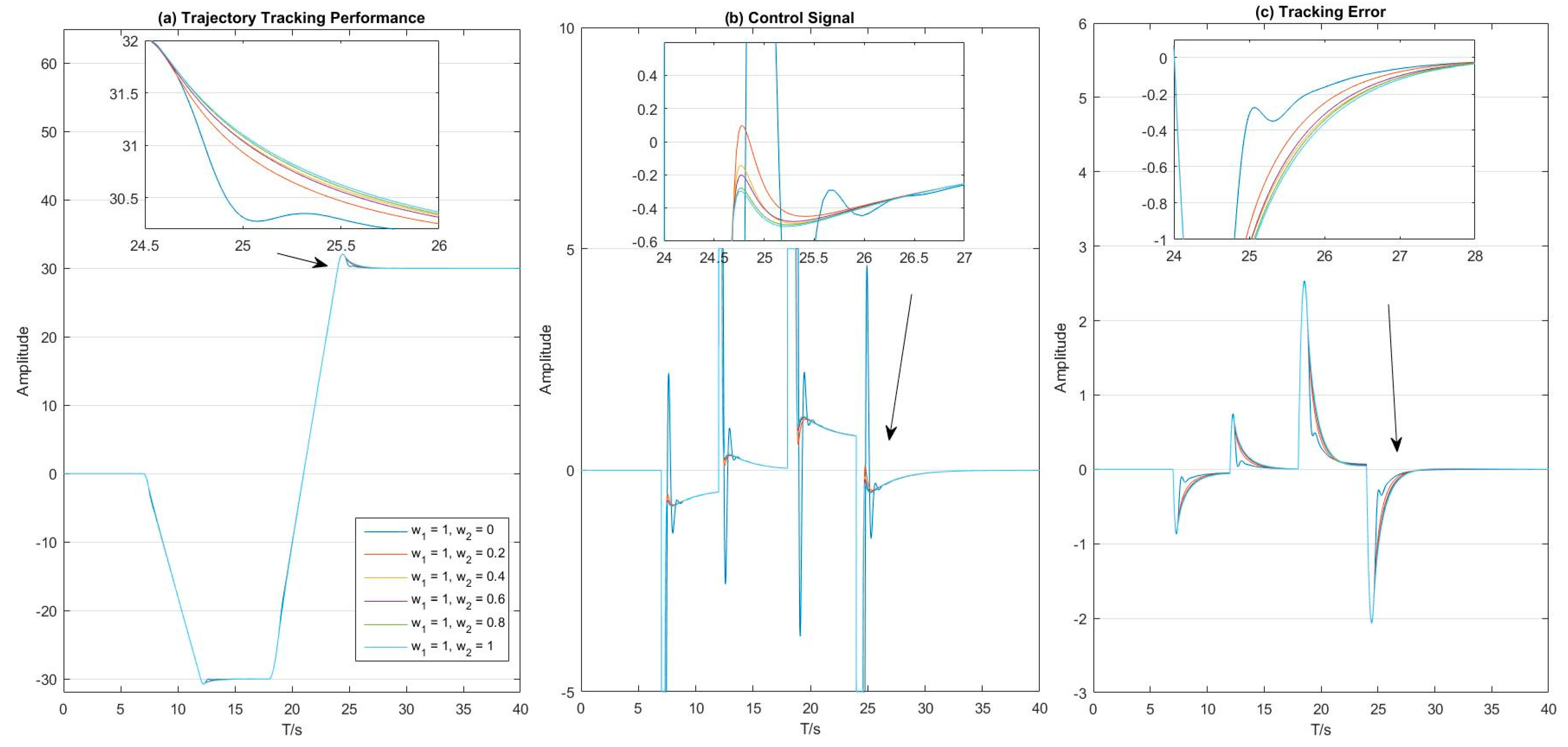
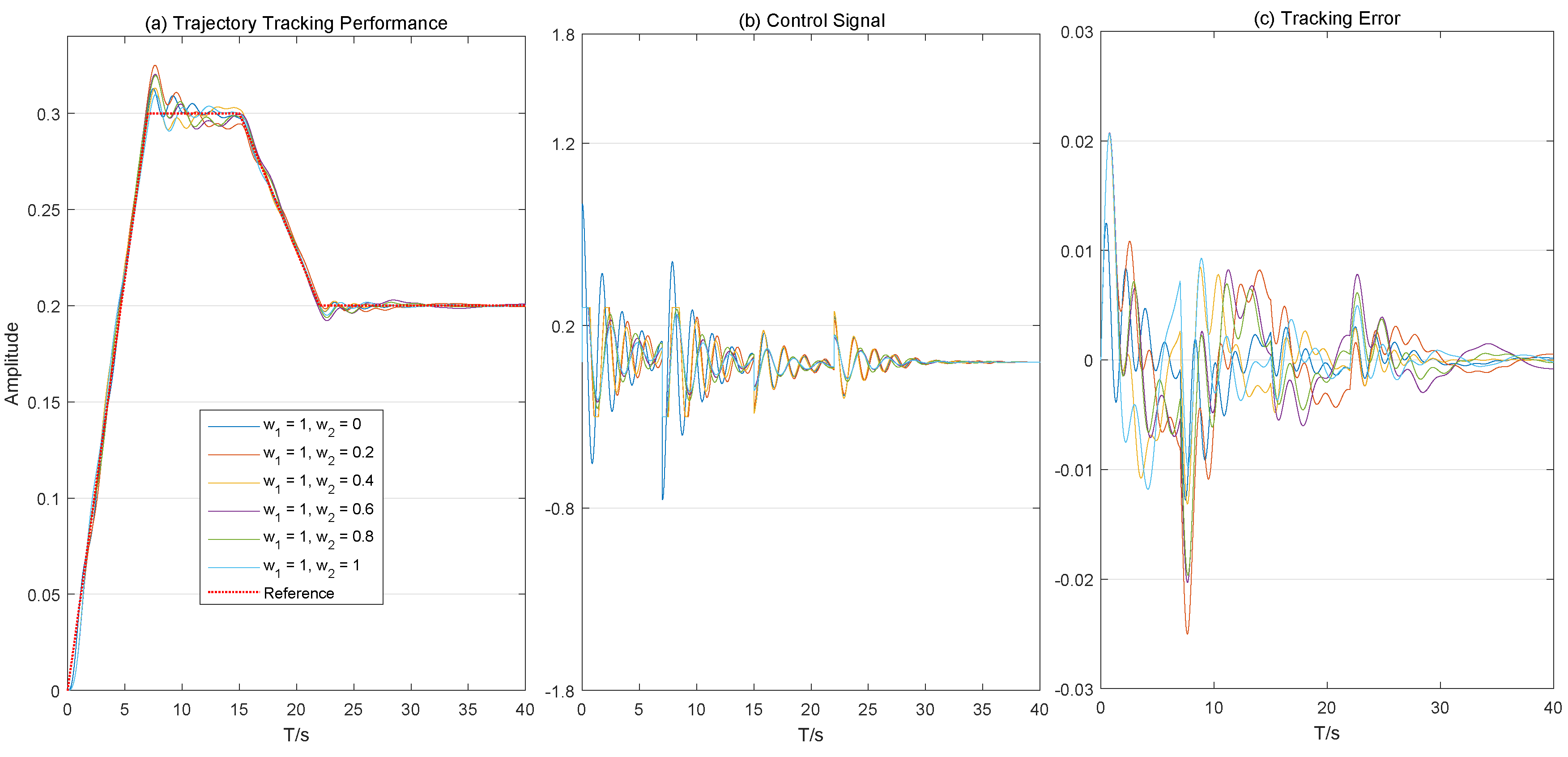
5. Simulations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Ge, H.; Chen, G.; Xu, G. Multi-AUV cooperative target hunting based on improved potential field in a surface water environment. Appl. Sci. 2018, 8, 973. [Google Scholar] [CrossRef]
- Wynn, R.B.; Huvenne, V.A.; Le Bas, T.P.; Murton, B.J.; Connelly, D.P.; Bett, B.J.; Ruhl, H.A.; Morris, K.J.; Peakall, J.; Parsons, D.R.; et al. Autonomous underwater vehicles (AUVs): Their past, present and future contributions to the advancement of marine geoscience. Mar. Geol. 2014, 352, 451–468. [Google Scholar] [CrossRef]
- Fossen, T.I.; Johansen, T.A. A survey of control allocation methods for ships and underwater vehicles. In Proceedings of the IEEE Mediterranean Conference on Control and Automation, Ancona, Italy, 28–30 June 2006. [Google Scholar]
- Wang, J. Research on motion control of underwater vehicle. In Proceedings of the Chinese Control and Decision Conference, Taiyuan, China, 23–25 May 2012; pp. 1–6. [Google Scholar]
- Xiang, X.; Yu, C.; Lapierre, L.; Zhang, J.; Zhang, Q. Survey on fuzzy-logic-based guidance and control of marine surface vehicles and underwater vehicles. Int. J. Fuzzy Syst. 2017, 20, 572–586. [Google Scholar] [CrossRef]
- Cui, R.; Zhang, X.; Cui, D. Adaptive sliding-mode attitude control for autonomous underwater vehicles with input nonlinearities. Ocean. Eng. 2016, 123, 45–54. [Google Scholar] [CrossRef]
- Perrier, M.; Canudas-De-Wit, C. Experimental comparison of PID vs. PID plus nonlinear controller for subsea robots. Auton. Robot. 1996, 3, 195–212. [Google Scholar] [CrossRef]
- Liu, S.; Wang, D.; Poh, E.K.; Chia, C.S. Nonlinear output feedback controller design for tracking control of ODIN in wave disturbance condition. In Proceedings of the IEEE Oceans Conference, Washington, DC, USA, 17–23 September 2005. [Google Scholar]
- Pettersen, K.Y. Output feedback control of slender body underwater vehicles with current estimation. Int. J. Control 2007, 80, 1136–1150. [Google Scholar]
- Adhami-Mirhosseini, A.; Aguiar, A.P.; Yazdanpanah, M.J. Seabed tracking of an autonomous underwater vehicle with nonlinear output regulation. In Proceedings of the IEEE Conference on Decision & Control, Orlando, FL, USA, 12–15 December 2011. [Google Scholar]
- Podlubny, I. Fractional-order systems and PIλDμ controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Oustaloup, A.; Sabatier, J.; Lanusse, P.; Malti, R.; Melchior, P.; Moreau, X.; Moze, M. An overview of the CRONE approach in system analysis, modeling and identification, observation and control. IFAC Proc. Vol. 2008, 41, 14254–14265. [Google Scholar] [CrossRef]
- Liu, L.; Xue, D.; Zhang, S. Closed-loop time response analysis of irrational fractional-order systems with numerical Laplace transform technique. Appl. Math. Comput. 2018, 350, 122–152. [Google Scholar] [CrossRef]
- Gao, Z. Kalman filters for continuous-time fractional-order systems involving fractional-order colored noises using tustin generating function. Int. J. Control Autom. Syst. 2018, 16, 1049–1059. [Google Scholar] [CrossRef]
- Xue, D. Fractional-Order Control Systems Fundamentals and Numerical Implementations; De Gruyter: Berlin, Germany, 2017. [Google Scholar]
- Liu, L.; Zhang, S.; Xue, D.; Chen, Y. General robustness analysis and robust fractional-order PD controller design for fractional-order plants. IET Control Theory Appl. 2018, 12, 1730–1736. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, Y.; Wang, H. Mittag-Leffler stability of fractional-order Hopfield neural networks. Nonlinear Anal. Hybrid Syst. 2015, 16, 104–121. [Google Scholar] [CrossRef]
- Liu, L.; Pan, F.; Xue, D. Variable-order fuzzy fractional PID controller. ISA Trans. 2015, 55, 227–233. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Yu, Y.; Wang, Q. Stability analysis of fractional-order Hopfield neural networks with discontinuous activation functions. Neurocomputing 2016, 171, 1075–1084. [Google Scholar] [CrossRef]
- Yin, C.; Huang, X.; Chen, Y.; Dadras, S.; Zhong, S.M.; Cheng, Y. Fractional-order exponential switching technique to enhance sliding mode control. Appl. Math. Model. 2018, 44, 705–726. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, L.; Cui, X. Robust FOPID controller design for fractional-order delay systems using positive stability region analysis. Int. J. Robust Nonlinear Control 2019, 29, 5195–5212. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, S.; Xue, D.; Chen, Y. Robust stability analysis for fractional-order systems with time-delay based on finite spectrum assignment. Int. J. Robust Nonlinear Control 2019, 29, 2283–2295. [Google Scholar] [CrossRef]
- Cheng, S.; Wei, Y.; Chen, Y.; Wang, Y.; Liang, Q. Fractional-order multivariable composite model reference adaptive control. Int. J. Adapt. Control. Signal Process. 2017, 31, 1467–1480. [Google Scholar] [CrossRef]
- Liu, L.; Tian, S.; Xue, D.; Zhang, T.; Chen, Y. Continuous fractional-order Zero Phase Error Tracking Control. ISA Trans. 2018, 75, 226–235. [Google Scholar] [CrossRef]
- Rosas-Jaimes, O.A.; Munoz-Hernandez, G.A.; Mino-Aguilar, G.; Castaneda-Camacho, J.; Gracios-Marin, C.A. Evaluating fractional PID control in a nonlinear MIMO model of a hydroelectric power station. Complexity 2019, 2019, 9367291. [Google Scholar] [CrossRef]
- Muñoz-Vázquez, A.J.; Ramírez-Rodríguez, H.; Parra-Vega, V.; Sánchez-Orta, A. Fractional sliding mode control of underwater ROVs subject to non-differentiable disturbances. Int. J. Control Autom. Syst. 2017, 15, 1314–1321. [Google Scholar]
- Talange, D.B.; Joshi, S.D.; Gaikwad, S. Control of autonomous underwater vehicle using fractional order PIλ controller. In Proceedings of the IEEE Oceans Conference, Hyderabad, India, 28–30 August 2013. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: London, UK, 1999. [Google Scholar]
- Sabatier, J.; Merveillaut, M.; Malti, R.; Oustaloup, A. How to impose physically coherent initial conditions to a fractional system? Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1318–1326. [Google Scholar] [CrossRef]
- Achar, N.; Lorenzo, C.; Hartley, T. Initialization and the Caputo fractional derivative. In Lewis Field Report; NASA John H. Glenn Research Center: Brook Park, OH, USA, 2003. [Google Scholar]
- Aguiar, B.; González, T.; Bernal, M. A way to exploit the fractional stability domain for robust chaos suppression and synchronization via LMIs. IEEE Trans. Autom. Control 2016, 61, 2796–2807. [Google Scholar] [CrossRef]
- Campos, E.; Chemori, A.; Creuze, V.; Torres, J.; Lozano, R. Saturation based nonlinear depth and yaw control of underwater vehicles with stability analysis and real-time experiments. Mechatronics 2017, 45, 49–59. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Lu, L.Y. Motion Control and Path Planning of Underwater Vehicle. Ph.D. Thesis, Yangzhou University, Yangzhou, China, 2013. [Google Scholar]
- Das, S.; Pan, I.; Das, S.; Gupta, A. A novel fractional order fuzzy PID controller and its optimal time domain tuning based on integral performance indices. Eng. Appl. Artif. Intell. 2012, 25, 430–442. [Google Scholar] [CrossRef]
- Barton, R.R.; Ivey, J.S. Nelder-Mead simplex modifications for simulation optimization. Manag. Sci. 1996, 42, 954–973. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
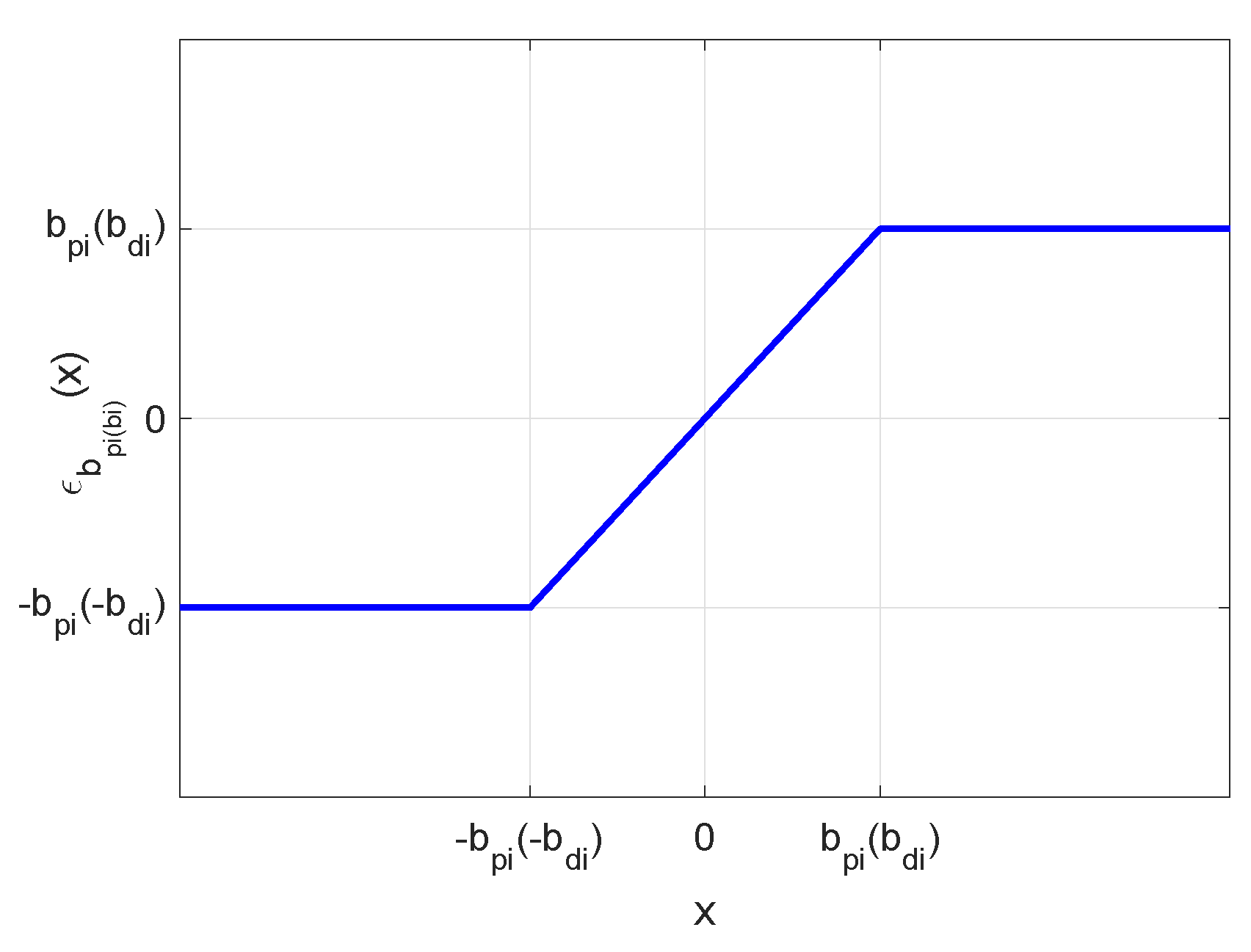
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Liu, L.; Zhang, S.; Cao, S. Saturation Based Nonlinear FOPD Motion Control Algorithm Design for Autonomous Underwater Vehicle. Appl. Sci. 2019, 9, 4958. https://doi.org/10.3390/app9224958
Zhang L, Liu L, Zhang S, Cao S. Saturation Based Nonlinear FOPD Motion Control Algorithm Design for Autonomous Underwater Vehicle. Applied Sciences. 2019; 9(22):4958. https://doi.org/10.3390/app9224958
Chicago/Turabian StyleZhang, Lichuan, Lu Liu, Shuo Zhang, and Sheng Cao. 2019. "Saturation Based Nonlinear FOPD Motion Control Algorithm Design for Autonomous Underwater Vehicle" Applied Sciences 9, no. 22: 4958. https://doi.org/10.3390/app9224958
APA StyleZhang, L., Liu, L., Zhang, S., & Cao, S. (2019). Saturation Based Nonlinear FOPD Motion Control Algorithm Design for Autonomous Underwater Vehicle. Applied Sciences, 9(22), 4958. https://doi.org/10.3390/app9224958





