Inversion of Thermal Conductivity in Two-Dimensional Unsteady-State Heat Transfer System Based on Finite Difference Method and Artificial Bee Colony
Abstract
1. Introduction
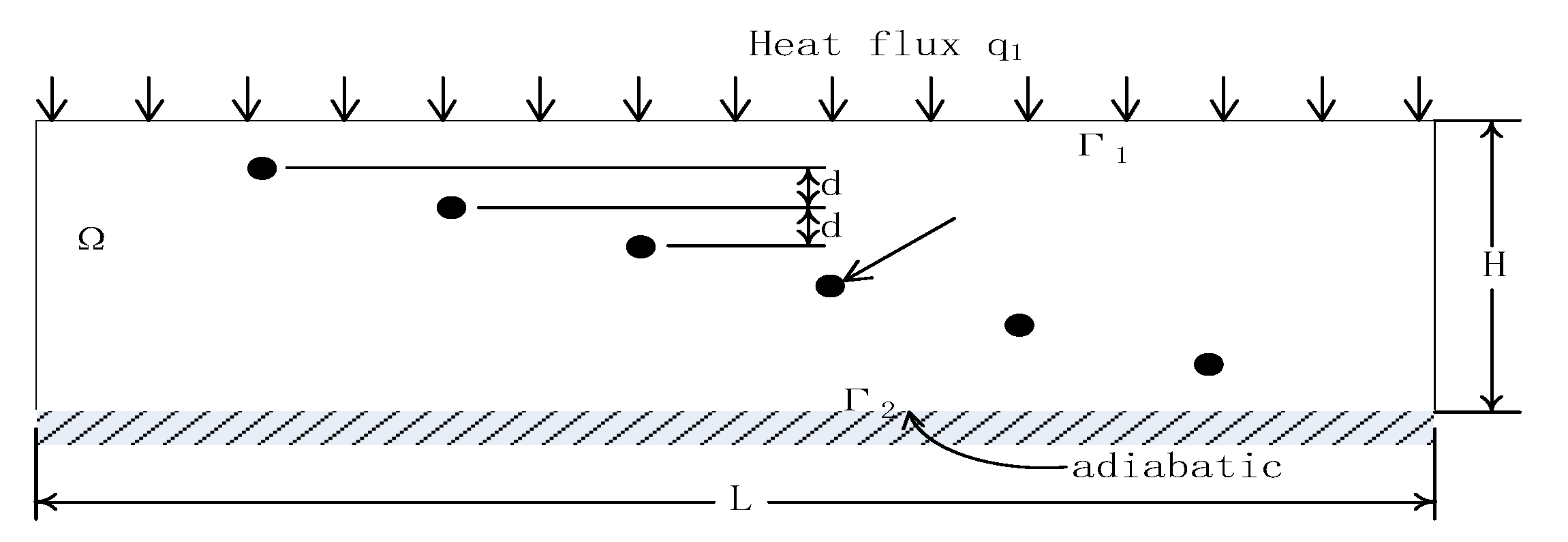
2. Forward Problem Description
3. The Inverse Problem
3.1. Objective Function of Inverse Problem
3.2. Artificial Bee Colony Algorithm
3.3. Improved Artificial Bee Colony Algorithm
3.4. Inverse Problem Solving Process
- (1)
- Randomly generate the initial value of thermal conductivity using Equation (5);
- (2)
- Solve the forward problem, calculate the objective function, and calculate the probability of each employed bee;
- (3)
- According to Equation (6), employed bees search for the solution. After the forward problem is solved, calculate the value of the objective function and probability, and determine if it needs to be updated by the greedy algorithm;
- (4)
- The onlooker bees search for the solution according to Equation (6). After the forward problem is solved, calculate the value of the objective function.
- (5)
- According to Equation (7), the scout bee searches for the solution. After the forward problem is solved, update the value of the objective function and probability. Select the optimal and update the optimal solution using Equation (11), then determine if it needs to be updated by the greedy algorithm.
- (6)
- Stop iteration once the stop criterion or the maximum number of iterations is satisfied, otherwise, return to step 2.
4. Numerical Experiment and Analysis
4.1. Contrast of Convergence Rate of IABCA and ABCA
4.2. Impact of Colony Size
4.3. Impact of the Number of Measuring Points
- When the measurement error was 0: When M = 2, the relative error of was −0.33%; when M = 4, the relative error of was 0.04%; and when M = 6, the relative error of was 0.00%.
- When the measurement error was ±0.1%: When M = 2, the relative error of was −0.43%; when M = 4, the relative error of was −0.25%; and when M = 6, the relative error of was −0.11%.
4.4. Impact of Measurement Error
- when measurement error was 0%, the average relative error of was 0.00%;
- when measurement error was ±0.3%, the average relative error of was 0.50%;
- when measurement error was ±0.5%, the average relative error of was 0.84%;
- when measurement error was ±1.0%, the average relative error of was −1.40%;
- when measurement error was ±2.0%, the average relative error of was −1.94%.
4.5. Impact of the Relative Placement
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, S.; Zhang, L.; Sun, X.; Jia, H. Inversion of Thermal Conductivity in Two-Dimensional Unsteady-State Heat Transfer System Based on Boundary Element Method and Decentralized Fuzzy Inference. Complexity 2018, 2018, 8783946. [Google Scholar] [CrossRef]
- Wang, S.; Jia, H.; Sun, X. Two-Dimensional Steady Boundary Shape Inversion of CGM-SPSO Algorithm on Temperature information. Adv. Mater. Sci. Eng. 2017, 2017, 2461498. [Google Scholar] [CrossRef]
- Fan, C.; Sun, F.; Yang, L. A simple method for inverse estimation of surface temperature distribution on a flat plate. Inverse Probl. Sci. Eng. 2009, 17, 885–899. [Google Scholar] [CrossRef]
- Cui, M.; Gao, X.; Liu, Y. Inversion of Temperature-dependent Thermal Conductivity Based on Transient Inverse Heat Conduction Problem. Proc. CSEE 2012, 32, 82–87. [Google Scholar]
- Wang, S.; Zhang, L.; Sun, X. Solution to Two-Dimensional Steady Inverse Heat Transfer Problems with Interior Heat Source Based on the Conjugate Gradient Method. Math. Probl. Eng. 2017, 2017, 1–9. [Google Scholar] [CrossRef]
- Baranov, V.L.; Zasyad’ko, A.A.; Frolov, G.A. Integro-differential method of solving the inverse coefficient heat conduction problem. J. Eng. Phys. Thermophys. 2010, 83, 60–71. [Google Scholar] [CrossRef]
- Sriram, S.B.; Sravan, S.; Gnanasekaran, N. Numerical Estimation of Heat Flux and Convective Heat Transfer Coefficient in a One Dimensional Rectangular Plate by Levenberg-Marquardt Method. Indian J. Sci. Technol. 2016, 9. [Google Scholar] [CrossRef]
- Ruan, Z.H.; Yuan, Y.; Chen, Q.X.; Zhang, C.X.; Shuai, Y.; Tan, H.P. A new multi-function global particle swarm optimization. Appl. Soft Comput. 2016, 49, 279–291. [Google Scholar] [CrossRef]
- Kosaka, M.; Monde, M. Simultaneous measurement of thermal diffusivity and thermal conductivity by means of inverse solution for one-dimensional heat conduction (anisotropic thermal properties of CFRP for FCEV). Int. J. Thermophys. 2015, 36, 2590–2598. [Google Scholar] [CrossRef]
- Czél, B.; Gróf, G. Genetic algorithm-based method for determination of temperature-dependent thermophysical properties. Int. J. Thermophys. 2009, 30, 1975–1991. [Google Scholar] [CrossRef]
- Mohebbi, F.; Sellier, M.; Rabczuk, T. Estimation of linearly temperature-dependent thermal conductivity using an inverse analysis. Int. J. Therm. Sci. 2017, 117, 68–76. [Google Scholar] [CrossRef]
- Bozzoli, F.; Mocerino, A.; Rainieri, S.; Vocale, P. Inverse heat transfer modeling applied to the estimation of the apparent thermal conductivity of an intumescent fire retardant paint. Exp. Therm. Fluid Sci. 2017, 90, 143–152. [Google Scholar] [CrossRef]
- Peng, C. Simultaneous determination of thickness, thermal conductivity and porosity in textile material design. J. Inverse Ill-Posed Probl. 2016, 24, 59–66. [Google Scholar]
- Huang, S.J. An Ant Colony Optimization Algorithm Suitable for Searching Heat Source Location in IHCP. J. Eng. Thermophys. 2013, 34, 694–697. [Google Scholar]
- Mahmud, K.; Mohsen, D.A. Inclusion Identification by Inverse Application of Boundary Element Method, Genetic Algorithm and Conjugate Gradient Method. Am. J. Appl. Sci. 2008, 5, 1158–1166. [Google Scholar]
- D’Haeyer, S.; Johansson, B.T.; Slodička, M. Reconstruction of a Spacewise-Dependent Heat Source in a Time-Dependent Heat Diffusion Process. IMA J. Appl. Math. 2014, 79, 33–53. [Google Scholar] [CrossRef]
- Chen, H.T.; Wu, X.Y. Investigation of Heat Transfer Coefficient in Two-Dimensional Transient Inverse Heat Conduction Problems Using the Hybrid Inverse Scheme. Int. J. Numer. Methods Eng. 2008, 73, 107–122. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, G.; Chen, H. Estimating Steady Multi-variables Inverse Heat Conduction Problem by Using Conjugate Gradient Method. Proc. CSEE 2011, 31, 58–61. [Google Scholar]
- Yu, X. Inverse Analysis of Thermal Conductivities in Non-Homogeneous Heat Conductions Using Boundary Element Mehod. Master’s Thesis, Dalian University of Technology, Dalian, China, 2013. [Google Scholar]
- Sawaf, B.; Ozisik, M.N. An inverse analysis to estimate linearly temperature dependent thermal conductivity components and heat capacity of an orthotropic medium. Int. J. Heat Mass Transf. 1995, 38, 3005–3010. [Google Scholar] [CrossRef]
- Ukrainczyk, N. Thermal diffusivity estimation using numerical inverse solution for 1D heat conduction. Int. J. Heat Mass Transf. 2009, 52, 5675–5681. [Google Scholar] [CrossRef]
- Huang, C.H.; Yan, J.Y. An inverse problem in simultaneously measuring temperature-dependent thermal conductivity and heat capacity. Int. J. Heat Mass Transf. 1995, 38, 3433–3441. [Google Scholar] [CrossRef]
- Huang, C.H.; Chin, S.C. A two-dimensional inverse problem in imaging the thermal conductivity of a non-homogeneous medium. Int. J. Heat Mass Transf. 2000, 43, 4061–4071. [Google Scholar] [CrossRef]
- Zhou, H.; Xu, X. Identifaction of Temperature-Dependent Thermal Conductivity for 2-D transient Heat Conduction Problem. Appl. Math. Mech. 2014, 12, 1341–1351. [Google Scholar]
- Cui, M.; Zhu, Q.H.; Gao, X.W. A modified conjugate gradient method for transient nonlinear inverse heat conduction problems: A case study for identifying temperature-dependent thermal conductivities. Heat Transf.-Trans. ASME 2014, 136, 091301. [Google Scholar] [CrossRef]
- Cao, K.; Lesnic, D.; Colaco, M.J. Determination of thermal conductivity of inhomogeneous orthotropic materials from temperature measurements. Inverse Probl. Sci. Eng. 2019, 27, 1372–1398. [Google Scholar] [CrossRef]
- Ardakani, M.D.; Khodadad, M. Identification of thermal conductivity and the shape of an inclusion using the boundary elements method and the particle swarm optimization algorithm. Inverse Probl. Sci. Eng. 2009, 17, 855–870. [Google Scholar] [CrossRef]
- Chanda, S.; Yenni, G.R.; Ambirajan, A.; Balaji, C.; Venkateshan, S.P. An Inverse Analysis for Estimation of Thermal Conductivity of Orthotropic Composite Medium Using Artificial Neural Network. In Proceedings of the 21st National and 10th ISHMT-ASME Heat and Mass Transfer Conference, IIT Madras, India, 27–30 December 2011. [Google Scholar]
- Tang, Z.H.; Qian, G.H.; Qian, W.Q. Estimation of temperature-dependent function of thermal conductivity for a material. Chin. J. Comput. Mech. 2011, 28, 377–382. [Google Scholar]
- Zhao, J.; Fu, Z.; Jia, X.; Cai, Y. Inverse determination of thermal conductivity in lumber based on genetic algorithms. Holzforschung 2016, 70, 235–241. [Google Scholar] [CrossRef]
- Lei, C. Research on Inversion Algorithms of the Thermo Physical Properties. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2015. [Google Scholar]
- Lotfi, M.; Mezrigui, L.; Heyd, R. Study of heat conduction through a self-heated composite cylinder by Laplace transfer functions. Appl. Math. Model. 2016, 40, 10360–10376. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization, Technical Report-TR06; Erciyes University, Engineering Faculty, Computer Engineering Department: Kayseri, Turkey, 2005. [Google Scholar]
- Karaboga, D. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (abc) algorithm. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B. A comparative study of artifcial bee colony algorithm. Appl. Math. Comput. 2009, 214, 108–132. [Google Scholar]
- Zhang, W. Reseach on Artificial Bee Colony Based Hybrid Optimization Algorithms and Application. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2013. [Google Scholar]
- Omars, S.; Senthilnath, J.; Khandelwal, R. Artificial bee colony (abc) for multi-objective design optimization of composite structures. Appl. Soft Comput. 2011, 11, 489–499. [Google Scholar]
- Hetmaniok, E. Inverse problem for the solidifcation of binary alloy in the casting mould solved by using the bee optimization algorithm. Heat Mass Transf. 2016, 52, 1369–1379. [Google Scholar] [CrossRef][Green Version]
- Hetmaniok, E.; Słota, D.; Zielonka, A. Identification of the Heat Transfer Coefficient in the Inverse Stefan Problem by Using the ABC Algorithm. Arch. Foundry Eng. 2012, 12, 27–32. [Google Scholar]
- Wong, L.-P.; Low, M.Y.H.; Chong, C.S. A Bee Colony Optimization Algorithm to Job Shop Scheduling. Ph.D. Thesis, Nanyang Technological University, Singapore, 2007. [Google Scholar]
- Pham, D.T.; Castellani, M. The bees algorithm: Modeling foraging behaviour to solve continuous optimization problems. Proc. Inst. Mech. Eng. Part C 2009, 223, 2919–2938. [Google Scholar] [CrossRef]
- Hemamalini, S.; Simon, S.P. Artifcial bee colony algorithm for economic load dispatch problem with non-smooth cost functions. Electr. Power Compon. Syst. 2010, 38, 786–803. [Google Scholar] [CrossRef]
- Singh, A. An Artificial Bee Colony Algorithm for the Leaf-constrained Minimum Spanning Tree Problem. Appl. Soft Comput. 2009, 9, 625–631. [Google Scholar] [CrossRef]
- Bahamish, H.; Abdullah, R.; Salam, R. Protein Tertiary Structure Prediction Using Artificial Bee Colony Algorithm. In Proceedings of the Third Asia International Conference on Modelling & Simulation, Bali, Indonesia, 25–29 May 2009; pp. 258–263. [Google Scholar]
- Karaboga, N. A New Design Method Based on Artificial Bee Colony Algorithm for Digital IIR filters. J. Frankl. Inst. 2009, 346, 328–348. [Google Scholar] [CrossRef]
- Rao, R.S.; Narasimham, S.; Ramalingaraju, M. Optimization of Distribution Network Configuration for Loss Reduction Using Artificial Bee Colony Algorithm. Int. J. Electr. Power Energy Syst. Eng. (IJEPESE) 2008, 1, 709–715. [Google Scholar]
- Bi, X.; Wang, Y. An improved artificial bee colony algorithm. In Proceedings of the 2011 3rd International Conference on Computer Research and Development (ICCRD 2011), Shanghai, China, 11–13 March 2011; pp. 174–179. [Google Scholar]
- Yu, X.; Zhan, D.; Nie, L. An artificial bee colony algorithm for resource-constrained project scheduling problem with spatial resource. J. Comput. Inf. Syst. 2012, 8, 6723–6732. [Google Scholar]
- Zhang, C.; Zhen, J.; Zhou, Y. Two modified artificial bee colony algorithms inspired by grenade explosion method. Neuro Comput. 2015, 151, 1198–1207. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, N.; Yang, S. Hybrid artificial bee colony algorithm for parameter estimation of proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2013, 38, 5796–5806. [Google Scholar] [CrossRef]






| Test Points | Relative Error (%) | Relative Error (%) | ||
|---|---|---|---|---|
| Measurement Error = 0 | Measurement Error = ± 0.1% | |||
| 2 | 11.9610 | −0.33 | 11.9490 | −0.43 |
| 4 | 12.0049 | 0.04 | 11.9700 | −0.25 |
| 6 | 12.0000 | 0.00 | 11.9871 | −0.11 |
| Measurement Error (%) | Relative Error (%) | |
|---|---|---|
| 0 | 12.0000 | 0.00 |
| ±0.3 | 12.0600 | 0.50 |
| ±0.5 | 12.1005 | 0.84 |
| ±1.0 | 11.8316 | −1.40 |
| ±2.0 | 11.7669 | −1.94 |
| Relative Placement (mm) | Relative Error (%) | |
|---|---|---|
| 4.3 | 11.9490 | −0.43 |
| 8.6 | 11.9337 | −0.55 |
| 12.9 | 11.9635 | −0.31 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Sun, B.; Sun, X. Inversion of Thermal Conductivity in Two-Dimensional Unsteady-State Heat Transfer System Based on Finite Difference Method and Artificial Bee Colony. Appl. Sci. 2019, 9, 4824. https://doi.org/10.3390/app9224824
Yang L, Sun B, Sun X. Inversion of Thermal Conductivity in Two-Dimensional Unsteady-State Heat Transfer System Based on Finite Difference Method and Artificial Bee Colony. Applied Sciences. 2019; 9(22):4824. https://doi.org/10.3390/app9224824
Chicago/Turabian StyleYang, Liangliang, Bojun Sun, and Xiaogang Sun. 2019. "Inversion of Thermal Conductivity in Two-Dimensional Unsteady-State Heat Transfer System Based on Finite Difference Method and Artificial Bee Colony" Applied Sciences 9, no. 22: 4824. https://doi.org/10.3390/app9224824
APA StyleYang, L., Sun, B., & Sun, X. (2019). Inversion of Thermal Conductivity in Two-Dimensional Unsteady-State Heat Transfer System Based on Finite Difference Method and Artificial Bee Colony. Applied Sciences, 9(22), 4824. https://doi.org/10.3390/app9224824





