Abstract
Formation of compound drops by breakup of an axisymmetric compound jet injected from a coaxial nozzle into another immiscible coflowing fluid, at various density and viscosity ratios, is numerically investigated. The fluids are assumed to be Newtonian and incompressible and gravity is neglected for simplicity. A Finite Difference Method with Front Tracking is used to track the evolution and breakup of the compound jet. The outcomes of our numerical results show how density and viscosity ratios affect the compound jet’s transition from dripping to jetting mode. The density ratios of inner-to-outer and intermediate-to-outer fluids affect compound jet breakup length, drop diameter and drop formation time more than comparable viscosity ratios. At high density and viscosity ratios, due to high inertia and viscous force respectively, the drop formation is more chaotic and mostly multi-core drops are formed.
Keywords:
laminar flow; compound jet; front-tracking; density ratio; viscosity ratio; dripping; jetting; coflowing fluid 1. Introduction
Compound liquid jet formation and breakup has been studied extensively due to its attractive industrial applications such as atomization, microencapsulation, and drug delivery [1,2,3,4,5,6]. For example, magnetic drug targeting applies compound droplets that are formed by coating a layer of ferrofluid around the core region of the drug [7].
A compound jet consists of two fluids, namely an “intermediate fluid” enclosing an “inner fluid”, extruded through a coaxial nozzle into the surrounding “outer fluid” which is coaxially resting or flowing. The resulting compound jet then decomposes into droplets due to the effects of surface tension forces. This phenomenon is known as capillary instability [8]. Several researchers have numerically and experimentally studied the formation of a compound jet in the dripping and jetting modes [3,4,6,8,9,10,11,12,13]. In the dripping mode, breakup of the drops occurs near the nozzle exit whereas in jetting mode, breakup takes place farther downstream. These two modes are essential in the application of compound jets [6,14]. Recently, the effect of outer coflowing fluid on a compound jet was experimentally examined by Lee et al. [15] and Utada et al. [16]. They demonstrated that increasing the volumetric flow rate of the external coflowing fluid not only changes the jet’s transition mode, but also affects the compound drop’s diameter. Vu et al. [12,13] numerically investigated the breakup modes in laminar compound jets in an external coflowing fluid by varying parameters such as Reynolds number, Weber number, surface tension, velocity, and nozzle size. However, the effect of differences of density and viscosity on the dynamics of a compound jet has received far less attention, especially when the outer fluid is coflowing.
Kendall et al. [17] experimentally examined the effect of flow rate and surfactants on the compound jet instabilities. They described drop formation with special attention to the conditions yielding concentricity. Chauhan et al. [9] conducted linear stability analysis and found absolute instability under certain parametric ranges. Vu et al. [13] considered the effect of outer fluid properties neglected by Chauhan et al. [9], and varied parameters such as Reynolds number, Weber number, interfacial tension ratio, velocity ratio, and jet radii ratio, when the outer fluid is either at rest or coflowing. Experimental investigations by Nadler et al. [14] and Utada et al. [16] confirm that when a compound jet forms with an outer coflowing fluid, it can breakup into simple, one-core and multi-core drops types.
The effect of inner to outer fluid viscosity ratios on the dynamics of a compound jet in a flow focusing device was studied by Zhou et al. [18]. By using the diffuse-interface model, they noticed that with increase in the viscosity ratio, multi-core compound drops form. On the other hand, Suryo et al. [19] studied the density and viscosity ratios effect on the breakup time of the inner fluid and encapsulated volume percentage of the inner fluid after drop breakup by using a Galerkin/finite element method. However, their calculations stopped when the compound jet accomplished stable shape and the domain used was half of the wavelength of the perturbation in the axial direction. Hence, later development of the jet and drop motion from dripping to jetting was not seen in their results.
As the above review shows, little consideration has been paid on the transition of a compound jet from dripping to jetting in a density-stratified and viscosity-stratified systems. Motivated by the importance of the compound jet in several industrial applications [1,2,3,4,5,6], the present study extends the work of Vu et al. [13] to numerically compute the breakup of a compound jet at fairly moderate density and viscosity ratios, when the outer fluid is coflowing.
2. Formulation
We consider an axisymmetric compound jet, comprising three viscous immiscible liquids, in a cylindrical tube of length L and diameter , as shown in Figure 1. The inner fluid (“ 1”) and intermediate fluid (“ 2”) are respectively injected from the inner nozzle and the annular region between the inner and outer nozzle into another outer coflowing fluid (“ 3”) within the cylindrical tube. We denote the inner radius of the inner nozzle by , and the inner radius of the outer nozzle by . We assume the wall of the cylinder to be rigid, with inlet at and outlet at . The fluids are assumed to be Newtonian and incompressible, with densities and dynamic viscosities of , , , and , respectively. The average velocity of inner, intermediate and outer fluids are denoted by , and respectively. = 0 represents the state where the outer fluid is at rest and reflects outer fluid coflowing. Both these configurations drastically affect the formation of compound jets and drop [14,16]. At the inlet, we apply fully developed laminar profiles, as specified in Equation (4). Also, the interfacial tension of the two fluid interfaces is assumed to be constant.
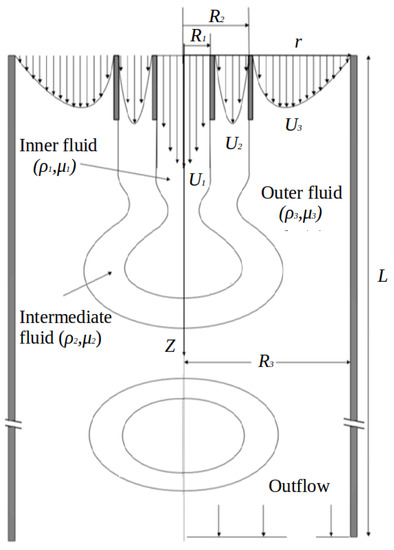
Figure 1.
Schematic of breakup of a compound jet, and a resulting compound drop.
Here, we use the cylindrical coordinate system to solve the three immiscible fluid flow problem, where r denotes the radial coordinate and z denotes the axial coordinate. The calculations are assumed to be axisymmetric along z axis. The flow dynamics are governed by the continuity and Navier-Stokes equations, given by:
wherein = () denotes the velocity in which u and v represent the radial and axial velocity components, respectively; p represents the pressure and t is the time; denotes the interfacial tension and f denotes the interfaces. The gravity is set to zero. The Dirac delta function is zero everywhere except that it provides unit impulse at the interface and S defines the inner and outer surfaces of the jets and drops. is twice the mean curvature, and represents the unit normal vector to the interface.
Here, we solve Equations (1) and (2) using no-slip and no penetration conditions on the cylindrical tube and nozzle walls. At the symmetric axis r = 0, symmetrical B.C is applied. To avoid recirculation in the computing domain, the outflow B.C, and / = 0 are enforced at . At the inlet, a constant flow rate and a fully-developed velocity profile are imposed:
With the thickness of the nozzle denoted by , we express = + and = +. We specify the nozzle thickness to be 0.2, and the length of the nozzle in the axial direction () as 2. The radius () of the cylindrical tube is assumed to be and its length L to be . At t = 0, we assign a hemispherical shape to the two interfaces forming the nascent compound jet with the outer fluid at resting.
The dimensionless parameters that control the dynamics of a gravity-free compound liquid jet are given by the Reynolds number and Weber number:
and by the following ratios:
The time t, as non-dimensionalized with respect to and (), is denoted = /.
3. Numerical Method
We use the Eulerian-Lagrangian method of Front Tracking, which applies the finite difference method to solve Equations (1) and (2) by the marker-and-cell (MAC) method [20] on a fixed, staggered grid. The Lagrangian front points are used to track the interfaces, which are transferred by the flow velocity interpolated from the fixed staggered grid. The momentum equation is discretized by second-order centered spatial differences and an explicit second-order time-integration method. The updated front point locations are used to spread the interfacial jumps of density and viscosity to the nearby grid points by area weighting, then density and viscosity fields are solved by Poisson equations. The interfacial tension force is calculated from the curvature formed by the linked front points which is spread to the Eulerian grid cells within a radius of one grid spacing by the discretized function. For detailed description of the method used, we refer readers to Tryggvason et al. [21]. This solver has been thoroughly confirmed for a compound jet by Vu et al. [11,12] by comparing with previous numerical and experimental results.
A grid refinement test was conducted with 64 × 960, 128 × 1920 and 256 × 3840 resolutions. Figure 2 shows the results of the interfacial evolution using the 128 × 1920 grid compared with the 256 × 3840 grid. The results were nearly the same with breakup length changing by less than 0.5–1.5% for the 128 × 1920 and 256 × 3840 grid resolutions, whereas 64 × 960 yielded some differences. Similar grid refinement tests were also conducted by Homma et al. [22] and Vu et al. [13] to numerically investigate the formation of a single and compound jet, by using the Front Tracking Method in both resting and coflowing outer fluid. For the results presented below, we incorporate 1920 grid points in the axial direction and 128 grid points in the radial direction. In the previous works, method validations have been conducted carefully. A validation case is shown in Figure 3a,b where comparison with the non-coflowing experiments of Hertz and Hermanrud [3] has been presented. Such validations are satisfactory and confirm the accuracy of the method used in this analysis. We also assume that the drop doesn’t merge with the jets so as to obtain the most suitable results that are observed in experiments [16].
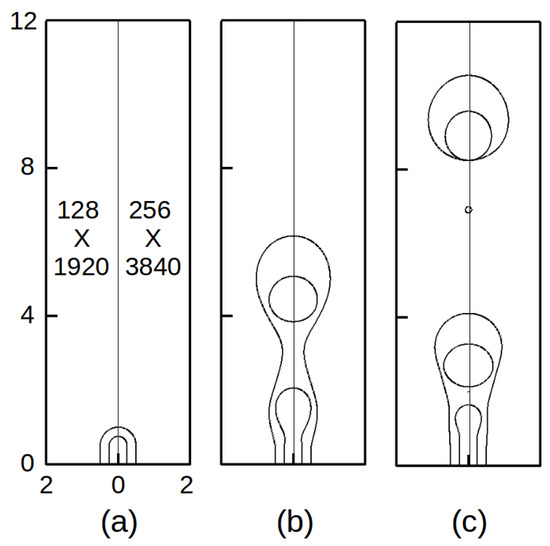
Figure 2.
Grid refinement test for = 1, = 1, = 1, = 1 at non-dimensional times of: (a) = 0; (b) = 6.42 and (c) = 8.72, with the rest of the parameters as and .

Figure 3.
A comparison between experimental jets of Hertz and Hermanrud [3] (top section) and the computed jet (bottom section) profiles at computational time: (a) = 251 and (b) = 253. The parameter used to generate the figures, calculated based on the inner most fluid, are , , , = 1, = 1, = 0.38, = 1, = 0, = 2, for both experimental and computed jets. = = 0.05 is for the computed jet; = 0.001 for the experimental jet. The figure is taken from Vu et al. [11]
Here, the properties of inner, intermediate and outer fluids are kept constant to focus on the effects of density and viscosity difference between the inner and intermediate fluids, for example, compound jets of immiscible liquids such as an aqueous solution of a k-Carrageenan or aqueous solution of polyethylene glycol injected from the inner and outer nozzles and sunflower oil injected from the annular nozzle [23]. Such liquid systems have nearly the same values of density, surface tension and the effect of viscosity can be studied by varying the weight fraction of k-Carrageenan in the aqueous solution. For the effect of density, examples such as immiscible liquids of water/Heptane/water or water/n-Decane/water system having nearly the same viscosity but different densities values may be considered [22]. Some density ratios simulated in the current study lie outside the range achievable by realistic choices of standard liquids. However such density ratios might be produced with bubbly suspensions having high volumetric gas fractions dispersed in a liquids which can produce fluids of rather exceptionally low bulk density and viscosity [24]. We keep the Reynolds number, Weber number, velocity ratios, surface tension ratio and jet radii ratio constant: , , , , and . The selection of such parametric values i.e., , , , and form compound drops near the nozzle, dripping mode [13,25]. The ranges for inner and intermediate fluid density and viscosity ratios used in the current study are displayed in Table 1.

Table 1.
Investigated ranges of parameters in the present study.
4. Results and Discussion
4.1. Baseline Case
We investigate the effect of density ratios , and viscosity ratios , on the breakup modes of the compound jet, focusing on the transition of a compound jet from dripping to jetting. We first consider the “baseline case” with all fluids having the same density and viscosity, = = = = 1, , , and , for which results are illustrated in Figure 4. In such conditions, the only destabilizing forces are the surface tension forces. Herein we set the criterion for “dripping” to be when the drops detach at a length less than 10, i.e., 5 non-dimensional units herein. For jet breakup above this length, we refer to such drop formation as being in the “jetting mode”.
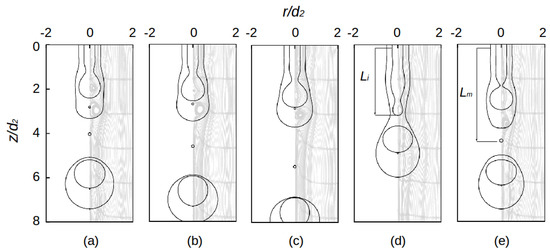
Figure 4.
Snapshots of phase boundaries of compound liquid jets for = 1, = 1, = 1, = 1, with the rest of the parameters as and , with streamlines superposed in the right halves at non-dimensional times of: (a) = 23.68; (b) = 24.08; (c) = 24.56; (d) = 27.04 and (e) = 28.08. Readers can refer to Video “S1:Baseline case” in the Supplementary Materials for better understanding of the breakup process of the baseline case.
In Figure 4a–e, the inner and intermediate jets are ejected from the coaxial nozzle into the outer co-flowing fluid and proceed to form compound drops. In the initial stages, a vortex forms inside the inner drop as shown in Figure 4a. The right sides of the snapshots in Figure 4 show the streamlines, whence the vortex formation process can be clearly seen. The vortex in the inner drop starts to weaken when the diameter of the growing inner drop reaches 0.75 times its ultimate value. This weakening of the vortex formation in the inner drop (Figure 2b) is basically due to more fluid accumulation in the growing inner drop which later results in pinch-off [13]. This growing drop detaches from the inner jet and then is carried away by the intermediate fluid motion (Figure 4d). Similarly, in the initial stages, vortex formation starts to occur on the inner surface of the intermediate fluid (Figure 4a,b). The vortex in the intermediate drop starts to weaken after the diameter ratio of the growing intermediate drop to the fully developed intermediate drop reaches 0.68 (Figure 4c). The motion of the inner drop further weakens the vortex formation inside the nascent intermediate drop (Figure 4d), which results in necking and detachment of the intermediate drop (Figure 4e).
After the pinch-off of the inner drop, the interface of the inner jet retracts due to surface tension. This causes a collision in the inner fluid streams, coming from opposite directions within the inner jet which gives rise to new vortex formation in the inner jet (Figure 4d). Similarly, after the detachment of the intermediate drop, surface tension causes the interface of the intermediate jet to retract. The retraction of the intermediate fluid gives rise to a new vortex formation due to the fluid collision from the opposite directions within the jet, leading in most cases to periodic compound drop formation (Figure 4e). Apart from compound drops, small inner and intermediate “satellite drops” are also formed due to capillary instability, is seen in Figure 4b. The intermediate satellite drops, which have larger volumes compared to the inner satellite drops, after breakup are carried away by the outer fluid motion. Whereas, the inner satellite drop having size less than 2 grid spacing are so small that after the breakup it disappears (Figure 4a,d). So, for such very tiny inner drops, we neglect its formation [13]. We define the jet breakup length as the length of the jet measured right after the breakup, as shown in Figure 4b where stands for jet breakup length of the inner jet, and in Figure 4c where denotes breakup length of the intermediate jet. In Figure 4b,c, the jet breakup lengths of both jets lie in the dripping region. The drops formed in this case are single-core. The breakup of a compound jet in the dripping region may also produce multi-core compound drops, i.e., a compound drop enclosing more than one core drop, which can break the periodicity of the drop formation. Such cases are discussed in Section 4.2.
4.2. Effect of Inner-to-Outer Density Ratio
The density ratio was varied in the range from 0.1 to 5. Here 1 corresponds to the situation where the inner fluid is less dense compared to the intermediate and outer fluids. The effect of inner-to-outer density ratio on the compound jet is shown in Figure 5a–c for = 0.5, 2 and 4.5, respectively. The rest of the parameters used to generate these figures are = 1, = 1 and = 1. For density ratio = 0.5 (Figure 5a), the compound drops are formed in the dripping mode; both the inner and intermediate drops form near the nozzle exit and the compound drops are single core. As the density ratio is increased (), the jet breakup length of both inner and intermediate fluids increases, transiting from dripping to jetting mode (Figure 5c).
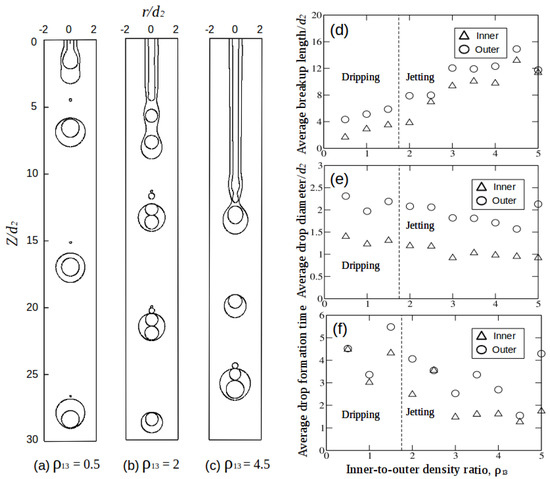
Figure 5.
Snapshots of compound liquid jets for (a) = 0.5; (b) = 2 and (c) = 4.5. The rest of the parameters are = 1, = 1, = 1, and . Graphs (d–f) represents the average breakup length, drop diameter and drop formation time for variable inner-to-outer density ratios. Readers can refer to Video “S2:Inner-to-outer Density ratio” in the Supplementary Materials for better understanding of the jetting mode and the chaotic drop formation process.
To understand the transitional behavior of the jet from dripping to jetting, let us consider the rate of necking of the inner interface when (Figure 5a), as compared with the baseline case (Figure 4). Clearly, the faster the necking rate, the shorter the breakup length (Figure 5d). By analogy to the classical analysis of Plateau-Rayleigh instability, we neglect viscosity. Then the necking is driven by the spatial gradients of surface tension, which from Equation (23.31) of [26] is inversely proportional to the radius of curvature at the interface and is resisted by the inertia of the fluid that must escape from the necking region. From consideration of this balance, we expect that fluid can escape faster from the necking region when , as compared with , and correspondingly that the necking proceeds more rapidly. The early instability of the inner jet also appears to influence the jet breakup length (Figure 5d) of the intermediate jet (compound drops).
In Figure 5d, it can be seen that for , both the inner and intermediate jet breakup lengths are lower than that of the baseline case (). On the other hand, for , due to the higher density of the inner fluid, the inertia tends to stabilize the inner jet and thereby increase its jet length. Also, as the inner jet is enclosed by the intermediate jet, the inner jet carries the intermediate jet along with it and the jet length of the intermediate jet increases. In general, increasing favors the jetting mode for both inner and intermediate jet. The transition from dripping to jetting, in this case, was found in the range of , as shown in Figure 5d by a thin dotted line that separates the dripping and jetting regions. Note the drop diameter, formation time and jet breakup length calculated in Figures 5, 7, 9 and 11 are over 5–10 drops on average. The number of drops is increased to more than 15 in the case of chaotic drops. Figure 6 shows the percent of multi-core compound drops formed with varying density ratios. For density ratio , the compound drops are single-core. As the density ratio is increased, the compound drops formed are two/three-core, and for higher values, four-core compound drops are formed. The percent of one-core, two-core, three-core and four-core inner drops are different due to which the drop types formed are not periodic. In this paper, the phenomenon of alternating formation of single and multi-core drops is termed “chaotic drop formation”.
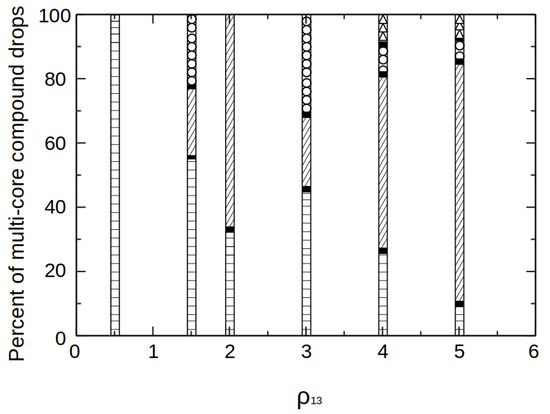
Figure 6.
Percent of multi-core compound drops formed vs inner-to-outer density ratio. The horizontal and slant lines depicted in this plot correspond to 1-core and 2-core compound drops respectively whereas circles and triangles denote 3-core and 4-core compound drops formation respectively.
In Figure 5e, on increasing the density ratio, slight decrease in inner and compound drop diameter can be seen. Similar outcomes were also recorded by Zhou et al. [18] where increasing the density ratio of inner-to-intermediate fluid resulted in decrease in the volume of the inner drop. In Figure 5f, the effect on the drop formation time for various density ratios has been plotted. It can be seen that the inner and compound drop formation time decreases with increasing density of the inner fluid. Also, the difference in the drop formation time of the inner and the compound drops reflects the formation of different types of compound drops (see Vu et al. [13]). For single-core drop formation, the difference in the drop formation time is small, while multi-core drop formation usually has a large difference.
4.3. Effect of Intermediate-to-Outer Density Ratio (
The density ratio of is varied in the range from 1 to 5. In Figure 7a–c, snapshots of the compound liquid jets are presented for = 1.5, 2.5 and 4.5 respectively, with = 1, = 1 and = 1. For = 1.5 (Figure 7a), it can be seen that both the jets breakup in the dripping mode. Increasing increases the breakup length of the intermediate jet, which accordingly transitions from dripping to jetting mode (Figure 7b,c). Trends similar to the previous section were observed for this case. As increases, due to higher inertia of the intermediate fluid that delays necking of the intermediate jet, the length of the intermediate jet increases, and thus the drops are formed in the jetting mode. Similar results were also observed by Afzaal et al. [27] for a compound jet, where increase in density ratio of intermediate to outer fluid resulted in longer breakup lengths. By contrast, increasing barely affects the breakup length of the inner jet (Figure 7d) yielding the inner-dripping and intermediate-jetting mode (mixed dripping-jetting). Although motion of the intermediate fluid is stabilized by the inertia, we infer that the density of the inner fluid dominates the resistance to necking that is driven by the surface tension force. Despite increase in , this “mixed” mode often results in two or more drops of inner fluid occupying compound drops and hence at high ratio, multi-core drop formation is seen. As compared with Figure 5c, Figure 7c shows less multi-core drop formation and the effect of is lesser in this case. Figure 8 illustrates the percentage of multi-core compound drops versus intermediate-to-outer density ratios plot. For values of = 1, the compound drops formed are single-core. Whereas for higher values of , formation of two-core and three-core compound drops is seen. In other words, for high values of , the compound jet formation falls in the inner-dripping and outer-jetting mode forming more multi-core compound drops.
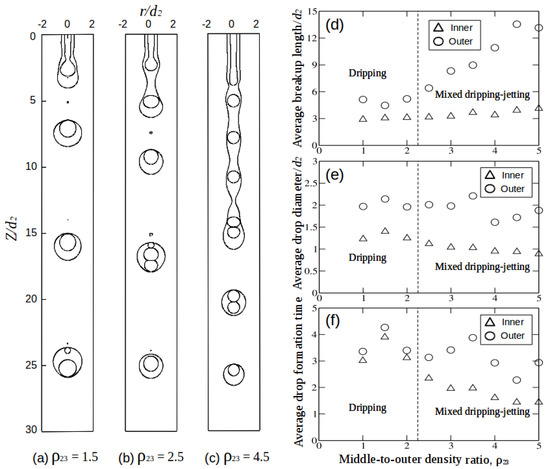
Figure 7.
Snapshots of compound liquid jets for (a) = 1.5; (b) = 2.5 and (c) = 4.5. The rest of the parameters are = 1, = 1 and = 1. Graphs (d–f) represents the average breakup length, drop diameter and drop formation time for variable intermediate-to-outer density ratios.
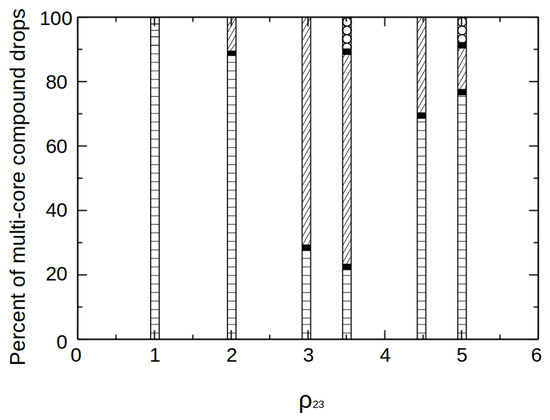
Figure 8.
Percent of multi-core compound drops formed vs intermediate-to-outer density ratio. The horizontal and slant lines depicted in this plot correspond to 1-core and 2-core compound drops respectively whereas circles denote 3-core compound drops formation.
Figure 7e,f shows the averaged drop diameter vs. and drop formation time vs. i.e., as the intermediate fluid density is varied, with inner and outer fluid densities kept constant. Figure 7e shows that as is increased, the average drop diameter of the inner drop decreases slightly. Slight decreasing behavior is observed in case of inner drop diameter whereas the compound drop diameter has increasing-decreasing behavior which is mainly due to the multi-core compound drops formation which sometimes encloses more than one drop leading to accumulation of large volume of the inner fluid. The transition from dripping to jetting, in this case, was found at density ratio 2, shown in Figure 7d by a thin dotted line which separates the dripping and jetting regions. Like the previous case, this case too shows that the system is more sensitive to parameter.
The effect of , on the time when the inner and compound drops form is shown in Figure 7f. 2.5, the difference in the time of inner and compound drops formed is small, which corresponds to single-core drop formation. Whereas, for 2.5, this difference in drop formation time is much greater, which reflects multi-core drop formation. The results obtained from and show that varying the density of the inner and intermediate fluid has a significant effect on the breakup length, drop type formation and drop diameter of inner and compound jets.
4.4. Effect of Inner-to-Outer Viscosity Ratio (
We now investigate the effect of viscosity ratio = on the dynamics of the compound liquid jet where ratio of 0.18 to 5 is varied. As compared to moderate density ratios, such viscosity ratios are more commonly found and studied experimentally [23]. In Figure 9a–c, snapshots of the compound liquid jets are presented for = 0.18, 1 (the “baseline case”) and 5 respectively. The rest of the parameters used for figures are = 1, = 1 and = 1.
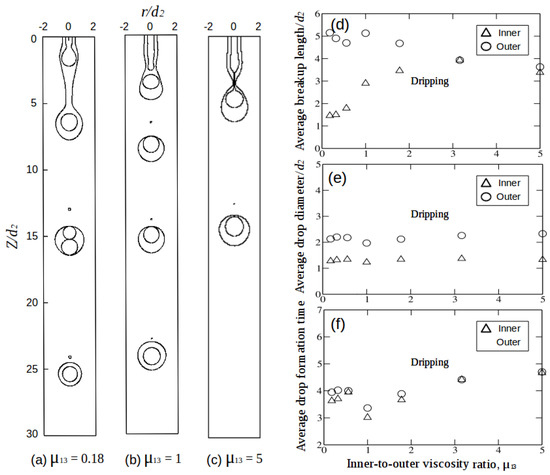
Figure 9.
Snapshots of compound liquid jets for (a) = 0.18; (b) = 1 and (c) = 5. The rest of the parameters are = 1, = 1 and = 1. Graphs (d–f) represents the average breakup length, drop diameter and drop formation time for variable inner-to-outer viscosity ratios. Readers can refer to the Video “S3:Inner-to-outer Viscosity ratio” in the Supplementary Materials for better understanding of the multi-core drop formation process in the dripping mode.
For = 0.18 (Figure 9a), it can be seen that the inner drop forms in the dripping mode and the compound drops form close to the jetting mode. The lower viscosity of inner fluid reduces the resistance to capillary-driven necking instability, facilitating the breakup of the inner fluid jet, and thus results in decreased inner jet length. Such observations are also seen in viscous fingering phenomena, in which less viscous fluid displacing a more viscous immiscible fluid tends to become unstable [28]. Due to the lower viscosity of inner fluid ( = 0.18) which break up more easily than the intermediate fluid, several drops formed at early stages can occupy the core of an intermediate drop, and hence form multi-core compound drops. On the other hand, with = 0.18, the intermediate fluid is approximately 5.5 times more viscous than the inner fluid. Due to the large viscous resistance of the intermediate fluid, which stabilizes the interface and delays necking, the breakup length of the compound drop increases.
As we increase the viscosity ratio from 0.18 to 2, the inner jet breakup length increases while the intermediate jet breakup length slightly decreases, and both jets remain in the dripping mode (Figure 9d). Omocea et al. [29] also reported similar outcomes in a two-phase system wherein water-glycerol solution (dispersed phase) of different viscosities was injected in oil (continuous phase). For viscosity ratios, , the inner and intermediate jets break at the same length forming mostly single-core drops whereas, for , multi-core drop formation is observed. Figure 10 shows the plot of percent of multi-core compound drops formed versus the inner-to-outer viscosity ratios. For the case where , the compound drops formed contain a mixture of single-core and double-core drops. Whereas for , the compound drops are single-core. For inner-to-outer viscosity ratio less than 5, no transition from dripping to jetting was observed. All the jet breakup lengths fall at or below the value of 2.5.
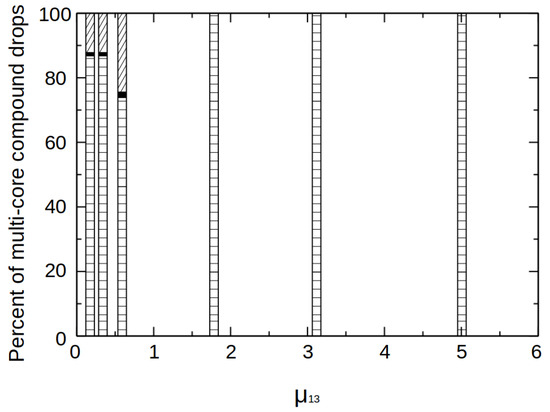
Figure 10.
Percent of multi-core compound drops formed versus inner-to-outer viscosity ratio. The horizontal and slant lines depicted in this plot correspond to 1-core and 2-core compound drops formation respectively.
Figure 9e,f shows average drop diameter vs. and average drop formation time vs. plot. For , there is no drastic change in the drop diameter of inner and compound drops. Such conclusions were also reached by Zhanga et al. [30] for drop formation in two-phase viscous flow system.
4.5. Effect of Intermediate-to-Outer Viscosity Ratio (
Finally, we consider variations in . Figure 11a–c shows snapshots of the compound liquid jets for viscosity ratio = = 0.18, 1 and 5 respectively, with = 1, = 1 and = 1. Initially, for lower values of , the inner and compound drops form in the dripping mode (Figure 11a). Compared to Figure 9a–c, Figure 11a–c situation is opposite. For = 0.18, the outer and inner fluids are approximately 5.5 times more viscous than the intermediate fluid. Due the lower viscous resistance of the intermediate fluid, the intermediate jet deforms faster [28], whence jet breakup length is shorter. The inner fluid is more viscous than the intermediate fluid, so the inner jet might be expected to break slowly. But due to the early necking of the intermediate jet, which encloses the inner fluid, the inner jet is forced to break up at an early stage, and compound drops form in the dripping mode. As we increase , both inner and compound drops are seen to form in mixed dripping-jetting mode. Similar to the previous section, an increase in the viscosity of intermediate fluid resists the formation and breakup of the drops, and formation takes place in the jetting mode.
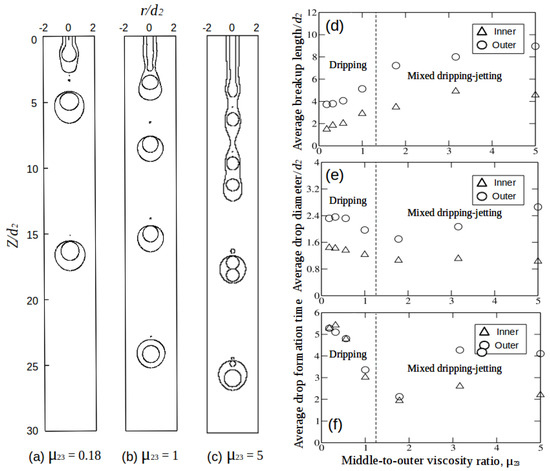
Figure 11.
Snapshots of compound liquid jets for (a) = 0.18; (b) = 1 and (c) = 5. The rest of the parameters are = 1, = 1 and = 1. Graphs (d–f) represents the average breakup length, drop diameter and drop formation time for variable intermediate-to-outer viscosity ratios.
The transition from jetting to dripping for was found in the range of . Compared to Figure 9c, Figure 11c shows more multi-core drops. For , the inner jet breaks at fairly short breakup length, and the intermediate jet breaks up at longer lengths i.e., in jetting mode (Figure 11d). As the inner drops are formed at early stages, more inner drops are enclosed in the intermediate jet, and many two-core drops are observed at high ratios. Figure 12 shows the plot of percent of multi-core inner drops occupied in the compound drop. For less values of , the compound drops formed are single-core. Whereas, increasing the ratio increases the percentage of two-core compound drops.
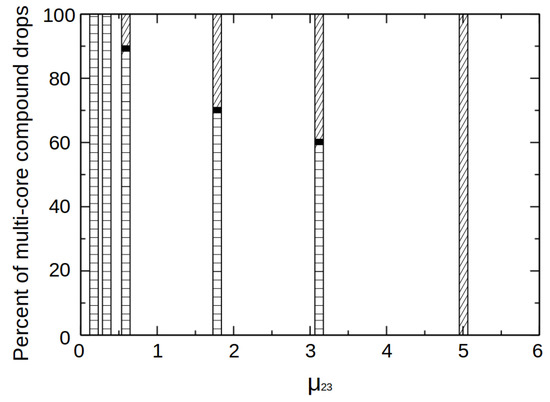
Figure 12.
Percent of multi-core compound drops formed vs. intermediate-to-outer viscosity ratio. The horizontal and slant lines depicted in this plot correspond to 1-core and 2-core compound drops formation respectively.
Figure 11e,f shows the average drop diameter vs. and average drop formation time vs. for the case where = . Increasing results in larger compound drops (Figure 11e), but with little change in average inner drop diameter. In Figure 11f, drop formation time for various values of has been plotted. For , it is seen that inner and compound drop formation time decreases and for 2, only the compound drops formation time increases. The sudden increase of the compound drop formation time is due to more resistive viscous force of the intermediate jet which deforms at later stages. For 1.56, the difference in drop formation times between inner and compound drops is small, which reflects single-core drop formation. For 3, the difference in drop formation time increases gradually, which corresponds to multi-core drop formation.
5. Conclusions
We have numerically investigated the effects of density and viscosity on the formation and breakup of a compound liquid jet in coflowing outer fluid in an axisymmetric cylindrical tube. The study showed the influence of density and viscosity ratios, i.e., , , and on the dynamics of the compound jet. The simulations show that, according to the density and viscosity ratios, the compound jet can transition to jetting or dripping mode. For low values of and , the inner and compound drops favor dripping mode and at higher values, they form in jetting and mixed dripping-jetting mode respectively. At higher values of and , the inertia force increasingly dominates, which causes more instabilities in the system and hence, more multi-core drop formation occurs. By contrast, for variation in , no jet transition from dripping to jetting was observed. For low values of viscosity ratio , dripping is more favorable for inner and compound drops, but at higher values of , both the drops form in the jetting mode. Variations in viscous resistance are the main cause of such behavior. Increasing the values of and leads to significant variation of average drop diameter, whereas changes in and yielded less change in the diameter. This shows that compared to viscosity ratios, the system is more sensitive towards density ratios.
This work provides overviews on the effect of density and viscosity ratios in a coflowing liquid-liquid-liquid system which has specific applications to industrial processes. However, some unresolved questions still exist. There is a need to analyze in detail the non-monotonic nature of the formation of multi-core drops (Figure 6) and the conditions for satellite drops formation during the breakup of a compound jet. The effect of nozzle geometry on the compound jet modes, drop size and formation time also merits further research.
Supplementary Materials
The supporting videos article are available at https://www.mdpi.com/2076-3417/9/22/4817/s1.
Author Contributions
K.D.B., T.V.V. and J.C.W. designed the study. T.V.V. modified the Front Tracking Code and K.D.B. performed the simulations. K.D.B., T.V.V. and J.C.W. wrote the manuscript. All authors discussed the results and contributed to the final manuscript.
Funding
This research received no external funding.
Acknowledgments
Kunal D. Bhagat is thankful to JICA (Japan International Cooperation Agency) for their support under the JICA-Friendship Scholarship Program 2016-2019. Truong V. Vu is thankful to the Phenikaa University Foundation for Science and Technology Development for their support. The front-tracking code was adapted from a program provided by G. Tryggvason and S. Homma.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abate, A.R.; Thiele, J.; Weitz, D.A. One-step formation of multiple emulsions in microfluidics. Lab Chip 2011, 11, 253–258. [Google Scholar] [CrossRef] [PubMed]
- Denn, M.M. Continuous Drawing of Liquids to form Fibers. Annu. Rev. Fluid Mech. 1980, 12, 365–387. [Google Scholar] [CrossRef]
- Hertz, C.H.; Hermanrud, B. A liquid compound jet. J. Fluid Mech. 1983, 131, 271. [Google Scholar] [CrossRef]
- Shen, J. Experiments on annular liquid jet breakup. At. Sprays 2001, 11, 18. [Google Scholar] [CrossRef]
- Mathiowitz, E.; Jacob, J.S.; Jong, Y.S. Biologically erodable microspheres as potential oral drug delivery systems. Nature 1997, 386, 410–414. [Google Scholar] [CrossRef]
- Herrada, M.A.; Montanero, J.M.; Ferrera, C.; Gañán-calvo, A.M. Analysis of the dripping–jetting transition in compound capillary jets. J. Fluid Mech. 2010, 649, 523. [Google Scholar] [CrossRef]
- Andreas, S.; Alexiou, C.; Bergemann, C. Clinical Applications of Magnetic Drug Targeting. J. Fluid Mech. 2001, 95, 200–206. [Google Scholar]
- Rayleigh, L. On the capillary phenomena of jets. Proc. R. Soc. Lond. 1879, 29, 71–97. [Google Scholar]
- Chauhan, A.; Maldarelli, C.; Papageorgiou, D.T.; Rumschitzki, D.S. Temporal instability of compound threads and jets. J. Fluid Mech. 2000, 420, 1–25. [Google Scholar] [CrossRef]
- Subramani, H.J.; Yeoh, H.K.; Suryo, R.; Xu, Q.; Ambravaneswaran, B.; Basaran, O.A. Simplicity and complexity in a dripping faucet. Phys. Fluids 2006, 18, 1–13. [Google Scholar] [CrossRef]
- Vu, T.V.; Homma, S.; Wells, J.C.; Takakura, H.; Tryggvason, G. Numerical simulation of formation and breakup of a three-fluid compound jet. J. Fluid Sci. Technol. 2011, 6, 252–263. [Google Scholar] [CrossRef]
- Vu, T.V.; Wells, J.C.; Takakura, H.; Homma, S.; Tryggvason, G. Numerical calculations of pattern formation of compound drops detaching from a compound jet in a coflowing immiscible fluid. J. Chem. Eng. Jpn. 2012, 45, 721–726. [Google Scholar] [CrossRef]
- Vu, T.V.; Homma, S.; Tryggvason, G.; Wells, J.C.; Takakura, H. Computations of breakup modes in laminar compound liquid jets in a coflowing fluid. Int. J. Multiph. Flow 2013, 49, 58–69. [Google Scholar] [CrossRef]
- Nadler, J.H.; Sanders, T.H., Jr.; Cochran, J.K. Aluminum hollow sphere processing. Mater. Sci. Forum 2000, 331, 495–500. [Google Scholar] [CrossRef]
- Lee, S.Y.; Snider, C.; Park, K.; Robinson, J.P. Compound jet instability in a microchannel for mononuclear compound drop formation. J. Micromech. Microeng. 2007, 17, 1558–1566. [Google Scholar] [CrossRef][Green Version]
- Utada, A.S. Monodisperse double emulsions generated from a microcapillary device. Science 2005, 308, 537–541. [Google Scholar] [CrossRef]
- Kendall, J.M. Experiments on annular liquid jet instability and on the formation of liquid shells. Phys. Fluids 1986, 29, 2086. [Google Scholar] [CrossRef]
- Zhou, C.; Yue, P.; Feng, J.J. Formation of simple and compound drops in microfluidic devices. Phys. Fluids 2006, 18, 092105. [Google Scholar] [CrossRef]
- Suryo, R.; Doshi, P.; Basaran, O.A. Nonlinear dynamics and breakup of compound jets. Phys. Fluids 2006, 18, 082107. [Google Scholar] [CrossRef]
- Harlow, F.H.; Welch, J.E. Numerical calculation of time-dependent Viscous incompressible flow of fluid with free surface. Phys. Fluids 1965, 8, 2185–2189. [Google Scholar] [CrossRef]
- Tryggvason, G.; Bunner, B.; Esmaeeli, A.; Juric, D.; Al-Rawahi, N.; Tauber, W.; Han, J.; Nas, S.; Ja, Y.J. A front-tracking method for the computations of multiphase flow. J. Comput. Phys. 2001, 169, 708–759. [Google Scholar] [CrossRef]
- Homma, S.; Koga, J.; Matsumoto, S.; Song, M.; Tryggvason, G. Breakup Mode of an Axisymmetric Liquid Jet Injected into Another Immiscible Liquid. Chem. Eng. Sci. 2006, 61, 3986–3996. [Google Scholar] [CrossRef]
- Cramer, C.; Fischer, P.; Windhab, E.J. Drop formation in a co-flowing ambient fluid. Chem. Eng. Sci. 2004, 59, 3045–3058. [Google Scholar] [CrossRef]
- Pal, R. Rheological Constitutive Equation for Bubbly Suspensions. Ind. Eng. Chem. Res. 2004, 43, 5372–5379. [Google Scholar] [CrossRef]
- Scheele, G.F.; Meister, B.J. Drop formation at low velocities in liquid-liquid systems. AIChE J. 1968, 14, 9–15. [Google Scholar] [CrossRef]
- Rappa, B.E. Microfluidics: Modeling, Mechanics and Mathematics; Elsevier: Amsterdam, The Netherlands, 2017; pp. 745–754. [Google Scholar]
- Afzaal, M.F.; Uddin, J.; Alsharif, A.M.; Mohsin, M. Temporal and spatial instability of a compound jet in a surrounding gas. Phys. Fluids 2015, 27, 044106. [Google Scholar] [CrossRef]
- Homsy, G.M. Viscous Fingering in Porous Media. Annu. Rev. Fluid Mech. 1987, 19, 271–311. [Google Scholar] [CrossRef]
- Omocea, I.L.; Patrascu, C.; Turcanu, M.; Balan, C. Breakup of Liquid Jets. Energy Procedia 2016, 85, 383–389. [Google Scholar] [CrossRef]
- Zhang, D.F.; Stone, H.A. Drop formation in viscous flows at a vertical capillary tube. Phys. Fluids 1997, 9, 2234–2242. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).