Ant Colony Optimization Algorithm for Maintenance, Repair and Overhaul Scheduling Optimization in the Context of Industrie 4.0

Featured Application

Production scheduling for MRO sector.

Abstract

Maintenance, Repair, and Overhaul (MRO) is a crucial sector in the remanufacturing industry and scheduling of MRO processes is significantly different from conventional manufacturing processes. In this study, we adopted a swarm intelligent algorithm, Ant Colony Optimization (ACO), to solve the scheduling optimization of MRO processes with two business objectives: minimizing the total scheduling time (make-span) and total tardiness of all jobs. The algorithm also has the dynamic scheduling capability which can help the scheduler to cope with the changes in the shop floor which frequently occur in the MRO processes. Results from the developed algorithm have shown its better solution in comparison to commercial scheduling software. The dependency of the algorithm’s performance on tuning parameters has been investigated and an approach to shorten the convergence time of the algorithm is emerging.

1. Introduction

Maintenance, Repair, and Overhaul (MRO) is a crucial sector in the remanufacturing industry [1]. In the context of Industrie 4.0, predictive maintenance has gained much attention in maintenance and asset management. Adopting reliability methods are one of the most interesting aspects to be considered. The works of [2,3] proposed a novel model for inspection scheduling of welded components as well as additive manufacturing parts. This marks a clear pathway of interest in the scientific community that evolves to the industrial domain in enhancements of products and processes.

Another aspect of MRO industry is on job scheduling of MRO parts which are typically low-process volume, high-value and complex components such as engine blades, compressor blisks and turbine disks. An engine blade, for example, its MRO processes generally consist of four fundamental phases comprising pre-treatment, material deposit, recontouring, and post-treatment. Various methods and machines can be utilized in each phase of the aforesaid sequence. Furthermore, due to the diversity of damages on components, the MRO process of each component might have to adapt to the sequence of these fundamental steps fully or partly and the processing time for each operation also varies due to this uncertainty. Therefore, scheduling of MRO processes is significantly different from conventional manufacturing processes. Some characteristics of MRO processes that scheduling task should take into accounts are disassembly process, uncertainty of material recovery, material matching requirements, stochastic routings and variable processing times [4].

In order to solve the scheduling optimization problem, numerous approaches and algorithms have been proposed and developed such as swarm intelligence algorithms, genetic algorithms, state-space search algorithms, GraphPlan algorithm and critical path method [5]. Among these approaches, the swarm intelligence algorithms such as Ant Colony Optimization (ACO), Fish Swarm Optimization, Bee-Inspired Algorithms and Bacterial Foraging Optimization have been demonstrated as effective methods to solve complex optimization problems [6]. The most prevalent swarm intelligence algorithm is ACO that has been successfully implemented for a variety of optimization problems such as scheduling, routing, assignment and machine learning [7]. The implementation of the ACO algorithm does not require a complex mathematical model of the problem. Furthermore, the complexity of process routings in MRO processes can be straightforwardly defined in the ACO algorithm.

Research on scheduling problem of MRO processes is scarce in the literature. Among the limited results, simulation optimization was usually adopted to formulate scheduling problem [4,5,6,7,8]. Liu et al. [4] used hybrid algorithms based on nested partition framework to address stochastic routings and variable processing times. Multi-fidelity optimization based on ordinal transformation and optimal sampling proposed by Huang et al. [8] was shown to achieve feasible solutions with low tardiness. Li et al. [9] implemented the genetic algorithm to optimize the scheduling of MRO resources considering the complexity of products. However, to the best of our knowledge, there is no paper that addresses scheduling MRO processes using swarm intelligence algorithms.

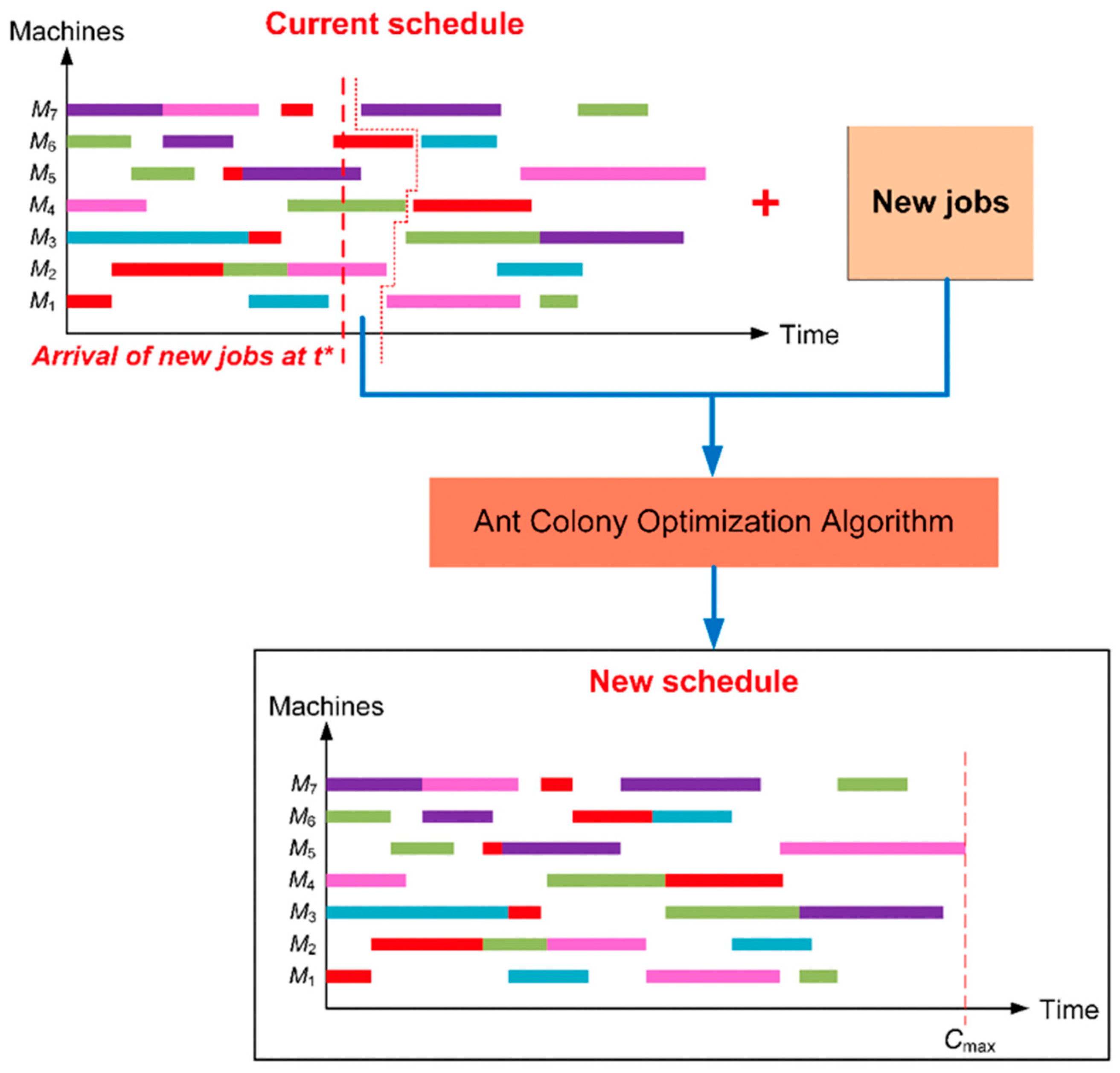
In this paper, we adopt the ACO algorithm to solve the scheduling optimization for MRO processes in the Industrie 4.0 context. According to Posada, et al. [10], in order to adopt Industrie 4.0, digital systems and applications must be able to address several challenges, including complex variation requirements of production processes. Therefore, the ACO algorithm developed in this paper considers the complexity of process routings, variable process times and rescheduling. A use-case is defined reflecting the complexity of process routings and variable processing time MRO processes. Rescheduling is also included for illustrating the dynamic scheduling capacity of the algorithm. Initially, minimization of make-span was selected as the objective function in order to develop the algorithm. Results from the developed algorithm are compared with a commercial scheduling software solution to show its effectiveness. Subsequently, the dependency of performance of the algorithm on the tuning parameters has been investigated. In addition, an alternative for the objective function, which was minimization of tardiness, was implemented for the algorithm to cater for practical use cases. Last but not least, the ACO algorithm has been further developed for the dynamic scheduling capability in an application deployed in the Model Factory at the Advanced Remanufacturing and Technology Centre (ARTC), which is a research and development program of the Agency for Science, Technology, and Research (A*STAR), Singapore. The outcome of the research can benefit not only MRO but any industrial sector with complex and variable process routings as well as dynamic changes in the shop floor.

The structure of the paper is as follows. First, we define the problem in Section 2. After that, state of art and the developed ACO algorithm for solving scheduling problem is described in Section 3. Section 4 presents and discusses numerical results that include the comparison with a commercial software, effects of tuning parameters on performance of the algorithm, the expansion to using minimization of total weighted tardiness as the objective function and the dynamic scheduling capability. The conclusion and further improvements are pointed out in Section 5.

2. Modelling of the Scheduling Optimization Problem of MRO Processes

First and foremost, the MRO process is required to be properly defined in order to model the scheduling optimization problem. Figure 1 describes an example of the MRO processes that have been defined in this paper. All components are initially inspected at an inspection station. Based on the identified damages on each component, a particular process flow will be assigned for that component. The process flow defines a series of operations to process the component. The operations of each process flow follow a defined sequence. After all operations of a process flow have been executed, the component is released from the MRO. Each operation is executed via various types of resources such as personnel, machines, materials, and tools. As a simplification, a machine represents all resources required to execute an operation. The different colored arrows in Figure 1 indicate the process flows of different components. The numbers of operations in process flows can be different from component to component. Depending on damages on the components, the processing times of the operations are also different from each other. The scheduling optimization problem in this paper covers the operations to process the components after they have been inspected at the inspection station.

The MRO process must be modelled in order to implement the ACO algorithm for scheduling optimization. The MRO process flow of a single component is represented as a job. There are $n$ jobs assigned for the corresponding $n$ components to be processed. Let $J=J_i$ is the set of n jobs, where $1\le i\le n$. There are $m$ machines to process the jobs. Each job $J_i$ consists of a predetermined sequence of $j$ operations. An operation is represented as $O_{i,j}$, which means it is the $j$-th operation of job $i$. Each of the operations can only be processed on a specific machine in the set of $m$ machines. The operation $O_{i,j}$ takes the processing time $p_{i,j}$ to be completed. The objective of the scheduling optimization is to minimize the makespan or scheduling time, $C_{max}$, which is the time required to finish all the operations of all the jobs. The constraints to the objective function are:

• The machine’s set-up time and transportation time required between operations are not considered.
• There is no dependency between machines.
• A machine can only execute other operations if the current operation is completed.
• The precedence constraints which indicate the sequence to execute the operations are only applicable for the operations in the same job.
• Only one operation of the same job can be executed at a time.

3. Ant Colony Optimization (ACO) Algorithm

ACO algorithm [11,12,13] was developed based on the foraging behavior of ants in their colonies where pheromone is the substance used to communicate amongst the individuals. The ant that finds a food source will come back to its nest and deposits an amount of pheromone along the path. The ants tend to follow the path that has more pheromone deposited. Pheromone also evaporates over time. In this way, by depositing pheromone and following pheromone trails, ants can find a good approximation to the shortest path of the food source from their nest.

ACO algorithm addressed job-shop scheduling problem firstly appeared in the literature which was known as Ant System (AS) in 1990s by Dorigo, Marco, et al. [14,15]. Since then, several ACO variations were proposed such as ASElite, ASRank, Ant Colony System (ACS), Max–Min Ant System (MMAS) and Best–Worst Ant System (BWAS) [16]. Each algorithm enhanced the base algorithm in different ways. ASElite only used the best solution to update the pheromone. ASRank has a ranking system of subsets of solutions so only these are used for pheromone update. MMAS has bounded value of pheromone and BWAS updated the pheromone only using the best and the worst solutions. Both exploration and exploitation mechanisms are adopted in ACS in order to widen the decision of path chosen in construction stage [17]. In addition, ACS also used local pheromone updating calculated at the end of each ant’s construction step to diversify the path built by subsequent ants. ACS has been applied to job-shop scheduling problem to minimize the makespan [18,19,20] or tardiness [21,22,23]. In this paper, ACS is implemented to address MRO scheduling problem and described below.

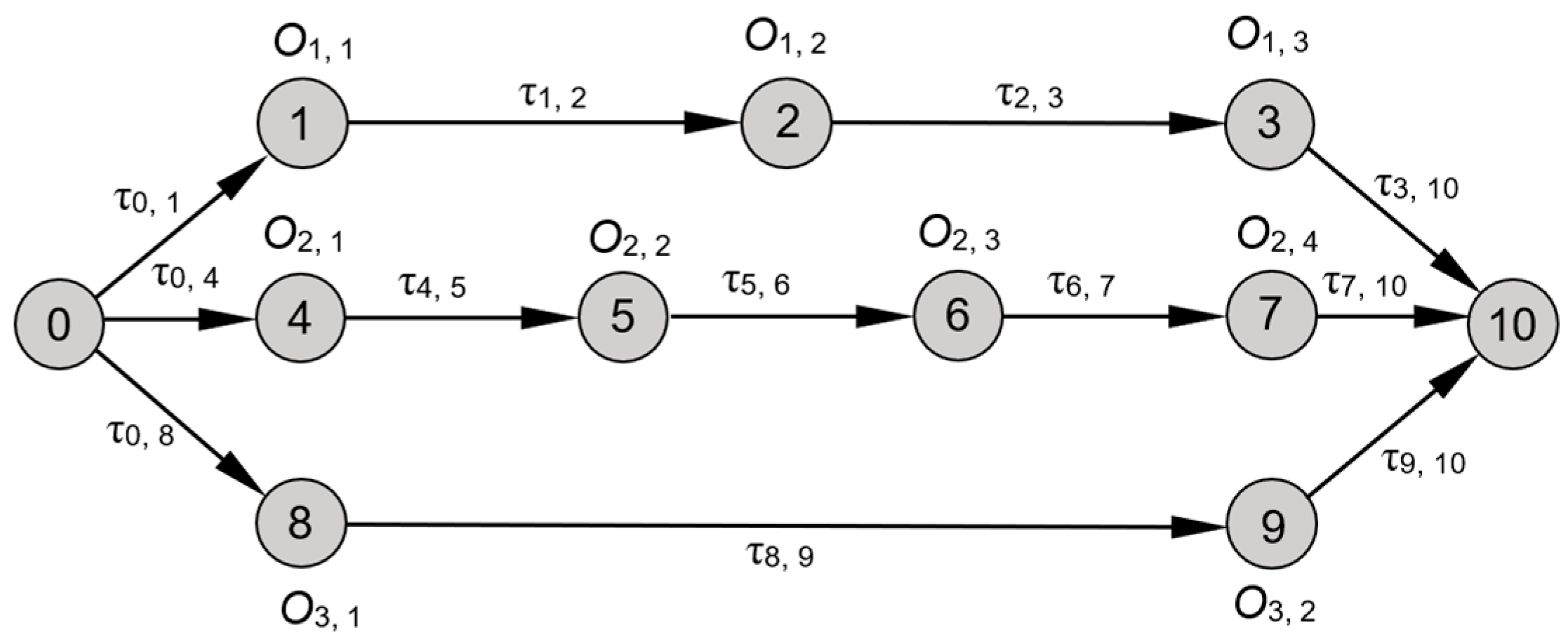
Figure 2 is a disjunctive graph to define the mathematical model of the ACO algorithm. Each node in the graph represents one operation of the jobs to be scheduled. Two more nodes are added into the graph, representing the starting and ending points. In the algorithm, each ant starts to visit all the nodes one-by-one from the starting node and complete its journey at the ending node. The schedule of the operations to be executed is constructed based on the sequence of the nodes that the ant has visited. All the operations are re-indexed from (0, 1, 2,..., N, N + 1), where 0 and (N + 1) are the starting and ending nodes, respectively. The value ${\tau }_{r,s}$ is the pheromone on the path that connects nodes r and s. The arrowhead lines indicate the precedence constraints between the operations within the same job. For example, the arrowhead line connecting nodes 1 and 2 indicates that the ant must visit node 1 before it can visit node 2. In other words, the operation $O_{1,1}$ must be executed before the operation $O_{1,2}$

Initially, the pheromone values of all the possible paths are equal to an initial value, τ₀. Each ant of the colony builds a tour by repetitively using a random greedy rule called the state transition rule as defined in Equation (1). According to this rule, an ant will decide which path to follow based on the pheromone deposited on each feasible path.

$$\{\begin{array}{cc}\arg {\max }_{u\in J\left(r\right)}\left\{\left[\tau \left(r, u\right)\right]·\left[\eta {\left(r,u\right)}^{\beta }\right]\right\},& \mathrm{if} q\le q_0 \left(\mathrm{exploitation}\right)\hfill \\ s,& \mathrm{otherwise} \left(\mathrm{biased} \mathrm{exploitation}\right)\hfill \end{array}$$

(1)

(r, u) represents the path connecting nodes r and u, and $\tau \left(r, u\right)$ is the pheromone value on that path. If the ant is travelling from node r to node u, the value $\eta \left(r, u\right)$ is calculated as $\eta \left(r, u\right) = 1/p_{i,j}$ where $p_{i,j}$ is the processing time of the operation $O_{ij}$ that corresponds to node u, q is a uniformly distributed random number in [0,1], $q_0$ is a predefined parameter with ($0\le q_0\le 1$), β is the controlled parameter relating the importance of processing times of the operations. J(r) is the set of nodes to which the ant can choose to travel from the current node. This set of possible nodes includes the nodes that have not been visited and follows the precedence constraints. The variable s is randomly chosen using the probability distribution given below.

$$P\left(r,s\right)=\{\begin{array}{cc}\frac{\left[\tau \left(r, s\right)\right]·\left[\eta {\left(r,s\right)}^{\beta }\right]}{{{\displaystyle \sum }}_{u\in J\left(r\right)}\left[\tau \left(r, u\right)\right]·\left[\eta {\left(r,u\right)}^{\beta }\right]},& \mathrm{if}s\in J\left(r\right)\hfill \\ 0,& \mathrm{otherwise} \hfill \end{array}$$

(2)

While an ant travels from node r to node s, it deposits an amount of pheromone along the path. This action is realized in the algorithm by the local pheromone updating rule as follow.

$$\tau \left(r,s\right)\leftarrow \left(1-\rho \right)·\tau \left(r,s\right)+\rho ·{\tau }_0$$

(3)

where ρ is the local pheromone evaporation rate $(0<\rho < 1)$.

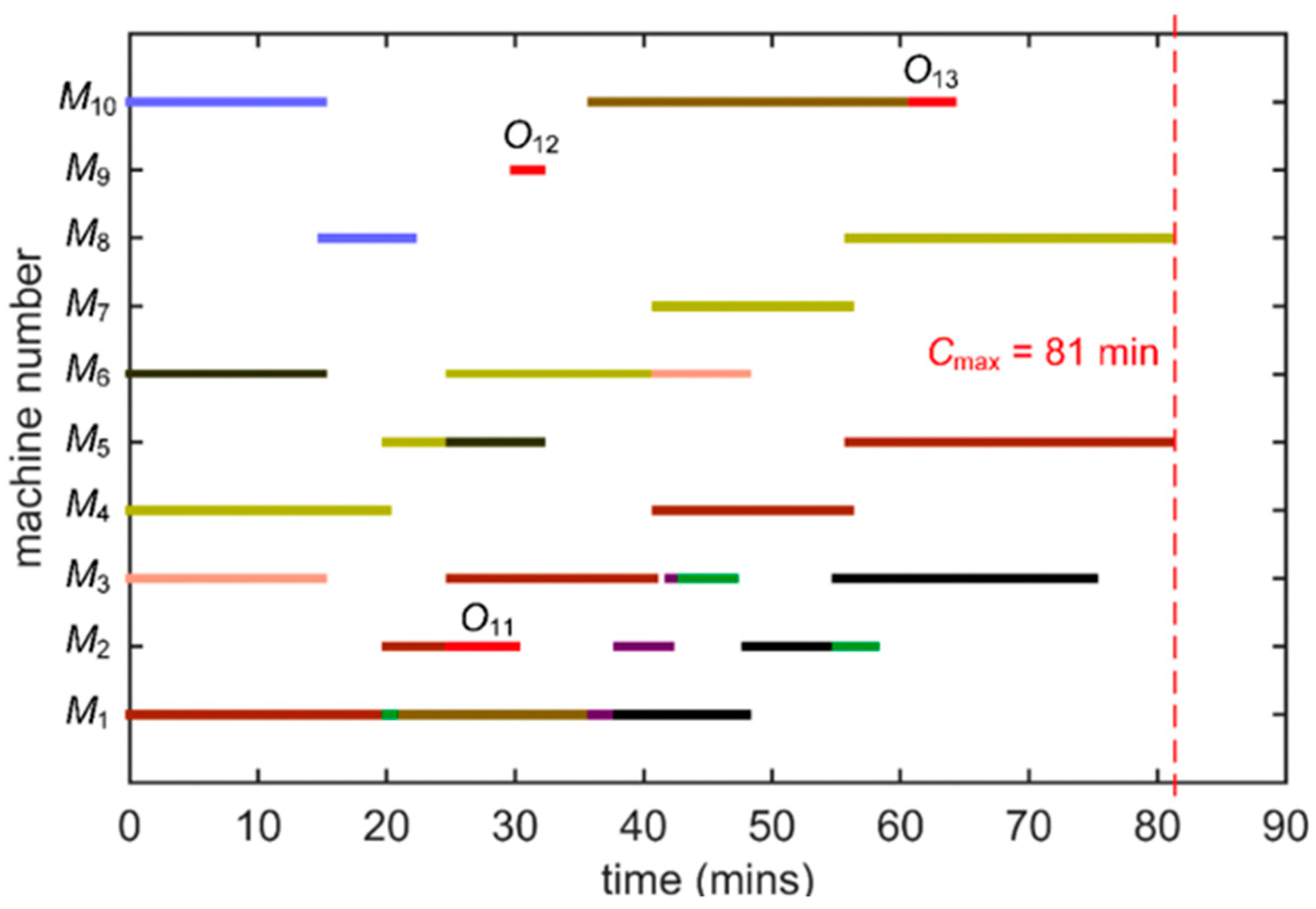
Once all the ants of the colony have completed their tours, the schedule to execute the operations can be built based on the sequence of nodes that each ant has visited during the tour. The operations are scheduled by following the sequence of the nodes as soon as the required machines are available. Afterwards, the time to complete all the operations of each ant, $C_{max}$, is defined from the schedule. The best tour provides the minimum value of $C_{max}$. Subsequently, the global pheromone updating rule is performed as follow.

$$\tau \left(r,s\right)\leftarrow \left(1-\alpha \right)·\tau \left(r,s\right)+Q·\alpha ·\Delta \tau \left(r,s\right)$$

(4)

where

$$\mathsf{\Delta }\tau \left(r,s\right)=\{\begin{array}{cc}\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\min C_{\max }$}\right.,& \mathrm{if} \left(r,s\right)\in \mathrm{global}-\mathrm{best}-\mathrm{tour}\hfill \\ 0,& \mathrm{otherwise}\hfill \end{array}$$

(5)

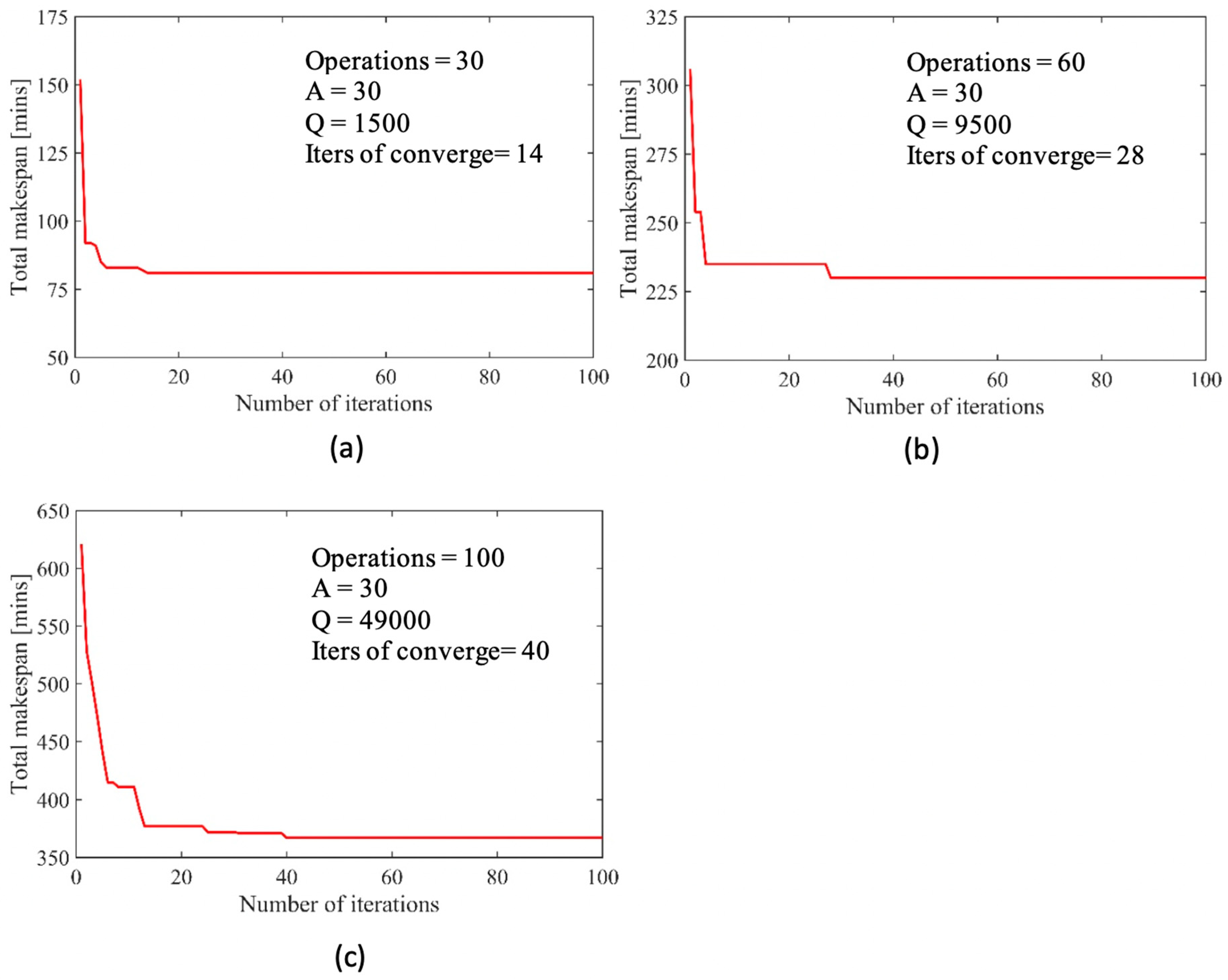
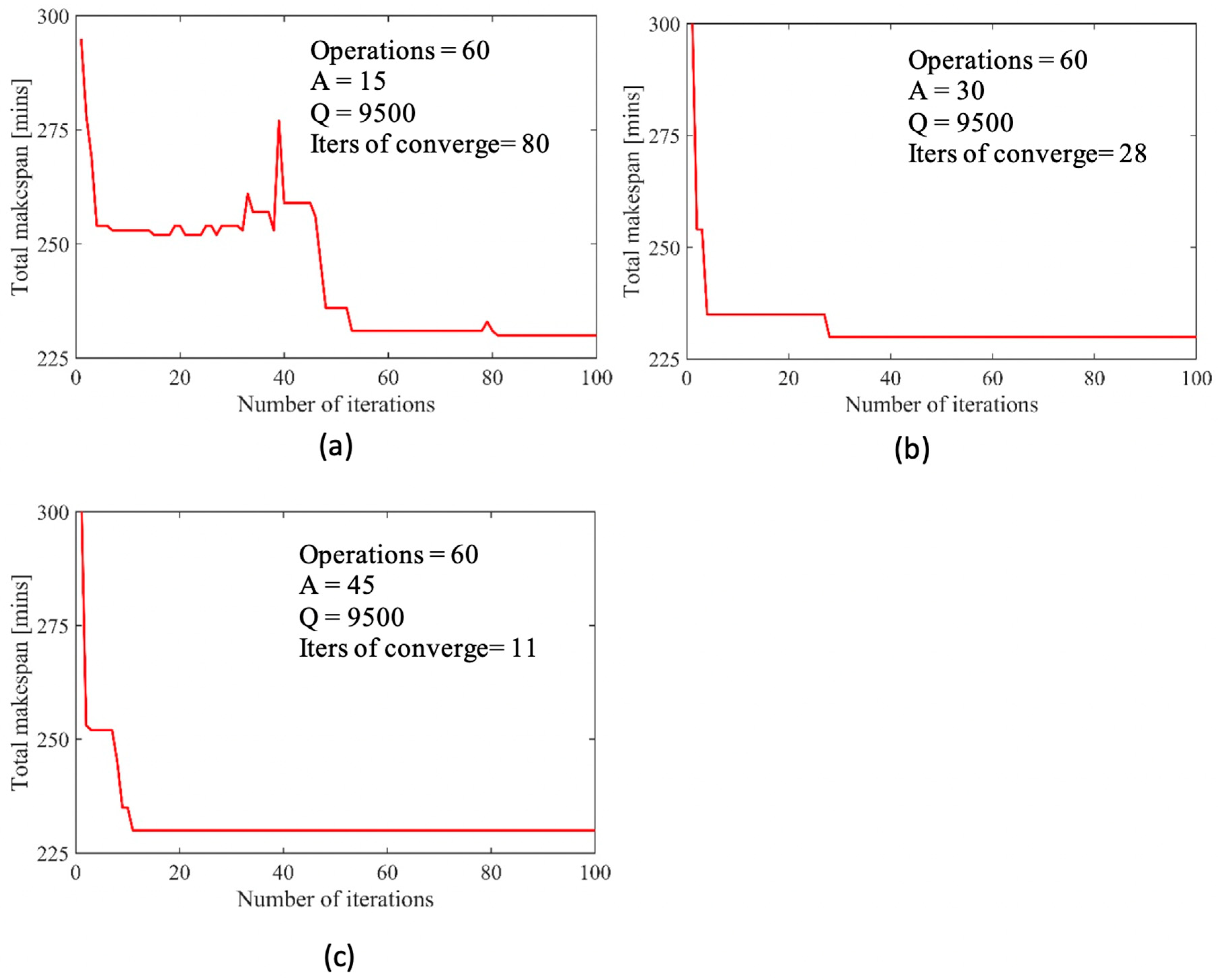
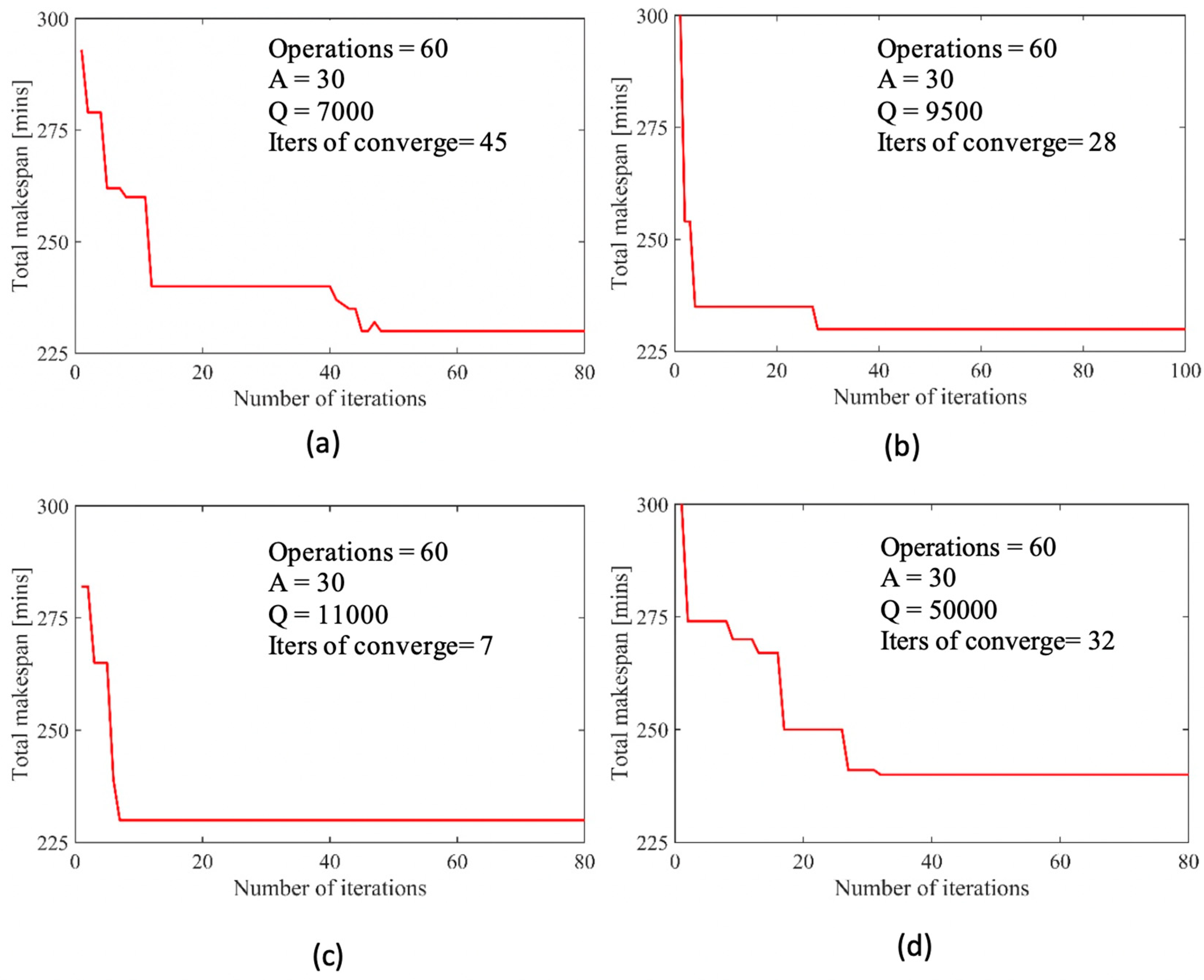
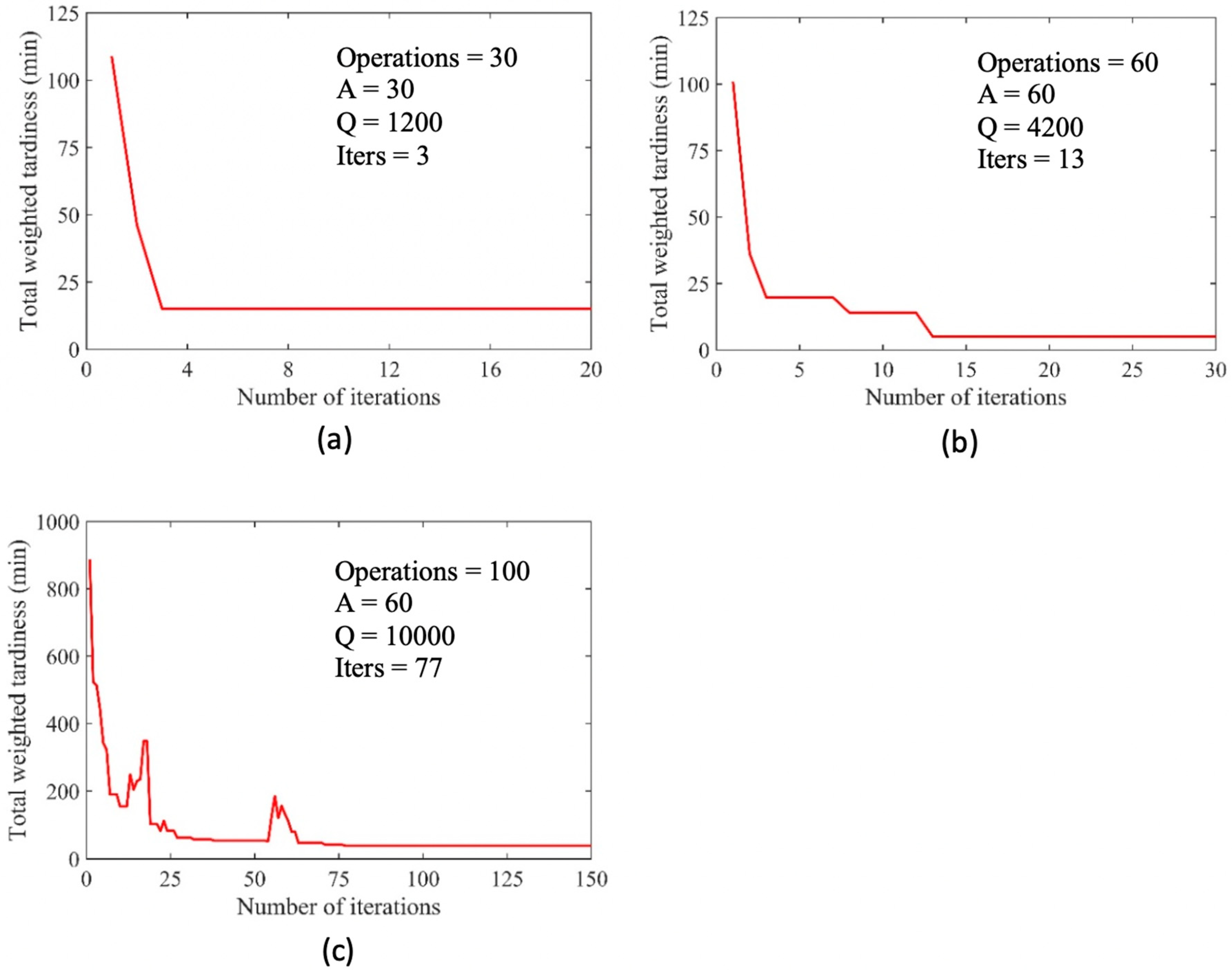
α is the global pheromone evaporation rate which control the influence of the new best solution, Q is a tuning parameter. With the new updated values of pheromone on all the possible paths, the process, where all the ants build their tours until the global pheromone updating rule is performed, is iterated until the solution ${\left({\mathrm{C}}_{max}\right)}_{min}$ converges and the scheduling optimization is completed.

4. Numerical Results

4.1. Minimizing Make-Span

The ACO algorithm explained in previous section has been implemented in MATLAB. The input includes all jobs for scheduling, their operations as well as processing time and machine of each operation. Users can input the required information into a csv file. Subsequently, the ACO program loads the information from the csv file and executes the optimization algorithm. Once the optimization operation has been performed, a schedule or Gantt chart is generated as output.

A use case has been deployed in order to demonstrate the performance of ACO algorithm. In this use case, there are 10 components that correspond to 10 jobs to be scheduled. After damages on these components were identified at an inspection station, the operations of the jobs, their sequences, required machines and processing times were defined as shown in

Table 1. Required machines and processing times of operations in the use case to execute the ACO algorithm.

	Operation	Operation 1		Operation 2		Operation 3		Operation 4		Operation 5
Job		Process time	Machine	Process time	Machine	Process time	Machine	Process time	Machine	Process time	Machine
Job 1		5 (min)	2	2 (min)	9	3 (min)	10	-	-	-	-
Job 2		2 (min)	1	4 (min)	2	1 (min)	3	-	-	-	-
Job 3		1 (min)	1	4 (min)	3	3 (min)	2	-	-	-	-
Job 4		20 (min)	1	5 (min)	2	16 (min)	3	15 (min)	4	25 (min)	5
Job 5		15 (min)	1	25 (min)	10	-	-	-	-	-	-
Job 6		15 (min)	6	7 (min)	5	-	-	-	-	-	-
Job 7		10 (min)	1	7 (min)	2	20 (min)	3	-	-	-	-
Job 8		20 (min)	4	5 (min)	5	16 (min)	6	15 (min)	7	25 (min)	8
Job 9		15 (min)	10	7 (min)	8	-	-	-	-	-	-
Job 10		15 (min)	3	7 (min)	6	-	-	-	-	-	-

. These data are also included in the input file for the algorithm to run. Values of the parameters of algorithm are selected as follows: $\alpha = 0.1$; $\rho = 0.1$;$\beta = 0$; $q_0= 0.8$; ${\tau }_0=0.1$. Values of the other parameters which are $Q$ and $A$ will be discussed in the next sub-section as they have significant impacts to performance of the algorithm.

Figure 3a presents the solution of the ACO algorithm, which is the scheduling time, $C_{max}$, resulted in each iteration during the execution of the algorithm. It can be observed that the solution starts to converge to the minimum value, $C_{max}=81 \min$, after about 10 iterations. Figure 4 shows the Gantt chart that corresponds to the optimized solution. The operations displayed in the same color belong to the same job. For example, three operations of Job 1 $O_{11}$, $O_{12}$ and $O_{13}$ are presented in Figure 4.

In order to further validate performance of the ACO algorithm, the commercial software Siemens SIMATIC IT Preactor AS has been utilized to schedule the jobs in this use case. Preactor AS uses order at a time scheduling method where each order is loaded in sequence according to predefined dispatching rule. Once an order is selected, all of its operations are loaded in a straightforward manner. Figure 5 presents the Gantt chart provided by this software. The scheduling time is resulted at ${\mathrm{C}}_{max}=84\min$, whereas the ACO algorithm provided the schedule with ${\mathrm{C}}_{max}=81\min$. Therefore, the ACO algorithm offers a better result in terms of optimizing the schedule with the objective of minimizing the scheduling time or makespan, ${\mathrm{C}}_{max}$.

To further test the performance of the developed ACO algorithm with the total number of operations, apart from this use case (defined as small case) that consists of 30 operations of all the jobs (Figure 3a), two more cases are defined including medium case (60 operations, Figure 3b) and large case (100 operations, Figure 3c). It can be observed in Figure 3 that the parameters such as number of ants in the colony $A$, and tuning parameter $Q$, needs to be adjusted accordingly to the number of operations in the problem. In addition, problems with more operations might require more iterative steps for the solution to converge. In the next sub-section, effects of these tuning parameters on performance of the algorithm and the number of required iterations will be discussed in details.

4.2. Effect of Parameters

It has been observed that the two parameters $A$ and $Q$ noticeably impact performance of the algorithm. Therefore, the investigations their effects have been carried out. Firstly, in order to investigate effect of $A$, which denotes the number of ants in the colony, the use case that has 60 operations was experimented with different values of $A$, while all other parameters remained the same. The results of this experiment are show in Figure 6. It can be seen that when the number of ants in the colony is increased, less iterations are required for the solution to converge. This can be explained as the more ants mean the more possibilities for the solution are explored in each iteration. Therefore, the best solution can be discovered in less iterations. Nonetheless, it should be noted that more computation is required for more ants in each iteration and this might slow down the overall running time of the algorithm.

In order to investigate effect of the parameter $Q$, the same use case that has 60 operations was also used. Three test cases were experimented with the value of $Q$ varied, while other parameters were kept the same. The results of these test cases are shown in Figure 7. It can be observed from Figure 7a–c that the higher value of $Q$ is defined, the lesser iterations are required for the solution to converge. This is because based on Equation (4), the effect of $Q$ is to amplify the enhancement of pheromone when the global updating rule is applied for the best solution. Therefore, the convergence rate towards the best solution is increased. However, it should be noted that an excessively high value of $Q$ might lead to a local optimal solution. For example, in Figure 7d, the value of $Q$ is increased to 50,000 and the best solution found is 240 min, while in the other cases, the best solution found is 230 min.

4.3. Minimizing Total Weighted Tardiness

In practical use cases, due dates are usually assigned for work orders. Therefore, in other to consider this feature, the developed algorithm is tested with another performance objective which is minimizing the total weighted tardiness defined as:

$${{\displaystyle \sum }}^{}{w}_i{T}_i$$

(6)

where $w_i$ is the weightage of job $i$. $T_i=\max \left\{0,C_i-d_i\right\}$ is tardiness of job $i$, $C_i$ and $d_i$ are completion time and due date respectively. In this case study, the weightage of all jobs is set to be equal to each other. The input data of machines, operations and processing time is obtained from the minimizing make-span case. The due date is set based on due date tightness factor which is also fixed value for all jobs [21].

Similar to minimizing the make span, three cases with variable number of operations: small (30 operations), medium (60 operations) and large (100 operations) are used to test the developed algorithm. The tuning parameters are the same as previous simulation, which are number of ants in the colony A and parameter Q.

The convergence graphs of the problems with different numbers of operations and the parameters adjusted are presented in Figure 8. When we increase the number of operations, different combinations of A and Q are needed to ensure converged solutions. Small value of A = 30 and Q = 1200 are sufficient for small number of operations. However, for larger size problem, the number of ants A and Q should be increased. Large value of A requires more computing time; therefore, for the largest number of operations, increasing Q is preferred to speed up the running time.

4.4. Dynamic scheduling

We have extended the ACO to solve the problem of dynamic scheduling or re-scheduling. In practical scenarios, during the execution of the scheduled jobs, there are usually arrivals of new or urgent work orders that need to be executed at the same time with the on-going work orders. Therefore, the current schedule needs to be updated in order to include new jobs. The ACO algorithm was developed to accommodate this requirement. Assuming that during the execution process, there are new jobs arriving at the shop floor at the time point t*. The solver firstly extracts the operations that have not been started from current schedule. Then, the ACO algorithm is implemented for these operations together with the new jobs in order to produce a new updated schedule. This process is summarized in Figure 9.

This dynamic scheduling capability has been demonstrated in our use case. Assuming that the operations were executed based on the schedule presented in Figure 4. At the time point $t^{*}= 40 \min$, there are 10 new jobs arriving. The performance metric used is make-span, $C_{max}$. Figure 10 has shown the capability of the solver in modelling dynamic job shop problem.

5. Conclusions

In this paper, motivated by the Industrie 4.0 concept, in which the complex variations of production processes must be systematically addressed, we have presented a solution of scheduling MRO processes. Our approach is based on the well-known ACO algorithm enhancing its parameters to optimize the schedule of MRO processes. Our approach was also proven to show good performance for dynamic scheduling scenarios and has been tested in Model Factory @ARTC.

In response to the state-of-the-art research gap where implementing ACO algorithm for MRO environment is scarce, the contribution of this research is on developing and studying an ACO algorithm for an MRO use-case with two business objectives which are minimizing the total scheduling time and tardiness of all jobs. The developed algorithm also has a capacity of dynamic scheduling. Result from the developed algorithm has shown its better solution in comparison with commercial scheduling software. Also emerging is an approach to shorten the convergence time of the algorithm by investigating the dependency of the algorithm’s performance on tuning parameters. Applying the developed ACO algorithm in this research can bring out various practical business values to companies. For example, complex MRO processes with various product routings can be optimally scheduled to improve productivity. The dynamic scheduling capability developed in this study can help production planners efficiently adjust the current product schedules to accommodate urgent work orders or additional work orders induced during the production process which frequently occurs in the MRO environment.

There are several areas where the research can be carried on in the future. First, the algorithm can be improved to shorten the overall time required for the solution to converge. One of the possibilities is to modify the local and global pheromone updating strategies. Industrial applicability of the developed algorithm can be enhanced by considering more constraints such as sequence-dependent setup times, availabilities of materials and personnel. The integration of the developed algorithm to commercial scheduling software to harvest all advantages of the algorithm and the software is also under consideration with the support of middleware option [24]. Finally, alternative optimization algorithms such as bee colony for scheduling optimization will be also explored and developed.