1. Introduction
The steel industry is a resource- and energy-intensive industry, and is also a high-pollution, high-energy, and high-emission industry. In 2015, the energy consumption of the steel industry accounted for 26.1% of the total industrial energy consumption, which accounted for 14.9% of the total energy consumption in China [
1]. The integrated steel enterprises include main steel production systems, energy systems, and auxiliary systems. The main steel production systems include sintering, pellet production, blast furnace (BF), coke oven, converting, refining, continuous casting, hot rolling, cold rolling, and so on. The energy systems include power and steam production systems, chemical product manufacturing systems, and technical gas production systems. The auxiliary systems include transportation equipment and warehousing processes. As large material energy input and output systems, steel companies include complex energy distribution networks that use multiple energy sources. Among them, 34% of the primary energy (cleaned coal and anthracite coal) is transformed to byproduct gases during the iron and steel production process [
2,
3]. As the Chinese steel industry pays increasing attention to environmental protection [
4], people are paying increasing attention to the recycling, conversion, and utilization of secondary energy. In the iron and steel production process, there is often a surplus or shortage of secondary energy, which will lead to an increase in operating costs and environmental pollution costs. Therefore, optimizing the utilization of secondary energy and improving the conversion efficiency of secondary energy are of great significance to the steel industry [
5]. Therefore, the design and optimization of energy systems in steel enterprises are receiving increasing attention.
The secondary energy utilization of iron and steel enterprises has been widely studied by researchers [
6,
7,
8]. Previous studies have focused on the production or consumption prediction and optimal scheduling of byproduct gases, steam, and electricity. In terms of energy forecasting, Lei et al. [
9] forecasted the surplus gas in the iron and steel industry to make full use of gas resources and stabilize the pipe network pressure. Zhang Qi et al. [
10] made comprehensive use of the grey model and back-propagation (BP) neural network to establish a prediction model of the blast furnace gas (BFG) system. In addition, several researchers, based on the ARIMA model, neural network, and least-squares support vector machine (LSSVM), have established composite prediction models to predict the production and consumption levels of energy source in steel enterprises [
11,
12,
13,
14]. In terms of energy scheduling, Kim et al. [
15] proposed an optimal distribution model of the gas supply and demand by considering constraints such as boiler fuel fluctuations, boiler efficiencies, and gasholder capacities. Kong et al. [
16] used a dynamic mixed-integer linear programming (MILP) model to optimize the multi-cycling of byproduct gas. Zhao et al. [
17,
18,
19] used MILP to establish an optimal distribution model for surplus gas and considered the influences of peak and valley electricity prices on the optimization results, thereby making the model closer to reality. Based on analysis of the supplies and demands of gas, steam, and electricity in the production cycle, Zhang Qi et al. [
20,
21,
22] established a multi-cycle optimal distribution model of the surplus gas, steam, and electric power. The model considered the impacts of polluting gases on the environment.
The above research aims to predict and optimize the distribution of one or several secondary energy sources (gas, steam, electricity, etc.) under the premise of determining the production processes and energy conversion devices. There are few types of energy sources involved in the above studies, and there is no comprehensive consideration of the interactions and the different uses of multiple energy sources.
The distribution of energy source is also different if steel plants are equipped with different energy conversion devices [
23]. For example, the introduction of desalination plants will change the distribution of steam in steel plants [
24]. In their research on the configurations of energy conversion equipment in iron and steel enterprises, Li et al., [
25] combined the analyses of the Angang Iron and Steel Group’s gas balance and gas power generation configurations and analyzed the process flows, overall benefits, technical advantages, and disadvantages of the high temperature and high-pressure power generation and combined cycle power plant (CCPP). Wang et al. [
26] proposed a technical route for the utilization of BFG and evaluated the environmental economy of methanol made from BFG. Joseck et al. [
27] studied the energy and emission effects of coke oven gas (COG) hydrogen production and compared these effects with those of other hydrogen production options. Although the above studies have proposed the impact of the choice of energy conversion method on the production efficiency, the evaluation of only a single energy conversion technology lacks the systematic consideration of the configurations of different energy conversion technologies (devices).
At present, in the design process of steel enterprises, the design steps of the energy systems are as follows: First, energy consumption analysis and evaluation of the production capacity of each process of the steel plant are conducted [
28]; then, selection of the energy conversion technology (equipment) occurs according to experience [
29]; and finally, the balance of the energy supply and demand is evaluated. The power determination and energy source distribution scheme determination of the energy conversion equipment are performed. The existing design methods do not comprehensively consider the interaction between energy conversion equipment types and the interaction between multiple energy sources. The design of an energy system has, in general, not been optimized.
In view of the drawbacks of the previous research work, this study proposes a linear programming model for the optimization design of the energy systems in steel plants. The model involves more than 20 energy sources and 27 equipment types/processes in iron and steel enterprises. At the same time, the model emphasizes the impacts of energy conversion devices on the energy distribution and the interaction between different energy sources and provides guidance for the optimization design of the energy systems in steel enterprises from the perspective of system optimization.
2. Problem Analysis
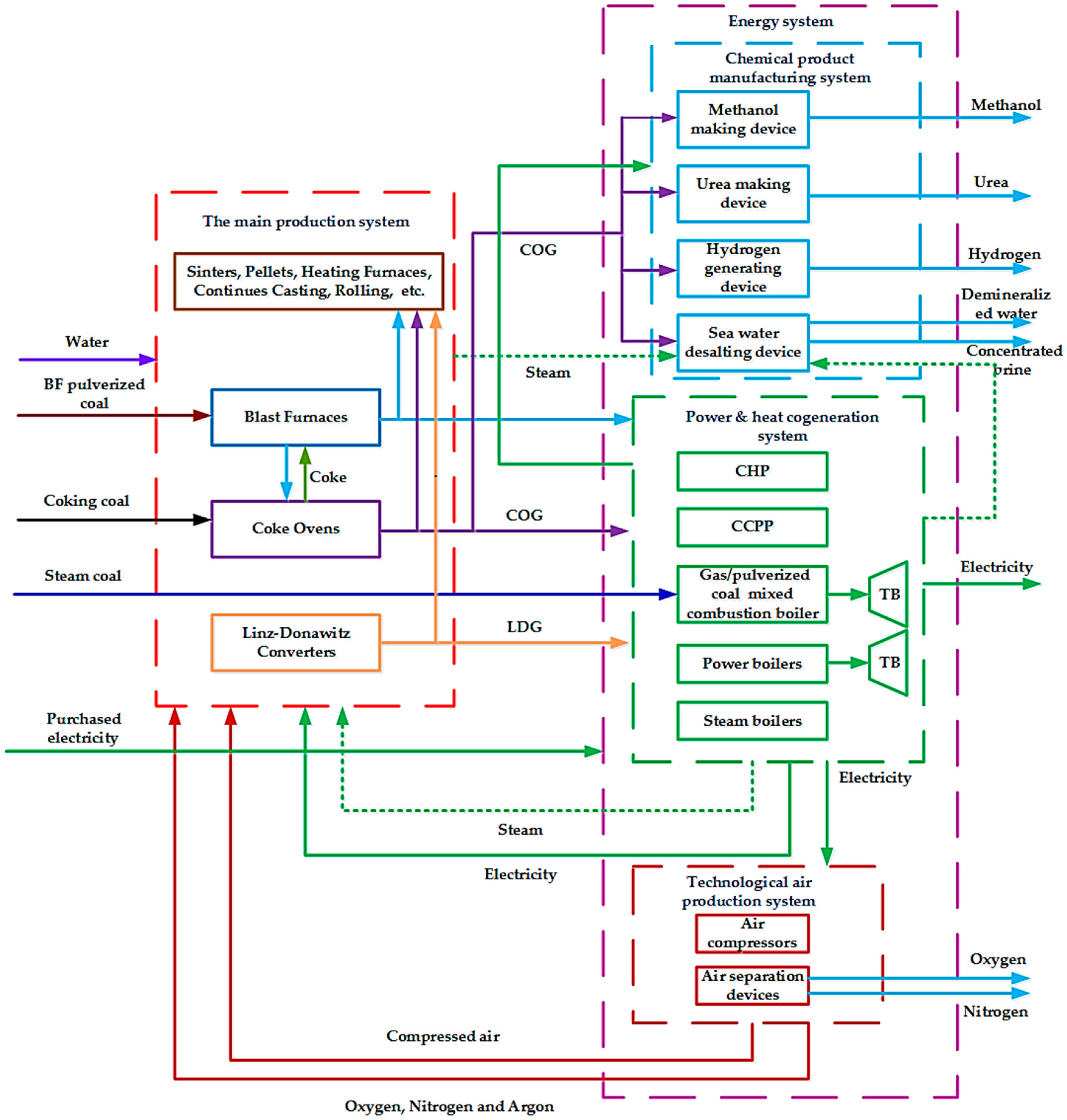
Portions of the BFG, COG, and Linz–Donawitz process gas (LDG) produced by a steel enterprise are used inside the steel system to meet the production demands of iron and steel, and the remaining byproduct gas is supplied to energy systems. The production of the iron and steel system is relatively stable, in which the amount and consumption of byproduct gas remain unchanged, and thus the amount of byproduct gas supplied to the energy systems does not change.
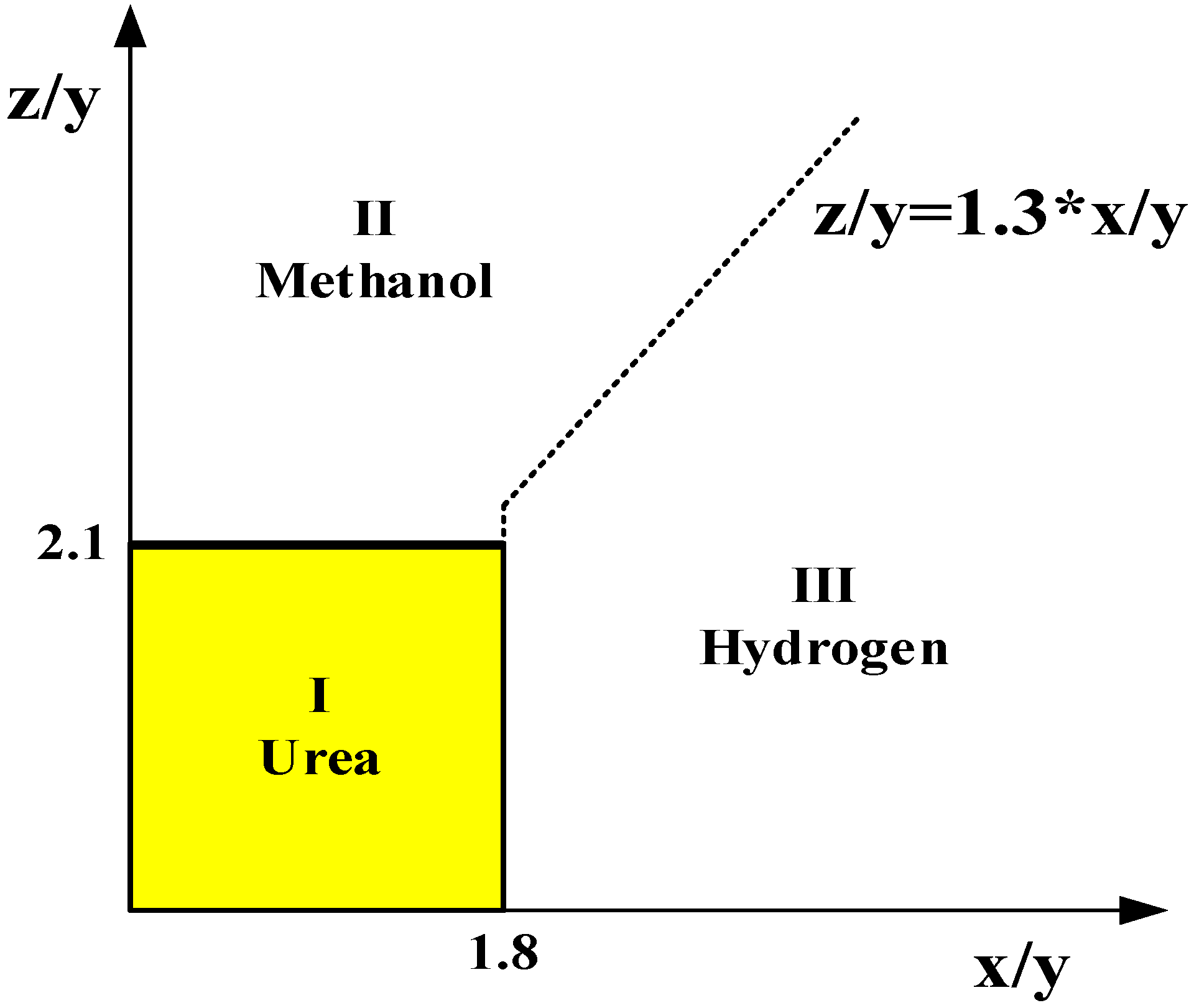
In energy systems, chemical product production systems can choose from the following processes: hydrogen production, methanol production, urea production, and seawater desalination. The corresponding products include hydrogen, methanol, urea, saltwater, and concentrated saltwater, and these products can be sold [
30,
31]. Power and steam production systems and optional equipment types, including CCPPs [
32], combined heat and power (CHP) systems [
33], gas/pulverized coal-fired generator sets [
34], electric boilers, and steam boilers, use byproduct gas and steam coal to produce electricity and steam. At the same time, electricity and steam support the steel production process and part of the steam supply desalination. Technical gas systems include air compressors and air separation units that primarily consume power and produce technical gases, including compressed air, argon, nitrogen, and oxygen. The technical gas supply outside the steel production system, which consists of the remaining liquid nitrogen and liquid oxygen, are sold. The energy systems of integrated steel enterprises are shown in
Figure 1. In
Figure 1, the energy system of the iron and steel enterprise contains almost all possible energy conversion equipment types. In fact, certain energy conversion equipment types are selected by an iron and steel enterprise.
As shown in the above figure, the energy source distribution is different if the energy system has different process configurations. Due to the existence of energy substitution, the distributions of different energy sources affect each other. For example, a power boiler can simultaneously use BFG, LDG, and COG, and the three types of gases can be substituted for each other within a certain range. In a gas/pulverized coal-fired generator unit, gas and pulverized coal can also be substituted for each other within a certain range [
35]. It is necessary to optimize the configuration of energy conversion equipment in the energy system and the coupled optimal distribution of various energy sources. This consideration means that we should choose the right energy conversion equipment and determine the types and quantities of energy sources to be distributed, thereby realizing the design optimization of the energy system of an iron and steel enterprise. At present, the design of an energy system is mainly based on experience and lacks evaluation of the overall structure of the energy system and energy conversion efficiency. In this paper, the overall optimization design of an energy system will be carried out to achieve the rational distribution and utilization of energy source.
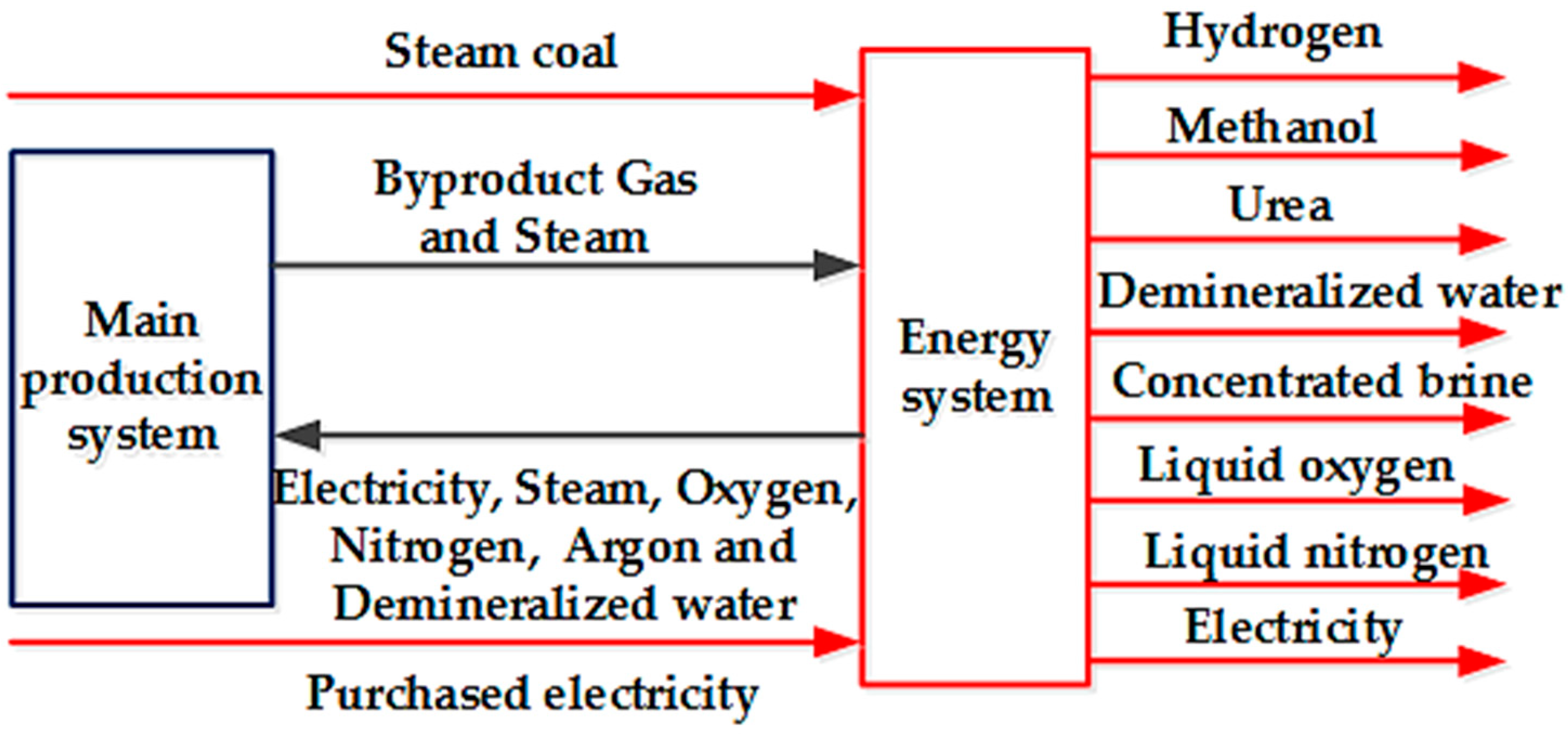
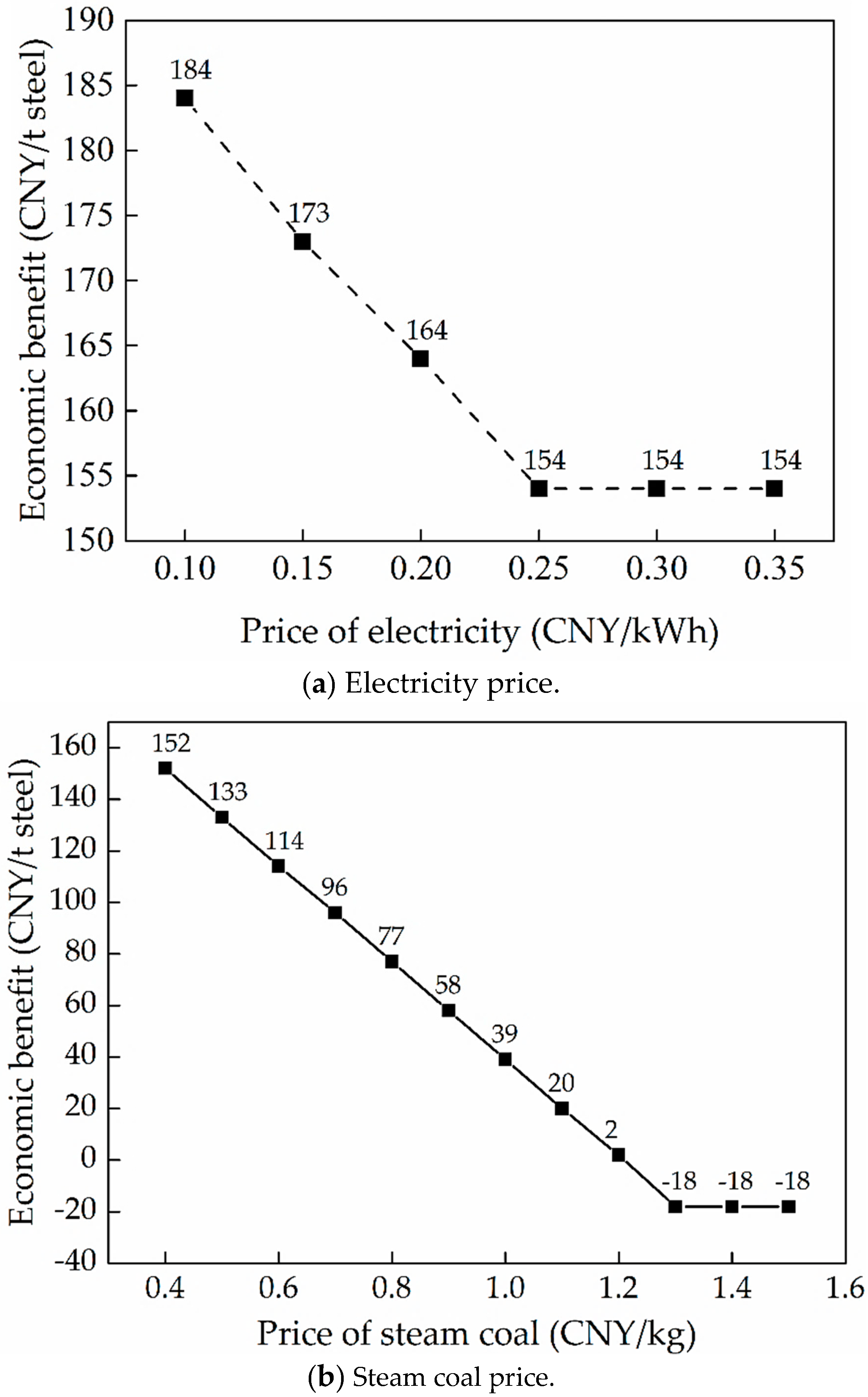
To ensure power demand and reduce cost, most integrated iron and steel corporations have built on-site power plants (OSPP) to cover 50–80% of the power demand, and the remaining demand is supplied by the main grid [
36], which should be purchased. Both the purchased electricity and the self-produced electricity maintain the power balance of iron and steel enterprises. The goal of energy system design optimization is to optimize the equipment configuration of the energy system and energy source distribution to meet the energy source requirements of the steel production system and to maximize the economic benefits of the energy system. That is, maximum the economic benefits of the energy system is equal to the value of the maximum energy system products for sale minus the purchase cost of the input energy source. Since the input energy source, such as coking coal, pulverized coal injection into a BF, and water input, are determined by the production scale of the steel production system, the output scale is unchanged, and the input levels of the three media are constant, and optimization is not considered. Therefore, the above formula is transformed into: Maximum economic benefits of the energy system is equal to the value of the maximum energy system products for sale minus the purchase cost of the steam coal, and then minus the purchase cost of electricity, and the specific optimizable input and output energy source are shown in
Figure 2.