A Systematic Error Compensation Method Based on an Optimized Extreme Learning Machine for Star Sensor Image Centroid Estimation
Abstract
1. Introduction
2. Error Analysis of the Center of Mass Method
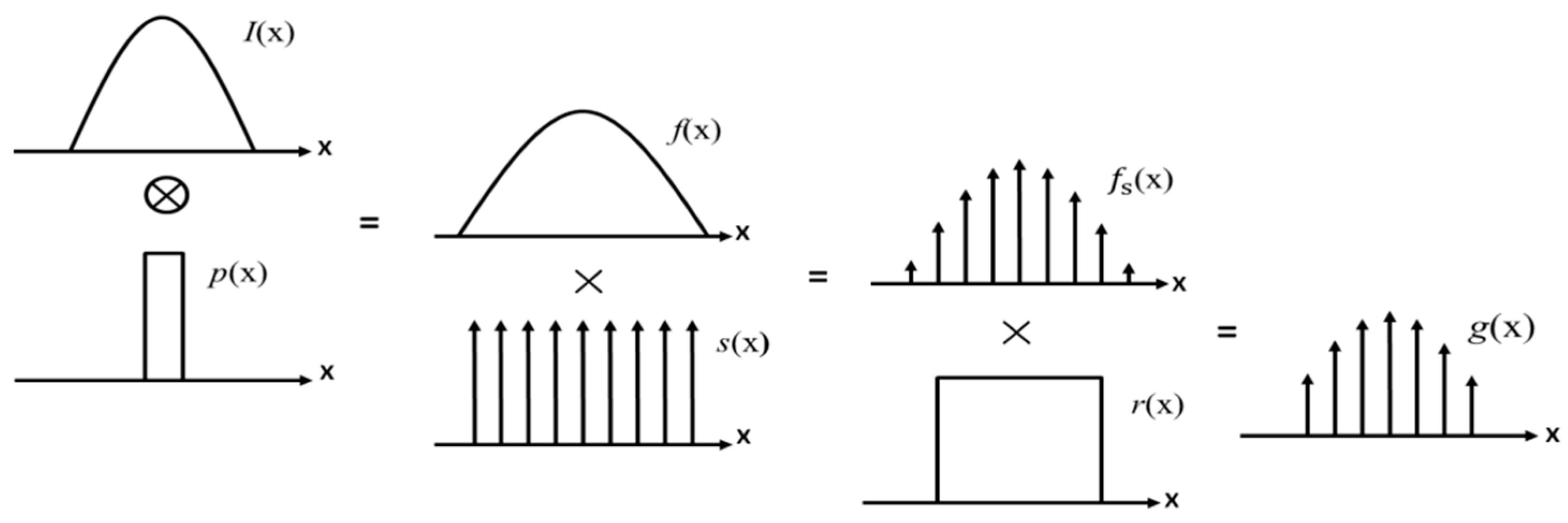
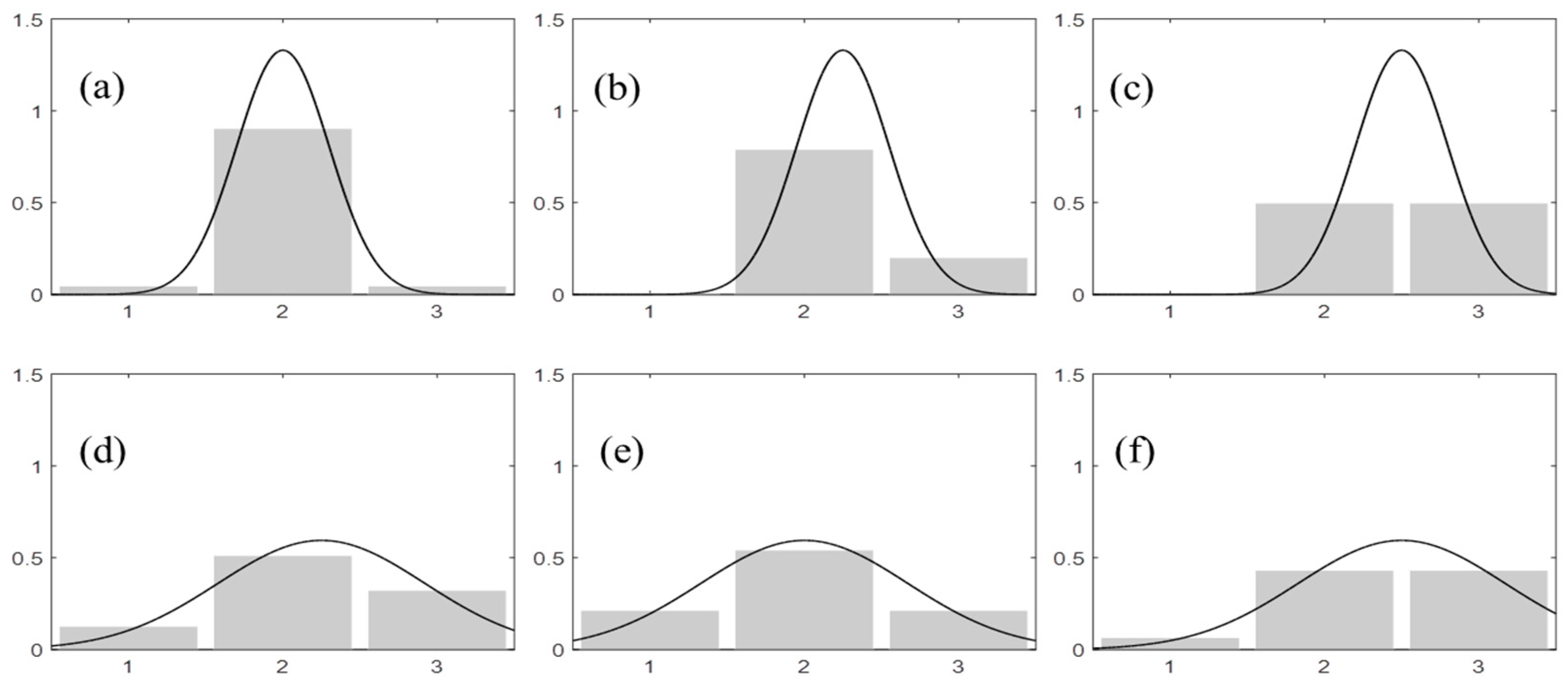
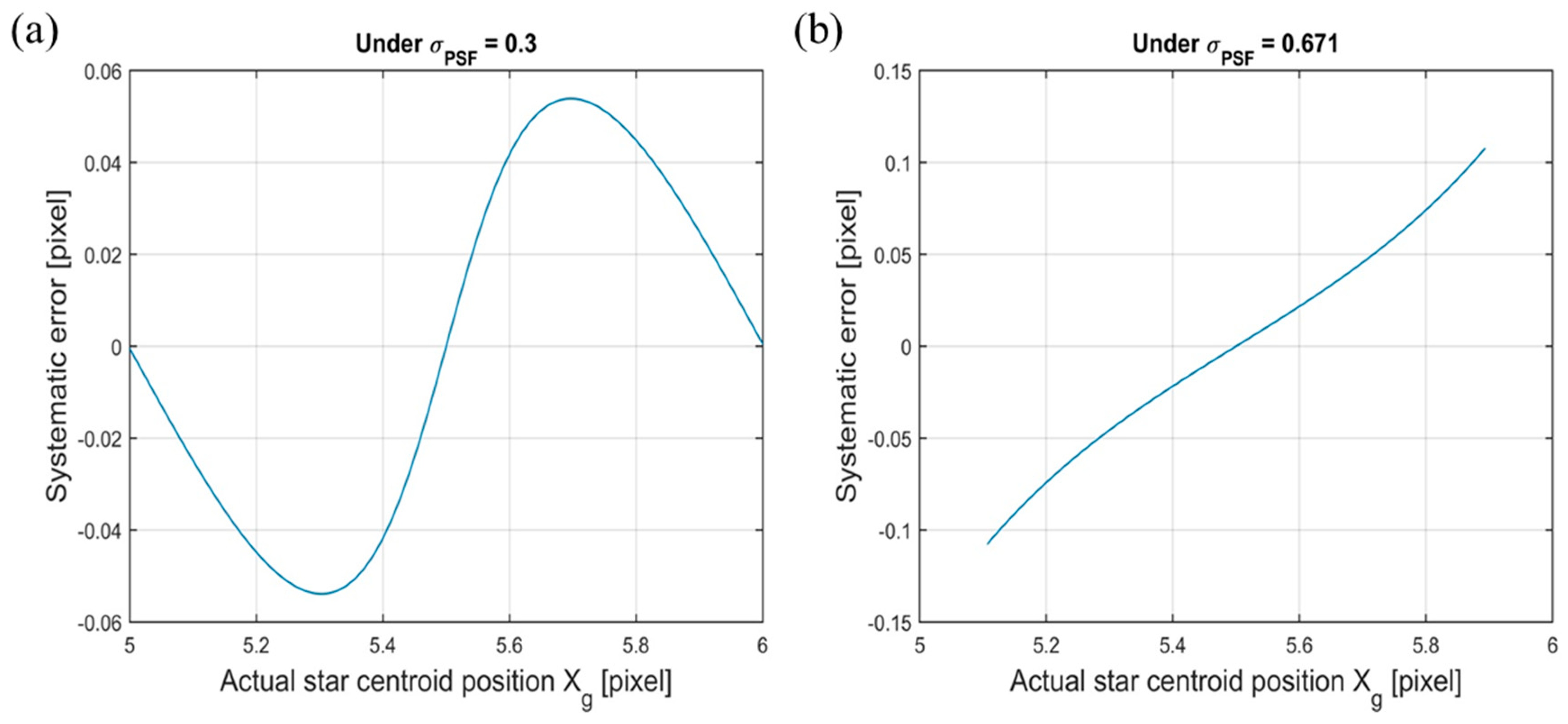
2.1. Discrete Approximation Error
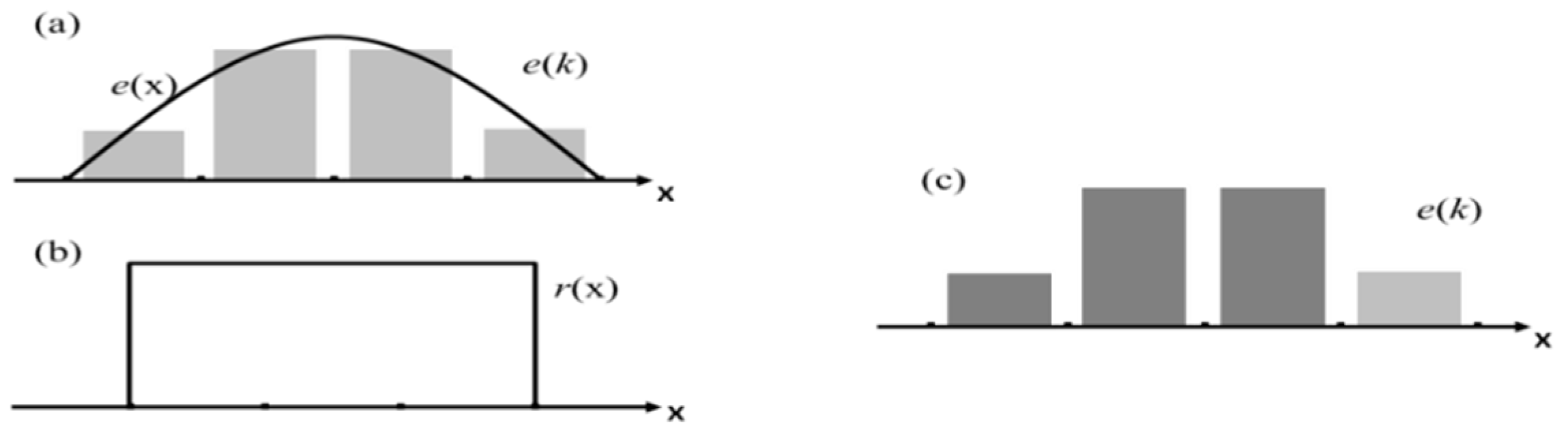
2.2. Sampling Window Truncation Error
3. Materials and Methods
3.1. Extreme Learning Machine
3.2. Bat Algorithm
| Algorithm 1. The pseudo code of the bat algorithm. |
| Initialize the bat population xi and vi (i = 1, 2, …, n) Initialize frequencies Fi, pulse rates ri and the loudness Ai while (t < max number of iterations) Generate new solutions by adjusting frequency, update velocities and locations if (rand > ri) Select a solution among the best solutions Generate a local solution around the selected best solution end if Generate a new solution by flying randomly if (rand < Ai & f(xi) < f(x*)) Accept the new solutions Increase ri and reduce Ai end if Rank the bats and find the current best x* end while |
3.3. Optimized Extreme Learning Machine
3.4. BA-ELM for Systematic Error Compensation
4. Simulations and Discussion
4.1. Preprocessing the Sample Data
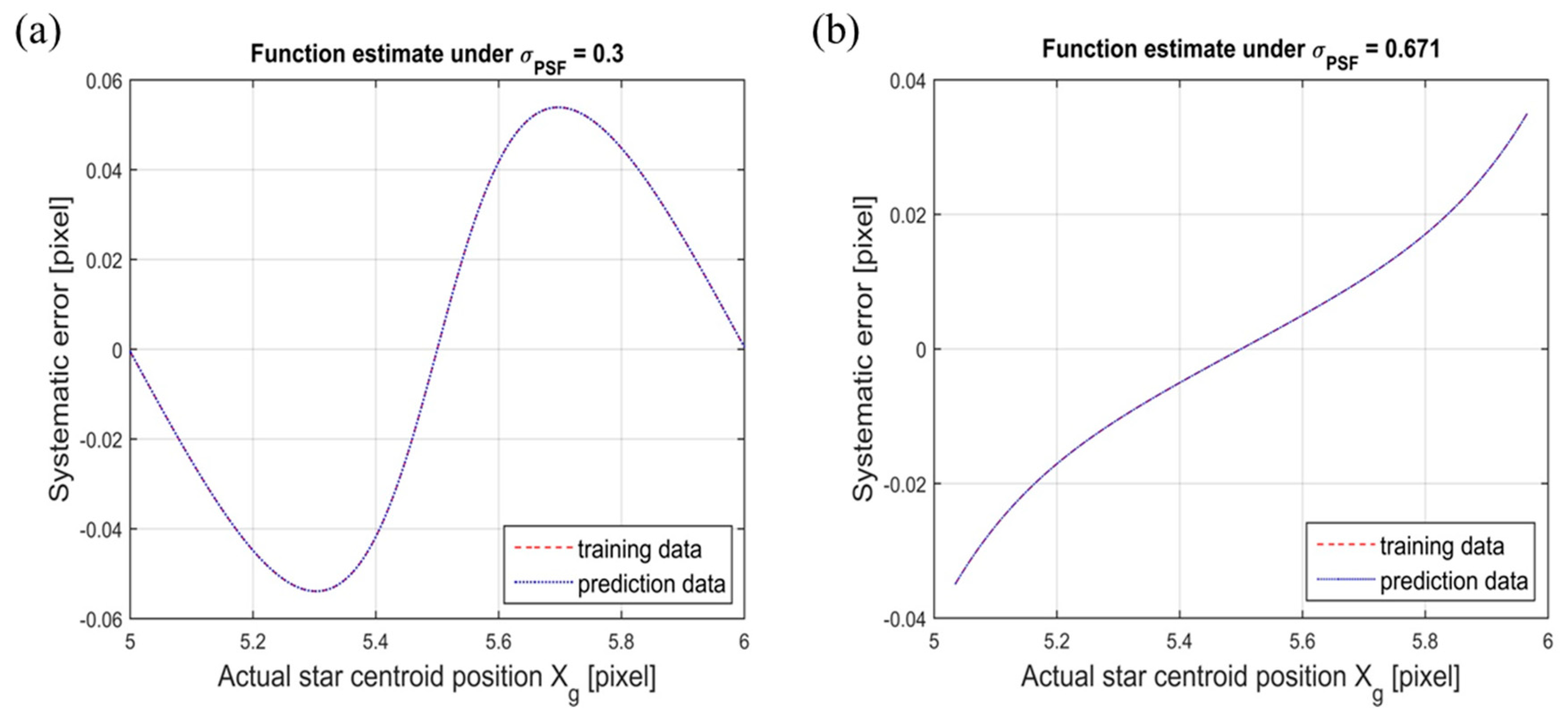
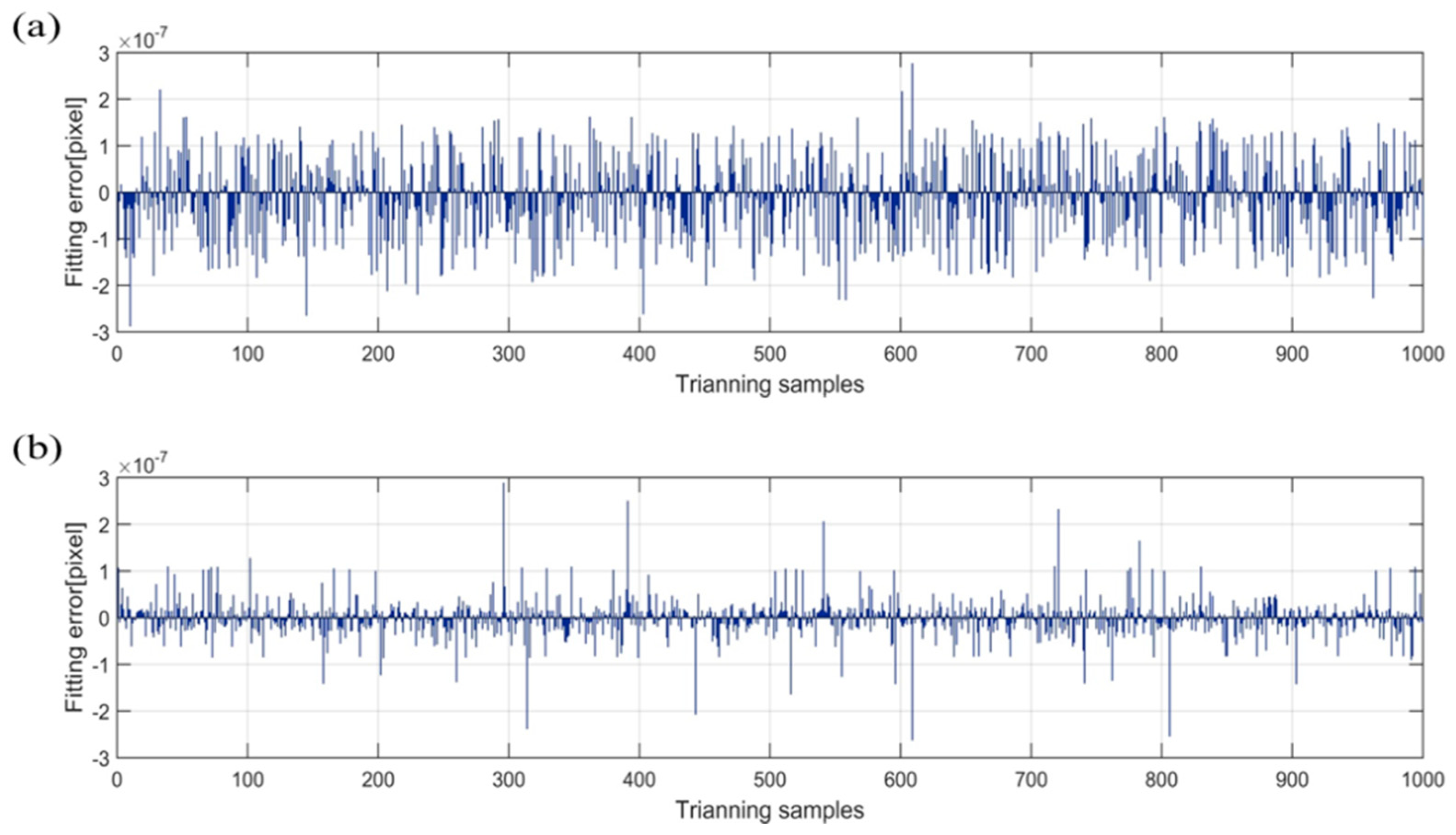
4.2. The Fitting Accuracy of the BA-ELM
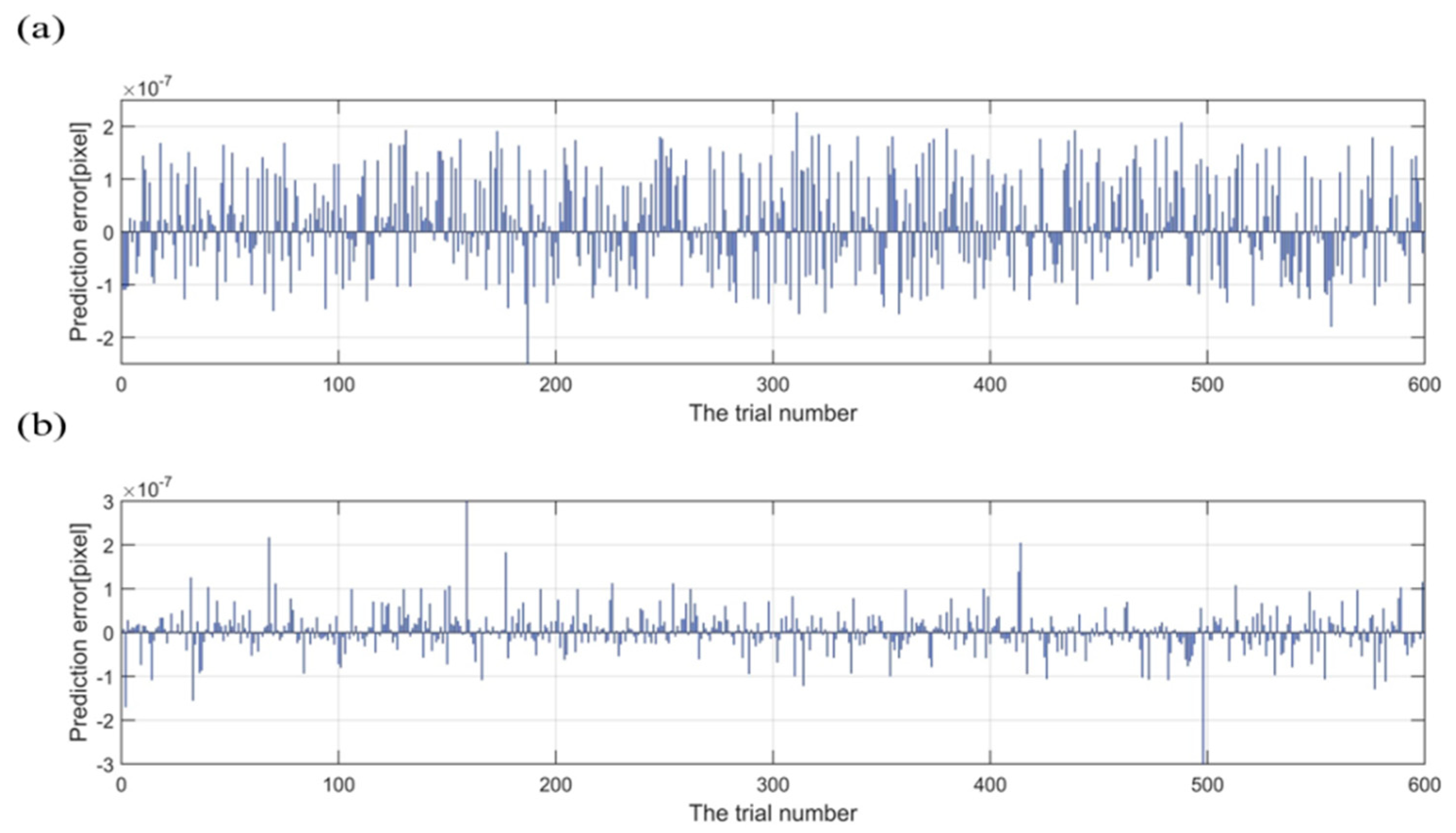
4.3. The Prediction Accuracy of the BA-ELM
4.4. The Compensation Performance in Star Images
4.5. Comparison and Discussion
5. Conclusions
- (1)
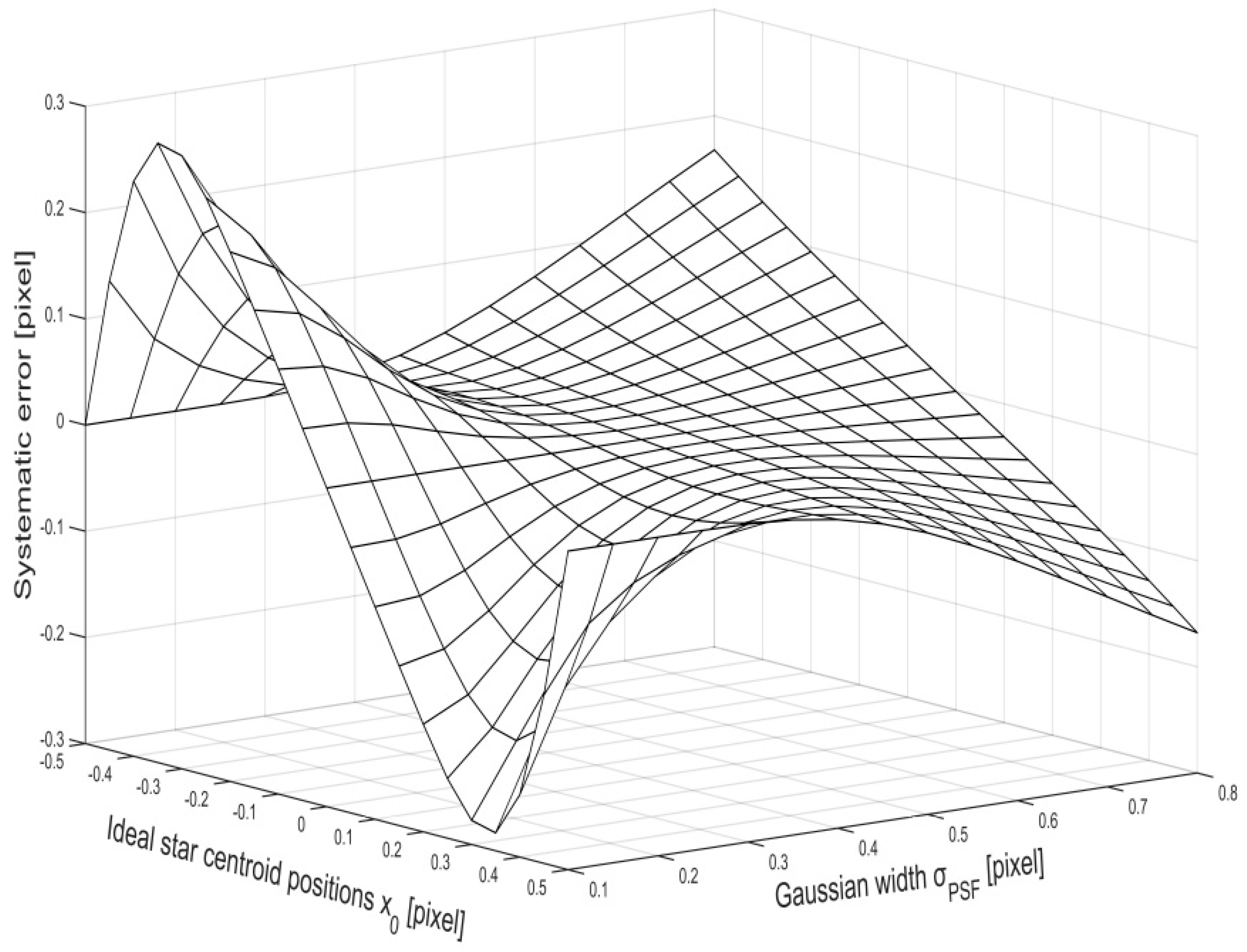
- Through a frequency field and numerical simulations approach, the characteristics and causes of two types of systematic error in the CoM method, namely, discrete approximation error and truncation error, were illustrated, and the relationships between the systematic error and actual star centroid position under different Gaussian widths were obtained. This helped us to design the compensation method.
- (2)
- BA was adopted to improve the prediction accuracy and stability of the ELM. The random parameters in the BA-ELM model were optimized during the off-line training process. Through the verification of the results, the proposed BA-ELM compensation method was shown to effectively eliminate the systematic error and enhance the accuracy of the CoM method in estimating star centroid locations.
- (3)
- Comparing the simulation results of the BP neural network method, analysis compensation method, LSSVR compensation method, and basic ELM showed that the BA-ELM compensation method performed better in terms of prediction accuracy than did the other methods during the systematic error compensation process.
Author Contributions
Funding
Conflicts of Interest
References
- Mehta, D.S.; Chen, S.; Low, K.S. A robust star identification algorithm with star shortlisting. Adv. Space Res. 2018, 61, 2647–2660. [Google Scholar] [CrossRef]
- Wang, G.; Lv, W.; Li, J.; Wei, X. False Star Filtering for Star Sensor Based on Angular Distance Tracking. IEEE Access 2019, 7, 62401–62411. [Google Scholar] [CrossRef]
- Zhu, H.; Liang, B.; Zhang, T. A robust and fast star identification algorithm based on an ordered set of points pattern. Acta Astronaut. 2018, 148, 327–336. [Google Scholar] [CrossRef]
- Mehta, D.S.; Chen, S.; Low, K.S. A Rotation-Invariant Additive Vector Sequence Based Star Pattern Recognition. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 689–705. [Google Scholar] [CrossRef]
- Fan, Q.; Cai, Z.; Wang, G. Plume Noise Suppression Algorithm for Missile-Borne Star Sensor Based on Star Point Shape and Angular Distance between Stars. Sensors 2019, 19, 3838. [Google Scholar] [CrossRef] [PubMed]
- Liebe, C.C. Accuracy performance of star trackers—A tutorial. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 587–599. [Google Scholar] [CrossRef]
- Quine, B.M.; Tarasyuk, V.; Mebrahtu, H.; Hornsey, R. Determining star-image location: A new sub-pixel interpolation technique to process image centroids. Comput. Phys. Commun. 2007, 177, 700–706. [Google Scholar] [CrossRef]
- Stone, R.C. A comparison of digital centering algorithms. Astron. J. 1989, 97, 1227–1237. [Google Scholar] [CrossRef]
- Delabie, T.; Schutter, J.D.; Vandenbussche, B. An accurate and efficient gaussian fit centroiding algorithm for star trackers. J. Astronaut. Sci. 2014, 61, 60–84. [Google Scholar] [CrossRef]
- He, Y.; Wang, H.; Feng, L.; You, S.; Lu, J.; Jiang, W. Centroid extraction algorithm based on grey-gradient for autonomous star sensor. Optik 2019, 194, 162932. [Google Scholar] [CrossRef]
- Tian, H. Noise Analysis in CMOS Image Sensors. Ph.D. Thesis, Standford University, College Station, CA, USA, 2000. [Google Scholar]
- Grossman, S.B.; Emmons, R.B. Performance analysis and size optimization of focal planes for point-source tracking algorithm applications. Opt. Eng. 1984, 23, 232167. [Google Scholar] [CrossRef]
- Stanton, R.H.; Alexander, J.W.; Dennison, E.W.; Glavich, T.A.; Hovland, L.F. Optical tracking using charge-coupled devices. Opt. Eng. 1987, 26, 930–938. [Google Scholar] [CrossRef]
- Hancock, B.R.; Stirbl, R.C.; Cunningham, T.J.; Pain, B.; Wrigley, C.J.; Ringold, P.G. CMOS active pixel sensor specific performance effects on star tracker/imager position accuracy. Proc. SPIE 2001, 4284, 43–53. [Google Scholar] [CrossRef]
- Alexander, B.F.; Ng, K.C. Elimination of systematic error in subpixel accuracy centroid estimation. Opt. Eng. 1991, 30, 1320–1332. [Google Scholar] [CrossRef]
- Rufino, G.; Accardo, D. Enhancement of the centroiding algorithm for star tracker measure refinement. Acta Astronaut. 2003, 53, 135–147. [Google Scholar] [CrossRef]
- Jia, H.; Yang, J.; Li, X.; Yang, J.; Yang, M.; Liu, Y.; Hao, Y. Systematic error analysis and compensation for high accuracy star centroid estimation of star tracker. Sci. China Technol. Sci. 2010, 53, 3145–3152. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, T.; Song, J.Y.; Liang, B. High accuracy error compensation algorithm for star image sub-pixel subdivision location. Opt. Precis. Eng. 2010, 18, 1002–1010. [Google Scholar]
- Yang, J.; Liang, B.; Zhang, T.; Song, J. A novel systematic error compensation algorithm based on least squares support vector regression for star sensor image centroid estimation. Sensors 2011, 11, 7341–7363. [Google Scholar] [CrossRef]
- Wei, X.; Xu, J.; Li, J.; Zhang, G. S-curve centroiding error correction for star sensor. Acta Astronaut. 2014, 99, 231–241. [Google Scholar] [CrossRef]
- Faraji, H.; Maclean, W.J. CCD noise removal in digital images. IEEE Trans. Image Process. 2006, 15, 2676–2685. [Google Scholar] [CrossRef]
- Katake, A.B. Modeling, Image Processing and Attitude Estimation of High Speed Star Sensors. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2006. [Google Scholar]
- Wang, H.; Wang, Y.; Li, Z.; Song, Z. Systematic centroid error compensation for the simple Gaussian PSF in an electronic star map simulator. Chin. J. Aeronaut. 2014, 27, 884–891. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. Part B 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Huang, K.; Cheng, H.; Li, Y.; Su, C.Y. Haptic identification by ELM-controlled uncertain manipulator. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2398–2409. [Google Scholar] [CrossRef]
- Mohammed, A.A.; Minhas, R.; Wu, Q.M.J.; Sid-Ahmed, M.A. Human face recognition based on multidimensional pca and extreme learning machine. Pattern Recognit. 2011, 44, 2588–2597. [Google Scholar] [CrossRef]
- Peng, X.; Lin, P.; Zhang, T.; Wang, J. Extreme learning machine-based classification of adhd using brain structural mri data. PLoS ONE 2013, 8, e79476. [Google Scholar] [CrossRef]
- Sun, Z.L.; Choi, T.M.; Au, K.F.; Yu, Y. Sales forecasting using extreme learning machine with applications in fashion retailing. Decis. Support Syst. 2008, 46, 411–419. [Google Scholar] [CrossRef]
- Wang, G.; Zhao, Y.; Wang, D. A protein secondary structure prediction framework based on the extreme learning machine. Neurocomputing 2008, 72, 262–268. [Google Scholar] [CrossRef]
- Vasileios, C.; Tsipouras, M.G.; Nikolalos, G.; Tzallas, A.T.; Brown, G. Hybrid extreme learning machine approach for heterogeneous neural networks. Neurocomputing 2019, 361, 137–150. [Google Scholar] [CrossRef]
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm. In Studies in Computational Intelligence; González, J., Pelta, D., Cruz, C., Terrazas, G., Krasnogor, N., Eds.; Springer: Heidelberg, Germany, 2010; Volume 284, pp. 65–74. [Google Scholar]
- Li, L.L.; Sun, J.; Tseng, M.L.; Li, Z.G. Extreme learning machine optimized by whale optimization algorithm using insulated gate bipolar transistor module aging degree evaluation. Expert Syst. Appl. 2019, 127, 58–67. [Google Scholar] [CrossRef]
- Yu, P.; Cao, J.; Jegatheesan, V.; Du, X. A real-time BOD estimation method in wastewater treatment process based on an optimized extreme learning machine. Appl. Sci. 2019, 9, 523. [Google Scholar] [CrossRef]
- Mariani, V.C.; Och, S.H.; Coelho, L.D.S.; Domingues, E. Pressure prediction of a spark ignition single cylinder engine using optimized extreme learning machine models. Appl. Energy 2019, 249, 204–221. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Image plane dimension | 512 pixels × 512 pixels |
| Field of view (FOV) | 12° × 12° |
| Principle point | (256 pixels, 256 pixels) |
| Pixel size | 15 mm × 15 mm |
| Magnitude threshold | 6.0 Mv |
| Number | IX | XBC | EXBC | XAC | EXAC |
|---|---|---|---|---|---|
| 1 | 51.2439 | 51.2978 | 0.0539 | 51.2439 | 1.2326 × 10−8 |
| 2 | 72.7366 | 72.6829 | 0.0537 | 72.7366 | 1.1070 × 10−7 |
| 3 | 361.2308 | 361.2483 | 0.0535 | 361.2308 | 2.1059 × 10−8 |
| 4 | 55.8758 | 55.8377 | 0.0382 | 55.8758 | 7.8417 × 10−8 |
| 5 | 199.6277 | 199.5891 | 0.0386 | 199.6277 | 1.8986 × 10−7 |
| 6 | 66.2154 | 66.2681 | 0.0527 | 66.2154 | 3.8834 × 10−8 |
| 7 | 69.2903 | 69.3424 | 0.0521 | 69.2903 | 4.5690 × 10−9 |
| 8 | 430.3110 | 430.3609 | 0.0499 | 430.3110 | 2.9145 × 10−8 |
| 9 | 108.1923 | 108.2428 | 0.0505 | 108.1923 | 1.5801 × 10−9 |
| 10 | 43.2980 | 43.3493 | 0.0514 | 43.2980 | 1.9520 × 10−8 |
| Number | IX | XBC | EXBC | XAC | EXAC |
|---|---|---|---|---|---|
| 1 | 387.9959 | 387.8897 | 0.1062 | 387.9959 | 8.5532 × 10−8 |
| 2 | 85.2216 | 85.2741 | 0.0525 | 85.2216 | 1.0517 × 10−7 |
| 3 | 55.9882 | 55.8842 | 0.1040 | 55.9882 | 3.4377 × 10−8 |
| 4 | 486.1995 | 486.2568 | 0.0072 | 486.1995 | 3.4220 × 10−8 |
| 5 | 464.0505 | 464.1439 | 0.0933 | 464.0505 | 2.9580 × 10−9 |
| 6 | 378.8036 | 378.7457 | 0.0579 | 378.8036 | 2.3147 × 10−8 |
| 7 | 507.9022 | 507.8212 | 0.0811 | 507.9022 | 3.9890 × 10−9 |
| 8 | 307.8156 | 307.7550 | 0.0606 | 307.8156 | 2.3306 × 10−8 |
| 9 | 240.8466 | 240.7790 | 0.0676 | 240.8466 | 2.2531 × 10−7 |
| 10 | 89.8935 | 89.8146 | 0.0789 | 89.8935 | 3.7056 × 10−8 |
| Method | Training Time | RMSE | Prediction Error |
|---|---|---|---|
| BP | 549.8 ms | 3.6230 × 10−4 | 2.0 × 10−3 |
| AC | -- | 1.8460 × 10−4 | 5.0 × 10−4 |
| ELM | 11.5 ms | 5.5251 × 10−6 | 4.0 × 10−5 |
| LSSVR | 204.6 ms | 3.0387 × 10−5 | 6.0 × 10−5 |
| BA-ELM | 50,400 ms | 2.4532 × 10−8 | 3.0 × 10−7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, X.; Wen, D.; Song, Z.; Xi, J.; Zhang, W.; Liu, G.; Li, Z. A Systematic Error Compensation Method Based on an Optimized Extreme Learning Machine for Star Sensor Image Centroid Estimation. Appl. Sci. 2019, 9, 4751. https://doi.org/10.3390/app9224751
Wei X, Wen D, Song Z, Xi J, Zhang W, Liu G, Li Z. A Systematic Error Compensation Method Based on an Optimized Extreme Learning Machine for Star Sensor Image Centroid Estimation. Applied Sciences. 2019; 9(22):4751. https://doi.org/10.3390/app9224751
Chicago/Turabian StyleWei, Xin, Desheng Wen, Zongxi Song, Jiangbo Xi, Weikang Zhang, Gang Liu, and Zhixin Li. 2019. "A Systematic Error Compensation Method Based on an Optimized Extreme Learning Machine for Star Sensor Image Centroid Estimation" Applied Sciences 9, no. 22: 4751. https://doi.org/10.3390/app9224751
APA StyleWei, X., Wen, D., Song, Z., Xi, J., Zhang, W., Liu, G., & Li, Z. (2019). A Systematic Error Compensation Method Based on an Optimized Extreme Learning Machine for Star Sensor Image Centroid Estimation. Applied Sciences, 9(22), 4751. https://doi.org/10.3390/app9224751





