1. Introduction
The classical use of regression in physics, sometimes also referred to as non-linear fitting, is to try to determine
d quantities
from a set of
n measurements
with
, using a theoretical mathematical model
that depends on a certain number
p of parameters
. Typically, this is achieved by choosing the parameters
w to minimize a selected error function, like the mean square error (MSE), with specific algorithms. To find the best solution for
f is a classical optimization problem [
1,
2,
3]. This method, however, fails to deliver stable and accurate results, for example, when the quantities
with
have different physical meanings and, consequently, depend on different components of the parameter vector
w in fundamentally distinct ways. As a result, the mathematical model may be an insufficient approximation, may be too complex for a stable implementation or may be simply unknown [
3].
An example where the usual multi-dimensional regression approach fails is in the determination of a substance from changes in its luminescence when several environmental conditions vary in an unknown and uncontrolled way. Luminescence quenching for oxygen detection represents a widespread application relevant in many fields like biomedical imaging, environmental monitoring, or process control [
4] (see
Section 4 for details). In this application, the quantity of interest is the concentration of molecular oxygen
. The measured quantity, either the luminescence intensity or luminescence intensity decay time of a special molecule (luminophore), is however, equally strongly dependent on the concentration
and the temperature
T. As a result, it is difficult to extract two different physical quantities, namely,
and
T, from the same set of data. Usually,
T is measured separately with another device and given as an input to a mathematical model describing the dependency of those two quantities from the input data. The complexity increases further if more than one luminophore is present, and several parameters (e.g.,
,
,
) have to be determined [
5,
6,
7,
8,
9].
A possible method, which recently attracted great interest, is the use of feed-forward neural network (FFNN) architectures, with a certain number of hidden layers and an appropriate number of output neurons, each responsible for predicting the desired variables
with
. In the example of oxygen sensing, the output layer would have a neuron for the oxygen concentration
and one for the temperature
T. This work shows that, since the output neurons must use the same features (the output of the last hidden layer) for all variables [
10,
11], FFNNs are insufficiently flexible. For the cases when the variables depend on fundamentally different ways from the inputs, this approach will give a result that is at best acceptable, and at worst unusable.
This work proposes a new approach, which is based on multi-task learning (MTL) neural network architectures. This type of architectures are characterized by multiple branches of layers, that get their input from a common set of layers. This type of network can improve the model prediction performance by jointly learning correlated tasks [
10,
11,
12,
13,
14]. In particular, the proposed MTL architectures are applied to the problem of luminescence quenching for oxygen sensing. Their performance in the prediction of oxygen concentration and temperature is analyzed and compared to that of a classical feed-forward neural network.
In general, the proposed MTL approach may be of particular relevance in all those cases where the mathematical model is not known, too complex or not really of interest and the only goal of the regression problem is to build a system that is able to determine y as accurately as possible.
The paper is organized as follows:
Section 2 describes non-linear regression and MTL with neural networks.
Section 3 describes the implementation of MTL and the different neural network studied in this work.
Section 4 reviews luminescence quenching for oxygen sensing. The results are discussed in
Section 5.
3. Neural Network Architectures and Implementation
In this paper, three architectures, one classical FFNN and two MTL, were investigated and compared in the simultaneous prediction of oxygen concentration and temperature. To make the comparison meaningful, the parameters, which are not architecture-specific, were not varied. The details of the architectures are described in the next subsections.
In the three architectures investigated the sigmoid activation functions was used for all the neurons
All the results were obtained with a training of 4000 epochs. The target variables
y were normalized to vary between 0 and 1. Thus, the sigmoid activation function was used also for the output neurons
and
. The input measurement, as will be explained in detail in
Section 4, is a vector in
with
.
To minimize the cost function, the optimizer Adaptive Moment Estimation (Adam) [
15,
25] was used. The training was performed with a starting learning rate of
and using batch-learning, which means that the weights were updated only after the entire training dataset has been fed to the network. Batch-learning was chosen because of its stability and speed since it reduces the training time of a few orders of magnitude in comparison to, for example, stochastic gradient descent [
15]. Therefore, it makes experimenting with different networks a feasible endeavor. The implementation was performed using the TensorFlow
™ library.
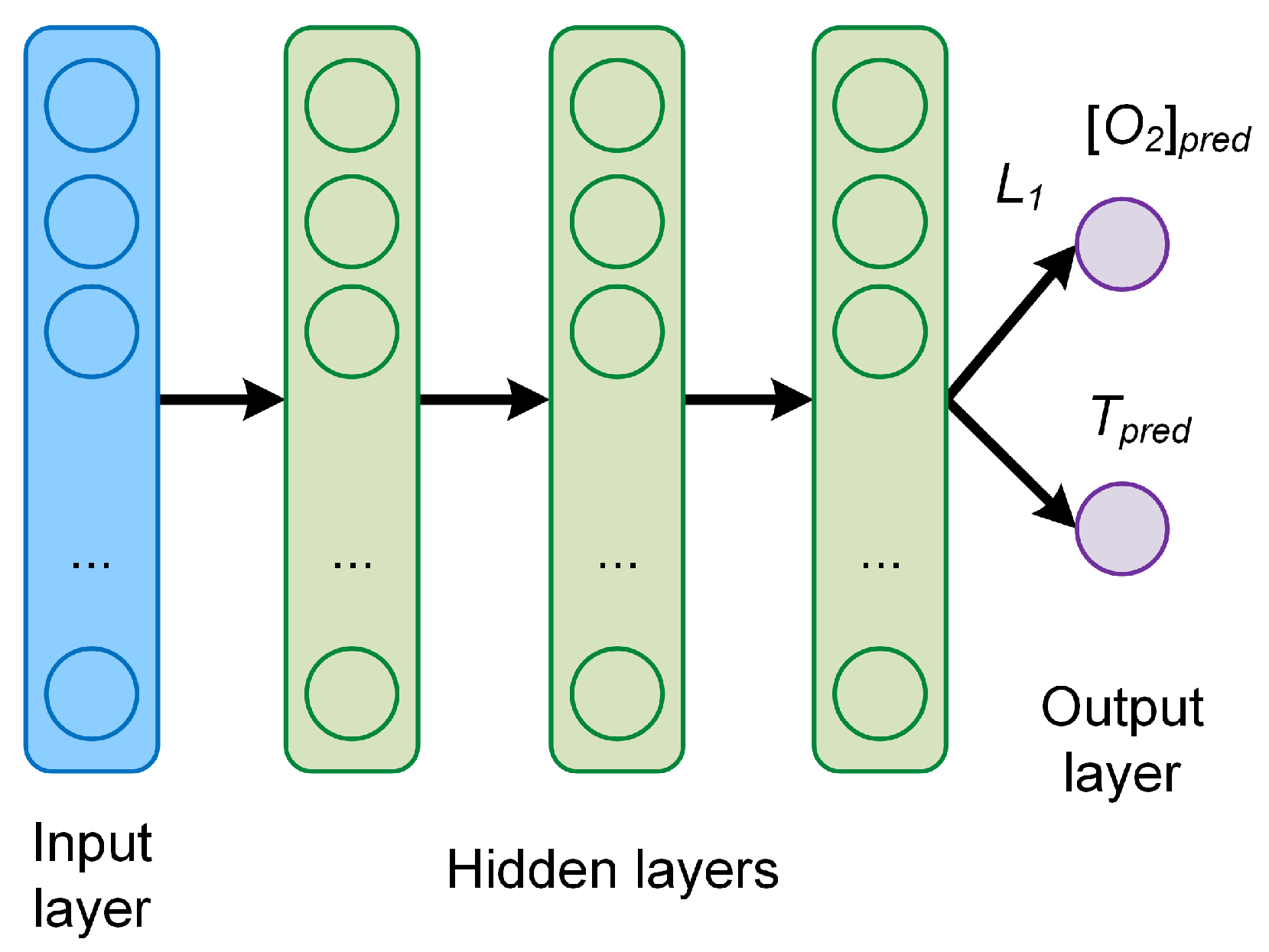
3.1. Network A
The first type of neural network investigated has a classical feed-forward architecture, consisting of an input layer, three hidden layers, and an output layer with two neurons
and
. This architecture, labeled here as Network A, is schematically shown in
Figure 2. The number of neurons of each hidden layer
is the same.
Each neuron in each layer gets as input the output of all neurons in the previous layer, and feeds its output to each neuron in the subsequent layer. To test the performance network A hyperparameter tuning was performed by varying the number of neurons in each of the four layers (). The number of neurons that was tested is . Additional hyperparameters, like the learning rate, were not optimized and the mentioned values were kept constant.
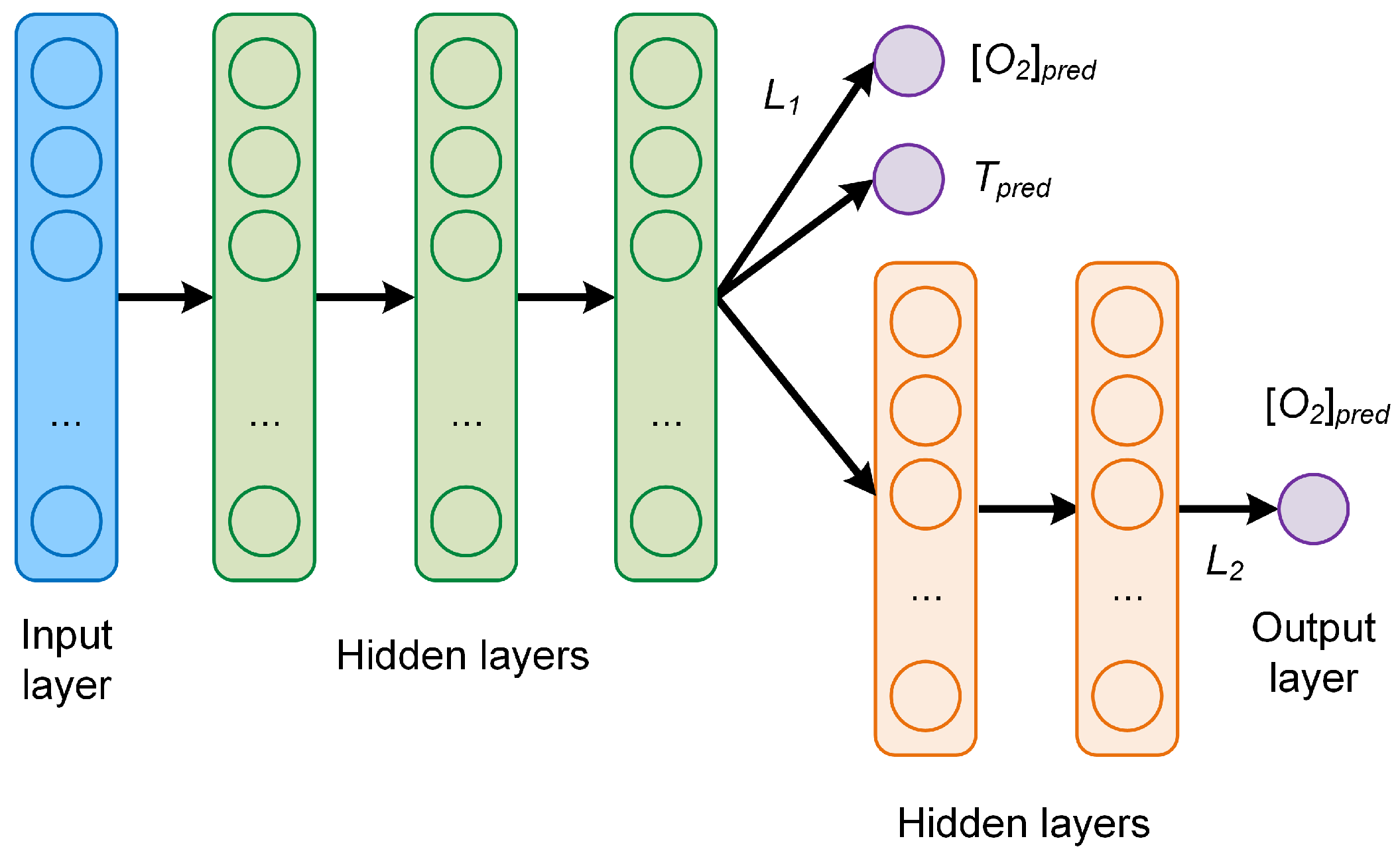
3.2. Network B
The first MTL network studied is depicted in
Figure 3. It consists of three common hidden layers with 50 neurons each, followed by two branches, one with two additional task-specific hidden layers used to predict
, and one branch without hidden layers used to predict both
and
T at the same time. The number of neurons of each task-specific hidden layer is 5. The idea behind this network is to have a system that learns to predict
well, thanks to the further task-specific layers. The predicted
T is not expected to be exceptionally good since the common hidden layers must learn to predict
and
at the same time. This architecture can be of applied when one of the outputs
, here
, needs to be predicted with higher accuracy than the other ones. For this network, the global cost function weights used were
and
.
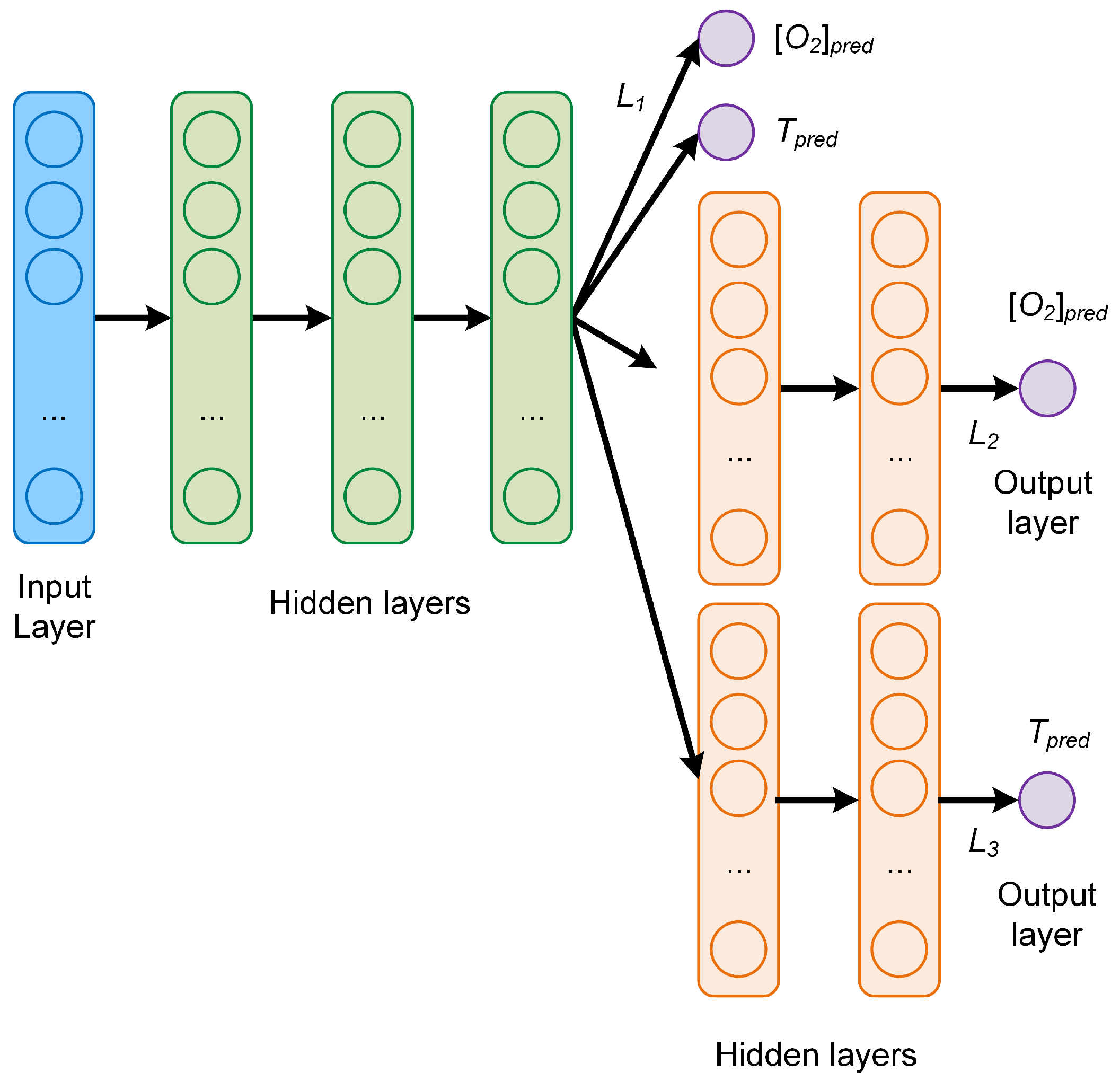
3.3. Network C
The last MTL network, depicted in
Figure 4, consists again of three common hidden layers with 50 neurons each, followed by three branches, two with each two additional task-specific layers to predict respectively
and
T, and then one without additional layers to predict
and
T at the same time. The number of neurons of each task-specific hidden layer is 5, as in the network B. The global cost function weights used for the plots were
,
and
. Those values were chosen because they result in the lowest
MAEs (see discussion in
Section 5).
This network is of interest because of the additional task-specific layers, which are expected to improve the ability of predicting the temperature compared to the network B.
3.4. Metrics
The metric used to compare results from different network models is the absolute error () defined as the absolute value of the difference between the predicted and the expected value for a given observation. For the oxygen concentration of the jth observation the is
The further quantity used to analyze the performance of the network is the mean absolute error (
), defined as the average of the absolute value of the difference between the predicted and the expected oxygen concentration or temperature. For example, for the oxygen prediction using the training dataset
,
is defined as
where
is the size (or cardinality) of the training dataset. For example, in this work
= 20,000. The
and
are similarly defined.
4. Luminescence Quenching for Oxygen and Temperature Sensing
To demonstrate its advantages, the MTL approach was applied to the simultaneous determination of the oxygen concentration and temperature of a medium. There are different optical methods used to determine oxygen concentration since this is of great relevance for numerous research and application fields, ranging from biomedical imaging, packaging, environmental monitoring, process control, and chemical industry, to mention only a few [
26]. Among the optical methods, a well-known approach is based on luminescence quenching [
27,
28,
29].
The measuring principle is based on the quenching of the luminescence of a specific molecule (luminophore) by oxygen molecules. Because of the collisions of the luminophore with oxygen, both the luminescence intensity and decay time are reduced. Sensors based on this principle rely on approximate empirical models to parametrize the dependence of the sensing quantity (e.g., luminescence intensity or intensity decay time) on influencing factors. The most relevant parameter, which can be a major source of error in sensors based on luminescence sensing, is the temperature of the luminophore, since both the luminescence and the quenching phenomena are strongly dependent on temperature [
26].
The conventional approach consists in relating the change of the luminescence decay time from the oxygen concentration through a multi-parametric model, called Stern–Volmer equation [
28]. The value of the device-specific constants is then determined through calibration. The decay time can be easily measured by modulating the intensity of the excitation. The emitted luminescence is also modulated but shows a phase shift
which depends on the decay time. Without going into the details of the analytical model, the measured quantity, the phase shift
, is most frequently related to the oxygen concentration
and temperature
T through the approximate equation [
30]
where
and
, respectively, are the phase shifts in the absence and presence of oxygen,
f and
indicate the fraction of the total emission of two components under unquenched conditions,
and
are associated (Stern–Volmer) constants for each component. Since the phenomena of luminescence and luminescence quenching are strongly influenced by the temperature, the parameters
,
,
, and
f need to be modeled through different temperature dependencies [
30]. The value of the parametrisation quantities is determined through non-linear regression.
is the angular frequency of the modulation of the excitation light. Finally, Equation (
7) must be inverted to obtain
as a function of
, T, and
. To be able to have more information as input to our network, we will not use a single
frequency value, but 16. Let’s define
The goal of the network is to predict the oxygen concentration and temperature from an array of values of evaluated at a discrete set of sixteen , with , that have been used for the measurements. The jth measurement can be written as with and . Each measurement j corresponds to a specific tuple of the oxygen concentration and temperature .
Summarizing, the conventional approach relies on the measurement of the temperature, which is then used to correct the parameters of the analytical model used to calculate the oxygen concentration
from the measured quantity, the phase shift
of Equation (
7). The inadequate determination of the luminophore temperature is one of the major sources of error in an optical oxygen sensor.
The neural network proposed in this work defies the difficulties described above by simultaneously predicting both the oxygen concentration and the temperature using 16 values of evaluated at a discrete set of sixteen values of .
Data Generation
To have a large enough dataset to train and test the neural networks, synthetic data were used. The model described by Equation (
7) was chosen to create the data, being as simple as possible but still capable to describe experimental observations. The values of the parameters for the synthetic data were determined from measurement performed under varying oxygen concentration and temperature conditions. For details on the samples and setup used for the determination of all the parameters the reader is referred to [
30].
The synthetic data consist of a set S of m = 25,000 observations using oxygen concentration values uniformly distributed between 0% air and 100% air and five temperatures and 45 C. Please note that in the following, the concentration of oxygen is be given in% of the oxygen concentration of dry air and indicated with% air. This means that 100% air corresponds to 20% vol . The m data were split randomly in a training dataset containing 80% of the data ( = 20,000), used to train the network, and a development dataset containing 20% of the data ( = 5000), used to test the generalization efficiency of the network when applied to unseen data.
Typically, when training neural network models, it is important to check if we are in a so-called overfitting regime. The essence of overfitting is to have unknowingly extracted some of the residual variation (i.e., the noise or errors) as if that variation represented an underlying model structure [
31]. In the case discussed in this work, with increasing network complexity, the network will never go into such a regime since the development dataset is a perfect representation of the training dataset. This leads to almost identical metric values for the
for both
and
, regardless of the network architecture effective complexity. This is what we observed while checking the metrics on the two different dataset
and
. Overfitting becomes relevant when dealing with real measurements and not synthetic data.
5. Results and Discussion
As described in
Section 4, the applied problem investigated in this work is a complex one since the two quantities to be extracted from the data (
and
T) depend from the input in different ways. It is, therefore, not obvious that is possible to build a model which is able to predict both
and
T at the same time with good accuracy.
The fist network investigated is the simple FFNN A described in
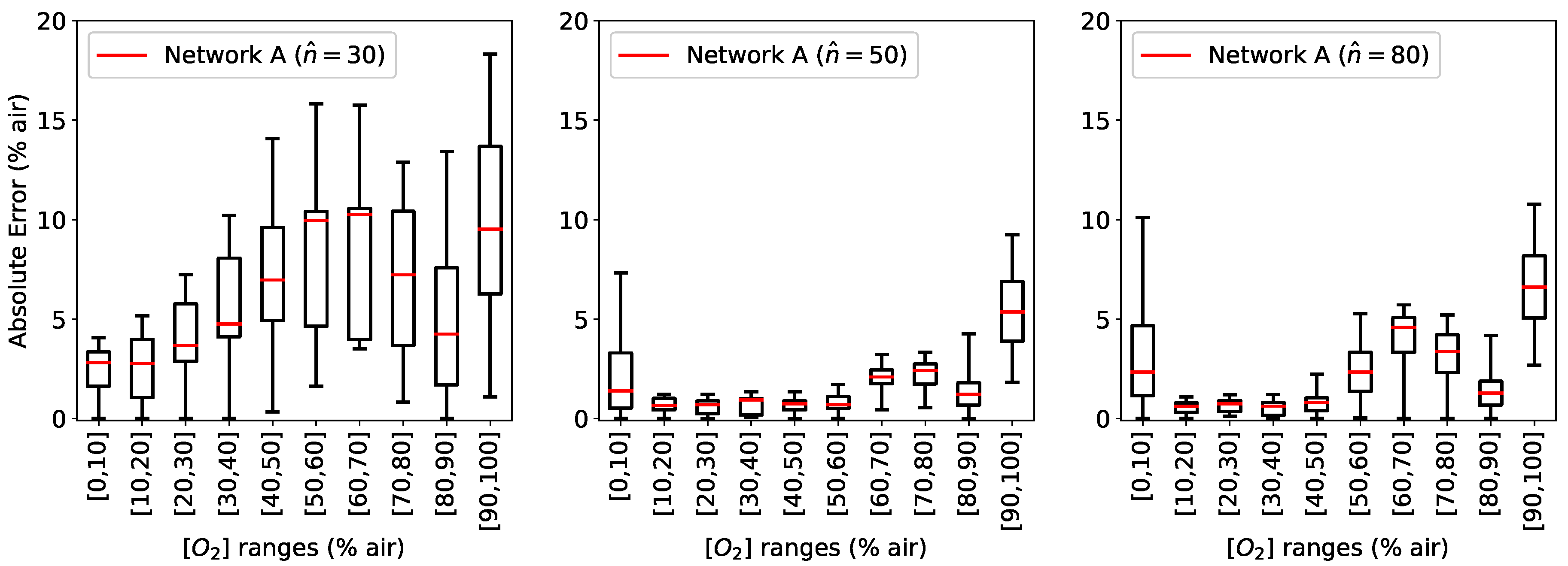
Section 3.1. For this network, the number of neurons was progressively increased (
) to study how
and
are affected by an increasingly complex network and to determine if it is possible to obtain a good prediction. The calculated
for different
concentrations were grouped in bins of 10% air for a clearer illustration and are shown in
Figure 5 as a box plot, where the median is visible as a red line. In all the boxplots in this paper the central box is the interquartile range and contains the middle 50% of the results, while the whiskers indicates the minimum and maximum of all the data [
32].
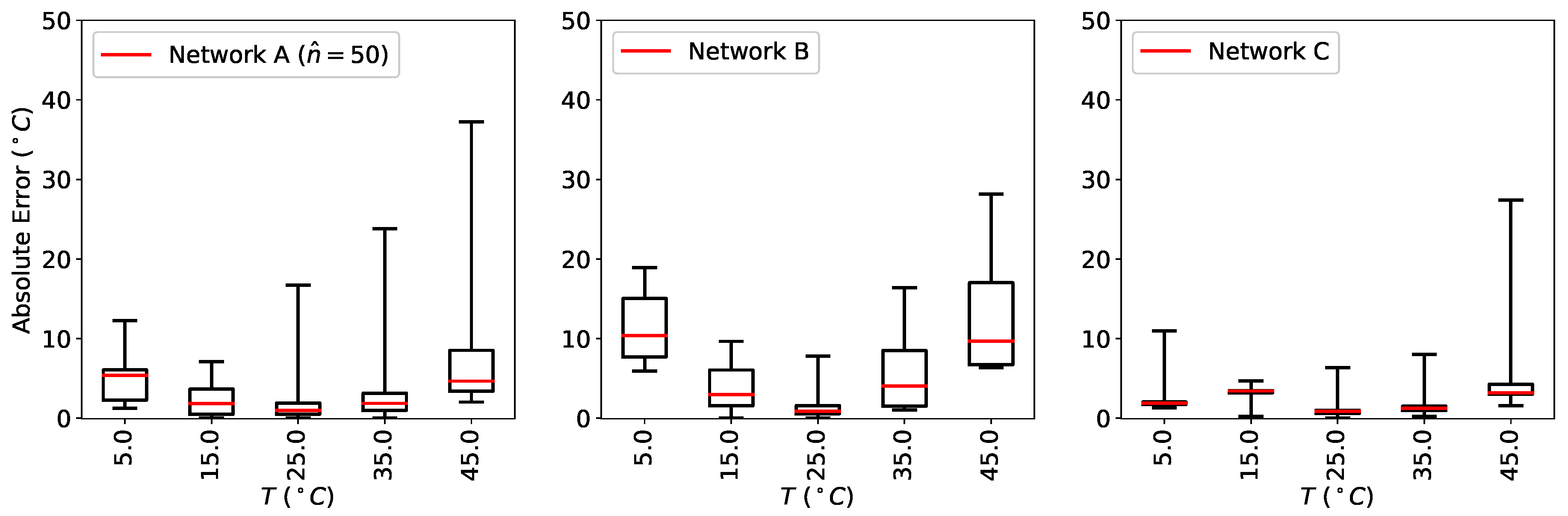
As can be seen in
Figure 5, the results are quite poor if
(results for
are comparable to those with
and are not shown here).
can assume values as big as 18% air, with a broad distribution. Increasing the number of neurons in the hidden layers to
improves the prediction, reducing both the median and the distribution. A further increase to
, however, does not result in better a prediction, showing the limits of this architecture to capture the details of the physical system.
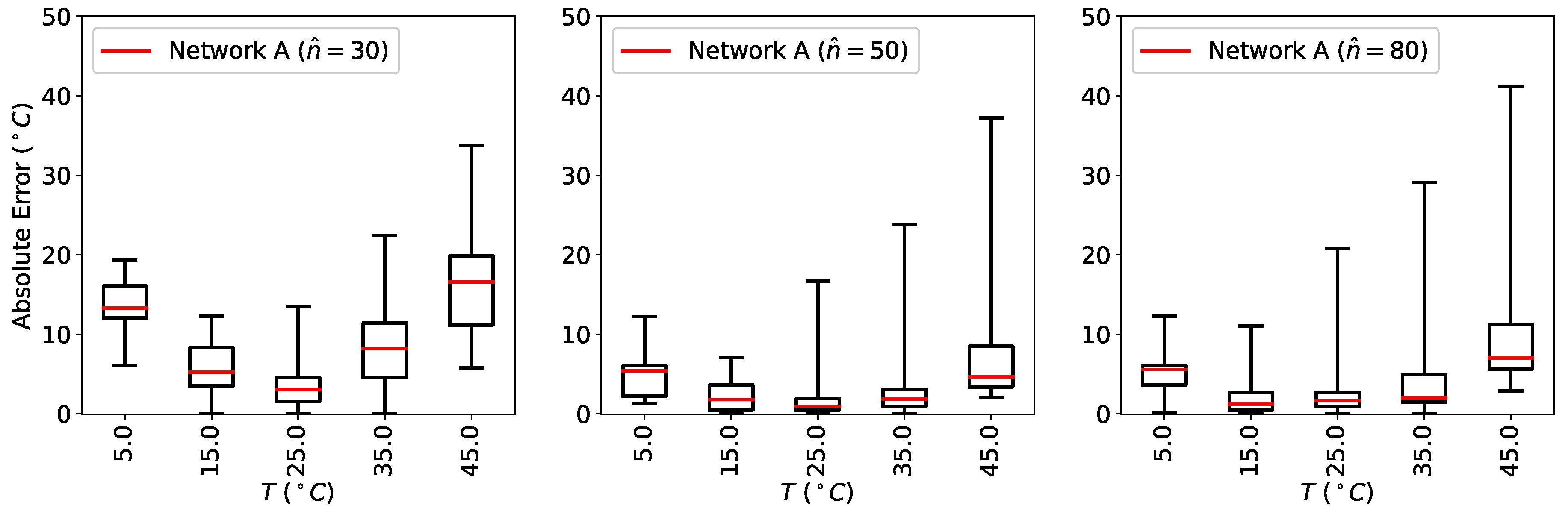
The results for the prediction of the temperature for the same three networks are shown in
Figure 6. Also
improves initially by increasing the number of neurons to
, but does not get any better when the number of neurons is further increased to
. The boxplots of
Figure 5 and
Figure 6 show that
and
can assume quite high values, therefore demonstrating how the model is not really able to make a prediction with an accuracy that may be used in any commercial application.
The performance of the three FFNN of type A can be summarized calculating the
as defined in Equation (
6). The results are listed in
Table 1. Consistently with what previously observed for the absolute error, the best network performance is obtained with
, achieving a mean absolute error of
air and
C.
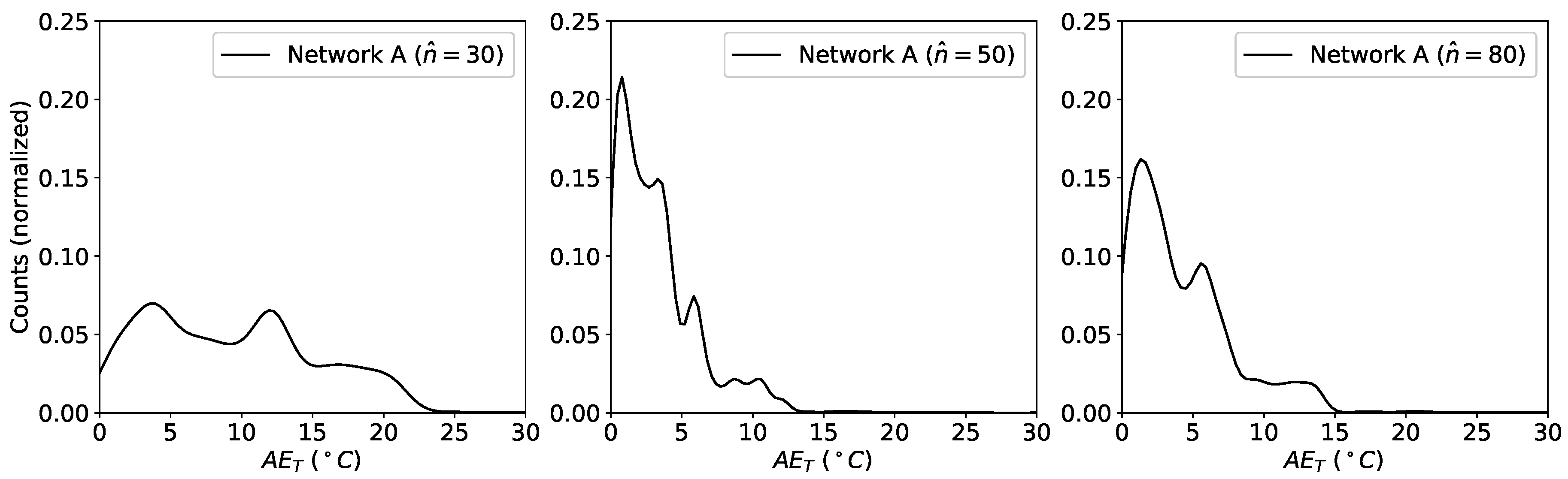
For a practical application, the probability density distributions of the
s for both parameters represent a much fundamental quantity since it carries information on the probability of the network to predict the expected value. For this reason, the kernel density estimate (KDE) of the distributions of the
s was used for analysis. KDE is a non-parametric algorithm to estimate the probability density function of a random variable by inferring the population distribution based on a finite data sample [
33]. For the plots we have used a Gaussian Kernel and a Scott bandwidth estimation using the seaborn Python package [
34]. The results for
and
for the three variations of FFNN A are shown in
Figure 7 and
Figure 8, respectively.
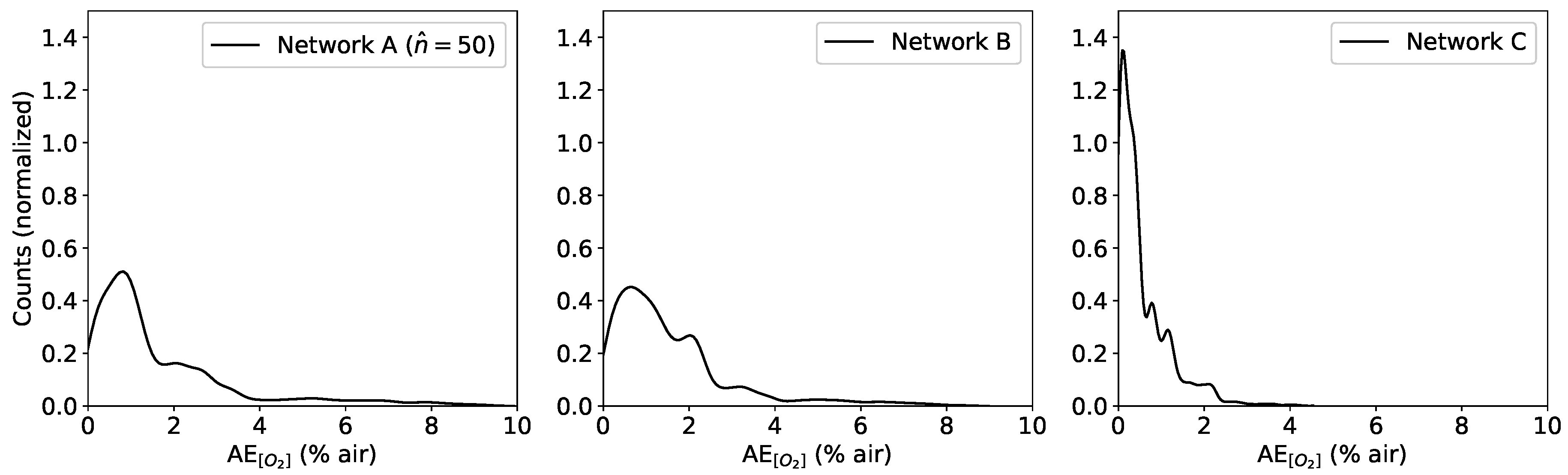
From
Figure 7 and
Figure 8 can clearly be seen that increasing the number of neurons helps at the beginning. A further increase in
does not produce an improvement in prediction quality, on the contrary it gets worse. These results indicate that this simple FFNN can extract at the same time the two quantities with an accuracy which is at best poor and at worst unusable.
Networks B and C try to address this problem by adding, as described in previous sections, respectively one and two branches after the last hidden layer in network A. The results of the prediction from the networks B and C are then compared to those from network A with
.
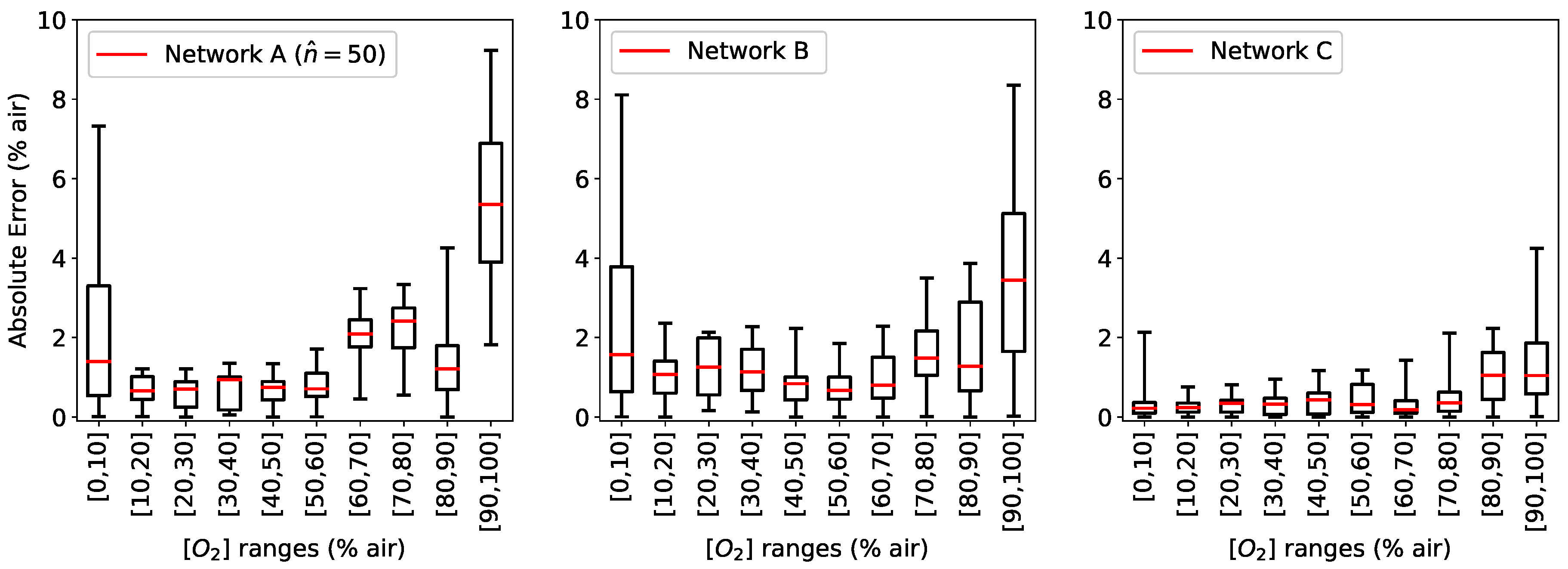
Figure 9 shows the calculated
for the three networks for the same
intervals as before as a box plot, where the median is visible as a red line.
As it can be seen from
Figure 9, the error in the prediction of network B is similar to that of network A. However,
is significantly improved when using network C. The additional branch in network C compared to network B clearly make the predictions much more accurate and, more importantly, much less spread around the median.
The distribution of the
is better illustrated by plotting the KDE (
Figure 10). The results indicate that the distribution assumes much smaller values and is peaked around zero for network C, in contrast with network A and B that have a quite wide tail that propagates toward higher values, reaching values as high as 10% air for network A and 8% air for network B.
Finally, the results of the same analysis for the prediction of the temperature are shown in
Figure 11. Here the calculated
for the same three networks is shown as a box plot, where the median is visible as a red line.
As it can be seen from
Figure 11,
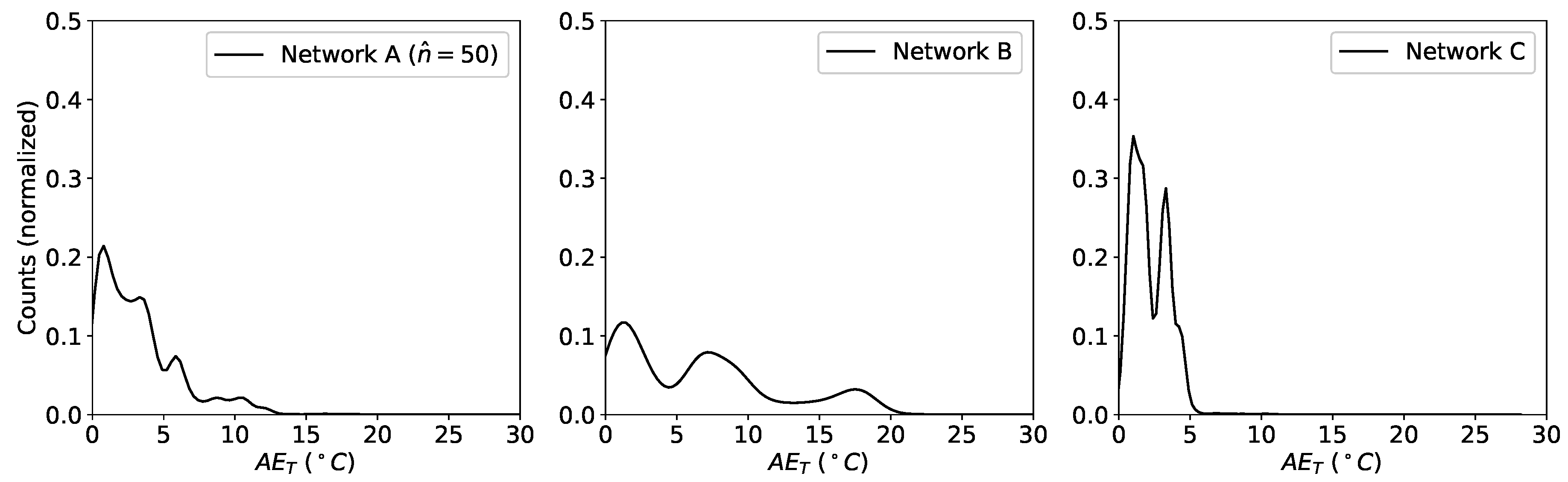
is much more concentrated around the median when using network C. These results indicate that the prediction of the temperature is substantially improved when using this network.
The distribution of the
using the KDE is shown in
Figure 12. Thanks to the additional task-specific hidden layer of the network C compared to network B, the KDE is higher and peaked around zero, with practically no contributions above 5
C.
Finally, the performance of the three neural networks are be summarized by calculating the
as defined in Equation (
6) for the oxygen concentration and the temperature prediction. The results are listed in
Table 2. The network C outperforms all the other networks analyzed in predicting both
and
T, achieving a mean absolute error of only 0.5% air for the oxygen concentration and of 2.2
C for the temperature.
The results of
Table 2 show that a simple FFNN as network A is not suitable to extract the two quantities of interest at the same time with good accuracy, since it is not flexible enough. The reason is that the two predicted quantities will depend on the same set of features generated by the hidden layers of network A. When network A tries to learn better weights to predict, for example, the temperature, these will, however, influence also the
prediction and vice-versa. So the common set of weights that are learned can not be optimized for each quantity separately at the same time. The MTL network B tries to address this problem with a separate branch of task-specific layers for
. The tests show however that this architecture is only marginally better for the prediction of
and even worse for the prediction of
T. This is probably due an insufficient flexibility of the network and shows that even if only one parameter were of interest, e.g.,
one single additional branch is not sufficient. A significant improvement is achieved with the MTL network C: the two task-specific branches give the network the flexibility of learning a set of weights (the ones in the branches) specific to each quantity, therefore achieving exceptionally good predictions on both
and
T. Note that in this work the hyper-parameter tuning [
15] for each network was not performed since the goal is not to achieve the lowest possible
s but rather to demonstrate the advantages and potential of MTL compared to classical FFNN approaches. For the implementation in a measuring instrument, therefore, a further phase of parameter tuning specifically dependent on the application would be needed.
An interesting question is what is the mutual influence of the branches in network C when the loss weights
are varied. To answer this question, a study was performed with various values of the global cost function weights. The results are shown in
Table 3.
By increasing progressively the weight for the temperature branch, , the MAE is not reduced further and appears rather insensitive to . However, increases slightly, since the higher values of shift the relative importance of the tasks the network is trying to learn. Increasing the weight for the oxygen branch negatively affects the oxygen prediction since increases slightly. The reason why this is happening is that the is becoming much bigger than . This shows that for the prediction of the oxygen concentration both the branches predicting T and at the same time and the one predicting are important: neglecting one will make the other works less efficiently. The temperature, on the other had, is predicted almost with the same kind of accuracy independently of the weights , indicating that the temperature branch is not dependent from the branch.