Featured Application
The new variable-diameter wheel is not only applicable in planet rovers for rough-terrain planetary explorations but also in earth-based mobile robots for agriculture and forestry, military applications, rescue operations, and disaster areas.
Abstract
Variable-diameter wheels balance the high mobility and limited volume of a planetary rover. Moreover, these wheels allow a rover to adjust its body attitude to adapt to rough terrains. These functions are achieved through the expansion–retraction motion of the variable-diameter mechanisms in the wheels. Thus, the traditional wheel design focuses on these mechanisms. To further facilitate its application, we propose a new concept variable-diameter wheel that considers the mechanism characteristics and wheel performances. This new wheel configuration is presented along with the corresponding transmission system, design, and analysis methods. Kinematic equations of the mechanism were established and then applied to synthesize the wheel dimensions. The load–deflection relationship of the wheels was analytically derived by developing a modified pseudo-rigid-body model (PRBM). Finite element analysis (FEA) simulations were performed to validate the design and analysis. In conclusion, the proposed novel wheel is extremely beneficial for rough-terrain locomotion systems. Furthermore, the design and analysis approaches used in this study are applicable for other expandable wheels.
1. Introduction
Wheeled rovers are one of the best candidates for planetary surface exploration due to their power-efficient performance [1]. Wheels are essential in improving the mobility of wheeled rovers, including trafficability and obstacle-surmounting capability on unstructured environments [2]. On soft terrain, conventional circular wheels slip and cause poor rover mobility [3]. Therefore, to optimize mobility on unknown and soft terrain, growing research interest has focused on various unconventional wheels [4,5,6]. However, despite the satisfactory trafficability of rovers with unconventional wheels, their obstacle-surmounting capabilities remain insufficient.
By increasing its diameter, a wheel can enhance the tractive performance and obstacle-surmounting capability of a vehicle [7,8]. Therefore, expandable wheels were developed. Expandable mechanisms allow the adjustment of wheel diameter, and different types have been proposed in recent years. The diagrams of the principles behind these mechanisms are provided in [9]. These mechanisms can be categorized into rigid-body mechanisms [10,11,12,13] and compliant mechanisms [14,15,16]. Compliant mechanisms perform movement through their part deflections and usually have reduced weight [17,18]. Moreover, these traditional mechanisms can be classified as expandable in the axial and radial planes of the wheels. Unlike the former, the ratio of the wheel width to diameter is unconstrained for the latter. However, several of these mechanisms are only capable of expanding once. By contrast, repeatedly expandable mechanisms with real-time self-locking can continuously adjust the wheel diameter according to different terrain conditions.
A repeatedly deployable compliant mechanism in the radial plane is desired for an expandable wheel. The mechanism in a variable-diameter wheel, which is an expandable wheel, is an example [9,19,20].
Previous studies had only considered mechanisms in the design of expandable wheels. Despite the importance of deployable mechanism in such designs, wheel performance cannot be ignored. At the least, the mechanism should not affect the normal operation of the wheel (e.g., maneuverability). Wheel performance is crucial for reliability and availability in real situations. Thus, the design of variable-diameter wheels should consider not only the mechanism but also meet the requirements of wheel performance.
In the existing variable-diameter wheel [9], the wheel feet may deviate from the initial orientation position because of the relative rotation between two hubs in the mechanism movement, resulting in a torque action on each foot. Moreover, because the supporting structure of each wheel foot consists of two spoke links that are not on the same plane, the support easily causes wheel camber or inclination. These conditions may influence the maneuverability of a wheeled rover. Every wheel leg has four flexure pivots on the radial plane of the wheels. Hence, with the compliance of the torsion springs, a single wheel leg approaches a four-bar mechanism. As a result, the structure of the wheel spoke may not transmit sufficient torque from the wheel’s hub to its feet.
To address these issues of the existing variable-diameter wheel, we designed a novel variable-diameter wheel in this study. Wheel performance was considered and improved in the new design. First, to increase stability of the supporting structure and avoid additional moment, the novel wheel configuration and its transmission system were considered. Kinematic equations of the mechanism were then established and applied to synthesize the wheel dimensions. The load–deflection relationship of the mechanism was analytically obtained by building a modified pseudo-rigid-body model (PRBM). Finally, finite element analysis (FEA) simulations were performed to validate the design and analysis.
2. Wheel Configuration and Transmission System
2.1. Wheel Configuration
As mentioned in Section 1, various expandable mechanisms have been invented to facilitate changes in the diameter of expandable wheels. In the present study, the traditional expandable mechanisms are classified into diverse types according to their different characteristics before summarizing their advantages. These characteristics are integrated in the proposed mechanism for the new variable-diameter wheel.
In compliant mechanisms, flexural pivots or hinges perform the function of pin joints for rigid-body kinematics [21,22,23]. Helical torsion springs serve as flexural hinges and can achieve large angular deformations, as shown in Figure 1. In addition, the springs are used with pins to maintain alignment and provide buckling resistance when necessary. Therefore, springs that can simplify the assembly are applied to the new mechanism in the wheel.

Figure 1.
Two limit working positions of new variable-diameter wheel prototype.
The proposed wheel with six circumferentially arranged wheel legs is composed of three hubs that house a planetary gear train system, helical torsion springs (the spring arms serve as the spokes), and 12 wheel feet. A single wheel leg consists of two wheel feet and geometrically symmetric helical torsion springs (Figure 2). These springs (including four spoke links) and the two wheel feet in a single wheel leg are connected by two concentric pins. One of the two wheel feet is fixed to two middle spoke bars, whereas the other foot is fixed to the two spoke bars on both sides. This setting allows the two wheel feet to rotate around each other. The ends of the middle two torsion springs in the wheel leg are positioned at the middle wheel hub, whereas the ends of the two torsion springs on both sides are positioned at the two wheel hubs on both sides. Therefore, when the middle hub rotates around the side hubs with the same speed, the helical torsion springs experience angular deflections, and the mechanism gains mobility (i.e., changes in wheel diameter). The relative rotation between the three hubs can prevent the movement interferences between the spoke bars and remove the additional moments on the wheel feet. Moreover, the supporting structure of the two wheel feet in each wheel leg, which is supported by four spoke links, has greater stability than that of the existing variable-diameter wheel.

Figure 2.
Single wheel leg configuration.
Each wheel leg can be treated as a triangular structure with three flexure pivots in the radial plane of the wheel. Hence, the structural stiffness of the wheel leg increases compared with that of the conventional variable-diameter wheel. In addition, the structure with the three flexure pivots reduces the linkages in the movement plane, which simplifies the design and analysis of the wheel.
Note that each wheel foot comprises three spaced metal cleats with segmented circular-arc outer edges. For its folded limit position, the wheel is circular with an outer contour that comprises the segmented circular-arc cleats. This condition provides good ride performance on flat and rigid terrains. Moreover, the spacing between these cleats creates a longer shearing surface that extends deep into soft terrains and thus develops more traction than the continuous wheel foot of the existing variable-diameter wheel [4]. When the wheel exits the folded limit position, the wheel feet separate from each other, except for the two wheel feet in the same wheel leg. As the wheel diameter increases, the angle between the two fixed wheel feet on the spoke links in a single wheel leg decreases and vice versa.
2.2. Transmission System
The planetary gear train of a variable-diameter wheel can transmit two power sources that are used to enable the wheel’s rolling and changes in diameter. The three ring gears in the transmission system and the three wheel hubs are assembled under the corresponding interference fits. The three wheel hubs (left, middle, and right) transfer the rotations from the transmission system to the spring spokes. The electric motor M1 adjusts the wheel diameter, whereas the electric motor M2 provides the energy for the wheel rotation. Figure 3 shows that M2 drives the rotation of the three ring gears with the same speed when M1 is locked (M1’s worm reducer has a self-locking ability). Thus, the wheel with an invariant diameter rotates on the terrain. If M2 rotates, then the wheel diameter adjusts.
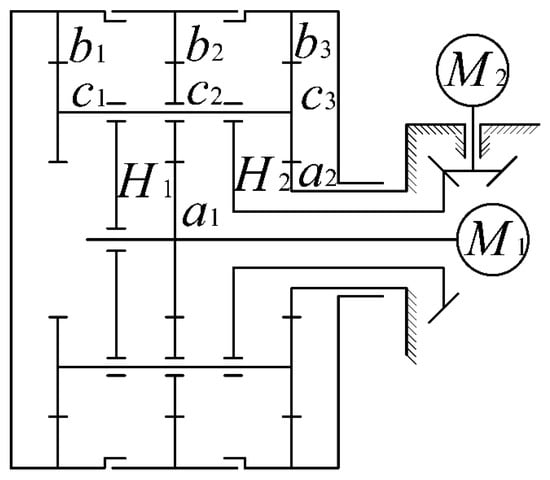
Figure 3.
Schematic of planetary gear train.
Therefore, to match the two power sources, the transmission system has two routes.
First, if M1 does not rotate (i.e., the left sun gear a1 is locked), then the three ring gears have the same rotating speed. The route can be elaborated as follows.
Electric motor (M2) → right (H2) and left planet carriers (H1) → left (c1), middle (c2), and right planet gears (c3) → left (b1), middle (b2), and right ring gears (b3).
Second, if M1 rotates, the three ring gears rotate at different speeds. Note that the two ring gears on both sides have the same speed.
- (1)
- M1 → left sun gear (a1) → middle planet gear (c2) → middle ring gear (b2).
- (2)
- Electric motor (M2) → right planet carrier (H2) and left planet carrier (H1) → left (c1), middle (c2), and right planet gears (c3) → left (b1), middle (b2), and right ring gears (b3).
In summary, on the basis of the power-transmitting routes of the transmission system, the three hubs rotate at different speeds. Consequently, the relative rotations between the hubs cause deflections of the helical torsion springs, from where the wheel feet gain radial mobility.
3. Design Methodology
The mechanism is the key component of variable-diameter wheels. Once the geometric parameters of the mechanism are obtained, the wheel dimensions can be determined. In this study, a kinematic synthesis was performed for the mechanism. The kinematic behavior for the mechanism must be analyzed before using the synthesis method [24].
3.1. Kinematic Analysis
For the kinematic synthesis of a compliant mechanism, the rigid-body replacement method was adopted [25], wherein the helical torsion springs were regarded as the pivoted links (Figure 1 and Figure 4). The left and right hubs were treated as the left crank, whereas the middle hub was considered as the right crank. The revolute joints that were placed at the center of the pins connected an imaginary spoke link to an imaginary crank or other spoke link (dashed lines in Figure 4) in the same wheel leg. Hence, the lengths of the imaginary spoke links were represented by the in-between distances of the revolute joints, and the length of an imaginary crank was the radius of the corresponding wheel hub. Moreover, because the three hubs had the same diameter, the two imaginary cranks had the same length.
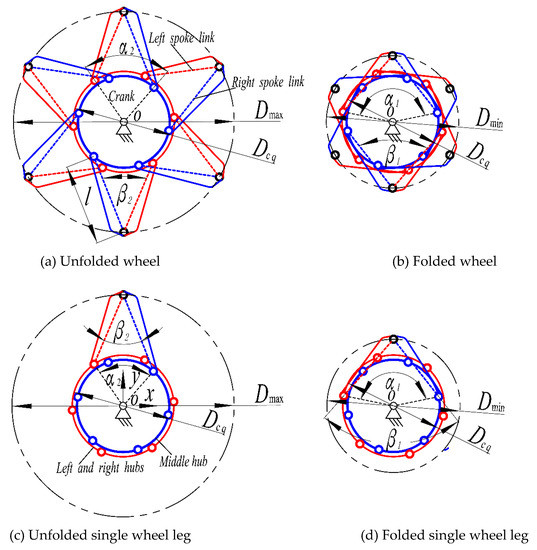
Figure 4.
Deformation of spring spokes in two limit positions.
Figure 4 presents the deformations of the spring spokes in the two limit positions of the mechanism, and Figure 4c displays the coordinate system of the mechanism. In Figure 4, α2 and α1 are the angles between two cranks that correspond to the largest and smallest wheel diameters, respectively; l is the length of the left (or right) spoke link; β2 and β1 are the angles between two spoke links that correspond to the largest and smallest wheel diameters, respectively; and Dcq is the diameter of each hub. As noted in Section 2, when the middle wheel hub rotates around the two hubs on both sides, the initial angle α2 increases to α1 while β2 increases to β1. As a result, the wheel diameter decreases and vice versa.
Using the difference between the above two equations, the length of a spoke link is obtained as
3.2. Optimization Design
According to the kinematic analysis, an optimization design approach could be used to gain the wheel dimensions.
3.2.1. Design Variables
According to Equation (3), when α1, α2, β1, β2, and Dcq are known, l can be obtained. Moreover, based on Equations (4) and (5), the maximum and minimum wheel radii can be calculated. Therefore, five independent design variables are available:
3.2.2. Objective Function
The two limit wheel diameters are the primary focus in the wheel design. For simplicity, the objective function is defined as the least-square deviation between the calculated and desired wheel radii for the two limit positions, such as
where Dmin and Dmax are the two desired wheel diameters.
3.2.3. Constraint Function
With respect to the practical assembly requirements and the possible movement interferences, the link lengths and relative positions in the mechanism are constrained.
To prevent the red (or blue) spoke bars on the same hub from contact with each other during mechanism movement, α1 should be smaller than 180° (Figure 4b) [9], and thus
For a variable-diameter wheel with six wheel legs, if α2 = 60°, only the wheel leg contacting the terrain will suffer the lateral forces because no lateral contact occurs among the spoke links for the largest wheel diameter position. If α2 > 60°, the wheel configuration improves the lateral stiffness (Figure 4a) [9], where
Note that an inscribed angle subtended by a diameter in a circle is always 90°. In an extreme case, when the mechanism contracts to the circular wheel, β1 = 90° (i.e., α1 = 180°) if the wheel feet lies on the hub circles. Figure 4d suggests that if β1 < 90°, the undesired interferences between the spoke links and the hub can be avoided [9], such as
From Figure 4d,
Every wheel leg requires sufficient structural stiffness, and thus β2 should be greater than 30° but less than 60° [9]:
3.2.4. Optimization Results
Optimization was performed in MATLAB using Equations (1)–(12) to solve the problem using the minimization function fmincon().
The optimization steps were as follows:
Step 1: The two limit wheel diameters (420 and 260 mm) and the initial values (160, 75, 60, 40, 150) of the design variables were given.
Step 2: According to the initial values in Step 1 or the changed design parameters, the constraint equations (Equations (7)–(12)) were checked. If one of these equations was unsatisfied, then the values were adjusted based on the step size (MATLAB default). This step continued until the optimization objective was achieved.
Step 3: Equations (4)–(6) and the parameters obtained in Step 2 were used to solve the objective function value. When the value was out of the specific tolerances (MATLAB default), the design variables were adjusted. Then, Steps 2 and 3 continued until the tolerance was within the allowable range. Table 1 summarizes the optimization results.

Table 1.
Optimization results.
4. Load–Deflection Relationship
4.1. Pseudo-Rigid-Body Model
The PRBM proposed by Howell [26] was used to analyze the compliant mechanism in the proposed wheel. In the model, the helical torsion springs and hubs are replaced by pivoted links with torsional springs [27]. When the wheel rolls, only one of its feet touches the ground. Therefore, in this study, a PRBM that only includes the wheel leg in contact with the ground and the two cranks (Figure 5) was established. This model was then utilized to analyze the load–deflection relationship of the wheel [28].
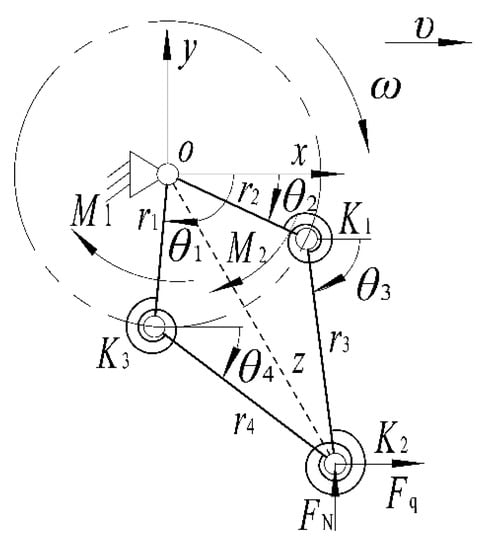
Figure 5.
Simplified pseudo-rigid-body model (PRBM) for a wheel.
First, the operating speeds of the wheel were assumed to be slow [29], and the model was analyzed on the basis of static equilibrium. For simplicity, the wheel was assumed to roll on rigid terrain during the mechanism movement. The action area of the distributed forces acting on the wheel foot in touch with the rigid terrain is small. Therefore, the concentrated forces replaced the distributed forces. To facilitate the mechanism analysis, the concentrated forces from the terrain were applied to the hinge point of the two wheel feet in the wheel leg.
As discussed in Section 2.2, the wheel is a system with two degrees of freedom (DOF). Applying the principle of virtual work, Figure 5 shows the corresponding coordinate system. θ1 is the angle between the left crank and the x-direction, and θ2 is the angle between the right crank and the x-direction, both of which are selected as the generalized coordinates. In addition, θ3 is the angle between the right spoke link and the x-axis, θ4 is the angle between the left spoke link and the x-axis, and Z is the distance between the hinge point of the two wheel feet and the fixed hinge center. M1 is applied to the left crank, whereas M2 is applied to the right. The forces in the x- and y-directions, Fq and FN, respectively, are applied to the hinge point of the two wheel feet. From Figure 5, r1 (or r2) is the hub radius, and r3 (or r4) is equal to l.
The PRBM describes the changes in wheel diameter through the rolling of the wheel. During this process, only one wheel leg is presumed to touch the ground. M1 and M2 are the inputs. When M2 decelerates (accelerates) the middle hub, the angle between the two spoke links increases (decreases). Consequently, the wheel diameter decreases (increases). When the two cranks have the same rotation, the angle stays constant, and the wheel diameter does not change.
4.2. Virtual Work of Forces
To gain the relationships between δθ1, δθ2, and δθ3, according to the reference [30], a loop closure equation for the PRBM is established as
where θ3 and θ4 are the respective functions of θ1 and θ2. Differentiating Equation (13) with respect to the two generalized coordinates yields
where
Differentiating Equation (17) yields
Substituting Equations (15) through (18) into Equation (14) yields
Thus, δθ3 can be expressed as
where
The position vector for the hinge point between the two wheel feet is obtained as
where
Differentiating Equation (23) yields
The force vector is then expressed as
Hence, the virtual work of the forces can be obtained as
4.3. Virtual Work of Moments
The angular displacement Θi of the ith crank is defined as
where θi0 is the initial angle.
Differentiating the two equations,
Therefore, the virtual work of the moments can be obtained as
4.4. Virtual Work of Springs
The intersection angle change among links or cranks is defined as
Differentiating Equations (33)–(35) yields
where ψ1 is the difference between the angle (π − θ2 + θ3) between links r2 and r3 in any position and the angle (π − θ20 + θ30) in the initial position, whereas ψ2 is the difference between the angle (2π+ θ1 + θ2 − 2θ3) between links r3 and r4 in any position and the initial angle (2π + θ10 + θ20 − 2θ30). For the initial position, the springs do not experience stress. Thus, when the wheel contracts, the following expressions are obtained:
where ki is the ith spring constant.
Moreover, a spring torque direction in the wheel expansion is opposite to that of the contraction. Thus, when the wheel unfolds, the above expressions become
where,
Combining Equations (36)–(43) with Equations (18)–(20), the virtual work of springs for a wheel with n wheel legs can be expressed as
Hence, the total virtual work for the wheel can be obtained as
In summary, the total virtual work of springs can be derived from Equations (27), (32), and (44).
4.5. Load–Deflection Behavior
For a wheel with two DOFs,
where Qi is the ith generalized force.
When Qi becomes zero, static equilibrium for the wheel is achieved [31]. Therefore, the load–deflection relationship can be expressed as
Equations (13)–(49) can be utilized to obtain θ1 of the left crank (left and right hubs) and θ2 of the right crank (middle hub) caused by M1 and M2. The two rotations result in variations of the wheel diameter, as suggested by Equations (24) and (45).
5. Modified PRBM and Validation
5.1. Modified PRBM
The suitability of a PRBM in modeling a compliant mechanism depends on the torsional spring constants. Thus, to better clarify the load–deflection behavior of the wheel, the torsional spring constants of the PRBM need to adjust. Generally, the spring constant of a helical coil torsion can be obtained from the following equation [32]:
where E is Young’s modulus, l represents the length of a spring arm, ni represents the number of active coils in the ith spring, d represents the steel-wire diameter, and D represents the spring pitch diameter.
This formula is similarly derived as the classic beam theory, which is also known as the Bernoulli–Euler beam theory. However, the equation is limited to a single torsion spring (i.e., without long spring arms) subjected to a pure bending moment.
For a single torsion spring with long arms, the spring constant must be adjusted to account for deflection when the arm length approaches the wire length. The end of the free spring arm connects a force F at a distance l from the coil axis to apply a moment (i.e., M = Fl). In this case, the working force causes additional bending to the arm. Thus, the long arm is treated as a cantilever subjected to a force. For small deflections, the transverse deflection (y) of the free end is expressed as
When viewed from the built-in end, the additional angle θa of the end deflection in the cantilever can be expressed as
The angular deflection of the wire in the spring body is defined as
The total angle can be obtained as
Finally, the torsion spring constant can be calculated as
However, for wheels, the torsion springs with the long spring arms in a single wheel leg possess a compliant structure. The main transmission is caused by the bending moments in the long spring arms, which should thus be treated as a cantilever with a bending moment rather than with a force. Then, the θa of the end deflection in the cantilever becomes
5.2. Validation
To validate the effectiveness of the modified PRBM, an application example is presented, in which only the contraction process was analyzed. This example clarifies the contraction process using seven loading cases. Figure 6 shows the initial position (i.e., the first case) of a variable-diameter wheel. The right wheel leg is presumed to touch the terrain and the angle between its Z and x-axis near the terrain is 60°. Based on Section 3, the initial angle between the two cranks in the example is α2 (67°). Therefore, when the mechanism exits the initial position, θ10 = 93.5° and θ20 = 26.5°.
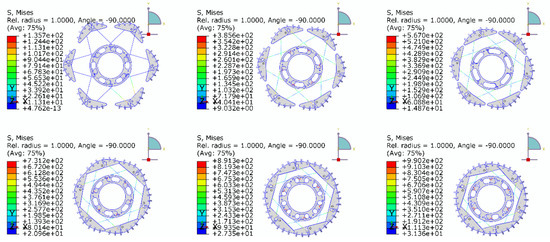
Figure 6.
Contraction process of wheel.
According to Equation (45), θ30 can be obtained as
The springs are made of steel (60Si2MnA). Poisson’s ratio is 0.3, and Young’s modulus is 206 GPa. Table 2 presents the geometric parameters of helical torsion springs [9]. Based on Equation (57) and the parameters in Table 2, the ith torsion spring constant ki can be obtained. The concentrated forces are hypothesized to be FN = 57.17 N and Fq = 40.02 N [9,33]. On the basis of these parameters, the deflections in the wheel caused by M1 and M2 can be calculated using Equations (13)–(49).

Table 2.
Parameters used in modified PRBM.
To validate the modified PRBM, the finite-element software ABAQUS was used. The angles (θ1 and θ2) were given, and the other five DOFs at the wheel center were fixed. Furthermore, FN and Fq acted on the hinge points of the two wheel feet in the wheel leg in contact with the ground. Linear Timoshenko beam elements were applied to the springs. The three hubs and the 12 wheel feet in the wheel were treated as the rigid bodies.
The contraction process of the wheel with six loading cases is described in Figure 6. For the first case, deflections existed only in the wheel leg in contact with the terrain. The wheel did not generate any mechanism movement. However, each wheel leg almost had the same deflections in the other loading cases, and the wheel was gradually contracting with the hub rotations.
After departing from the initial position, M1 increased the rotation (θ1) of the left crank in a clockwise direction, whereas M2 decreased the rotation (θ2) of the right crank in the opposite direction. As a result, the difference between θ1 and θ2 gradually increased in the latter five cases (Figure 6), while the angle between the two spoke links gradually increased. Consequently, the wheel diameter decreased. Finally, the wheel was folded into a circular wheel.
For the six load conditions (Table 3), the moments acting on the left and right cranks during the mechanism motion were calculated using Equations (13)–(49) and compared with the corresponding FEA results in Table 3. However, the modified PRBM was not suitable for the first case, which is a structural analysis and is not included in Table 3.

Table 3.
Comparison of results between modified PRBM and finite element analysis (FEA).
The results in Table 3 indicate that the absolute values of the moments increased when the wheel folded. The elastic potential energy of these springs always increases due to wheel contraction, which can be attributed to the work of M1 and M2. Hence, the input moments during the mechanism movement should increase. In the cases presented in Table 3, the different hub rotations caused the direction of M1 to be opposite to that of M2, which corresponded to the changes in wheel diameter. When the wheel with a constant diameter rotated, both moments acted on the same direction (first case in Figure 6). The stresses in the springs did not exceed the material yield strength (1372 MPa) in the wheel contraction. Starting from the first case, with the wheel rotation, the wheel feet contracted along the radial direction until the last case. This phenomenon shows that changes in wheel diameter and wheel rolling occur simultaneously. In all cases, the absolute value of M1 was higher than that of M2 because parts of the former needed to overcome ground resistance to carry out wheel rolling, whereas the rest was used to change the wheel diameter. The wheel diameter varied from an unfolded wheel to a folded circular wheel without any movement interferences and additional moments on the wheel feet.
Table 3 suggests that the FEA and PRBM results achieved good agreement. Both analyses had relative errors less than 1.2%. Therefore, the modified PRBM is reliable for analysis of the variable-diameter wheel. On the one hand, the clearance between the torsional spring and the pin prevents the actual rotation center of the spring from always overlapping with the original center [34]. On the other hand, the modified torsional spring constant is just an approximation for the spring deflections. As previously mentioned in Section 5.1, helical torsion springs are compliant structures. Thus, the torsion springs are subject not only to the bending moments but also to the axial and transverse forces transferred by the arms during mechanism movement.
6. Conclusions
In this study, the influence of mechanisms on wheel performance was considered for wheel design. The mechanism characteristics are achieved without weakening the wheel’s performance. This design guideline has significance for future design and development of deployable wheels. To improve the performance of the existing variable-diameter wheels, we have developed a novel variable-diameter wheel with an innovative compliant mechanism. The proposed wheel uses the same mechanism characteristics as the conventional variable-diameter mechanism but includes more advantages. The wheel’s spoke structure eliminates the additional moments acting on the wheel feet during mechanism motion and improves the support stability for the wheel feet. In addition, the wheel leg structure that has three flexure pivots reduces the number of links in the mechanism movement plane, thereby simplifying the kinematic equations for the design and the PRBM for analysis. This structure enables a more compact and reliable mechanism compared with conventional variable-diameter wheels. The presented planetary gear train helps the wheels to continuously adjust in diameter so that the rover can adapt to rough terrains. This feature can improve the rover’s obstacle-surmounting capability and stability. In conclusion, the proposed wheel enhances the wheel performance and practicability in real applications. Thus, the new variable-diameter wheel can be utilized not only in planet rovers for rough-terrain planetary explorations but also in earth-based mobile robots for agriculture and forestry, military applications, rescue operations, and disaster areas. Moreover, the novel wheel is applicable in locomotion systems, especially on unstructured and soft terrains.
Practical design and analysis approaches for the proposed wheel were also considered. The established kinematic equations were applied to the motion control of the wheel mechanism. The load–deflection relationship was derived from the modified PRBM. The results in Table 3 indicate that the proposed design and analysis tools are suitable for the proposed wheel. The modified PRBM can help operators control changes in the wheel diameter on rigid terrains. Furthermore, the design and analysis methods used in this study are applicable to other deployable wheels.
Author Contributions
G.X. and F.G. conducted this study and proofread the manuscript together; W.Z. conceived the idea, designed and analyzed the wheel, and wrote this manuscript; H.J. contributed to the FEA for the wheel and proofread the manuscript.
Funding
This research was funded in part by the National Natural Science Foundation of China under grant number 51675027 and in part by the National Key Technology R&D Program of China under grant number 2016YFD0700503-1
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alamdari, A.; Krovi, V.N. Design of articulated leg–wheel subsystem by kinetostatic optimization. Mech. Mach. Theory 2016, 100, 222–234. [Google Scholar] [CrossRef]
- Ghotbi, B.; González, F.; Kövecses, J.; Angeles, J. Mobility evaluation of wheeled robots on soft terrain: Effect of internal force distribution. Mech. Mach. Theory 2016, 100, 259–282. [Google Scholar] [CrossRef]
- Xie, X.; Gao, F.; Huang, C.; Zeng, W. Design and development of a new transformable wheel used in amphibious all-terrain vehicles (A-ATV). J. Terramech. 2017, 69, 45–61. [Google Scholar] [CrossRef]
- Asnani, V.; Delap, D.; Creager, C. The development of wheels for the lunar roving vehicle. J. Terramech. 2009, 46, 89–103. [Google Scholar] [CrossRef]
- Zakrajsek, J.; McKissock, D.; Woytach, J.; Zakrajsek, J.; Oswald, F.; McEntire, K.; Goodnight, T. Exploration Rover Concepts and Development Challenges. In Proceedings of the 1st Space Exploration Conference: Continuing the Voyage of Discovery, Orlando, FL, USA, 30 January–1 February 2005; pp. 1–23. [Google Scholar]
- Bekker, M.G. Introduction to Terrain-Vehicle Systems, 1st ed.; University of Michigan Press: Ann Arbor, MI, USA, 1969; pp. 1–20. ISBN 0472041444. [Google Scholar]
- Bekker, M.G. Off-The-Road Locomotion: Research and Development in Terramechanics, 1st ed.; University of Michigan Press: Ann Arbor, MI, USA, 1960; pp. 1–30. ISBN 0472041428. [Google Scholar]
- Siddiqi, A.; Weck, O.L. Reconfigurability in planetary surface vehicles. Acta Astronaut. 2009, 64, 589–601. [Google Scholar] [CrossRef]
- Zeng, W.; Gao, F.; Jiang, H.; Huang, C.; Liu, J.; Li, H. Design and analysis of a compliant variable-diameter mechanism used in variable-diameter wheels for lunar rover. Mech. Mach. Theory 2018, 125, 240–258. [Google Scholar] [CrossRef]
- Abad-Manterola, P.; Burdick, J.W.; Nesnas, I.A.; Chinchali, S.; Fuller, C.; Zhou, X. Axel Rover Paddle Wheel Design, Efficiency, and Sinkage on Deformable Terrain. In Proceedings of the IEEE International Conference on Robotics and Automation(ICRA), Anchorage, AK, USA, 3–7 May 2010; pp. 2821–2827. [Google Scholar]
- Ming, H.; Bao-Long, S.; Wen-Hua, C.; Dan-Min, H.; De-Bei, L.; Ya-Di, H. Structure Synthesis & Configuration Transformation of Variable Topology Repeated Foldable Wheel. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), ShenZhen, China, 12–14 December 2013; pp. 85–90. [Google Scholar]
- Bidaud, P.; Benamar, F.; Poirier, S. An Expandable Mechanism for Deployment and Contact Surface Adaptation of Rover Wheels. In Climbing and Walking Robots; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1053–1060. [Google Scholar]
- Grand, C.; Bidaud, P.; Jarrassé, N. Innovative Concept of Unfoldable Wheel with an Active Contact Adaptation Mechanism. In Proceedings of the 12th IFToMM World Congress, Besancon, France, 17–21 June 2007. [Google Scholar]
- Hirose, S.; Kuwabara, H. Design of three-wheeled planetary rover Tri-star II. J. Robot. Mechatron. 2000, 12, 446–452. [Google Scholar] [CrossRef]
- Aoki, T.; Murayama, Y.; Hirose, S. Development of a transformable three-wheeled lunar rover: Tri-star IV. J. Field Robot. 2014, 31, 206–223. [Google Scholar] [CrossRef]
- Sun, G.; Gao, F.; Sun, P. Design and mobility performance study of spring wheel for lunar rover. China Mech. Eng. 2009, 20, 134–137. [Google Scholar]
- Midha, A.; Norton, T.W.; Howell, L.L. On the nomenclature, classification, and abstractions of compliant mechanisms. ASME J. Mech. Des. 1994, 116, 270–279. [Google Scholar] [CrossRef]
- Howell, L.L.; Magleby, S.P.; Olsen, B.M. Handbook of Compliant Mechanisms, 1st ed.; Wiley: New York, NY, USA, 2013; pp. 1–2. ISBN 1119953456. [Google Scholar]
- Sun, P.; Gao, F.; Li, W.; Sun, G. Analysis of traction trafficability of diameter-variable wheel for planetary rover. J. Beijing Univ. Aeronaut. Astronaut. 2007, 33, 1404–1407. [Google Scholar]
- Cui, Y.; Gao, F. Kinematic modeling and analysis of variable diameter wheeled lunar rover. J. Beijing. Univ. Aeronaut. Astronaut. 2008, 34, 348–352. [Google Scholar]
- Machekposhti, D.F.; Tolou, N.; Herder, J.L. A review on compliant joints and rigid-body constant velocity universal joints toward the design of compliant homokinetic couplings. ASME J. Mech. Des. 2015, 137, 032301. [Google Scholar] [CrossRef]
- Valentini, P.P.; Pennestrì, E. Second-order approximation pseudo-rigid model of leaf flexure hinge. Mech. Mach. Theory 2017, 116, 352–359. [Google Scholar] [CrossRef]
- Hongzhe, Z.; Dong, H.; Shusheng, B. Modeling and analysis of a precise multibeam flexural pivot. ASME J. Mech. Des. 2017, 139, 081402. [Google Scholar] [CrossRef]
- Norton, R.L. Design of Machinery: An Introduction to the Synthesis and Analysis of Mechanisms and Machines; McGraw-Hill Higher Education: Boston, MA, USA, 2004; pp. 188–232. ISBN 0-07-247076-1. [Google Scholar]
- Sanò, P.; Verotti, M.; Bosetti, P.; Belfiore, N.P. Kinematic synthesis of a D-Drive MEMS Device with rigid-body replacement method. ASME J. Mech. Des. 2018, 140, 075001. [Google Scholar] [CrossRef]
- Howell, L.L. Compliant Mechanisms; John Wiley & Sons: New York, NY, USA, 2001; pp. 162–168. ISBN 0-471-38478-X. [Google Scholar]
- Venkiteswaran, V.K.; Su, H.J. Pseudo-rigid-body models for circular beams under combined tip loads. Mech. Mach. Theory 2016, 106, 80–93. [Google Scholar] [CrossRef]
- Venkiteswaran, V.K.; Su, H.J. A versatile 3R pseudo-rigid-body model for initially curved and straight compliant beams of uniform cross section. ASME J. Mech. Des. 2018, 140, 092305. [Google Scholar] [CrossRef]
- Tanık, E.; Parlaktaş, V. Compliant cardan universal joint. ASME J. Mech. Des. 2012, 134, 021011–021015. [Google Scholar] [CrossRef]
- Tanık, E.; Söylemez, E. Analysis and design of a compliant variable stroke mechanism. Mech. Mach. Theory 2010, 45, 1385–1394. [Google Scholar] [CrossRef]
- Tanık, E. Analysis and design of an underactuated compliant five-bar mechanism. Mech. Mach. Theory 2016, 102, 123–134. [Google Scholar] [CrossRef]
- Beitz, W.; Kuttner, K.H. Dubbel-Handbook of Mechanical Engineering; Springer: London, UK, 1994; pp. 50–63. ISBN 3-540-19868-7. [Google Scholar]
- Xiao, W.; Zhang, Y. Design of manned lunar rover wheels and improvement in soil mechanics formulas for elastic wheels in consideration of deformation. J. Terramech. 2016, 65, 61–71. [Google Scholar] [CrossRef]
- Jouaneh, M.; Yang, R. Modeling of flexure-hinge type lever mechanisms. Precis. Eng. 2003, 27, 407–418. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).