Crack Initiation and Propagation Fatigue Life of Ultra High-Strength Steel Butt Joints
Abstract
1. Introduction
1.1. Fatigue Assessment of Welds Considering Crack Initiation and Propagation
1.2. Detection of the Crack Initiation Point
1.3. Effect of Local Weld Geometry on Fatigue Performance
2. Experimental Investigations
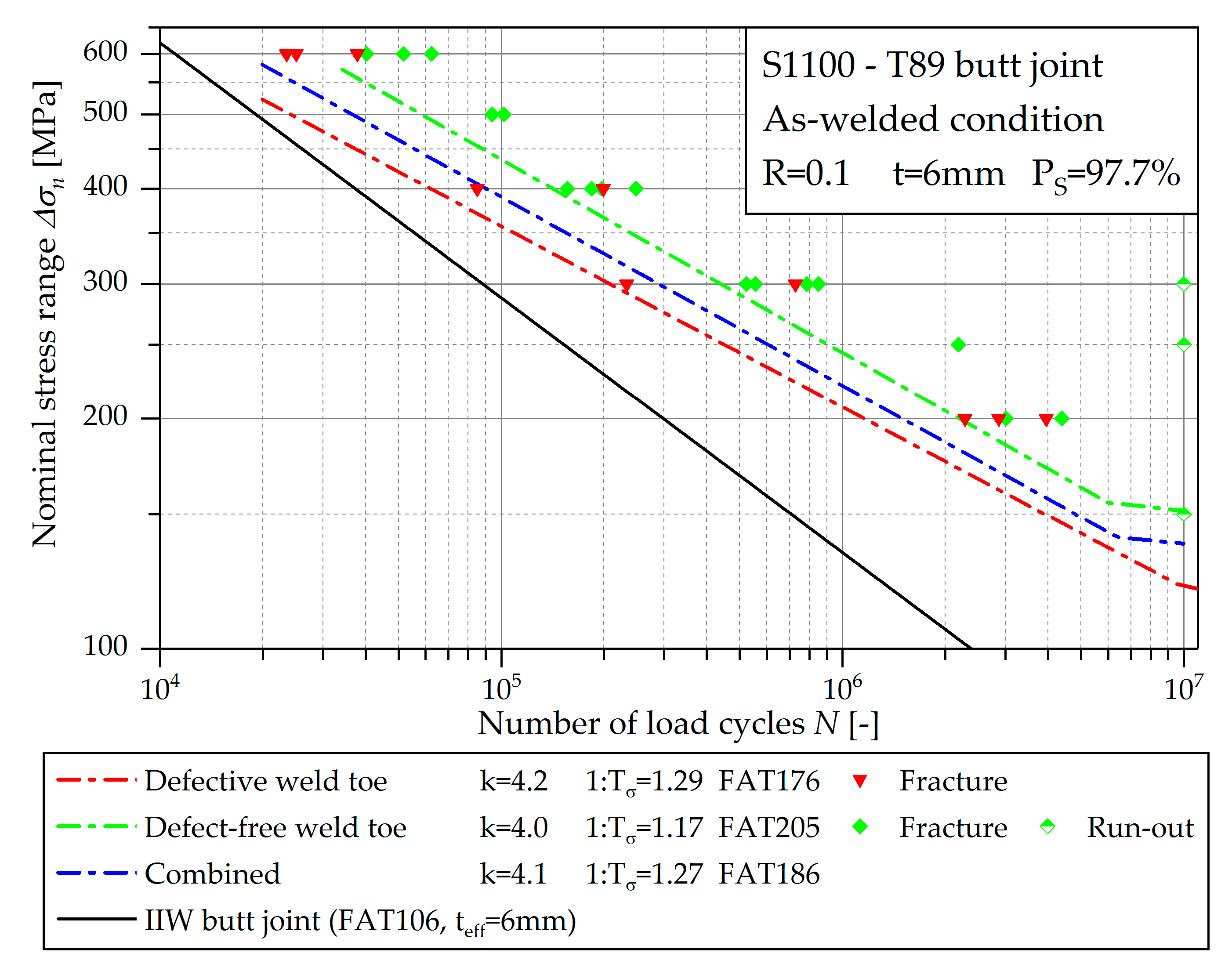
2.1. Fatigue Tests
2.2. Determination of Crack Propagation Parameters
3. Optical Detection of Crack Initiation and Propagation
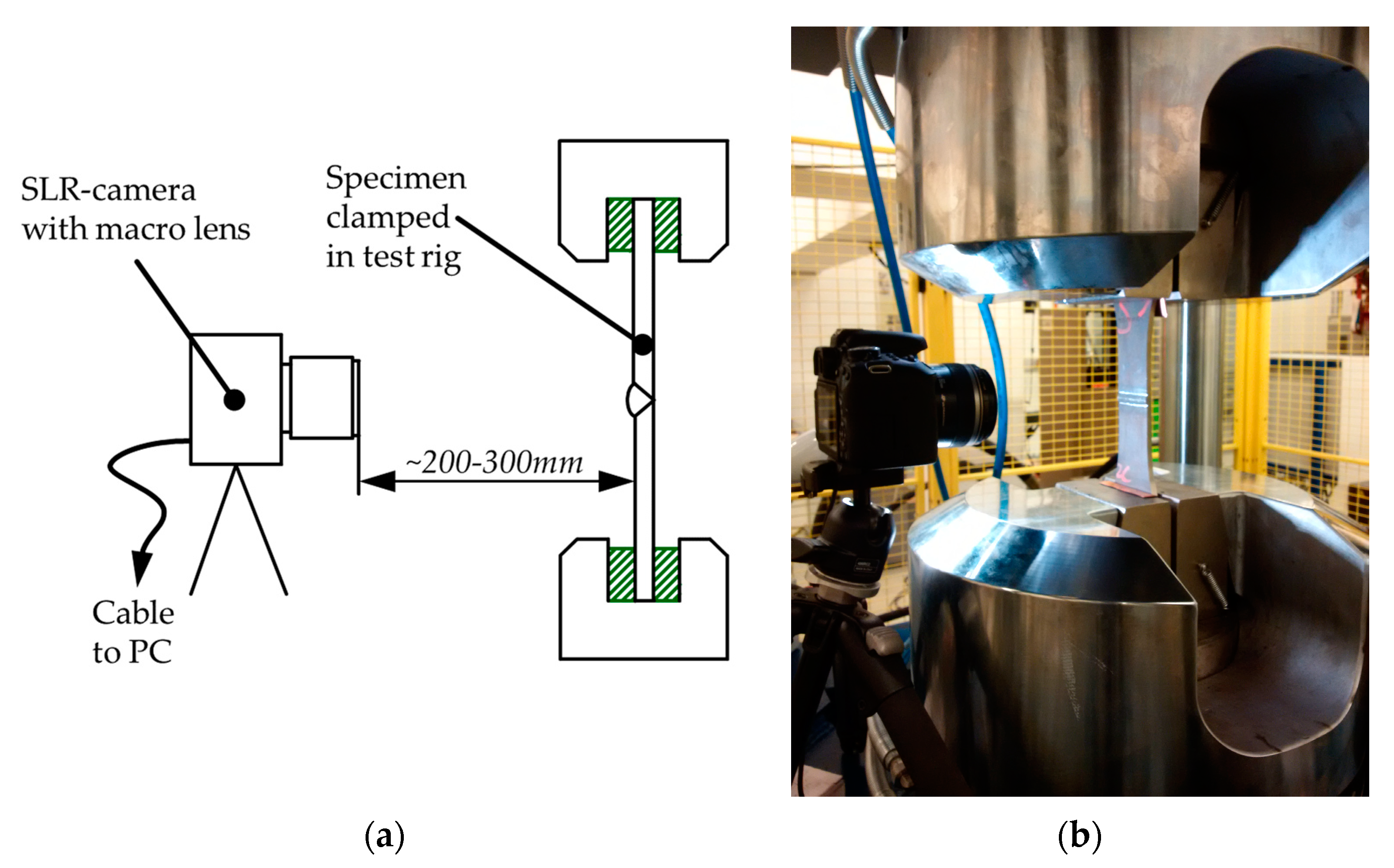
3.1. Experimental Setup
3.2. Crack Detection and Tracking Procedure
3.2.1. Local Distortion Field of the Specimen’s Surface
3.2.2. Crack Detection and Tracking
3.3. Validation of the Procedure
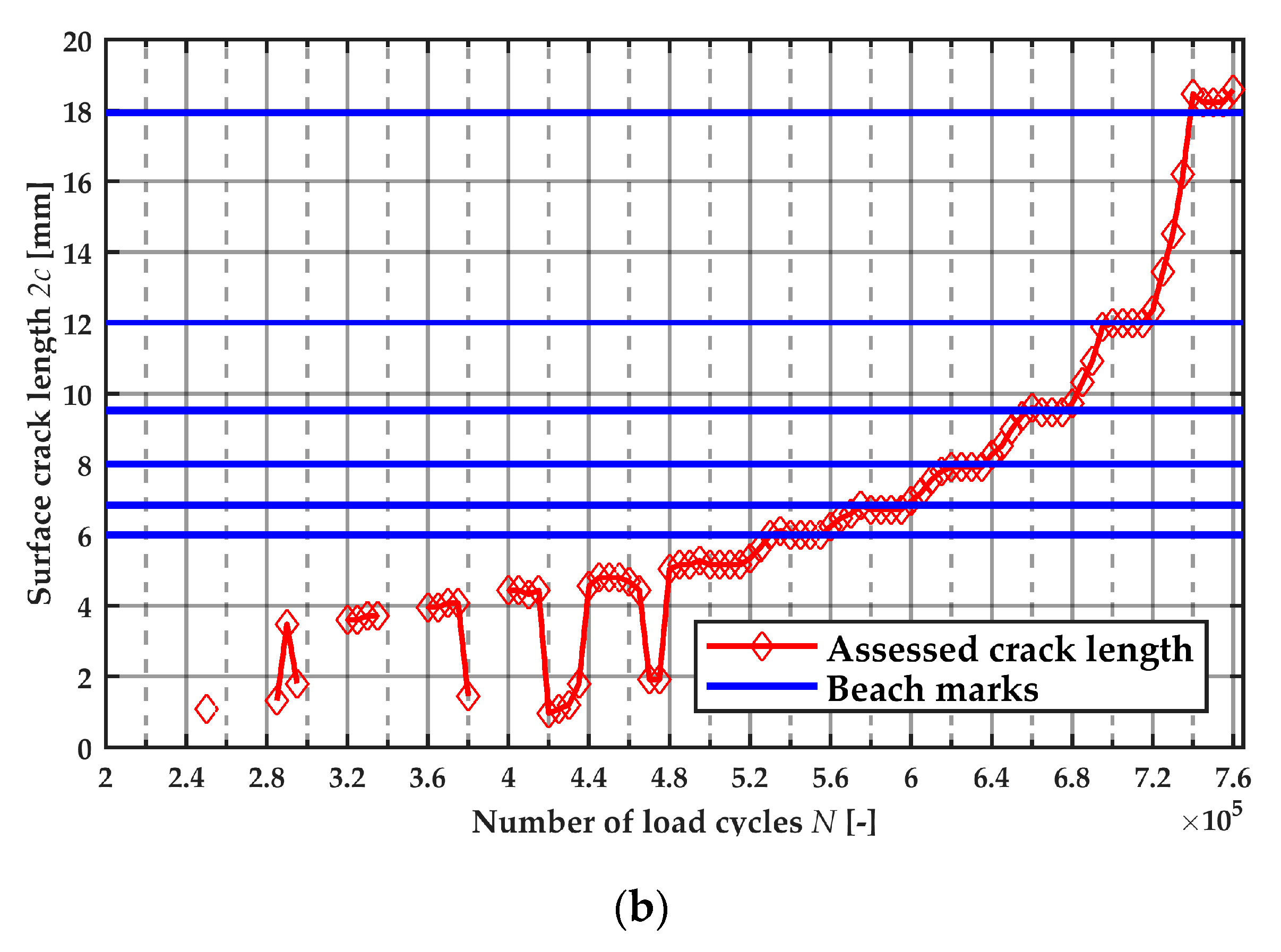
3.3.1. Beach Marks
3.3.2. Fracture Surfaces
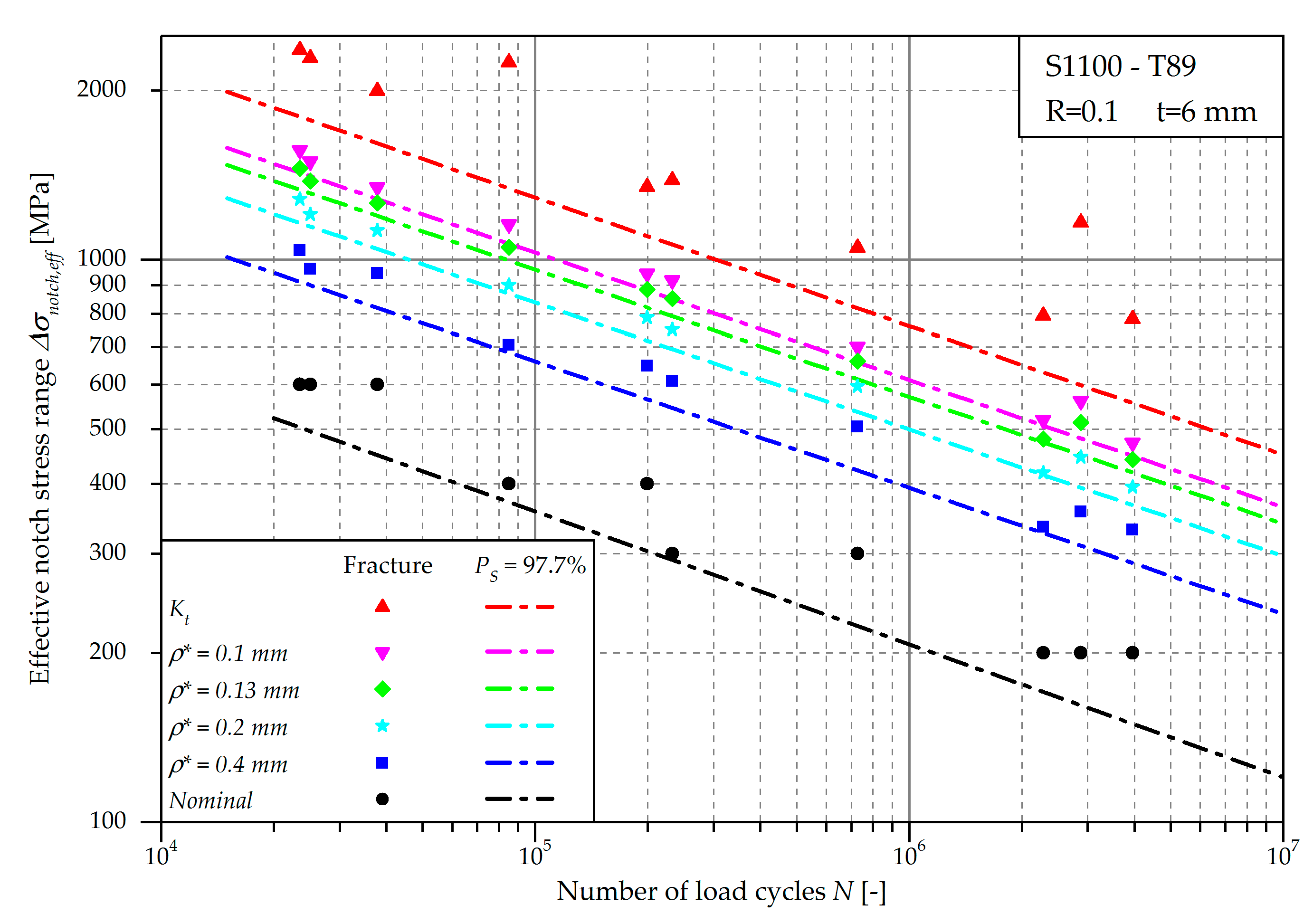
4. Fatigue Assessment
4.1. Neuber’s Stress Averaging Method
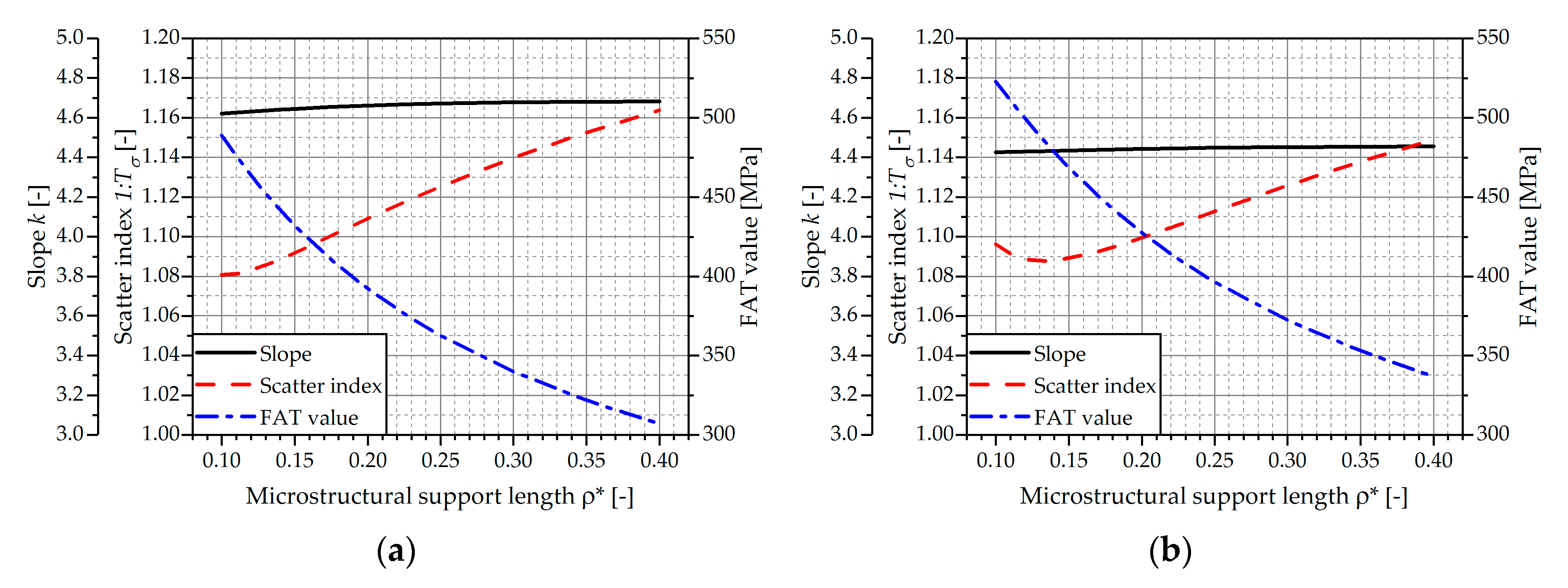
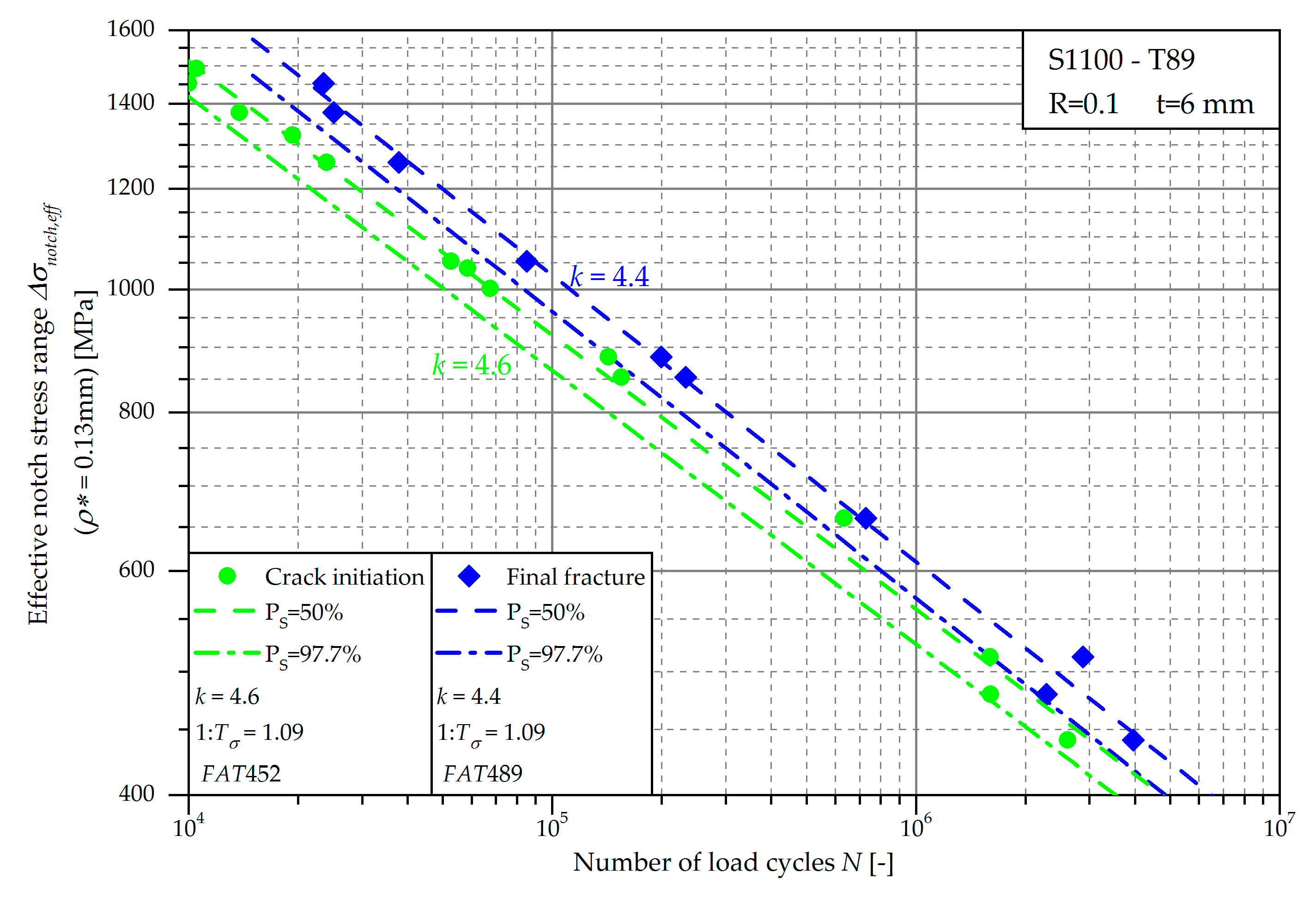
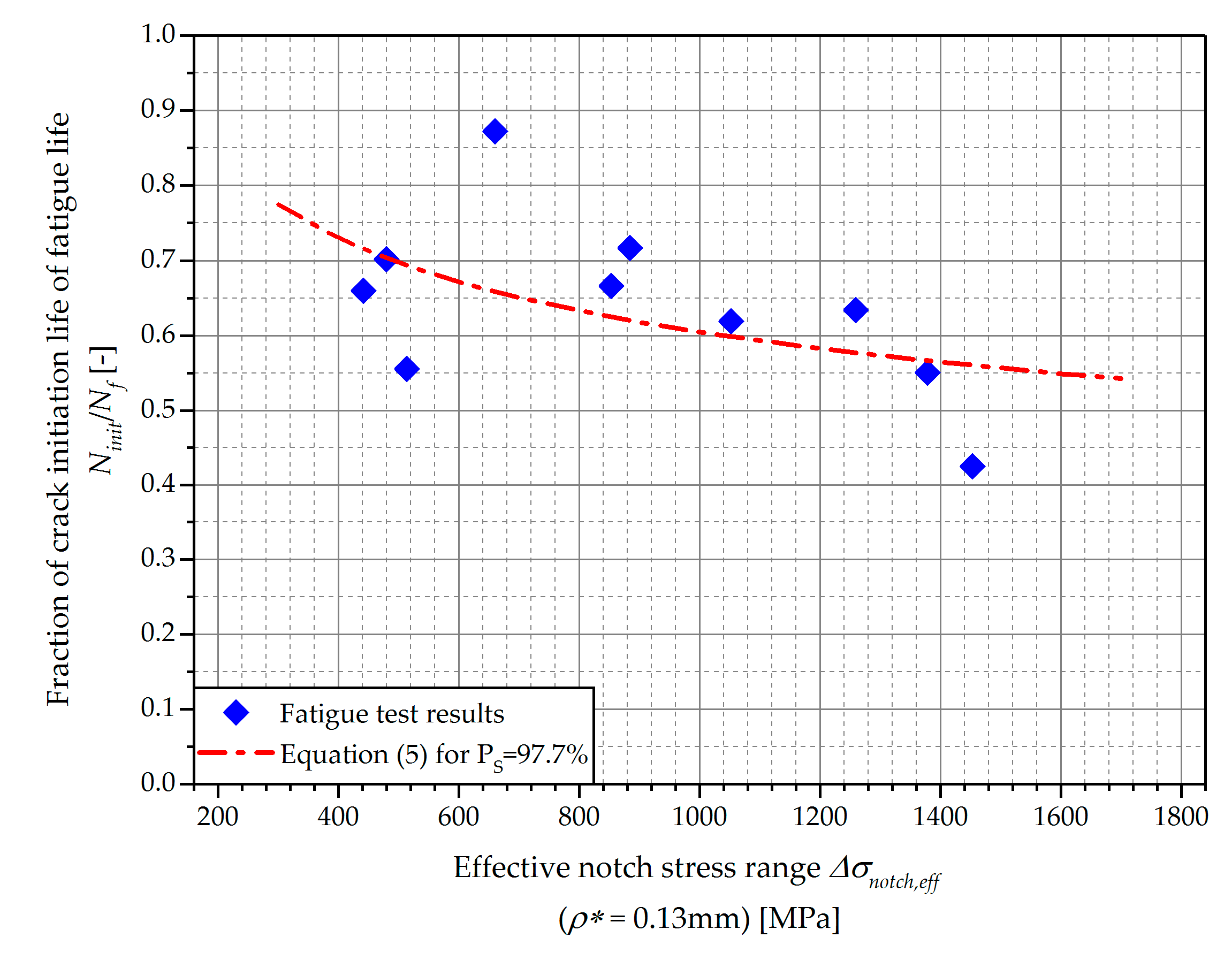
4.2. Crack Initiation and Propagation Life
4.3. Assessment of Crack Propagation Life by Fracture Mechanics
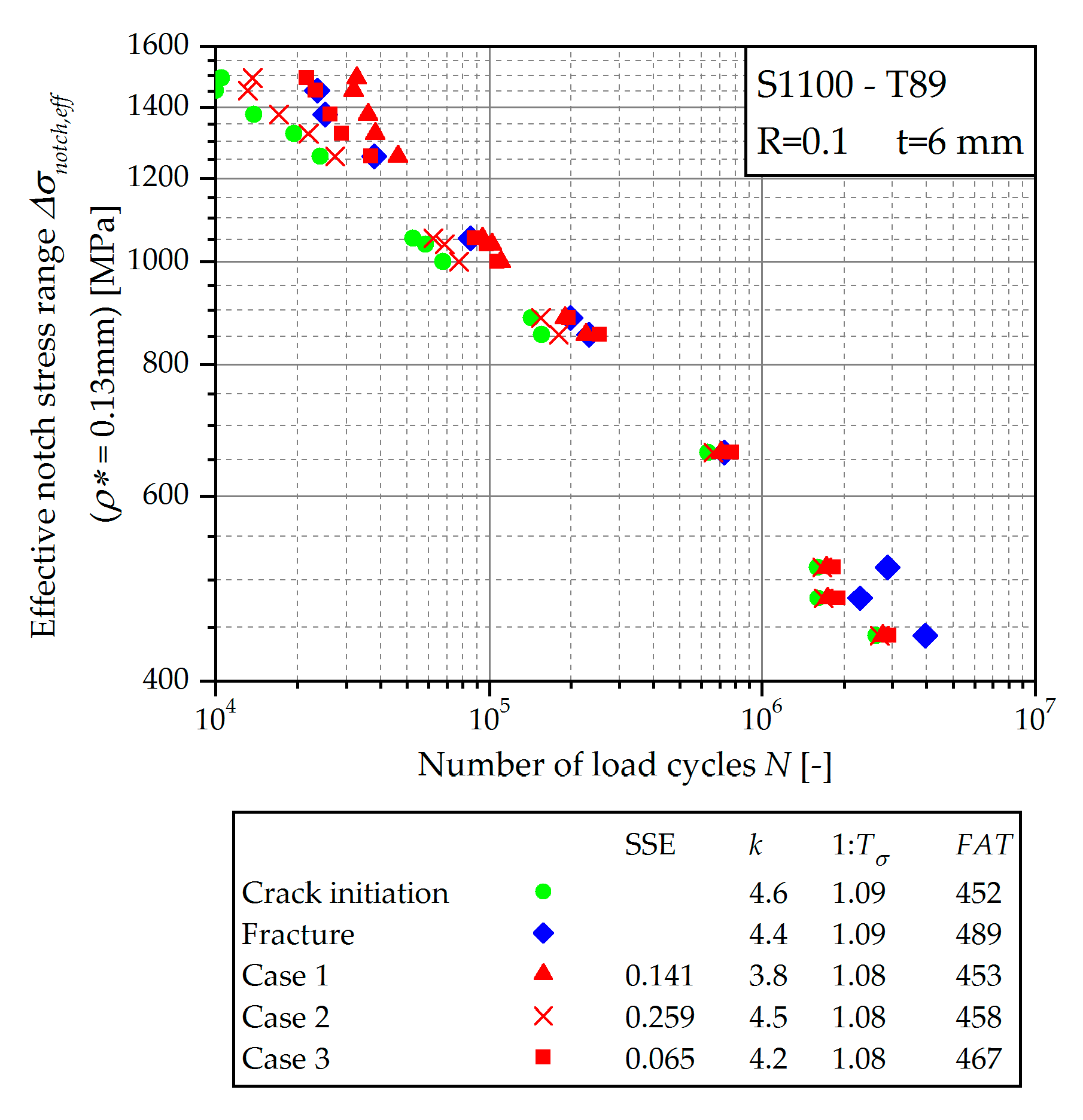
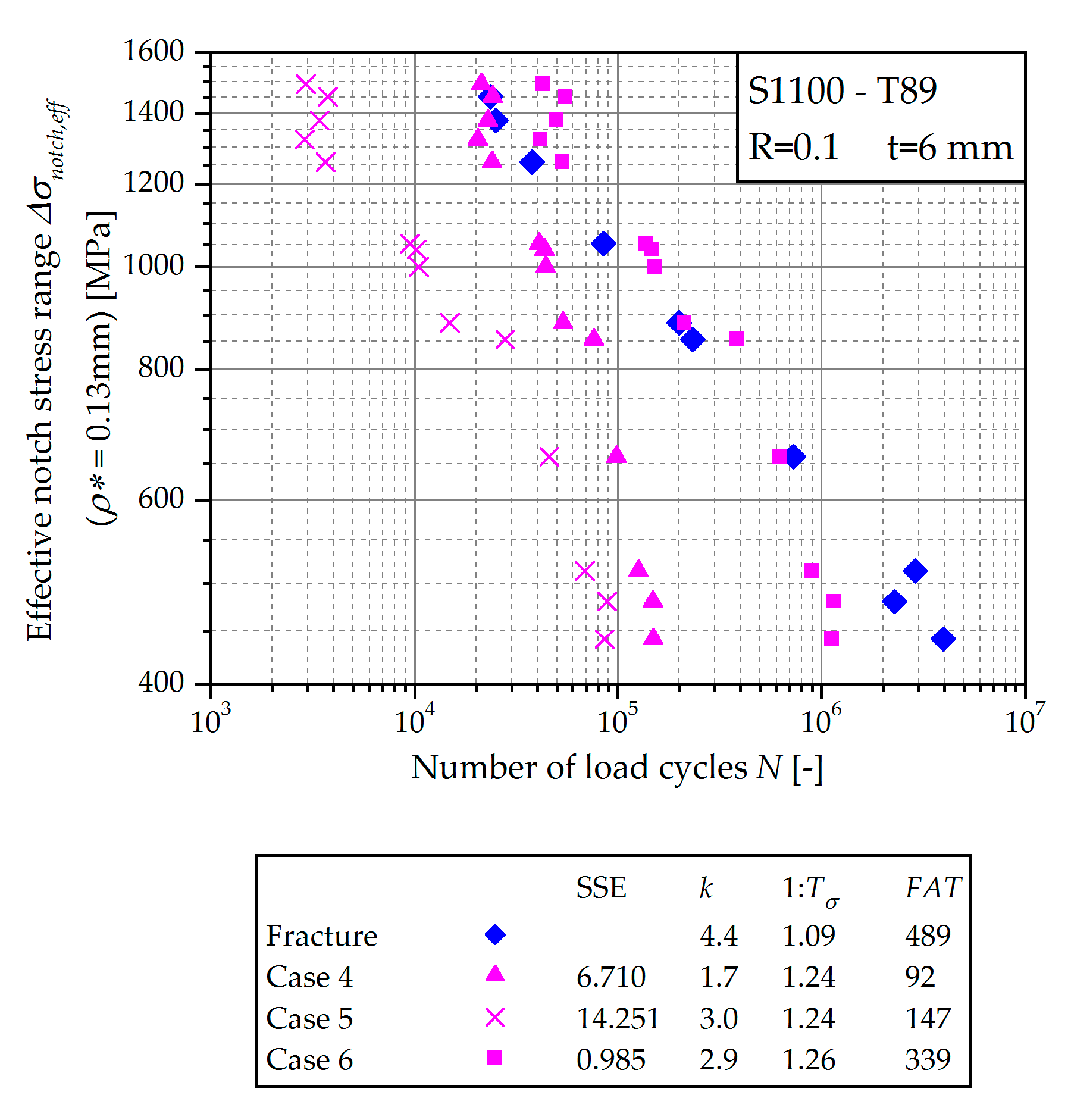
- Start of calculation at the previously determined threshold load cycle number Nth with an initial crack length of ainit = ath = 0.5 mm.
- Calculation from the test start with an initial crack length of ainit = u + 0.1 mm as recommended in [38].
- S1100 base material determined in Section 2.2.;
- IIW parameters for welds suggested in [38]; and
- Best fit parameters resulting by a least square fit of the fatigue test results.
4.3.1. Crack Propagation Analysis
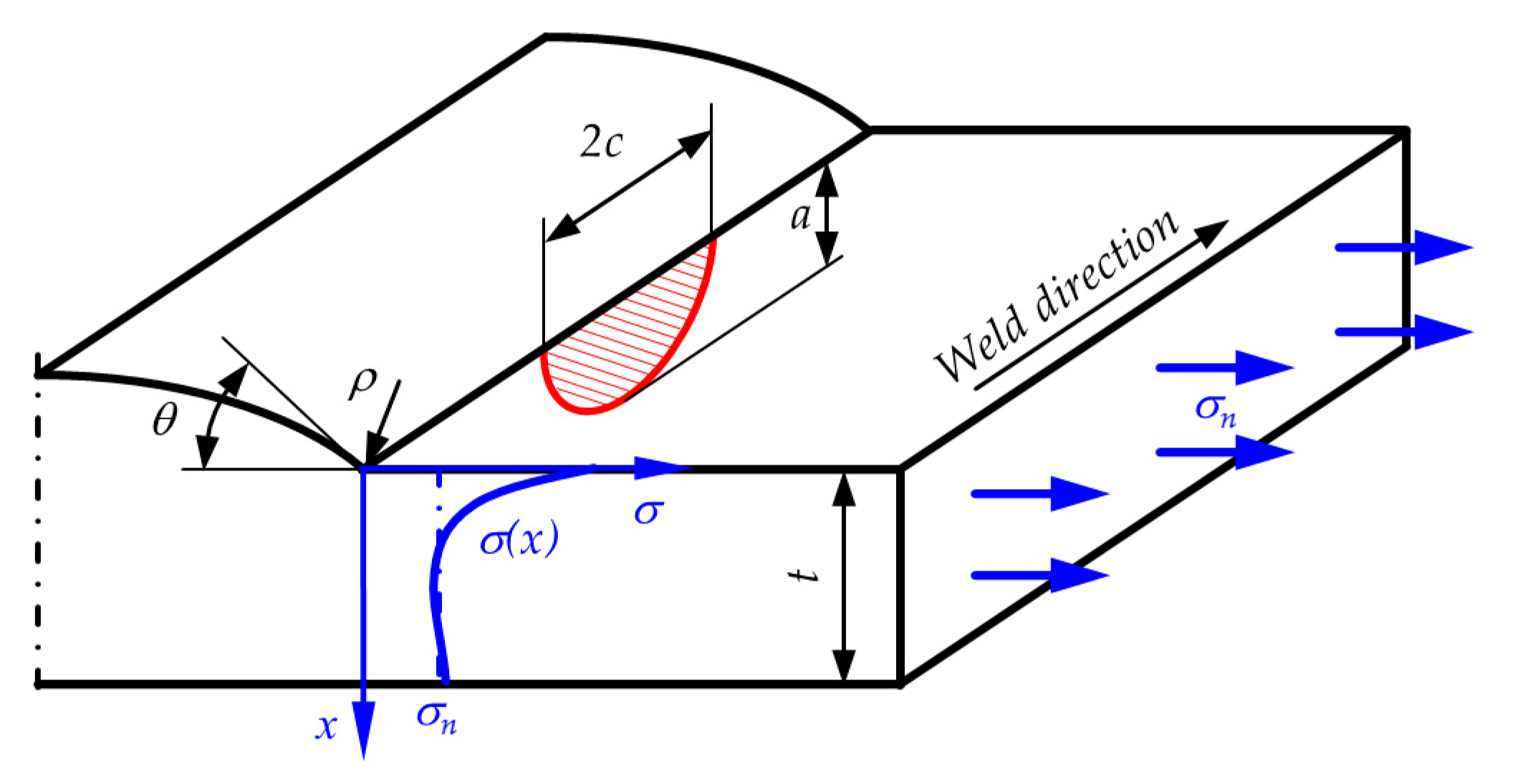
4.3.2. Weight Functions Approach
4.3.3. Stress Distribution
4.3.4. Calculation of Crack Propagation
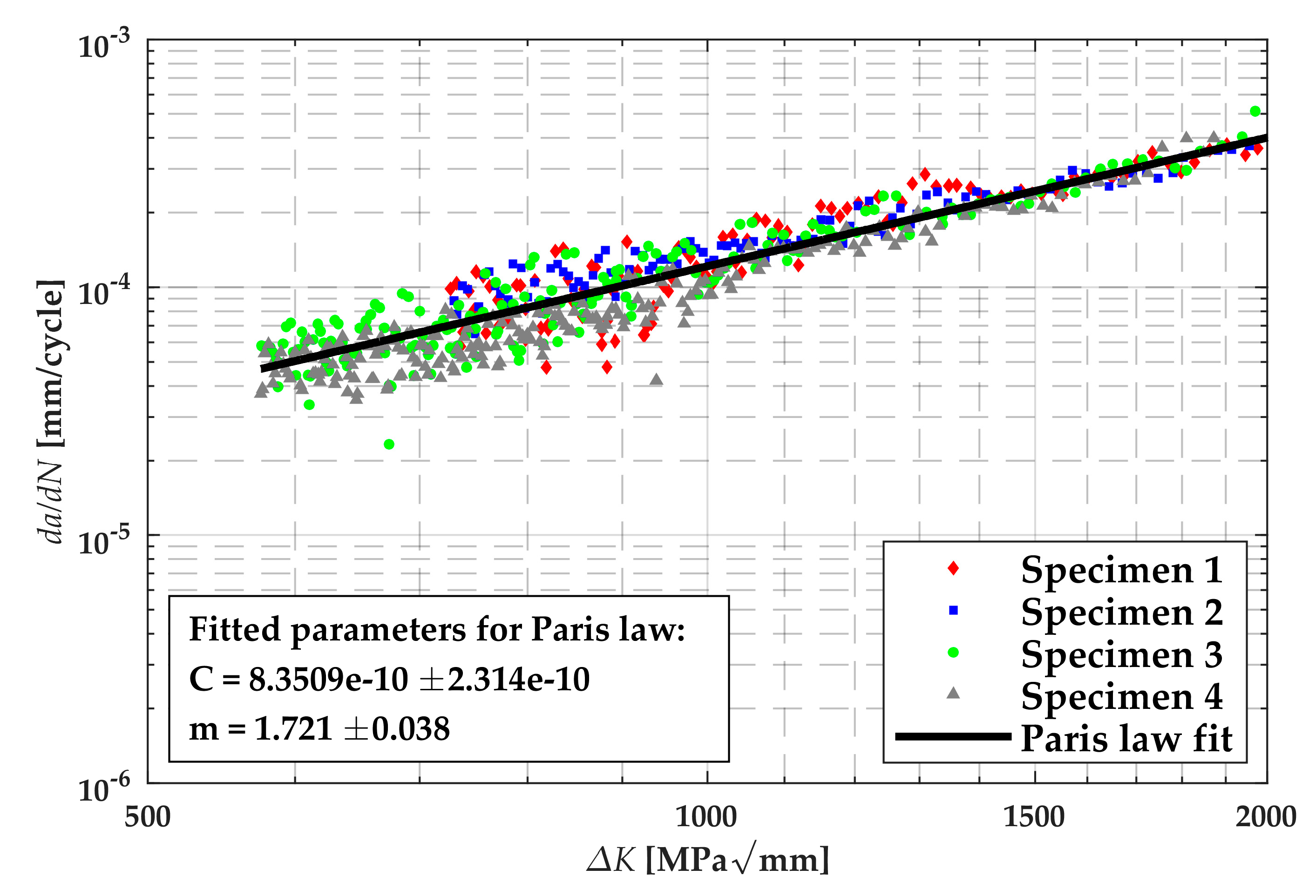
4.3.5. Determination of “Best Fit” Parameters for the Paris Power Law
4.3.6. Crack Propagation Results
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Crack depth (mm) | |
| Final crack depth for crack propagation calculation (mm) | |
| ainit | Initial crack depth for crack propagation calculation (mm) |
| Threshold crack depth between crack initiation and propagation (mm) | |
| Crack aspect ratio (–) | |
| Half surface crack length, half width of elliptical crack (mm) | |
| Crack growth rate coefficient according to Paris law (ΔK in MPa√mm; da/dN in mm/cycle) | |
| Young’s modulus (MPa) | |
| Fatigue class according to IIW, stress range Δσ at N = 2·106 load cycles and PS = 97.7% (MPa) | |
| Stress intensity factor (MPa√mm) | |
| Fatigue notch factor (–) | |
| Stress concentration factor (–) | |
| Inverse slope of S/N-curve (–) | |
| Weight function parameters for deepest point of a surface crack | |
| Weight function for deepest point of surface crack | |
| Weight function parameters for surface point of a surface crack | |
| Weight function for surface point of surface crack | |
| mp | Slope of crack growth rate curve according to Paris law (–) |
| Load cycle number (–) | |
| Load cycle number at specimen burst fracture (–) | |
| Load cycle number before start of image acquisition (–) | |
| Interval load cycle number between two image acquisitions (–) | |
| Load cycle number at crack length ath, threshold between crack initiation and propagation (–) | |
| Load cycle number of crack propagation until burst fracture (–) | |
| Transition knee point of S/N-curve (–) | |
| Probability of survival (–) | |
| Load stress ratio (–) | |
| Displacement in y-direction (specimen loading direction) (pixel) | |
| Gradient of displacement in y-direction (–) | |
| Threshold for gradient of displacement in y-direction (–) | |
| Sum of squared errors (–) | |
| Sheet thickness (mm) | |
| Scatter index of S/N-curve, ratio of stress range Δσ at PS = 10% and PS = 90% (–) | |
| Weld toe radius (mm) | |
| Microstructural support length (mm) | |
| Weld flank angle (°) | |
| Stress (MPa) | |
| Recurring indices | |
| Effective value | |
| Nominal value | |
| Notch value | |
| Range, difference of upper and lower value | |
References
- Radaj, D. Review of fatigue strength assessment of nonwelded and welded structures based on local parameters. Int. J. Fatigue 1996, 18, 153–170. [Google Scholar] [CrossRef]
- Lassen, T.; Recho, N. Fatigue Life Analyses of Welded Structures; ISTE: London, UK; Newport Beach, CA, USA, 2006. [Google Scholar]
- Chattopadhyay, A.; Glinka, G.; El-Zein, M.; Qian, J.; Formas, R. Stress analysis and fatigue of welded structures. Weld. World 2011, 55, 2–21. [Google Scholar] [CrossRef]
- Hou, C.-Y.; Charng, J.-J. Models for the estimation of weldment fatigue crack initiation life. Int. J. Fatigue 1997, 19, 537–541. [Google Scholar] [CrossRef]
- Remes, H. Strain-based Approach to Fatigue Strength Assessment of Laser-welded Joints. Ph.D. Thesis, Helsinki University of Technology, Espoo, Finland, 2008. [Google Scholar]
- Lihavainen, V.-M. A Novel Approach for Assessing the Fatigue Strenght of Ultrasonic Impact Treated Welded Structures. Ph.D. Thesis, Lappeenranta University of Technology, Lappeenranta, Finland, 2006. [Google Scholar]
- Peterson, R.E. Notch sensitivity. In Metal Fatigue; Sines, G., Waisman, J.L., Dolan, T.J., Eds.; McGraw-Hill: New York, NY, USA, 1959; pp. 293–306. [Google Scholar]
- Neuber, H. Über die Berücksichtigung der Spannungskonzentration bei Festigkeitsberechnungen. Konstruktion 1968, 20, 245–251. [Google Scholar]
- Radaj, D. Design and Analysis of Fatigue Resistant Welded Structures; Abington: Cambridge, UK, 1990. [Google Scholar]
- Lawrence, F.V.; Ho, N.J.; Mazumdar, P.K. Predicting the fatigue resistance of welds. Ann. Rev. Mater. Sci. 1981, 11, 401–425. [Google Scholar] [CrossRef]
- Seeger, T. Grundlagen für Betriebsfestigkeitsnachweise. Stahlbau-Handbuch, 3rd ed.; Stahlbau-Verl.-Ges: Köln, Germany, 1996; pp. 5–123. [Google Scholar]
- Atzori, B.; Lazzarin, P. Notch sensitivity and defect sensitivity under fatigue loading: Two sides of the same medal. Int. J. Fract. 2001, 107, 1–8. [Google Scholar] [CrossRef]
- Glinka, G. Energy density approach to calculation of inelastic strain-stress near notches and cracks. Eng. Fract. Mech. 1985, 22, 485–508. [Google Scholar] [CrossRef]
- Haibach, E. Betriebsfestigkeit. Verfahren und Daten zur Bauteilberechnung; Springer: Berlin, Germany, 2006. [Google Scholar]
- Krebs, J.; Hübner, P.; Kassner, M. Eigenspannungseinfluss auf Schwingfestigkeit und Bewertung in geschweißten Bauteilen; DVS-Verlag: Düsseldorf, Germany, 2004. [Google Scholar]
- Lieurade, H.-P.; Huther, I.; Maddox, S.J. Recommendations on the Fatigue Testing of Welded Components; LETS Global: Rotterdam, The Netherlands, 2006. [Google Scholar]
- Stoschka, M.; Leitner, M.; Fössl, T.; Posch, G. Effect of high-strength filler metals on fatigue. Weld. World 2012, 56, 20–29. [Google Scholar] [CrossRef]
- Maddox, S.J. The effect of mean stress on fatigue crack propagation a literature review. Int. J. Fract. 1975, 11, 389–408. [Google Scholar]
- Verreman, Y.; Nie, B. Short-crack growth and coalescence along the toe of a manual fillet weld. Fatigue Frac. Eng. Mat. Struct. 1991, 14, 337–349. [Google Scholar] [CrossRef]
- Fricke, W. Fatigue analysis of welded joints: State of development. Mar. Struct. 2003, 16, 185–200. [Google Scholar] [CrossRef]
- Baumgartner, J.; Bruder, T. Influence of weld geometry and residual stresses on the fatigue strength of longitudinal stiffeners. Weld. World 2013, 57, 841–855. [Google Scholar] [CrossRef]
- Leitner, M.; Barsoum, Z.; Schäfers, F. Crack propagation analysis and rehabilitation by HFMI of pre-fatigued welded structures. Weld. World 2016, 60, 581–592. [Google Scholar] [CrossRef]
- Baumgartner, J.; Waterkotte, R. Crack initiation and propagation analysis at welds—Assessing the total fatigue life of complex structures. Mat. Wiss. Werkstofftech. 2015, 46, 123–135. [Google Scholar] [CrossRef]
- Simunek, D.; Leitner, M.; Grün, F. In-situ crack propagation measurement of high-strength steels including overload effects. Proc. Eng. 2018, 213, 335–345. [Google Scholar] [CrossRef]
- Simunek, D.; Leitner, M.; Maierhofer, J.; Gänser, H.-P. Crack growth under constant amplitude loading and overload effects in 1:3 scale specimens. Proc. Struct. Integr. 2017, 4, 27–34. [Google Scholar] [CrossRef]
- Todorov, E.I.; Mohr, W.C.; Lozev, M.G.; Thompson, D.O.; Chimenti, D.E. Detection and Sizing of Fatigue Cracks in Steel Welds with Advanced Eddycurrent techniques. In Proceedings of the AIP Conference—34th Annual Review of Progress in Quantitative Nondestructive Evaluation, Golden, CO, USA, 22–27 July 2007; pp. 1058–1065. [Google Scholar]
- Lamtenzan, D.; Glenn, W.; Lozev, M.G. Detection and Sizing of Cracks in Structural Steel Using the Eddy Current Method; US Department of Transportation Federal Highway Administration FHWA-RD-00-018; Turner-Fairbank Highway Research Center: McLean, VA, USA, 2000.
- Roux, S.; Réthoré, J.; Hild, F. Digital image correlation and fracture: An advanced technique for estimating stress intensity factors of 2D and 3D cracks. J. Phys. D Appl. Phys. 2009, 42, 214004. [Google Scholar] [CrossRef]
- Mathieu, F.; Hild, F.; Roux, S. Identification of a crack propagation law by digital image correlation. Int. J. Fatigue 2012, 36, 146–154. [Google Scholar] [CrossRef]
- Ozelo, R.R.M.; Sollero, P.; Sato, M.; Barros, R.S.V. Monitoring crack propagation using digital image correlation and cod technique. In Proceedings of the COBEM 2009 20th International Congress of Mechanical Engineering, ABCM, Gramado, Brazil, 15–20 November 2009. [Google Scholar]
- Alam, M.M.; Barsoum, Z.; Jonsén, P.; Kaplan, A.F.H.; Häggblad, H.Å. The influence of surface geometry and topography on the fatigue cracking behaviour of laser hybrid welded eccentric fillet joints. Appl. Surf. Sci. 2010, 256, 1936–1945. [Google Scholar] [CrossRef]
- Caccese, V.; Blomquist, P.A.; Berube, K.A.; Webber, S.R.; Orozco, N.J. Effect of weld geometric profile on fatigue life of cruciform welds made by laser/GMAW processes. Mar. Struct. 2006, 19, 1–22. [Google Scholar] [CrossRef]
- Lillemäe, I.; Remes, H.; Liinalampi, S.; Itävuo, A. Influence of weld quality on the fatigue strength of thin normal and high strength steel butt joints. Weld. World 2016, 60, 731–740. [Google Scholar] [CrossRef]
- Rennert, R.; Kullig, E.; Vormwald, M.; Esderts, A.; Siegele, D. Analytical Strength Assessment of Components Made of Steel, Cast Iron and Aluminium Materials in Mechanical Engineering: FKM Guideline, 6th ed.; VDMA-Verl: Frankfurt, Germany, 2012. [Google Scholar]
- Olivier, R.; Köttgen, V.B.; Seeger, T. Welded Joints I—Fatigue Strength Assessment Method for Welded Joints Based on Local Stresses; Forschungshefte No. 143; Forschungskuratorium Maschinenbau: Frankfurt, Germany, 1989. [Google Scholar]
- Olivier, R.; Köttgen, V.B.; Seeger, T. Welded Joints II—Investigation of Inclusion into Codes of a Novel Fatigue Strength Assessment Method for Welded Joints in Steel; No. 180; Forschungskuratorium Maschinenbau: Frankfurt, Germany, 1994. [Google Scholar]
- Morgenstern, C.; Sonsino, C.M.; Hobbacher, A.; Sorbo, F. Fatigue design of aluminium welded joints by the local stress concept with the fictitious notch radius of rf = 1 mm. Int. J. Fatigue 2006, 28, 881–890. [Google Scholar] [CrossRef]
- Hobbacher, A. Recommendations for Fatigue Design of Welded Joints and Components, 2nd ed.; Springer: New York, NY, USA, 2016. [Google Scholar]
- Nykänen, T.; Björk, T.; Laitinen, R. Fatigue strength prediction of ultra high strength steel butt-welded joints. Fatigue Frac. Eng. Mater. Struct. 2013, 36, 469–482. [Google Scholar] [CrossRef]
- Liinalampi, S.; Remes, H.; Lehto, P.; Lillemäe, I.; Romanoff, J.; Porter, D. Fatigue strength analysis of laser-hybrid welds in thin plate considering weld geometry in microscale. Int. J. Fatigue 2016, 87, 143–152. [Google Scholar] [CrossRef]
- Nykänen, T.; Marquis, G.; Björk, T. Effect of weld geometry on the fatigue strength of fillet welded cruciform joints. In Proceedings of the International Symposium on Integrated Design and Manufacturing of Welded Structures; Lappeenranta University of Technology: Lappeenranta, Finland, 2007. [Google Scholar]
- Schork, B.; Kucharczyk, P.; Madia, M.; Zerbst, U.; Hensel, J.; Bernhard, J.; Tchuindjang, D.; Kaffenberger, M.; Oechsner, M.; Zerbst, U. The effect of the local and global weld geometry as well as material defects on crack initiation and fatigue strength. Eng. Fract. Mech. 2018, 198, 103–122. [Google Scholar] [CrossRef]
- Madia, M.; Zerbst, U.; Th. Beier, H.; Schork, B. The IBESS model—Elements, realisation and validation. Eng. Fract. Mech. 2018, 198, 171–208. [Google Scholar] [CrossRef]
- Mashiri, F.R.; Zhao, X.L.; Grundy, P. Effects of weld profile and undercut on fatigue crack propagation life of thin-walled cruciform joint. Thin Walled Struct. 2001, 39, 261–285. [Google Scholar] [CrossRef]
- Steimbreger, C.; Chapetti, M.D. Fatigue strength assessment of butt-welded joints with undercuts. Int. J. Fatigue 2017, 105, 296–304. [Google Scholar] [CrossRef]
- Steimbreger, C.; Chapetti, M.; Hénaff, G. Undercut tolerances in industry from a fracture mechanic perspective. MATEC Web Conf. 2018, 165, 21009. [Google Scholar] [CrossRef][Green Version]
- Ottersböck, M.J.; Leitner, M.; Stoschka, M.; Maurer, W. Effect of Weld Defects on the Fatigue Strength of Ultra High-strength Steels. Proc. Eng. 2016, 160, 214–222. [Google Scholar] [CrossRef]
- ASTM. Practice for Statistical Analysis of Linear or Linearized Stress-Life (S-N) and Strain-Life (-N) Fatigue Data; E739; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- Dengel, D.; Harig, H. Estimation of the fatigue limit by progressively-increasing load tests. Fatigue Frac. Eng. Mat. Struct. 1980, 3, 113–128. [Google Scholar] [CrossRef]
- Sonsino, C.M. Course of SN-curves especially in the high-cycle fatigue regime with regard to component design and safety. Int. J. Fatigue 2007, 29, 2246–2258. [Google Scholar] [CrossRef]
- Ottersböck, M.J.; Leitner, M.; Stoschka, M. Characterisation of actual weld geometry and stress concentration of butt welds exhibiting local undercuts. Eng. Fail. Anal. 2019. in review. [Google Scholar]
- ASTM. Standard Test Method for Measurement of Fatigue Crack Growth Rates; E647; ASTM International: West Conshohocken, PA, USA, 2000. [Google Scholar]
- Tada, H.; Paris, P.C.; Irwin, G.R. The Stress Analysis of Cracks Handbook, 3rd ed.; ASME: New York, NY, USA, 2000. [Google Scholar]
- Beden, S.M.; Abdullah, S.; Ariffin, A.K. Review of fatigue crack propagation models for metallic components. Eur. J. Sci. Res. 2009, 28, 364–397. [Google Scholar]
- Richard, H.A.; Sander, M. Ermüdungsrisse. In Erkennen, Sicher Beurteilen, Vermeiden, 3rd ed.; Springer Vieweg: Wiesbaden, Germany, 2012. [Google Scholar]
- Paris, P.; Erdogan, F. A critical analysis of crack propagation laws. J. Basic Eng. 1963, 85, 528. [Google Scholar] [CrossRef]
- Jones, E.M.C. Improved Digital Image Correlation; Version 4; University of Illinois: Champaign, IL, USA, 2015. [Google Scholar]
- Reu, P.L.; Toussaint, E.; Jones, E.M.C.; Bruck, H.A.; Iadicola, M.; Balcaen, R.; Turner, D.Z.; Siebert, T.; Lava, P.; Simonsen, M. DIC Challenge: Developing images and guidelines for evaluating accuracy and resolution of 2D analyses. Exp. Mech. 2018, 58, 1067–1099. [Google Scholar] [CrossRef]
- Jones, E.M.C. Documentation for Matlab-Based DIC Code; Version 4; University of Illinois: Champaign, IL, USA, 2015. [Google Scholar]
- Ottersböck, M.J. Einfluss von Imperfektionen auf die Schwingfestigkeit hochfester Stahlschweißverbindungen. Ph.D. Thesis, Montanuniversität Leoben, Leoben, Austria, 2019. [Google Scholar]
- Simunek, D.; Leitner, M.; Maierhofer, J.; Gänser, H.-P. Fatigue crack growth under constant and variable amplitude loading at semi-elliptical and V-notched steel specimens. Proc. Eng. 2015, 133, 348–361. [Google Scholar] [CrossRef]
- Engesvik, K.M. Analysis of Uncertainties in the Fatigue Capacity of Welded Joints. Ph.D. Thesis, University of Trondheim, Trondheim, Norway, 1981. [Google Scholar]
- Baumgartner, J. Enhancement of the fatigue strength assessment of welded components by consideration of mean and residual stresses in the crack initiation and propagation phases. Weld. World 2016, 60, 547–558. [Google Scholar] [CrossRef]
- Radaj, D.; Sonsino, C.M.; Fricke, W. Fatigue Assessment of Welded Joints by Local Approaches, 2nd ed.; Woodhead Publishing: Sawston, UK, 2006. [Google Scholar]
- Goyal, R.; Glinka, G. Fracture mechanics-based estimation of fatigue lives of welded joints. Weld. World 2013, 57, 625–634. [Google Scholar] [CrossRef]
- Newman, J.C.; Raju, I.S. Stress-intensity factor equations for cracks in three-dimensional finite bodies, ASTM STP 791. In Fracture Mechanics: Fourteenth Symposium—Volume I: Theory and Analysis; Lewis, J.C., Sines, G., Eds.; ASTM International: West Conshohocken, PA, USA, 1983; pp. I238–I265. [Google Scholar]
- Murakami, Y.; Murakami, Y. Stress Intensity Factors Handbook; Pergamon Press: Oxford, UK, 1990. [Google Scholar]
- Bueckner, H.F. Novel principle for the computation of stress intensity factors. J. Appl. Math. Mech. 1970, 50. [Google Scholar]
- Shen, G.; Glinka, G. Weight functions for a surface semi-elliptical crack in a finite thickness plate. Theor. Appl. Fract. Mech. 1991, 15, 247–255. [Google Scholar] [CrossRef]
- Glinka, G.; Shen, G. Universal features of weight functions for cracks in mode I. Eng. Fract. Mech. 1991, 40, 1135–1146. [Google Scholar] [CrossRef]
- Wang, X.; Lambert, S.B. Stress intensity factors for low aspect ratio semi-elliptical surface cracks in finite-thickness plates subjected to nonuniform stresses. Eng. Fract. Mech. 1995, 51, 517–532. [Google Scholar] [CrossRef]
- Hall, M.S.; Topp, D.A.; Dover, W.D. Parametric Equations for Stress Intensity Factors in Weldments; Project Report TSC/MSH/0244; Technical Software Consultants Ltd.: Milton Keynes, UK, 1990. [Google Scholar]
- Monahan, C.C. Early Fatigue Crack Growth at Welds; Computational Mechanics: Southampton, UK, 1995. [Google Scholar]



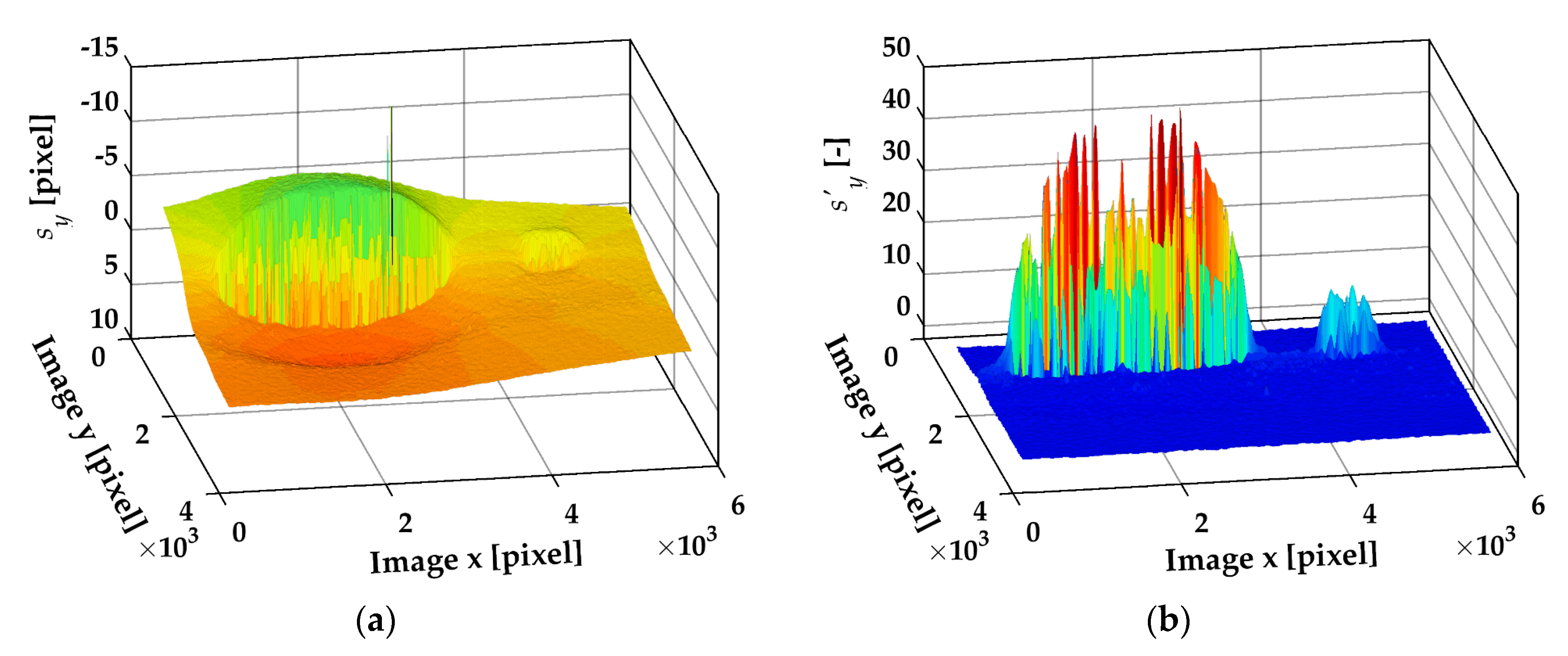

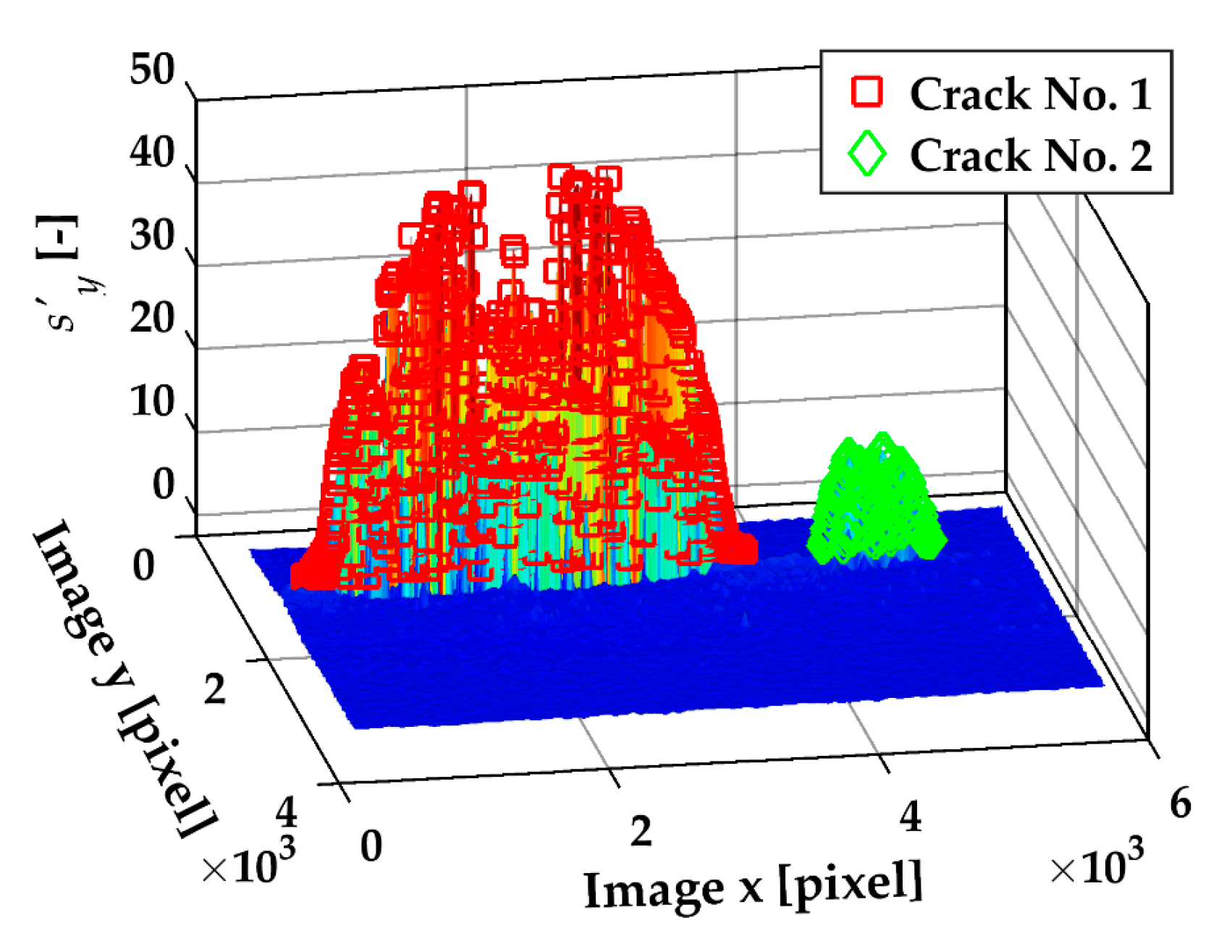
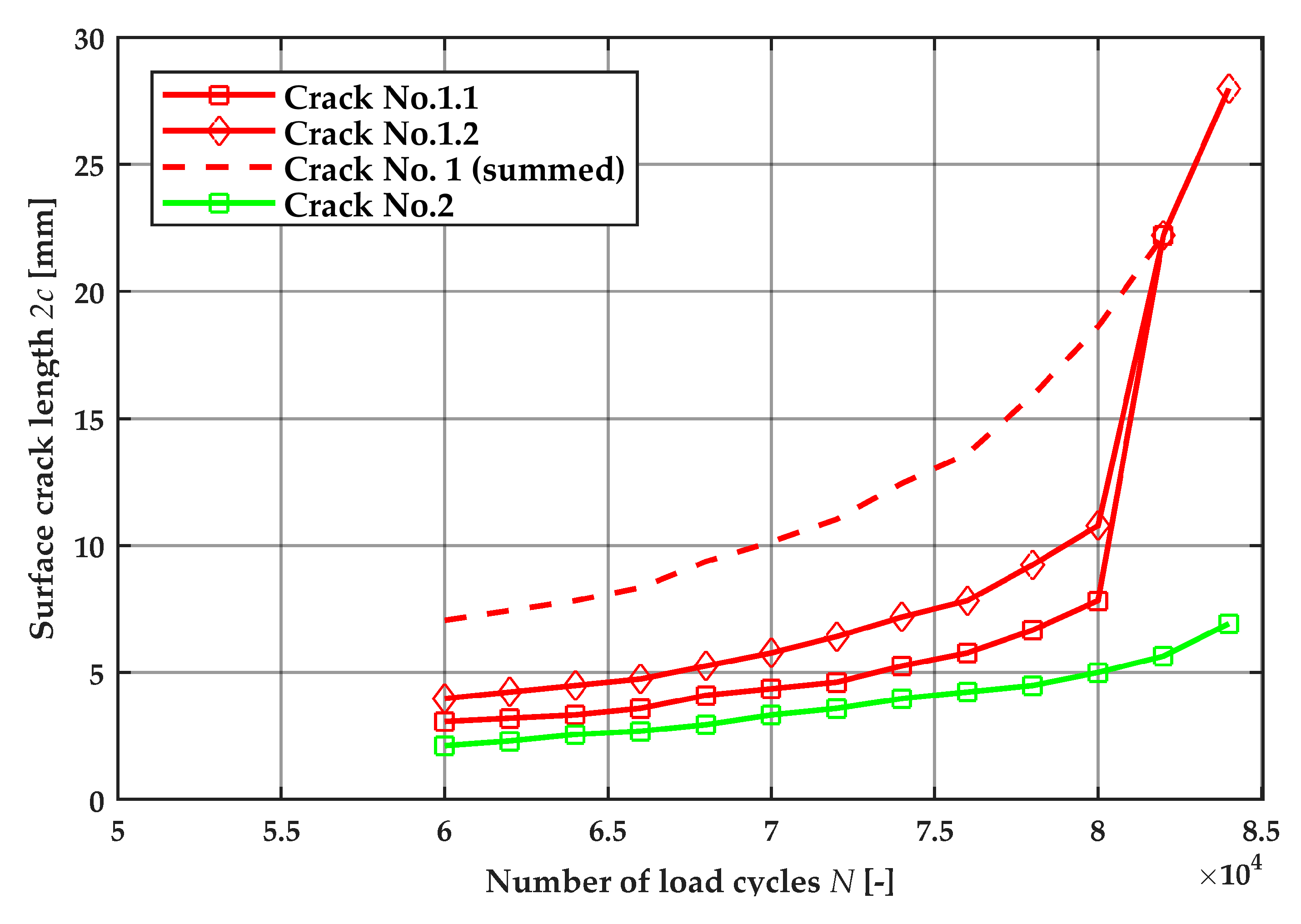



| Material | Yield Strength σy (MPa) | Tensile Strength σu (MPa) | Elongation A (%) | Impact Work ISO-V KV (J) |
|---|---|---|---|---|
| Base, S1100 | ≥1100 | ≥1140 | ≥8 | ≥ 27 @ −20 °C |
| Filler, T89 | ≥890 | ≥940 | ≥15 | ≥ 47 @ −40 °C |
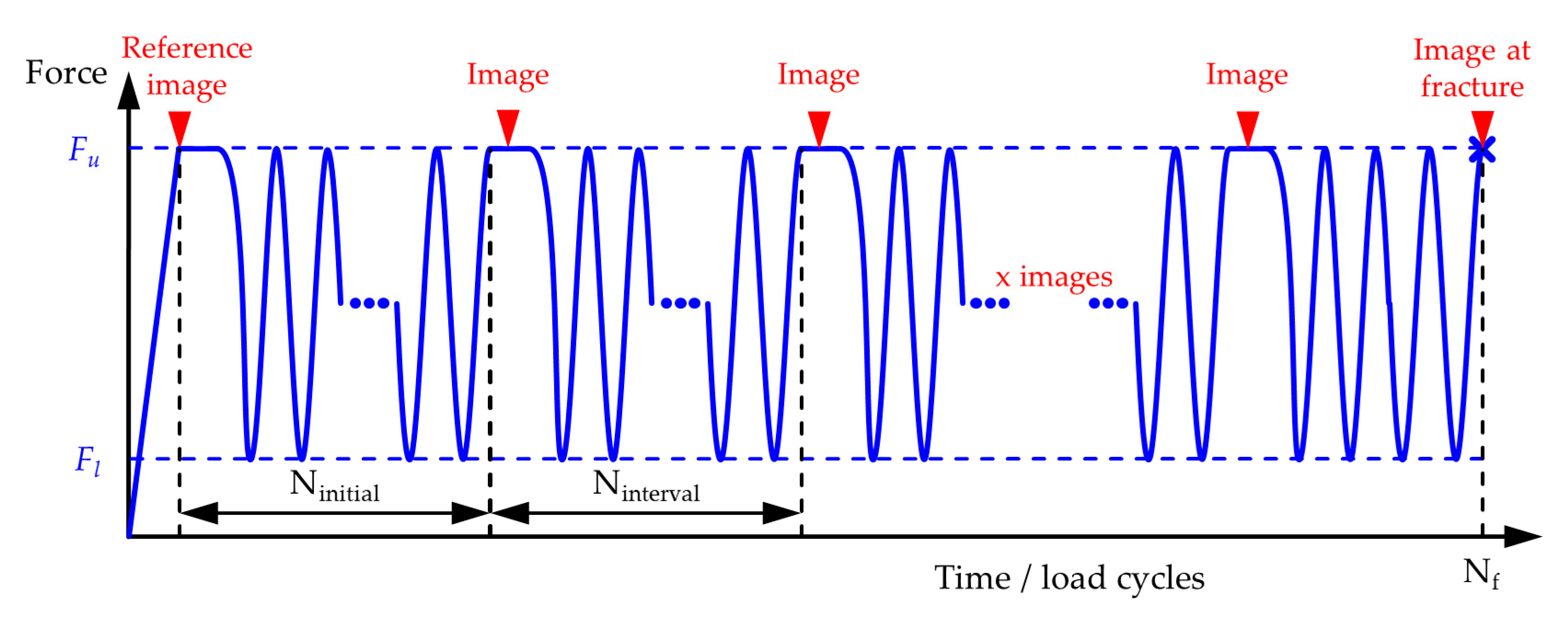
| Current Load Cycle Number N (–) | Interval between Image Acquisition Ninterval (–) | ||
|---|---|---|---|
| 0≤ | N | <100,000 | 2000 |
| 100,000≤ | N | <400,000 | 5000 |
| 400,000≤ | N | <800,000 | 10,000 |
| 800,000≤ | N | <1500,000 | 25,000 |
| 1500,000 ≤ | N | 50,000 | |
| Beach Mark | Measured Crack Length 2c (mm) | Assessed Crack Length 2c (mm) | Deviation (%) | |
|---|---|---|---|---|
| No. | N (–) | |||
| 1 | 740,000 | 17.94 | 18.23 | 1,62 |
| 2 | 700,000 | 11.98 | 11.97 | −0,08 |
| 3 | 660,000 | 9.52 | 9.52 | 0 |
| 4 | 620,000 | 8.00 | 7.92 | −1.00 |
| 5 | 580,000 | 6.84 | 6.72 | −1.75 |
| 6 | 540,000 | 6.00 | 6.00 | 0 |
| Specimen 1 | Specimen 2 | ||||
|---|---|---|---|---|---|
| Number of Load Cycles N (–) | Assessed Crack Length 2c (mm) | Measured Crack Length 2c after Final Rupture (mm) | Number of Load Cycles N (–) | Assessed Crack Length 2c (mm) | Measured Crack Length 2c after Final Rupture (mm) |
| 60,000 | 1.41 | 7.76 | 20,000 | - | 3.70 |
| 62,000 | 2.31 | 22,000 | - | ||
| 64,000 | 2.56 | 24,000 | 1.19 | ||
| 66,000 | 2.70 | 26,000 | 1.70 | ||
| 68,000 | 2.95 | 28,000 | 2.39 | ||
| 70,000 | 3.34 | 30,000 | 3.24 | ||
| 72,000 | 3.59 | 30,871 | 3.67 * | ||
| 74,000 | 3.98 | ||||
| 76,000 | 4.24 | ||||
| 78,000 | 4.49 | ||||
| 80,000 | 5.01 | ||||
| 82,000 | 5.65 | ||||
| 84,000 | 6.93 | ||||
| 85,039 | 7.66 * | ||||
| Evaluation Method | Crack Initiation | Burst Fracture | ||||
|---|---|---|---|---|---|---|
| Slope k (–) | FAT Value (MPa) | Scatter Index 1:Tσ (–) | Slope k (–) | FAT Value (MPa) | Scatter Index 1:Tσ (–) | |
| Nominal stress | 4.43 | 160 | 1.30 | 4.20 | 176 | 1.29 |
| Eff. notch stress (ρ* = 0.4 mm) | 4.68 | 307 | 1.16 | 4.46 | 337 | 1.15 |
| Eff. notch stress (ρ* = 0.3 mm) | 4.68 | 340 | 1.14 | 4.45 | 372 | 1.13 |
| Eff. notch stress (ρ* = 0.2 mm) | 4.66 | 392 | 1.11 | 4.44 | 427 | 1.10 |
| Eff. notch stress (ρ* = 0.13 mm) | 4.64 | 452 | 1.09 | 4.43 | 489 | 1.09 |
| Eff. notch stress (ρ* = 0.1 mm) | 4.62 | 489 | 1.08 | 4.43 | 523 | 1.10 |
| Notch stress (Kt) | 4.37 | 626 | 1.41 | 4.38 | 650 | 1.51 |
| Specimen No. | Kt (–) | Kf (–) | Δσeff (MPa) | Nth (–) | Nf (–) | Nth /Nf (%) | |
|---|---|---|---|---|---|---|---|
| ρ = 0.10 mm | ρ = 0.13 mm | ||||||
| 1 | 3.93 | 2.60 | 2.42 | 1453.5 | 10,000 | 23,497 | 43 |
| 4.50 | 2.69 | 2.49 | 1492.2 | 10,520 | - | - | |
| 2 | 3.37 | 2.36 | 2.21 | 884.5 | 142,840 | 199,292 | 71 |
| 3 | 3.97 | 2.60 | 2.40 | 479.8 | 1601,800 | 2281,981 | 70 |
| 4 | 5.61 | 2.89 | 2.63 | 1052.6 | 52,650 | 85,039 | 53 |
| 4.75 | 2.83 | 2.60 | 1039.5 | 58,530 | - | - | |
| 4.45 | 2.71 | 2.50 | 1001.2 | 67,580 | - | - | |
| 5 | 5.82 | 2.80 | 2.57 | 513.6 | 1596,300 | 2873,617 | 52 |
| 6 | 3.50 | 2.33 | 2.20 | 660.0 | 635,190 | 728,340 | 87 |
| 7 | 3.92 | 2.36 | 2.21 | 441.5 | 2610,560 | 3958,013 | 67 |
| 8 | 3.33 | 2.24 | 2.10 | 1259.4 | 24,000 | 37,839 | 66 |
| 4.60 | 2.40 | 2.20 | 1322.7 | 19,330 | - | - | |
| 9 | 3.81 | 2.49 | 2.30 | 1378.7 | 13,790 | 25,060 | 52 |
| 10 | 4.61 | 3.06 | 2.84 | 852.9 | 155,070 | 232,717 | 67 |
| Start Crack Length ainit (mm) | Start Load Cycle Number Nstart (–) | Parameters for Paris Law | SSE (–) | Statistical Evaluation of S-N Curve | |||||
|---|---|---|---|---|---|---|---|---|---|
| Material | CP | mP | Slope k (–) | FAT Value (MPa) | Scatter Index 1:Tσ (–) | ||||
| Case 1 | 0.5 | Nth | S1100 | 8.35×10−10 | 1.72 | 0.141 | 3.80 | 453 | 1.077 |
| Case 2 | 0.5 | Nth | IIW | 5.21×10−13 | 3.00 | 0.259 | 4.47 | 458 | 1.076 |
| Case 3 | 0.5 | Nth | Best fit | 1.78×10−13 | 2.90 | 0.065 | 4.17 | 467 | 1.084 |
| Case 4 | u + 0.1 | 0 | S1100 | 8.35×10−10 | 1.72 | 6.710 | 1.73 | 92 | 1.239 |
| Case 5 | u + 0.1 | 0 | IIW | 5.21×10−13 | 3.00 | 14.251 | 3.03 | 147 | 1.243 |
| Case 6 | u + 0.1 | 0 | Best fit | 1.00×10−13 | 2.85 | 0.985 | 2.92 | 339 | 1.255 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ottersböck, M.J.; Leitner, M.; Stoschka, M.; Maurer, W. Crack Initiation and Propagation Fatigue Life of Ultra High-Strength Steel Butt Joints. Appl. Sci. 2019, 9, 4590. https://doi.org/10.3390/app9214590
Ottersböck MJ, Leitner M, Stoschka M, Maurer W. Crack Initiation and Propagation Fatigue Life of Ultra High-Strength Steel Butt Joints. Applied Sciences. 2019; 9(21):4590. https://doi.org/10.3390/app9214590
Chicago/Turabian StyleOttersböck, Markus J., Martin Leitner, Michael Stoschka, and Wilhelm Maurer. 2019. "Crack Initiation and Propagation Fatigue Life of Ultra High-Strength Steel Butt Joints" Applied Sciences 9, no. 21: 4590. https://doi.org/10.3390/app9214590
APA StyleOttersböck, M. J., Leitner, M., Stoschka, M., & Maurer, W. (2019). Crack Initiation and Propagation Fatigue Life of Ultra High-Strength Steel Butt Joints. Applied Sciences, 9(21), 4590. https://doi.org/10.3390/app9214590






