Glottal Source Contribution to Higher Order Modes in the Finite Element Synthesis of Vowels †
Abstract
1. Introduction
2. Methodology
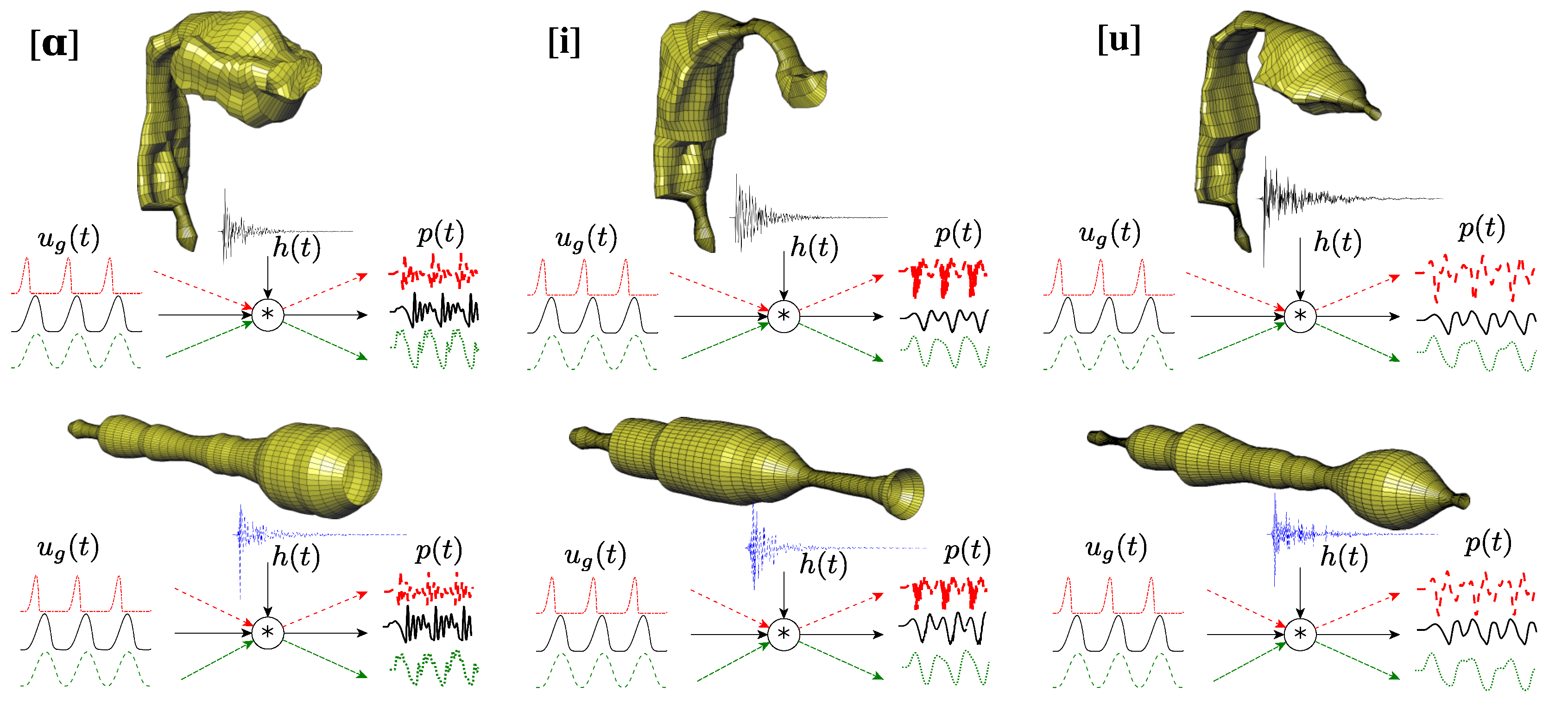
2.1. Vocal Tract Geometries
2.2. Vocal Tract Impulse Response
2.3. Voice Source Signal
2.4. Acoustic Analysis
3. Results
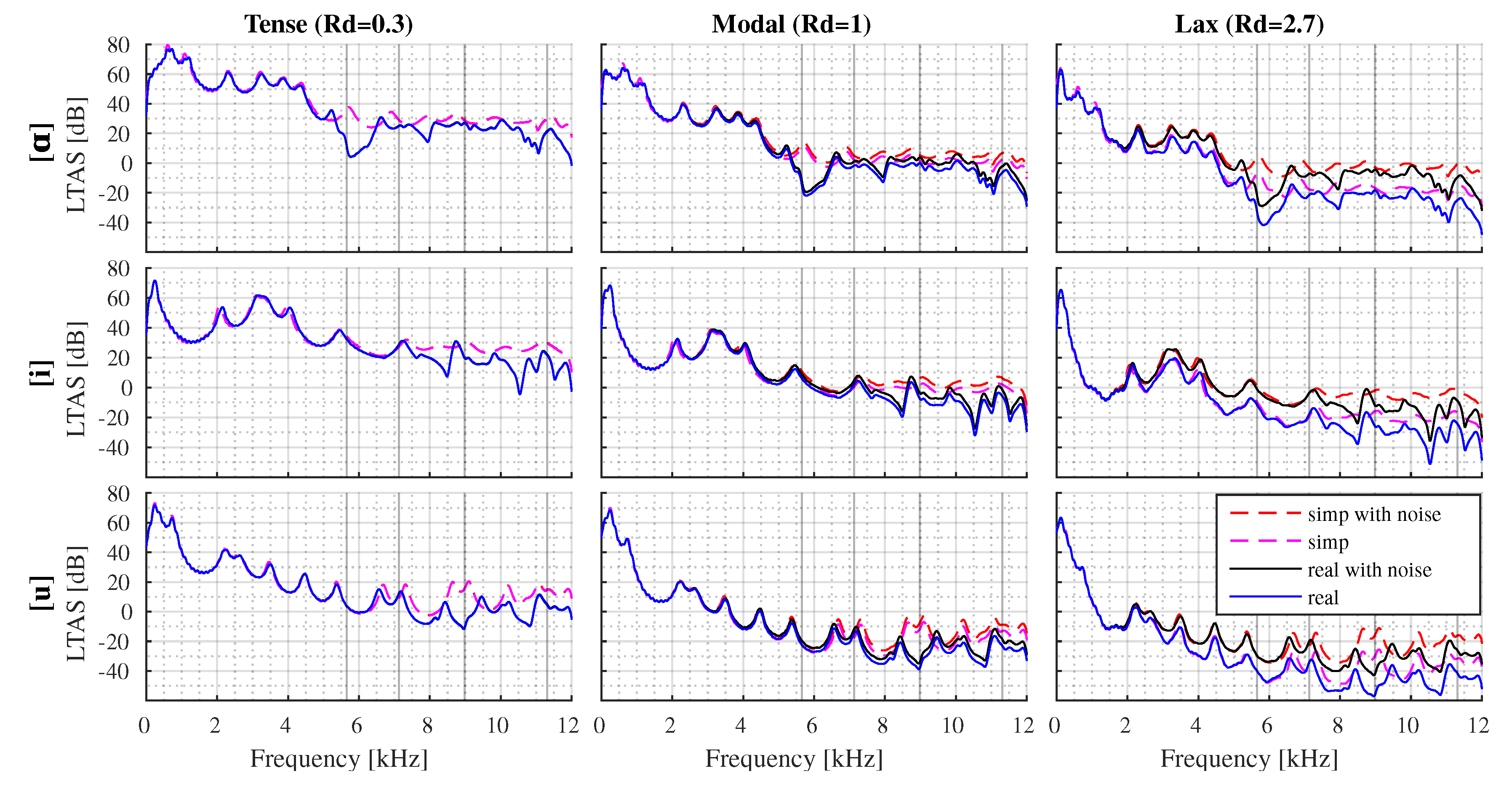
3.1. Analysis of Tense, Modal, and Lax Phonations for Fixed and Values
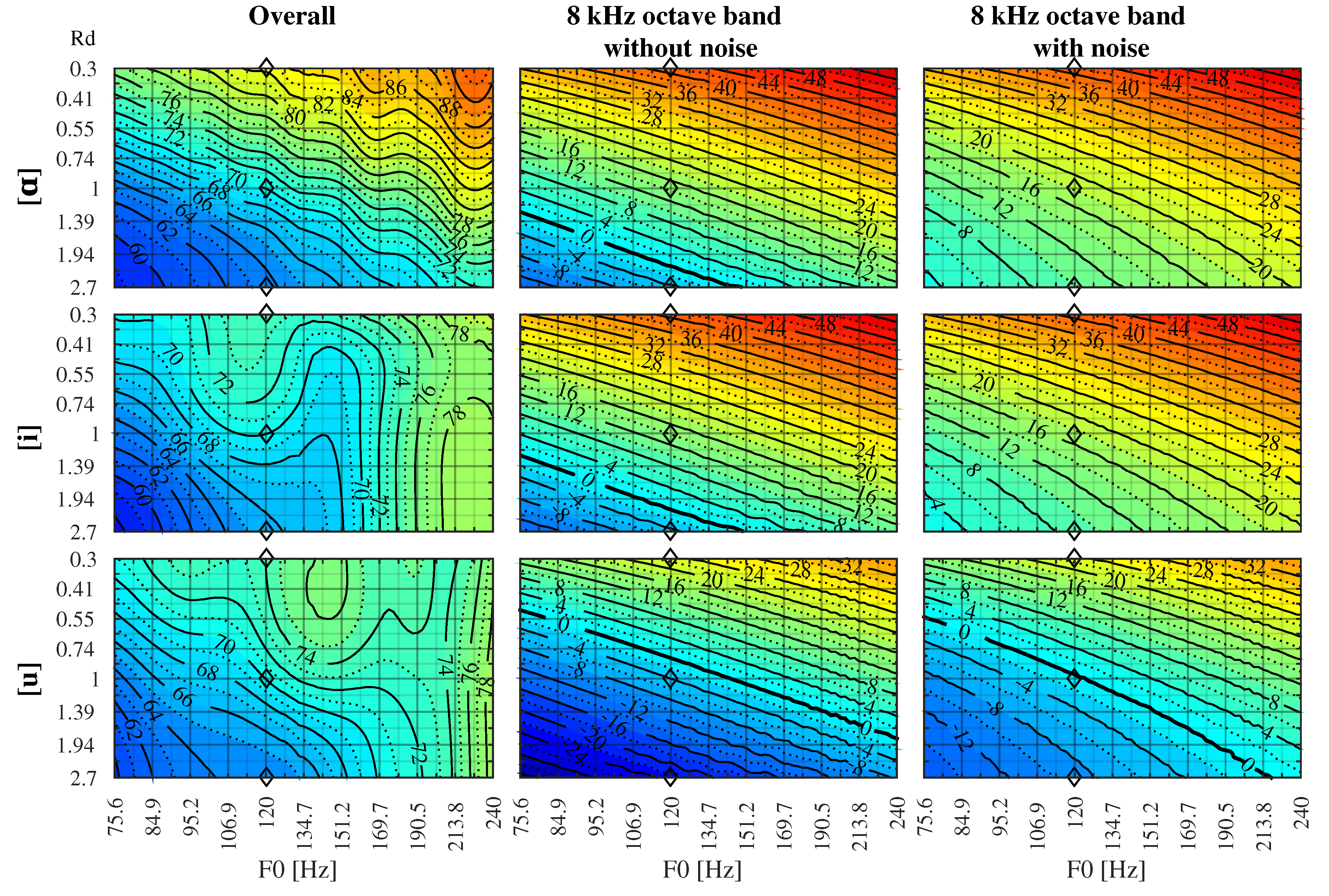
3.2. Analysis for the Whole Phonation Range
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| HFE | High Frequency Energy |
| FEM | Finite Element Method |
| LF | Liljencrants–Fant |
| MRI | Magnetic Resonance Imaging |
| PML | Perfectly Matched Layer |
| PSD | Power Spectral Density |
| LTAS | Long-Term Average Spectrum |
References
- Story, B.H. Phrase-level speech simulation with an airway modulation model of speech production. Comput. Speech Lang. 2013, 27, 989–1010. [Google Scholar] [CrossRef][Green Version]
- Birkholz, P. Modeling Consonant-Vowel Coarticulation for Articulatory Speech Synthesis. PLoS ONE 2013, 8, e60603. [Google Scholar] [CrossRef]
- Arnela, M.; Dabbaghchian, S.; Guasch, O.; Engwall, O. MRI-based vocal tract representations for the three-dimensional finite element synthesis of diphthongs. IEEE/ACM Trans. Audio Speech Lang. Process. 2019, 27, 2173–2182. [Google Scholar] [CrossRef]
- Blandin, R.; Arnela, M.; Laboissière, R.; Pelorson, X.; Guasch, O.; Hirtum, A.V.; Laval, X. Effects of higher order propagation modes in vocal tract like geometries. J. Acoust. Soc. Am. 2015, 137, 832–838. [Google Scholar] [CrossRef]
- Arnela, M.; Dabbaghchian, S.; Blandin, R.; Guasch, O.; Engwall, O.; Van Hirtum, A.; Pelorson, X. Influence of vocal tract geometry simplifications on the numerical simulation of vowel sounds. J. Acoust. Soc. Am. 2016, 140, 1707–1718. [Google Scholar] [CrossRef]
- Monson, B.B.; Hunter, E.J.; Lotto, A.J.; Story, B.H. The perceptual significance of high-frequency energy in the human voice. Front. Psychol. 2014, 5, 587. [Google Scholar] [CrossRef]
- Vampola, T.; Horáček, J.; Švec, J.G. FE Modeling of Human Vocal Tract Acoustics. Part I: Production of Czech vowels. Acta Acust. United Acust. 2008, 94, 433–447. [Google Scholar] [CrossRef]
- Takemoto, H.; Mokhtari, P.; Kitamura, T. Acoustic analysis of the vocal tract during vowel production by finite-difference time-domain method. J. Acoust. Soc. Am. 2010, 128, 3724–3738. [Google Scholar] [CrossRef]
- Arnela, M.; Blandin, R.; Dabbaghchian, S.; Guasch, O.; Alías, F.; Pelorson, X.; Van Hirtum, A.; Engwall, O. Influence of lips on the production of vowels based on finite element simulations and experiments. J. Acoust. Soc. Am. 2016, 139, 2852–2859. [Google Scholar] [CrossRef]
- Monson, B.B.; Lotto, A.J.; Ternström, S. Detection of high-frequency energy changes in sustained vowels produced by singers. J. Acoust. Soc. Am. 2011, 129, 2263–2268. [Google Scholar] [CrossRef]
- Arnela, M.; Guasch, O. Finite element computation of elliptical vocal tract impedances using the two-microphone transfer function method. J. Acoust. Soc. Am. 2013, 133, 4197–4209. [Google Scholar] [CrossRef]
- Fant, G.; Liljencrants, J.; Lin, Q. A four-parameter model of glottal flow. Speech Transm. Lab. Q. Prog. Status Rep. 1985, 26, 1–13. [Google Scholar]
- Murtola, T.; Alku, P.; Malinen, J.; Geneid, A. Parameterization of a computational physical model for glottal flow using inverse filtering and high-speed videoendoscopy. Speech Commun. 2018, 96, 67–80. [Google Scholar] [CrossRef]
- Erath, B.D.; Zañartu, M.; Stewart, K.C.; Plesniak, M.W.; Sommer, D.E.; Peterson, S.D. A review of lumped-element models of voiced speech. Speech Commun. 2013, 55, 667–690. [Google Scholar] [CrossRef]
- Murphy, A.; Yanushevskaya, I.; Chasaide, A.N.; Gobl, C. Rd as a Control Parameter to Explore Affective Correlates of the Tense-Lax Continuum. In Proceedings of the Interspeech 2017, Stockholm, Sweden, 20–24 August 2017; pp. 3916–3920. [Google Scholar] [CrossRef]
- Fant, G. The LF-model revisited. Transformations and frequency domain analysis. Speech Transm. Lab. Q. Prog. Status Rep. 1995, 36, 119–156. [Google Scholar]
- Freixes, M.; Arnela, M.; Socoró, J.C.; Alías, F.; Guasch, O. Influence of tense, modal and lax phonation on the three-dimensional finite element synthesis of vowel [A]. In Proceedings of the IberSPEECH 2018, Barcelona, Spain, 21–23 November 2018; pp. 132–136. [Google Scholar] [CrossRef]
- Aalto, D.; Aaltonen, O.; Happonen, R.P.; Jääsaari, P.; Kivelä, A.; Kuortti, J.; Luukinen, J.M.; Malinen, J.; Murtola, T.; Parkkola, R.; et al. Large scale data acquisition of simultaneous MRI and speech. Appl. Acoust. 2014, 83, 64–75. [Google Scholar] [CrossRef]
- Arnela, M.; Guasch, O.; Alías, F. Effects of head geometry simplifications on acoustic radiation of vowel sounds based on time-domain finite-element simulations. J. Acoust. Soc. Am. 2013, 134, 2946–2954. [Google Scholar] [CrossRef]
- Takemoto, H.; Adachi, S.; Mokhtari, P.; Kitamura, T. Acoustic interaction between the right and left piriform fossae in generating spectral dips. J. Acoust. Soc. Am. 2013, 134, 2955–2964. [Google Scholar] [CrossRef]
- Story, B.H.; Titze, I.R.; Hoffman, E.A. Vocal tract area functions from magnetic resonance imaging. J. Acoust. Soc. Am. 1996, 100, 537–554. [Google Scholar] [CrossRef]
- Kawahara, H.; Sakakibara, K.I.; Banno, H.; Morise, M.; Toda, T.; Irino, T. A new cosine series antialiasing function and its application to aliasing-free glottal source models for speech and singing synthesis. In Proceedings of the Interspeech 2017, Stockholm, Sweden, 20–24 August 2017; pp. 1358–1362. [Google Scholar] [CrossRef]
- Davis, P.J.; Rabinowitz, P. Methods of Numerical Integration; Courier Corporation: North Chelmsford, MA, USA, 2007. [Google Scholar]
- Gobl, C. Modelling aspiration noise during phonation using the LF voice source model. In Proceedings of the Interspeech 2006, Pittsburgh, PA, USA, 17–21 September 2006; pp. 965–968. [Google Scholar]
- Pabon, P.; Ternström, S. Feature Maps of the Acoustic Spectrum of the Voice. J. Voice 2018, in press. [Google Scholar] [CrossRef]
- Monson, B.B.; Lotto, A.J.; Story, B.H. Analysis of high-frequency energy in long-term average spectra of singing, speech, and voiceless fricatives. J. Acoust. Soc. Am. 2012, 132, 1754–1764. [Google Scholar] [CrossRef]

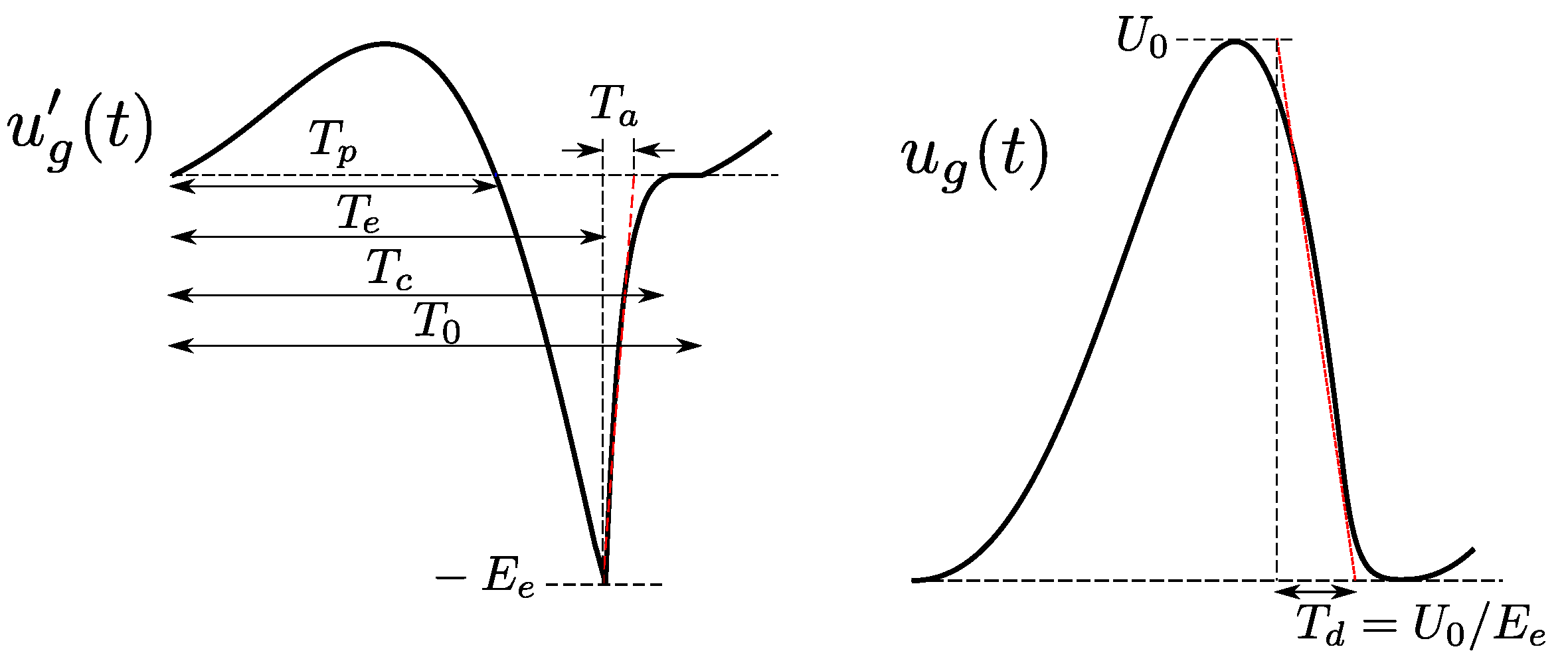
| Vowel | Geometry | Overall | 1/1 Octave Band | 1/3 Octave Band | |||
|---|---|---|---|---|---|---|---|
| 8 kHz | 6.3 kHz | 8 kHz | 10 kHz | ||||
| realistic | 0.3 | 82.3 (+0.0) | 41.5 (+0.2) | 35.3 (+0.1) | 37.6 (+0.2) | 37.2 (+0.2) | |
| 1.0 | 70.0 (+0.0) | 14.5 (+3.8) | 8.7 (+3.0) | 10.6 (+3.7) | 9.8 (+4.4) | ||
| 2.7 | 63.5 (+0.0) | −4.5 (+14.4) | −10.3 (+13.1) | −8.5 (+14.3) | −9.1 (+15.2) | ||
| simplified | 0.3 | 83.5 (+0.0) | 47.4 (+0.1) | 43.4 (+0.1) | 42.4 (+0.2) | 41.9 (+0.2) | |
| 1.0 | 71.4 (+0.0) | 20.5 (+3.5) | 17.0 (+2.8) | 15.3 (+3.6) | 14.5 (+4.4) | ||
| 2.7 | 64.9 (+0.0) | 1.6 (+13.8) | −1.8 (+12.4) | −3.7 (+14.3) | −4.4 (+15.3) | ||
| realistic | 0.3 | 73.6 (+0.0) | 41.0 (+0.2) | 37.0 (+0.1) | 37.9 (+0.2) | 31.8 (+0.2) | |
| 1.0 | 70.0 (+0.0) | 14.2 (+3.3) | 10.6 (+2.7) | 10.9 (+3.5) | 4.4 (+4.4) | ||
| 2.7 | 65.6 (+0.0) | −4.7 (+13.4) | −8.2 (+12.3) | −8.0 (+13.8) | −14.5 (+15.2) | ||
| simplified | 0.3 | 73.4 (+0.0) | 44.8 (+0.2) | 38.5 (+0.1) | 40.7 (+0.2) | 40.5 (+0.2) | |
| 1.0 | 70.0 (+0.0) | 17.8 (+3.7) | 12.2 (+2.7) | 13.7 (+3.6) | 13.1 (+4.4) | ||
| 2.7 | 65.6 (+0.0) | −1.0 (+14.0) | −6.6 (+12.2) | −5.0 (+13.8) | −5.7 (+15.2) | ||
| realistic | 0.3 | 74.0 (+0.0) | 22.8 (+0.2) | 19.6 (+0.1) | 16.3 (+0.2) | 18.0 (+0.3) | |
| 1.0 | 70.0 (+0.0) | −4.0 (+3.6) | −6.9 (+3.0) | −10.6 (+3.3) | −9.4 (+4.5) | ||
| 2.7 | 64.2 (+0.0) | −23.2 (+14.1) | −26.4 (+13.5) | −29.3 (+13.3) | −28.3 (+15.3) | ||
| simplified | 0.3 | 75.0 (+0.0) | 29.9 (+0.2) | 21.5 (+0.1) | 25.4 (+0.2) | 27.0 (+0.2) | |
| 1.0 | 71.1 (+0.0) | 2.7 (+4.0) | −5.2 (+3.2) | −1.7 (+3.7) | −0.4 (+4.4) | ||
| 2.7 | 64.2 (+0.0) | −16.0 (+14.4) | −23.6 (+12.6) | −20.5 (+14.2) | −19.2 (+15.1) | ||
| Vowel | 1/1 Octave Band | 1/3 Octave Band | ||
|---|---|---|---|---|
| 8 kHz | 6.3 kHz | 8 kHz | 10 kHz | |
| 6.0 (−0.2) | 8.2 (−0.2) | 4.8 (+0.0) | 4.7 (+0.0) | |
| 3.6 (+0.3) | 1.5 (+0.0) | 2.8 (+0.1) | 8.8 (+0.0) | |
| 6.8 (+0.4) | 1.8 (+0.0) | 9.2 (+0.3) | 9.0 (+0.0) | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Freixes, M.; Arnela, M.; Socoró, J.C.; Alías, F.; Guasch, O. Glottal Source Contribution to Higher Order Modes in the Finite Element Synthesis of Vowels. Appl. Sci. 2019, 9, 4535. https://doi.org/10.3390/app9214535
Freixes M, Arnela M, Socoró JC, Alías F, Guasch O. Glottal Source Contribution to Higher Order Modes in the Finite Element Synthesis of Vowels. Applied Sciences. 2019; 9(21):4535. https://doi.org/10.3390/app9214535
Chicago/Turabian StyleFreixes, Marc, Marc Arnela, Joan Claudi Socoró, Francesc Alías, and Oriol Guasch. 2019. "Glottal Source Contribution to Higher Order Modes in the Finite Element Synthesis of Vowels" Applied Sciences 9, no. 21: 4535. https://doi.org/10.3390/app9214535
APA StyleFreixes, M., Arnela, M., Socoró, J. C., Alías, F., & Guasch, O. (2019). Glottal Source Contribution to Higher Order Modes in the Finite Element Synthesis of Vowels. Applied Sciences, 9(21), 4535. https://doi.org/10.3390/app9214535







