Abstract
An air pollutant proxy is a mathematical model that estimates an unobserved air pollutant using other measured variables. The proxy is advantageous to fill missing data in a research campaign or to substitute a real measurement for minimising the cost as well as the operators involved (i.e., virtual sensor). In this paper, we present a generic concept of pollutant proxy development based on an optimised data-driven approach. We propose a mutual information concept to determine the interdependence of different variables and thus select the most correlated inputs. The most relevant variables are selected to be the best proxy inputs, where several metrics and data loss are also involved for guidance. The input selection method determines the used data for training pollutant proxies based on a probabilistic machine learning method. In particular, we use a Bayesian neural network that naturally prevents overfitting and provides confidence intervals around its output prediction. In this way, the prediction uncertainty could be assessed and evaluated. In order to demonstrate the effectiveness of our approach, we test it on an extensive air pollution database to estimate ozone concentration.
1. Introduction
Air pollution describes the presence of harmful substances in the atmosphere, which are detrimental to human health as well as the Earth’s climate. The World Health Organization (WHO) estimates that ~7 million people die every year from exposure to fine particles in polluted air. Such particles induce a variety of diseases such as strokes, heart diseases, lung cancer, chronic obstructive pulmonary diseases and respiratory infections, including pneumonia [1]. Furthermore, air pollution trace gases, such as ozone, has proven to accelerates the progression of emphysema of the lung [2]. In urban environments, air pollution is mostly generated from vehicle emission as well as industrial and domestic fossil fuel combustion [3]. Such processes, i.e., the extraction and burning of fossil fuels, also emit carbon dioxide (), which is found to be a key driver of climate change [4,5].
Air quality indicators are typically monitored by environmental or government authorities using networks of fixed monitoring stations [6], equipped with instruments specialised for measuring a number of pollutants, such as carbon monoxide (), nitrogen oxides (NOx), sulphur dioxide (), ozone () and particulate matter (PM) [7]. In practice, a comprehensive measurement covering a large area may not always be possible as air pollutant analysers are generally complicated, bulky and labour-intensive [7,8]. Furthermore, instrument failure, fault in data acquisition or data corruption often result in missing data during research campaigns or continuous measurements [9,10,11]. If the data gap is relatively large, interpolation methods become ineffective. As a result, these problems pose a significant obstacle for comprehensive air pollution data analysis and time series prediction scheme.
There are several solutions in order to deal with the aforementioned challenges, including low-cost air quality sensor networks [12], chemical transport simulation models [13] and satellite remote sensing data [14]. Here, we propose the solution by developing a pollutant proxy that is also known as a model or an estimator. A pollutant proxy can be defined as a mathematical model that estimates an unobserved air pollutant using other measured variables. Such a proxy acts as a virtual sensor or an expert system to fill missing data or to substitute one or more real measurements, thus the number of operated instruments can be minimised leading to a reduction in operational cost as well as the operators involved. Therefore, the area with pollution information can also be widened. A pollutant proxy is also useful to support scientists in studying the impact of relevant variables to pollutants. Their relationship can be simulated and then analysed.
Physics-based approaches are usually first to solve the aforementioned problems. These are models based on the fundamental description of atmospheric physical and chemical processes, such as Lagrangian and Eulerian models [15]. However, this approach is very computationally demanding. Simple statistical predictive models are usually the next attempt to solve the aforementioned problems, such as described in Clifford et al. [16], Mølgaard et al. [17], von Bismarck-Osten et al. [18], Khalil et al. [19], Alghamdi et al. [20]. However, these proxies may not always be suitable or perform well due to the poor input choice, nonlinearity in data and the complexity in establishing appropriate physics-based models.
As an alternative approach, data-driven methods have recently gained much attention for developing pollutant proxies. For examples, various types of data-driven proxies were developed based on adaptive neuro-fuzzy inference by Taylan [21], artificial neural network (ANN) by Gao et al. [22], Arroyo et al. [23], support vector machine (SVM) by Ortiz-García et al. [24] and based on ANN and SVM by Luna et al. [25]. However, those methods mainly attempt to use all input combinations to obtain the best model performance during the training phase. This method may not always be effective for large data sets because of the computational cost and analysis issues. Recently, a large number of instruments involved in research campaigns as well as continuous measurements produces massive amounts of data. Additionally, many developed methods are mostly based on deterministic data-driven approaches where these proxies only estimate mean values of pollutant concentrations. Consequently, these proxies are unable to evaluate and assess the estimation uncertainty. For instance, if there is a sudden increase of pollutant concentration estimation, it is not possible to assess its confidence interval [26,27]. Therefore, additional measurements and validation may be required to confirm the estimation.
The main contributions of this paper lie in dealing with the aforementioned problems as part of design solutions. First, we apply mutual information (MI) method for selecting appropriate data as proxy inputs. This method is also complemented by the evaluation of performance metrics as well as data loss accumulation to select the number of maximum inputs involved. Second, a probabilistic machine learning (ML) method is implemented, where in this case we use a Bayesian neural network (BNN). Neural networks (NNs) have been a popular choice among ML methods for approximating complex functions [28] and have been used in a wide variety of problems in various disciplines [29]. However, standard NNs general formulation typically gives single point based output estimates. The Bayesian inference implementation in the NNs does not solely prevent overfitting in the training phase, but it also provides confidence interval around its prediction [30,31,32]. Third, this work is a continuation of our previous work in developing proxy [20] that was based on physics-based approaches using an extensive air pollution measurement campaign database. In this work, using the same data sets, we demonstrate that the proposed data-driven-based proxy outperforms the previous developed proxy. Finally, we discuss the practical implementation on deploying the developed proxy including the compromise between an automatic input selector based MI and the number of used instruments for minimising the costs as well as the number of operators involved, so as to gain maximum benefit in practice.
2. Methods
This section describes our proposed methodology for developing a pollutant proxy. Figure 1 presents a generic data-driven-based methodology for a pollutant proxy development and deployment. The concept is mainly based on two key approaches. The first is called a mutual information (MI) approach that is used to select the most relevant proxy inputs. The second is a probabilistic machine learning (ML) method that is used to model an air pollutant.
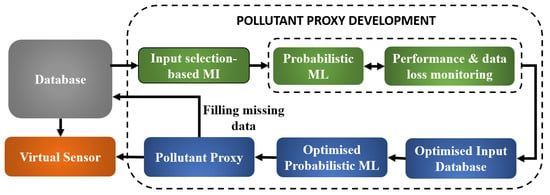
Figure 1.
The block diagram of general methodology for pollutant proxy development.
Having a large amount of field measurement data, the first step is to explore the available database. For example, data analysis is typically performed to understand data statistical properties, such as mean, standard deviation, minimum and maximum values of each variable, the number of missing data, the linear correlation, etc. From data exploration, it is known how one measured variable is related to other measured variables. Standard correlation methods, such as Pearson correlation coefficient (PCC), is typically applied. However, as air pollution is a complex process, the relationship between the measured variables may not always be linear. Therefore, we complement the correlation analysis by an information theory-based technique, named mutual information (MI), to search relevant measured variables correlated linearly and nonlinearly to an air pollutant to be modelled.
From the data exploration, it is known that there is a substantial amount of missing data. To solve the problem in practice, an additional guidance method is required for inputs selection. When generating a proxy, we are often limited to the measurement period during which data of all variables exist (i.e., the data with same time index). This leads to fewer data points available as the inputs for training phase of the pollutant proxy. The missing data scenario results in significant data loss for the training purposes. Furthermore, the use of a large number of inputs typically increases the model complexity leading to poor proxy performance. Limiting the number of inputs also allows the proxy to be used flexibly without relying on many other measurements in practice. Therefore, it is vital to consider these effects when determining the number of inputs involved in modelling, shown as the box of performance and data loss monitoring in Figure 1. The selected input data is then used for ML training and validation data. Finally the results are validated and analysed. This whole process can be called pollutant proxy development. The development results in the pollutant proxy where it can then be deployed for filling the missing data in the database and/or act as a virtual sensor.
2.1. Input Selector: Mutual Information
The mutual information (MI) of two random variables is a measure of the mutual dependence between these two variables. MI is thus a method for measuring the degree of relationship between data sets. This method has been widely used in various modern disciplines of science and technology, such as medical imaging [33], search engine [34] and DNA sequencing [35]. In the field related to atmospheric and environmental sciences, MI has been introduced to large data sets to detect nonlinear relationship between new-particle formation and other ambient variables in Hyytiälä Forest, Finland, as described in our previous work [36]. In this case, we adopt the same strategy for finding the relationship between a pollutant proxy and other measured variables.
The concept of MI is depicted in Figure 2. Suppose X and Y are the measured variables and the variable of interest. The area covered by red and orange is the entropy of X, , whereas the area covered by yellow and orange represents the entropy of Y, . The red area is the conditional entropy of X given by Y, , whereas the yellow area is the conditional entropy of Y given by X, . The area contained by both circles is the joint entropy and the orange area is the mutual information between X and Y, . Therefore, MI can be found by calculating
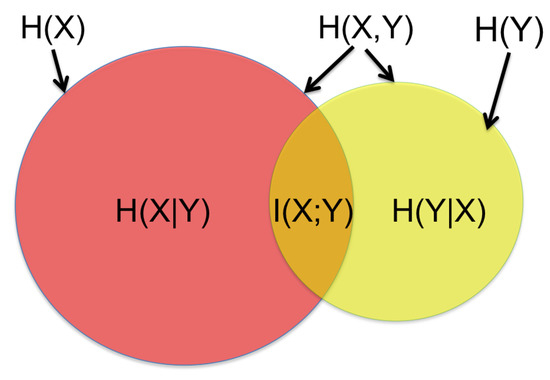
Figure 2.
Venn diagram of entropy properties. is the mutual information between entropy X and Y, symbolised by and , respectively.
As used in Zaidan et al. [36], we also adopt a nearest-neighbour MI implementation based on Kraskov et al. [37]. The nearest neighbour concept assumes the space . We can rank for each point , its neighbours by distance and similar rankings can also be done for the subspaces X and Y. So, the distance can then be found by finding the maximum norm: where the distance from to its kth neighbour is denoted by . The MI estimation is then given by
where the symbol represents the digamma function. N is the number of all data points and k constitutes the number of nearest neighbours (the user choice). Parameters is the number of point whose distance from is strictly less than , and similarly for y instead of x. The symbol denotes the averages both over all data points N. The can then be normalised between 0 and 1 by a scaling factor [38], so the final MI formulation is given by
where symbol sign represents a signum function and notation is the absolute value. The mathematical details of the used MI method can be found in Kraskov et al. [37], and its implementation in this field can be found in Zaidan et al. [36].
2.2. Probabilistic Machine Learning: Bayesian Neural Networks
Machine learning (ML) infers plausible models to explain observed data where the models are capable to make predictions about unseen data and take decisions that are rational given these predictions. However, there are many forms of uncertainty in modelling, such as measurement noise and model general structure. Probabilistic modelling framework takes into account the uncertainty in modelling by using probability theory to express all forms of uncertainty [39]. One of the most popular ML methods is neural networks [28]. The rise of deep learning and related methods have made neural network based approaches become even more popular [40,41]. However, their standard implementations are mostly based on deterministic methods, providing point-based estimations [42]. Although, there are many strategies in preventing overfitting, such as cross-validation, early stopping and regularisation, the standard implementation does not provide confidence-interval around its prediction. A Bayesian neural network (BNN) is a type of probabilistic modelling method [43], and here we adopt this method for estimating pollutant concentration. However, other types of probabilistic models may also be applicable if they are implemented appropriately.
BNNs were popularised by MacKay [44], Neal [45]. The methods have been advancing since then to cope with many issues, such as challenging inference and computational costs. Several improved BNN versions have been developed, including variational inference [46], sampling-based variational inference [47] and expectation propagation [48]. In this case, we adopt one of the most recent version of BNNs where it uses dropout applied before every weight layer as Bayesian approximation [49]. For the case of a single hidden layer, dropout NN structure can be shown mathematically as
where and are output and input models, respectively. The notation of is a weight matrix connecting the first layer to the hidden layer and is a matrix connecting the hidden layer to the output layer. The symbol is K dimensional vector biases, whereas is a nonlinear activation function. Dropout can be applied through the sampling of two binary vectors and of dimensions Q and K, respectively. They are modelled as Bernoulli distribution with some parameters . The process can be repeated for multiple layers. To optimise the weights, regularisation weighted by some decay is used, given by
where L is the total number of layers and E is Euclidean loss, defined by
that is, simply the loss function between the predicted and the real data. New realisations are sampled for the binary vectors for every input point and every forward pass when evaluating the model’s output, and the same values are also used in the backward pass. The architecture of dropout NN based method is depicted in Figure 3. The use of dropout, applied before every weight layer, trained in deep NN with arbitrary depth and nonlinearity has been shown as approximate Bayesian inference in deep Gaussian process. As the posterior distributions of weight matrices, , are intractable, variational inference [50,51] is applied to approximate the distributions. The details of the approximate predictive distribution and other mathematical formulations are described in Gal and Ghahramani [49], whereas the implementation, such as designing network architecture and its inference, is done in an open source machine learning library called PyTorch [52].
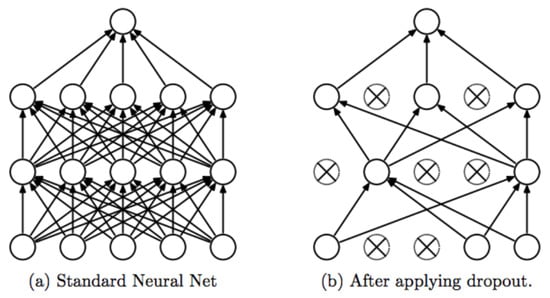
Figure 3.
The difference between standard NN and Dropout NN [53]. Dropout method randomly drops units (along with their connections) from the NN during training, which prevents units from learning too much and thus potentially avoid overfitting. The dropout NN can also be seen as BNN.
3. Case Study
In this section, we explain a case study, including the sampling site and the data sets used for evaluating the proposed method. The proposed pollutant proxy is tested using an extensive measurement data obtained in Jeddah, Saudi Arabia. In particular, we choose to develop a proxy of Ozone () concentration, but the proposed method is also generic for other types of air pollutant.
The used data set is one of the most comprehensive measurement in the Middle Eastern region [54]. The sampling was performed in an urban background area of Jeddah city, Kingdom of Saudi Arabia (Figure 4). The site is located at 21.4869° N, 39.2517° E and the altitude is 38.7 m above sea level. The measurement site is about 105 m and 1.7 km to the nearest road and the major highway, respectively. The measurements were performed at the height of 3.5 m and 6.7 m for gaseous air pollutants and meteorological parameters above the ground level, respectively. The sampling originally took place from 31 July 2011 to 28 February 2013. However, the concentration data is only available for 258 days.
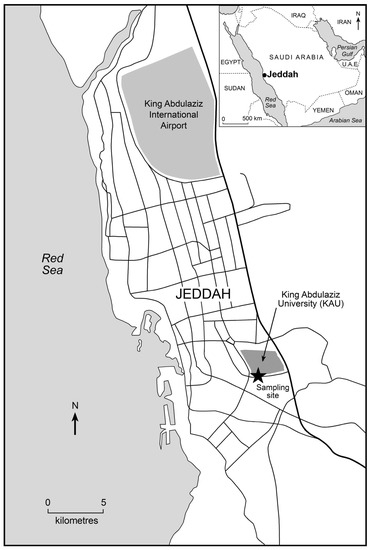
Figure 4.
Map of Jeddah with the sampling site marked with a star [54]. Map data ©Google, 2013 Terra Metrics.
A variety of scientific instruments were involved in the measurement campaign. concentration was monitored by an UV Absorption Ozone Analyser (Model 400E, Teledyne Technologies Company, San Diego, CA, USA), whereas , and concentrations were measured using a chemiluminescence // analyser (Model 200E, Teledyne Technologies Company, San Diego). Syntech Spectras BTEX analyser GC 955, type 600 (Syntech Spectras, Groningen, the Netherlands) was used to measure a specific volatile organic compound (VOC) concentrations, that are benzene, toluene, ethylbenzene and xylenes (BTEX). Particulate matter concentrations, such as PM, PM and PM, and the number concentration (TC) of particles in the diameter size range of to 32 m were measured with one-minute average by an optical scattering spectrometer (EDM-180D, Grimm Aerosol, Germany). A solar radiation sensor (Vantage Pro2™Accessories, Davis Instruments, Hayward, CA, USA) was used for continuous measurement of solar radiation. Finally, meteorological variables, such as wind speed, temperature and relative humidity, were measured using Lufft WS600-UMB Compact Weather Station. The detailed explanation of the sampling site, data sets and the instruments used in this research campaign can be found in the previous works by Alghamdi et al. [54,55], Hussein et al. [56].
concentration is the major gas component of air pollution in cities. Among other photochemical oxidants, is one of the widely studied subjects worldwide under the category of air pollution [20]. For example, air pollution in Jeddah was investigated by analysing temporal variations of and [54] and formation affected by benzene, toluene, ethylbenzene and xylenes [55].
Several reasons motivate this study to establish an proxy as the case study. First, there are missing values spread across the data, including a large number of concentration data, due to the instruments maintenance as well as other issues [56]. The proxy is expected to contribute in filling the missing data to allow better air pollution analysis. Second, the cost operation of official air pollution monitoring stations is typically high due to the number of instruments used. To substitute monitoring, the proxy can be deployed to mimic the real measurement based on “Ozone Analyzer”. In this way, the number of instruments involved can be minimised. As a result, the operational cost can be reduced and the number of monitoring stations can be scaled up. Finally, human involvement is typically required to operate some instruments, including “Ozone Analyzer” [57]. The proxy acts as a virtual sensor where the number of operators can be reduced. The aforementioned proxy advantages can be even greater if the proxy is deployed in one or several long-term continuous measurement stations.
4. Results and Discussion
This section comprises three subsections. First, we describe data analysis to get insight about the available database. Second, the results of proxy implementation and its performance are presented and explained. Finally, we discuss about the proxy deployment in practice.
4.1. Data Analysis
Linear correlation analysis is performed on every measured variables in the database. As described in Section 2, we also perform an additional MI analysis to ensure all possible relationships are captured between measured variables, either linear or nonlinear. Pearson correlation coefficient (PCC) is used here representing linear correlation method whereas mutual information (MI) acts as a nonlinear method. To make both methods comparable, as described in Zaidan et al. [36], we take absolute values of PCC because MI does not capture the correlation direction. In this case, the correlation direction is insignificant to be analysed because the air pollutant proxy will be modelled based on a black block approach (i.e., ML). Figure 5 shows the correlation analysis in the form of matrix plots. It can be seen that the linear correlation method (a) does not find strong correlation between and several variables that are known to be connected to formation, such as and . On the other hand, MI method (b) demonstrates that presents good connection to these two variables.
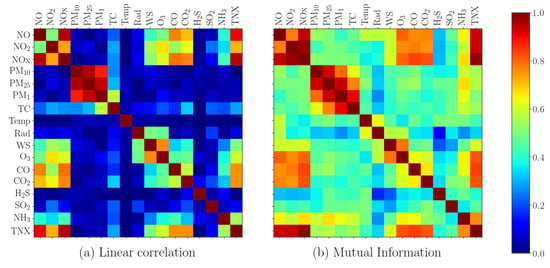
Figure 5.
Matrix plot correlation analysis between ozone () and other measured variables. It can be seen that linear correlation (a) does not capture well the relationship between and other measured variables, such as m,p-xylene (TNX), and .
From the MI scores, the variables that share the highest correlation to are , wind speed (WS), m,p-Xylene (TNX) and . It is well known from previous studies [20,58,59] that is strongly connected to and as well as concentrations. Furthermore, TNX was found as the largest contributor to formation [55]. However, the relationship between these concentrations cannot be captured well by PCC analysis as shown in Figure 5.
Figure 6 presents the scatter plots of some selected variables. It can be seen that the three variables (e.g., , and TNX) are shaped to a specific pattern (i.e., exponential functions), indicating that they correlate nonlinearly to concentration (these variables also behave nonlinearly in logarithmic scale). Their linear correlation coefficients and MI scores are also not similar. Nevertheless, both methods are able to capture good linear correlation between and wind speed (WS) at R and MI = 0.79. WS has been known to affect concentration in urban area as described in previous studies, such as explained by Hidy [60] and Klein et al. [61]. In summary, the use of MI allows the detection of linear and nonlinear correlation between variables of interest where the correlated variables can then be used as potential inputs for the pollutant proxy.
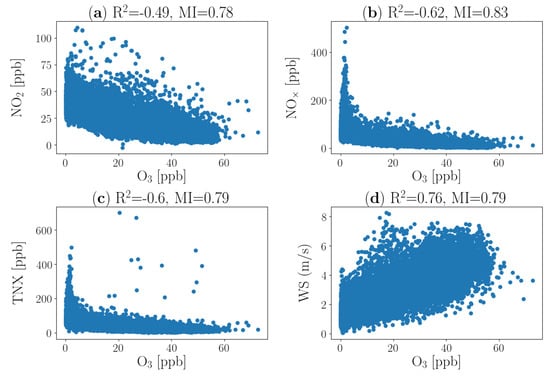
Figure 6.
The scatter plot between concentration and several selected variables, including , wind speed, m,p-Xylene (TNX) and . R is Pearson correlation coefficient (PCC), whereas MI is mutual information score. The concentration unit of trace gases and TNX is in part per billion (ppb) whereas the unit of wind speed is in m/s.
4.2. Performance Analysis
The results of the previous subsection justify our choice to utilise the strength of MI method for proxy inputs selection as proposed in Section 2. This subsection presents several results obtained from the proposed proxy development.
Figure 7 presents the rank of MI score of the measured variables correlated to concentration. The variables with high MI score indicate the higher association with the concentration. Based on the bar chart, we can select the appropriate inputs for training the pollutant proxy. We first explore the possibility to divide the proxies into two: day and night proxies as previously proposed in our previous work [20], and then also generate one single full day proxy. Therefore, MI between concentration and other measured variables are applied on data sets for entire day, day only and night only. Figure 7 shows the MI level between and other measured variables for two main types of proxy. The subplot (a) is the MI level for a full day analysis, whereas the subplots (b) and (c) constitute the MI level for day and night measurements, respectively. The analysis for the subplot (a) is used to select the inputs for the single proxy, whereas information on the subplots (b) and (c) are utilised to select the divided proxy. It is noted that the bar chart results also support the scientific findings discovered earlier in the previous section.
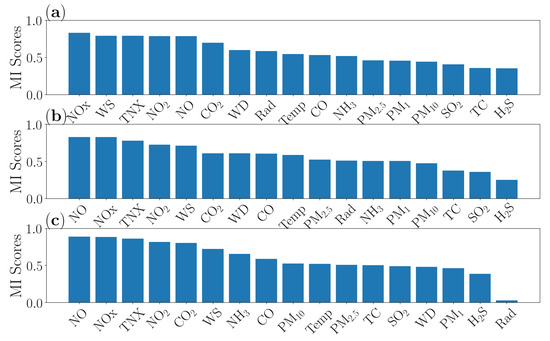
Figure 7.
Mutual information level between ozone concentration and other measured variables on full day (a), day only (b) and night only (c).
All proxies use at least two inputs at the first modelling attempt and then the inputs fed into BNN training following the order as shown in Figure 7. In order to evaluate the developed proxies, three types of performance metric are used. The first metric is called mean absolute error (MAE). It has a simple interpretation as the average absolute difference between the predicted proxy values () and the real measurement data points (). It can be defined mathematically as
where , y and n are the predicted value from proxy, the real measurement value and the number of data points, respectively. The second metric is root-mean-squared error (RMSE) that is also known as the standard deviation of the residuals (prediction errors). It is given by
The third metric is called coefficient of determination, denoted by R. It provides a measure of how well observed outcomes are replicated by the proxy, based on the proportion of total variation of outcomes explained by the proxy. It can be defined as
where is the mean of the number of measurement data points, .
Figure 8 shows proxy performance metrics and the percentage of data loss. The Figure 8a demonstrates the proxy performance after incorporating different number of inputs into BNN, including MAE, RMSE and R. It is known that incorporating more inputs into ML models improves their performance generally, as shown in Figure 8a. Figure 8b demonstrates that after incorporating four input variables, the model performance still improves, but the number of data loss increases significantly, i.e., to be almost 80% because the need to find some common training data from all variables used in the training process. In a real-world problem, this is not always possible, some data points may be missing from several measurements at different time frames. As a result, the number of data points may be very less when we take many inputs into the ML training process. Using the remaining data that is less than 80% may not be optimal in data-driven approach because the use of more data is a key in proxy training. The good performance obtained may be because the number of validation data points becomes much fewer. It can also be seen that when the number of inputs is increased to be 10, the proxy performance deteriorates rapidly because there are not enough validation points at all.
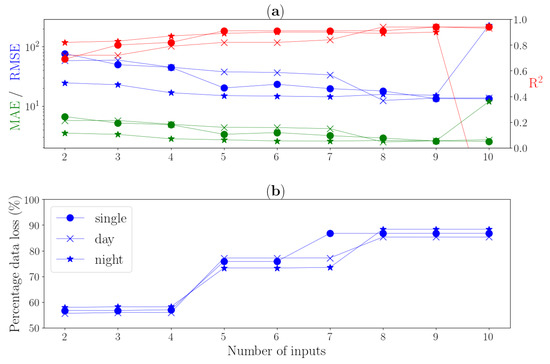
Figure 8.
Proxy performance metrics and the percentage of data loss evaluated on testing data. In the subplot (a), the green, blue and red constitute the metrics of Mean Absolute Error (MAE), Root-Mean-Squared Error (RMSE) and coefficient of determination (R), respectively. The subplot (b) presents the percentage of data loss due to the involvement of more input numbers. For both subplots as shown the legend in subplot (b), the symbols ◯, × and ⋆ denotes the performances of single, day and night models, respectively.
Furthermore, the use of many input variables is also impractical when deploying the proxy. The deployed proxy will require many instruments working simultaneously at the same location to supply the same type of input data used in the training. Using many inputs from instruments indicates that the developed proxy is becoming less independent from real measurements. The real value of having a pollutant proxy will then be less because the deploying cost would rise. Therefore, as a compromise, we determine to select the number of inputs to be four. In this case, the number of missing data excluded can be minimised and we can still gain relatively good proxy performance.
After all, we decided to exclude the two separate proxies, i.e., day and night models. The main reason is that the proxy performances do not vary significantly between the single proxy and the coupled proxies as shown in Figure 8. Therefore, for simplification, we will present the results of single proxy only from now on.
A brute-force method is used to search the most optimal architecture of the BNN structure. In this case, we found that the best network consists of one hidden layer with rectifier activation functions and linear output layer. The hidden layer comprises 100 neurons, but the “drop-out” method (with 50% initial drop-out rate) is also applied as explained earlier to remove unnecessary neurons. For optimisation, an adaptive learning rate optimisation algorithm (Adam) [62] is used for tuning the BNN parameters. Once the top four inputs are selected, we applied cross-validation methods to find the optimal training/testing data that generate the best BNN. However, we found that this implementation does not result in significant difference in term of performance. It is also preferred to have continuous training and testing data in this case. Hence, we determine the used training data is from 21 December 2011 until 21 July 2012 whereas the validation data is selected from 22 July 2012 until 10 October 2012. This selection constitutes 70% training and 30% testing data. In this work, we do not compare the proposed probabilistic ML method with other ML methods, as the focus emphasises the concept of proxy development. The concept should be generic to be applied on other types of air pollutant proxy with different ML methods.
As discussed earlier, the objective of deploying proxy is to reduce the number of operated instruments in an air pollution station, and then to minimises the cost as well as the operators involved in the measurement processes. Table 1 displays the performance metrics of different inputs combination from the selected proxy inputs. Please note that the inputs of and are not separated since they are measured from the same instrument. From Figure 5, it is found that TNX correlates highly with which is another input of the proxy. Therefore, this variable can be discarded. It can be seen in the table’s last row that, by excluding TNX input, a very similar proxy performance can still be gained. This means that the optimal proxy can be deployed by utilising only two instruments: the // analyser and a WS measurement device. The following results will then present only the three inputs based proxy that are , and WS.

Table 1.
The above table shows that the combination of the best four variables to understand the impact of proxy performance by reducing the required instruments for computing proxy.
Figure 9 presents a fraction of the time series results of real measurement of concentration (red) and its proxy (blue) as well as its confidence interval (light green). Even though the prediction does not fit perfectly the real measurement data, some parts of predicted uncertainty capture the real data. Furthermore, it can be seen that the proxy tracks very well the concentration pattern, which is a good successful indicator from the developed proxy performance. The full time series data is not displayed because it is visually unclear to plot the whole time series of validation data set.
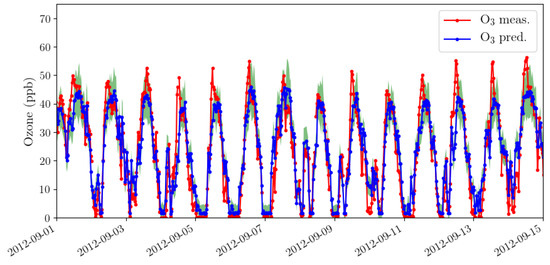
Figure 9.
The time series data of real measurement (red), the estimation (blue) produced by the BNN and its confidence interval (light green).
To understand the overall performance of developed model, we produce a regression plot and an error histogram as shown in Figure 10. Regression plot, subplot (a), displays the scatter plot between the measured (x-axis) and the estimated (y-axis). The light blue represents 2 uncertainty around the mean of predictive distribution. It can be seen that the majority of estimations lie within 2 of uncertainty. Furthermore, the obtained R performance is at on the scatter plot that is considerably higher than considering the simple dual model (day and night) as our previous work presented (R) by Alghamdi et al. [20]. The error histogram, subplot (b), displays the difference between the measured and estimated concentration. The evaluation through error histogram is also promising because it follows a Normal distribution where the peak is centred around zero with standard deviation is only ~5 parts per billion (ppb).
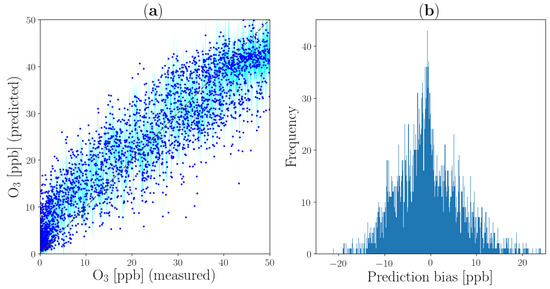
Figure 10.
Regression plot (a) and the prediction bias (b) between the test data of concentration measurement and the estimated concentration generated by BNN.
4.3. Discussion
As mentioned earlier, in addition of filling missing data, an air pollutant proxy is advantageous for several reasons. This subsection discusses two scenarios where the developed proxy is beneficial to be deployed in practice. The first scenario is related to the proxy deployment in an official air pollution monitoring station. It is known that the pollutant concentration differs between weekend and weekday, as well as day and night, due to the variation of traffic volumes in big cities [63]. An investigation of weekday and weekend differences in – levels is an important indicator to understand whether has its origin in local photochemical production or in transport processes [54,64]. Figure 11 presents the average of the measured and estimated concentration on weekday and weekend. It can be seen that lower levels and higher values at weekends than on weekdays took place in Jeddah. This phenomenon is common to be observed mainly within areas with an influence from urban emissions. This occurs due to weekly changes in emissions from human activities. The relationship of emission–concentration relationship at urban, suburban and rural sites is discussed in Stephens et al. [65]. Considering the significance of having both measurements of and concentration, the developed proxy performance on the is evaluated on the concentration characteristic in the area as shown in Figure 11. It can be seen clearly that our developed estimated concentration fits very well the average measurement data on weekday and weekend. This suggests that the developed proxy is reliable and accurate as the substitution of real measurement. Having the virtual measurement is then beneficial to study the pollutant sources by reducing the cost and operator involvement.
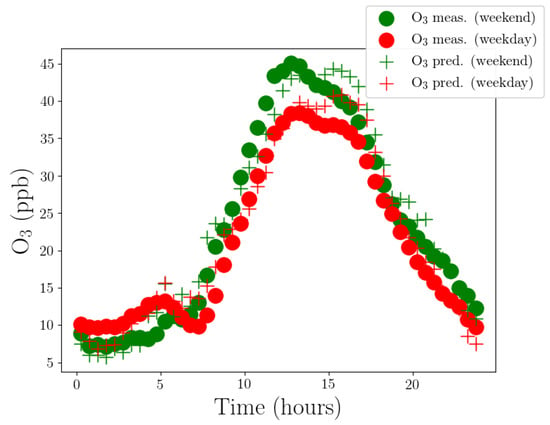
Figure 11.
The average of the measurement and estimation of Ozone concentration from two different models on weekday and weekend.
The second scenario concerns the proxy deployment to complement low-cost sensor measurements in dense air pollution networks. Air quality networks in cities are usually sparse because air pollution is difficult to measure, instrumental and operational costs of official measurement stations are typically expensive [66]. On the other hand, air pollutant concentrations vary highly over both space and time [67]. Therefore, real-time and high-resolution measurements are then required that enable the mapping of air pollutants and air quality index in higher resolution. Over the last few years, the deployment of low cost sensors have been assessed for their viability in monitoring ambient air quality [68]. However, their accuracy and reliability are still challenging. For example, although testing low-cost sensors demonstrates good performance under controlled labouratory conditions [69], their performances decline significantly under field conditions [70,71]. The performance degradation is mainly related to interference with other air pollutants as well as with meteorological conditions [72,73,74,75]. Therefore, it is also advantageous to substitute low-cost sensors by proxies. Although low-cost WS devices are also available, such as described in Pan et al. [76], but this variable may be neglected as the proxy input because the proxy performance is still reasonable well (see Table 1). The proxy can then be deployed by taking inputs from the measurements of low-cost // sensors. The combination of low-cost sensors and virtual sensors is promising because virtual sensors are not affected directly by physical sensor failures and environmental conditions. However, the proxy accuracy might drift over time because there may be new measured data that has not been involved at all in the process of proxy development, which is known as extrapolation. This phenomenon can be detected through uncertainty quantification from the probabilistic ML based proxy and then the proxy can be retrained and updated accordingly.
5. Conclusions
This paper demonstrates the development of an air pollutant proxy based on data-driven methods. The deployment of air pollutant proxy is beneficial to replace missing data, to substitute a real measurement that are typically expensive and required operators and to be embedded in low-cost sensors as a virtual sensor. This work presents two main contributions in air pollutant proxy development: (1) mutual information (MI) for selecting appropriate inputs and (2) the proxy based on a probabilistic ML that is a Bayesian neural network (BNN).
The MI method demonstrates the effectiveness in finding other relevant variables to a pollutant to be modelled (as a proxy) where standard correlation method is unable to discover them. The proposed method guarantees to capture linear and nonlinear relationship among the variables. The most relevant variables as the proxy inputs are determined based on several highest MI scores obtained and based on proxy performance metrics as well as data loss monitoring. For practicality, the selected proxy inputs are then evaluated based on the number of instruments involved and their respective performance metrics. In this way, testing all combinations of measured variables can be avoided. A probabilistic ML method, named BNN, is then used to establish a pollutant proxy. The proposed method offers confidence interval for further analysis. The use of Bayesian method also prevents overfitting naturally due to the presence of regularisation and dropout method.
In particular, establishing an concentration proxy is selected as a case study. The and other variables’ databases are obtained from an extensive air pollution research campaign in Jeddah, Saudi Arabia. The MI application in the data results in the associated variables to which have also been reported in other studies separately. The variables are , , WS and TNX. The overall implementation of our proposed methodology on the case study leads to adequate performance in general and the obtained results are also considerably better in comparison with the previous attempt using the same dataset. As this is a general methodology, the strategy is also promising to be adopted to estimate any other types of air pollutant concentration.
Several future works can be continued from this approach. First, the proxy performance and accuracy can still be improved. The slight bias in the proposed proxy might take place due to the presence of autocorrelated effect in the data or the drifting in other measured variables. The former can be solved by applying dynamic ML models where they typically accommodate some previous steps of historical data in model inputs and outputs into the model. The latter can be checked by diagnosing the drift. For example, anomalies in the variables involved should be detected in the estimation given the absent of ground truth which can be performed using a predictive distribution analysis. If the drifting occurs, the remedy is then to develop an adaptive proxy which is capable to modify automatically its parameters based on the nature change in the data. Second, the capability of developed proxy has a potential to be enhanced for acting as a pollutant forecasting. Therefore, the proxy does not only estimate the current pollutant concentration, but also forecast it a couple of hours/days in advance, so better mitigation can be taken by policy makers. This can be done by applying MI between variables at different times for analysing and determining the dynamic relationships between air pollution variables. Then, the proxy can be upgraded into a dynamic model, such as Bayesian recurrent neural network (BRNN). In this case, a forecast proxy is fitted on newly available data prior to each prediction. Third, the developed proxy may not work well in other geographical locations. The proxy needs to be improved to ensure that it works robustly at other sites too. The involvement of Bayesian method in the proxy already allows the evaluation of the drifting effect which inform about the model performance through its uncertainty quantification. In addition, the proxy needs to be upgraded into a dynamic model as mentioned earlier. This makes the proxy becoming more adaptive because the model is updated when there is new data coming into the proxy. The involvement of additional inputs, such as meteorological variables, will also produce a generalised proxy, because these types of input distinguish different sites. However, the proxy needs to be trained at several different locations. Fourth, the extra measurements should be carried out in the same location using low-cost sensor devices next to the reference station. the developed proxy is then taken inputs from low-cost sensors’ measurements as inputs. In this way, we can further validate the usefulness of our proxy. Finally, as the developed method is generic, the proposed concept should be applied to the same/different types of air pollutant in same or different cities/regions.
Author Contributions
M.A.Z. and T.H. designed the study. M.A.Z. developed the methodology, applied it on the case study and performed analysis. T.H. and L.D. suggested the use of experimental data. M.A.A., H.A.-J., H.L., A.H. and T.H. carried out the experiment. M.A.Z., L.D. and T.H. contributed to the interpretation of the data and the results. All authors contributed to writing the manuscript.
Funding
This research was part of a close collaboration between King Abdulaziz University and the Institute for Atmospheric and Earth System Research (INAR/Physics) University of Helsinki via ERA-PLANET (www.era-planet.eu), transnational project SMURBS (www.smurbs.eu) (Grant Agreement n. 689443), funded under the EU Horizon 2020 Framework Programme and Academy of Finland via the Center of Excellence in Atmospheric sciences (grant no. 272041) and NanoBioMass (project number 1307537). The first author (M.A.Z.) was supported by the Academy of Finland Centre of Excellence in Atmospheric Sciences (project number 307331) and the EU Urban Innovative Actions via HOPE project (grant number UIA03-240). The research campaign was funded by Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, under grant no. (I-122-30). The authors acknowledge with thanks DSR for technical and financial support. This manuscript was written and completed during the sabbatical leave of the last author’s (T.H.) that was spent at the University of Helsinki and supported by the University of Jordan during 2019.
Acknowledgments
The authors acknowledge use of the CSC-IT Center for Science Ltd. Finland for computational resources.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BNN | Bayesian Neural Network |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| MI | Mutual Information |
| NN | Neural Network |
| Nitric oxide | |
| Nitrogen dioxide | |
| Nitrogen oxides | |
| Ozone | |
| PCC | Pearson Correlation Coefficient |
| ppb | part per billion |
| RMSE | Root Mean Squared Error |
| SVM | Support Vector Machine |
| TNX | Xylene |
| WS | Wind Speed |
| WHO | World Health Organization |
References
- WHO Global Ambient Air Quality Database. Available online: https://www.who.int/airpollution/data/en/ (accessed on 17 August 2019).
- Wang, M.; Aaron, C.P.; Madrigano, J.; Hoffman, E.A.; Angelini, E.; Yang, J.; Laine, A.; Vetterli, T.M.; Kinney, P.L.; Sampson, P.D.; et al. Association between long-term exposure to ambient air pollution and change in quantitatively assessed emphysema and lung function. JAMA 2019, 322, 546–556. [Google Scholar] [CrossRef] [PubMed]
- Cairncross, E.K.; John, J.; Zunckel, M. A novel air pollution index based on the relative risk of daily mortality associated with short-term exposure to common air pollutants. Atmos. Environ. 2007, 41, 8442–8454. [Google Scholar] [CrossRef]
- Helmers, E.; Leitão, J.; Tietge, U.; Butler, T. CO2-equivalent emissions from European passenger vehicles in the years 1995–2015 based on real-world use: Assessing the climate benefit of the European “diesel boom”. Atmos. Environ. 2019, 198, 122–132. [Google Scholar] [CrossRef]
- Rockström, J.; Schellnhuber, H.J.; Hoskins, B.; Ramanathan, V.; Schlosser, P.; Brasseur, G.P.; Gaffney, O.; Nobre, C.; Meinshausen, M.; Rogelj, J.; et al. The world’s biggest gamble. Earth’s Future 2016, 4, 465–470. [Google Scholar] [CrossRef]
- Mølgaard, B.; Birmili, W.; Clifford, S.; Massling, A.; Eleftheriadis, K.; Norman, M.; Vratolis, S.; Wehner, B.; Corander, J.; Hämeri, K.; et al. Evaluation of a statistical forecast model for size-fractionated urban particle number concentrations using data from five European cities. J. Aerosol Sci. 2013, 66, 96–110. [Google Scholar] [CrossRef]
- Kumar, P.; Morawska, L.; Martani, C.; Biskos, G.; Neophytou, M.; Di Sabatino, S.; Bell, M.; Norford, L.; Britter, R. The rise of low-cost sensing for managing air pollution in cities. Environ. Int. 2015, 75, 199–205. [Google Scholar] [CrossRef]
- Chong, C.Y.; Kumar, S.P. Sensor networks: Evolution, opportunities, and challenges. Proc. IEEE 2003, 91, 1247–1256. [Google Scholar] [CrossRef]
- Junninen, H.; Niska, H.; Tuppurainen, K.; Ruuskanen, J.; Kolehmainen, M. Methods for imputation of missing values in air quality data sets. Atmos. Environ. 2004, 38, 2895–2907. [Google Scholar] [CrossRef]
- Rohde, R.A.; Muller, R.A. Air pollution in China: Mapping of concentrations and sources. PLoS ONE 2015, 10, e0135749. [Google Scholar] [CrossRef]
- Junger, W.; De Leon, A.P. Imputation of missing data in time series for air pollutants. Atmos. Environ. 2015, 102, 96–104. [Google Scholar] [CrossRef]
- Strigaro, D.; Cannata, M.; Antonovic, M. Boosting a weather monitoring system in low Income economies using open and non-conventional systems: data quality analysis. Sensors 2019, 19, 1185. [Google Scholar] [CrossRef] [PubMed]
- Carnevale, C.; Finzi, G.; Pisoni, E.; Volta, M.; Guariso, G.; Gianfreda, R.; Maffeis, G.; Thunis, P.; White, L.; Triacchini, G. An integrated assessment tool to define effective air quality policies at regional scale. Environ. Model. Softw. 2012, 38, 306–315. [Google Scholar] [CrossRef]
- Gupta, P.; Christopher, S.A.; Wang, J.; Gehrig, R.; Lee, Y.; Kumar, N. Satellite remote sensing of particulate matter and air quality assessment over global cities. Atmos. Environ. 2006, 40, 5880–5892. [Google Scholar] [CrossRef]
- Sofiev, M.; Galperin, M.; Genikhovich, E. A construction and evaluation of Eulerian dynamic core for the air quality and emergency modelling system SILAM. In Air Pollution Modeling and Its Application XIX; Springer: New York, NY, USA, 2008; pp. 699–701. [Google Scholar]
- Clifford, S.; Choy, S.L.; Hussein, T.; Mengersen, K.; Morawska, L. Using the generalised additive model to model the particle number count of ultrafine particles. Atmos. Environ. 2011, 45, 5934–5945. [Google Scholar] [CrossRef]
- Mølgaard, B.; Hussein, T.; Corander, J.; Hämeri, K. Forecasting size-fractionated particle number concentrations in the urban atmosphere. Atmos. Environ. 2012, 46, 155–163. [Google Scholar] [CrossRef]
- Von Bismarck-Osten, C.; Birmili, W.; Ketzel, M.; Weber, S. Statistical modelling of aerosol particle number size distributions in urban and rural environments—A multi-site study. Urban Clim. 2015, 11, 51–66. [Google Scholar] [CrossRef]
- Khalil, M.; Butenhoff, C.L.; Harrison, R. Ozone balances in urban Saudi Arabia. NPJ Clim. Atmos. Sci. 2018, 1, 27. [Google Scholar] [CrossRef]
- Alghamdi, M.A.; Al-Hunaiti, A.; Arar, S.; Khoder, M.; Abdelmaksoud, A.S.; Al-Jeelani, H.; Lihavainen, H.; Hyvärinen, A.; Shabbaj, I.I.; Almehmadi, F.M.; et al. A predictive model for steady state ozone concentration at an urban-coastal site. Int. J. Environ. Res. Public Health 2019, 16, 258. [Google Scholar] [CrossRef]
- Taylan, O. Modelling and analysis of ozone concentration by artificial intelligent techniques for estimating air quality. Atmos. Environ. 2017, 150, 356–365. [Google Scholar] [CrossRef]
- Gao, M.; Yin, L.; Ning, J. Artificial neural network model for ozone concentration estimation and Monte Carlo analysis. Atmos. Environ. 2018, 184, 129–139. [Google Scholar] [CrossRef]
- Arroyo, Á.; Herrero, Á.; Tricio, V.; Corchado, E.; Woźniak, M. Neural models for imputation of missing ozone data in air-quality datasets. Complexity 2018, 2018, 7238015. [Google Scholar] [CrossRef]
- Ortiz-García, E.; Salcedo-Sanz, S.; Pérez-Bellido, Á.; Portilla-Figueras, J.; Prieto, L. Prediction of hourly O3 concentrations using support vector regression algorithms. Atmos. Environ. 2010, 44, 4481–4488. [Google Scholar] [CrossRef]
- Luna, A.; Paredes, M.; De Oliveira, G.; Corrêa, S. Prediction of ozone concentration in tropospheric levels using artificial neural networks and support vector machine at Rio de Janeiro, Brazil. Atmos. Environ. 2014, 98, 98–104. [Google Scholar] [CrossRef]
- Li, S.T.; Shue, L.Y. Data mining to aid policy making in air pollution management. Expert Syst. Appl. 2004, 27, 331–340. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X.; Guo, Z.; Lu, H. Developing an early-warning system for air quality prediction and assessment of cities in China. Expert Syst. Appl. 2017, 84, 102–116. [Google Scholar] [CrossRef]
- Maren, A.J.; Harston, C.T.; Pap, R.M. Handbook of Neural Computing Applications; Academic Press: New York, NY, USA, 2014. [Google Scholar]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H.; De Jesús, O. Neural Network Design; PWS Publishing Company: Boston, MA, USA, 2014; Volume 20, pp. 1.5–1.7. [Google Scholar]
- Zaidan, M.A.; Mills, A.R.; Harrison, R.F. Bayesian framework for aerospace gas turbine engine prognostics. In Proceedings of the 2013 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013; pp. 1–8. [Google Scholar]
- Zaidan, M.A.; Harrison, R.F.; Mills, A.R.; Fleming, P.J. Bayesian hierarchical models for aerospace gas turbine engine prognostics. Expert Syst. Appl. 2015, 42, 539–553. [Google Scholar] [CrossRef]
- Zaidan, M.; Haapasilta, V.; Relan, R.; Junninen, H.; Aalto, P.; Kulmala, M.; Laurson, L.; Foster, A. Predicting atmospheric particle formation days by Bayesian classification of the time series features. Tellus B Chem. Phys. Meteorol. 2018, 70, 1–10. [Google Scholar] [CrossRef]
- Diamant, I.; Klang, E.; Amitai, M.; Konen, E.; Goldberger, J.; Greenspan, H. Task-driven dictionary learning based on mutual information for medical image classification. IEEE Trans. Biomed. Eng. 2017, 64, 1380–1392. [Google Scholar] [CrossRef]
- Almasri, M.; Berrut, C.; Chevallet, J.P. A comparison of deep learning based query expansion with pseudo-relevance feedback and mutual information. In European Conference on Information Retrieval; Springer: Cham, Switzerland, 2016; pp. 709–715. [Google Scholar]
- Jiao, D.; Han, W.; Ye, Y. Functional association prediction by community profiling. Methods 2017, 129, 8–17. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Haapasilta, V.; Relan, R.; Paasonen, P.; Kerminen, V.M.; Junninen, H.; Kulmala, M.; Foster, A.S. Exploring nonlinear associations between atmospheric new-particle formation and ambient variables: A mutual information approach. Atmos. Chem. Phys. 2018, 18, 12699–12714. [Google Scholar] [CrossRef]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- Numata, J.; Ebenhöh, O.; Knapp, E.W. Measuring correlations in metabolomic networks with mutual information. In Genome Informatics 2008: Genome Informatics Series Vol. 20; World Scientific: Singapore, 2008; pp. 112–122. [Google Scholar]
- Ghahramani, Z. Probabilistic machine learning and artificial intelligence. Nature 2015, 521, 452. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Kendall, A.; Gal, Y. What uncertainties do we need in Bayesian deep learning for computer vision? In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017; pp. 5574–5584. [Google Scholar]
- Zaidan, M.A.; Canova, F.F.; Laurson, L.; Foster, A.S. Mixture of clustered Bayesian neural networks for modeling friction processes at the nanoscale. J. Chem. Theory Comput. 2016, 13, 3–8. [Google Scholar] [CrossRef]
- MacKay, D.J. A practical Bayesian framework for backpropagation networks. Neural Comput. 1992, 4, 448–472. [Google Scholar] [CrossRef]
- Neal, R. Bayesian Learning for Neural Networks. Ph.D. Thesis, Department of Computer Science, University of Toronto, Toronto, ON, Canada, 1995. [Google Scholar]
- Barber, D.; Bishop, C.M. Ensemble learning in Bayesian neural networks. Nato ASI Ser. F Comput. Syst. Sci. 1998, 168, 215–238. [Google Scholar]
- Paisley, J.; Blei, D.M.; Jordan, M.I. Variational Bayesian inference with stochastic search. In Proceedings of the International Conference on Machine Learning (ICML), Edinburgh, Scotland, 26 June–1 July 2012; Citeseer: University Park, PA, USA, 2012. [Google Scholar]
- Hernández-Lobato, J.M.; Adams, R. Probabilistic backpropagation for scalable learning of Bayesian neural networks. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1861–1869. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1050–1059. [Google Scholar]
- Zaidan, M.A.; Mills, A.R.; Harrison, R.F.; Fleming, P.J. Gas turbine engine prognostics using Bayesian hierarchical models: A variational approach. Mech. Syst. Signal Process. 2016, 70, 120–140. [Google Scholar] [CrossRef]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in PyTorch. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Alghamdi, M.; Khoder, M.; Harrison, R.M.; Hyvärinen, A.P.; Hussein, T.; Al-Jeelani, H.; Abdelmaksoud, A.; Goknil, M.; Shabbaj, I.; Almehmadi, F.; et al. Temporal variations of O3 and NOx in the urban background atmosphere of the coastal city Jeddah, Saudi Arabia. Atmos. Environ. 2014, 94, 205–214. [Google Scholar] [CrossRef]
- Alghamdi, M.; Khoder, M.; Abdelmaksoud, A.; Harrison, R.; Hussein, T.; Lihavainen, H.; Al-Jeelani, H.; Goknil, M.; Shabbaj, I.; Almehmadi, F.; et al. Seasonal and diurnal variations of BTEX and their potential for ozone formation in the urban background atmosphere of the coastal city Jeddah, Saudi Arabia. Air Qual. Atmos. Health 2014, 7, 467–480. [Google Scholar] [CrossRef]
- Hussein, T.; Alghamdi, M.A.; Khoder, M.; AbdelMaksoud, A.S.; Al-Jeelani, H.; Goknil, M.K.; Shabbaj, I.I.; Almehmadi, F.M.; Hyvärinen, A.; Lihavainen, H.; et al. Particulate matter and number concentrations of particles larger than 0.25 μm in the urban atmosphere of Jeddah, Saudi Arabia. Aerosol Air Qual. Res. 2014, 14, 1383–1391. [Google Scholar] [CrossRef]
- Sklaveniti, S.; Locoge, N.; Stevens, P.S.; Wood, E.; Kundu, S.; Dusanter, S. Development of an instrument for direct ozone production rate measurements: Measurement reliability and current limitations. Atmos. Meas. Tech. 2018, 11, 741–761. [Google Scholar] [CrossRef]
- Melkonyan, A.; Kuttler, W. Long-term analysis of NO, NO2 and O3 concentrations in North Rhine-Westphalia, Germany. Atmos. Environ. 2012, 60, 316–326. [Google Scholar] [CrossRef]
- Hagenbjörk, A.; Malmqvist, E.; Mattisson, K.; Sommar, N.J.; Modig, L. The spatial variation of O3, NO, NO2 and NOx and the relation between them in two Swedish cities. Environ. Monit. Assess. 2017, 189, 161. [Google Scholar] [CrossRef]
- Hidy, G. Ozone process insights from field experiments—Part I: Overview. Atmos. Environ. 2000, 34, 2001–2022. [Google Scholar] [CrossRef]
- Klein, P.M.; Hu, X.M.; Xue, M. Impacts of mixing processes in nocturnal atmospheric boundary layer on urban ozone concentrations. Bound.-Layer Meteorol. 2014, 150, 107–130. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimisation. In Proceedings of the 3rd International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Blanchard, C.L.; Tanenbaum, S.; Lawson, D.R. Differences between weekday and weekend air pollutant levels in Atlanta; Baltimore; Chicago; Dallas–Fort Worth; Denver; Houston; New York; Phoenix; Washington, DC; and surrounding areas. J. Air Waste Manag. Assoc. 2008, 58, 1598–1615. [Google Scholar] [CrossRef]
- Tzima, F.A.; Mitkas, P.A.; Voukantsis, D.; Karatzas, K. Sparse episode identification in environmental datasets: The case of air quality assessment. Expert Syst. Appl. 2011, 38, 5019–5027. [Google Scholar] [CrossRef]
- Stephens, S.; Madronich, S.; Wu, F.; Olson, J.; Ramos, R.; Retama, A.; Munoz, R. Weekly patterns of México City’s surface concentrations of CO, NOx, PM10 and O3 during 1986–2007. Atmos. Chem. Phys. 2008, 8, 5313–5325. [Google Scholar] [CrossRef]
- Mijling, B.; Jiang, Q.; De Jonge, D.; Bocconi, S. Field calibration of electrochemical NO2 sensors in a citizen science context. Atmos. Meas. Tech. 2018, 11, 1297–1312. [Google Scholar] [CrossRef]
- Afshar-Mohajer, N.; Zuidema, C.; Sousan, S.; Hallett, L.; Tatum, M.; Rule, A.M.; Thomas, G.; Peters, T.M.; Koehler, K. Evaluation of low-cost electro-chemical sensors for environmental monitoring of ozone, nitrogen dioxide, and carbon monoxide. J. Occup. Environ. Hyg. 2018, 15, 87–98. [Google Scholar] [CrossRef] [PubMed]
- Popoola, O.A.; Carruthers, D.; Lad, C.; Bright, V.B.; Mead, M.I.; Stettler, M.E.; Saffell, J.R.; Jones, R.L. Use of networks of low cost air quality sensors to quantify air quality in urban settings. Atmos. Environ. 2018, 194, 58–70. [Google Scholar] [CrossRef]
- Rai, A.C.; Kumar, P.; Pilla, F.; Skouloudis, A.N.; Di Sabatino, S.; Ratti, C.; Yasar, A.; Rickerby, D. End-user perspective of low-cost sensors for outdoor air pollution monitoring. Sci. Total Environ. 2017, 607, 691–705. [Google Scholar] [CrossRef]
- Broday, D.; Citi-Sense Project Collabourators. Wireless distributed environmental sensor networks for air pollution measurement—The promise and the current reality. Sensors 2017, 17, 2263. [Google Scholar] [CrossRef]
- Mukherjee, A.; Stanton, L.; Graham, A.; Roberts, P. Assessing the utility of low-cost particulate matter sensors over a 12-week period in the Cuyama Valley of California. Sensors 2017, 17, 1805. [Google Scholar] [CrossRef]
- Aleixandre, M.; Gerboles, M. Review of small commercial sensors for indicative monitoring of ambient gas. Chem. Eng. Trans 2012, 30. [Google Scholar]
- Spinelle, L.; Gerboles, M.; Aleixandre, M. Performance evaluation of amperometric sensors for the monitoring of O3 and NO2 in ambient air at ppb level. Procedia Eng. 2015, 120, 480–483. [Google Scholar] [CrossRef]
- Spinelle, L.; Gerboles, M.; Villani, M.G.; Aleixandre, M.; Bonavitacola, F. Field calibration of a cluster of low-cost available sensors for air quality monitoring. Part A: Ozone and nitrogen dioxide. Sens. Actuators B Chem. 2015, 215, 249–257. [Google Scholar] [CrossRef]
- Spinelle, L.; Gerboles, M.; Villani, M.G.; Aleixandre, M.; Bonavitacola, F. Field calibration of a cluster of low-cost commercially available sensors for air quality monitoring. Part B: NO, CO and CO2. Sens. Actuators B Chem. 2017, 238, 706–715. [Google Scholar] [CrossRef]
- Pan, Y.; Zhao, Z.; Zhao, R.; Fang, Z.; Wu, H.; Niu, X.; Du, L. High accuracy and miniature 2-D wind sensor for boundary layer meteorological observation. Sensors 2019, 19, 1194. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).