Exploiting Deep Learning for Wind Power Forecasting Based on Big Data Analytics
Abstract
1. Introduction
2. Related Work
3. Contributions
- A novel big data-driven wind power prediction model is proposed that combines the strengths of both the univariate and multivariate wind power forecasting techniques by using decomposed and exogenous inputs for forecasting; consequently, the forecasting accuracy is significantly enhanced.
- The proposed model employs an existing method wavelet packet decomposition and an enhanced method Efficient DCNN (EDCNN) for feature extraction and forecasting, respectively.
- A DSM algorithm is also proposed. The proposed DSM algorithm takes into account the day-ahead demand, day-ahead price and wind power.
- The proposed DSM algorithm reduces the consumption cost and improves the load profile to almost a normal shape.
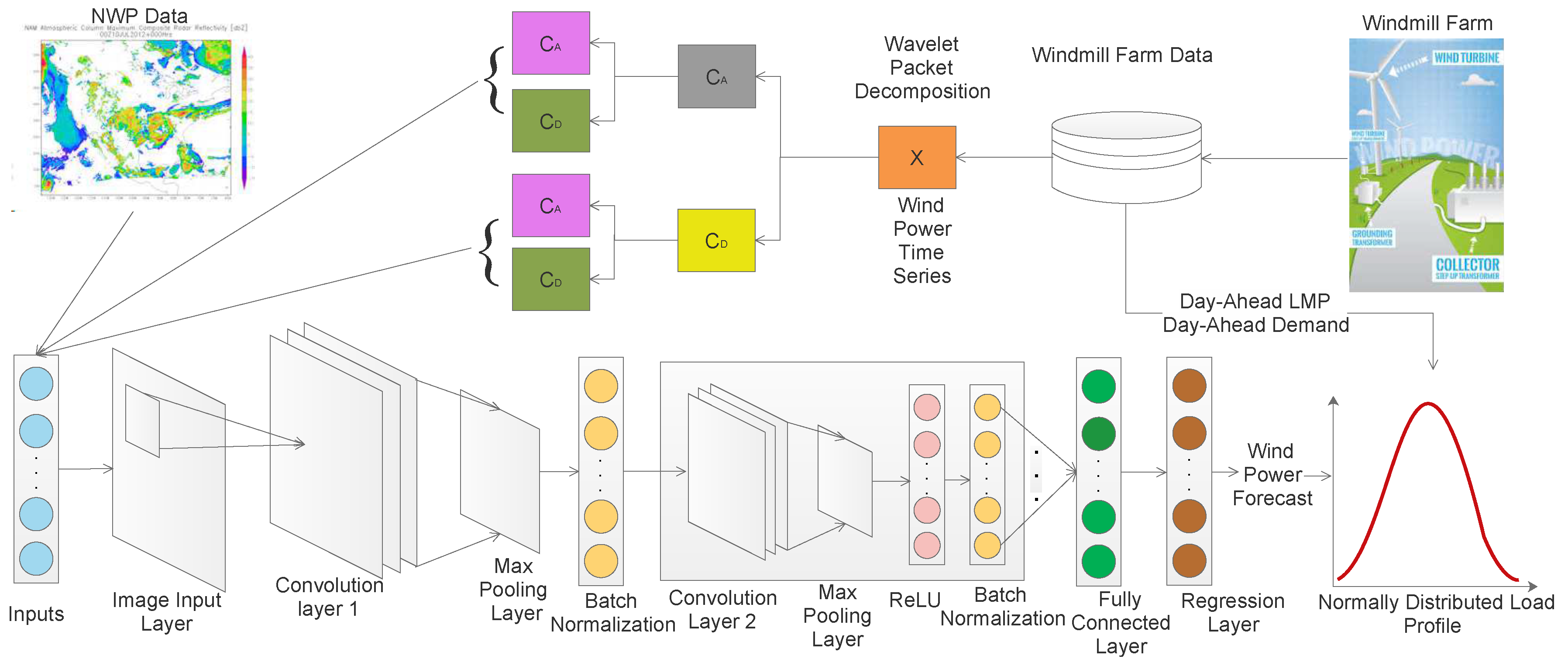
4. Proposed Model
4.1. Data Preprocess
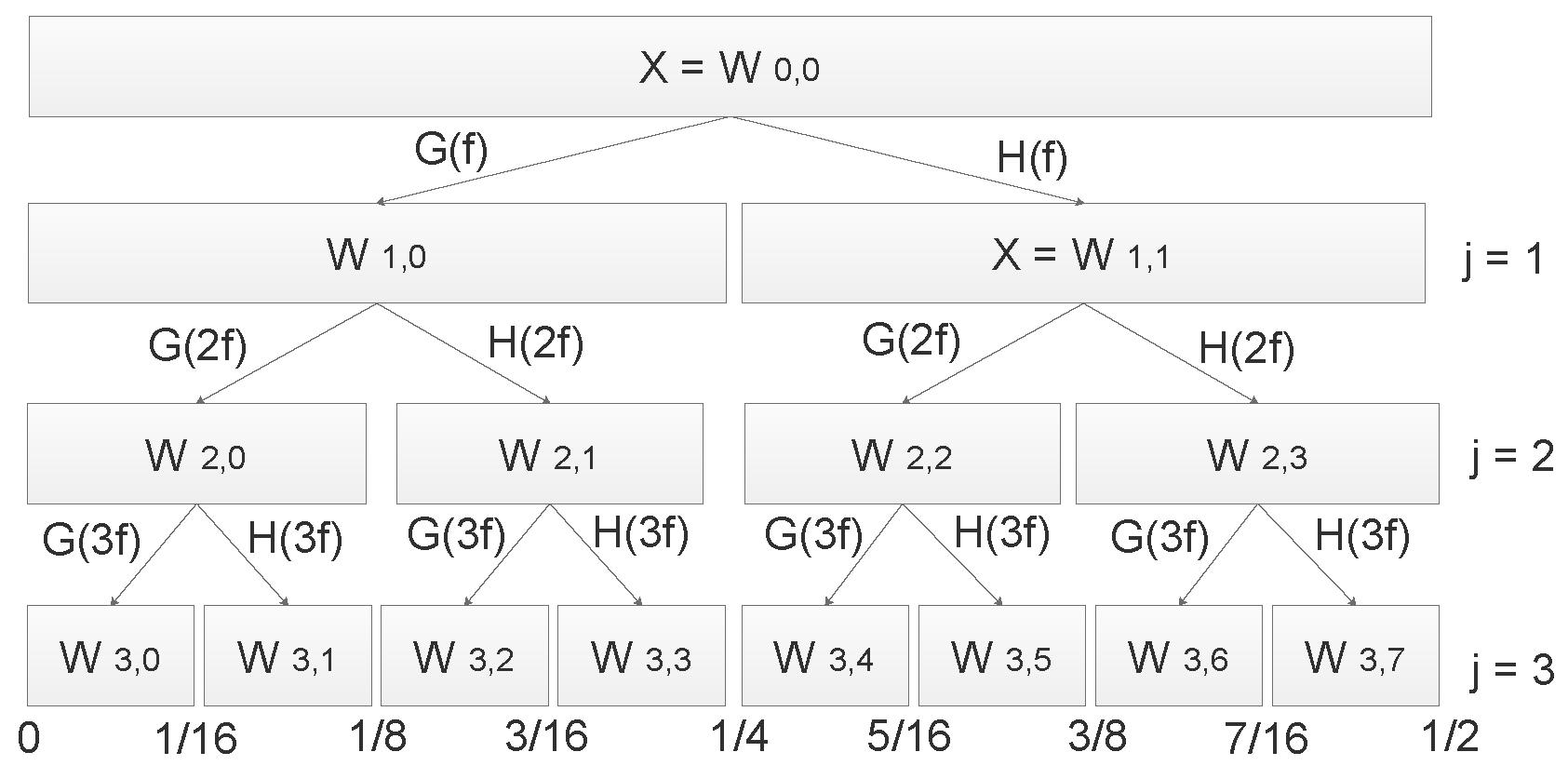
4.2. Feature Engineering
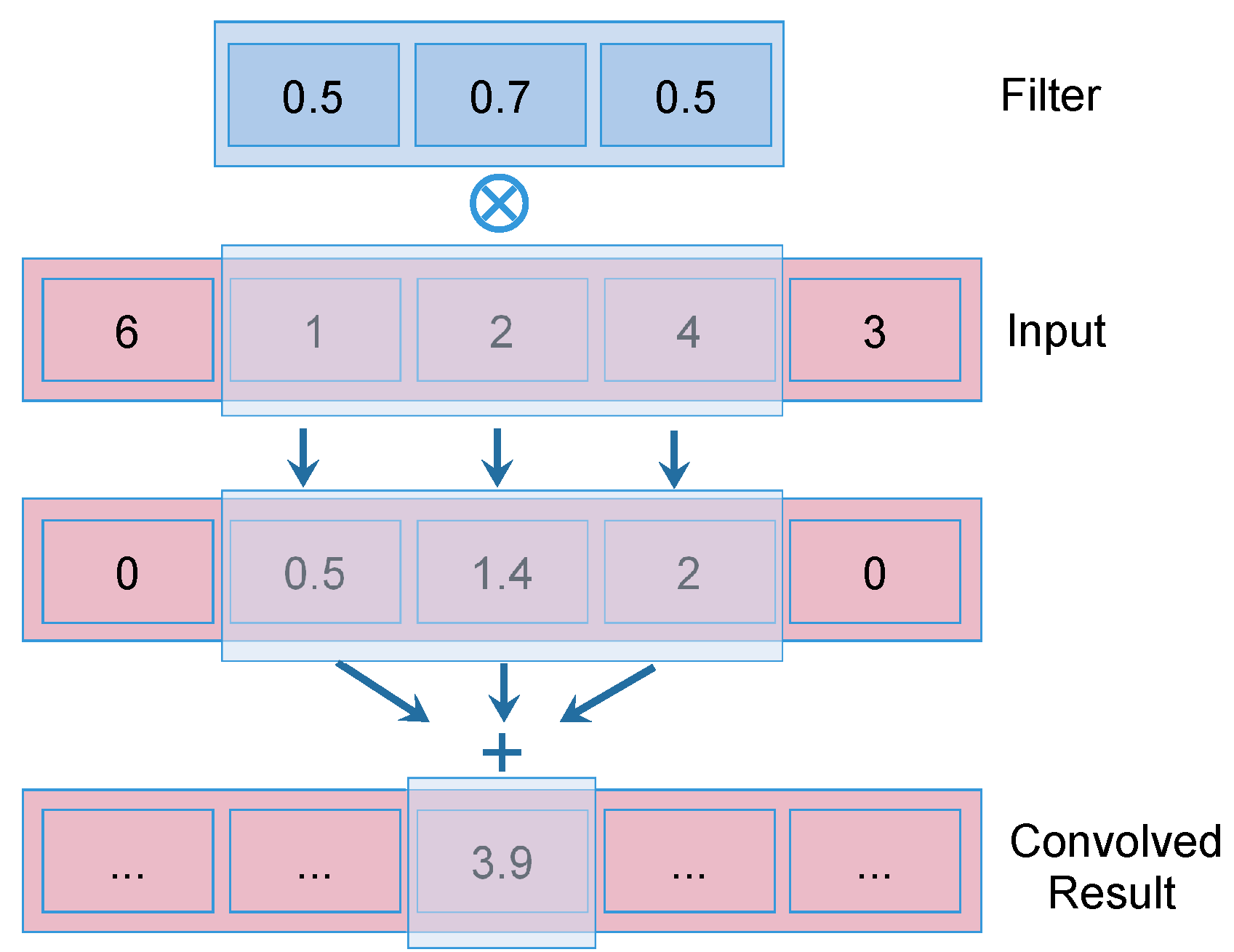
4.3. Efficient DCNN
5. System Description
5.1. Case 1
5.2. Case 2
5.3. Case 3
- -
- Load factor maximization
- -
- Consumption cost minimization
6. Problem Formulation
| Algorithm 1 Algorithm for Demand Side Management (DSM). | ||
| Require:Input: [W, L, P] | ||
| 1: Output: C | ||
| 2: if W = L then | ▹ Wind power is sufficient to fulfill demand | |
| 3: | ▹ Wind power is sufficient that has no cost | |
| 4: | ▹ Load is equal to wind power, so load adjustment is not performed | |
| 5: | ▹ Calculating consumption cost | |
| 6: else if W > L then | ▹ Wind power is greater than demand | |
| 7: | ▹ Excessive wind power is transmitted to the SG | |
| 8: S = 0.9 | ▹ 10 % reduction in price is subsidiary for next power purchase | |
| 9: | ▹ Wind power is sufficient that has no cost | |
| 10: | ▹ Load is lesser than wind power, so load adjustment is not performed | |
| 11: | ▹ Calculating the consumption cost | |
| 12: else if then | ▹ Wind power is not sufficient to fulfill the demand | |
| 13: | ▹ Finding demand that have to be fulfilled by the SG | |
| 14: | ▹ Managing demand to distribute it normally | |
| 15: if S = 0.9 then | ▹ If there is subsidiary on the price, the price will be adjusted | |
| 16: | ▹ 10% reduction on price by subsidiary | |
| 17: | ▹ Calculating consumption cost | |
| 18: else | ||
| 19: | ▹ If there is no subsidiary on price, price remains same | |
| 20: | ▹ Calculating consumption cost | |
| 21: end if | ||
| 22: end if | ||
| 23: Manage_Demand Function | ||
| 24: Function | ||
| 25: | ▹ Average of demand to be fulfilled by the SG | |
| 26: | ▹ Standard deviation of demand to be fulfilled by the SG | |
| 27: | ▹ Sum of demand to be fulfilled by the SG | |
| 28: if DWD < then | ▹ Checking each value of demand vector if it is smaller than mean | |
| 29: | ▹ When value is smaller, add standard deviation to make it closer to mean | |
| 30: else if DWD > then | ▹ Checking each value of demand vector if it is greater than mean | |
| 31: | ▹ When value is larger, subtract standard deviation to make it closer to mean | |
| 32: end if | ||
| 33: | ▹ Taking sum of all values of new adjusted load vector | |
| 34: d = SL – SD | ▹ Taking the difference of demanding load and new adjusted load | |
| 35: ⊳ | ▹ Now the demanded load and new load are adjusted to be equal | |
| 36: if d > 0 then | ▹ Difference greater than zero means the new adjusted load is more than the demanded load | |
| 37: | ▹ Count is the number of values greater than average and index are their index | |
| 38: | ▹ Subtracting the difference from all the larger values | |
| 39: else if d < 0 then | ▹ Difference smaller than zero means the new adjusted load is lesser than the demanded | |
| 40: load | ||
| 41: | ▹ Count is the number of values that are smaller than average load | |
| 42: | ▹ Adding the difference in all the smaller values | |
| 43: end if | ||
| 44: [index ] = Sort() | ▹ Sort will sort the in ascending order and return index of the sorted array | |
| 45: | ||
| 46: For i = 1 to 6 | ▹ Shift the peak load to the lowest load | |
| 47: j = i-1, sf = 5*i a = length() | ▹ Defining shifting factor | |
| 48: if index(i) > 6 then | ▹ Shift the load to the lowest load that is not late night | |
| 49: shftFac = | ||
| 50: (index(i)) = (index(i)) - shftFac | ▹ Subtracting the shifting factor from the highest load | |
| 51: (index(a-j)) = (index(a-j)) + shftFac | ▹ Adding the shifting factor to the lowest load | |
| 52: end if | ||
| 53: End For | ||
| 54: End Function | ||
7. Results and Analysis
7.1. Data Description
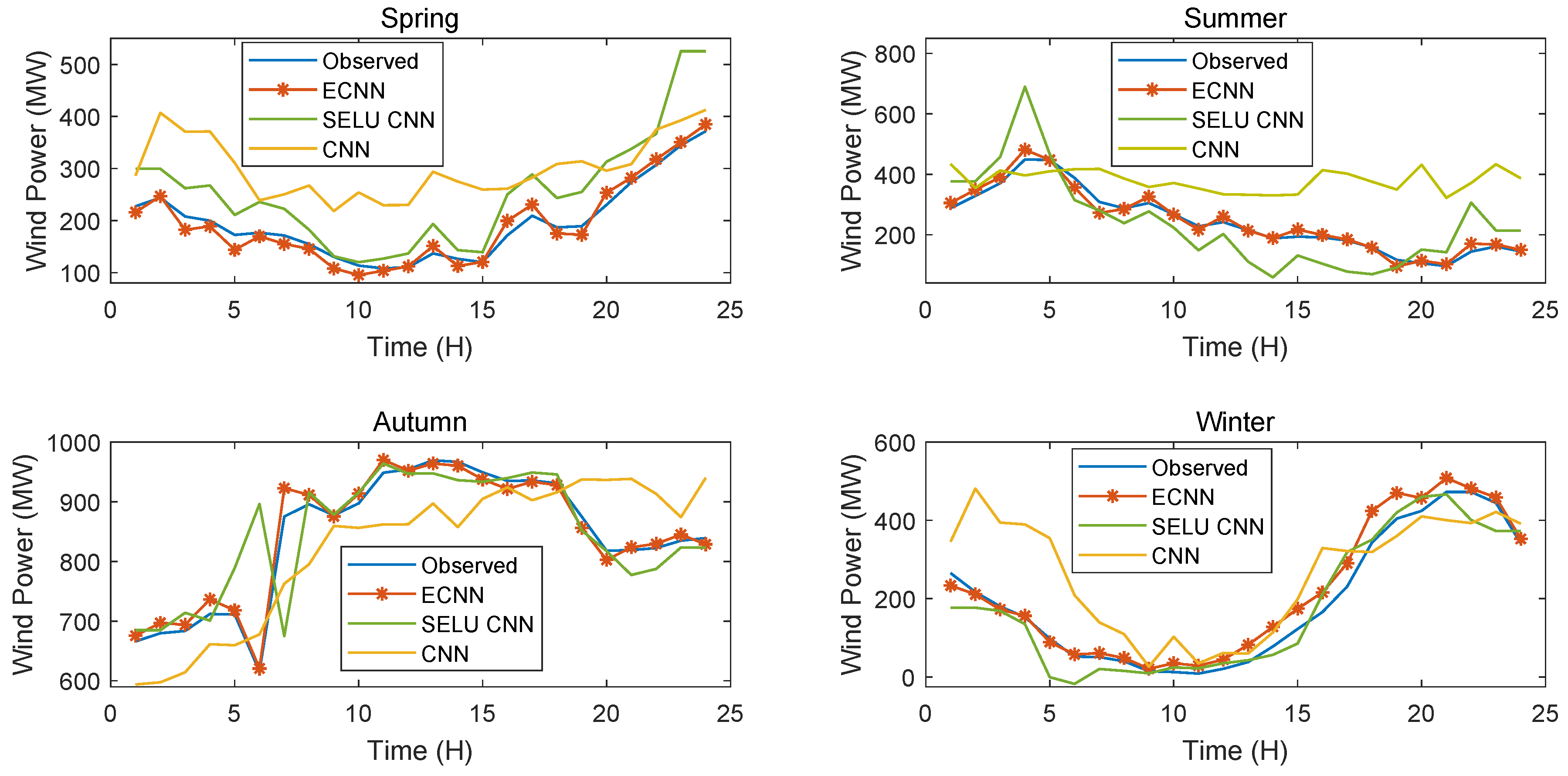
7.2. Wind Power Analysis
7.3. EDCNN Performance Evaluation
7.4. Statistical Analysis of EDCNN
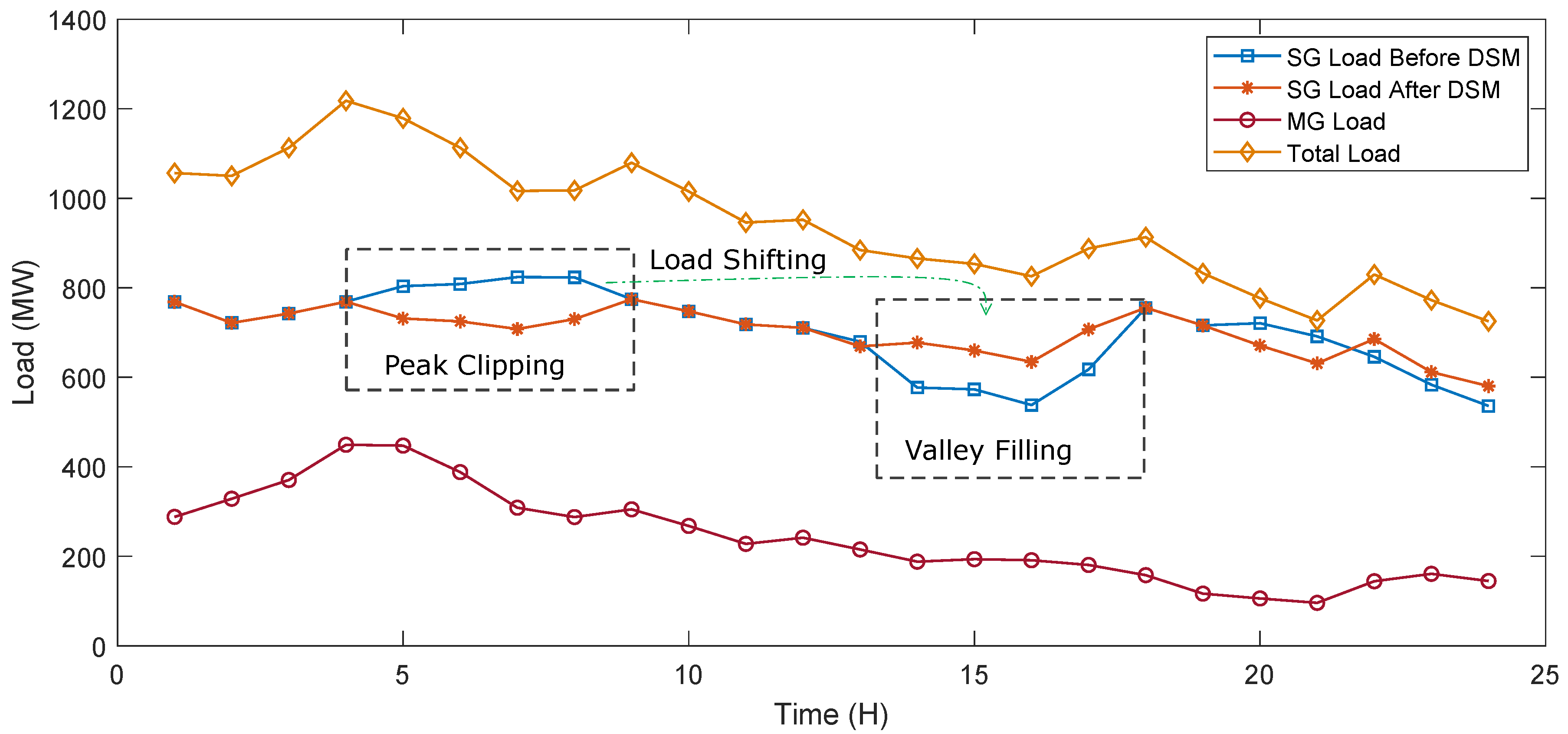
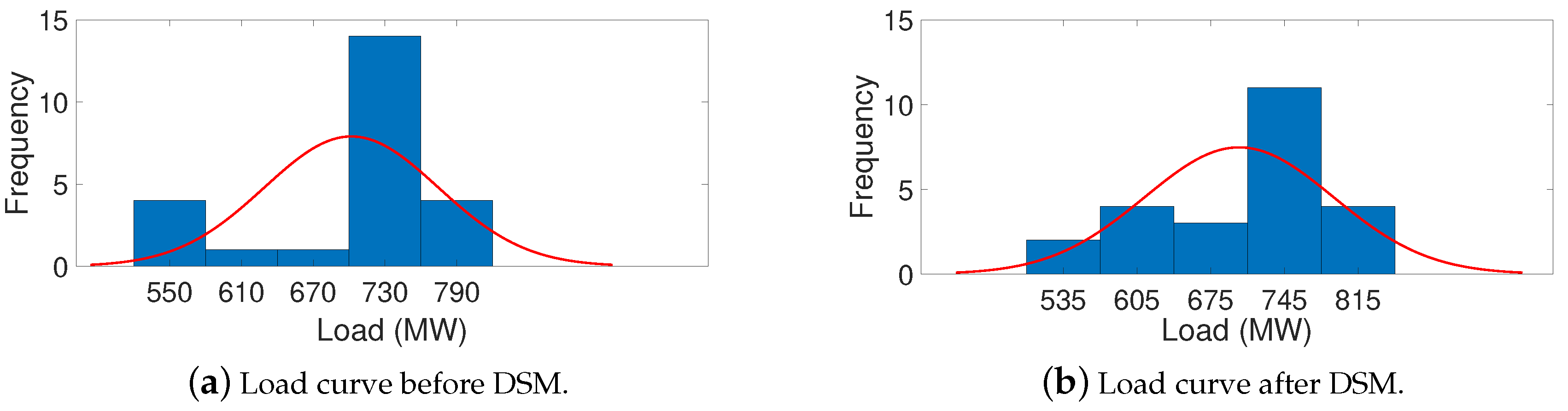
7.5. Analysis of Proposed DSM Algorithm
8. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| ABC | Artificial Bee Colony |
| ANN | Artificial Neural Networks |
| AEMO | Australia Electricity Market Operator |
| ARIMA | Autoregressive Integrated Moving Average |
| CASIO | California Independent System Operators |
| CNN | Convolution Neural Networks |
| DWT | Discrete Wavelet Transform |
| DM | Diebold–Mariano (statistical test) |
| DNN | Deep Neural Networks |
| DSM | Demand Side Management |
| ELM | Extreme Learning Machine |
| EROL | Enhanced Regression Output Layer |
| ISO NE | Independent System Operator New England |
| LSSVM | Least Square Support Vector Machine |
| LSTM | Long Short Term Memory |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MISO | Mid-continent Independent System Operator |
| NRMSE | Normalized Root Mean Square Error |
| ReLU | Rectified Linear Unit |
| RNN | Recurrent Neural Network |
| SAE | Sparse Auto Encoders |
| SCADA | Supervisory Control And Data Acquisition |
| STLF | Short-Term Load Forecast |
| TV | Time Varying |
| WPP | Wind Power Plant |
| WPT | Wavelet Packet Transform |
| a | Input signal to wavelet transform |
| Bias of mth hidden layer | |
| C | Power consumption cost |
| Differential loss of forecasting models’ error | |
| Demand and wind generation difference | |
| Sigmoid function | |
| L | Load vector |
| Load factor | |
| P | Price vector |
| S | Subsidiary |
| Error of forecasting model | |
| Radial base function | |
| Wavelet function | |
| Weights of mth layer | |
| Feature map of , mth layer |
References
- Zhao, Y.N.; Ye, L.; Li, Z.; Song, X.R.; Lang, Y.S.; Su, J. A novel bidirectional mechanism based on time series model for wind power forecasting. Appl. Energy 2016, 177, 793–803. [Google Scholar] [CrossRef]
- U.S. Department of Energy. Staff Report to the Secretary on Electricity Markets and Reliability. 2017. Available online: https://www.energy.gov/downloads/download-staff-report-secretary-electricity-markets-and-reliability (accessed on 8 June 2019).
- Jong, P.; Kiperstok, A.; Sanchez, A.S.; Dargaville, R.; Torres, E.A. Integrating large scale wind power into the electricity grid in the Northeast of Brazil. Energy 2016, 100, 401–415. [Google Scholar] [CrossRef]
- Global Wind Energy Council. GWEC Global Wind Report 2016. Available online: https://gwec.net/publications/global-wind-report-2/global-wind-report-2016 (accessed on 8 June 2019).
- Shafiee, M.; Brennan, F.; Espinosa, I.A. A parametric whole life cost model for offshore wind farms. Int. J. Life Cycle Assess. 2016, 21, 961–975. [Google Scholar] [CrossRef]
- Tomporowski, A.; Flizikowski, J.; Kasner, R.; Kruszelnicka, W. Environmental control of wind power technology. Rocznik Ochrona Srodowiska 2017, 19, 694–714. [Google Scholar]
- U.S. Department of Energy, 20% Wind Energy by 2030: Increasing Wind Energy’s Contribution to US Electricity Supply, Energy Efficiency and Renewable Energy (EERE). 2008. Available online: https://www.energy.gov/eere/wind (accessed on 8 June 2019).
- Athari, M.H.; Wang, Z. Impacts of Wind Power Uncertainty on Grid Vulnerability to Cascading Overload Failures. IEEE Trans. Sustain. Energy 2018, 9, 128–137. [Google Scholar] [CrossRef]
- Wang, Q.; Martinez-Anido, C.B.; Wu, H.; Florita, A.R.; Hodge, B.M. Quantifying the economic and grid reliability impacts of improved wind power forecasting. IEEE Trans. Sustain. Energy 2016, 7, 1525–1537. [Google Scholar] [CrossRef]
- Swinand, G.P.; Mahoney, A.O. Estimating the impact of wind generation and wind forecast errors on energy prices and costs in Ireland. Renew. Energy 2015, 75, 468–473. [Google Scholar] [CrossRef]
- Chen, Z. Wind power in modern power systems. J. Mod. Power Syst. Clean Energy 2013, 1, 2–13. [Google Scholar] [CrossRef]
- Haque, A.U.; Nehrir, M.H.; Mandal, P. A hybrid intelligent model for deterministic and quantile regression approach for probabilistic wind power forecasting. IEEE Trans. Power Syst. 2014, 29, 1663–1672. [Google Scholar] [CrossRef]
- Juban, J.; Siebert, N.; Kariniotakis, G.N. Probabilistic short-term wind power forecasting for the optimal management of wind generation. In Proceedings of the 2007 IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007; pp. 683–688. [Google Scholar]
- Zhou, K.; Fu, C.; Yang, S. Big data driven smart energy management: From big data to big insights. Renew. Sustain. Energy Rev. 2016, 56, 215–225. [Google Scholar] [CrossRef]
- Haupt, S.E.; Kosovic, B. Variable generation power forecasting as a big data problem. IEEE Trans. Sustain. Energy 2016, 8, 725–732. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, M.; Hodge, B.M.; Florita, A.; Freedman, J. Ramp forecasting performance from improved short-term wind power forecasting over multiple spatial and temporal scales. Energy 2017, 122, 528–541. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, L.T.; Chen, Z.; Li, P. A survey on deep learning for big data. Inf. Fusion 2018, 42, 146–157. [Google Scholar] [CrossRef]
- Najafabadi, M.M.; Villanustre, F.; Khoshgoftaar, T.M.; Seliya, N.; Wald, R.; Muharemagic, E. Deep learning applications and challenges in big data analytics. J. Big Data 2015, 2, 1–15. [Google Scholar] [CrossRef]
- Mujeeb, S.; Javaid, N.; Gul, H.; Daood, N.; Shabbir, S.; Arif, A. Wind Power Forecasting Based on Efficient Deep Convolution Neural Networks. In Proceedings of the 3PGCIC Conference, Antwerp, Belgium, 7–9 November 2019. [Google Scholar]
- Xu, Q.; He, D.; Zhang, N.; Kang, C.; Xia, Q.; Bai, J.; Huang, J. A short-term wind power forecasting approach with adjustment of numerical weather prediction input by data mining. IEEE Trans. Sustain. Energy 2015, 6, 1283–1291. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, Y.; Wong, K.P.; Xu, Z.; Dong, Z.Y.; Herbert, H.C. An advanced approach for construction of optimal wind power prediction intervals. IEEE Trans. Power Syst. 2015, 30, 2706–2715. [Google Scholar] [CrossRef]
- Wang, J.; Niu, T.; Lu, H.; Yang, W.; Du, P. A Novel Framework of Reservoir Computing for Deterministic and Probabilistic Wind Power Forecasting. IEEE Trans. Sustain. Energy 2019. [Google Scholar] [CrossRef]
- Yang, S.; Xu, X.; Xiang, J.; Chen, R.; Jiang, W. The efficient market operation for wind energy trading based on the dynamic improved power forecasting. J. Renew. Sustain. Energy 2018, 10, 45908–45921. [Google Scholar] [CrossRef]
- Cavalcante, L.; Bessa, R.J.; Reis, M.; Browell, J. LASSO vector autoregression structures for very short-term wind power forecasting. Wind Energy 2017, 20, 657–675. [Google Scholar] [CrossRef]
- Yan, J.; Li, K.; Bai, E.; Zhao, X.; Xue, Y.; Foley, A.M. Analytical Iterative Multistep Interval Forecasts of Wind Generation Based on TLGP. IEEE Trans. Sustain. Energy 2018, 10, 625–636. [Google Scholar] [CrossRef]
- Lin, Y.; Yang, M.; Wan, C.; Wang, J.; Song, Y. A multi-model combination approach for probabilistic wind power forecasting. IEEE Trans. Sustain. Energy 2019, 10, 226–237. [Google Scholar] [CrossRef]
- Ellis, N.; Davy, R.; Troccoli, A. Predicting wind power variability events using different statistical methods driven by regional atmospheric model output. Wind Energy 2015, 18, 1611–1628. [Google Scholar] [CrossRef]
- Yan, J.; Li, K.; Bai, E.W.; Deng, J.; Foley, A.M. Hybrid probabilistic wind power forecasting using temporally local Gaussian process. IEEE Trans. Sustain. Energy 2016, 7, 87–95. [Google Scholar] [CrossRef]
- Li, S.; Wang, P.; Goel, L. Wind power forecasting using neural network ensembles with feature selection. IEEE Trans. Sustain Energy 2015, 6, 1447–1456. [Google Scholar] [CrossRef]
- Lee, D.; Baldick, R. Short-term wind power ensemble prediction based on Gaussian processes and neural networks. IEEE Trans. Smart Grid 2014, 5, 501–510. [Google Scholar] [CrossRef]
- Chitsaz, H.; Amjady, N.; Zareipour, H. Wind power forecast using wavelet neural network trained by improved Clonal selection algorithm. Energy Convers. Manag. 2015, 89, 588–598. [Google Scholar] [CrossRef]
- Wu, W.; Peng, M. A Data Mining Approach Combining K-Means Clustering With Bagging Neural Network for Short-Term Wind Power Forecasting. IEEE Internet Things J. 2017, 4, 979–986. [Google Scholar] [CrossRef]
- Qureshi, A.S.; Khan, A.; Zameer, A.; Usman, A. Wind power prediction using deep neural network based meta regression and transfer learning. Appl. Soft Comput. 2017, 58, 742–755. [Google Scholar] [CrossRef]
- Shao, H.; Deng, X.; Jiang, Y. A novel deep learning approach for short-term wind power forecasting based on infinite feature selection and recurrent neural network. J. Renew. Sustain. Energy 2018, 10, 43303–43314. [Google Scholar] [CrossRef]
- Torres, J.M.; Aguilar, R.M.; Zuniga-Meneses, K.V. Deep learning to predict the generation of a wind farm. J. Renew. Sustain. Energy 2018, 10, 013305. [Google Scholar] [CrossRef]
- Wang, H.Z.; Li, G.Q.; Wang, G.B.; Peng, J.C.; Jiang, H.; Liu, Y.T. Deep learning based ensemble approach for probabilistic wind power forecasting. Appl. Energy 2017, 188, 56–70. [Google Scholar] [CrossRef]
- Torres, J.M.; Aguilar, R.M. Using deep learning to predict complex systems: A case study in wind farm generation. Complexity 2018, 2018, 9327536. [Google Scholar] [CrossRef]
- Stephens, E.R.; Smith, D.B.; Mahanti, A. Game theoretic model predictive control for distributed energy demand-side management. IEEE Trans. Smart Grid 2015, 6, 1394–1402. [Google Scholar] [CrossRef]
- Ghasemi, A.; Shayeghi, H.; Moradzadeh, M.; Nooshyar, M. A novel hybrid algorithm for electricity price and load forecasting in smart grids with demand-side management. Appl. Energy 2016, 177, 40–59. [Google Scholar] [CrossRef]
- Pascual, J.; Barricarte, J.; Sanchis, P.; Marroyo, L. Energy management strategy for a renewable-based residential microgrid with generation and demand forecasting. Appl. Energy 2015, 158, 12–25. [Google Scholar] [CrossRef]
- Mujeeb, S.; Javaid, N.; Ilahi, M.; Wadud, Z.; Ishmanov, F.; Afzal, M.K. Deep long short-term memory: A new price and load forecasting scheme for big data in smart cities. Sustainability 2019, 11, 987. [Google Scholar] [CrossRef]
- Mujeeb, S.; Javaid, N. ESAENARX and DE-RELM: Novel schemes for big data predictive analytics of electricity load and price. Sustain. Cities Soc. 2019, 51, 101642. [Google Scholar] [CrossRef]
- Coifman, R.R.; Wickerhauser, M.V. Entropy-based algorithms for best basis selection. IEEE Trans. Inf. Theory 1992, 38, 713–718. [Google Scholar] [CrossRef]
- Burrus, C.S.; Gopinath, R.; Guo, H. Introduction to Wavelets and Wavelet Transforms: A Primer; Prentice Hall Press: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Zahid, M.; Ahmed, F.; Javaid, N.; Abbasi, R.A.; Kazmi, Z.; Syeda, H.; Javaid, A.; Bilal, M.; Akbar, M.; Ilahi, M. Electricity price and load forecasting using enhanced convolutional neural network and enhanced support vector regression in smart grids. Electronics 2019, 8, 122. [Google Scholar] [CrossRef]
- ISO NE Market Operations Data. Available online: https://www.iso-ne.com (accessed on 20 January 2019).
- Wang, Y.; Hu, Q.; Srinivasan, D.; Wang, Z. Wind power curve modeling and wind power forecasting with inconsistent data. IEEE Trans. Sustain. Energy 2018, 10, 16–25. [Google Scholar] [CrossRef]
- Zhao, Y.; Ye, L.; Pinson, P.; Tang, Y.; Lu, P. Correlation-constrained and sparsity-controlled vector autoregressive model for spatio-temporal wind power forecasting. IEEE Trans. Power Syst. 2018, 33, 5029–5040. [Google Scholar] [CrossRef]
- Martin, P.; Moreno, G.; Rodriguez, F.; Jimenez, J.; Fernandez, I. A Hybrid Approach to Short-Term Load Forecasting Aimed at Bad Data Detection in Secondary Substation Monitoring Equipment. Sensors 2018, 18, 3947. [Google Scholar] [CrossRef]
- Derrac, J.; Garcia, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Diebold, F.X.; Mariano, R.S. Comparing predictive accuracy. J. Bus. Econ. Stat. 1995, 13, 253–263. [Google Scholar]
- Lago, J.; De Ridder, F.; De Schutter, B. Forecasting spot electricity prices: Deep learning approaches and empirical comparison of traditional algorithms. Appl. Energy 2018, 221, 386–405. [Google Scholar] [CrossRef]
- Chen, H.; Wan, Q.; Wang, Y. Refined Diebold-Mariano test methods for the evaluation of wind power forecasting models. Energies 2014, 7, 4185–4198. [Google Scholar] [CrossRef]
| Inputs | Dataset | Algorithms |
|---|---|---|
| Past wind power | Delaware wind farm data, American National Renewable Energy Laboratory, 2006 | Nelder–Mead simplex optimization algorithm, Bidirectional backward Extreme learning machine [1] |
| Wind power, IEEE 118-bus system parameters | Wind Integration National Dataset , National Renewable Energy Laboratory, CASIO, MISO, ISO NE, 2007–2013 | PLEXOS tool, Flexible Energy Scheduling Tool for Integrating Variable generation tool [9] |
| Past hourly wind power | 66 wind power plants data, Supervisory Control And Data Acquisition (SCADA) | Vector autoregression model, Least absolute shrinkage and selection operator [24] |
| Past wind power | Wind farm, Donegal, North West Ireland, June–July 2004 | Temporally local Gaussian process [25] |
| 10-min resolution: wind speed, wind power | Global Energy Forecasting Competition (GEFCom) 2014 | Multi-model combination method: Sparse Bayesian learning, Kernel density estimation and Beta distribution fitting method [26] |
| 5-minute resolution: wind speed, wind power | Wind power data, Australian Energy Market Operator (AEMO), 2005 | Spatial empirical decomposition, Random Forest, Gradient boosting, Support vector machine [27] |
| Wind power, wind speed | Wind farm data, Ireland and USA, August 2006, October 2008 | Hybrid deterministic-probabilistic method with Gaussian process [28] |
| 10-min resolution: wind speed, wind power | National Renewable Energy Laboratory, 2005–2006 | Ensemble method: Wavelet transform, Partial least squares regression, ANN [29] |
| Wind speed, wind power | GEFCom 2012 | ANN, Gaussian process [30] |
| Past hourly wind power, past weather forecast: wind speed, wind direction, temperature and humidity | Wind power generation, Alberta, Canada | Improved Clonal selection algorithm, Wavelet neural networks, Maximum correntropy criterion [31] |
| Wind turbine parameters, wind speed, wind power | 10-min wind farm data, SCADA | K-means clustering, Bagging ANN [32] |
| Wind power, weather forecasts | 5 Wind farms data, Europe | Mutual information, Deep auto-encoders, Deep belief network [33] |
| Wind speed, wind power | National Renewable Energy Laboratory (NREL), 2004 | Infinite feature selection method, RNN [34] |
| Day of the year, hour, wind speed, wind direction, temperature, humidity, pressure, generators out of service | MADE wind farm, ITER, Tenerife Island, Spain, January 2014–April 2016 | Multi-layer perceptron with ReLU, Long short-term memory, Nonlinear autoregressive network with exogenous inputs [35] |
| 5-min intervals past wind power | SIWF wind farm, China, 2011–2013 | Wavelet transform, Ensemble CNN [36] |
| Wind speed, wind direction, temperature, humidity, pressure | MADE wind farm, ITER, Tenerife Island, Spain | Feed Forward ANN, SELU CNN, RNN [37] |
| Past consumption, solar radiation | Victorian solar dataset | Game theory model [38] * |
| Historic price and load | Hourly load and price data, NYISO, PJM, AEMO, 2010, 2013, 2014 | Flexible wavelet packet transform, Nonlinear least square support vector machine, ARIMA, TV-ABC [39] * |
| Historic consumption, wind power, photovoltaic power | Micro grid data, Renewable Energy Laboratory, UPNa, 2014 | Simple moving average, Central moving average [40] * |
| Input | Description |
|---|---|
| Dew point temperature | Past NWP forecast |
| Dry bulb temperature | Past NWP forecast |
| Wind speed | Past NWP forecast |
| Lagged wind power 1 | Wind power (t-24) |
| Lagged wind power 2 | Wind power (t-25) |
| Decomposed wind power | Wavelet decomposed past wind power |
| Hour | Time of the day |
| Method | Season | MAPE | NRMSE | MAE |
|---|---|---|---|---|
| Spring | 8.42 | 2.34 | 3.34 | |
| Summer | 8.23 | 2.27 | 3.24 | |
| CNN | Autumn | 7.9 | 2.65 | 3.36 |
| Winter | 8.1 | 2.71 | 2.89 | |
| Spring | 3.47 | 0.12 | 3.1 | |
| Summer | 3.62 | 0.13 | 3.3 | |
| SELU CNN | Autumn | 3.45 | 0.12 | 3.4 |
| Winter | 3.27 | 0.17 | 3.2 | |
| Spring | 2.67 | 0.092 | 2.4 | |
| Summer | 2.43 | 0.096 | 2.24 | |
| EDCNN | Autumn | 2.56 | 0.085 | 2.67 |
| Winter | 2.62 | 0.094 | 2.18 |
| DM Score | |||
|---|---|---|---|
| Season | EDCNN Compared to SELU CNN | SELU CNN Compared to CNN | EDCNN Compared to CNN |
| Spring DM-MAE | 1.4252 | 0.0842 | 1.4256 |
| Spring p-value | 0.0432 | 0.9242 | 0.1248 |
| Summer DM-MAE | 1.3262 | 0.1024 | 1.3692 |
| Summer p-valve | 0.0326 | 0.8624 | 0.2142 |
| Autumn DM-MAE | 1.2714 | 0.1762 | 1.6728 |
| Autumn p-vale | 0.0196 | 0.0242 | 0.9242 |
| Winter DM-MAE | 1.4632 | 1.1426 | 1.2464 |
| Winter p-value | 0.02762 | 0.9862 | 0.7642 |
| Consumption Cost / Day ($) | Reduction / Day | |||
|---|---|---|---|---|
| Season | Before DSM | After DSM | Amount ($) | Percentage |
| Spring | 483,330 | 475,170 | 8153$ | 1.7% |
| Summer | 793,930.5 | 784,403 | 7527$ | 1.2% |
| Autumn | 417,980.5 | 413,770.5 | 4210$ | 1% |
| Winter | 3,347,106 | 3,305,006 | 42,109$ | 1.3% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mujeeb, S.; Alghamdi, T.A.; Ullah, S.; Fatima, A.; Javaid, N.; Saba, T. Exploiting Deep Learning for Wind Power Forecasting Based on Big Data Analytics. Appl. Sci. 2019, 9, 4417. https://doi.org/10.3390/app9204417
Mujeeb S, Alghamdi TA, Ullah S, Fatima A, Javaid N, Saba T. Exploiting Deep Learning for Wind Power Forecasting Based on Big Data Analytics. Applied Sciences. 2019; 9(20):4417. https://doi.org/10.3390/app9204417
Chicago/Turabian StyleMujeeb, Sana, Turki Ali Alghamdi, Sameeh Ullah, Aisha Fatima, Nadeem Javaid, and Tanzila Saba. 2019. "Exploiting Deep Learning for Wind Power Forecasting Based on Big Data Analytics" Applied Sciences 9, no. 20: 4417. https://doi.org/10.3390/app9204417
APA StyleMujeeb, S., Alghamdi, T. A., Ullah, S., Fatima, A., Javaid, N., & Saba, T. (2019). Exploiting Deep Learning for Wind Power Forecasting Based on Big Data Analytics. Applied Sciences, 9(20), 4417. https://doi.org/10.3390/app9204417





