Monin–Obukhov Similarity Theory for Modeling of Wind Turbine Wakes under Atmospheric Stable Conditions: Breakdown and Modifications
Abstract
1. Introduction
2. Monin–Obukhov Similarity Theory
3. Models for Wind Turbine Wakes under Stable Conditions
3.1. Modeling of Wind Turbine
3.1.1. Actuator Disk Model Based on Thrust Coefficient (-CT)
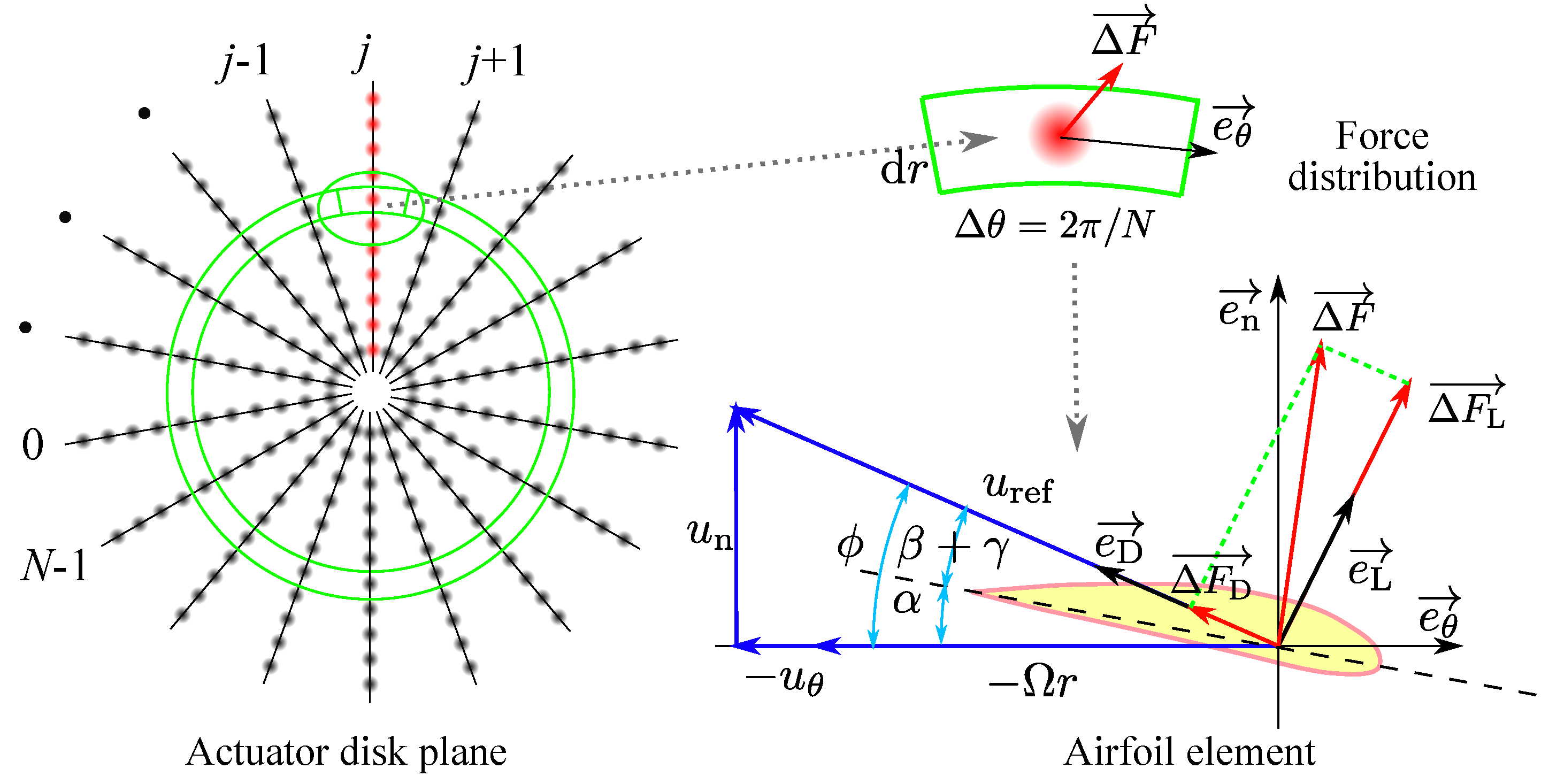
3.1.2. Actuator Disk Model Based on Blade Element Method
3.2. Turbulence Modeling
4. Breakdown and Modifications of MOST under Stable Conditions
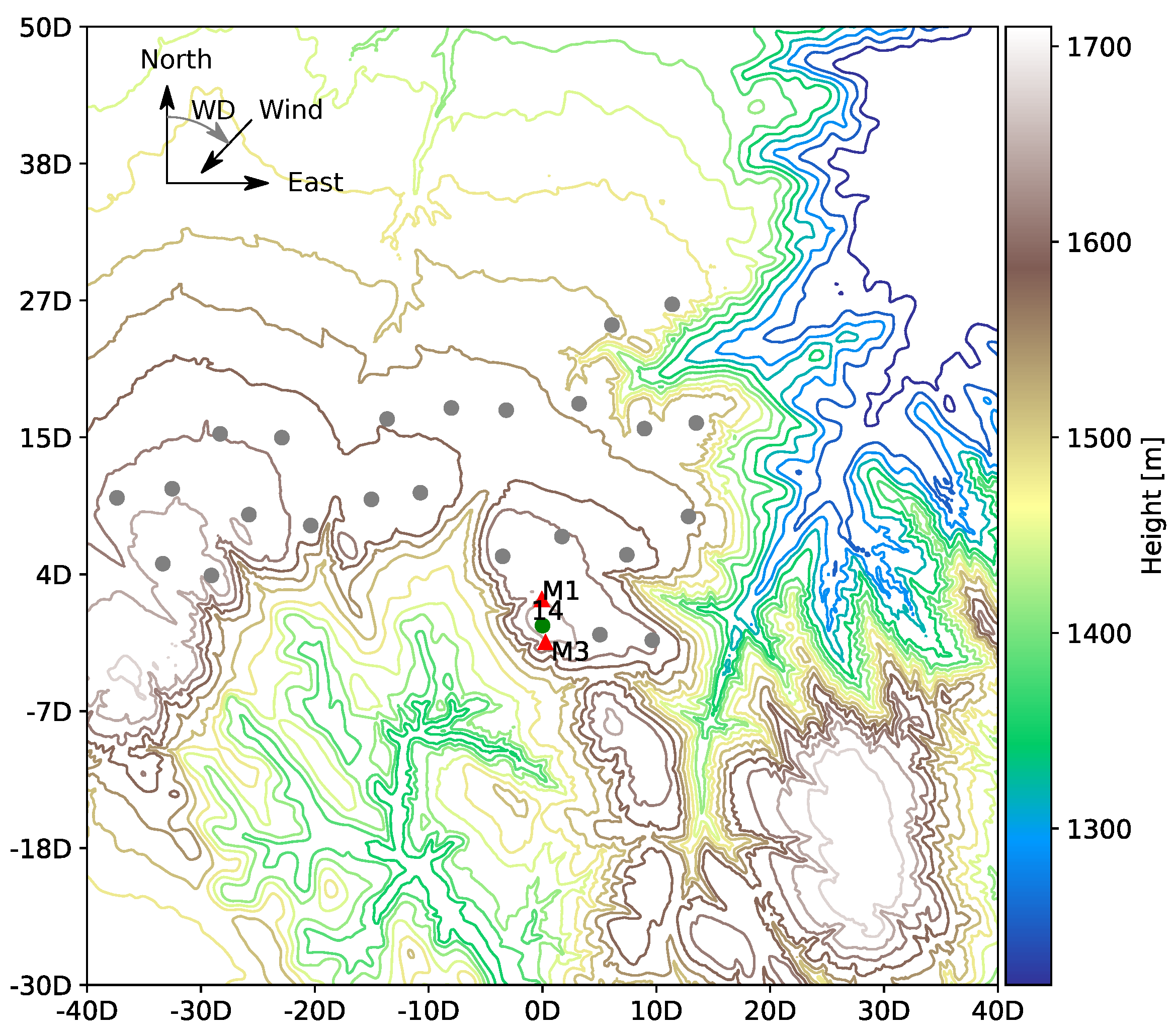
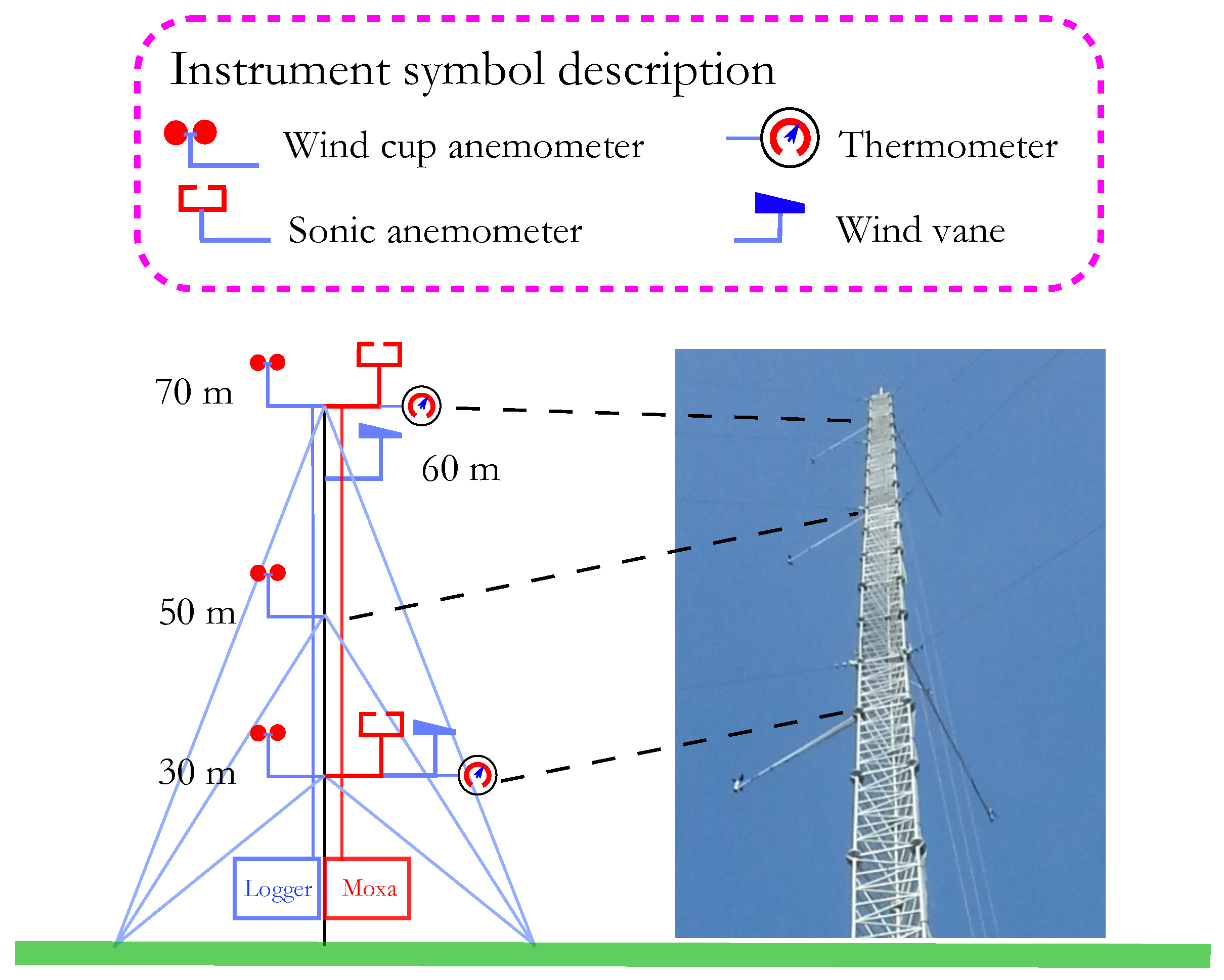
4.1. Experimental Data
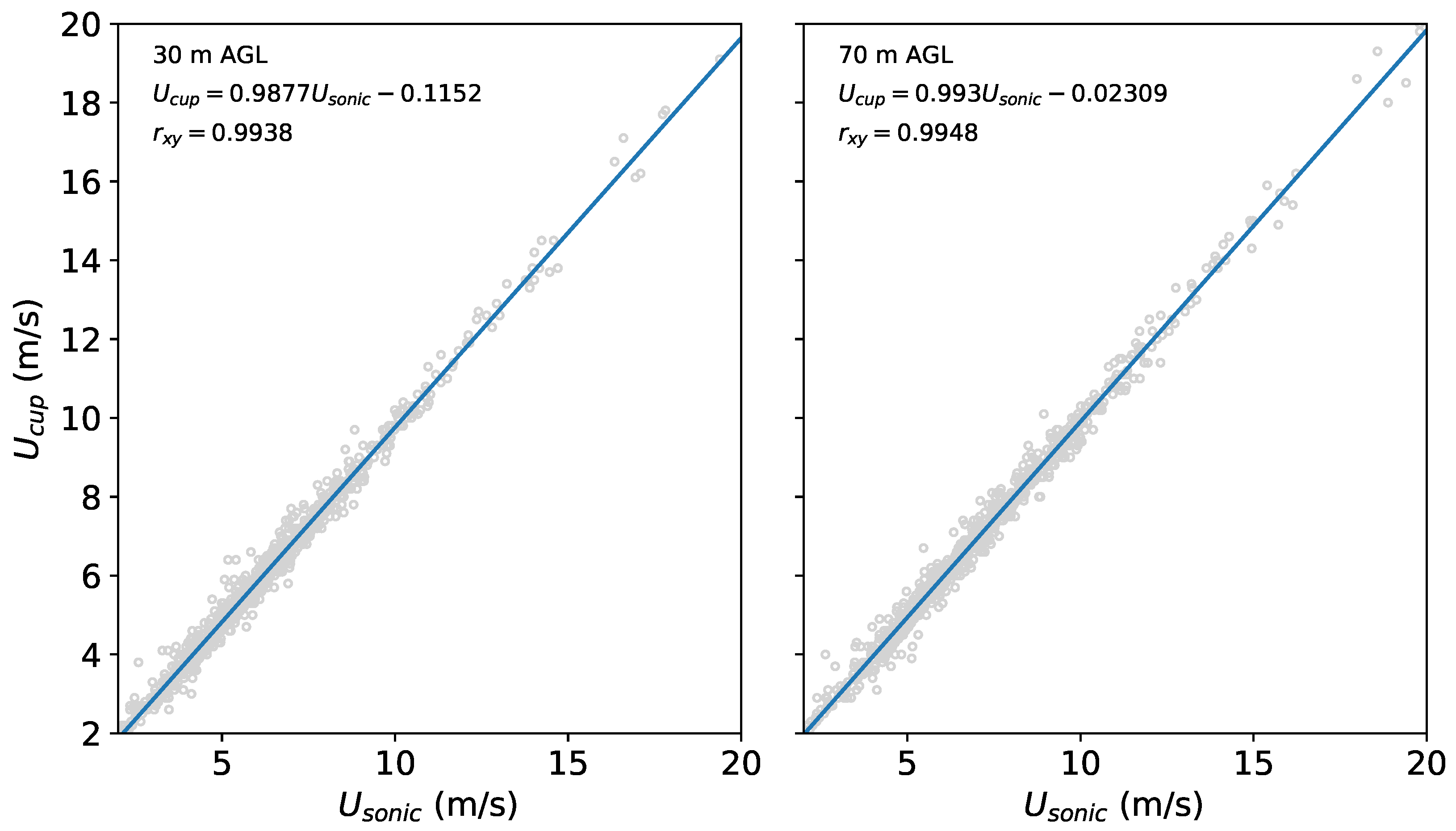
4.2. Data Processing
4.3. Limitations and Breakdown of MOST
4.4. Assessment of Similarity Functions for Predicting Wind Profiles
4.5. The Proposed Similarity Functions
5. Simulation Details
5.1. Test Cases
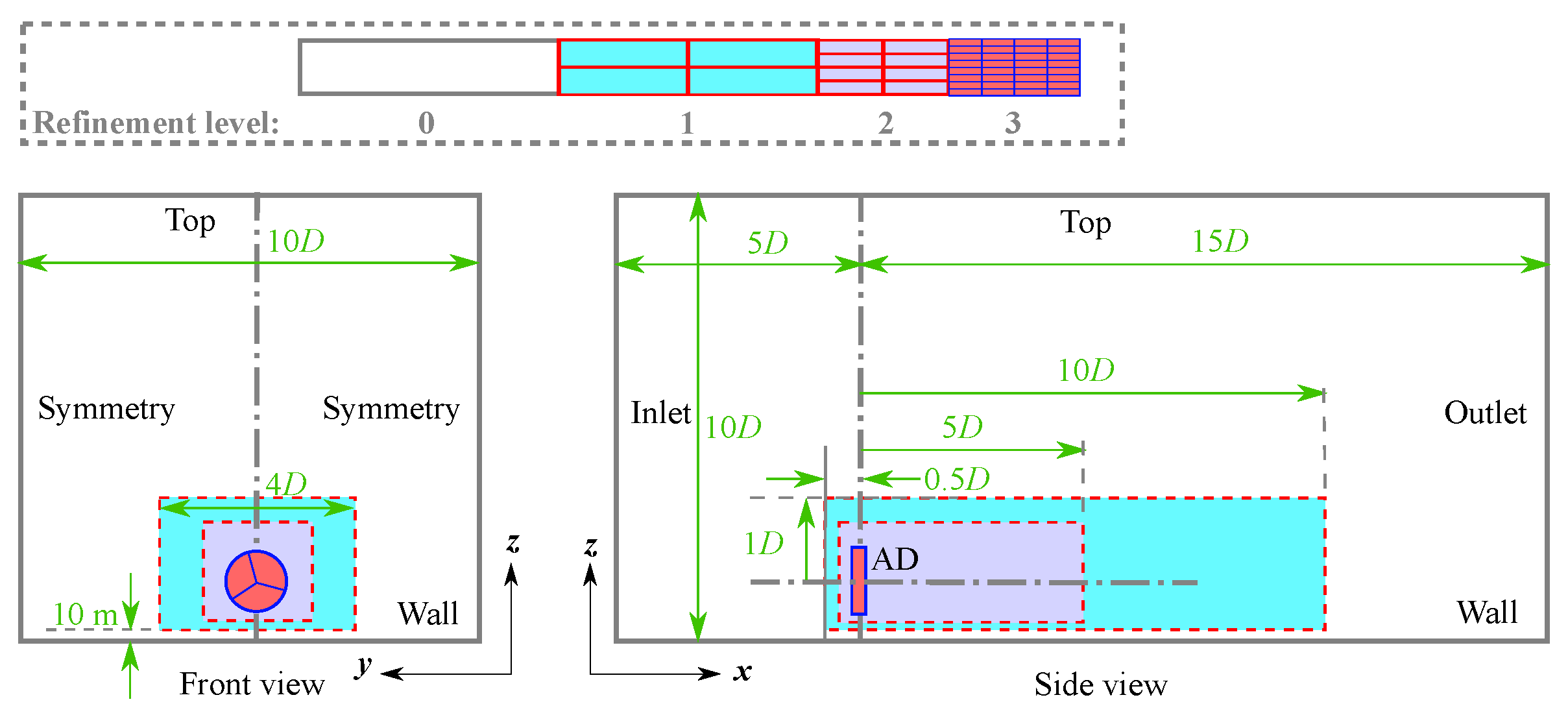
5.2. Computational Domain and Meshing
5.3. Boundary Conditions
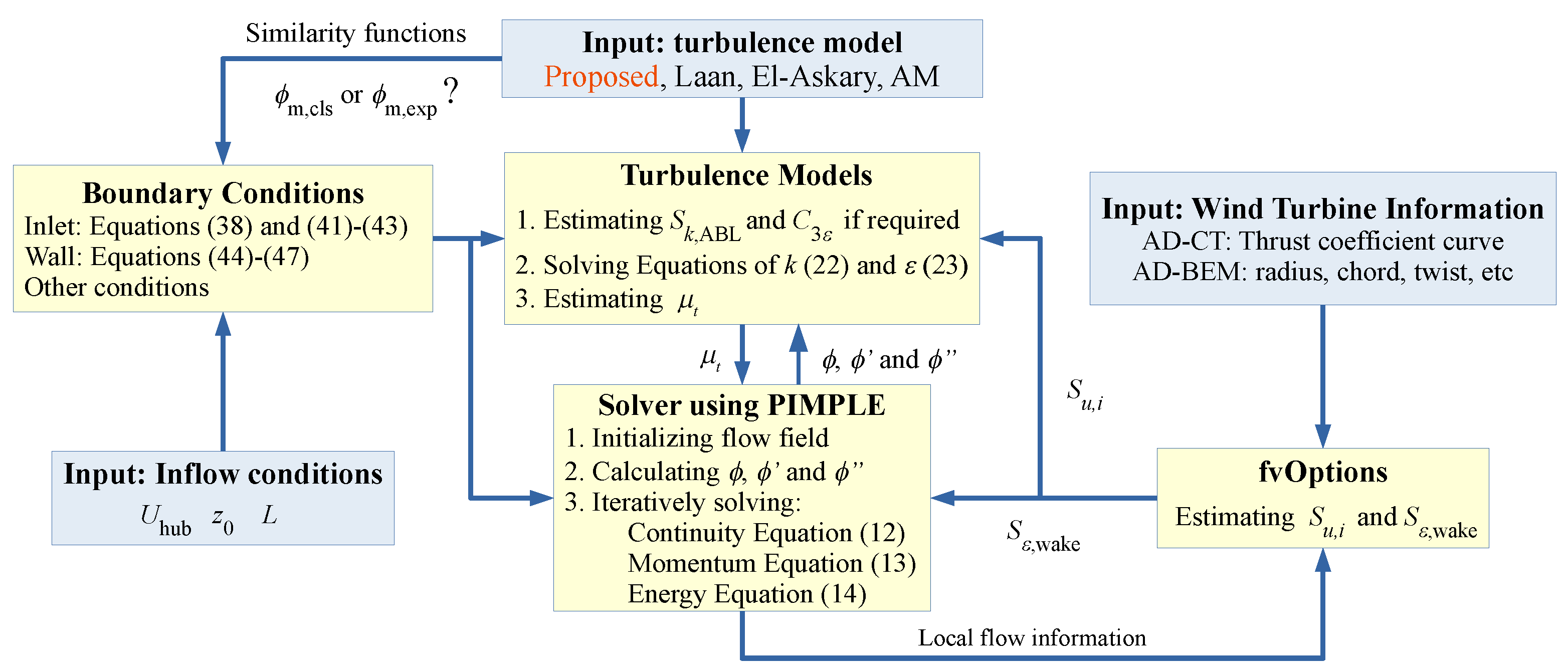
5.4. Implementations of Wake Models
6. Results of Wake Simulations
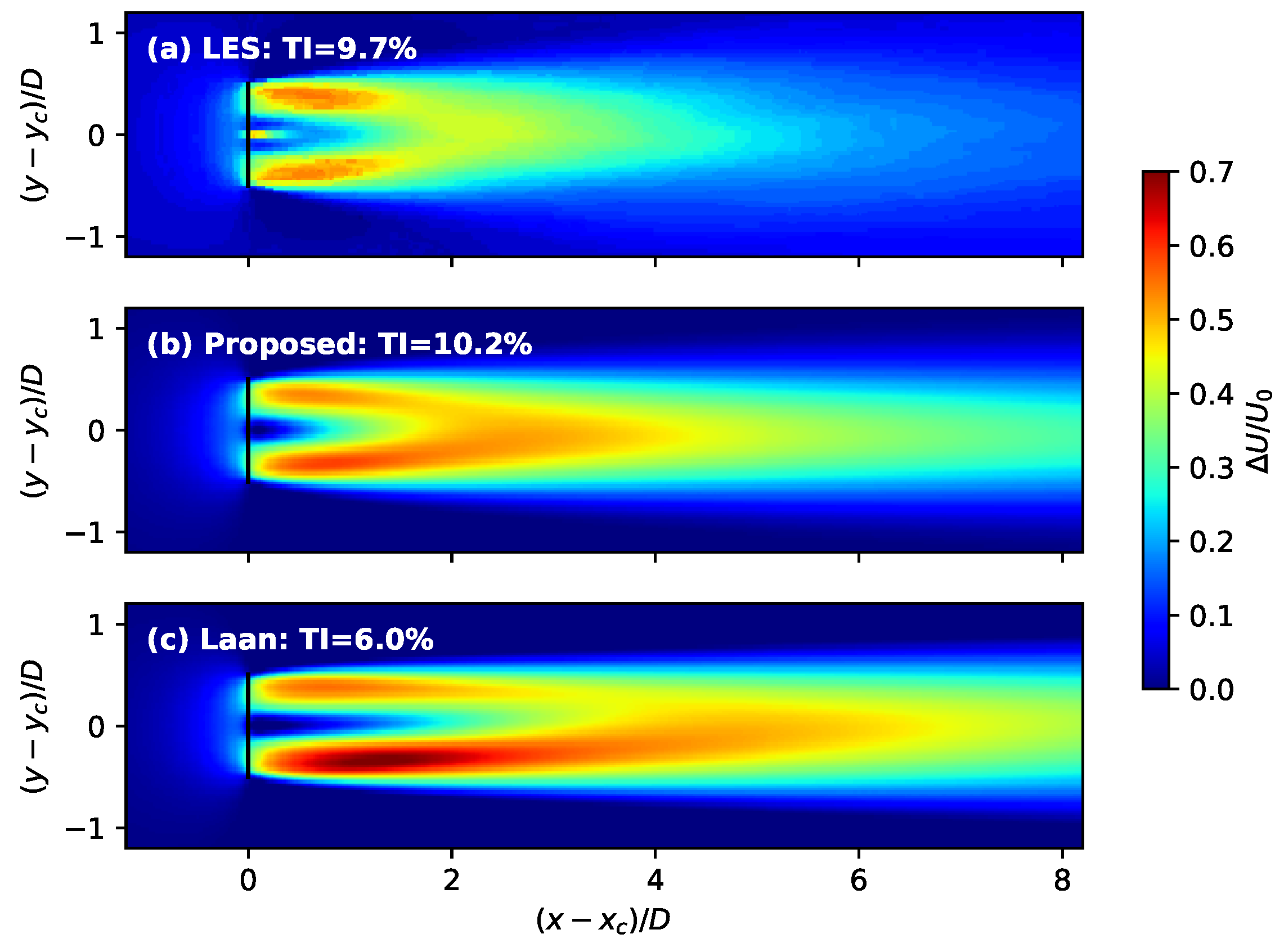
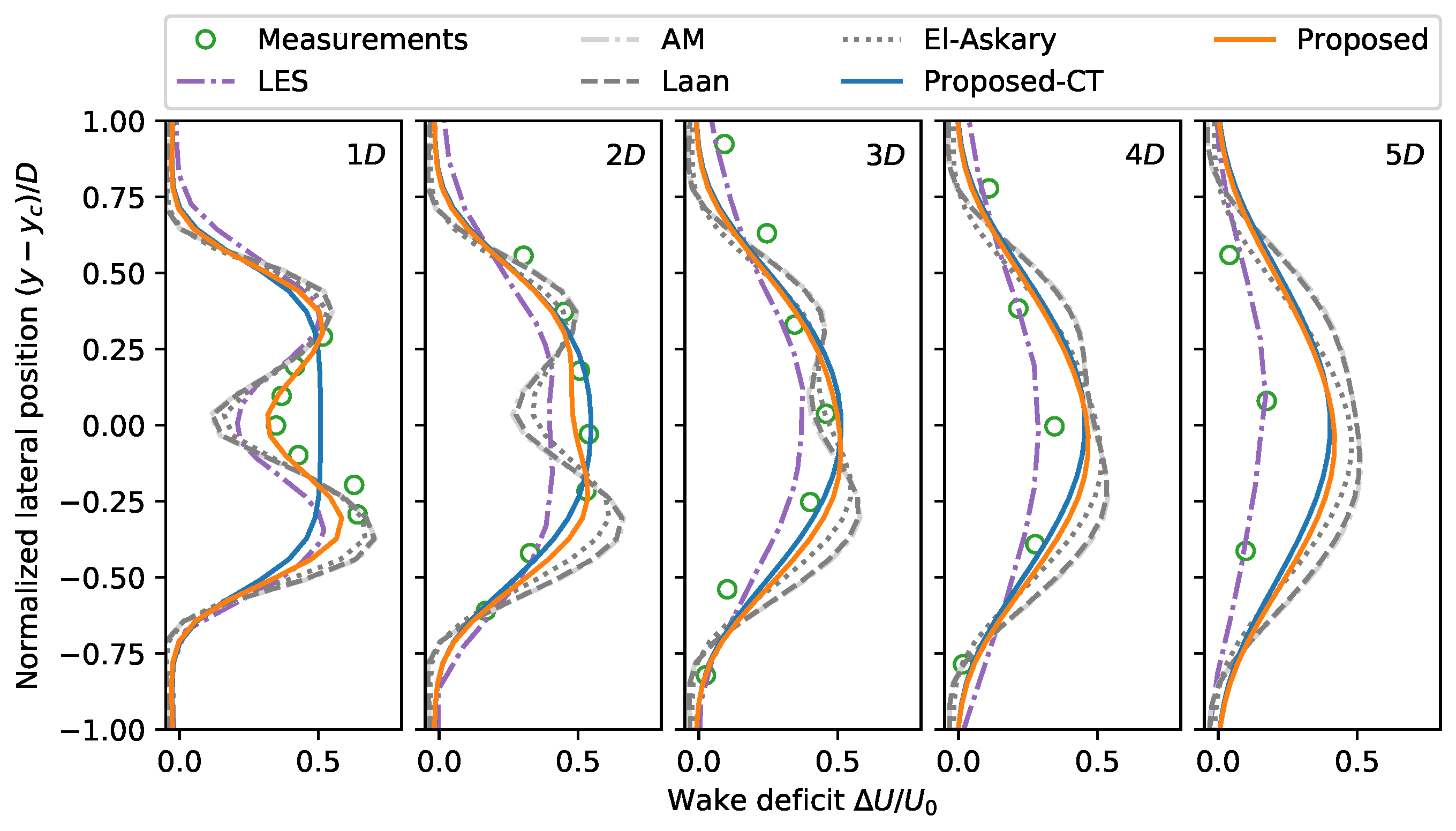
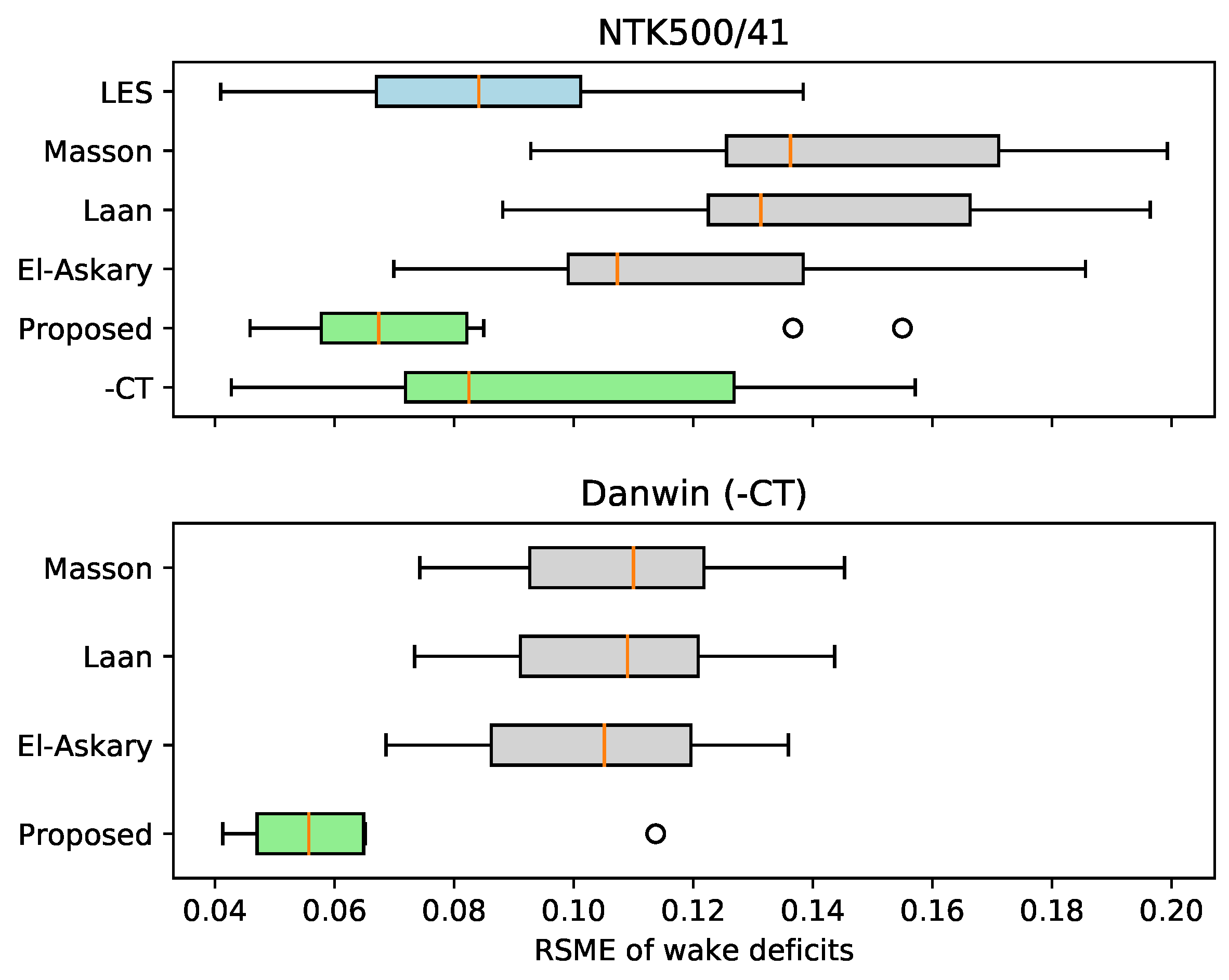
6.1. Case 1: Wakes of a NTK500/41 Wind Turbine
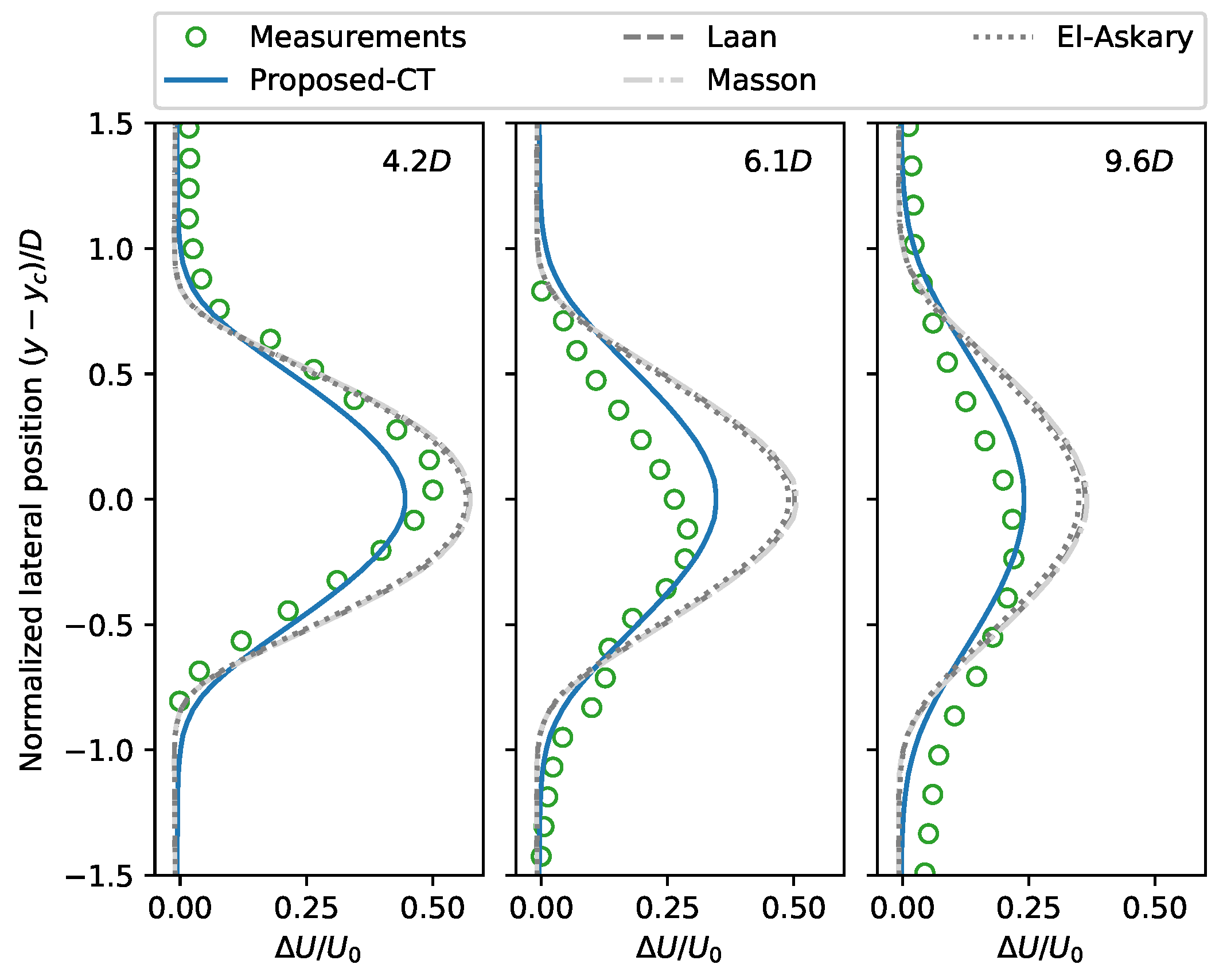
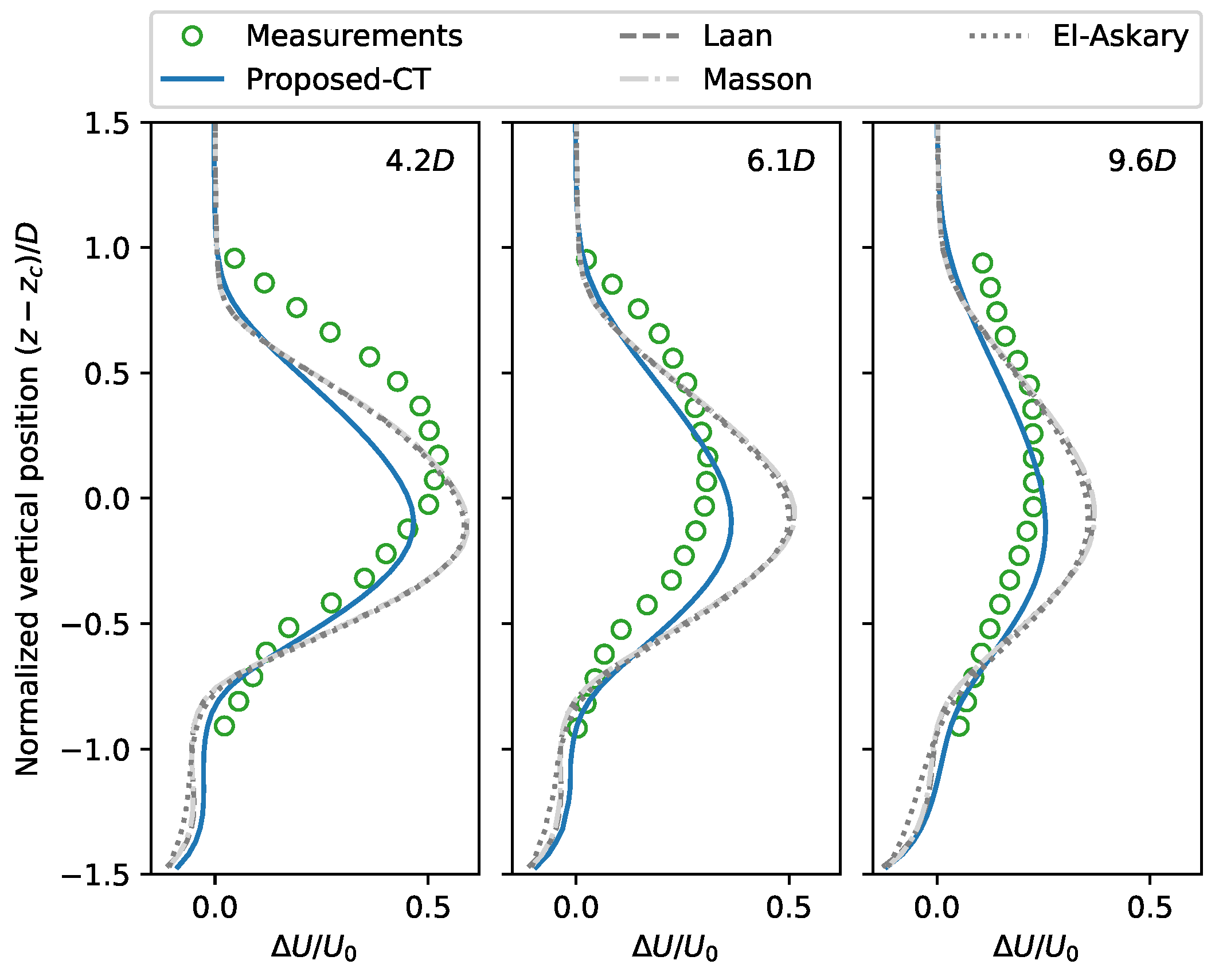
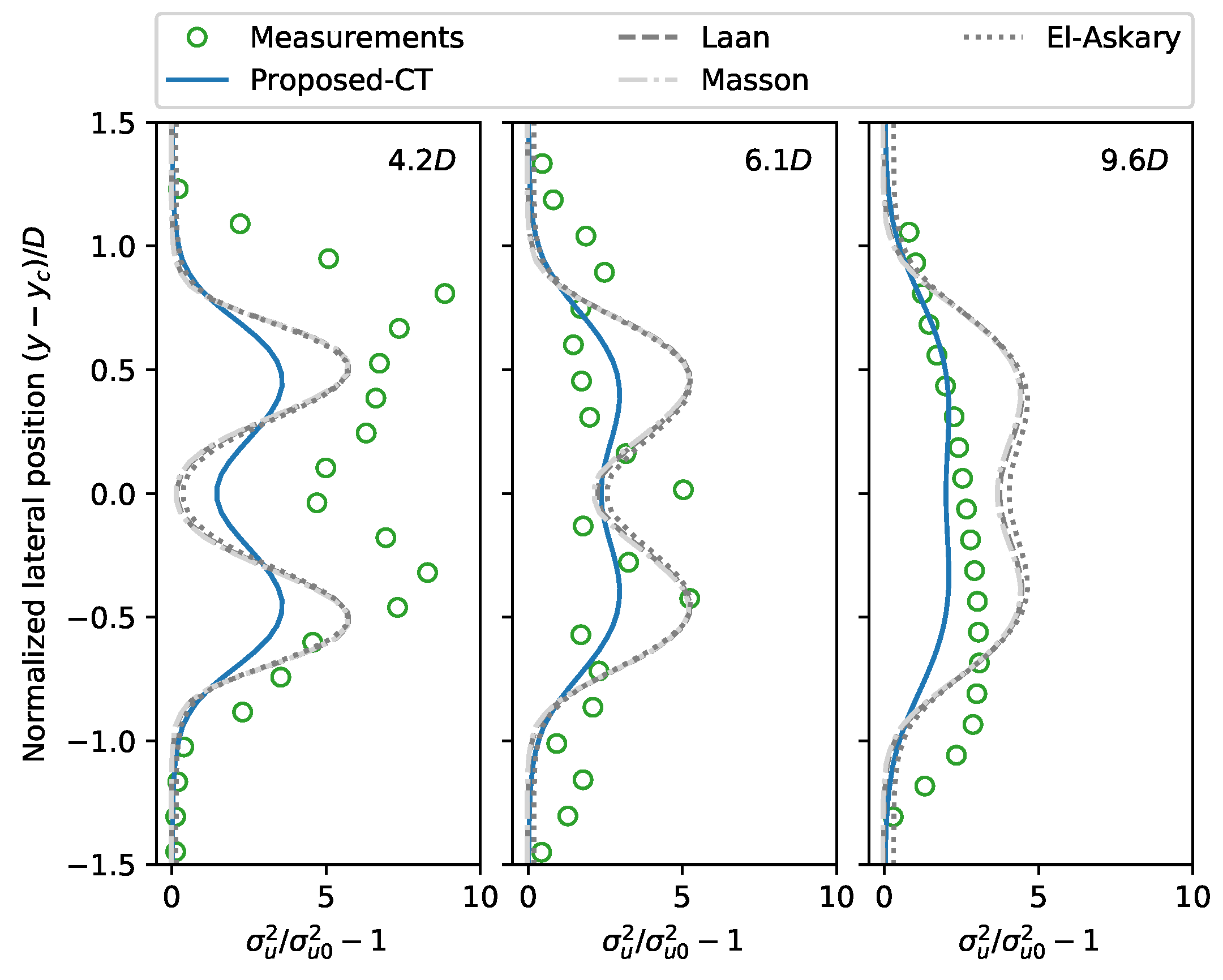
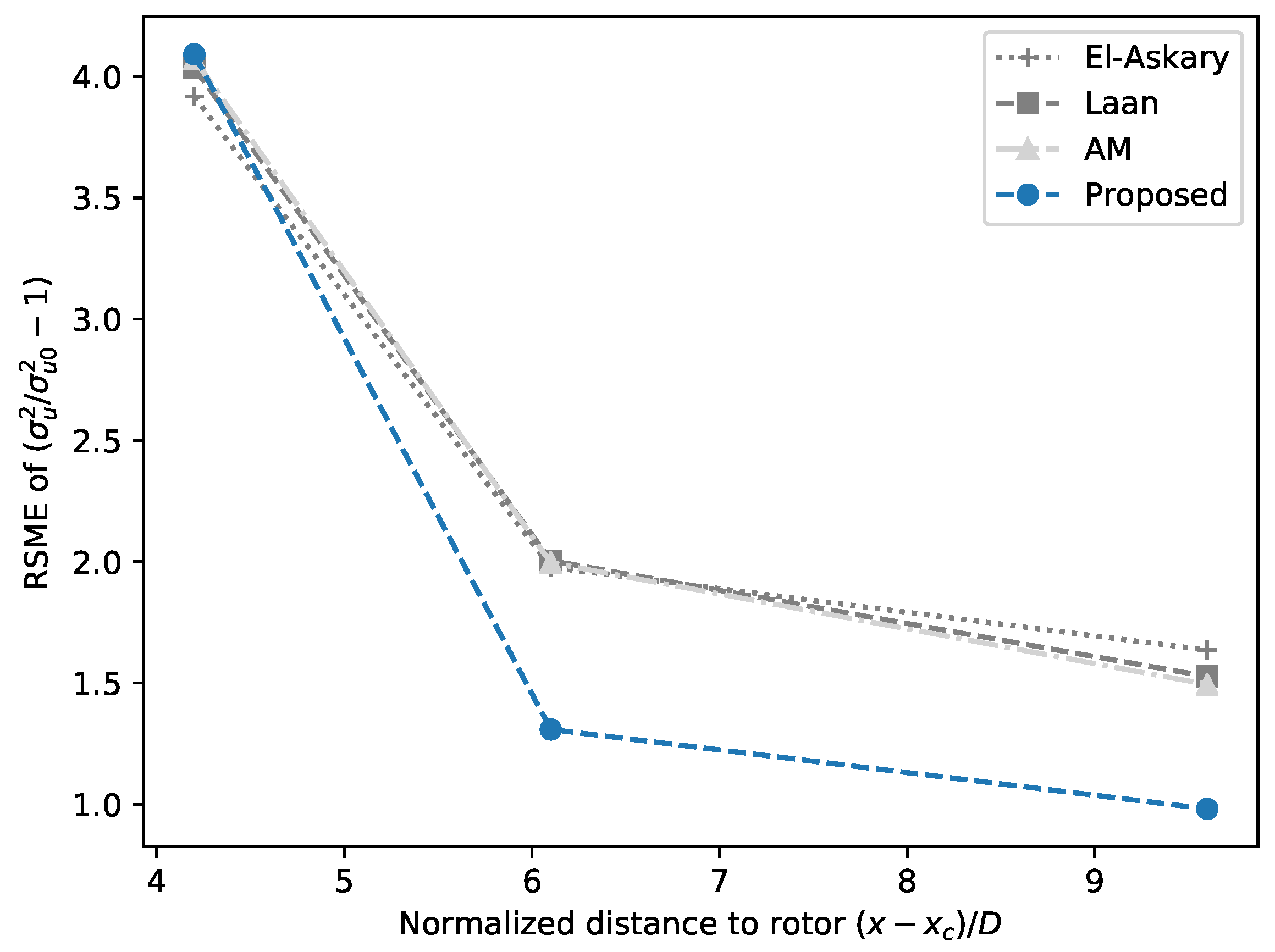
6.2. Case 2: Wakes of Danwin 180 kW Wind Turbines
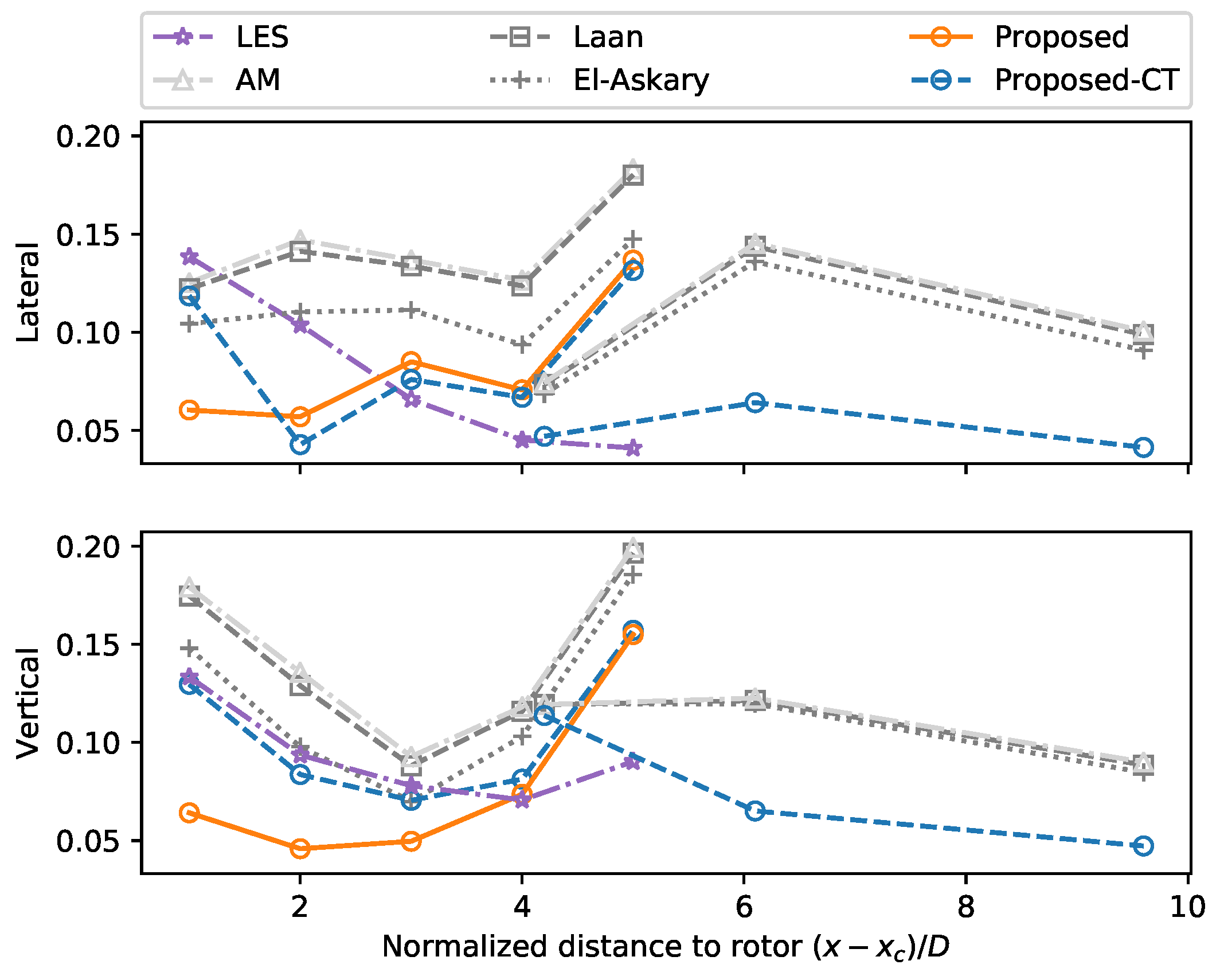
6.3. Model Assessment
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AD | Actuator Disk |
| AGL | Above Ground Level |
| AL | Actuator Line |
| BEM | Blade Element Theory |
| CFD | Computational Fluid Dynamics |
| LES | Large Eddy Simulation |
| LiDAR | Light Detection and Ranging |
| MOST | Monin–Obukhov Similarity Theory |
| OpenFOAM | Open-Source Field Operation And Manipulation |
| RANS | Reynolds-averaged Navier–Stokes Equations |
| TKE | Turbulence Kinetic Energy |
| WD | Wind Direction |
References
- Machefaux, E.; Larsen, G.C.; Koblitz, T.; Troldborg, N.; Kelly, M.C.; Chougule, A.; Hansen, K.S.; Rodrigo, J.S. An experimental and numerical study of the atmospheric stability impact on wind turbine wakes. Wind Energy 2016, 19, 1785–1805. [Google Scholar] [CrossRef]
- Han, X.; Liu, D.; Xu, C.; Shen, W.Z. Atmospheric stability and topography effects on wind turbine performance and wake properties in complex terrain. Renew. Energy 2018, 126, 640–651. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Porté-Agel, F. Effects of Thermal Stability and Incoming Boundary-Layer Flow Characteristics on Wind-Turbine Wakes: A Wind-Tunnel Study. Bound.-Layer Meteorol. 2010, 136, 515–533. [Google Scholar] [CrossRef]
- Zhang, W.; Markfort, C.D.; Porté-Agel, F. Wind-turbine wakes in a convective boundary layer: A wind-tunnel study. Bound.-Layer Meteorol. 2013, 146, 161–179. [Google Scholar] [CrossRef]
- Hancock, P.; Zhang, S.; Pascheke, F.; Hayden, P. Wind tunnel simulation of a wind turbine wake in neutral, stable and unstable wind flow. J. Phys. Conf. Ser. 2014, 555, 012047. [Google Scholar] [CrossRef]
- Magnusson, M.; Smedman, A.S. Influence of atmospheric stability on wind turbine wakes. Wind Eng. 1994, 18, 139–152. [Google Scholar]
- Iungo, G.V.; Porté-Agel, F. Volumetric lidar scanning of wind turbine wakes under convective and neutral atmospheric stability regimes. J. Atmos. Ocean. Technol. 2014, 31, 2035–2048. [Google Scholar] [CrossRef]
- Menke, R.; Vasiljević, N.; Hansen, K.S.; Hahmann, A.N.; Mann, J. Does the wind turbine wake follow the topography? A multi-lidar study in complex terrain. Wind Energy Sci. 2018, 3, 681–691. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porté-Agel, F. Atmospheric turbulence effects on wind-turbine wakes: An LES study. Energies 2012, 5, 5340–5362. [Google Scholar] [CrossRef]
- Xie, S.; Archer, C.L. A numerical study of wind-turbine wakes for three atmospheric stability conditions. Bound.-Layer Meteorol. 2017, 165, 87–112. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porté-Agel, F. Large-eddy simulation of wind-turbine wakes: Evaluation of turbine parametrisations. Bound.-Layer Meteorol. 2011, 138, 345–366. [Google Scholar] [CrossRef]
- Keck, R. A Numerical Investigation of Nacelle Anemometry for a HAWT Using Actuator Disc and Line Models in CFX. Renew. Energy 2012, 48, 72–84. [Google Scholar] [CrossRef]
- Prospathopoulos, J.M.; Politis, E.S.; Rados, K.G.; Chaviaropoulos, P.K. Evaluation of the Effects of Turbulence Model Enhancements on Wind Turbine Wake Predictions. Wind Energy 2011, 14, 285–300. [Google Scholar] [CrossRef]
- El-Askary, W.; Sakr, I.; AbdelSalam, A.M.; Abuhegazy, M. Modeling of Wind Turbine Wakes under Thermally-Stratified Atmospheric Boundary Layer. J. Wind Eng. Ind. Aerodyn. 2017, 160, 1–15. [Google Scholar] [CrossRef]
- Alinot, C.; Masson, C. k–varepsilon Model for the Atmospheric Boundary Layer Under Various Thermal Stratifications. J. Sol. Energy Eng. 2005, 127, 438–443. [Google Scholar] [CrossRef]
- Van der Laan, M.P.; Kelly, M.C.; Sørensen, N.N. A new k-epsilon model consistent with Monin–Obukhov similarity theory. Wind Energy 2017, 20, 479–489. [Google Scholar] [CrossRef]
- Grachev, A.A.; Andreas, E.L.; Fairall, C.W.; Guest, P.S.; Persson, P.O.G. The critical Richardson number and limits of applicability of local similarity theory in the stable boundary layer. Bound.-Layer Meteorol. 2013, 147, 51–82. [Google Scholar] [CrossRef]
- Van Der Avoird, E.; Duynkerke, P.G. Turbulence in a katabatic flow. Bound.-Layer Meteorol. 1999, 92, 37–63. [Google Scholar] [CrossRef]
- Foken, T. 50 years of the Monin–Obukhov similarity theory. Bound.-Layer Meteorol. 2006, 119, 431–447. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1990, 3, 269–289. [Google Scholar] [CrossRef]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Dyer, A. A review of flux-profile relationships. Bound.-Layer Meteorol. 1974, 7, 363–372. [Google Scholar] [CrossRef]
- Koblitz, T.; Sørensen, N.N.; Bechmann, A.; Sogachev, A. CFD Modeling of Non-Neutral Atmospheric Boundary Layer Conditions; DTU Wind Energy: Lyngby, Denmark, 2013. [Google Scholar]
- Shen, W.Z.; Mikkelsen, R.; Sørensen, J.N.; Bak, C. Tip Loss Corrections for Wind Turbine Computations. Wind Energy 2005, 8, 457–475. [Google Scholar] [CrossRef]
- Drela, M. XFOIL: An analysis and design system for low Reynolds number airfoils. In Low Reynolds Number Aerodynamics; Springer: Berlin/Heidelberg, Germany, 1989; pp. 1–12. [Google Scholar]
- Du, Z.; Selig, M. A 3-D Stall-Delay Model for Horizontal Axis Wind Turbine Performance Prediction. In Proceedings of the 1998 ASME Wind Energy Symposium, Reno, NV, USA, 12–15 January 1998; p. 21. [Google Scholar]
- Shen, W.Z.; Zhu, W.J.; Sørensen, J.N. Actuator Line/Navier–Stokes Computations for the MEXICO Rotor: Comparison with Detailed Measurements. Wind Energy 2012, 15, 811–825. [Google Scholar] [CrossRef]
- Glauert, H. Airplane propellers. In Aerodynamic Theory; Springer: Berlin/Heidelberg, Germany, 1935; pp. 169–360. [Google Scholar]
- El Kasmi, A.; Masson, C. An extended k–ε model for turbulent flow through horizontal-axis wind turbines. J. Wind Eng. Ind. Aerodyn. 2008, 96, 103–122. [Google Scholar] [CrossRef]
- Grachev, A.A.; Andreas, E.L.; Fairall, C.W.; Guest, P.S.; Persson, P.O.G. On the turbulent Prandtl number in the stable atmospheric boundary layer. Bound.-Layer Meteorol. 2007, 125, 329–341. [Google Scholar] [CrossRef]
- Pedersen, T.F.; Dahlberg, J.Å.; Busche, P. ACCUWIND-Classification of Five Cup Anemometers According to IEC 61400-12-1; Forskningscenter Risoe: Roskilde, Denmark, 2006. [Google Scholar]
- IEC. 61400-12-1: Wind Turbines—Part 12-1: Power Performance Measurements of Electricity Producing Wind Turbines; IEC: Geneva, Switzerland, 2005. [Google Scholar]
- Lira, A.; Rosas, P.; Araújo, A.; Castro, N. Uncertainties in the estimate of wind energy production. In Proceedings of the Energy Economics Iberian Conference—EEIC, Lisboa, Portugal, 4–5 February 2016; pp. 4–5. [Google Scholar]
- Coquilla, R.V.; Obermeier, J. Calibration Uncertainty Comparisons between Various Anemometers; American Wind Energy Association: Washington, DC, USA, 2008. [Google Scholar]
- Lindelöw-Marsden, P.; Pedersen, T.F.; Gottschall, J.; Vesth, A.; Wagner, R.; Paulsen, U.; Courtney, M. Flow Distortion on Boom Mounted Cup Anemometers; Risø-R-Report-1738 (EN); DTU Wind Energy: Lyngby, Denmark, 2010. [Google Scholar]
- Högström, U. Non-dimensional wind and temperature profiles in the atmospheric surface layer: A re-evaluation. In Topics in Micrometeorology. A Festschrift for Arch Dyer; Springer: Berlin/Heidelberg, Germany, 1988; pp. 55–78. [Google Scholar]
- Nieuwstadt, F.T. The turbulent structure of the stable, nocturnal boundary layer. J. Atmos. Sci. 1984, 41, 2202–2216. [Google Scholar] [CrossRef]
- Dyer, A.; Hicks, B. Flux-gradient relationships in the constant flux layer. Q. J. R. Meteorol. Soc. 1970, 96, 715–721. [Google Scholar] [CrossRef]
- Paulson, C.A. The mathematical representation of wind speed and temperature profiles in the unstable atmospheric surface layer. J. Appl. Meteorol. 1970, 9, 857–861. [Google Scholar] [CrossRef]
- Coppin, P.; Bradley, E.F.; Finnigan, J. Measurements of flow over an elongated ridge and its thermal stability dependence: The mean field. Bound.-Layer Meteorol. 1994, 69, 173–199. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, L.; Wang, Y.; Cao, X.; Zhang, Q.; Wang, H.; Zhang, B. Turbulence regimes and the validity of similarity theory in the stable boundary layer over complex terrain of the Loess Plateau, China. J. Geophys. Res. Atmos. 2014, 119, 6009–6021. [Google Scholar] [CrossRef]
- Grachev, A.A.; Andreas, E.L.; Fairall, C.W.; Guest, P.S.; Persson, P.O.G. SHEBA flux–profile relationships in the stable atmospheric boundary layer. Bound.-Layer Meteorol. 2007, 124, 315–333. [Google Scholar] [CrossRef]
- Sorbjan, Z. An examination of local similarity theory in the stably stratified boundary layer. Bound.-Layer Meteorol. 1987, 38, 63–71. [Google Scholar] [CrossRef]
- Blackadar, A.K.; Tennekes, H. Asymptotic similarity in neutral barotropic planetary boundary layers. J. Atmos. Sci. 1968, 25, 1015–1020. [Google Scholar] [CrossRef]
- Tennekes, H. The logarithmic wind profile. J. Atmos. Sci. 1973, 30, 234–238. [Google Scholar] [CrossRef]
- Bak, C.; Fuglsang, P.; Sørensen, N.N.; Madsen, H.A.; Shen, W.Z.; Sørensen, J.N. Airfoil Characteristics for Wind Turbines; Forskningscenter Risoe: Roskilde, Denmark, 1999. [Google Scholar]
- Johansen, J.; Sørensen, N.N. Aerofoil characteristics from 3D CFD rotor computations. Wind Energy Int. J. Prog. Appl. Wind Power Convers. Technol. 2004, 7, 283–294. [Google Scholar] [CrossRef]
- Vignaroli, A. UniTTe–MC1-Nordtank Measurement Campaign (Turbine and Met Masts); DTU Wind Energy: Lyngby, Denmark, 2016. [Google Scholar]
- Magnusson, M. Near-wake behaviour of wind turbines. J. Wind Eng. Ind. Aerodyn. 1999, 80, 147–167. [Google Scholar] [CrossRef]
- Zhang, X. CFD Simulation of Neutral ABL Flows; DTU Wind Energy: Lyngby, Denmark, 2009. [Google Scholar]
- Sørensen, J.N.; Mikkelsen, R.F.; Henningson, D.S.; Ivanell, S.; Sarmast, S.; Andersen, S.J. Simulation of wind turbine wakes using the actuator line technique. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140071. [Google Scholar] [CrossRef]
- Temel, O.; van Beeck, J. Two-equation eddy viscosity models based on the Monin–Obukhov similarity theory. Appl. Math. Model. 2017, 42, 1–16. [Google Scholar] [CrossRef]
- Chang, C.Y.; Schmidt, J.; Dörenkämper, M.; Stoevesandt, B. A consistent steady state CFD simulation method for stratified atmospheric boundary layer flows. J. Wind Eng. Ind. Aerodyn. 2018, 172, 55–67. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Sørensen, N.N. General Purpose Flow Solver Applied to Flow Over Hills; DTU Wind Energy: Lyngby, Denmark, 1995. [Google Scholar]
- Bodini, N.; Zardi, D.; Lundquist, J.K. Three-Dimensional Structure of Wind Turbine Wakes as Measured by Scanning Lidar. Atmos. Meas. Tech. 2017, 10, 2881–2896. [Google Scholar] [CrossRef]
- Ntinas, G.K.; Shen, X.; Wang, Y.; Zhang, G. Evaluation of CFD Turbulence Models for Simulating External Airflow Around Varied Building Roof with Wind Tunnel Experiment; Building Simulation; Springer: Berlin/Heidelberg, Germany, 2018; Volume 11, pp. 115–123. [Google Scholar]






| Turbulence Model | Energy Equation (14) | Similarity Functions | |||
|---|---|---|---|---|---|
| AM | √ | Equation (25) | − | −2.9 | classical |
| El-Askary | − | Equation (27) | − | 1 | classical |
| Laan | √ | Equation (25) | Equation (32) | Equation (33) | classical |
| Proposed | √ | Equation (25) | Equation (32) | Equation (33) | , , |
| Wind Turbine | D (m) | H (m) | Measurements | Wake Range |
|---|---|---|---|---|
| NTK500/41 | 41 | 36 | LiDAR scanning | 1D to 5D |
| Danwin | 23 | 35 | Mast measurements | 4.2D, 6.1D, and 9.6D |
| Model | Case 1 | Case 2 | ||
|---|---|---|---|---|
| (m/s) | TI | (m/s) | TI | |
| AM, Laan, El-Askary | 0.223 | 6.0% | 0.198 | 4.5% |
| Proposed | 0.297 | 10.2% | 0.228 | 6.5% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.; Liu, D.; Xu, C.; Shen, W.; Li, L.; Xue, F. Monin–Obukhov Similarity Theory for Modeling of Wind Turbine Wakes under Atmospheric Stable Conditions: Breakdown and Modifications. Appl. Sci. 2019, 9, 4256. https://doi.org/10.3390/app9204256
Han X, Liu D, Xu C, Shen W, Li L, Xue F. Monin–Obukhov Similarity Theory for Modeling of Wind Turbine Wakes under Atmospheric Stable Conditions: Breakdown and Modifications. Applied Sciences. 2019; 9(20):4256. https://doi.org/10.3390/app9204256
Chicago/Turabian StyleHan, Xingxing, Deyou Liu, Chang Xu, Wenzhong Shen, Linmin Li, and Feifei Xue. 2019. "Monin–Obukhov Similarity Theory for Modeling of Wind Turbine Wakes under Atmospheric Stable Conditions: Breakdown and Modifications" Applied Sciences 9, no. 20: 4256. https://doi.org/10.3390/app9204256
APA StyleHan, X., Liu, D., Xu, C., Shen, W., Li, L., & Xue, F. (2019). Monin–Obukhov Similarity Theory for Modeling of Wind Turbine Wakes under Atmospheric Stable Conditions: Breakdown and Modifications. Applied Sciences, 9(20), 4256. https://doi.org/10.3390/app9204256






