Evaluating Seismic Soil Liquefaction Potential Using Bayesian Belief Network and C4.5 Decision Tree Approaches
Abstract
1. Introduction
- (1)
- The BBN and C4.5 DT effective approaches are used to evaluate and compare the seismic soil liquefaction potential of the updated and relatively large cone penetration test (CPT) data set, which includes 251 case history records. In addition, the developed models are compared with the Youd et al. [6] and Rezania et al. [31] models to validate performance.
- (2)
- One of the major advantages of the presented models is the consideration and addition of earthquake parameters to the dataset—the causative fault type and closest distance to rupture surface parameter.
- (3)
- Data division for training and testing datasets was performed with due attention to statistical aspects, such as minimum, maximum, mean, and standard deviation of the datasets. The splitting of the datasets helped identify the predictive ability and generalization performance of the developed models, and evaluate them better.
- (4)
- This study presents probabilistic reasoning, most probable explanation of seismic soil liquefied sites, and parametric sensitivity analysis of the robust model.
2. Predictive Modeling Techniques
2.1. Bayesian Belief Network (BBN)
2.2. C4.5 Decision Tree (DT) Model
3. Development of Seismic Soil Liquefaction Modeling
3.1. Dataset, Date Preprocessing, and Predictor Variables
- A training dataset is required to train the models. In this research work, the authors used 80% of the data i.e., 201 out of 251 CPT case histories are considered for the training set.
- A testing dataset is needed to predict the developed models’ performance. In this study, the remaining 20% of data i.e., 50 out of 251 CPT case histories are considered as the testing dataset.
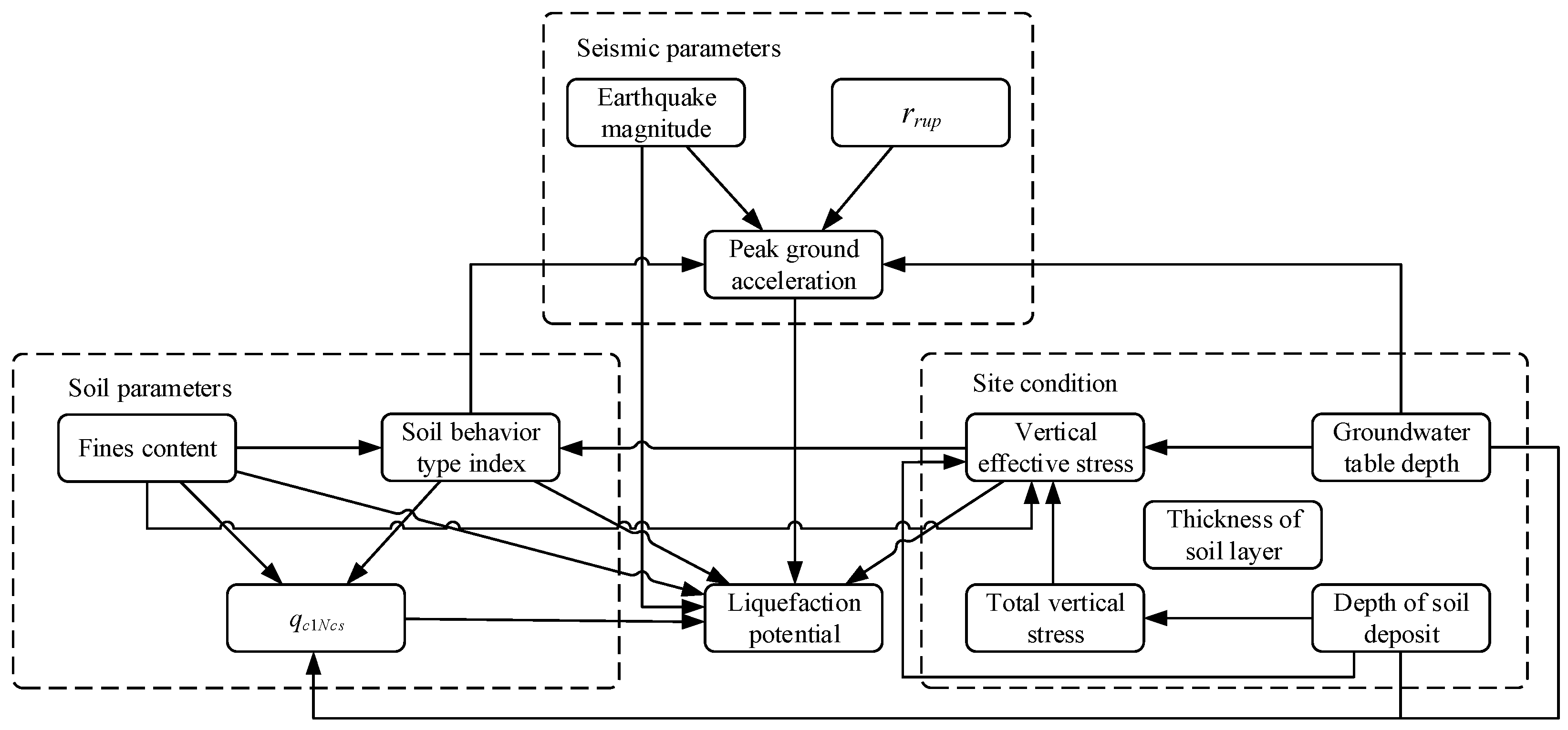
3.2. Model Development Using BBNs
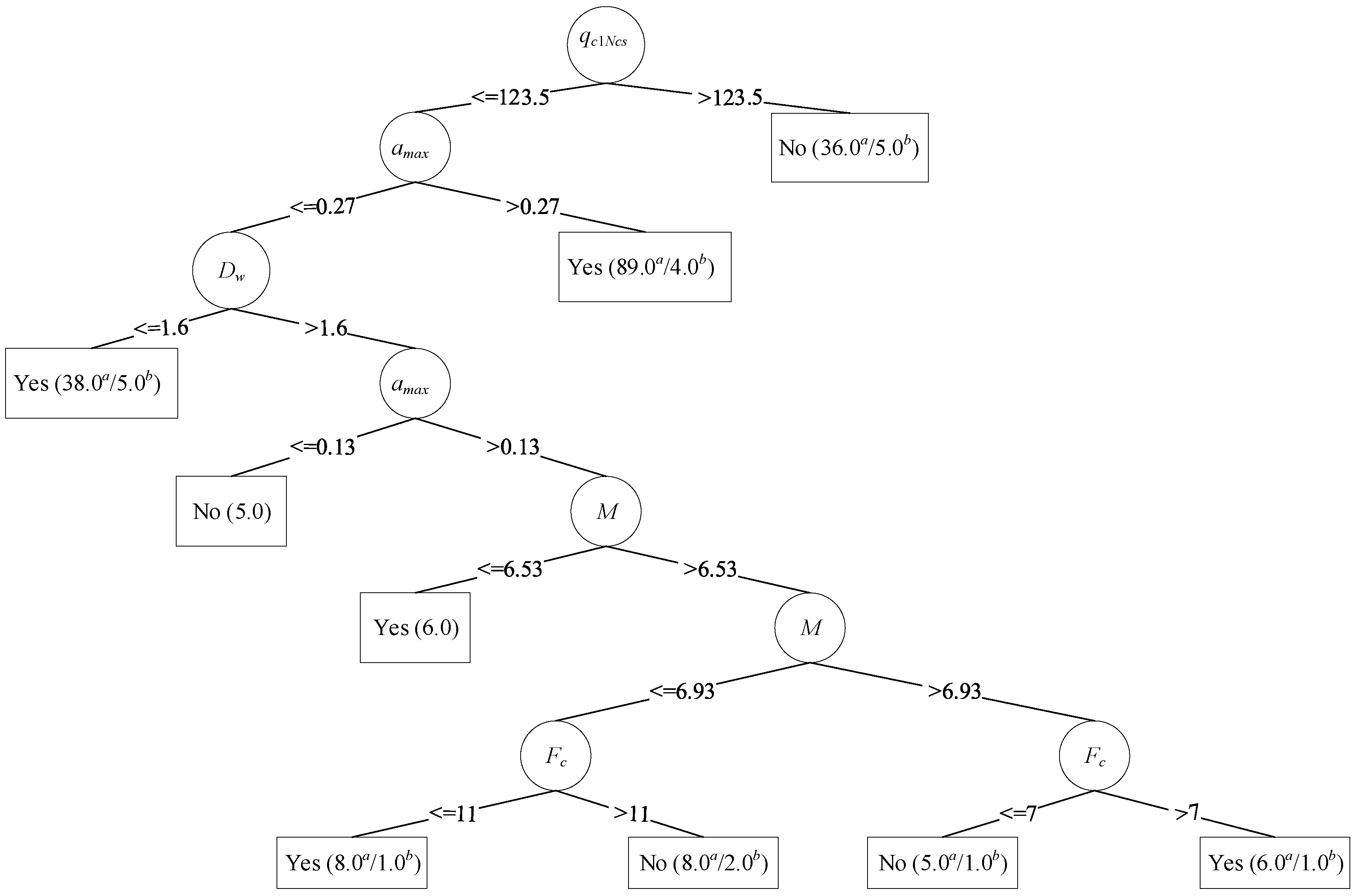
3.3. Model Development Using C4.5 Decision Tree
4. Performance Measure
- True positive (TP) and true negative (TN) indicate that the samples are predicted correctly.
- False positive (FP) represents the number of non-liquefied samples that are predicted incorrectly as positive.
- False negative (FN) denotes the number of liquefied samples that are predicted incorrectly as negative.
- Precision refers to the accuracy of the predictions for a single class (positive or negative).
- Recall measures the accuracy of predictions, considering only the predicted value.
5. Results
5.1. Comparative Performance of Training and Testing Datasets
5.2. Analysis of a Robust BBN Model
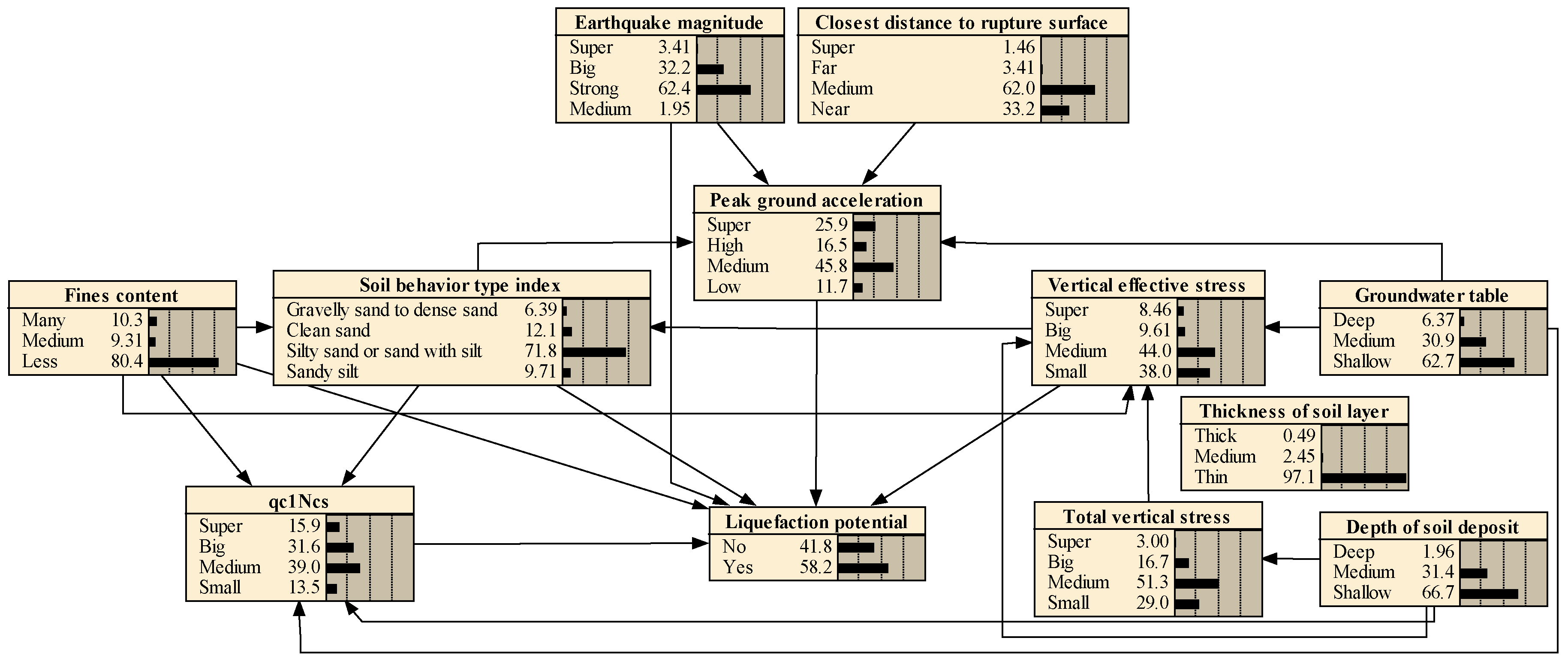
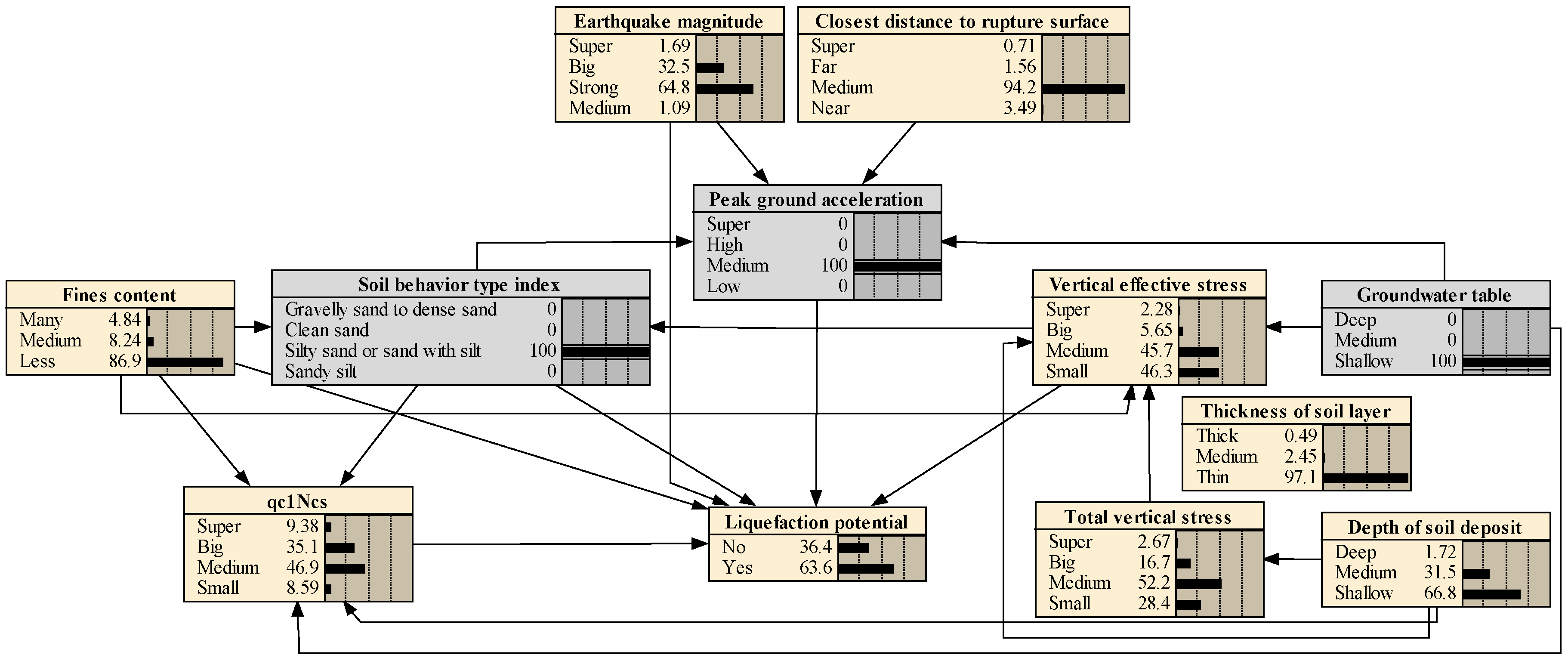
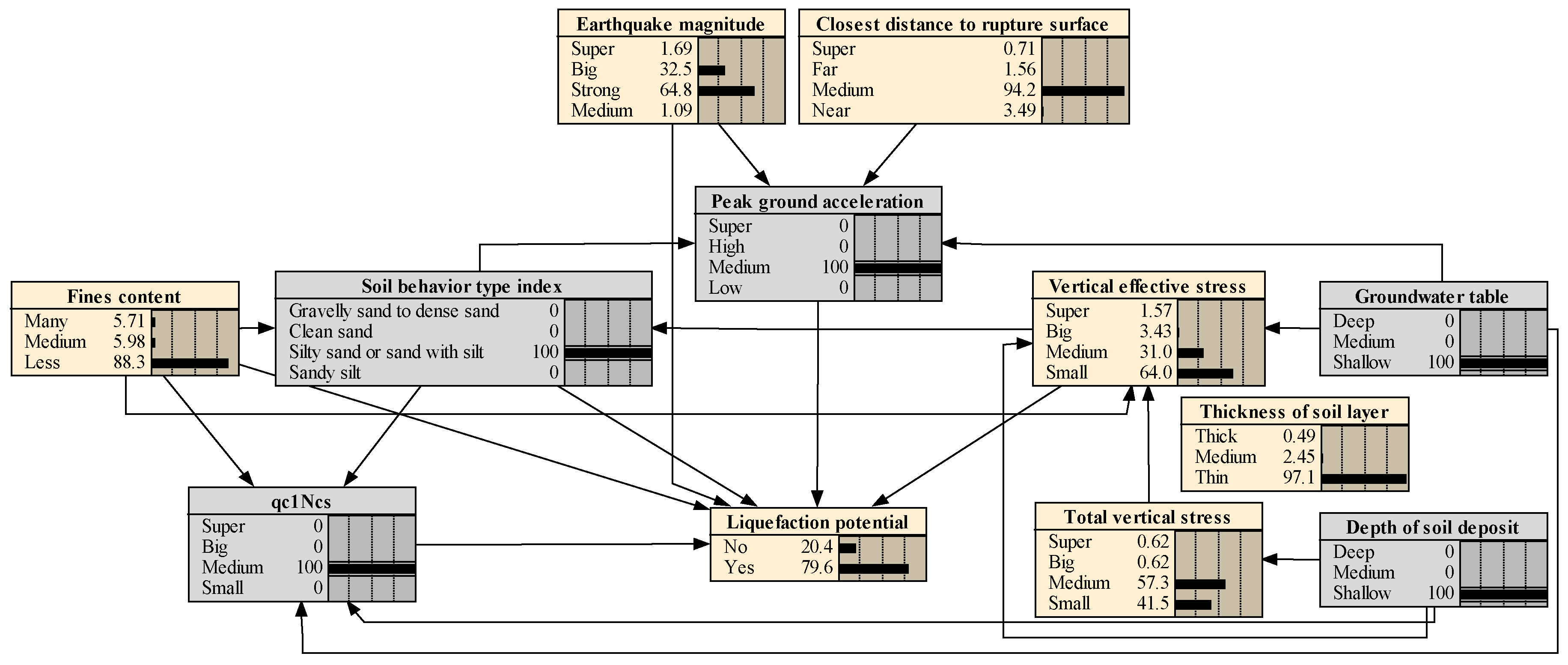
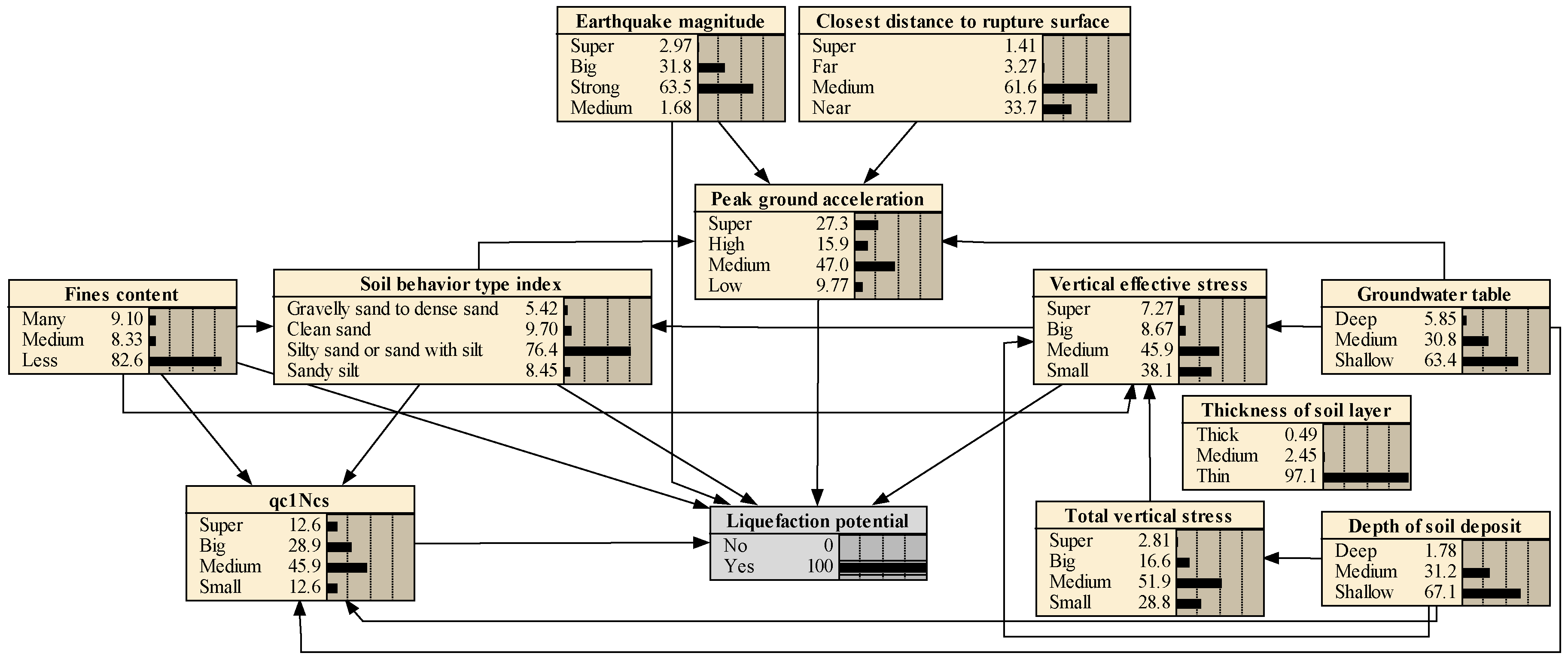
5.2.1. Probabilistic Reasoning
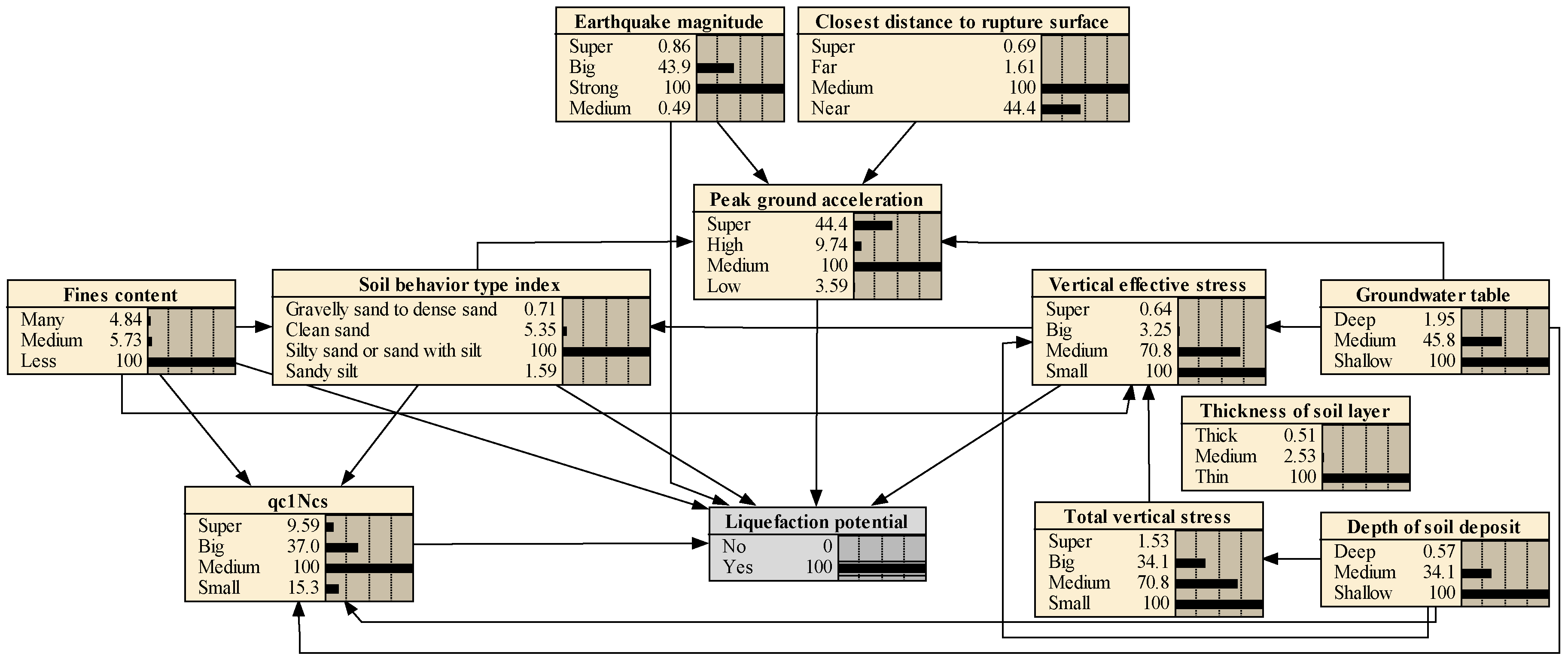
5.2.2. Most Probable Explanation
5.2.3. Sensitivity Analysis
6. Discussion and Conclusions
- The BBN model has relatively better results, as compared to the C4.5 DT, CPT-YD, and CPT-RA models. Considering its overall predictive accuracy, MCC, precision, recall, F-measure for liquefaction and non-liquefaction instances, AUC of ROC, simplicity in practice, data-driven characteristics, and the ability to map interactions between variables, the use of the BBN model in evaluating seismic soil liquefaction by multiple complex factors is quite promising.
- The proposed robust BBN model can not only quantitatively predict seismic soil liquefaction potential probability under certain influence factors (seismic, soil, and site conditions), but also identify the main diagnostic reasons and fault-finding states’ combinations presumed to support decisions on seismic soil liquefaction mitigation measures for sustainable development.
- The sensitivity analysis results conclude that “equivalent clean sand penetration resistance”, “soil behavior type index’, “groundwater table”, “peak ground acceleration’, “vertical effective stress”, and “fines content” are the most sensitive factors in descending order in the assessment of liquefaction potential, and are well matched with the literature.
- The “most probable explanation” function is used to provide the most likely cause set of seismic soil liquefied sites, which is: earthquake magnitude = strong, peak ground acceleration = medium, closest distance to rupture surface = medium, fines content = less, soil behavior type index = silty sand or silt with sand, qc1Ncs = medium, vertical effective stress = small, total vertical stress = small, groundwater table depth = shallow, and depth of soil deposit = shallow. This is considerably compatible and well matched with engineering judgment.
- The BBN model can be used to assess vulnerability of land damage resulting from seismic soil liquefaction by adding nodes of liquefaction land damage potential.
- Additional CPT case history records should be collected and an attempt made to avoid class imbalance in the dataset (caused by updating the BBN model’s conditional probability table) and improve the performance results of prediction.
- The nodes of ‘utility’ and ‘decision operations’ should be added to seismic soil liquefaction and the BBN’s land damage potential model, which can eventually be used as important decision-making information in case of expected utility of loss.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oommen, T.; Baise, L.G.; Vogel, R. Validation and Application of Empirical Liquefaction Models. J. Geotech. Geoenviron. Eng. 2010, 136, 1618–1633. [Google Scholar] [CrossRef]
- Tang, X.-W.; Bai, X.; Hu, J.-L.; Qiu, J.-N. Assessment of liquefaction-induced hazards using Bayesian networks based on standard penetration test data. Nat. Hazards Earth Syst. Sci. 2018, 18, 1451–1468. [Google Scholar] [CrossRef]
- Kohestani, V.R.; Hassanlourad, M.; Ardakani, A. Evaluation of liquefaction potential based on CPT data using random forest. Nat. Hazards 2015, 79, 1079–1089. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, D.; Liu, X.; Chen, C.; Li, X. P and S wave attenuation tomography of the Japan subduction zone. Geochem. Geophys. Geosyst. 2017, 18, 1688–1710. [Google Scholar] [CrossRef]
- Goh, A.T.; Goh, S. Support vector machines: Their use in geotechnical engineering as illustrated using seismic liquefaction data. Comput. Geotech. 2007, 34, 410–421. [Google Scholar] [CrossRef]
- Youd, T.L.; Idriss, I.M. Liquefaction resistance of soils: Summary report from the 1996 NCEER and 1998 NCEER/NSF workshops on evaluation of liquefaction resistance of soils. J. Geotech. Geoenviron. Eng. 2001, 127, 297–313. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M. Simplified procedure for evaluating soil liquefaction potential. J. Soil Mech. Found. Div. 1971, 97, 1249–1273. [Google Scholar]
- Juang, C.H.; Yuan, H.; Lee, D.-H.; Lin, P.-S. Simplified Cone Penetration Test-based Method for Evaluating Liquefaction Resistance of Soils. J. Geotech. Geoenviron. Eng. 2003, 129, 66–80. [Google Scholar] [CrossRef]
- Xue, X.; Yang, X. Application of the adaptive neuro-fuzzy inference system for prediction of soil liquefaction. Nat. Hazards 2013, 67, 901–917. [Google Scholar] [CrossRef]
- Goh, A.T.C. Neural-Network Modeling of CPT Seismic Liquefaction Data. J. Geotech. Eng. 1996, 122, 70–73. [Google Scholar] [CrossRef]
- Samui, P. Seismic liquefaction potential assessment by using Relevance Vector Machine. Earthq. Eng. Eng. Vib. 2007, 6, 331–336. [Google Scholar] [CrossRef]
- Pal, M. Support vector machines-based modelling of seismic liquefaction potential. Int. J. Numer. Anal. Methods Géoméch. 2006, 30, 983–996. [Google Scholar] [CrossRef]
- Kaveh, A.; Hamze-Ziabari, S.M.; Bakhshpoori, T. Patient rule-induction method for liquefaction potential assessment based on CPT data. Bull. Int. Assoc. Eng. Geol. 2016, 77, 849–865. [Google Scholar] [CrossRef]
- Zhou, J.; Li, E.; Wang, M.; Chen, X.; Shi, X.; Jiang, L. Feasibility of Stochastic Gradient Boosting Approach for Evaluating Seismic Liquefaction Potential Based on SPT and CPT Case Histories. J. Perform. Constr. Facil. 2019, 33, 04019024. [Google Scholar] [CrossRef]
- Liang, W.-J.; Zhuang, D.-F.; Jiang, D.; Pan, J.-J.; Ren, H.-Y. Assessment of debris flow hazards using a Bayesian Network. Geomorphology 2012, 171, 94–100. [Google Scholar] [CrossRef]
- Ardakani, A.; Kohestani, V.R. Evaluation of liquefaction potential based on CPT results using C4.5 decision tree. J. Artif. Intell. Data Min. 2015, 3, 85–92. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems; Morgan Kaufmann Publishers: San Mateo, CA, USA, 1988. [Google Scholar]
- Bayraktarli, Y.Y.; Baker, J.W.; Faber, M.H. Uncertainty treatment in earthquake modelling using Bayesian probabilistic networks. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2011, 5, 44–58. [Google Scholar] [CrossRef]
- Bensi, M.T.; Der, K.A.; Straub, D. A Bayesian Network framework for post–earthquake infrastructure system performance assessment. In Proceedings of the TCLEE 2009: Lifeline Earthquake Engineering in a Multi-hazard Environment, Oakland, CA, USA, 28 June–1 July 2009. [Google Scholar]
- Bayraktarli, Y.Y.; Faber, M.H. Bayesian probabilistic network approach for managing earthquake risks of cities. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2011, 5, 2–24. [Google Scholar] [CrossRef]
- Faizian, M.; Schalcher, H.R.; Faber, M.H. Consequence assessment in earthquake risk management using damage indicators. In Proceedings of the 9th International Conference on Structural Safety and Reliability (ICOSSAR 05), Rome, Italy, 19–23 June 2005; pp. 19–23. [Google Scholar]
- Jia, J.; Zhang, L.; Xu, Y.; Zhao, C. Diagnosis of embankment dam distresses using Bayesian networks. Part I. Global-level characteristics based on a dam distress database. Can. Geotech. J. 2011, 48, 1630–1644. [Google Scholar]
- Jia, J.; Xu, Y.; Zhang, L. Diagnosis of embankment dam distresses using Bayesian networks. Part II. Diagnosis of a specific distressed dam. Can. Geotech. J. 2011, 48, 1645–1657. [Google Scholar]
- Bayraktarli, Y.Y. Application of Bayesian probabilistic networks for liquefaction of soil. In Proceedings of the 6th International PhD Symposium in Civil Engineering, Zurich, Switzerland, 23–26 August 2006. [Google Scholar]
- Hu, J.-L.; Tang, X.-W.; Qiu, J.-N. A Bayesian network approach for predicting seismic liquefaction based on interpretive structural modeling. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2015, 9, 200–217. [Google Scholar] [CrossRef]
- Hu, J.-L.; Tang, X.-W.; Qiu, J.-N. Assessment of seismic liquefaction potential based on Bayesian network constructed from domain knowledge and history data. Soil Dyn. Earthq. Eng. 2016, 89, 49–60. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann: San Francisco, CA, USA, 1993. [Google Scholar]
- Duch, W.; Setiono, R.; Zurada, J. Computational intelligence methods for rule-based data understanding. Proc. IEEE 2004, 92, 771–805. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Fridline, M.M.; Roke, D.A. Decision Tree Approach for Soil Liquefaction Assessment. Sci. World J. 2013, 2013, 1–8. [Google Scholar] [CrossRef]
- Rezania, M.; Faramarzi, A.; Javadi, A.A. An evolutionary based approach for assessment of earthquake-induced soil liquefaction and lateral displacement. Eng. Appl. Artif. Intell. 2011, 24, 142–153. [Google Scholar] [CrossRef]
- Cooper, G.F.; Herskovits, E. A Bayesian Method for the Induction of Probabilistic Networks from Data. Mach. Learn. 1992, 9, 309–347. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Lauritzen, S.L. Sequential updating of conditional probabilities on directed graphical structures. Networks 1990, 20, 579–605. [Google Scholar] [CrossRef]
- Lauritzen, S.L. The EM algorithm for graphical association models with missing data. Comput. Stat. Data Anal. 1995, 19, 191–201. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; Wadsworth International Group: San Francisco, CA, USA, 1984. [Google Scholar]
- Mesarić, J.; Šebalj, D. Decision trees for predicting the academic success of students. Croat. Oper. Res. Rev. 2016, 7, 367–388. [Google Scholar] [CrossRef]
- Boulanger, R.; Idriss, I. CPT and SPT Based Liquefaction Triggering Procedures; Report No. UCD/CGM–14/01; Center for Geotechnical Modeling, Department of Civil and Environmental Engineering, University of California: Davis, CA, USA, 2014. [Google Scholar]
- Tranfield, D.; Denyer, D.; Smart, P. Knowledge by Means of Systematic Review. Br. J. Manag. 2003, 14, 207–222. [Google Scholar] [CrossRef]
- Okoli, C.; Schabram, K. A Guide to Conducting a Systematic Literature Review of Information Systems Research. Working Papers on Information Systems. SSRN Electron. J. 2010, 10, 1–51. [Google Scholar]
- Zhang, L.Y. Predicting Seismic Liquefaction Potential of Sands by Optimum Seeking Method. Soil Dyn. Earthq. Eng. 1998, 17, 219–226. [Google Scholar] [CrossRef]
- Ahmad, M.; Tang, X.-W.; Qiu, J.-N.; Ahmad, F. Interpretive Structural Modeling and MICMAC Analysis for Identifying and Benchmarking Significant Factors of Seismic Soil Liquefaction. Appl. Sci. 2019, 9, 233. [Google Scholar] [CrossRef]
- Sadigh, K.; Chang, C.-Y.; Egan, J.A.; Makdisi, F.; Youngs, R.R. Attenuation Relationships for Shallow Crustal Earthquakes Based on California Strong Motion Data. Seism. Res. Lett. 1997, 68, 180–189. [Google Scholar] [CrossRef]
- Matthews, B. Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochim. Biophys. Acta (BBA)-Protein Struct. 1975, 405, 442–451. [Google Scholar] [CrossRef]
- Baldi, P.; Brunak, S.; Chauvin, Y.; Andersen, C.A.F.; Nielsen, H. Assessing the accuracy of prediction algorithms for classification: An overview. Bioinformatics 2000, 16, 412–424. [Google Scholar] [CrossRef]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Hamdia, K.M.; Marino, M.; Zhuang, X.; Wriggers, P.; Rabczuk, T. Sensitivity analysis for the mechanics of tendons and ligaments: Investigation on the effects of collagen structural properties via a multiscale modeling approach. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3209. [Google Scholar] [CrossRef]
- Ayad, F.; Abdelmalek, B.; Youcef, H. Sensitivity Analysis of Soil Liquefaction Potential. Earth Sci. Res. 2014, 3, 14–24. [Google Scholar] [CrossRef]
- Cheng, J.; Greiner, R.; Kelly, J.; Bell, D.; Liu, W. Learning Bayesian networks from data: An information-theory based approach. Artif. Intell. 2002, 137, 43–90. [Google Scholar] [CrossRef]
- Tesfamariam, S.; Liu, Z. Seismic risk analysis using Bayesian belief networks. In Handbook of Seismic Risk Analysis and Management of Civil Infrastructure Systems; Woodhead Publishing: Cambridge, UK, 2013; pp. 175–208. [Google Scholar]
- Pirhadi, N.; Tang, X.; Yang, Q.; Kang, F. A New Equation to Evaluate Liquefaction Triggering Using the Response Surface Method and Parametric Sensitivity Analysis. Sustainability 2018, 11, 112. [Google Scholar] [CrossRef]
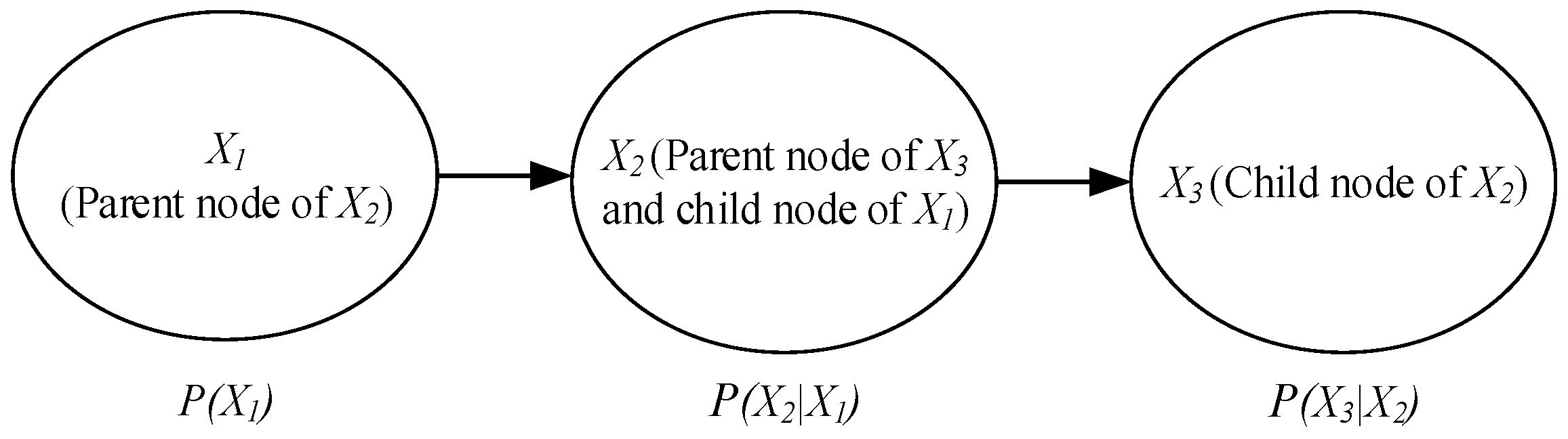
| Input : A complete dataset; . : The order of nodes (Assume it is consistent with variables’ subscripts). : The maximum number of parents. Output Bayesian belief network structure |
| Steps 1: 2: for j = 1 to n 3: 4: 5: while(true) 6: 7: 8: if ( and ) 9: 10: 11: 12: else 13: break 14: end if 15: end while 16: end for 17: return |
| Category | Seismic Soil Liquefaction Factors | Number of Grades | Explanation | Range |
|---|---|---|---|---|
| Seismic parameter | Earthquake magnitude, M | 4 | Super | 8 ≤ M |
| Big | 7 ≤ M < 8 | |||
| Strong | 6 ≤ M < 7 | |||
| Medium | 4.5 ≤ M < 6 | |||
| Peak ground acceleration (PGA), amax (g) | 4 | Super | 0.40 ≤ amax | |
| High | 0.30 ≤ amax < 0.40 | |||
| Medium | 0.15 ≤ amax < 0.30 | |||
| Low | 0 ≤ amax < 0.15 | |||
| Closest distance to rupture surface, rrup (km) | 4 | Super | 100 < rrup | |
| Far | 50 < rrup ≤ 100 | |||
| Medium | 10 < rrup ≤ 50 | |||
| Near | 0 < rrup ≤ 10 | |||
| Soil parameter | Fines content, Fc (%) | 3 | Many | 50 < Fc |
| Medium | 30 < Fc ≤ 50 | |||
| Less | 0 ≤ Fc ≤ 30 | |||
| Equivalent clean sand penetration resistance, qc1Ncs | 4 | Super | 135 ≤ qc1Ncs | |
| Big | 90 ≤ qc1Ncs < 135 | |||
| Medium | 45 ≤ qc1Ncs < 90 | |||
| Small | 0 ≤ qc1Ncs < 45 | |||
| Soil behavior type index, Ic | 4 | Gravelly sand to dense sand | Ic < 1.31 | |
| Clean sand | 1.31 ≤ Ic < 1.61 | |||
| Silty sand or sand with silt | 1.61 ≤ Ic < 2.40 | |||
| Sandy silt | 2.40 ≤ Ic < 2.60 | |||
| Site condition | Vertical effective stress, σ’v (kPa) | 4 | Super | 150 ≤ σ’v |
| Big | 100 ≤ σ’v < 150 | |||
| Medium | 50 ≤ σ’v < 100 | |||
| Small | 0 ≤ σ’v < 50 | |||
| Total vertical stress, σv (kPa) | 4 | Super | 165 ≤ σv | |
| Big | 110 ≤ σv < 165 | |||
| Medium | 55 ≤ σv < 110 | |||
| Small | 0 ≤ σv < 55 | |||
| Groundwater table depth, Dw (m) | 3 | Deep | 4 ≤ Dw | |
| Medium | 2 < Dw < 4 | |||
| Shallow | Dw ≤ 2 | |||
| Depth of soil deposit, Ds (m) | 3 | Deep | 10 ≤ Ds < 20 | |
| Medium | 5 ≤ Ds <10 | |||
| Shallow | 0 ≤ Ds <5 | |||
| Thickness of soil layer, Ts (m) | 3 | Thick | 10 ≤ Ts | |
| Medium | 5 ≤ Ts < 10 | |||
| Thin | 0 < Ts < 5 |
| Seismic Soil Liquefaction Factors | Dataset | Minimum | Maximum | Mean | Standard Deviation |
|---|---|---|---|---|---|
| Earthquake magnitude, M | Training | 5.9 | 9 | 7.01 | 0.55 |
| Testing | 5.9 | 9 | 6.88 | 0.56 | |
| Peak ground acceleration (PGA), amax (g) | Training | 0.09 | 0.84 | 0.32 | 0.14 |
| Testing | 0.09 | 0.8 | 0.32 | 0.17 | |
| Closest distance to rupture surface, rrup (km) | Training | 1 | 107.03 | 18.15 | 17.08 |
| Testing | 1 | 100.36 | 18.57 | 17.92 | |
| Fines content, Fc (%) | Training | 0 | 85 | 18.65 | 19.92 |
| Testing | 0 | 75 | 13.94 | 15.98 | |
| Equivalent clean sand penetration resistance, qc1Ncs | Training | 16.1 | 311.9 | 93.83 | 38.82 |
| Testing | 36.7 | 206.3 | 94.79 | 33.85 | |
| Soil behavior type index, Ic | Training | 1.16 | 2.59 | 1.98 | 0.29 |
| Testing | 1.34 | 2.5 | 1.90 | 0.25 | |
| Vertical effective stress, σ’v (kPa) | Training | 19 | 147 | 56.60 | 24.12 |
| Testing | 24 | 124 | 61.70 | 26.06 | |
| Total vertical stress, σv (kPa) | Training | 24 | 210 | 79.90 | 36.48 |
| Testing | 34 | 162 | 86.26 | 36.26 | |
| Groundwater table depth, Dw (m) | Training | 0.2 | 7.2 | 2.00 | 1.20 |
| Testing | 0.2 | 6.4 | 2.19 | 1.26 | |
| Depth of soil deposit, Ds (m) | Training | 1.4 | 11.8 | 4.38 | 1.96 |
| Testing | 1.9 | 8.7 | 4.71 | 1.93 | |
| Thickness of soil layer, Ts (m) | Training | 0.3 | 6.5 | 1.79 | 1.19 |
| Testing | 0.3 | 5 | 1.98 | 1.33 |
| Predicated Class | |||
|---|---|---|---|
| Yes | No | ||
| Actual Class | Yes | True Positive (TP) | False Negative (FN) |
| No | False Positive (FP) | True Negative (TN) | |
| Model | OA | AUC | MCC | Liquefaction | Non-Liquefaction | ||||
|---|---|---|---|---|---|---|---|---|---|
| Recall | Precision | F-Measure | Recall | Precision | F-Measure | ||||
| BBN | 0.9104 | 0.9168 | 0.7746 | 0.9583 | 0.9200 | 0.9388 | 0.7895 | 0.8824 | 0.8333 |
| C4.5 DT | 0.9055 | 0.9111 | 0.7640 | 0.9440 | 0.9250 | 0.9350 | 0.8070 | 0.8520 | 0.8290 |
| Model | OA | AUC | MCC | Liquefaction | Non-Liquefaction | ||||
|---|---|---|---|---|---|---|---|---|---|
| Recall | Precision | F-Measure | Recall | Precision | F-Measure | ||||
| BBN | 0.7600 | 0.7698 | 0.4910 | 0.7500 | 0.9000 | 0.8182 | 0.7857 | 0.5500 | 0.6471 |
| C4.5 DT | 0.7400 | 0.7450 | 0.3690 | 0.8060 | 0.8290 | 0.8170 | 0.5710 | 0.5330 | 0.5520 |
| CPT-YD | 0.7400 | 0.7103 | 0.3987 | 0.7778 | 0.8485 | 0.8116 | 0.6429 | 0.5294 | 0.5806 |
| CPT-RA | 0.7000 | 0.6607 | 0.3047 | 0.7500 | 0.8182 | 0.7826 | 0.5714 | 0.4706 | 0.5161 |
| Node | Mutual Info | Percent | Variance of Beliefs |
|---|---|---|---|
| Liquefaction potential | 0.980740 | 100.0000 | 0.243354 |
| Equivalent clean sand penetration resistance | 0.022310 | 2.270000 | 0.007442 |
| Soil behavior type index | 0.010800 | 1.100000 | 0.003674 |
| Peak ground acceleration | 0.004560 | 0.465000 | 0.001552 |
| Vertical effective stress | 0.003450 | 0.351000 | 0.001171 |
| Fines content | 0.002980 | 0.304000 | 0.001015 |
| Earthquake magnitude | 0.001150 | 0.118000 | 0.000394 |
| Groundwater table | 0.000490 | 0.050100 | 0.000167 |
| Total vertical stress | 0.000230 | 0.023800 | 0.000079 |
| Depth of soil deposit | 0.000200 | 0.020400 | 0.000068 |
| Closest distance to rupture surface | 0.000190 | 0.019500 | 0.000065 |
| Thickness of soil layer | 0.000000 | 0.000000 | 0.000000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, M.; Tang, X.-W.; Qiu, J.-N.; Ahmad, F. Evaluating Seismic Soil Liquefaction Potential Using Bayesian Belief Network and C4.5 Decision Tree Approaches. Appl. Sci. 2019, 9, 4226. https://doi.org/10.3390/app9204226
Ahmad M, Tang X-W, Qiu J-N, Ahmad F. Evaluating Seismic Soil Liquefaction Potential Using Bayesian Belief Network and C4.5 Decision Tree Approaches. Applied Sciences. 2019; 9(20):4226. https://doi.org/10.3390/app9204226
Chicago/Turabian StyleAhmad, Mahmood, Xiao-Wei Tang, Jiang-Nan Qiu, and Feezan Ahmad. 2019. "Evaluating Seismic Soil Liquefaction Potential Using Bayesian Belief Network and C4.5 Decision Tree Approaches" Applied Sciences 9, no. 20: 4226. https://doi.org/10.3390/app9204226
APA StyleAhmad, M., Tang, X.-W., Qiu, J.-N., & Ahmad, F. (2019). Evaluating Seismic Soil Liquefaction Potential Using Bayesian Belief Network and C4.5 Decision Tree Approaches. Applied Sciences, 9(20), 4226. https://doi.org/10.3390/app9204226





