A Damage Model Reflecting the Interaction between Delamination and Intralaminar Crack for Failure Analysis of FRP Laminates
Abstract
1. Introduction
2. Mechanics Model
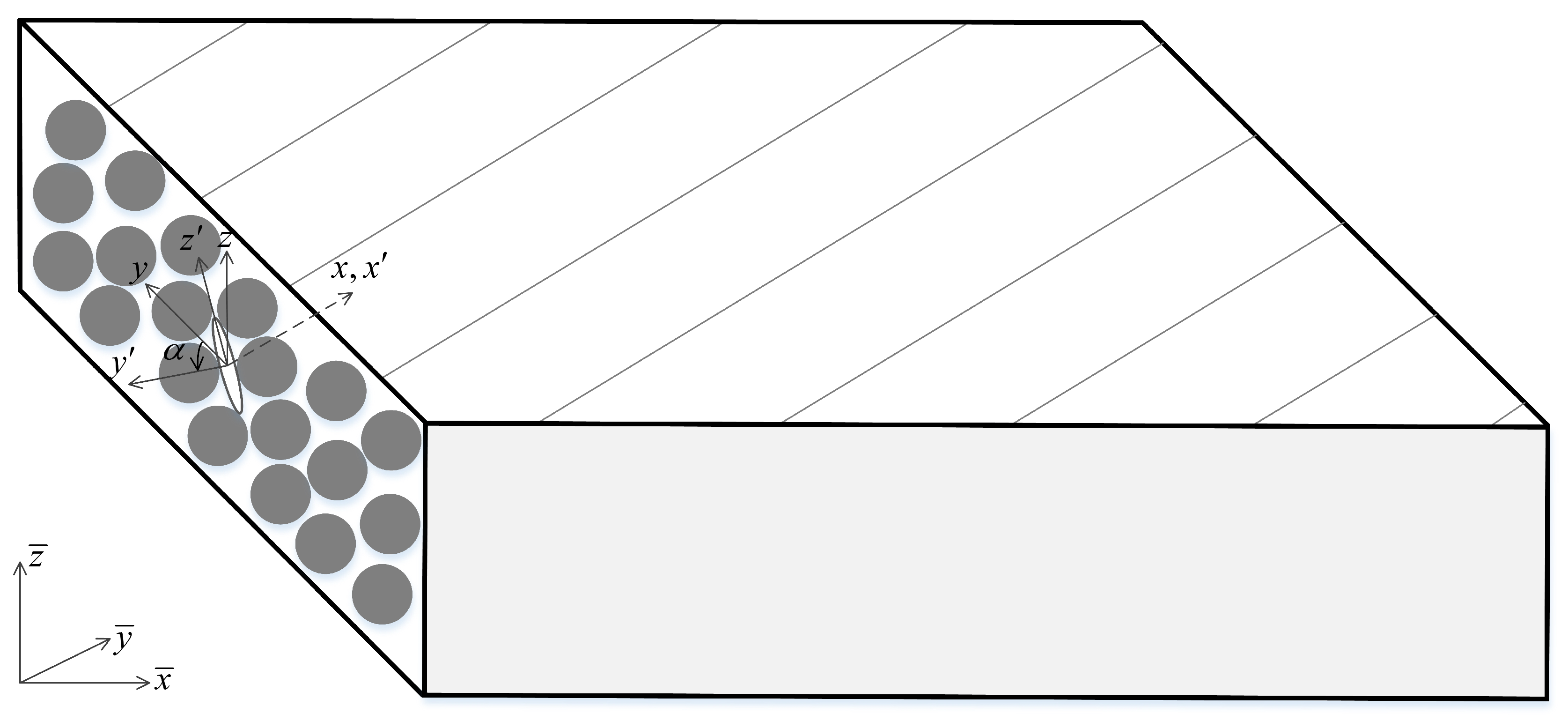
2.1. Material Damage Model for Intralaminar Failure
2.2. Modeling of Mixed-Mode Delamination
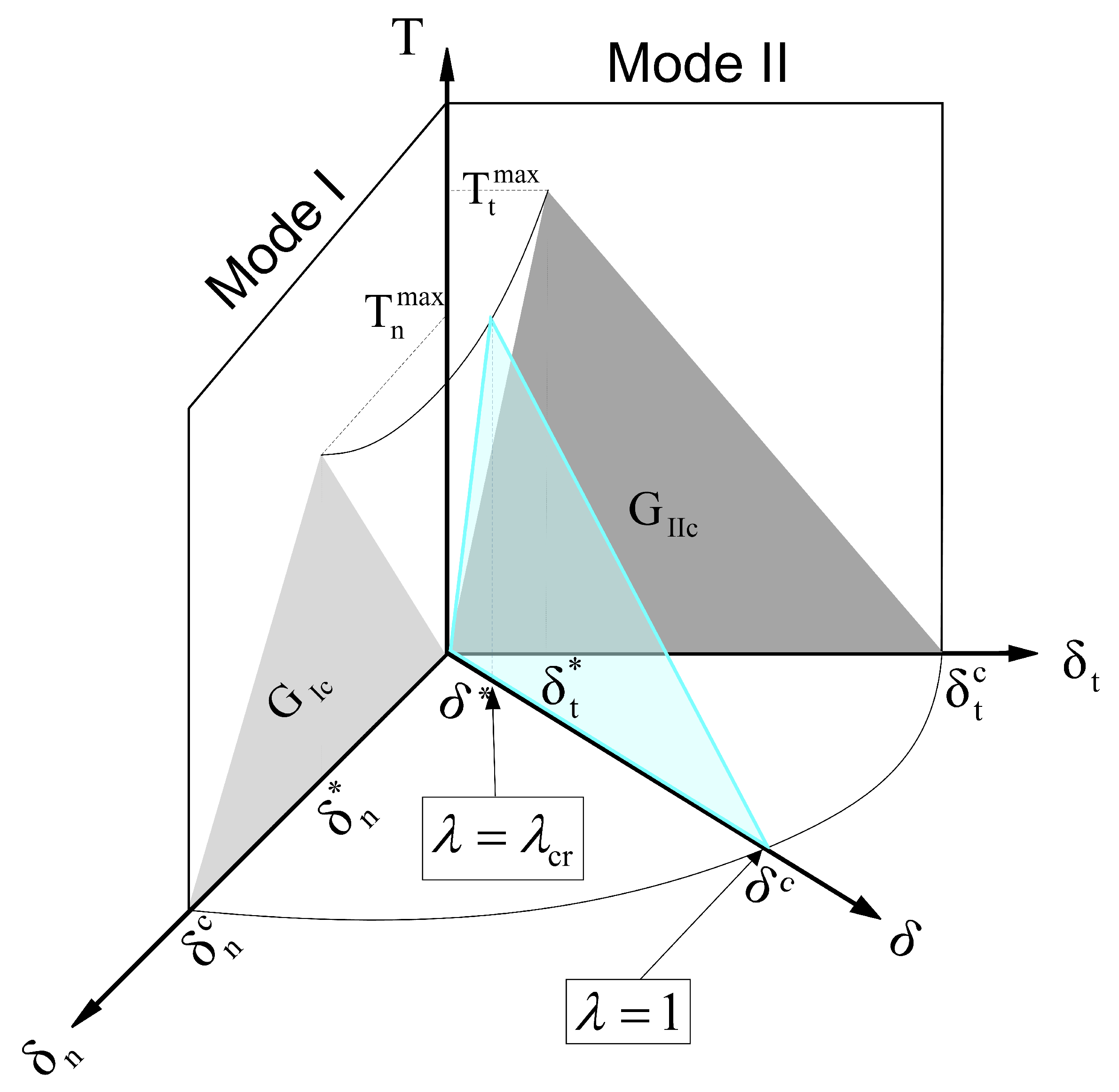
2.2.1. Mixed Mode Traction-Separation Law
2.2.2. Mixed Mode Damage Model
2.2.3. Fracture Mechanics-Based Criterion
2.3. Interaction between Delamination and Intralaminar Failure
3. Finite Element Modeling
4. Results and Discussion
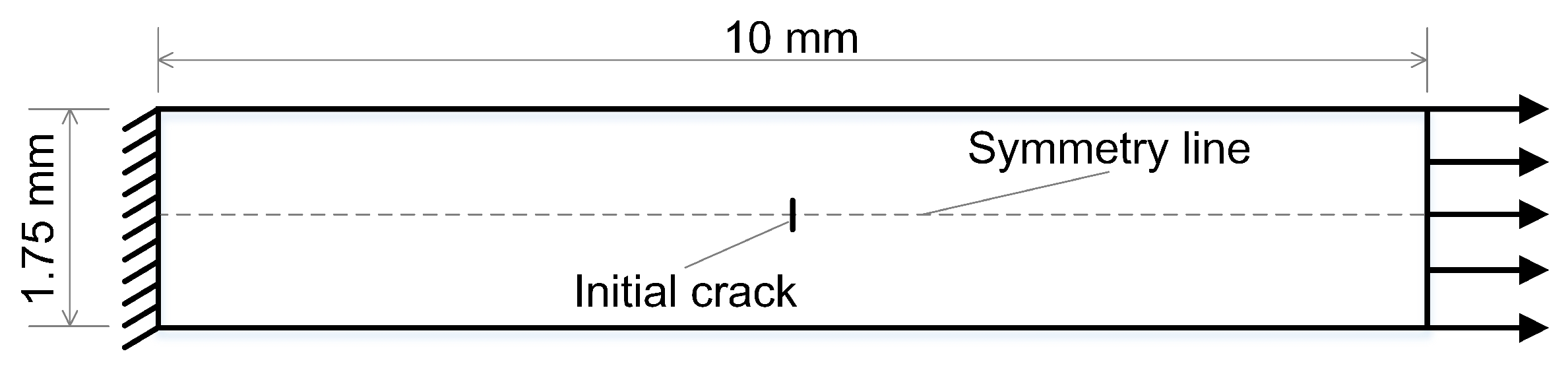
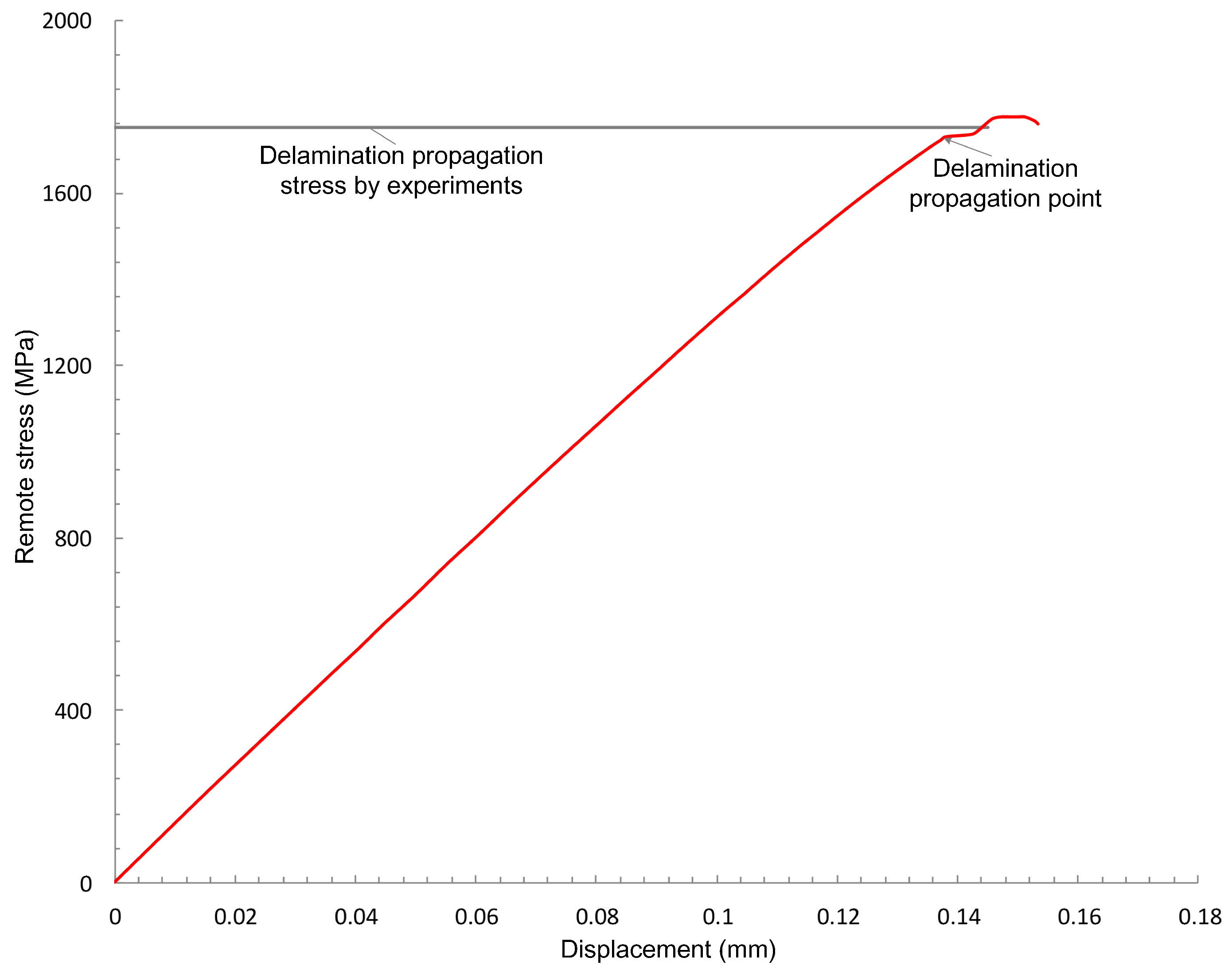
4.1. Unidirectional Specimen with a Central Cut under Tension
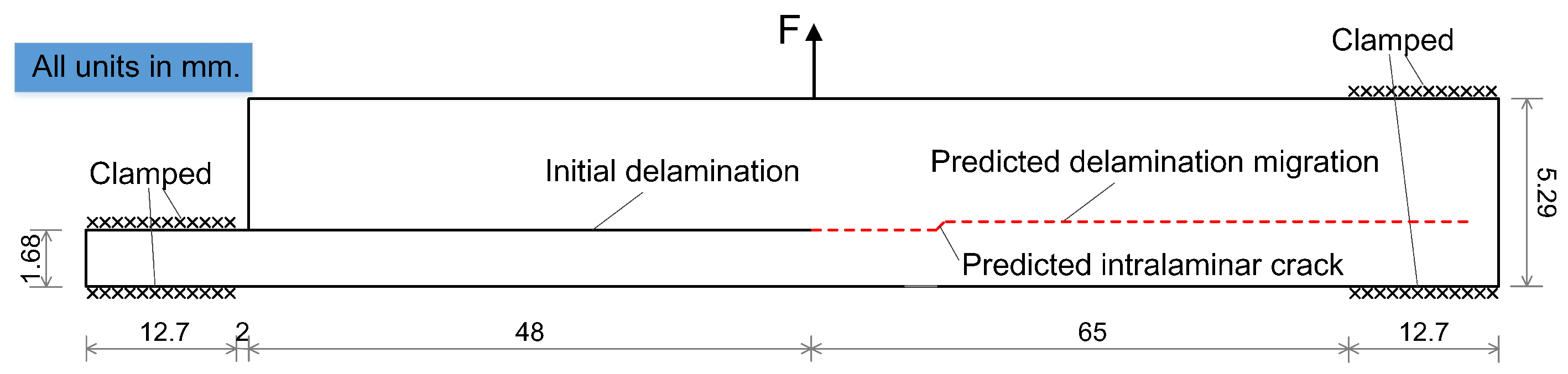
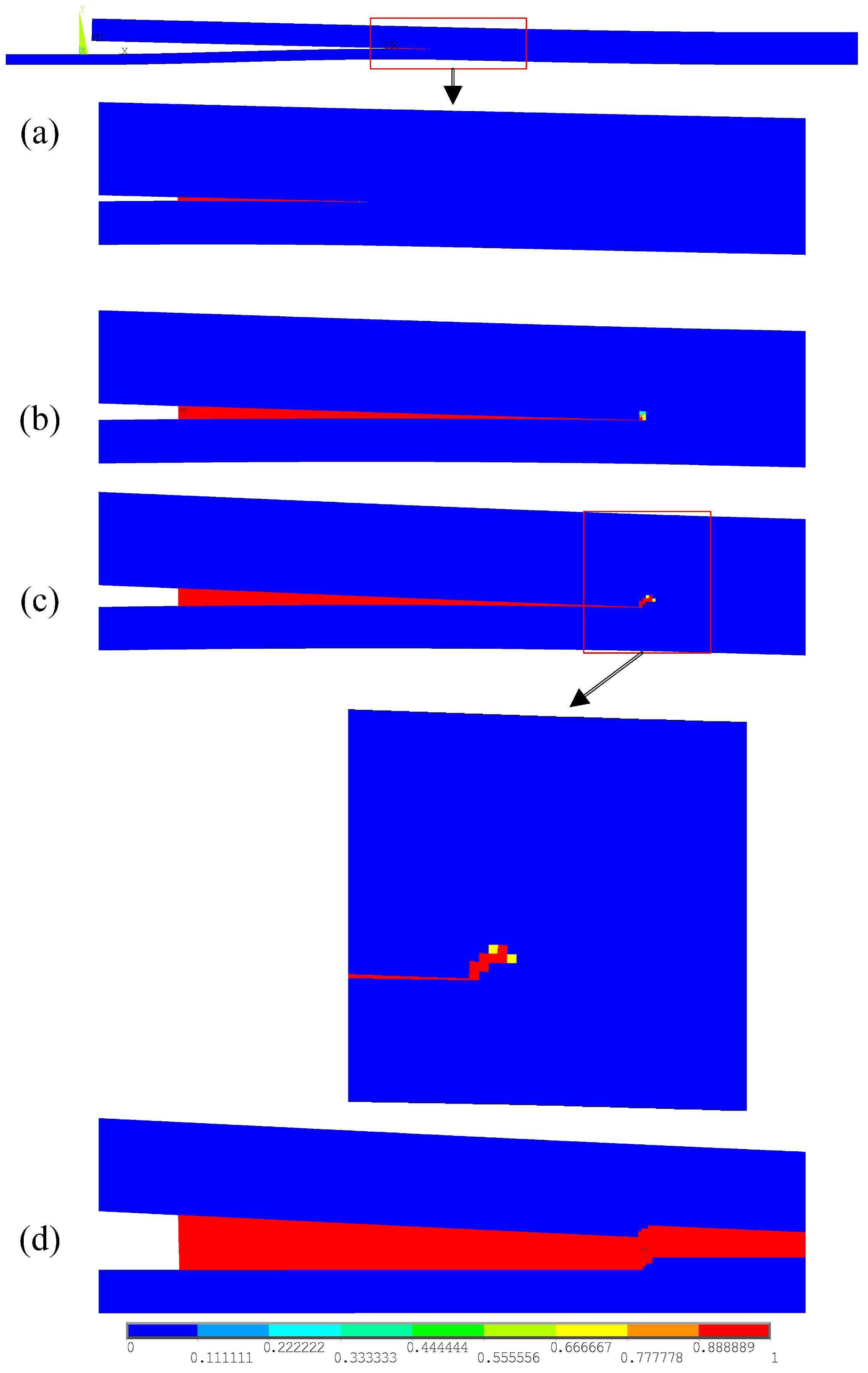
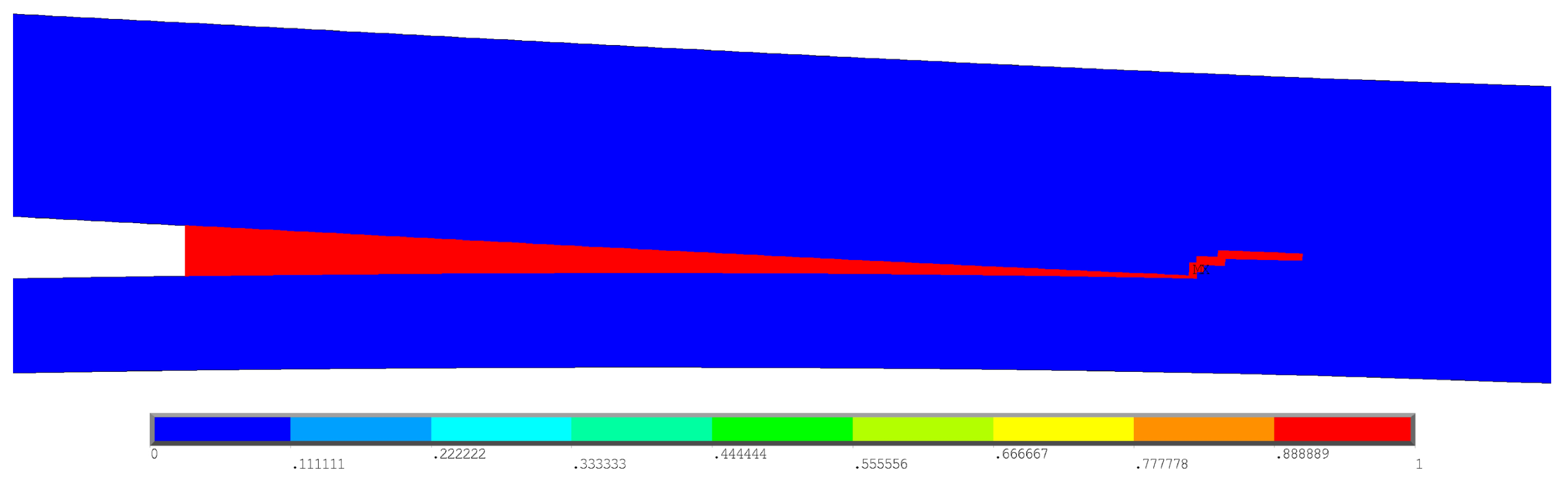
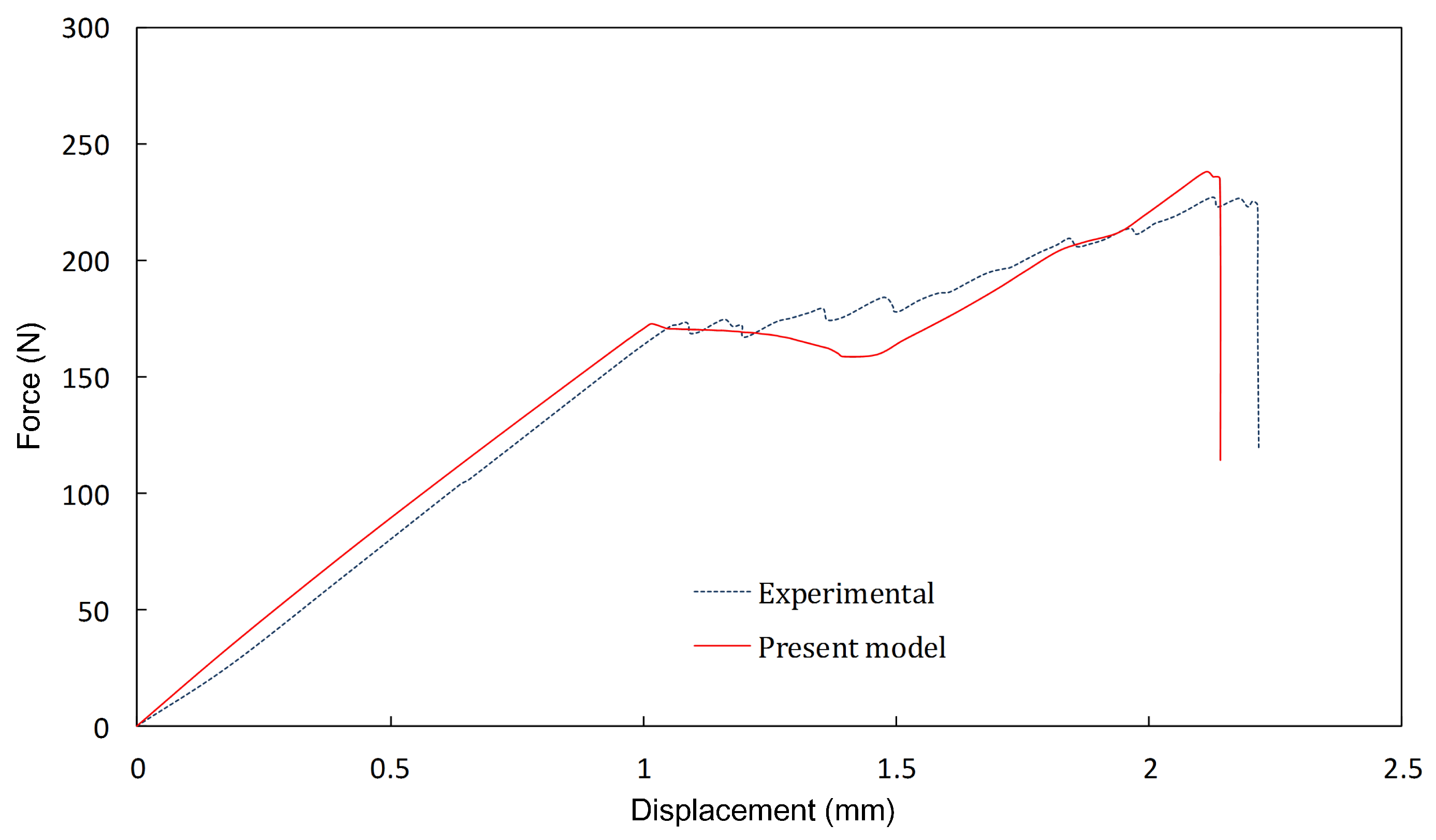
4.2. Delamination Migration
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xin, S.H.; Wen, H.M. A progressive damage model for fiber reinforced plastic composites subjected to impact loading. Int. J. Impact Eng. 2015, 75, 40–52. [Google Scholar] [CrossRef]
- Yang, D.; Ye, J.; Tan, Y.; Sheng, Y. Modeling progressive delamination of laminated composites by discrete element method. Comp. Mat. Sci. 2011, 50, 858–864. [Google Scholar] [CrossRef]
- Ullah, H.; Harland, A.R.; Silberschmidt, V.V. Damage modeling in woven-fabric CFRP laminates under large-deflection bending. Comp. Mat. Sci. 2012, 64, 130–135. [Google Scholar] [CrossRef]
- Fang, X.J.; Zhou, Z.Q.; Cox, B.N.; Yang, Q.D. High-fidelity simulations of multiple fracture processes in a laminated composite in tension. J. Mech. Phys. Solids 2011, 59, 1355–1373. [Google Scholar] [CrossRef]
- Salavatian, M.; Smith, L.V. An investigation of matrix damage in composite laminates using continuum damage mechanics. Comput. Struct. 2015, 131, 565–573. [Google Scholar] [CrossRef]
- Zhong, S.; Guo, L.; Liu, G.; Lu, H.; Zeng, T. A continuum damage model for three-dimensional woven composites and finite element implementation. Comput. Struct. 2015, 128, 1–9. [Google Scholar] [CrossRef]
- Yun, K.; Wang, Z.; Ronald, S.; Pak, Y. An advanced continuum damage mechanics model for predicting the crack progress process based on the consideration of the influence of crack direction under quasi-static load. Int. J. Mech. Sci. 2017, 130, 487–496. [Google Scholar] [CrossRef]
- Schreter, M.; Neuner, M.; Hofstetter, G. Evaluation of the Implicit Gradient-Enhanced Regularization of a Damage-Plasticity Rock Model. Appl. Sci. 2018, 8, 1004. [Google Scholar] [CrossRef]
- Kachanov, L.M. On the time to failure under creep condition. In Akad Nauk USSR; Otd Techn Nauk; AN SSSR: Moscow, Russian, 1958; Volume 8, pp. 26–31. [Google Scholar]
- Maimí, P.; Camanho, P.P.; Mayugo, J.A.; Dávila, C.G. A continuum damage model for composite laminates: Part I—Constitutive model. Mech. Mater. 2007, 39, 897–908. [Google Scholar] [CrossRef]
- Maimí, P.; Camanho, P.P.; Mayugo, J.A.; Dávila, C.G. A continuum damage model for composite laminates: Part II—Computational implementation and validation. Mech. Mater. 2007, 39, 909–919. [Google Scholar] [CrossRef]
- Chen, J.F.; Morozov, E.V.; Shankar, K. A combined elastoplastic damage model for progressive failure analysis of composite materials and structures. Compos. Struct. 2012, 94, 3478–3489. [Google Scholar] [CrossRef]
- Nuismer, R.J.; Tan, S.C. The role of matrix cracking in the continuum constitutive behavior of a damaged composite ply. In Mechanics of Composite Materials: Recent Advances; Pergamon Press Offices: New York, NY, USA, 1983; pp. 437–448. [Google Scholar]
- Salavatian, M.; Smith, L. An improved analytical model for shear modulus of fiber reinforced laminates with damage. Compos. Sci. Technol. 2014, 105, 9–14. [Google Scholar] [CrossRef]
- Yun, K.; Wang, Z. A damage model based on the introduction of a crack direction parameter for FRP composites under quasi-static load. Compos. Struct. 2018, 184, 388–399. [Google Scholar] [CrossRef]
- Cicco, D.D.; Taheri, F. Delamination Buckling and Crack Propagation Simulations in Fiber-Metal Laminates Using xFEM and Cohesive Elements. Appl. Sci. 2018, 8, 2440. [Google Scholar] [CrossRef]
- Yang, B.; Wang, Z.; Zhou, L. Study on the low-velocity impact response and CAI behavior of foam-filled sandwich panels with hybrid facesheet. Compos. Struct. 2015, 132, 1129–1140. [Google Scholar] [CrossRef]
- Yang, B.; Wang, Z.; Zhou, L. Experimental and numerical investigation of interply hybrid composites based on woven fabrics and PCBT resin subjected to low-velocity impact. Compos. Struct. 2015, 132, 464–476. [Google Scholar] [CrossRef]
- Dimitri, R.; Zavarise, G. Isogeometric treatment of frictional contact and mixed mode debonding problems. Comput. Mech. 2017, 60, 315–332. [Google Scholar] [CrossRef]
- Dimitri, R.; Tornabene, F.; Zavarise, G. Analytical and numerical modeling of the mixed-mode delamination process for composite moment-loaded double cantilever beams. Compos. Struct. 2018, 187, 535–553. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Barenblatt, G.I. The mathematical theory equilibrium cracks brittle fracture. Adv. Appl. Mech. 1962, 7, 55–129. [Google Scholar]
- Rose, J.H.; Ferrante, J.; Smith, J.R. Universal binding energy curves for metals and bimetallic interfaces. Phys. Rev. Lett. 1981, 47, 675–678. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cement. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Ataş, A.; Soutis, C. Application of cohesive zone elements in damage analysis of composites: Strength prediction of a single-bolted joint in CFRP laminates. Int. J. Nonlinear Mech. 2014, 66, 96–104. [Google Scholar] [CrossRef]
- Harper, P.W.; Hallett, S.R. Cohesive zone length in numerical simulations of composite delamination. Eng. Fract. Mech. 2008, 75, 4774–4792. [Google Scholar] [CrossRef]
- Schellekens, J.C.J.; Borst, R.D. On the numerical integration of interface elements. Int. J. Numer. Meth. Eng. 2010, 36, 43–66. [Google Scholar] [CrossRef]
- Chandra, N.; Li, H.; Shet, C. Some issues in the application of cohesive zone models for metal-ceramic interfaces. Int. J. Solids Struct. 2002, 39, 2827–2855. [Google Scholar] [CrossRef]
- Volokh, K.Y. Comparison between cohesive zone models. Int. J. Numer. Meth. Eng. 2010, 20, 845–856. [Google Scholar] [CrossRef]
- Dogan, F.; Hadavinia, H.; Donchev, T. Delamination of impacted composite structures by cohesive zone interface elements and tiebreak contact. Cent. Eur. J. Eng. 2012, 2, 612–626. [Google Scholar] [CrossRef]
- Park, K.; Paulino, G.H. Cohesive zone models: A critical review of traction-separation relationships across fracture surfaces. Appl. Mech. Rev. 2011, 64, 1–20. [Google Scholar] [CrossRef]
- Dimitri, R.; Cornetti, P.; Mantic, V. Mode-I debonding of a double cantilever beam: A comparison between cohesive crack modeling and Finite Fracture Mechanics. Int. J. Solids Struct. 2017, 124, 57–72. [Google Scholar] [CrossRef]
- Maimí, P.; Camanho, P.P.; Mayugo, J.A. Matrix cracking and delamination in laminated composites. Part II: Evolution of crack density and delamination. Mech. Mater. 2011, 43, 194–211. [Google Scholar] [CrossRef]
- Rebière, J.L.; Gamby, D. A criterion for modeling initiation and propagation of matrix cracking and delamination in cross-ply laminates. Compos. Sci. Technol. 2004, 64, 2239–2250. [Google Scholar] [CrossRef]
- Hallett, S.R.; Jiang, W.G.; Khan, B.; Wisnom, M.R. Modeling the interaction between matrix cracks and delamination damage in scaled quasi-isotropic specimens. Compos. Sci. Technol. 2008, 68, 80–89. [Google Scholar] [CrossRef]
- Mcelroy, A.M.; Ratcliffe, J.G.; Czabaj, M.; Wang, J.; Yuan, F.G. A numerical and experimental study of damage growth in a composite laminate. In American Society for Composites Technical Conference; NF1676L-18068; NASA Langley Research Center: Hampton, VA, USA, 2014. [Google Scholar]
- Carvalho, N.V.D.; Chen, B.Y.; Pinho, S.T. Modeling delamination migration in cross-ply tape laminates. Compos. Part A-Appl. Sci. Manuf. 2015, 71, 192–203. [Google Scholar] [CrossRef]
- Ullah, H.; Harland, A.R.; Silberschmidt, V.V. Characterisation of mechanical behaviour and damage analysis of 2D woven composites under bending. Compos. Part B-Eng. 2015, 75, 156–166. [Google Scholar] [CrossRef]
- Meer, F.P.V.D.; Sluys, L.J. Mesh-independent modeling of both distributed and discrete matrix cracking in interaction with delamination in composites. Eng. Fract. Mech. 2010, 77, 719–735. [Google Scholar] [CrossRef]
- Zhao, L.; Zhi, J.; Zhang, J. XFEM simulation of delamination in composite laminates. Compos. Part A-Appl. Sci. Manuf. 2016, 80, 61–71. [Google Scholar] [CrossRef]
- Li, X.; Chen, J. An extended cohesive damage model for simulating multicrack propagation in fiber composites. Compos. Struct. 2016, 143, 1–8. [Google Scholar] [CrossRef]
- Li, X.; Chen, J. The implementation of the extended cohesive damage model for multicrack evolution in laminated composites. Compos. Struct. 2016, 139, 68–76. [Google Scholar] [CrossRef]
- Fries, T.; Baydoun, M. Crack propagation with the extended finite element method and a hybrid explicit–implicit crack description. Int. J. Numer. Meth. Eng. 2012, 89, 1527–1558. [Google Scholar] [CrossRef]
- Carollo, V.; Reinoso, J.; Paggi, M. A 3D finite strain model for intralayer and interlayer crack simulation coupling the phase field approach and cohesive zone model. Compos. Struct. 2017, 182, 636–651. [Google Scholar] [CrossRef]
- Wang, Y.; Waisman, H. Progressive delamination analysis of composite materials using XFEM and a discrete damage zone model. Comput. Mech. 2015, 55, 1–26. [Google Scholar] [CrossRef]
- Wang, Y.; Waisman, H. From diffuse damage to sharp cohesive cracks: A coupled XFEM framework for failure analysis of quasi-brittle materials. Comput. Methods Appl. Mech. Eng. 2016, 299, 57–89. [Google Scholar] [CrossRef]
- Moura, M.F.S.F.D.; Gonçalves, J.P.M. Modeling the interaction between matrix cracking and delamination in carbon–epoxy laminates under low velocity impact. Compos. Sci. Technol. 2004, 64, 1021–1027. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, C.; Luo, H.; Wei, S.; Wei, Z. Continuum damage modeling and progressive failure analysis of carbon fiber/epoxy composite pressure vessel. Compos. Struct. 2015, 134, 475–482. [Google Scholar] [CrossRef]
- Maimí, P.; Mayugo, J.A.; Camanho, P.P. A Three-dimensional Damage Model for Transversely Isotropic Composite Laminates. J. Compos. Mater. 2008, 42, 2717–2745. [Google Scholar] [CrossRef]
- Alfano, G.; Crisfield, M.A. Finite element interface models for the delamination analysis of laminated composites: Mechanical and computational issues. Int. J. Numer. Meth. Eng. 2001, 50, 1701–1736. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, F.; Zhao, L. A progressive damage analysis based characteristic length method for multi-bolt composite joints. Compos. Struct. 2014, 108, 915–923. [Google Scholar] [CrossRef]
- Hashin, Z. Fatigue failure criteria for unidirectional fiber composites. J. Appl. Mech. 1981, 48, 846–852. [Google Scholar] [CrossRef]
- Espinosa, H.D.; Zavattieri, P.D. A grain level model for the study of failure initiation and evolution in polycrystalline brittle materials. Part II: Numerical examples. Mech. Mater. 2003, 35, 365–394. [Google Scholar] [CrossRef]
- Dávila, C.G.; Rose, C.A.; Camanho, P.P. A procedure for superposing linear cohesive laws to represent multiple damage mechanisms in the fracture of composites. Int. J. Fract. 2009, 158, 211–223. [Google Scholar] [CrossRef]
- Reeder, J.R. An evaluation of mixed-Mode delamination failure criteria. In Technical Memorandum-1992-104210; NASA Langley Research Centre: Hampton, VA, USA, 1992. [Google Scholar]
- Yuan, Z.; Fish, J. Are the cohesive zone models necessary for delamination analysis. Comput. Methods Appl. Mech. Eng. 2016, 310, 567–604. [Google Scholar] [CrossRef]
- Green, B.G.; Wisnom, M.R.; Hallett, S.R. An experimental investigation into the tensile strength scaling of notched composites. Compos. Part A-Appl. Sci. Manuf. 2007, 38, 867–878. [Google Scholar] [CrossRef]
- Lammerant, L.; Verpoest, I. Modeling of the interaction between matrix cracks and delaminations during impact of composite plates. Compos. Sci. Technol. 1996, 56, 1171–1178. [Google Scholar] [CrossRef]
- Lapczyk, I.; Hurtado, J.A. Progressive damage modeling in fiber-reinforced materials. Compos. Part A-Appl. Sci. Manuf. 2007, 38, 2333–2341. [Google Scholar] [CrossRef]
- Ratcliffe, J.G.; Czabaj, M.W.; Obrien, T.K. Characterizing Delamination Migration in Carbon/Epoxy Tape Laminates; Ratcliffe, J.G., Ed.; DEStech Publications Inc.: Lancaster, PA, USA, 2012. [Google Scholar]
- Ratcliffe, J.G.; Decarvalho, N.V. Investigating Delamination Migration in Composite Tape Laminates. In Proceedings of the European Conference on Composite Materials, Seville, Spain, 22–26 June 2014. [Google Scholar]
- Mcelroy, M.; Leone, F.; Ratcliffe, J. Simulation of delamination-migration and core crushing in a CFRP sandwich structure. Compos. Part A-Appl. Sci. Manuf. 2015, 79, 192–202. [Google Scholar] [CrossRef]




| (GPa) | (GPa) | (GPa) | (GPa) | ||
|---|---|---|---|---|---|
| 161 | 11.38 | 5.17 | 3.98 | 0.32 | 0.436 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yun, K.; Kwak, S.; Wang, Z.; Chang, M.; Kim, J.; Liu, J.; Ri, C. A Damage Model Reflecting the Interaction between Delamination and Intralaminar Crack for Failure Analysis of FRP Laminates. Appl. Sci. 2019, 9, 314. https://doi.org/10.3390/app9020314
Yun K, Kwak S, Wang Z, Chang M, Kim J, Liu J, Ri C. A Damage Model Reflecting the Interaction between Delamination and Intralaminar Crack for Failure Analysis of FRP Laminates. Applied Sciences. 2019; 9(2):314. https://doi.org/10.3390/app9020314
Chicago/Turabian StyleYun, Kumchol, Songhun Kwak, Zhenqing Wang, Mengzhou Chang, Jonggun Kim, Jingbiao Liu, and Cholsu Ri. 2019. "A Damage Model Reflecting the Interaction between Delamination and Intralaminar Crack for Failure Analysis of FRP Laminates" Applied Sciences 9, no. 2: 314. https://doi.org/10.3390/app9020314
APA StyleYun, K., Kwak, S., Wang, Z., Chang, M., Kim, J., Liu, J., & Ri, C. (2019). A Damage Model Reflecting the Interaction between Delamination and Intralaminar Crack for Failure Analysis of FRP Laminates. Applied Sciences, 9(2), 314. https://doi.org/10.3390/app9020314





