Dependency Model-Based Multiple Fault Diagnosis Using Knowledge of Test Result and Fault Prior Probability
Abstract
:1. Introduction
- The sequential diagnosis method [15,16,17,18]: Sequential diagnosis is a kind of testing and diagnosis method basing on a cycle process of “test–diagnosis–retest”. The sequential diagnosis method is especially suitable for a system which is at the phase of principle testing and prototype developing. To obtain the correct diagnosis results with the minimum test cost, an optimal test sequence in the diagnosis strategy should be constructed, which is a typical NP (Non-deterministic Polynomial)-complete problem. Currently, more research focuses on the hypotheses of single fault and reliable test results to reduce the hardship of solving the problem.
- Concurrent fault diagnosis method [19,20,21]: The concurrent fault diagnosis method is a traditional monitoring diagnosis method, where all the tests are completed before applying the diagnosis procedure. The whole diagnosis process only needs one cycle of testing and diagnosis procedure. Since it requires all the symptoms or at least most of the symptoms in advance to gain the correct diagnosis results, the concurrent fault diagnosis method is more suitable for a system where abundant sensing information can be acquired. A typical method for concurrent diagnosis is that the fault prior probability of the components in the system is known, the posterior probability of each component can be calculated and the maximum posteriori probability will be used to determine the corresponding fault component. The limitation of this method is that it only searches for one optimal solution and the suboptimal solution will be abandoned, which may easily fall into the local optimum.
2. Problem Formulation
- F means the set of independent fault states in the system. represents the lst fault state;
- P means the set of the prior probability among all the fault states that happens independently; represents the prior probability of the fault happens alone;
- T means a finite set consisting of all the available tests in the system. Here, assume that each test result is reliable with an output in the form of a binary number;
- represents the dependency matrix of fault test results, of which the expression is defined as follows:is a matrix with a scale of . The element denotes the correlation between a fault state in F and a test in T. If , then the fault state can be tested by the test . If , then the test fails to know the situation about the fault state . In this way, in Equation (3), the rows in the matrix denote the set of fault types, while the columns denote the set of tests;
- R is a set of the observation results according to the tests in the system, e.g., is the observation result of the test . For each test , the corresponding observation result will be only one of the following two states:
- –
- ‘Pass’, denoted by ‘0’. The system passes the test;
- –
- ‘Fail’, denoted by ‘1’. The system fails to pass the test.
3. A New Multiple Fault Diagnosis Method
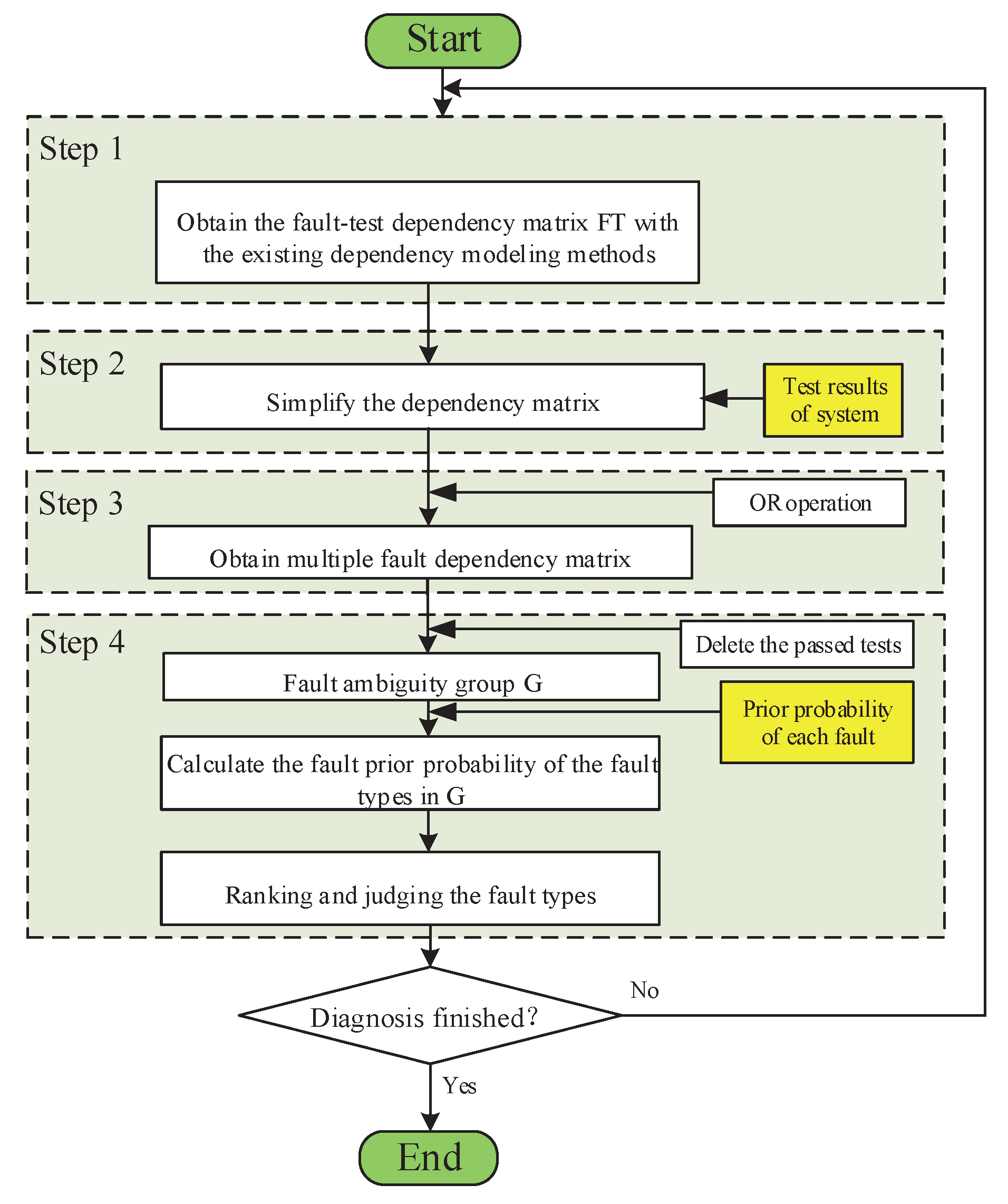
- Step 1. Build the fault-test dependency matrix based on the existing dependency modeling methods. Analyze the system and build its dependency model based on the information flows or the multisignal flow graphs model [12,25]. After that, the dependency matrix in the form of Equation (3) can be built based on the reachability algorithm [26] or experimental design method [21,27].
- Step 2. Simplify the dependency matrix according to the test results of the system. The purpose of this step is to delete the impossible fault states according to the test results. For example, if , which means the test is correlated with the fault type and the test result of is ‘Pass’ according to the observation result , then the fault type will definitely not happen. In this way, the logical judgment from experts or engineers is applied for simplifying the complex fault diagnosis processing. This can be regarded as a semisupervised diagnosis method.In detail, the principle of simplifying the dependency matrix based on the correlation between the test and the fault type can be analyzed as follows.
- For the element in the dependency matrix, which means the test is correlated with the fault type , the following cases may exist:
- –
- If the fault happens, the result of the test must be ‘1’ (Fail);
- –
- If the fault does not happen, the result of the test is unknown;
- –
- If the result of the test is ‘1’ (Fail), the state of the fault is unknown; in this case, may be caused by or the other fault like ;
- –
- If the result of the test is ‘0’ (Pass), the fault type will not happen.
- For the element in the dependency matrix, which means the test is not correlated with the fault type , the following cases may exist:
- –
- If the fault happens, the result of the test is unknown because there is no correlation between and ;
- –
- If the fault does not happen, the result of the test is unknown, too;
- –
- If the result of the test is ‘1’ (Fail), the state of the fault is unknown;
- –
- If the result of the test is ‘0’ (Pass), the state of the fault is unknown.
After analyzing the cases in the correlation between the test and the fault type , the method of simplifying the dependency matrix can be concluded as follows:- Delete the column vectors correlated to the test result (‘Pass’ the test) in the dependency matrix . Only the items correlated to the test (‘Fail’ to pass the test) are reserved.
- Delete the row vectors correlated to in the column that satisfies .
Finally, the simplified matrix can be formulated where , . - Step 3. Formulate the multiple fault dependency matrix by logic operation. Perform the logical ‘OR’ operation on each fault eigenvector (the row vector) in the simplified matrix to obtain the multiple fault dependency matrix . Define that the fault type of single faults is included in the ones of the multiple faults. Thus, the results of the ‘OR’ operation among each fault type vector in the matrix can be used to denote the state in which that multiple fault happens. For example, when the eigenvector of the fault and are and , respectively, then the corresponding eigenvector of the multiple fault is is . The results of the logic operation ware added at the bottom of the matrix as the new row vectors. Finally, the new matrix are defined as the multiple fault dependency matrix , in which the number of the column vector is k and the maximum of the row vector is .
- Step 4. Fault diagnosis based on the multiple fault dependency matrix . If the fault state happens, then all the tests corresponding to the element ‘1’ in the row vector fail. If the chosen tests all fail, then the row vectors in the matrix correlated to the fault are all ‘1’. Therefore, if the row vectors in the matrix correlated to the fault include the element ‘0’, then delete the corresponding rows where the element ‘0’ is included in. Now, the remaining fault states, in which the elements in the row vector are all ‘1’, are the suspicious fault types. All the suspicious fault types constitute the fault ambiguity group denoted as G.Ranking all the suspicious fault types in the fault ambiguity group G based on the fault prior probability, where the prior probability of the multiple fault type generated in the third step can be calculated as follows:Actions such as fault isolation or removal in the system will be based on the ranking results of the fault types.
4. Illustrative Experiment
- If the fault happens, the observation results of all the tests including , , and must be ‘Fail’;
- If the fault happens, the observation result of the test is definitely ‘Fail’.
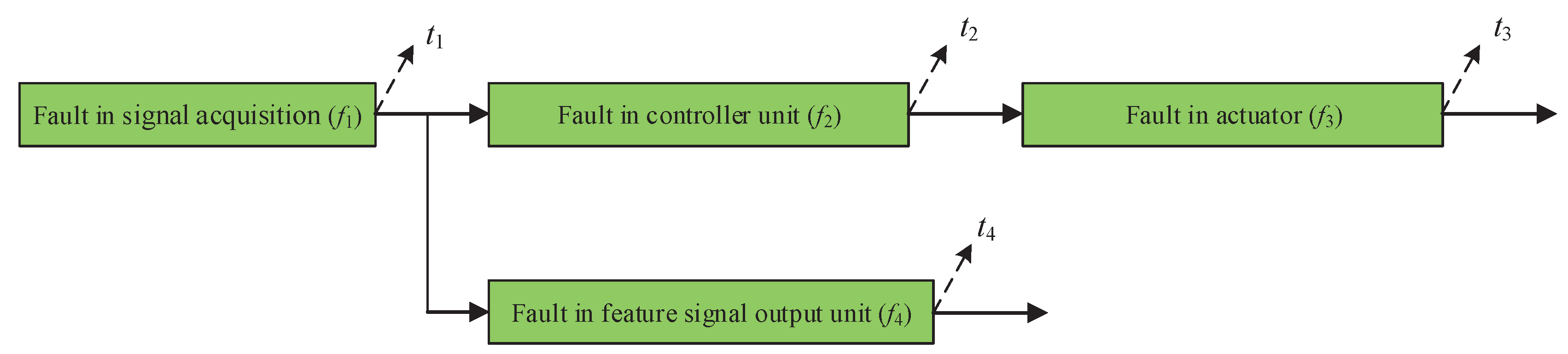
4.1. Experiment Process
- denotes a signal acquisition test,
- denotes a controller unit efficiency test,
- denotes an actuator action range test,
- denotes a feature signal output test,
- denotes a signal collector fault,
- denotes a controller unit fault,
- denotes an actuator fault, and
- denotes a feature signal output unit fault.
- Fault in Controller and Actuator unit ..
- Fault in Controller and Feature signal output unit ..
- Fault in Actuator and Feature signal output unit ..
- Fault in Controller unit, Actuator and Feature signal output unit ..
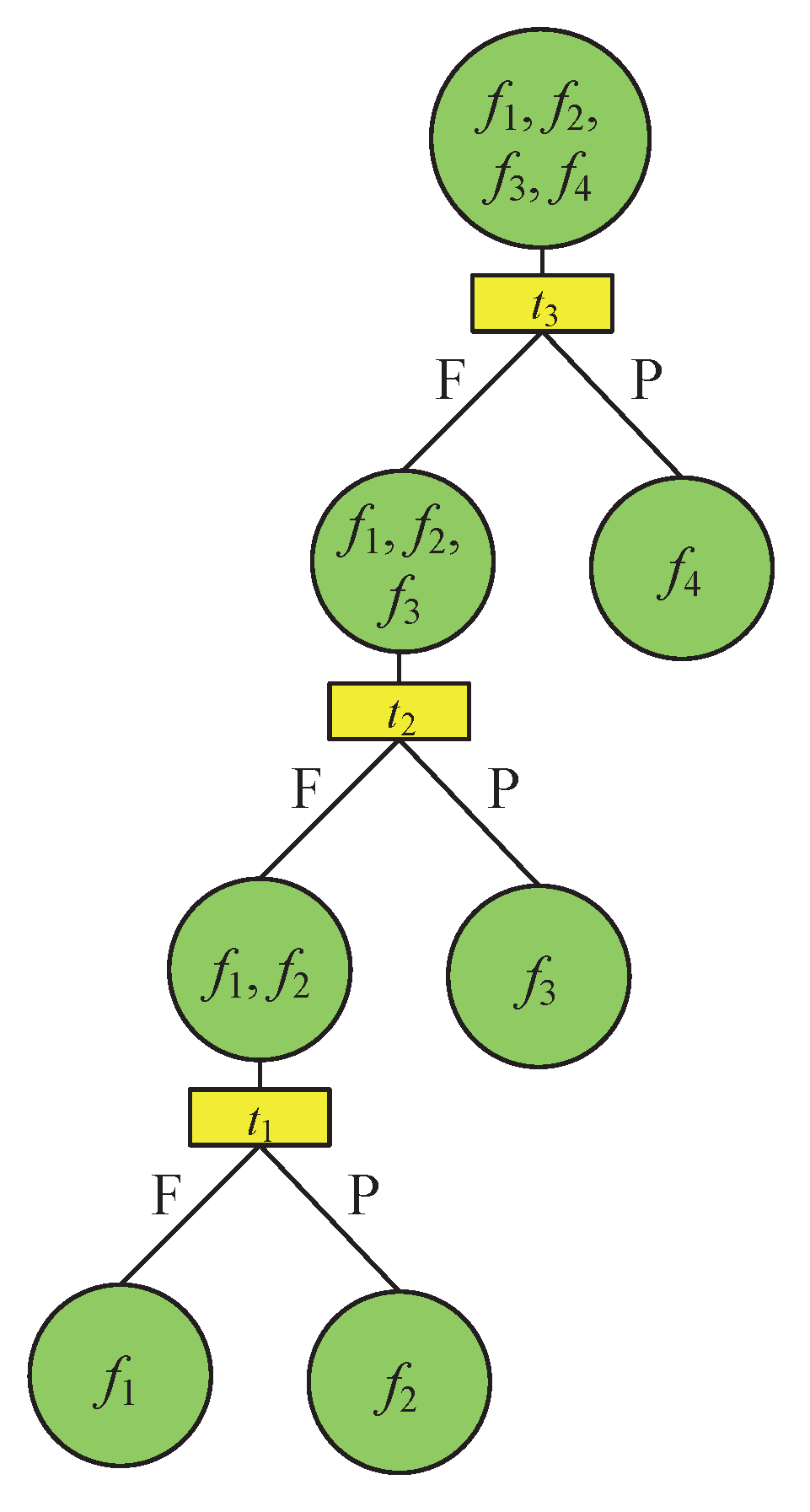
4.2. A Simple Discussion in Comparison With Diagnosis Tree
5. A Case Study
5.1. Experiment 1
5.1.1. Experiment Process
5.1.2. A Discussion
- Compare the experiment results with the hypothesis of a single fault. For the system under test where , , and are successfully passed and the rest of the tests are unqualified, if there is a single fault assumption, according to the diagnosis logic, the system will have no solution— while with the proposed method, the fault status can be located on , or , with a possibility suggestion of each diagnosis result for reference.
- Compare the experiment results with the method in the literature [29]. The method in Reference [29] shows that if the fault prior probability and the test results are known, the multiple fault diagnosis can be achieved through the criterion of maximum posterior probability. Although the method is effective, sometimes the result can be insufficient, because it only gives one diagnosis result ( in this case study), while the failure may exist in other fault types according to the proposed method.
5.2. Experiment 2
6. Conclusions and Future Work
- The proposed method is designed for multiple faults diagnosis. The potential multiple faults are modeled by formulating a multiple fault dependency matrix based on the test results and the dependency matrix;
- Each multiple fault type is assigned a possibility based on the prior probability of the original fault status. The possibility value of each fault type provides a basis of ranking and judging the failure for the following diagnosis and maintenance work.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- De Loza, A.F.; Cieslak, J.; Henry, D.; Davila, J.; Zolghadri, A. Sensor fault diagnosis using a non-homogeneous high-order sliding mode observer with application to a transport aircraft. IET Control Theory Appl. 2015, 9, 598–607. [Google Scholar] [CrossRef]
- Gao, Z.; Ma, C.; Song, D.; Liu, Y. Deep quantum inspired neural network with application to aircraft fuel system fault diagnosis. Neurocomputing 2017, 238, 13–23. [Google Scholar] [CrossRef]
- Glowacz, A. Fault diagnosis of single-phase induction motor based on acoustic signals. Mech. Syst. Signal Process. 2019, 117, 65–80. [Google Scholar] [CrossRef]
- Glowacz, A. Acoustic based fault diagnosis of three-phase induction motor. Appl. Acoust. 2018, 137, 82–89. [Google Scholar] [CrossRef]
- Karvelis, P.; Georgoulas, G.; Tsoumas, T.P.; Antonino-Daviu, J.A.; Climente-Alarcon, V.; Stylios, C.D. A Symbolic Representation Approach for the Diagnosis of Broken Rotor Bars in Induction Motors. IEEE Trans. Ind. Inform. 2015, 11, 1028–1037. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, Y.; Duan, Z.; Peng, Z. A new swarm intelligence optimized multiclass multi-kernel relevant vector machine: An experimental analysis in failure diagnostics of diesel engines. Struct. Health Monit. Int. J. 2018, 17, 1503–1519. [Google Scholar] [CrossRef]
- Bosso, N.; Gugliotta, A.; Zampieri, N. Wheel flat detection algorithm for onboard diagnostic. Measurement 2018, 123, 193–202. [Google Scholar] [CrossRef]
- Zhang, S.; Pattipati, K.R.; Hu, Z.; Wen, X.; Sankavaram, C. Dynamic coupled fault diagnosis with propagation and observation delays. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 1424–1439. [Google Scholar] [CrossRef]
- Zhang, S.; Pattipati, K.R.; Hu, Z.; Wen, X. Optimal selection of imperfect tests for fault detection and isolation. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 1370–1384. [Google Scholar] [CrossRef]
- Lv, X.; Zhou, D.; Tang, Y.; Ma, L. An improved test selection optimization model based on fault ambiguity group isolation and chaotic discrete PSO. Complexity 2018, 2018. [Google Scholar] [CrossRef]
- Tu, F.; Pattipati, K.R.; Deb, S.; Malepati, V.N. Computationally efficient algorithms for multiple fault diagnosis in large graph-based systems. IEEE Trans. Syst Man Cybern. Part A Syst. Hum. 2003, 33, 73–85. [Google Scholar]
- Deb, S.; Pattipati, K.R.; Raghavan, V.; Shakeri, M.; Shrestha, R. Multi-signal flow graphs: A novel approach for system testability analysis and fault diagnosis. In Proceedings of the AUTOTESTCON’94, IEEE Systems Readiness Technology Conference, ‘Cost Effective Support Into the Next Century’, Anaheim, CA, USA, 20–22 September 1994; pp. 361–373. [Google Scholar]
- Chessa, S.; Santi, P. Operative diagnosis of graph-based systems with multiple faults. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2001, 31, 112–119. [Google Scholar] [CrossRef]
- Cui, Y.; Shi, J.; Wang, Z. An analytical model of electronic fault diagnosis on extension of the dependency theory. Reliab. Eng. Syst. Saf. 2015, 133, 192–202. [Google Scholar] [CrossRef]
- Pattipati, K.R.; Alexandridis, M.G. Application of heuristic search and information theory to sequential fault diagnosis. IEEE Trans. Syst. Man Cybern. 1990, 20, 872–887. [Google Scholar] [CrossRef]
- Shakeri, M.; Raghavan, V.; Pattipati, K.R.; Patterson-Hine, A. Sequential testing algorithms for multiple fault diagnosis. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2000, 30, 1–14. [Google Scholar] [CrossRef]
- Huang, Y.; Jing, B.; Luo, B.; Li, J. Sequential multiple fault diagnosis strategy based on Rollout algorithm. Control Decis. 2015, 30, 572–576. [Google Scholar]
- Tian, H.; Duan, F.; Fan, L.; Sang, Y. Novel solution for sequential fault diagnosis based on a growing algorithm. Reliab. Eng. Syst. Saf. 2018. [Google Scholar] [CrossRef]
- Lee, K.; Kuo, C. Concurrent error detection, diagnosis, and fault tolerance for switched-capacitor filters. J. Inf. Sci. Eng. 1998, 14, 863–890. [Google Scholar]
- Far, B.; Nakamichi, M. Qualitative fault-diagnosis in systems with nonintermittent concurrent faults—A subjective approach. IEEE Trans. Syst. Man Cybern. 1993, 23, 14–30. [Google Scholar] [CrossRef]
- Hemmati, F.; Alqaradawi, M.; Gadala, M.S. Optimized statistical parameters of acoustic emission signals for monitoring of rolling element bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 897–906. [Google Scholar] [CrossRef]
- Khan, S.A.; Equbal, M.D.; Islam, T. A comprehensive comparative study of DGA based transformer fault diagnosis using fuzzy logic and ANFIS models. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 590–596. [Google Scholar] [CrossRef]
- Yan, H.; Xu, Y.; Cai, F.; Zhang, H.; Zhao, W.; Gerada, C. PWM-VSI Fault Diagnosis for a PMSM Drive Based on the Fuzzy Logic Approach. IEEE Trans. Power Electron. 2019, 34, 759–768. [Google Scholar] [CrossRef]
- Song, L.; Wang, H.; Chen, P. Step-by-step Fuzzy Diagnosis Method for Equipment Based on Symptom Extraction and Trivalent Logic Fuzzy Diagnosis Theory. IEEE Trans. Fuzzy Syst. 2018, 26, 3467–3478. [Google Scholar] [CrossRef]
- Pattipati, K.R.; Deb, S.; Dontamsetty, M.; Maitra, A. Start: System testability analysis and research tool. IEEE Aerosp. Electron. Syst. Mag. 1991, 6, 13–20. [Google Scholar] [CrossRef]
- Roditty, L.; Zwick, U. A fully dynamic reachability algorithm for directed graphs with an almost linear update time. SIAM J. Comput. 2016, 45, 712–733. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Wohl, J.G. Information Automation and the Apollo Program: A Retrospective. IEEE Trans. Syst. Man Cybern. 1982, 12, 469–478. [Google Scholar] [CrossRef]
- Ke, L.; Bing, L.; Wang, H.J. A Fault Diagnosis Approach of the Large Complex System Based on Bayes Theory. Acta Armamentarii 2008, 29, 352–356. [Google Scholar]
| Fault Type | ||||
|---|---|---|---|---|
| Signal collector fault | 1 | 1 | 1 | 1 |
| Controller unit fault | 0 | 1 | 1 | 0 |
| Actuator fault | 0 | 0 | 1 | 0 |
| Feature signal output unit fault | 0 | 0 | 0 | 1 |
| Fault Type | |||
|---|---|---|---|
| Controller unit fault | 1 | 1 | 0 |
| Actuator fault | 0 | 1 | 0 |
| Feature signal output unit fault | 0 | 0 | 1 |
| Fault Type | |||
|---|---|---|---|
| Controller unit fault | 1 | 1 | 0 |
| Actuator fault | 0 | 1 | 0 |
| Feature signal output unit fault | 0 | 0 | 1 |
| Fault in Controller and Actuator unit | 1 | 1 | 0 |
| Fault in Controller and Feature signal output unit | 1 | 1 | 1 |
| Fault in Actuator and Feature signal output unit | 0 | 1 | 1 |
| Fault in Controller, Actuator and Feature signal output unit | 1 | 1 | 1 |
| Fault Type | |||
|---|---|---|---|
| Controller unit and Feature signal output unit fault | 1 | 1 | 1 |
| Controller unit, Actuator and Feature signal output unit fault | 1 | 1 | 1 |
| Fault Type | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| Fault Type | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Fault Type | |||||
|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 1 | 1 |
| Fault Type | Prior Probability | |||||
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | 0.1 | |
| 1 | 1 | 0 | 1 | 0 | 0.1 | |
| 0 | 1 | 1 | 1 | 1 | 0.1 | |
| 1 | 1 | 0 | 1 | 1 | 0.01 | |
| 1 | 1 | 1 | 1 | 1 | 0.01 | |
| 1 | 1 | 1 | 1 | 1 | 0.01 | |
| 1 | 1 | 1 | 1 | 1 | 0.001 |
| Fault Type | Prior Probability | |||||
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 0.01 | |
| 1 | 1 | 1 | 1 | 1 | 0.01 | |
| 1 | 1 | 1 | 1 | 1 | 0.001 |
| Fault Type | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 |
| Fault Type | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| Fault Type | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Fault Type | Prior Probability | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.01 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.001 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.001 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.001 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.0001 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, X.; Zhou, D.; Ma, L.; Tang, Y. Dependency Model-Based Multiple Fault Diagnosis Using Knowledge of Test Result and Fault Prior Probability. Appl. Sci. 2019, 9, 311. https://doi.org/10.3390/app9020311
Lv X, Zhou D, Ma L, Tang Y. Dependency Model-Based Multiple Fault Diagnosis Using Knowledge of Test Result and Fault Prior Probability. Applied Sciences. 2019; 9(2):311. https://doi.org/10.3390/app9020311
Chicago/Turabian StyleLv, Xiaofeng, Deyun Zhou, Ling Ma, and Yongchuan Tang. 2019. "Dependency Model-Based Multiple Fault Diagnosis Using Knowledge of Test Result and Fault Prior Probability" Applied Sciences 9, no. 2: 311. https://doi.org/10.3390/app9020311
APA StyleLv, X., Zhou, D., Ma, L., & Tang, Y. (2019). Dependency Model-Based Multiple Fault Diagnosis Using Knowledge of Test Result and Fault Prior Probability. Applied Sciences, 9(2), 311. https://doi.org/10.3390/app9020311





