Next Article in Journal
Wheat Bread with Dairy Products—Technology, Nutritional, and Sensory Properties
Next Article in Special Issue
Characteristics of Postural Muscle Activity in Response to A Motor-Motor Task in Elderly
Previous Article in Journal
Transmission Performance Analysis of RV Reducers Influenced by Profile Modification and Load
Previous Article in Special Issue
Center of Pressure Feedback Modulates the Entrainment of Voluntary Sway to the Motion of a Visual Target
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 9
Issue 19
10.3390/app9194100
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Ankle Joint Dynamic Stiffness in Long-Distance Runners: Effect of Foot Strike and Shoes Features

by
Alessandro Garofolini
1,*,
Simon Taylor
1,
Patrick Mclaughlin
1,
Karen J Mickle
1 and
Carlo Albino Frigo
2
1
Institute for Health and Sport (IHeS), Victoria University, Melbourne 3011, Australia
2
Dipartimento di Elettronica, Informazione e Bioingegneria, Politecnico di Milano, 20133 Milan, Italy
*
Author to whom correspondence should be addressed.
Appl. Sci. 2019, 9(19), 4100; https://doi.org/10.3390/app9194100
Submission received: 3 September 2019 / Revised: 27 September 2019 / Accepted: 27 September 2019 / Published: 1 October 2019
(This article belongs to the Special Issue Movement Biomechanics and Motor Control)
Browse Figures
Versions Notes

Abstract

:
Foot strike mode and footwear features are known to affect ankle joint kinematics and loading patterns, but how those factors are related to the ankle dynamic properties is less clear. In our study, two distinct samples of experienced long-distance runners: habitual rearfoot strikers (n = 10) and habitual forefoot strikers (n = 10), were analysed while running at constant speed on an instrumented treadmill in three footwear conditions. The joint dynamic stiffness was analysed for three subphases of the moment–angle plot: early rising, late rising and descending. Habitual rearfoot strikers displayed a statistically (p < 0.05) higher ankle dynamic stiffness in all combinations of shoes and subphases, except in early stance in supportive shoes. In minimal-supportive shoes, both groups had the lowest dynamic stiffness values for early and late rising (initial contact through mid-stance), whilst the highest stiffness values were at late rising in minimal shoes for both rearfoot and forefoot strikers (0.21 ± 0.04, 0.24 ± 0.06 (Nm/kg/°∙100), respectively). In conclusion, habitual forefoot strikers may have access to a wider physiological range of the muscle torque and joint angle. This increased potential may allow forefoot strikers to adapt to different footwear by regulating ankle dynamic stiffness depending upon the motor task.

1. Introduction

There is an ongoing debate on whether the foot strike pattern of long-distance runners plays a role in defining performance and injury risk in this population [1,2,3]. Experienced long-distance runners are able to change their foot strike pattern during a competition [4] or if they are asked to [5]. Their ability to adopt a different foot strike pattern has been often interpreted as a sign of adaptability. The concepts of “adaptability” and ”ability to adopt different execution patterns”, however, are not equivalent [6]. Adaptability refers to the level of organisation embodied by the human locomotor control system [7]; it represents the richness of motor behaviours that equally can accomplish the task-goal [8]. In contrast, the ability to adopt different execution patterns refers to the ability to change joint kinematics (and kinetics) without necessarily meeting the task-goal. It is unknown if runners who adopt different execution patterns (i.e., rearfoot strikers versus forefoot strikers) have developed a different level of adaptability.
During the stance phase of running, the ankle plays a dominant role in storing and generating energy for propulsion [9,10]. The mode of foot/ground initial contact may affect the subsequent joint angle time course and the associated joint stiffness. According to Günther and Blickhan [11], the foot strike angle, stiffness and running velocity are crucial parameters for coordination of body movement dynamics. The concept of dynamic joint stiffness [12,13], defined “quasi-stiffness” by Latash and Zatsiorsky [14], can be used to characterize the ankle behaviour during the stance phase of running [15]. Here, the ankle exhibits a first loading state in which the internal plantarflexor moment rises during dorsiflexion, and the periarticular joint structures absorb energy. It follows an unloading state in which the plantarflexion moment decreases while the joint plantarflexes, and the periarticular joint structures produce energy. The level of stiffness (that is the variation of joint moment per unit of joint angle variation) can depend on both (i) structural adaptations of the muscle–tendon units surrounding this joint and (ii) neural adaptations that control instantly the characteristics of these muscle–tendon units [16,17,18]. For instance, long-term adaptations in muscle and tendon architecture in the lower limb, such as shorter gastrocnemius medialis fascicles [19], thicker Achilles tendon [20] and stiffer foot arch [21], were found in habitual forefoot strikers, who usually land with a plantar-flexed ankle. Such adaptations could lead to a different load distribution in the muscle–tendon unit [22], in which the role of the elastic components is increased and the muscle fibres contract at a slower rate, which is advantageous for maximal power output and efficiency [23]. Together, both the structural and the neural adaptations contribute to defining the dimensionality of the system (degrees of freedom of the neural control system), that is the number of structures (muscles) that can be actively controlled and can be used to regulate the ankle dynamic stiffness efficiently, according to the mechanical requirements [24].
Ankle dynamic stiffness can be computed as the slope of the tangent to the moment–angle curve [12]. Using similar approaches, previous studies investigated dynamic ankle stiffness during running [9,10,11]. To our knowledge, Hamill and Gruber [5] were the only researchers testing change in ankle joint stiffness in two groups of runners with distinct foot strike patterns. Participants were classified as either rearfoot or forefoot strikers based on the presence of an impact peak on the vertical ground reaction force and on the ankle angle at landing. Although using these criteria runners may have been misclassified [25], according to Hamill and Gruber [5], habitual forefoot strikers exhibited a more compliant ankle and absorbed more (negative) work than habitual rearfoot strikers when running with their preferred foot strike pattern (forefoot); however, no differences were found with habitual rearfoot strikers running with a forefoot strike pattern (nonpreferred mode).
It is common for studies concerning running and ankle stiffness to simplify the loading phase of the moment–angle loop by representing the linear slope from initial foot contact to peak moment [5,15,26,27,28] (Figure 1, dashed line). This approach overlooks the potentially meaningful details occurring within the loading phase. For instance, at initial foot contact, the ankle joint moment increases nonlinearly with the change in angle (red portion in Figure 1). This state represents the ankle joint response to foot/ground initial loading. Thereafter, the ankle dorsiflexes slowly, while the ankle moment increases fast (blue portion in Figure 1).
This is a less compliant condition, representing the loading of the passive structures of the muscle–tendon units, and can be seen as a different state [29]. Another interesting phase that deserves attention is the unloading phase (light-blue portion in Figure 1), where the movement of the joint reverses to plantarflexion and the joint moment decreases. To the best of our knowledge, no studies have investigated the stance phase of running by considering these three task-relevant subphases of the moment–angle loop, which we expect to yield a more sensitive insight of the differences between habitual rearfoot and forefoot strikers.
The aim of this study was to investigate if foot strike loading technique has an effect on the ankle moment–angle dynamics during the stance phase of running. We expected forefoot strikers to have lower dynamic stiffness during the loading phase, based on previous findings [5]. We also expected forefoot strikers to have a higher proportion of negative work relative to positive work because of their loading technique that allows them to store and return elastic potential energy in the foot–ankle structure. To test whether habitual foot strike loading technique compromises the control of ankle stiffness, shoes with different assistive constructs were considered. We expected differences in ankle stiffness and work ratio between groups to be greater in minimally assistive shoes, due to the unfamiliarity of rearfoot strikers to this condition. Because we expected forefoot strikers have a greater intrinsic foot–ankle adaptability to external loading (i.e., greater ability to control ankle stiffness), we expected their (forefoot strikers) ankle stiffness to have a higher time-dependency. That is, ankle stiffness during unloading will depend more on ankle stiffness during loading in forefoot strikers.

2. Materials and Methods

2.1. Participants

Forty male long-distance runners gave their personal consent to take part in this study. Participants were excluded if they had not been running for at least 5 years, with an average of at least 40 km/week, and had not been free of neurological, cardiovascular or musculoskeletal problems within the previous six months. A number of 21 runners were found eligible. One subject was unable to complete the study protocol, which resulted in a tested sample of 20 subjects (age: 31.2 ± 6.9 yrs, height: 1.77 ± 0.07 cm, weight: 73.4 ± 7.9 kg). Participants were classified as rearfoot strikers (RFS, n = 10) or forefoot strikers (FFS, n = 10) based on their habitual mode of foot/ground initial contact. To classify their foot strike loading type, the participants were asked to run on an instrumented treadmill (AMTI Pty, Watertown, MA, USA) at their preferred speed, wearing their habitual running shoes. After a standardized 7 min of progressive warm up (starting from 3 min at 6 km/h, followed by 2 min at 8 km/h, then 2 min at 10 km/h) and accommodation period (i.e., quantitatively assessed stable foot strike angle—around 2 min), participants ran for 3 min at their preferred running speed, which was identified from the protocol suggested by Jordan and Challis [30]. Habitual foot strike mode was assessed on the basis of data collected on the last minute of running (~60 steps). The ankle internal moment of the dominant leg was analysed to this purpose within a short period, from initial ground contact to the time at which the vertical ground reaction force exceeded a threshold corresponding to body weight. Runners displaying an internal plantarflexor moment for at least 90% of this period were classified as forefoot strikers (FFS); conversely, those who displayed an internal dorsiflexor moment for at least 90% of the analysed period were classified as rearfoot strikers (RFS). This foot strike classification method was shown to perform best among other conventional methods [25].

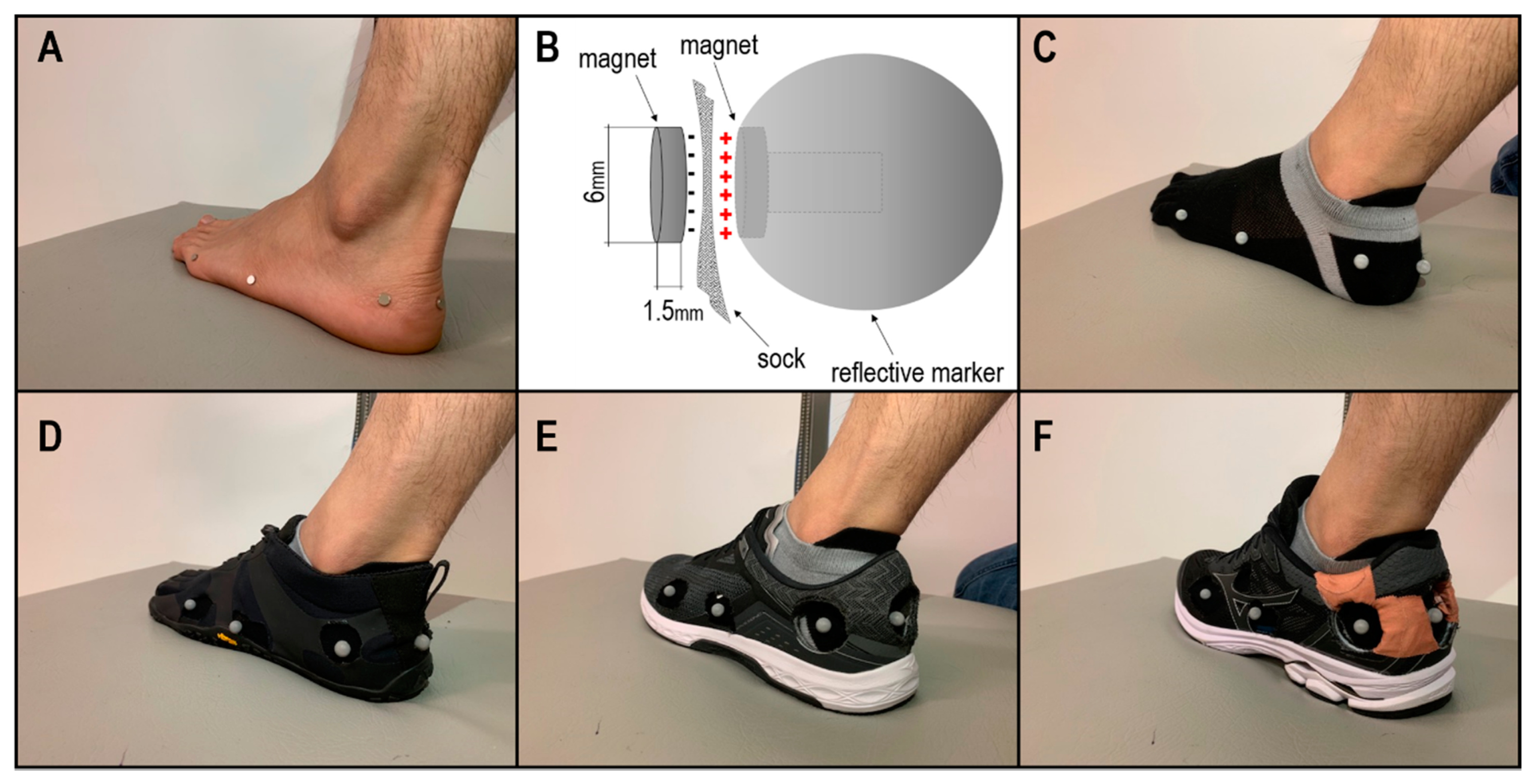
2.2. Experimental Protocol

Tests were performed on an instrumented treadmill (Advanced Mechanical Technology Inc., Watertown, MA, USA) that collects ground reaction forces [31] at a sampling rate of 1000 Hz. Three-dimensional kinematics data of the lower extremities was recorded at a sampling rate of 250 Hz from a 14-camera VICON B-10 system (Oxford Metrics Ltd., Oxford, UK). Kinematic and ground reaction force data were synchronised using a VICON MX-Net control box and collected through Nexus 2.6 software (Vicon Motion Systems Ltd., Oxford, UK). A biomechanical model was reconstructed from 45 retroreflective markers, placed on proper landmarks of body segments (Appendix A).
After completing a standardized and progressive 7 min warm-up, participants repeated three times a 5 min running test, with different shoes for each trial; the three shoe models were characterized by their different minimalist indexes (MI). The minimalist index is a classification that takes into account structure, flexibility, pronation support and other footwear features, and ranges from 0% (maximum assistance) to 100% (least interaction with the foot) [32]. The shoes adopted in our experiments were classified at low-MI (Mizuno® Wave Rider 21, MI = 18%), medium-MI (Mizuno® Wave Sonic, MI = 56%) and high-MI (Vibram® Five fingers, MI = 96%). The order of presentation was pseudorandom, which means that combinations were balanced within each group and equal between groups. Testing speed was fixed for all participants at 11 km/h.

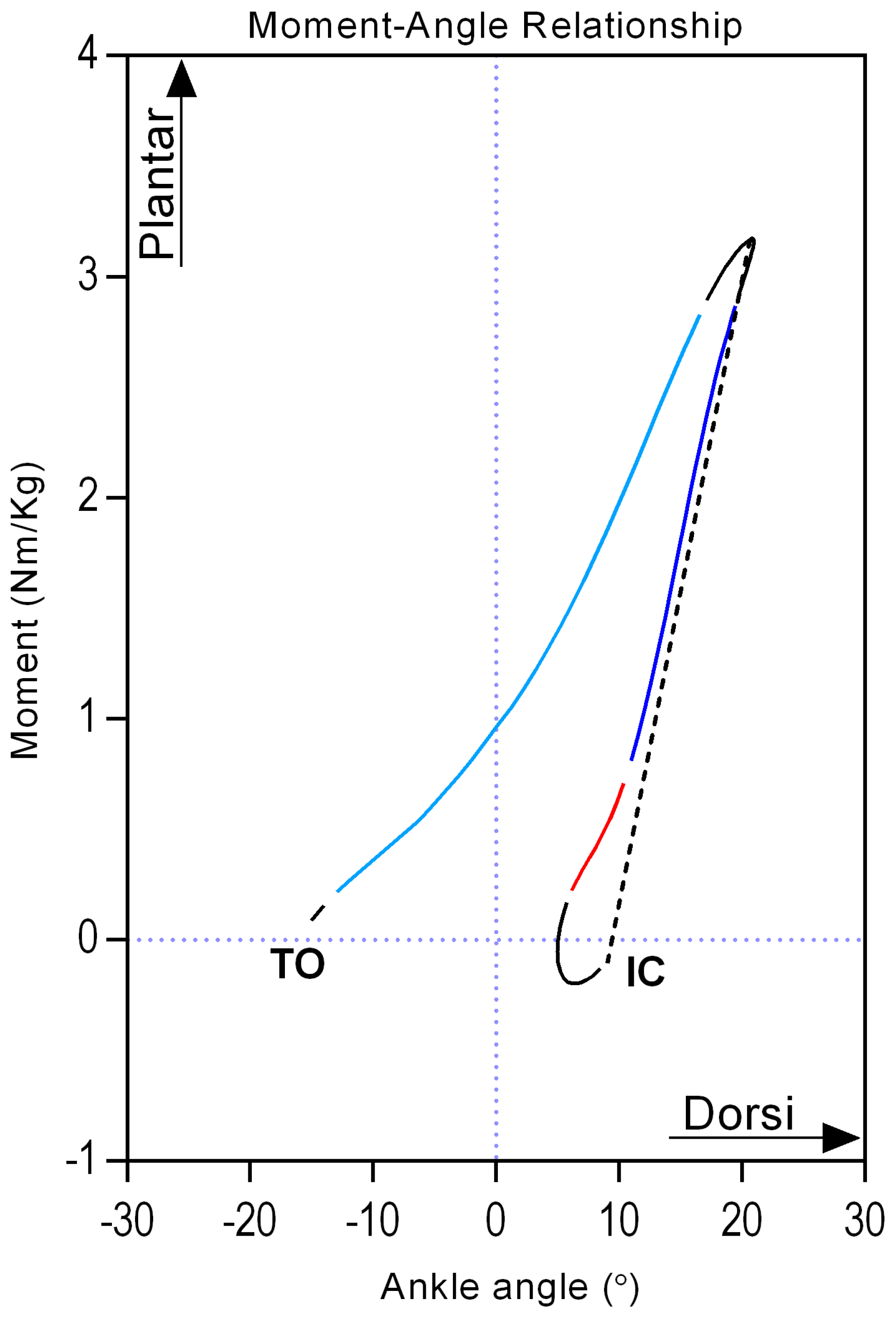
2.3. Data Analysis

Three-dimensional kinematics and kinetic data were analysed in Visual3D software (C-Motion, Inc, Rockville, MD, USA). A digital low-pass Butterworth filter (4th order, zero lag) was used to smooth raw kinematic and kinetic data with cut-off frequency of 15 and 35 Hz, respectively. The ankle joint angle was calculated as the relative angle between the foot and the shank longitudinal axes, and subtracted to the ankle joint angle computed during subject’s standing calibration posture (reference angle). Joint moments were computed around the ankle flexion/extension axis (the axis connecting the medial and lateral malleoli) using Newton–Euler inverse dynamics approach and normalized to body mass. Stance time was defined by gait events of initial and terminal foot contact (IC and TC) that were determined by a vertical ground reaction force threshold of 20 N. Stance time was normalised to 101 data points. The ankle (internal) moment was plotted as a function of the corresponding ankle angle (moment–angle plot), and the resultant curve was subdivided into three functionally relevant phases: early rising (ERP), late rising (LRP) and descending-phase (DP), similar to Crenna and Frigo [12]. The ERP was defined as the period between an ascending threshold of 0.2 peak plantarflexion moment and the first identified abrupt change in the statistical properties of the signal (i.e., mean and slope) going forward. The LRP was defined as the period between a threshold of 0.95 ascending moment to the first change in the statistical properties of the signal (i.e., mean and slope) going backwards.
The slope of the best regression line interpolating the angle–moment curve in each phase represents the average ankle joint stiffness (Kankle) in each functionally relevant phase (Figure S1). The area under the rising component and the descending component of the curve was integrated using a trapezoidal approximation. This gives the work absorbed (Wabs, during the loading phase) and the work produced (Wprod, during the unloading phase), respectively. The net work (Wnet) produced was computed as the difference between Wprod and Wabs. Finally, the work ratio (Wratio = Wabs/Wprod) was computed and was considered as a measure of muscle efficiency.

2.4. Statistical Analysis

An initial check for normal distribution (Shapiro–Wilk test) of the dependent variables and homogeneity of variance (Levene’s test) was performed. A three-way repeated-measures ANOVA was used to test the effect of the between-factor Group (RFS, FFS) and within-factors Shoe (LOW, MED and HIGH MI index), and Slope (ERP, LRP and DP) on Kankle. A two-way repeated measure ANOVA was used to test the effect of the between-factor Group (RFS, FFS) and within-factors Shoe for dependent variables Wabs, Wprod, Wnet and Wratio. If ANOVA was significant, a posthoc multiple comparison Tukey’s test was used to determine where the differences were. Pearson Correlation coefficient (r) was calculated for all couples of dependent variables, while the coefficient of determination (r2) was estimated from a linear regression model run among ERP, LRP, and DP. In case of non-normal distribution of data, the equivalent nonparametric tests (Kruskal–Wallis test, Dunn’s multiple comparisons test, Spearman correlation) were used. All statistical analyses were performed using SPSS (version 25.0. Armonk, NY, USA: IBM Corp.). Statistical significance was set at p < 0.05, with multiple pairwise comparisons corrected with Bonferroni adjustment method. Magnitude of changes (effect sizes) was assessed using partial Eta squared (ηp2) for the ANOVA, and Hedges’ g for pairwise (posthoc) comparisons.

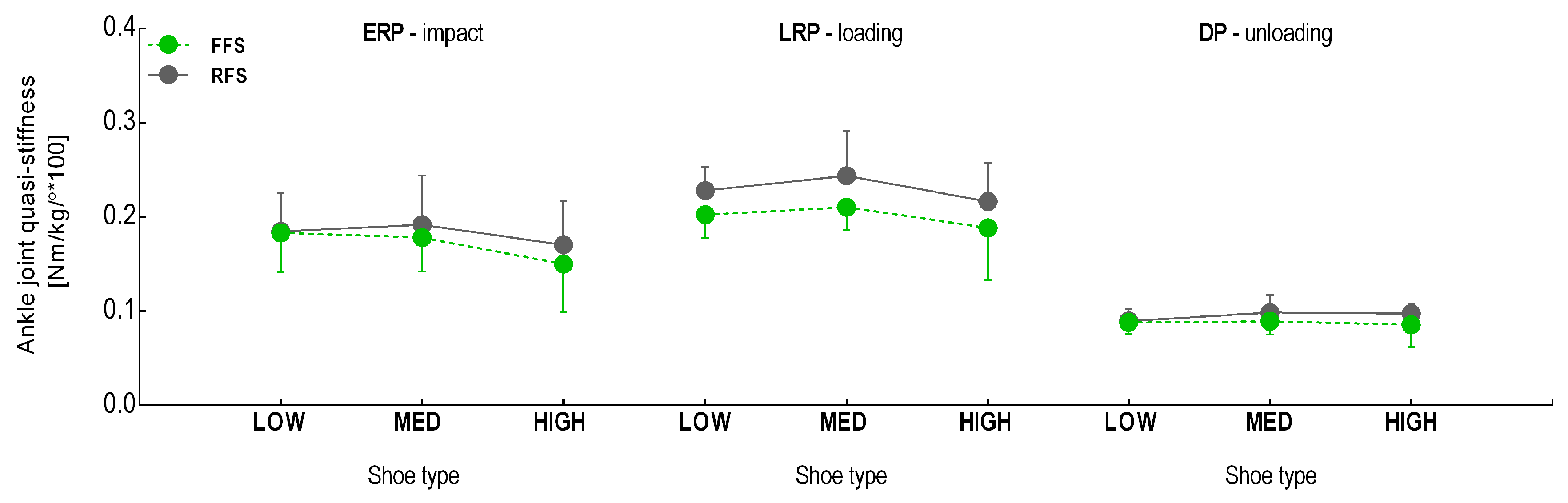
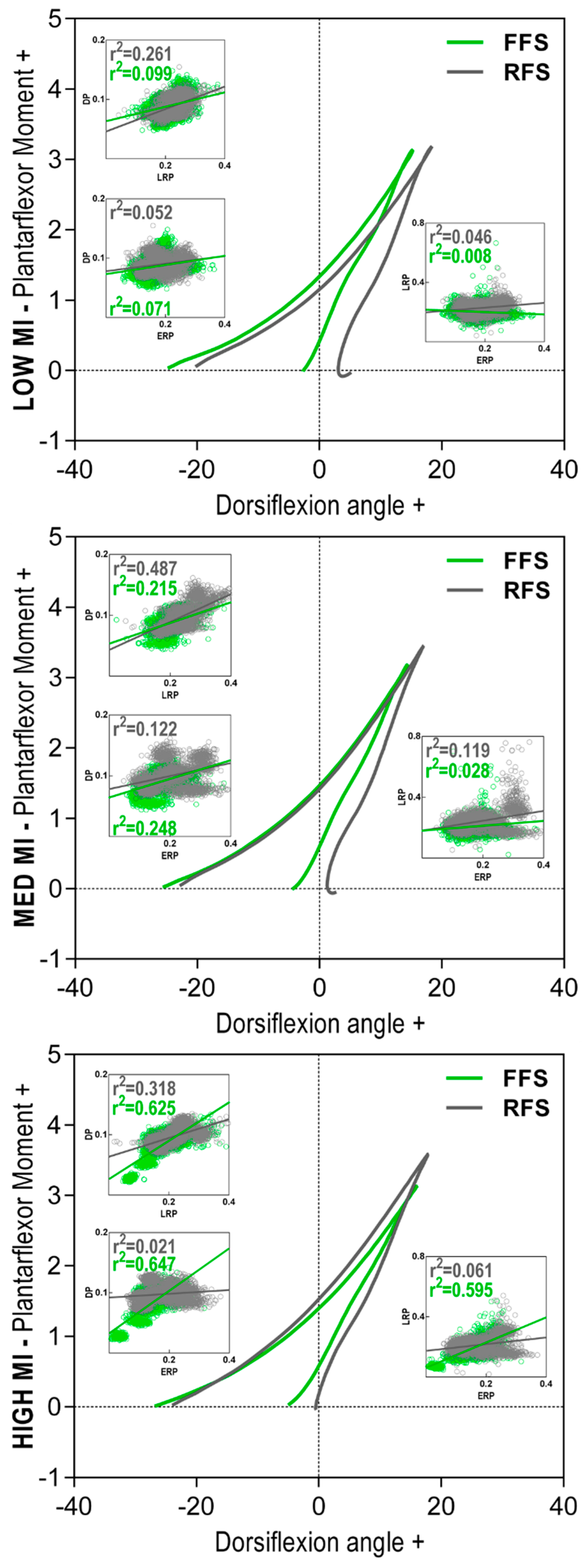
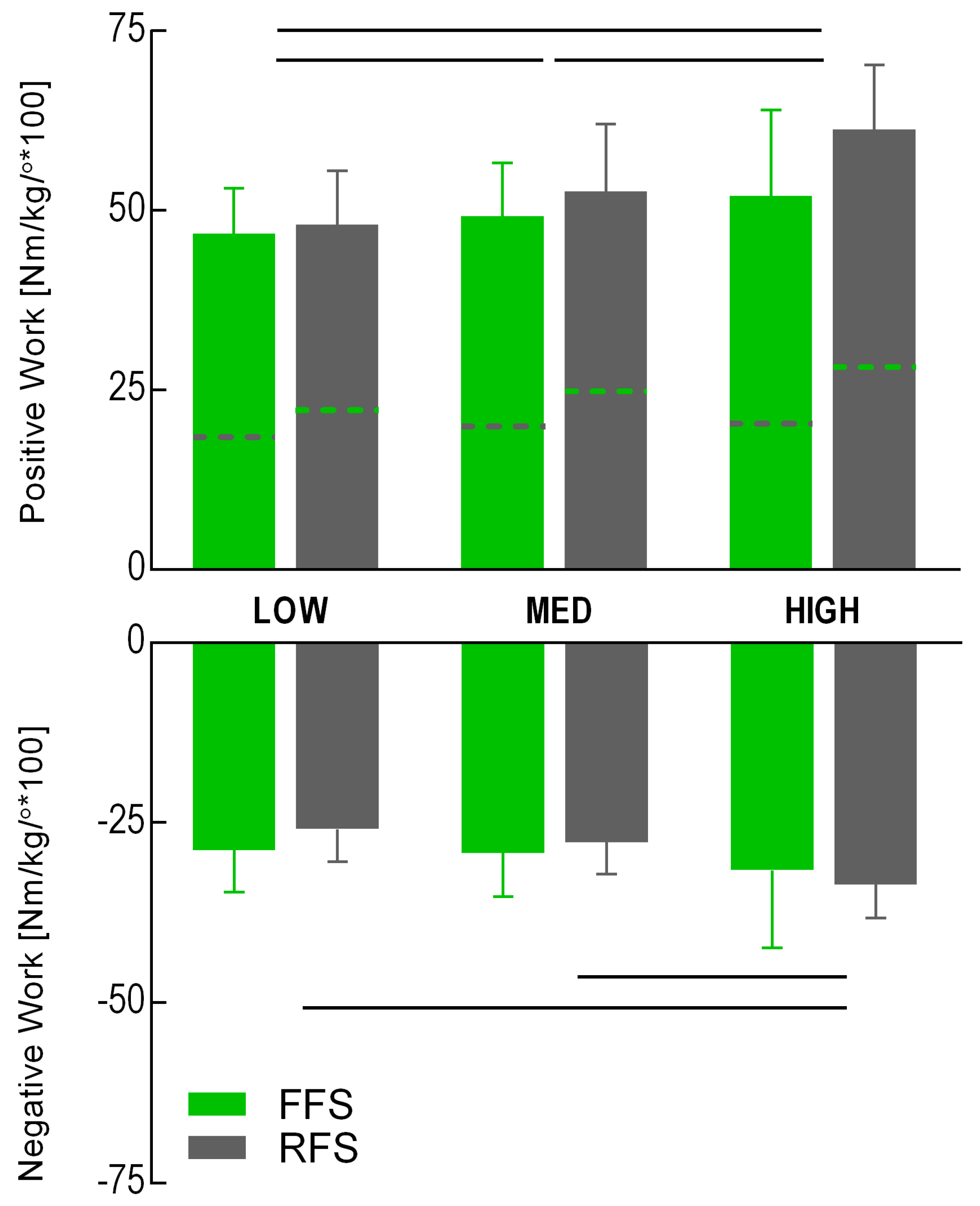
3. Results

No main effect of group was found for Kankle (p = 0.164; ηp2 = 0.105), but the main effects for shoe type (p = 0.008; ηp2 = 0.272) and slope (p < 0.001; ηp2 = 0.889) were obtained (Table S1). Posthoc analysis revealed that Kankle was 12% higher in med-MI compared with high-MI shoes (p = 0.007; g = 0.706). Table S2 and Figure 2 show mean and SD for Kankle in the three subphases of stance and among the three shoe conditions. Significant differences were found among all subphases: ERP–LRP (0.176 ± 0.01; 0.215 ± 0.01 Nm/kg/°∙100) p = 0.001; g = 3.9; ERP–DP (0.176 ± 0.01; 0.091 ± 0.01 Nm/kg/°∙100) p < 0.001; g = 9.5; LRP–DP (0.215 ± 0.01; 0.091 ± 0.01 Nm/kg/°∙100) p = 0.001; g = 12.4. Overall Kankle was highest when wearing med-MI shoes (although not statistically different from low-MI shoes; p = 0.246); Kankle was highest during the late rising phase (LRP) and lowest during the unloading phase (DP).
Runners in high-MI shoes exhibited a lower stiffness (more compliant ankle) during the impact phase (ERP) and late rising phase (LRP); during the unloading phase (DP), low-MI shoes allowed the most compliant ankle. There was a Shoe by Slope interaction effect (p = 0.008; ηp2 = 0.221; Table S1) for Kankle (Figure 2, Table S2). Pairwise multiple comparisons showed that during the impact phase (ERP), Kankle in high-MI shoes was lower compared with that in both low-MI and med-MI shoes (−15%, p = 0.013, g = 1.2; and −16%, p = 0.003, g = 1.25, respectively). During the late rising phase (LRP), Kankle was the highest in med-MI shoes (0.227 ± 0.01 Nm/kg/°∙100), but only statistically different from high-MI shoes (+12%, p = 0.011, g = 1.58). During the unloading phase (DP), differences between shoes were only significant for low-MI compared with med-MI shoes (−6%, p = 0.009, g = 0.5).
Figure 3 compares mean moment–angle loops for RFS and FFS. While curves are similar in low-MI shoes, (Figure 3, top) the base (ankle range of motion) is shifted toward the left for FFS. This is also true for medium-MI (Figure 3, middle), and high-MI shoes (Figure 3, bottom).
Overall, runners exhibiting high Kankle during the late rising phase (LRP) also have high Kankle during the unloading phase (DP) (Table 1). For FFS, the correlation between Kankle in the impact phase (ERP) and in late rising phase (LRP) increased with shoes’ MI, with the highest correlation (rs = 0.95; p < 0.01) in high-MI shoes. A similar trend was reported for correlations between Kankle in impact phase (ERP) and in unloading (DP), and between Kankle in late rising phase (LRP) and in unloading (DP), with highest values in the high-MI condition (rs = 0.84, p < 0.01; rs = 0.89, p < 0.01, respectively). Values were only significant in high-MI shoe conditions; this means that FFS in high-MI shoes with high Kankle during impact phase will also have high Kankle during the loading and unloading phases. For RFS, correlations between Kankle in impact phase (ERP) and in late rising phase (LRP) and correlations between Kankle in impact phase (ERP) and in unloading (DP) vary irrespectively to the shoe condition. The correlation between Kankle in late rising phase (LRP) and in unloading (DP) increased with shoes’ MI, with the highest correlation (rs = 0.92; p < 0.01) in high-MI shoes. This means, Kankle during impact has less of an effect on the subsequent subphases in RFS; instead, the late rising phase plays a central role.
In low-MI shoes, both groups presented low regression values (r2 ≤ 0.26, insets in Figure 3). In medium-MI shoes, Kankle of RFS during the loading phase (LRP) explained 49% of the Kankle variance during the unloading phase (DP), while for FFS, only 22% was explained. Kankle of FFS in high-MI shoes depended on the stiffness in the previous phase: that is, stiffness during the impact phase (ERP) explained 60% of the stiffness variance during the late rising phase (LRP) and 65% of the stiffness variance during the unloading phase (DP); likewise, stiffness during the late rising phase (LRP) explained 63% of the stiffness variance during the unloading phase (DP).
We found a main effect of shoes for Wabs and Wprod (p = 0.001, ηp2 = 0.425; p < 0.001, ηp2 = 0.517) but no main effect of group (p = 0.105; p = 0.716) or interaction effects for Groups by Shoes were found (p = 0.051; p = 0.097) (Table S1). Figure 4 shows that Wprod increased significantly from low-MI to med-MI shoes (7%, p = 0.004, g = 0.578) and from med-MI to high-MI shoes (11%, p = 0.017, g = 0.657); while Wabs decreased as an inverse function of shoe MI index, reaching highest values in high-MI shoes (−32.58 ± 1.71 Nm/kg/°∙100). The latter was significantly lower than Wabs in low-MI (−19%, p = 0.002, g = 0.839) and med-MI shoes (−14%, p = 0.009, g = 0.674). RFS exhibited higher Wnet compared with FFS (24.99 ± 1.25 versus 19.47 ± 1.25; p = 0.006, g = 4.420); Wnet increased with shoe MI index, with runners in low-MI shoes exhibiting statistically lower Wnet (−12%; p = 0.007, g = 0.456) compared with those in med MI-shoes, and compared with those in high-MI shoes (−20%; p = 0.028, g = 0.728).
Rear foot strikers in high-MI shoes had the highest net work values (27.8 ± 8 Nm/kg/°∙100) associated to increased work absorbed (+28% from LOW, p < 0.001 g = 2.09; +16% from MED, p < 0.001, g = 1.60) and produced (+30% from LOW, p < 0.001, g = 2.17; +21% from MED, p < 0.001, g = 1.17) (Figure 4); however, the work ratio (absorbed/produced) for RFS was statistically lower than for FFS (0.55 vs. 0.59, g = 0.533). FFS increased positive work going from LOW to MED (+5%; p < 0.001, g = 0.465) and from MED to HIGH (+6%; p < 0.001, g = 0.319); while negative work was not statistically different from LOW (28.84 ± 5.8 Nm/kg/°∙100) and MED (29.21 ± 6.0 Nm/kg/°∙100; p = 0.327), but in HIGH, negative work was higher than in both LOW (+9%; p < 0.001, g = 0.342) and MED (+8%; p < 0.001, g = 0.299); however, net work in HIGH (20.4 ± 5.5 Nm/kg/°∙100) was similar (p = 0.781) to MED (20.2 ± 5.0 Nm/kg/°∙100) and LOW (18.8 ± 6 Nm/kg/°∙100).
As for the correlation between energetic (work) measures (Table 1), FFS exhibited high negative correlations values between Wabs and Wprod in all shoe conditions (rs ≤ −0.69), meaning that the more work they absorbed during loading, the less work they needed to produce during the unloading phase. RFS did not show such correlations; instead, they exhibited high positive correlations (rs ≥ 0.60) between Wprod and Wnet, meaning that the net work increased as the produced work increased.

4. Discussion

The purpose of this study was to explore the effect of foot strike modes and footwear features on the dynamic control of the ankle dynamics stiffness. There was no group main effect for ankle stiffness, contrary to our hypothesis that FFS had a lower ankle stiffness than RFS. Hamill, Gruber [5] investigated stiffness during the phase of stance that corresponds most closely to the LRP region of our study. By examining a main effect of group within the LRP region (ignoring ERP and DP), we have also confirmed a statistically higher (+14%; p = 0.005, g = 0.725) ankle stiffness in the RFS group. However, within the LRP, there was not a main effect of Shoe on ankle stiffness (p = 0.163). Previous studies found that changing shoe support altered the level of joint stiffness [26,33]; where ankle dynamic stiffness increased as the shoe hardness decreased [34]. While increasing stiffness may be functional in preventing excessive joint movement [35], it has been identified as a possible risk of Achilles tendon injuries in runners [36].
The rearfoot strike loading technique generated more positive (produced) work by the ankle joint. This confirms our hypothesis and is consistent with previous studies that found ankle plantar flexor muscles to store more elastic energy (negative work) during the loading phase of fast running (i.e., forefoot strike) compared with positive work during unloading [37,38]. The RFS group in our study exhibited 34% higher net work compared with FFS (Table S2 and Table 1), which correlated strongly with the work produced (Figure 3); indicating that there was more muscle energy produced compared with elastic energy stored [39]. Efficient running is achieved by efficiently storing and releasing elastic energy at each step; our results are in line with previous literature data that found FFS to store and return more elastic energy than RFS [40,41,42]. Despite this energetic advantage, FFS is consistently reported to be energetically inefficient [43,44], probably because storing energy in passive structures requires muscle contraction [45]. Therefore, it may be concluded that saving and releasing energy in the plantarflexor muscles may not significantly reduce the whole-body metabolic cost of running with a forefoot strike pattern [46].
The FFS group demonstrated a time-dependent ankle stiffness across the stance phase, especially for the high-MI shoe condition, fulfilling our hypothesis. Furthermore, within the same shoe condition, the FFS group had strong correlations between ankle stiffness (Kankle) during both impact and loading phases and net work (Wnet). By controlling ankle stiffness, the work around the ankle was modulated, probably to achieve a functional redistribution of loading along the lower limb joints [10,47]. Furthermore, Figure 3 indicates that the Kankle of FFS running in minimally supportive shoes is constant through the impact, late rising (loading) and unloading subphases, suggesting that foot strike at landing is a determinant for ankle dynamic stiffness not only at impact, but also during the loading and unloading phases. A similar correlation has been found between the initial joint stiffness and maximal stiffness during the stance phase of hopping [48]. One possible explanation for a constant ankle stiffness is that in that configuration (ankle plantarflexion with minimal support) the ankle–foot complex can express its spring-like function [49,50,51]; while increasing shoe support may introduce a level of instability that requires a trade-off between the task-goals of energy recycling and stable locomotion [52].
Shoe characteristics influenced the control of ankle dynamic stiffness. Both groups were able to reduce ankle dynamic stiffness during impact and loading phase when wearing high-MI shoes (Figure 2, Table S2). However, both groups also increased the work produced and absorbed, so that the total net work done around the ankle during stance increased as a function of the shoe MI index (Figure 4, Table S2). Control and modulation of these loads need a certain level of adaptability of both the musculoskeletal and neuronal systems [53]. This may explain the high risk of certain injuries when changing from low- to high-MI shoes [54] or from RFS to FFS patterns [55].

Limitations

We acknowledge that the energy absorbed or produced at the foot/ankle is not only associated to flexion/extension, but also to foot/shoes deformation [56]. In addition, in this study, analysis was limited to the ankle joint. Indeed, adding analysis on the work done around knee and hip would have validated our assumption on leg-level force stabilization. Other limitations are the assumed symmetry between dominant and nondominant leg. The modulation of joint dynamic stiffness and the redistribution of joint work may vary if significant asymmetry exist [57].

5. Conclusions

In this study, we investigated the effect of habitual rearfoot strike loading pattern, and the assistance of shoes, on ankle stiffness control. Our results suggested that RFS has reduced adaptability when compared with FFS, but the constraint of this ability is dependent on the shoe worn. These findings reiterate the idea that functional changes at joint level are important to define the redistribution of load along the lower-limb kinetic chain in order to solve leg-level force control. Shoes with a low MI may limit the ability to utilize the spring-like function of the ankle–foot complex, while shoes with high MI may promote the exploitation of the system redundancy. However, further studies are warranted to confirm the effect of shoes on ankle neuromuscular adaptations.

Supplementary Materials

The following are available online at https://www.mdpi.com/2076-3417/9/19/4100/s1, Figure S1: Example of ankle moment–angle relationship for a FFS subject and a RFS subject for the normalized stance phase from initial contact to toe-off. Table S1: Primary statistical results for differences between Groups, Shoes, and Slopes for mean ankle stiffness (Kankle), work produced (Wprod), work absorbed (Wabs), work net (Wnet), and work ratio (Wratio). Table S2: Mean and (SD) for Groups, Shoes, and Slopes for mean ankle stiffness, work produced (Wprod), work absorbed (Wabs), work net (Wnet), and work ratio (Wratio).

Author Contributions

A.G.: Conceptualization, Methodology, Formal Analysis, Investigation, Data curation, Software, Visualization, Writing—Original draft preparation. S.T.: Conceptualization, Methodology, Supervision, Reviewing and Editing. P.M.: Methodology, Supervision, Reviewing and Editing. K.J.M.: Methodology, Supervision, Reviewing and Editing. C.A.F.: Writing-Reviewing and Editing.

Funding

This research received no external funding.

Acknowledgments

The authors gratefully acknowledge Mizuno Footwear Company for their financial support.

Conflicts of Interest

The authors declare no competing interests relevant to the content of this study.

Appendix A

Biomechanical Model

A set of retroreflective markers arranged in cluster setup were used to track 3D position of body segments, while landmark-derived virtual markers and movement-derived virtual markers were used to calibrate the position and orientation of the lower body skeletal system. Semirigid clusters of 4–5 markers were attached to lower-body segments so that the location of the cluster centroid was minimally affected by muscular contraction and related mass deformation. To minimize effects of skin movement artefact [58,59], we secured the semirigid clusters over extra-long neoprene bands made of antimigration material that wrapped and fastened on the thigh and shank segments. Individual trunk and pelvis retroreflective markers were placed over the 7th cervical vertebrae, sterno-clavicular notch, 10th thoracic vertebrae and posterior- and anterior-superior iliac spines. Virtual markers were used to identify medial and lateral epicondyles of the femur and medial and lateral malleoli. A custom version of the IOR multisegment foot model [60] was adopted for the foot marker setup. Retroreflective markers were placed on calcanei, first metatarsal bases and heads, second metatarsal bases and heads, navicular bones and base and heads of the 5th metatarsals.
To fix the 9.5 mm reflective markers on the foot, we removed the internal screw from the markers and replaced with a 6 mm diameter × 1.5 mm long Rare Earth Magnet fixed with superglue. After identifying the foot anatomical landmarks, we applied a similar magnet on the skin, fixed with topical skin adhesive glue. Participants performed testing in socks and shoes. All shoes were modified, with the circular holes cut at anatomical landmarks. Foot markers were attached to magnets that were preglued to the skin of the participants, ensuring repeatable marker location associated with reattachment process between footwear conditions (Figure A1).
Applsci 09 04100 g0a1 550
Figure A1. (A) Magnets glued to bony landmarks; (B) Schematic representation of magnets interaction; (C) markers placed over the sock, maintaining the same position; (D–F) markers position in the three shoe conditions: Vibram® Five fingers (D), Mizuno® Wave Sonic (E), Mizuno® Wave Rider 21 (F).
Figure A1. (A) Magnets glued to bony landmarks; (B) Schematic representation of magnets interaction; (C) markers placed over the sock, maintaining the same position; (D–F) markers position in the three shoe conditions: Vibram® Five fingers (D), Mizuno® Wave Sonic (E), Mizuno® Wave Rider 21 (F).
Applsci 09 04100 g0a1
Hip joint centre and knee joint axis of rotation were defined using functional movement trials according to Camomilla and Cereatti [61], and Schwartz and Rozumalski [62]. A six-degrees of freedom segment model was built for biomechanical analysis in Visual3D software (C-motion Inc., Rockville, MD, USA). Standard methods were used to calibrate segment pose from marker setup and reconstruct the subject biomechanical model in Visual3D. For joint rotations, we used a right-handed orthogonal coordinate systems, where the z-axis represented the axial direction of the segment. The x-axis lied in the frontal plane perpendicular to the z-axis. The y-axis lied on the sagittal plane in the antero-posterior direction. In Visual3D, joint angles were calculated using an x–y–z Cardan–Euler sequence representing flexion/extension, abduction/adduction and axial rotation of the thigh, shank and foot [63]. For the pelvis, the Cardan sequence was reversed (z–y–x), as recommended by Baker [64]. Joint angles were normalized to the subject static reference position, recorded as a “standing calibration trial”. For the scope of this study, the segment movements of interest were those within the sagittal plane only (i.e., flexion/extension rotations).
The force signal recorded was assigned to relevant foot segment based on detection software in Visual3D. The estimated foot assigned to the force is based on the proximity between the location of the centre of mass of the foot and the transverse plane location of the centre of pressure on the force plate. Force signals were then used to compute joint moment (through inverse dynamic calculations) represented in the joint coordinate system [65].

References

  1. Bramble, D.M.; Lieberman, D.E. Endurance running and the evolution of Homo. Nature 2004, 432, 345–352. [Google Scholar] [CrossRef] [PubMed]
  2. Davis, I.S.; Rice, H.M.; Wearing, S.C. Why forefoot striking in minimal shoes might positively change the course of running injuries. J. Sport Health Sci. 2017, 6, 154–161. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  3. Hamill, J.; Gruber, A.H. Is changing footstrike pattern beneficial to runners? J. Sport Health Sci. 2017, 6, 146–153. [Google Scholar] [CrossRef] [PubMed]
  4. Larson, P.; Higgins, E.; Kaminski, J.; Decker, T.; Preble, J.; Lyons, D.; McIntyre, K.; Normile, A. Foot strike patterns of recreational and sub-elite runners in a long-distance road race. J. Sport Health Sci. 2011, 29, 1665–1673. [Google Scholar] [CrossRef] [PubMed]
  5. Hamill, J.; Gruber, A.H.; Derrick, T.R. Lower extremity joint stiffness characteristics during running with different footfall patterns. Eur. J. Sport Sci. 2014, 14, 130–136. [Google Scholar] [CrossRef] [PubMed]
  6. Garofolini, A.; Taylor, S.; Mclaughlin, P.; Vaughan, B.; Wittich, E. Acute adaptability to barefoot running among professional AFL players. Footwear Sci. 2017, 9, S44–S45. [Google Scholar] [CrossRef]
  7. Lacquaniti, F.; Ivanenko, Y.P.; Zago, M. Patterned control of human locomotion. J. Physiol. 2012, 590, 2189–2199. [Google Scholar] [CrossRef]
  8. Todorov, E.; Jordan, M.I. Optimal feedback control as a theory of motor coordination. Nat. Neurosci. 2002, 5, 1226–1235. [Google Scholar] [CrossRef] [PubMed]
  9. Jin, L.; Hahn, M.E. Modulation of lower extremity joint stiffness, work and power at different walking and running speeds. Hum. Mov. Sci. 2018, 58, 1–9. [Google Scholar] [CrossRef] [PubMed]
  10. Schache, A.G.; Brown, N.A.T.; Pandy, M.G. Modulation of work and power by the human lower-limb joints with increasing steady-state locomotion speed. J. Exp. Biol. 2015, 218, 2472–2481. [Google Scholar] [CrossRef]
  11. Günther, M.; Blickhan, R. Joint stiffness of the ankle and the knee in running. J. Biomech. 2002, 35, 1459–1474. [Google Scholar] [CrossRef]
  12. Crenna, P.; Frigo, C. Dynamics of the ankle joint analyzed through moment–angle loops during human walking: Gender and age effects. Hum. Mov. Sci. 2011, 30, 1185–1198. [Google Scholar] [CrossRef] [PubMed]
  13. Gabriel, R.C.; Abrantes, J.; Granata, K.; Bulas-Cruz, J.; Melo-Pinto, P.; Filipe, V. Dynamic joint stiffness of the ankle during walking: Gender-related differences. Phys. Ther. Sport 2008, 9, 16–24. [Google Scholar] [CrossRef] [PubMed]
  14. Latash, M.L.; Zatsiorsky, V.M. Joint stiffness: Myth or reality? Hum. Mov. Sci. 1993, 12, 653–692. [Google Scholar] [CrossRef]
  15. Stefanyshyn, D.J.; Nigg, B.M. Dynamic angular stiffness of the ankle joint during running and sprinting. J. Appl. Biomech. 1998, 14, 292–299. [Google Scholar] [CrossRef] [PubMed]
  16. Feldman, A. Superposition of motor programs—I. Rhythmic forearm movements in man. Neuroscience 1980, 5, 81–90. [Google Scholar] [CrossRef]
  17. Guissard, N.; Duchateau, J. Neural Aspects of Muscle Stretching. Exerc. Sport Sci. Rev. 2006, 34, 154–158. [Google Scholar] [CrossRef]
  18. Duchateau, J.; Enoka, R.M. Neural control of lengthening contractions. J. Exp. Biol. 2016, 219, 197–204. [Google Scholar] [CrossRef] [Green Version]
  19. Cronin, N.J.; Finni, T. Treadmill versus overground and barefoot versus shod comparisons of triceps surae fascicle behaviour in human walking and running. Gait Posture 2013, 38, 528–533. [Google Scholar] [CrossRef]
  20. Lichtwark, G.A.; Cresswell, A.G.; Newsham-West, R.J. Effects of running on human Achilles tendon length–tension properties in the free and gastrocnemius components. J. Exp. Biol. 2013, 216, 4388–4394. [Google Scholar] [CrossRef]
  21. Lieberman, D.E. Strike type variation among Tarahumara Indians in minimal sandals versus conventional running shoes. J. Sport Health Sci. 2014, 3, 86–94. [Google Scholar] [CrossRef]
  22. Kubo, K.; Miyazaki, D.; Ikebukuro, T.; Yata, H.; Okada, M.; Tsunoda, N. Active muscle and tendon stiffness of plantar flexors in sprinters. J. Sports Sci. 2017, 35, 742–748. [Google Scholar] [CrossRef] [PubMed]
  23. Lichtwark, G.; Bougoulias, K.; Wilson, A. Muscle fascicle and series elastic element length changes along the length of the human gastrocnemius during walking and running. J. Biomech. 2007, 40, 157–164. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  24. Latash, M.L. The bliss (not the problem) of motor abundance (not redundancy). Exp. Brain Res. 2012, 217, 1–5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  25. Garofolini, A.; Taylor, S.; Mclaughlin, P.; Vaughan, B.; Wittich, E. Foot strike classification: A comparison of methodologies. Footwear Sci. 2017, 9, S129–S130. [Google Scholar] [CrossRef]
  26. Sinclair, J.; Atkins, S.; Taylor, P.J. The Effects of Barefoot and Shod Running on Limb and Joint Stiffness Characteristics in Recreational Runners. J. Mot. Behav. 2016, 48, 79–85. [Google Scholar] [CrossRef]
  27. Kuitunen, S.; Komi, P.V.; Kyröläinen, H. Knee and ankle joint stiffness in sprint running. Med. Sci. Sports Exerc. 2002, 34, 166–173. [Google Scholar] [CrossRef] [PubMed]
  28. Powell, D.W.; Williams, D.S., 3rd; Windsor, B.; Butler, R.J.; Zhang, S. Ankle work and dynamic joint stiffness in high-compared to low-arched athletes during a barefoot running task. Hum. Mov. Sci. 2014, 34, 147–156. [Google Scholar] [CrossRef]
  29. Roberts, T.J. Contribution of elastic tissues to the mechanics and energetics of muscle function during movement. J. Exp. Biol. 2016, 219, 266–275. [Google Scholar] [CrossRef] [Green Version]
  30. Jordan, K.; Challis, J.H.; Newell, K.M. Speed influences on the scaling behavior of gait cycle fluctuations during treadmill running. Hum. Mov. Sci. 2007, 26, 87–102. [Google Scholar] [CrossRef]
  31. Garofolini, A.; Taylor, S.; Lepine, J. Evaluating dynamic error of a treadmill and the effect on measured kinetic gait parameters: Implications and possible solutions. J. Biomech. 2019, 82, 156–163. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  32. Esculier, J.-F.; Dubois, B.; Dionne, C.E.; Leblond, J.; Roy, J.-S. A consensus definition and rating scale for minimalist shoes. J. Foot Ankle Res. 2015, 8, 1–9. [Google Scholar] [CrossRef] [PubMed]
  33. Apps, C.; Sterzing, T.; O’Brien, T.; Lake, M. Lower limb joint stiffness and muscle co-contraction adaptations to instability footwear during locomotion. J. Electromyogr. Kinesiol. 2016, 31, 55–62. [Google Scholar] [CrossRef] [PubMed]
  34. Baltich, J.; Maurer, C.; Nigg, B.M. Increased vertical impact forces and altered running mechanics with softer midsole shoes. PLoS ONE 2015, 10, e0125196. [Google Scholar] [CrossRef] [PubMed]
  35. Riemann, B.L.; Myers, J.B.; Lephart, S.M. Sensorimotor system measurement techniques. J. Athl. Train. 2002, 37, 85–98. [Google Scholar] [PubMed]
  36. Lorimer, A.V.; Hume, P.A. Stiffness as a Risk Factor for Achilles Tendon Injury in Running Athletes. Sports Med. 2016, 46, 1921–1938. [Google Scholar] [CrossRef]
  37. Lai, A.; Schache, A.G.; Brown, N.A.; Pandy, M.G. Human ankle plantar flexor muscle–tendon mechanics and energetics during maximum acceleration sprinting. J. R. Soc. Interface 2016, 13, 20160391. [Google Scholar] [CrossRef]
  38. Hof, A.; van Zandwijk, J.; Bobbert, M. Mechanics of human triceps surae muscle in walking, running and jumping. Acta Physiol. Scand. 2002, 174, 17–30. [Google Scholar] [CrossRef]
  39. Biewener, A.A.; Roberts, T.J. Muscle and tendon contributions to force, work, and elastic energy savings: A comparative perspective. Exerc. Sport Sci. Rev. 2000, 28, 99–107. [Google Scholar]
  40. Hasegawa, H.; Yamauchi, T.; Kraemer, W.J. Foot strike patterns of runners at the 15-km point during an elite-level half marathon. J. Strength Cond. Res. 2007, 21, 888–893. [Google Scholar]
  41. Lieberman; Venkadesan, M.; Werbel, W.A.; Daoud, A.I.; D’Andrea, S.; Davis, I.S.; Mang’Eni, R.O.; Pitsiladis, Y. Foot strike patterns and collision forces in habitually barefoot versus shod runners. Nature 2010, 463, 531–535. [Google Scholar] [CrossRef] [PubMed]
  42. Perl, D.P.; Daoud, A.I.; Lieberman, D.E. Effects of footwear and strike type on running economy. Med. Sci. Sports Exerc. 2012, 44, 1335–1343. [Google Scholar] [CrossRef] [PubMed]
  43. Gruber, A.H.; Umberger, B.R.; Braun, B.; Hamill, J. Economy and rate of carbohydrate oxidation during running with rearfoot and forefoot strike patterns. J. Appl. Physiol. (1985) 2013, 115, 194–201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  44. Ogueta-Alday, A.; Rodríguez-Marroyo, J.A.; García-López, J. Rearfoot striking runners are more economical than midfoot strikers. Med. Sci. Sports Exerc. 2014, 46, 580–585. [Google Scholar] [CrossRef]
  45. Holt, N.C.; Roberts, T.J.; Askew, G.N. The energetic benefits of tendon springs in running: Is the reduction of muscle work important? J. Exp. Biol. 2014, 217, 4365–4371. [Google Scholar] [CrossRef] [PubMed]
  46. Gruber, A.; Umberger, B.R.; Miller, R.H.; Hamill, J.H. Muscle mechanics and energy expenditure of the triceps surae during rearfoot and forefoot running. bioRxiv 2018. [Google Scholar] [CrossRef]
  47. Yen, J.T.; Auyang, A.G.; Chang, Y.-H. Joint-level kinetic redundancy is exploited to control limb-level forces during human hopping. Exp. Brain Res. 2009, 196, 439–451. [Google Scholar] [CrossRef] [PubMed]
  48. Rapoport, S.; Mizrahi, J.; Kimmel, E.; Verbitsky, O.; Isakov, E. Constant and variable stiffness and damping of the leg joints in human hopping. J. Biomech. Eng. 2003, 125, 507–514. [Google Scholar] [CrossRef]
  49. Farris Dominic, J.; Brent, J.R. Modulation of leg joint function to produce emulated acceleration during walking and running in humans. R. Soc. Open Sci. 2017, 4, 160901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  50. Kelly, L.A.; Farris, D.J.; Lichtwark, G.A.; Cresswell, A.G. The Influence of Foot-Strike Technique on the Neuromechanical Function of the Foot. Med. Sci. Sports Exerc. 2018, 50, 98–108. [Google Scholar] [CrossRef] [Green Version]
  51. Riddick, R.; Farris, D.J.; Kelly, L.A. The foot is more than a spring: Human foot muscles perform work to adapt to the energetic requirements of locomotion. J. R. Soc. Interface 2019, 16, 20180680. [Google Scholar] [CrossRef] [PubMed]
  52. Ferris, D.P.; Louie, M.; Farley, C.T. Running in the real world: Adjusting leg stiffness for different surfaces. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1998, 265, 989–994. [Google Scholar] [CrossRef] [PubMed]
  53. Cronin, N.J.; Carty, C.P.; Barrett, R.S. Triceps surae short latency stretch reflexes contribute to ankle stiffness regulation during human running. PLoS ONE 2011, 6, e23917. [Google Scholar] [CrossRef] [PubMed]
  54. Giuliani, J.; Masini, B.; Alitz, C.; Owens, B.D. Barefoot-simulating footwear associated with metatarsal stress injury in 2 runners. Orthopedics 2011, 34, e320–e323. [Google Scholar] [CrossRef] [PubMed]
  55. Daoud, A.I.; Geissler, G.J.; Wang, F.; Saretsky, J.; Daoud, Y.A.; Lieberman, D.E. Foot Strike and Injury Rates in Endurance Runners: A Retrospective Study. Med. Sci. Sports Exerc. 2012, 44, 1325–1334. [Google Scholar] [CrossRef] [PubMed]
  56. Farinelli, V.; Hosseinzadeh, L.; Palmisano, C.; Frigo, C. An easily applicable method to analyse the ankle-foot power absorption and production during walking. Gait Posture 2019, 71, 56–61. [Google Scholar] [CrossRef]
  57. Exell, T.A.; Irwin, G.; Gittoes, M.J.; Kerwin, D.G. Implications of intra-limb variability on asymmetry analyses. J. Sport Health Sci. 2012, 30, 403–409. [Google Scholar] [CrossRef]
  58. Taylor, W.R.; Ehrig, R.M.; Duda, G.N.; Schell, H.; Seebeck, P.; Heller, M.O. On the influence of soft tissue coverage in the determination of bone kinematics using skin markers. J. Orthop. Res. 2005, 23, 726–734. [Google Scholar] [CrossRef]
  59. Leardini, A.; Chiari, L.; Della Croce, U.; Cappozzo, A. Human movement analysis using stereophotogrammetry: Part 3. Soft tissue artifact assessment and compensation. Gait Posture 2005, 21, 212–225. [Google Scholar] [CrossRef]
  60. Leardini, A.; Benedetti, M.G.; Berti, L.; Bettinelli, D.; Nativo, R.; Giannini, S. Rear-foot, mid-foot and fore-foot motion during the stance phase of gait. Gait Posture 2007, 25, 453–462. [Google Scholar] [CrossRef]
  61. Camomilla, V.; Cereatti, A.; Vannozzi, G.; Cappozzo, A. An optimized protocol for hip joint centre determination using the functional method. J. Biomech. 2006, 39, 1096–1106. [Google Scholar] [CrossRef] [PubMed]
  62. Schwartz, M.H.; Rozumalski, A. A new method for estimating joint parameters from motion data. J. Biomech. 2005, 38, 107–116. [Google Scholar] [CrossRef] [PubMed]
  63. Robertson, D.G.E.; Robertson, G.; Caldwell, G.; Hamill, J.; Kamen, P.G.; Whittlesey, S. Research Methods in Biomech, 2nd ed.; Human Kinetics: Champaign, IL, USA, 2013. [Google Scholar]
  64. Baker, R. Pelvic angles: A mathematically rigorous definition which is consistent with a conventional clinical understanding of the terms. Gait posture 2001, 13, 1–6. [Google Scholar] [CrossRef]
  65. Schache, A.G.; Baker, R. On the expression of joint moments during gait. Gait Posture 2007, 25, 440–452. [Google Scholar] [CrossRef] [PubMed]
Applsci 09 04100 g001 550
Figure 1. Example of moment–angle loop for the ankle joint. IC = initial foot contact; TO = toe off. Dashed line represents commonly computed slope for ankle stiffness during the loading phase. Red line represents foot/ground initial loading; blue line represents loading phase; light-blue line represents unloading phase.
Figure 1. Example of moment–angle loop for the ankle joint. IC = initial foot contact; TO = toe off. Dashed line represents commonly computed slope for ankle stiffness during the loading phase. Red line represents foot/ground initial loading; blue line represents loading phase; light-blue line represents unloading phase.
Applsci 09 04100 g001
Applsci 09 04100 g002 550
Figure 2. Mean and SD values for ankle joint dynamic stiffness of FFS and RFS for the three phases of stance, in the three shoe conditions. ERP early rising phase, LRP late rising phase, DP descending phase. Shoes conditions are termed as low-MI (LOW), medium-MI (MED) and high-MI (HIGH). MI: minimalist indexes. FFS: forefoot strikers. RFS: rearfoot strikers
Figure 2. Mean and SD values for ankle joint dynamic stiffness of FFS and RFS for the three phases of stance, in the three shoe conditions. ERP early rising phase, LRP late rising phase, DP descending phase. Shoes conditions are termed as low-MI (LOW), medium-MI (MED) and high-MI (HIGH). MI: minimalist indexes. FFS: forefoot strikers. RFS: rearfoot strikers
Applsci 09 04100 g002
Applsci 09 04100 g003 550
Figure 3. Ankle moment–angle plot. Group mean profiles comparison for low-MI, medium-MI and high-MI shoes. Insets report linear regression lines among early rising phase (ERP), late rising phase (LRP) and descending phase (DP).
Figure 3. Ankle moment–angle plot. Group mean profiles comparison for low-MI, medium-MI and high-MI shoes. Insets report linear regression lines among early rising phase (ERP), late rising phase (LRP) and descending phase (DP).
Applsci 09 04100 g003
Applsci 09 04100 g004 550
Figure 4. Mean and SD of ankle work for the three footwear conditions. Values are shown for positive and negative work for FFS and RFS. Dashed lines across the bars indicate the net work. Horizontal solid lines above and below the bar graph signify a statistically significant (p < 0.05) difference between footwear conditions.
Figure 4. Mean and SD of ankle work for the three footwear conditions. Values are shown for positive and negative work for FFS and RFS. Dashed lines across the bars indicate the net work. Horizontal solid lines above and below the bar graph signify a statistically significant (p < 0.05) difference between footwear conditions.
Applsci 09 04100 g004
Table
Table 1. Correlations between moment–angle loop parameters (Spearman correlation coefficient rs). * represents statistically significant correlations (p < 0.05); ** represents statistically significant correlations (p < 0.01). Wabs: work absorbed. Wnet: net work. Wprod: work produced. Wratio: work ratio.
Table 1. Correlations between moment–angle loop parameters (Spearman correlation coefficient rs). * represents statistically significant correlations (p < 0.05); ** represents statistically significant correlations (p < 0.01). Wabs: work absorbed. Wnet: net work. Wprod: work produced. Wratio: work ratio.
FFS RFS
Slope LRPSlope DPWabsWprodWnetWratioSlope LRPSlope DPWabsWprodWnetWratio
LOW
Slope ERP−0.160.41−0.410.04−0.46−0.390.190.20−0.270.600.31−0.01
Slope LRP 0.100.47−0.220.260.38 0.58−0.030.440.360.35
Slope DP −0.520.09−0.65 *−0.71 * −0.240.02−0.41−0.39
Wabs −0.69 *0.370.64 * −0.500.270.60
Wprod 0.360.03 0.600.30
Wnet 0.93 ** 0.88 **
MED
Slope ERP0.410.67 *−0.440.32−0.09−0.220.190.42−0.600.350.29−0.02
Slope LRP 0.76 *−0.100.13−0.29−0.21 0.67 *−0.01−0.07−0.020.20
Slope DP −0.67 *0.55−0.27−0.44 −0.05−0.43−0.47−0.24
Wabs −0.82 **0.080.50 −0.61−0.530.16
Wprod 0.39−0.08 0.99 **0.53
Wnet 0.86 ** 0.61
HIGH
Slope ERP0.95 **0.84 **−0.190.300.71 *0.130.09−0.020.040.210.270.31
Slope LRP 0.89 **−0.220.300.65 *0.08 0.92 **0.26−0.080.210.43
Slope DP −0.530.580.580.07 0.14−0.080.150.25
Wabs −0.93 **−0.010.38 −0.520.190.66 *
Wprod 0.26−0.16 0.64 *0.21
Wnet 0.61 0.79 **

Share and Cite

MDPI and ACS Style

Garofolini, A.; Taylor, S.; Mclaughlin, P.; Mickle, K.J.; Frigo, C.A. Ankle Joint Dynamic Stiffness in Long-Distance Runners: Effect of Foot Strike and Shoes Features. Appl. Sci. 2019, 9, 4100. https://doi.org/10.3390/app9194100

AMA Style

Garofolini A, Taylor S, Mclaughlin P, Mickle KJ, Frigo CA. Ankle Joint Dynamic Stiffness in Long-Distance Runners: Effect of Foot Strike and Shoes Features. Applied Sciences. 2019; 9(19):4100. https://doi.org/10.3390/app9194100

Chicago/Turabian Style

Garofolini, Alessandro, Simon Taylor, Patrick Mclaughlin, Karen J Mickle, and Carlo Albino Frigo. 2019. "Ankle Joint Dynamic Stiffness in Long-Distance Runners: Effect of Foot Strike and Shoes Features" Applied Sciences 9, no. 19: 4100. https://doi.org/10.3390/app9194100

APA Style

Garofolini, A., Taylor, S., Mclaughlin, P., Mickle, K. J., & Frigo, C. A. (2019). Ankle Joint Dynamic Stiffness in Long-Distance Runners: Effect of Foot Strike and Shoes Features. Applied Sciences, 9(19), 4100. https://doi.org/10.3390/app9194100

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop