Dependence-Analysis-Based Data-Refinement in Optical Scatterometry for Fast Nanostructure Reconstruction
Abstract
1. Introduction
2. Method
3. Experiments
3.1. Experimental Setup
3.2. Experimental Results on 2D Grating
3.3. Experimental Results on 3D Grating
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fang, F.Z.; Zhang, X.D.; Gao, W.; Guo, Y.B.; Byrne, G.; Hansen, H.N. Nanomanufacturing – Perspective and applications. CIRP Ann. Manuf. Technol. 2017, 66, 683–705. [Google Scholar] [CrossRef]
- Bundary, B.; Solecky, E.; Vaid, A.; Bello, A.F.; Dai, X. Metrology capabilities and needs for 7nm and 5nm logic nodes. Proc. SPIE 2017, 10145, 101450G. [Google Scholar]
- Sunkoju, S.; Schujman, S.; Dixit, D.; Diebold, A.; Li, J.; Collins, R.; Haldar, P. Spectroscopic ellipsometry studies of 3-stage deposition of CuIn1 _ XGaXSe2 on Mo-coated glass and stainless steel substrates. Thin Solid Films 2016, 606, 113–119. [Google Scholar] [CrossRef]
- Lereu, A.L.; Passian, A.; Farahi, R.H.; Abel-Tiberini, L.; Tetard, L.; Thundat, T. Spectroscopy and imaging of arrays of nanorods toward nanopolarimetry. Nanotechnology 2012, 23, 045701. [Google Scholar] [CrossRef][Green Version]
- Hansen, H.N.; Carneiro, K.; Haitjema, H.; Chiffre, L.D. Dimensional micro and nano metrology. CIRP Ann. Manuf. Technol. 2006, 55, 721–743. [Google Scholar] [CrossRef]
- Huang, H.T.; Kong, W.; Terry, F.L., Jr. Normal-incidence spectroscopic ellipsometry for critical dimension monitoring. Appl. Phys. Lett. 2001, 78, 3983–3985. [Google Scholar] [CrossRef]
- Matthias, W.; Johannes, E.; Jürgen, P.; Max, S.; Alexander, D.; Bernd, B. Metrology of nanoscale grating structures by UV scatterometry. Opt. Express 2017, 25, 2460–2468. [Google Scholar]
- Faruk, M.G.; Zangooie, S.; Angyal, M.; Watts, D.K.; Sendelbach, M.; Economikos, L.; Herrera, P.; Wilkins, R. Enabling scatterometry as an in-line measurement technique for 32nm BEOL application. IEEE Trans. Semicond. Manuf. 2011, 24, 499–512. [Google Scholar] [CrossRef]
- Kim, Y.N.; Paek, J.S.; Rabello, S.; Lee, S.; Hu, J.; Liu, Z.; Hao, Y.; McGahan, W. Device based in-chip critical dimension and overlay metrology. Opt. Express 2009, 17, 21336–21343. [Google Scholar] [CrossRef] [PubMed]
- Patrick, H.J.; Gemer, T.A.; Ding, Y.F.; Ro, H.W.; Richter, L.J.; Soles, C.L. Scatterometry for in situ measurement of pattern flow in nanoimprinted polymers. Appl. Phys. Lett. 2008, 93, 233105. [Google Scholar] [CrossRef]
- Paz, V.F.; Peterhänsel, S.; Frenner, K.; Osten, W. Solving the inverse grating problem by white light interference Fourier scatterometry. Light Sci. Appl. 2012, 1, e36. [Google Scholar]
- Chen, X.; Liu, S.; Zhang, C.; Jiang, H. Measurement configuration optimization for accurate grating reconstruction by Mueller matrix polarimetry. J. Micro/Nanolith. MEMS MOEMS 2013, 12, 033013. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, S.; Zhang, C.; Chen, X.; Dong, Z. Identification and reconstruction of diffraction structures in optical scatterometry using support vector machine method. J. Micro/Nanolith. MEMS MOEMS 2013, 12, 013004. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, S.; Shi, T.; Tang, Z. Fitting-determined formulation of effective medium approximation for 3D trench structures in model-based infrared reflectrometry. J. Opt. Soc. Am. A 2011, 28, 263–271. [Google Scholar] [CrossRef] [PubMed]
- Zallat, J.; Aïnouz, S.; Stoll, M.P. Optimal configurations for imaging polarimeters: Impact of image noise and systematic errors. J. Opt. A Pure Appl. Opt. 2006, 8, 807–814. [Google Scholar] [CrossRef]
- Zaharov, V.V.; Farahi, R.H.; Snyder, P.J.; Davison, B.H.; Passian, A. Karhunen-Loève treatment to remove noise and facilitate data analysis in sensing, spectroscopy and other applications. Analyst 2014, 139, 5927–5935. [Google Scholar] [CrossRef] [PubMed]
- Mu, T.; Chen, Z.; Zhang, C.; Liang, R. Optimal configurations of full-Stokes polarimeter with immunity to both Poisson and Gaussian noise. J. Opt. 2016, 18, 055702. [Google Scholar] [CrossRef]
- Logofǎtu, P.C. Sensitivity analysis of grating parameter estimation. Appl. Opt. 2002, 41, 7179–7186. [Google Scholar] [CrossRef]
- Ku, Y.; Wang, S.; Shyu, D.; Smith, N. Scatterometry-based metrology with feature region signature matching. Opt. Express 2006, 14, 8482–8491. [Google Scholar] [CrossRef]
- Vagos, P.; Hu, J.; Liu, Z.; Rabello, S. Uncertainty and sensitivity analysis and its applications in OCD measurement. Proc. SPIE 2009, 7272, 72721N. [Google Scholar]
- Dong, Z.; Liu, S.; Chen, X.; Shi, Y.; Zhang, C.; Jiang, H. Optimization of measurement configuration in optical scatterometry for one-dimensional nanostructures based on local sensitivity analysis. J Infrared Millim Waves 2016, 1, 116–122. [Google Scholar]
- Dong, Z.; Liu, S.; Chen, X.; Zhang, C. Determination of an optimal measurement configuration in optical scatterometry using global sensitivity analysis. Thin Solid Films 2014, 562, 16–23. [Google Scholar] [CrossRef]
- Twomey, S. Indirect measurements of atmospheric temperature profiles from satellites: II. Mathematical aspects of the inverse problem. Mon Weather Rev 1966, 96, 363–366. [Google Scholar] [CrossRef]
- Twomey, S.; Howell, H.B. Some Aspects of the Optical Estimation of Microstructure in Fog and Cloud. Appl. Opt. 1967, 6, 2125–2131. [Google Scholar] [CrossRef] [PubMed]
- Twomey, S. Information content in remote sensing. Appl. Opt. 1973, 13, 942–945. [Google Scholar] [CrossRef] [PubMed]
- Al-Assaad, R.A. Scatterometry for Semiconductor Sub-Micrometer and Nanometer Critical Dimension Metrology. Ph. D. Thesis, University of Texas, Austin, TX, USA, 2006. [Google Scholar]
- Kirsch, A. Uniqueness theorems in inverse scattering theory for periodic structures. Inverse Probl. 1994, 10, 145–152. [Google Scholar] [CrossRef]
- Kirsch, A. An Introduction to the Mathematical Theory of Inverse Problems, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Yang, J.; Zhang, B. Uniqueness results in the inverse scattering problem for periodic structures. Math. Method. Appl. Sci. 2012, 35, 828–838. [Google Scholar] [CrossRef]
- Chen, X.; Liu, S.; Gu, H.; Zhang, C. Formulation of error propagation and estimation in grating reconstruction by a dual-rotating compensator Mueller matrix polarimeter. Thin Solid Films 2014, 571, 653–659. [Google Scholar] [CrossRef]
- Collins, R.W.; Koh, J. Dual rotating-compensator multichannel ellipsometer: Instrument design for real-time Mueller matrix spectroscopy of surfaces and films. J. Opt. Soc. Am. A 1999, 16, 1997–2006. [Google Scholar] [CrossRef]
- Liu, S.; Chen, X.; Zhang, C. Development of a broadband Mueller matrix ellipsometer as a powerful tool for nanostructure metrology. Thin Solid Films 2015, 584, 176–185. [Google Scholar] [CrossRef]
- Moharam, M.G.; Pommet, D.A.; Grann, E.B.; Gaylord, T.K. Stable implementation of the rigorous coupled-wave analysis for surface-relief gratings: Enhanced transmittance matrix approach. J. Opt. Soc. Am. A 1995, 12, 1077–1086. [Google Scholar] [CrossRef]
- Li, L. New Formulation of the Fourier modal method for crossed surface-relief gratings. J. Opt. Soc. Am. A 1997, 14, 2758–2767. [Google Scholar] [CrossRef]
- Liu, S.; Ma, Y.; Chen, X.; Zhang, C. Estimation of the convergence order of rigorous coupled-wave analysis for binary gratings in optical critical dimension metrology. Opt. Eng. 2012, 51, 081504. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipies: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007; Chapter 15. [Google Scholar]
- Herzinger, C.M.; Johs, B.; Mcgahan, W.A.; Woollam, J.A.; Paulson, W. Ellipsometric determination of optical constants for silicon and thermally grown silicon dioxide via a multi-sample, multi-wavelength, multi-angle investigation. J. Appl. Phys. 1998, 83, 3323–3336. [Google Scholar] [CrossRef]
- Forouhi, A.R.; Bloomer, I. Optical properties of crystalline semiconductors and dielectrics. Phys. Rev. B 1988, 38, 1865–1874. [Google Scholar] [CrossRef] [PubMed]
- Jellison, G.E., Jr.; Modine, F.A. Parameterization of the optical functions of amorphous materials in the interband region. Appl. Phys. Lett. 1996, 69, 371–373. [Google Scholar] [CrossRef]


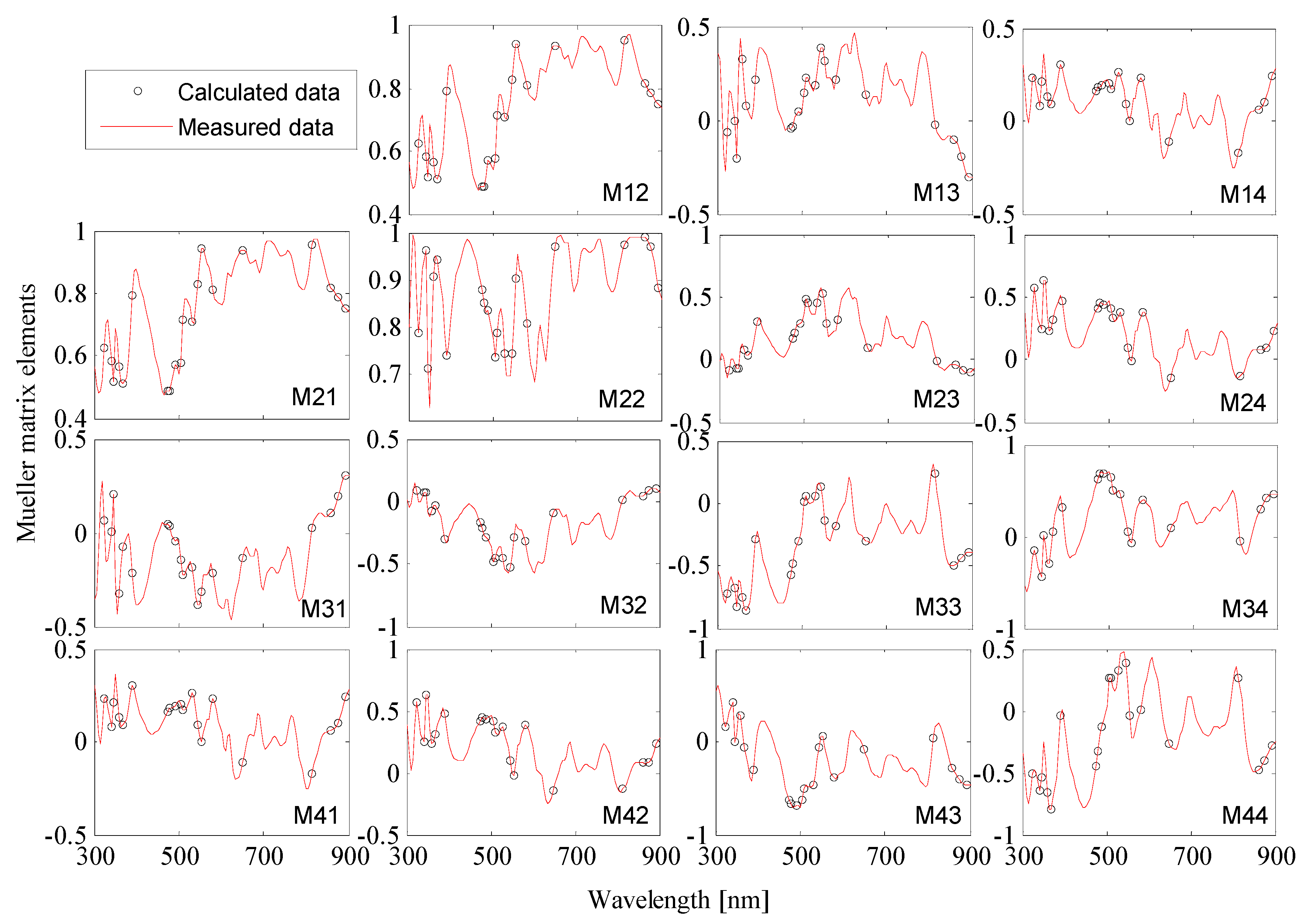
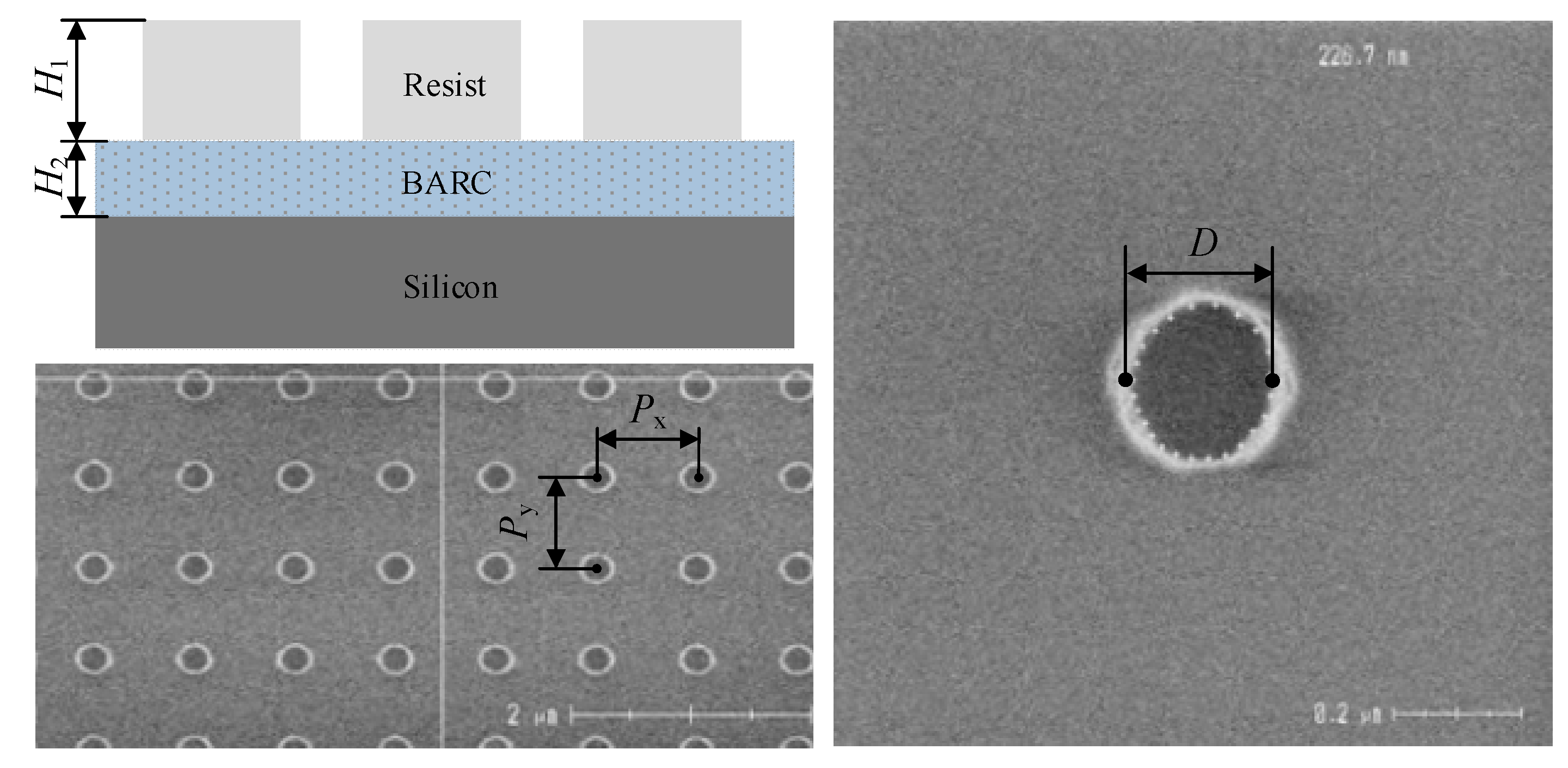
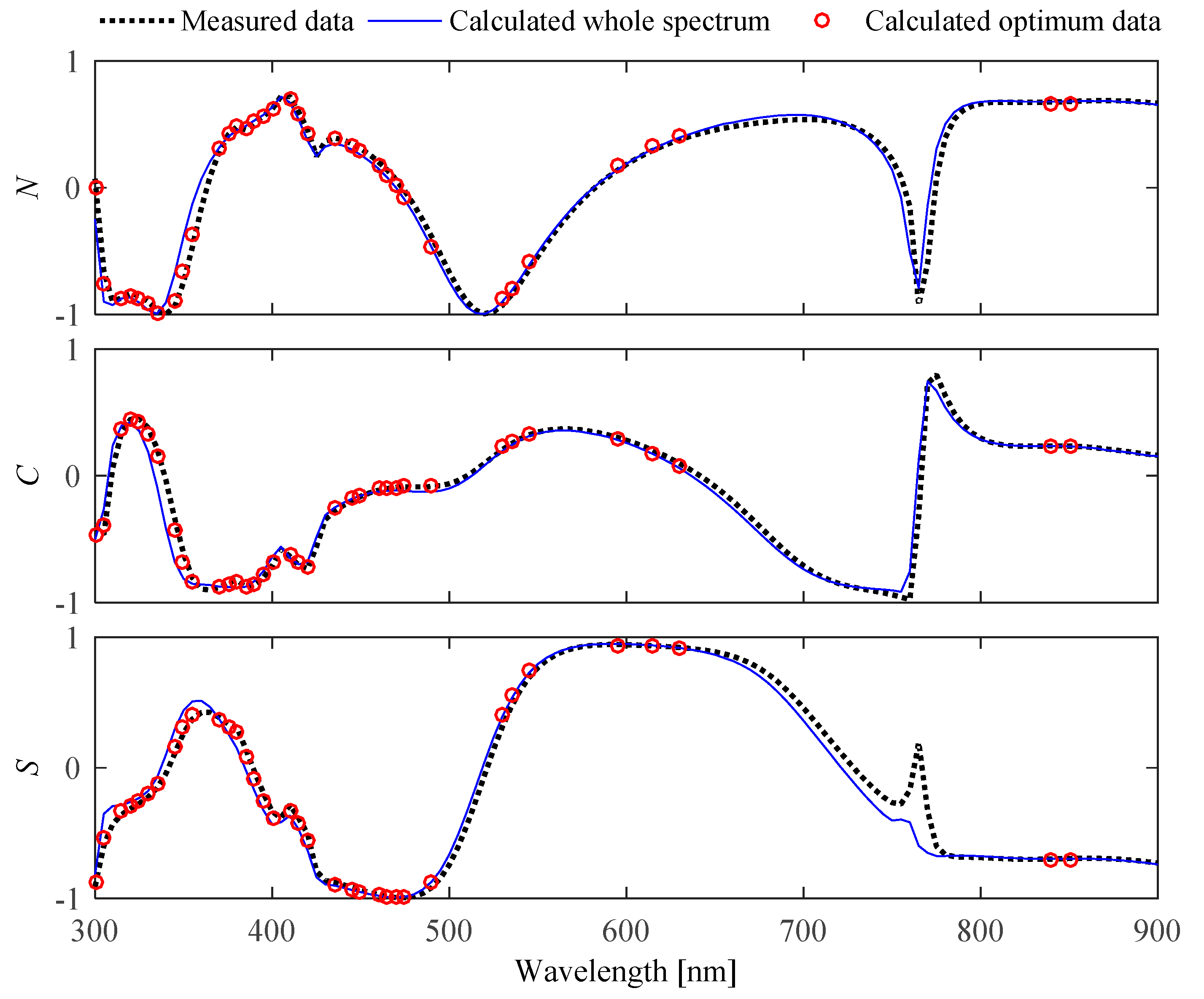
| Measuring Mode | Dimensions (nm/°) | RMSE | Time (s) | ||
|---|---|---|---|---|---|
| W /nm | H /nm | SWA /° | |||
| SEM | 350.3 ± 4.74 | 472.1 ± 4.87 | 87.63 ± 0.611 | — | — |
| Full spectrum | 347.3 ± 0.17 | 468.9 ± 0.20 | 86.89 ± 0.019 | 9.44 | 548 |
| Optimal (19) | 347.4 ± 0.15 | 476.9 ± 0.12 | 87.27 ± 0.008 | 8.27 | 143 |
| Random (19) | 345.2 ± 0.74 | 486.4 ± 0.86 | 86.31 ± 0.103 | 13.59 | 225 |
| Measuring Mode | Dimensions (nm) | RMSE | Time (hour) | ||
|---|---|---|---|---|---|
| D /nm | H1 /nm | H2 /nm | |||
| SEM | 226.7 ± 28.32 | 355.1 ± 2.05 | 104.3 ± 1.30 | — | — |
| Full spectrum | 249.8 ± 2.56 | 344.3 ± 1.44 | 107.6 ± 0.62 | 28.77 | 14 |
| Optimal (36) | 250.4 ± 2.21 | 343.9 ± 1.03 | 106.4 ± 0.51 | 17.45 | 4.5 |
| Random (36) | 262.4 ± 2.38 | 338.7 ± 2.42 | 108.1 ± 0.89 | 26.50 | 6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Z.; Chen, X.; Wang, X.; Shi, Y.; Jiang, H.; Liu, S. Dependence-Analysis-Based Data-Refinement in Optical Scatterometry for Fast Nanostructure Reconstruction. Appl. Sci. 2019, 9, 4091. https://doi.org/10.3390/app9194091
Dong Z, Chen X, Wang X, Shi Y, Jiang H, Liu S. Dependence-Analysis-Based Data-Refinement in Optical Scatterometry for Fast Nanostructure Reconstruction. Applied Sciences. 2019; 9(19):4091. https://doi.org/10.3390/app9194091
Chicago/Turabian StyleDong, Zhengqiong, Xiuguo Chen, Xuanze Wang, Yating Shi, Hao Jiang, and Shiyuan Liu. 2019. "Dependence-Analysis-Based Data-Refinement in Optical Scatterometry for Fast Nanostructure Reconstruction" Applied Sciences 9, no. 19: 4091. https://doi.org/10.3390/app9194091
APA StyleDong, Z., Chen, X., Wang, X., Shi, Y., Jiang, H., & Liu, S. (2019). Dependence-Analysis-Based Data-Refinement in Optical Scatterometry for Fast Nanostructure Reconstruction. Applied Sciences, 9(19), 4091. https://doi.org/10.3390/app9194091






