Mathematical Model and Numerical Simulation for Tissue Growth on Bioscaffolds
Abstract
1. Introduction
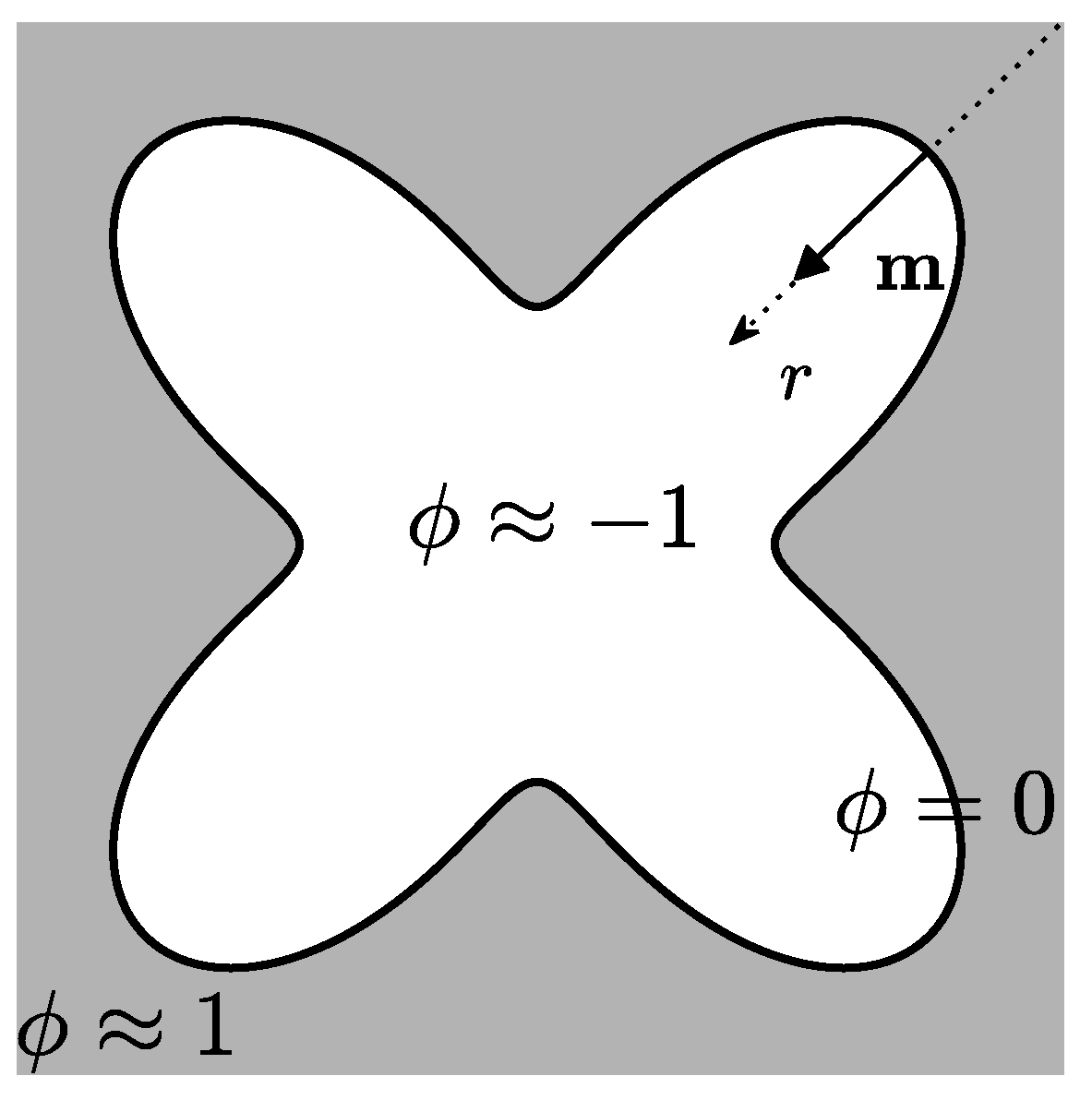
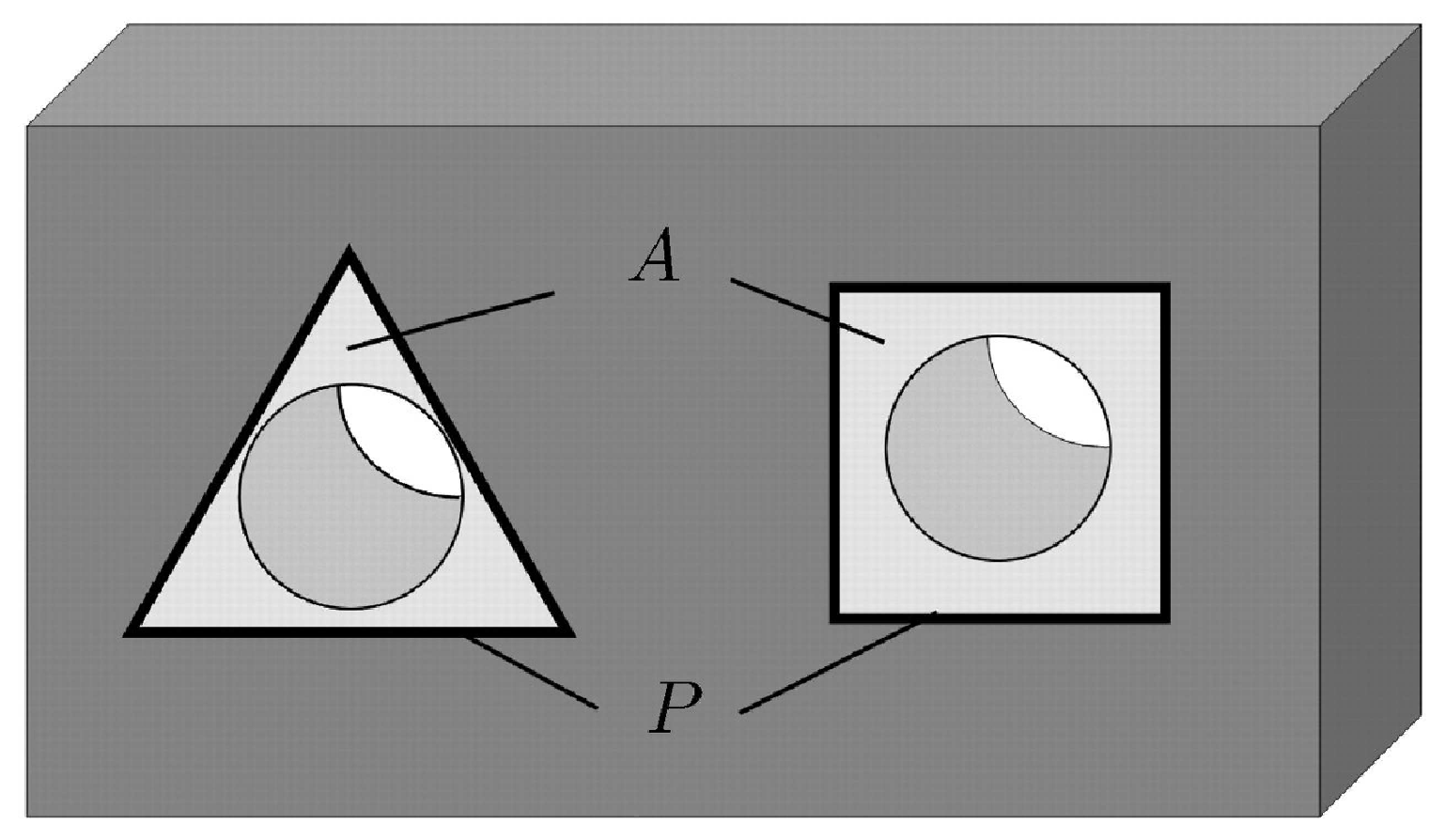
2. Mathematical Model
3. Numerical Solution
4. Numerical Experiments
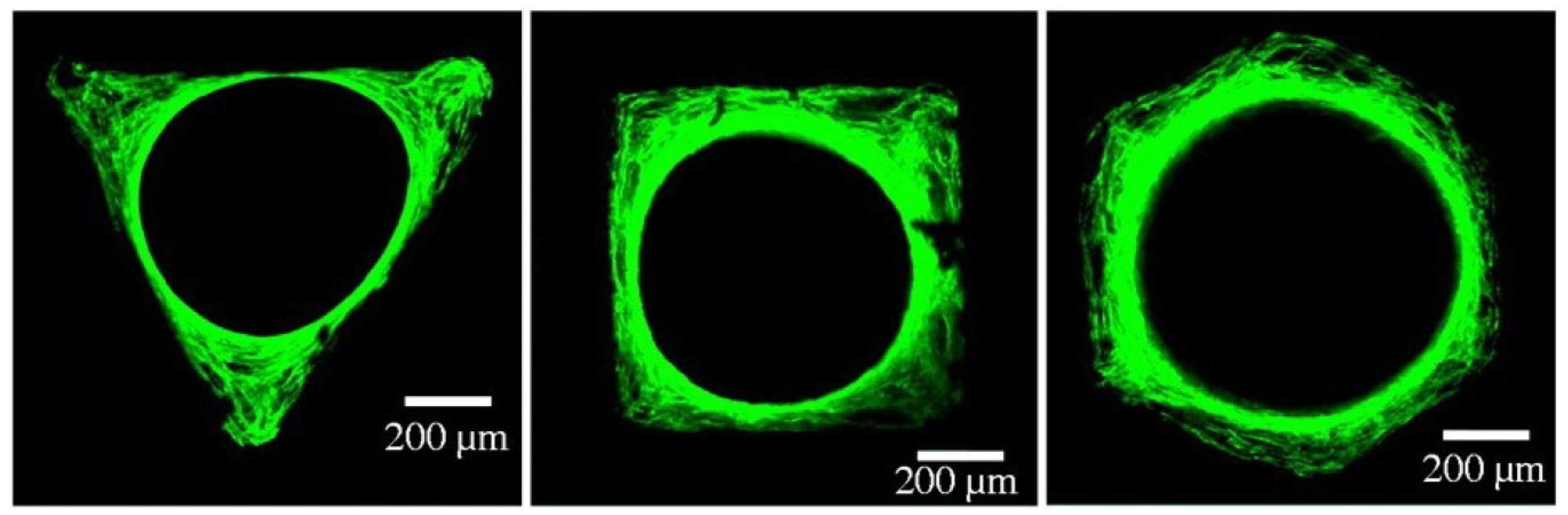
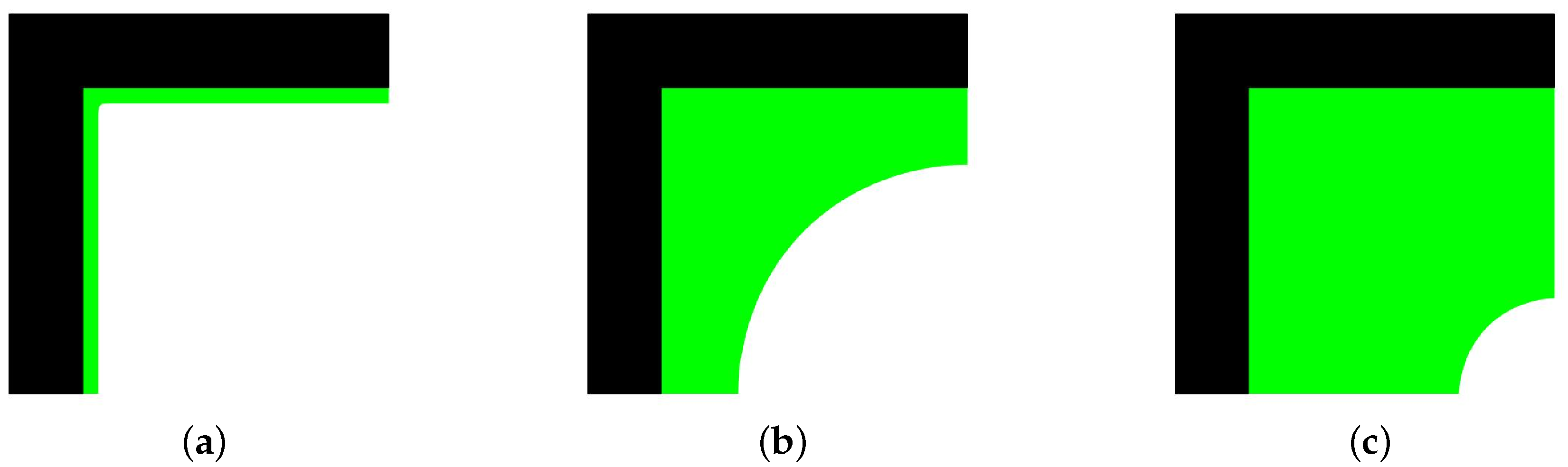
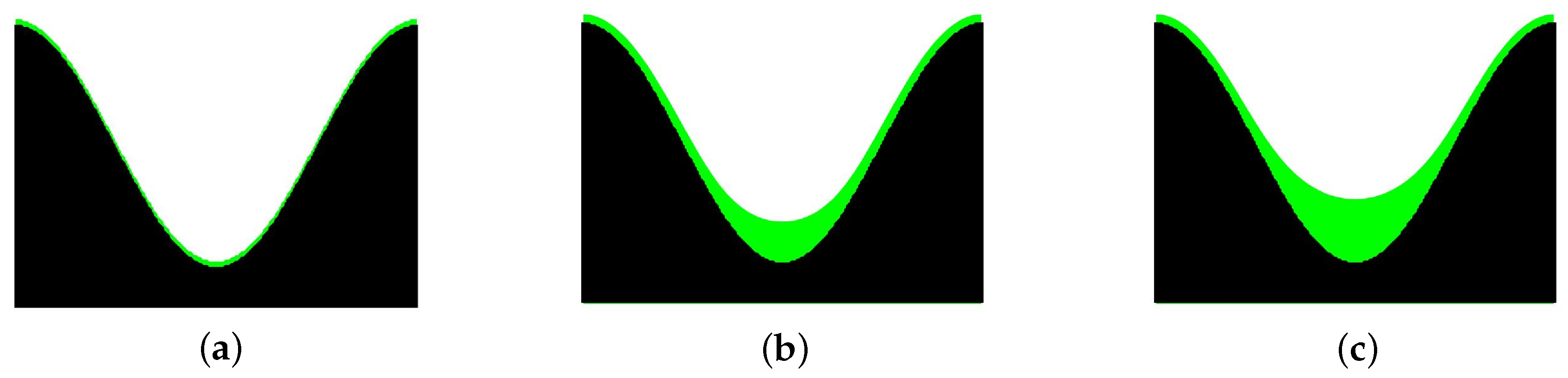
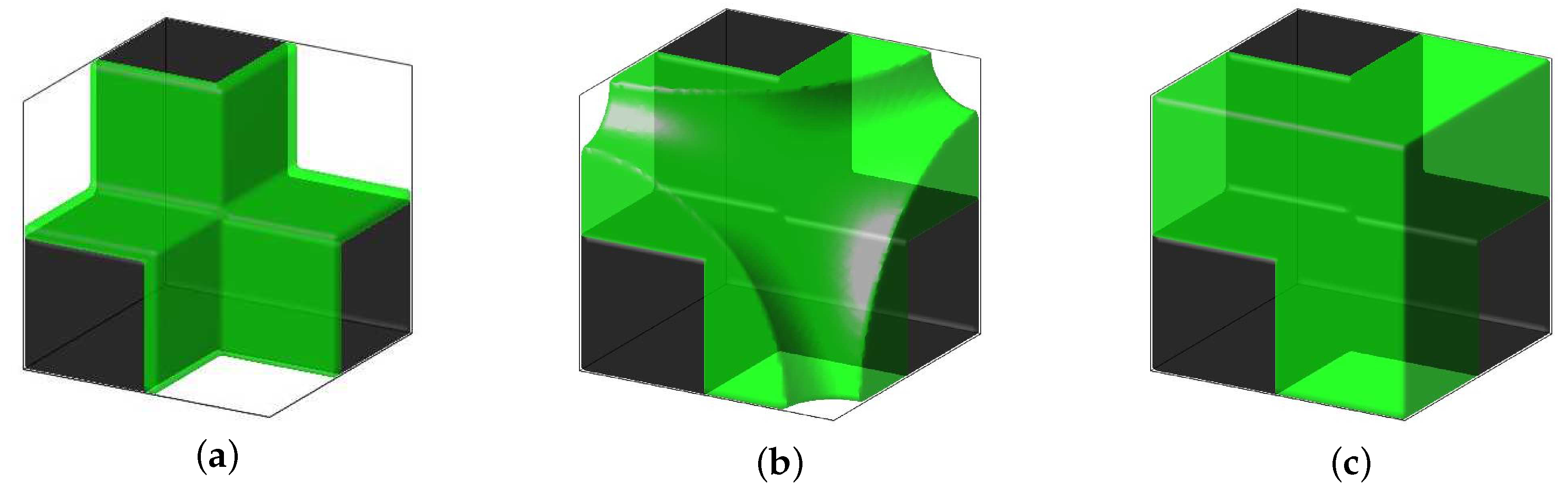
4.1. Simulation of Tissue Growth on Scaffold In 2D
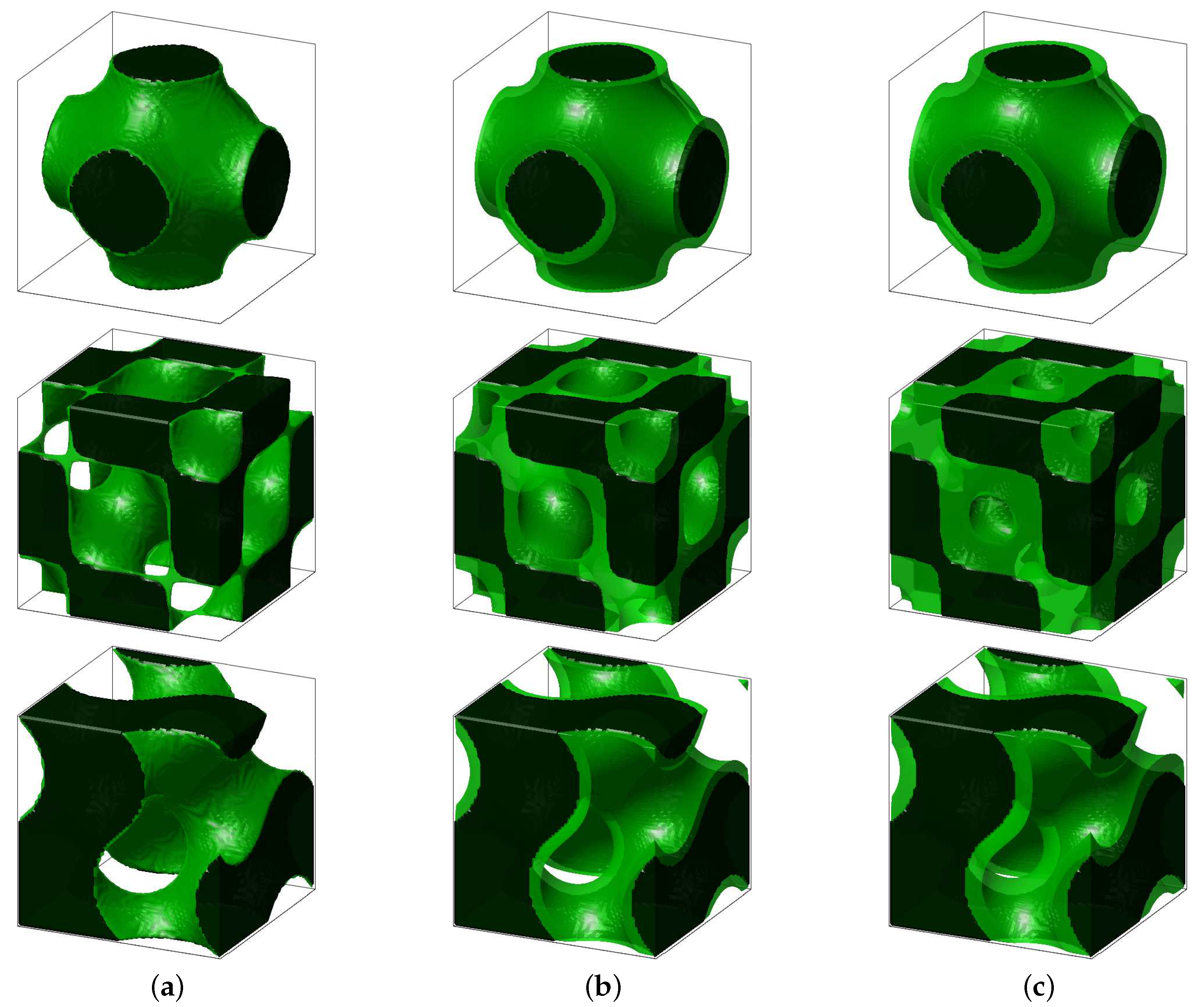
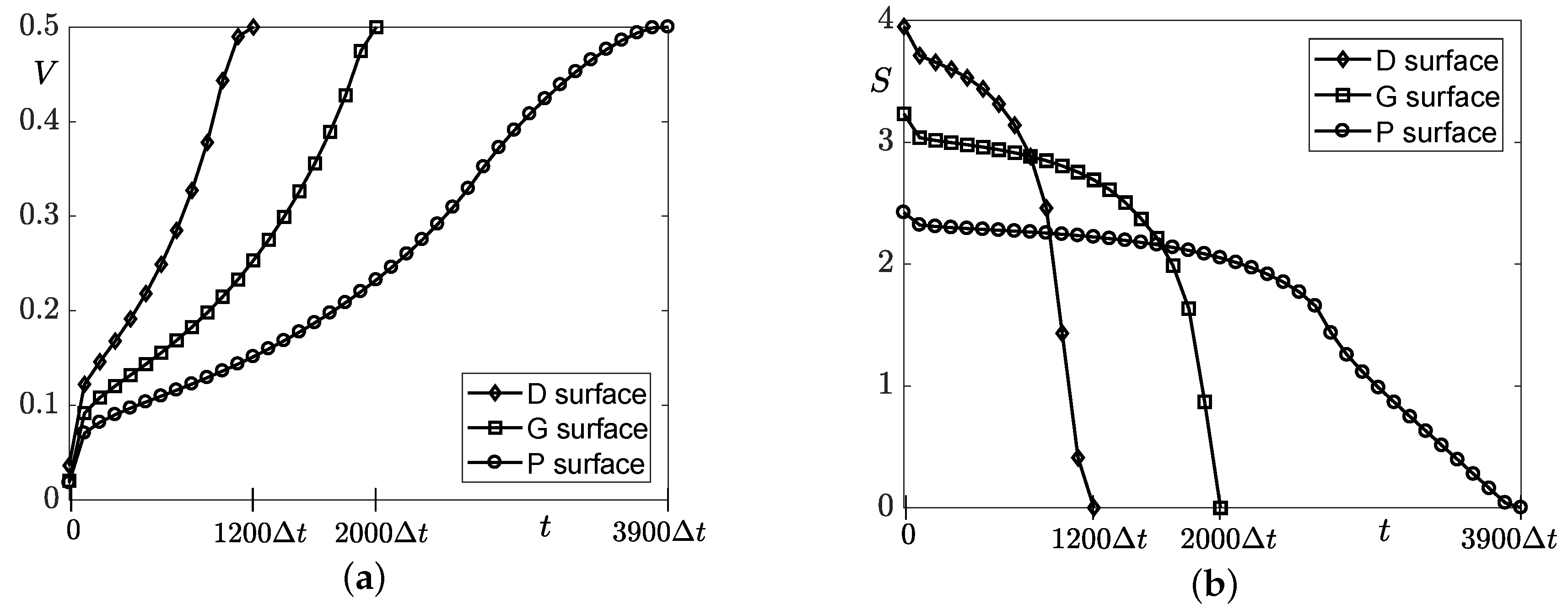
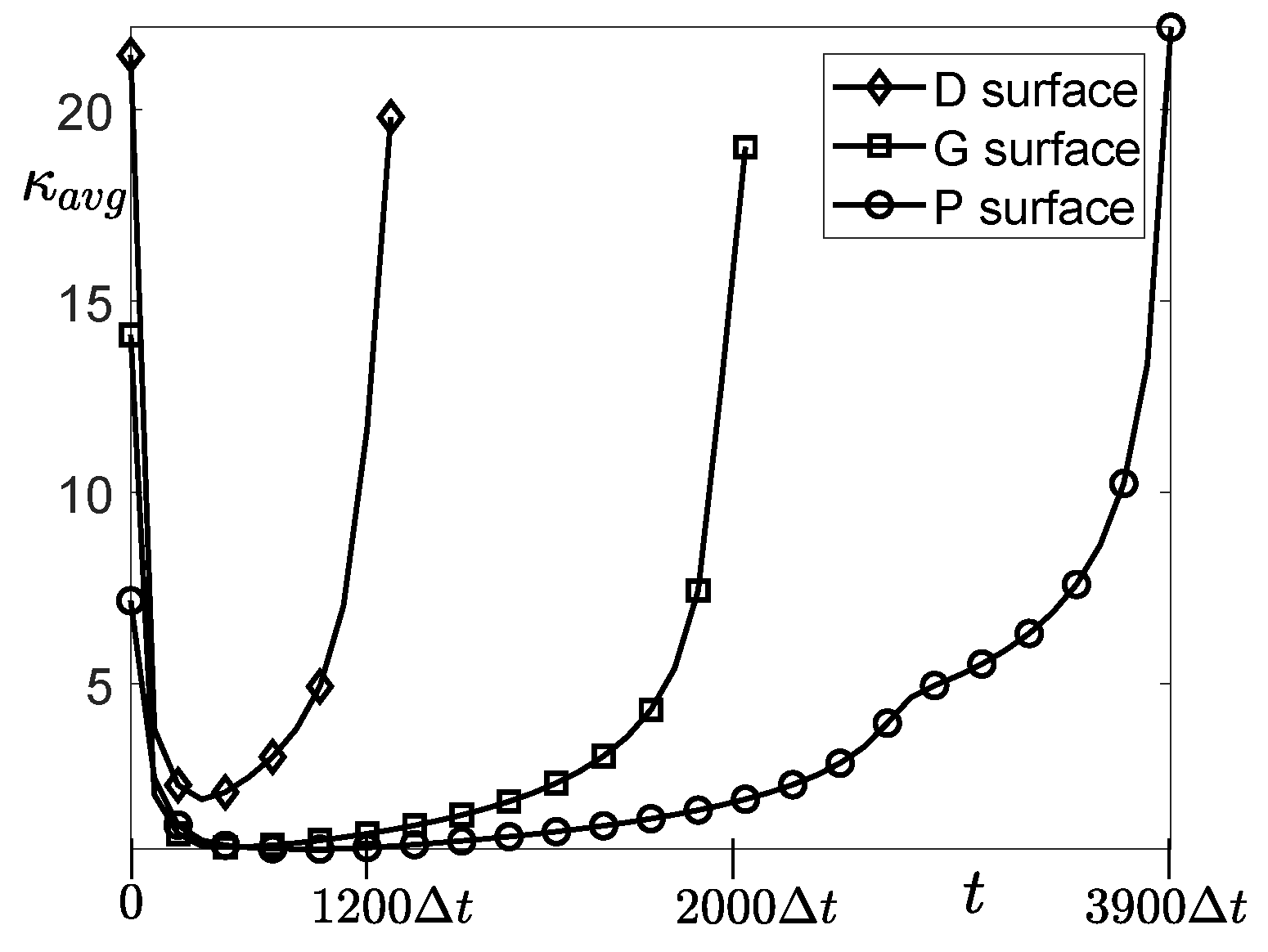
4.2. Simulation of Tissue Growth on Scaffold In 3D
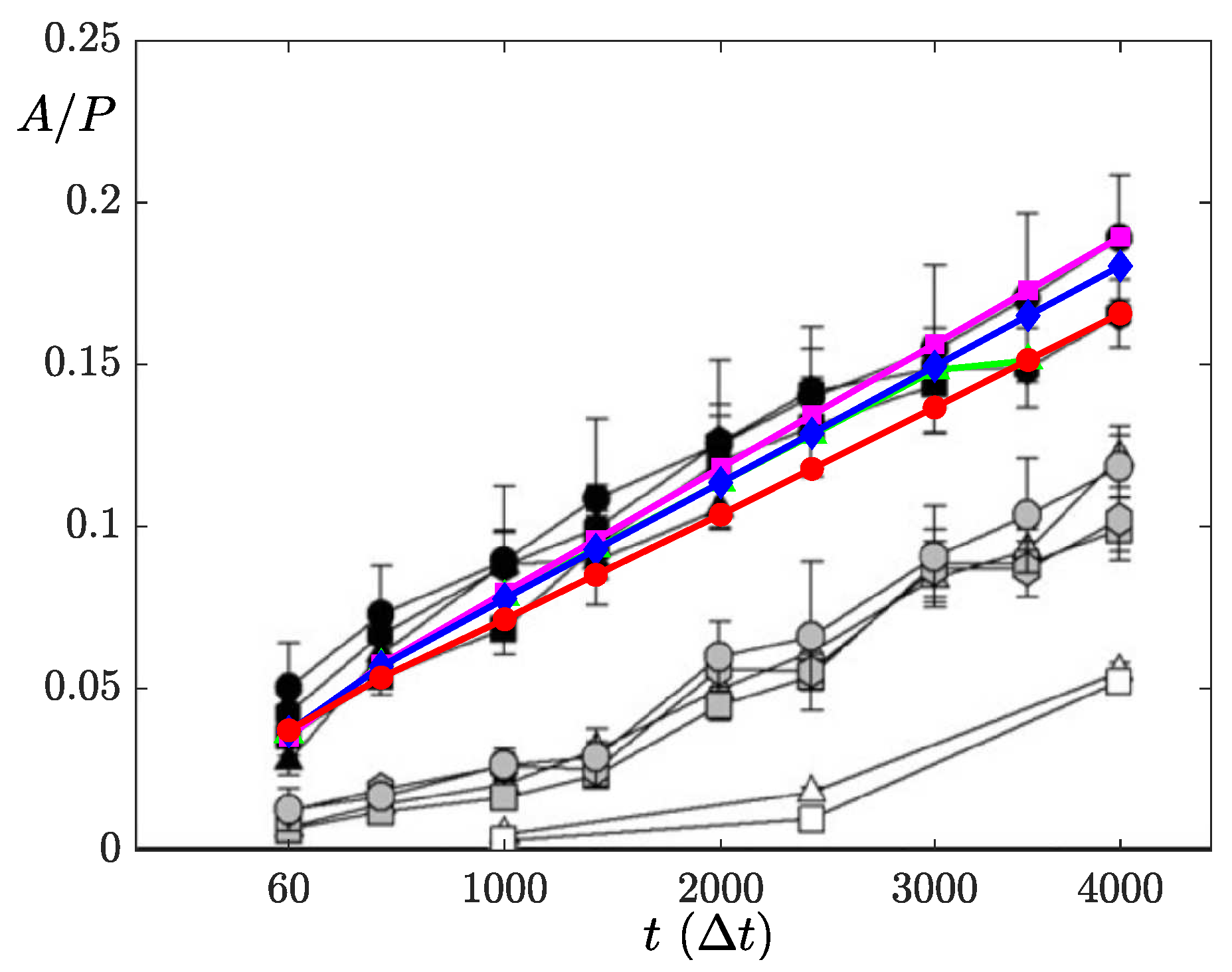
4.3. Comparison between Experiments and Simulations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Carlier, A.; van Gastel, N.; Geris, L.; Carmeliet, G.; Van Oosterwyck, H. Size Does Matter: An Integrative In Vivo-In Silico Approach for the Treatment of Critical Size Bone Defects. PLoS Comput. Biol. 2014, 10, e1003888. [Google Scholar] [CrossRef] [PubMed]
- Castro, A.P.G.; Lacroix, D. Micromechanical study of the load transfer in a polycaprolactone-collagen hybrid scaffold when subjected to unconfined and confined compression. Biomech. Model. Mechanobiol. 2018, 17, 531–541. [Google Scholar] [CrossRef] [PubMed]
- Martin, J.Y.; Schwartz, Z.; Hummert, T.W.; Schraub, D.M.; Simpson, J.; Lankford, J., Jr.; Dean, D.D.; Cochran, D.L.; Boyan, B.D. Effect of titanium surface roughness on proliferation, differentiation, and protein synthesis of human osteoblast-like cells (MG63). J. Biomed. Mater. Res. 1995, 29, 389–401. [Google Scholar] [CrossRef] [PubMed]
- Deligianni, D.D.; Katsala, N.D.; Koutsoukos, P.G.; Missirlis, Y.F. Effect of surface roughness of hydroxyapatite on human bone marrow cell adhesion, proliferation, differentiation and detachment strength. Biomaterials 2000, 22, 87–96. [Google Scholar] [CrossRef]
- Guyot, Y.; Papantoniou, I.; Luyten, F.P.; Geris, L. Coupling curvature-dependent and shear stress-stimulated neotissue growth in dynamic bioreactor cultures: A 3D computational model of a complete scaffold. Biomech. Model. Mechanobiol. 2016, 15, 169–180. [Google Scholar] [CrossRef] [PubMed]
- Dunn, G.A.; Heath, J.P. A new hypothesis of contact guidance in tissue cells. Exp. Cell Res. 1976, 101, 1–14. [Google Scholar] [CrossRef]
- Curtis, A.S.G.; Varde, M. Control of cell behavior: Topological factors. J. Natl. Cancer Inst. 1964, 33, 15–26. [Google Scholar] [PubMed]
- Alias, M.A.; Buenzli, P.R. Modeling the effect of curvature on the collective behavior of cells growing new tissue. Biophys. J. 2017, 112, 193–204. [Google Scholar] [CrossRef]
- Egan, P.F.; Shea, K.A.; Ferguson, S.J. Simulated tissue growth for 3D printed scaffolds. Biomech. Model. Mechanobiol. 2018, 17, 1481–1495. [Google Scholar] [CrossRef]
- Egan, P.F.; Ferguson, S.J.; Shea, K. Design of hierarchical three-dimensional printed scaffolds considering mechanical and biological factors for bone tissue engineering. J. Mech. Des. 2017, 139, 061401. [Google Scholar] [CrossRef]
- Bidan, C.M.; Wang, F.M.; Dunlop, J.W.C. A three-dimensional model for tissue deposition on complex surfaces. Comput. Methods Biomech. Biomed. Eng. 2013, 16, 1056–1070. [Google Scholar] [CrossRef] [PubMed]
- Olivares, A.L.; Marsal, É.; Planell, J.A.; Lacroix, D. Finite element study of scaffold architecture design and culture conditions for tissue engineering. Biomaterials 2009, 30, 6142–6149. [Google Scholar] [CrossRef]
- Zadpoor, A.A. Bone tissue regeneration: The role of scaffold geometry. Biomater. Sci. 2015, 3, 231–245. [Google Scholar] [CrossRef] [PubMed]
- Paris, M.; Götz, A.; Hettrich, I.; Bidan, C.M.; Dunlop, J.W.C.; Razi, H.; Zizak, I.; Hutmacher, D.W.; Fratzl, P.; Duda, G.N.; et al. Scaffold curvature-mediated novel biomineralization process originates a continuous soft tissue-to-bone interface. Acta Biomater. 2017, 60, 64–80. [Google Scholar] [CrossRef] [PubMed]
- Vassaux, M.; Milan, J.L. Stem cell mechanical behaviour modelling: Substrate’s curvature influence during adhesion. Biomech. Model. Mechanobiol. 2017, 16, 1295–1308. [Google Scholar] [CrossRef]
- De Aza, P.; Rodriguez, M.; Gehrke, S.; Maté-Sánchez de Val, J.E.; Calvo-Guirado, J. A Si-αTCP Scaffold for Biomedical Applications: An Experimental Study Using the Rabbit Tibia Model. Appl. Sci. 2017, 7, 706. [Google Scholar] [CrossRef]
- Ishikawa, S.; Iijima, K.; Sasaki, K.; Hashizume, M.; Kawabe, M.; Otsuka, H. Cartilage Differentiation of Bone Marrow-Derived Mesenchymal Stem Cells in Three-Dimensional Silica Nonwoven Fabrics. Appl. Sci. 2018, 8, 1398. [Google Scholar] [CrossRef]
- Rumpler, M.; Woesz, A.; Dunlop, J.W.C.; van Dongen, J.T.; Fratzl, P. The effect of geometry on three-dimensional tissue growth. J. R. Soc. Interface. 2008, 5, 1173–1180. [Google Scholar] [CrossRef]
- Allen, S.M.; Cahn, J.W. A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Mater. 1979, 27, 1085–1095. [Google Scholar] [CrossRef]
- Yang, X. Efficient linear, stabilized, second-order time marching schemes for an anisotropic phase field dendritic crystal growth model. Comput. Methods Appl. Mech. Eng. 2019, 347, 316–339. [Google Scholar] [CrossRef]
- Jing, X.; Wang, Q. Linear second order energy stable schemes of phase field model with nonlocal constraints for crystal growth. arXiv, 2018; arXiv:1812.04504. [Google Scholar]
- Li, Y.; Jeong, D.; Choi, J.; Lee, S.; Kim, J. Fast local image inpainting based on the Allen–Cahn model. Digit. Signal Process. 2015, 37, 65–74. [Google Scholar] [CrossRef]
- Li, Y.; Kim, J. An unconditionally stable hybrid method for image segmentation. Appl. Numer. Math. 2014, 82, 32–43. [Google Scholar] [CrossRef]
- Laux, T.; Simon, T.M. Convergence of the Allen–Cahn equation to multiphase mean curvature flow. Commun. Pure Appl. Math. 2018, 71, 1597–1647. [Google Scholar] [CrossRef]
- Liu, H.; Cheng, A.; Wang, H.; Zhao, J. Time-fractional Allen–Cahn and Cahn–Hilliard phase-field models and their numerical investigation. Comput. Math. Appl. 2018, 76, 1876–1892. [Google Scholar] [CrossRef]
- Lee, D.S.; Kim, J. Mean curvature flow by the Allen–Cahn equation. Eur. J. Appl. Math. 2015, 26, 535–559. [Google Scholar] [CrossRef]
- Jeong, D.; Kim, J. An explicit hybrid finited difference scheme for the Allen-Cahn equation. J. Comput. Appl. Math. 2018, 340, 247–255. [Google Scholar] [CrossRef]
- Kim, J. Phase-field models for multi-component fluid flows. Commun. Comput. Phys. 2012, 12, 613–661. [Google Scholar] [CrossRef]
- Castro, A.P.G.; Pires, T.; Santos, J.E.; Gouveia, B.P.; Fernandes, P.R. Permeability versus design in TPMS scaffolds. Materials 2019, 12, 1313. [Google Scholar] [CrossRef]
- Lee, H.G.; Kim, J. Regularized Dirac delta functions for phase field models. Int. J. Numer. Methods Eng. 2012, 91, 269–288. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.G.; Park, J.; Yoon, S.; Lee, C.; Kim, J. Mathematical Model and Numerical Simulation for Tissue Growth on Bioscaffolds. Appl. Sci. 2019, 9, 4058. https://doi.org/10.3390/app9194058
Lee HG, Park J, Yoon S, Lee C, Kim J. Mathematical Model and Numerical Simulation for Tissue Growth on Bioscaffolds. Applied Sciences. 2019; 9(19):4058. https://doi.org/10.3390/app9194058
Chicago/Turabian StyleLee, Hyun Geun, Jintae Park, Sungha Yoon, Chaeyoung Lee, and Junseok Kim. 2019. "Mathematical Model and Numerical Simulation for Tissue Growth on Bioscaffolds" Applied Sciences 9, no. 19: 4058. https://doi.org/10.3390/app9194058
APA StyleLee, H. G., Park, J., Yoon, S., Lee, C., & Kim, J. (2019). Mathematical Model and Numerical Simulation for Tissue Growth on Bioscaffolds. Applied Sciences, 9(19), 4058. https://doi.org/10.3390/app9194058





