A Mesh-Based Monte Carlo Study for Investigating Structural and Functional Imaging of Brain Tissue Using Optical Coherence Tomography
Abstract
Featured Application
Abstract
1. Introduction
2. Methods
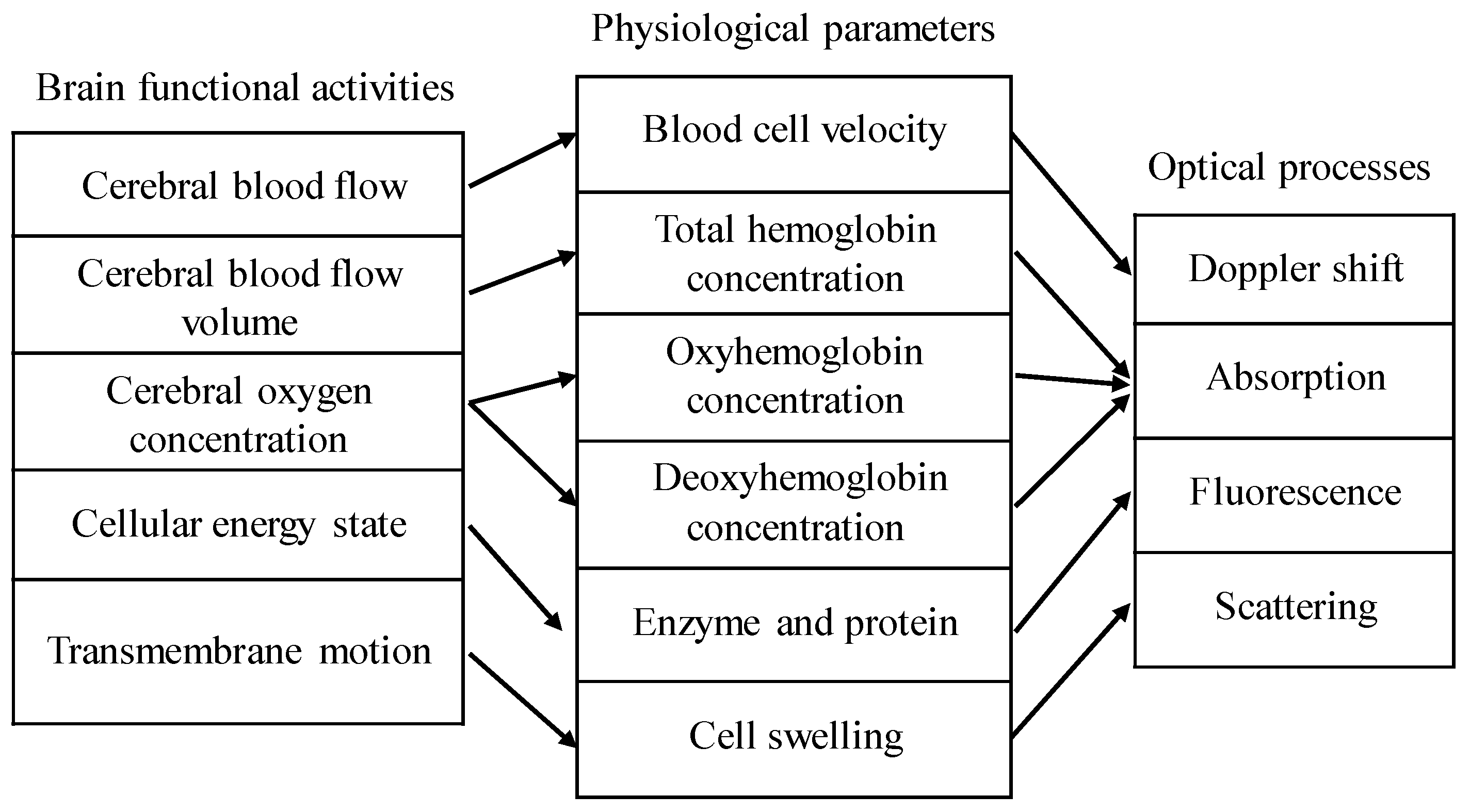
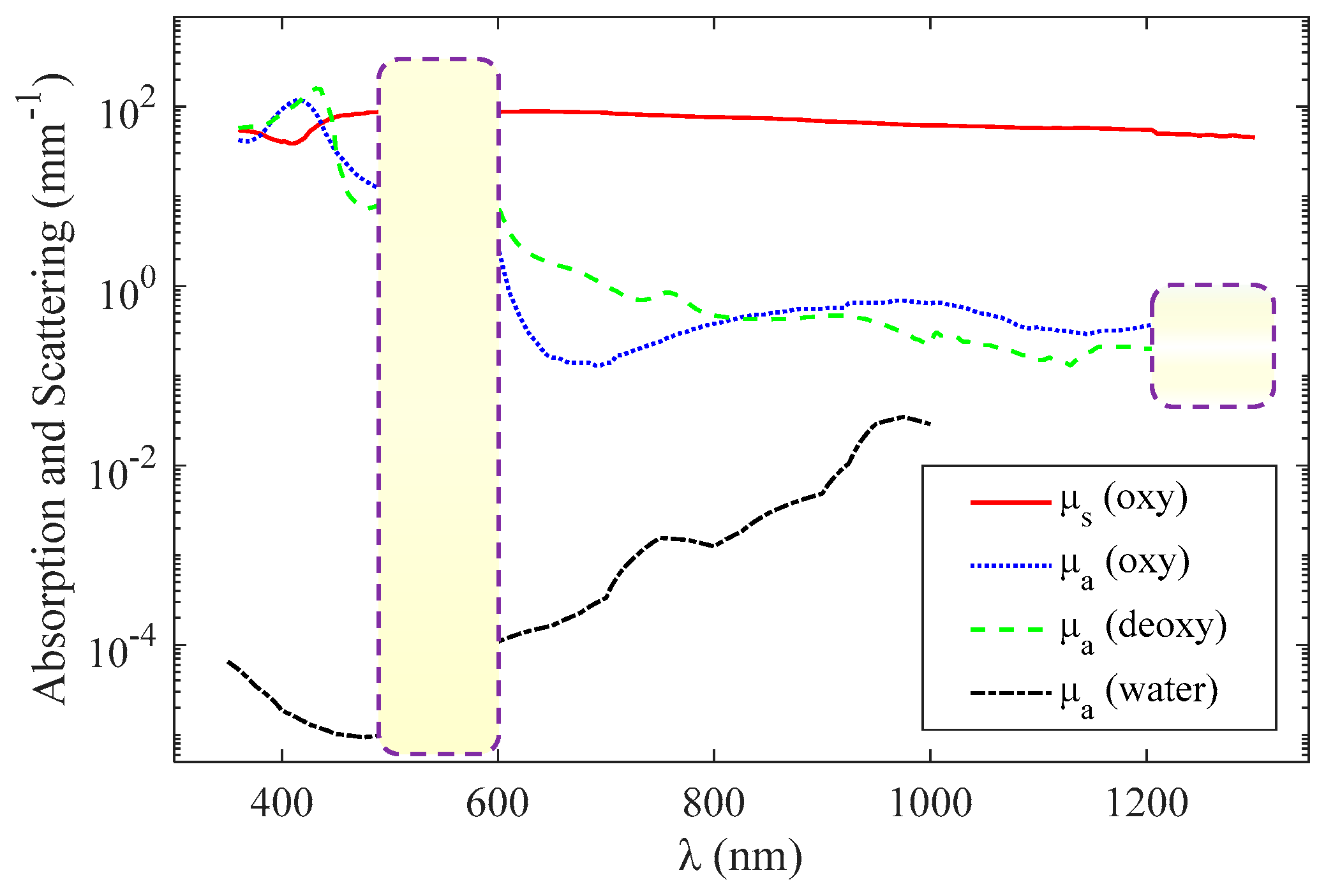
2.1. Structural and Functional Imaging Based on OCT
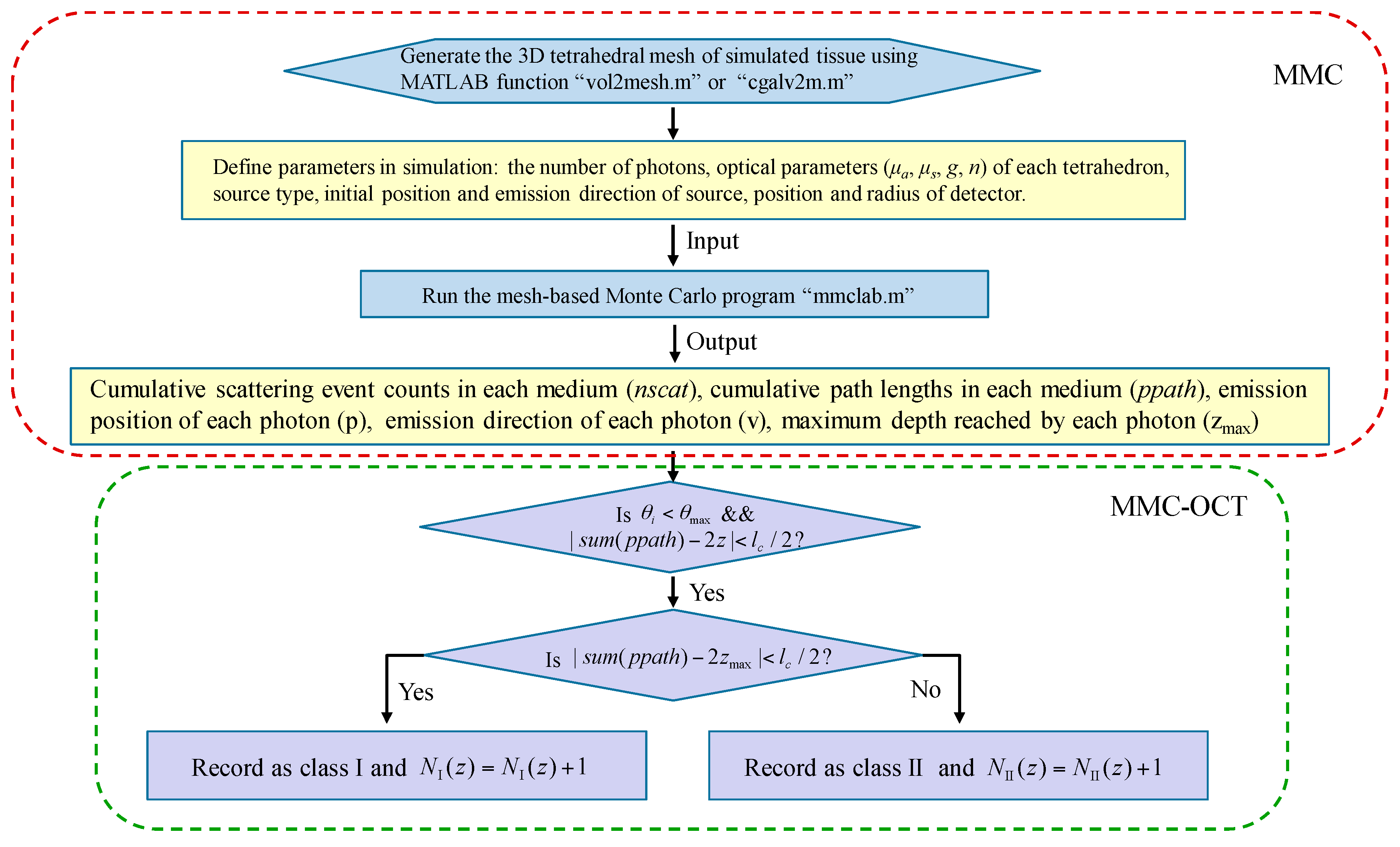
2.2. Mesh-Based Monte Carlo for Optical Coherence Tomography (MMC-OCT)
3. Results and Discussions
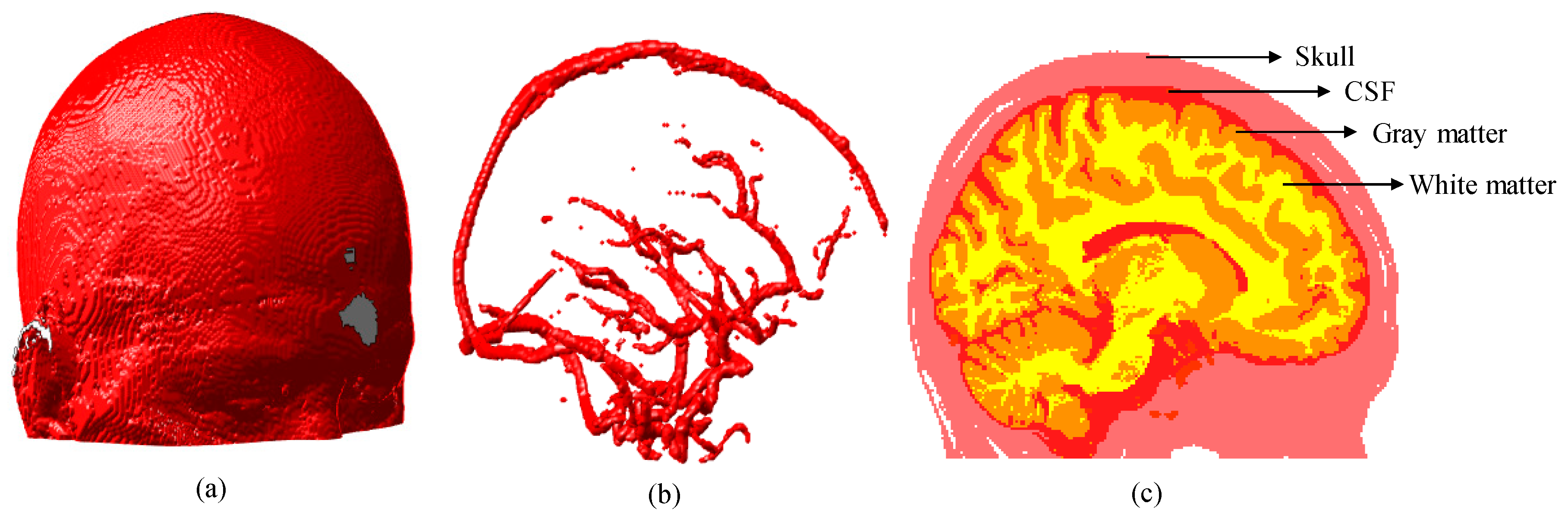
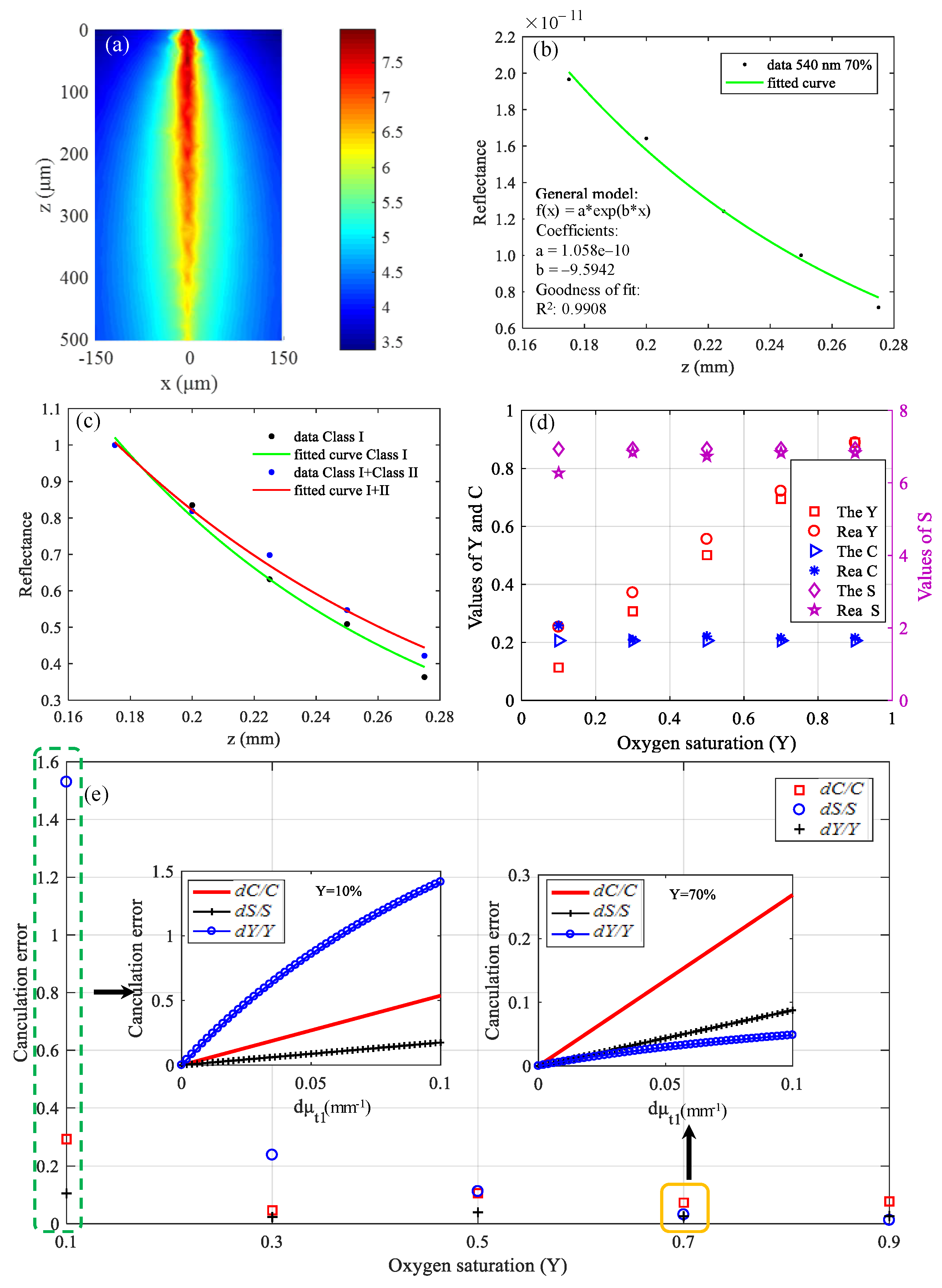
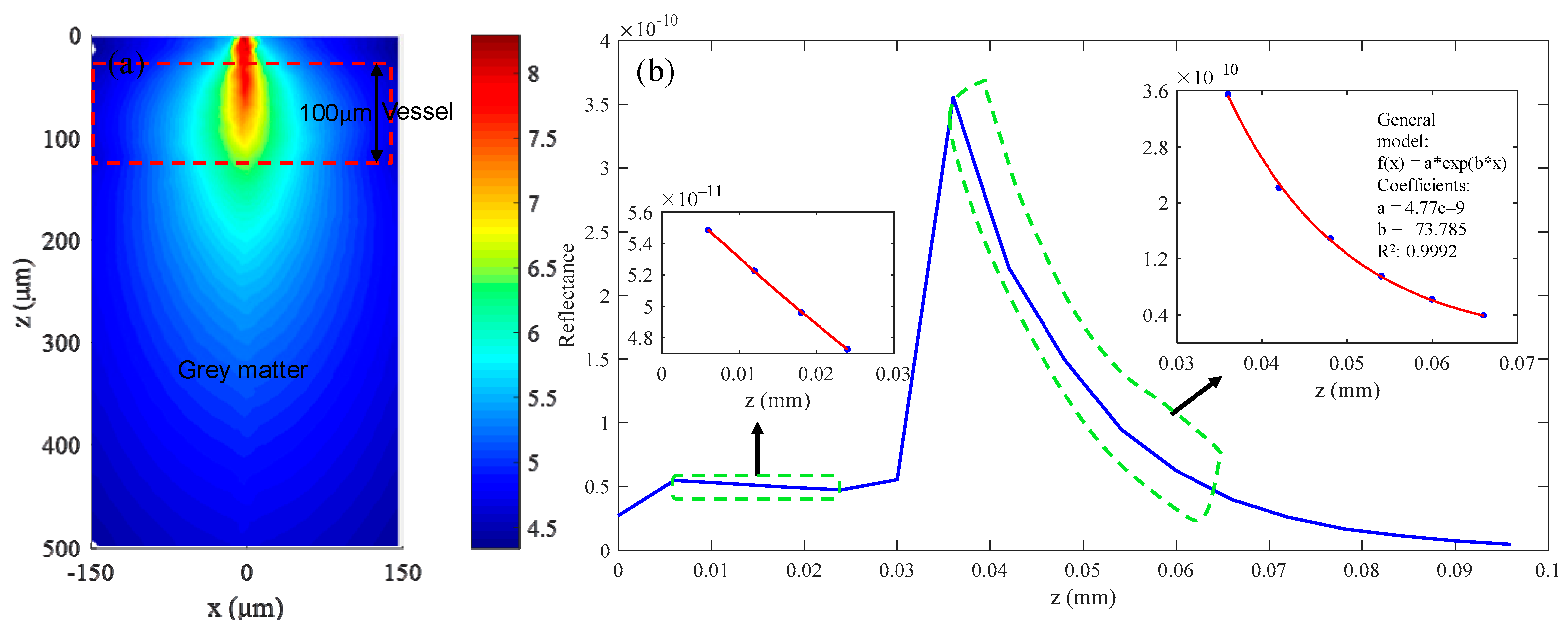
3.1. Simulation Results of Brain Structural Imaging
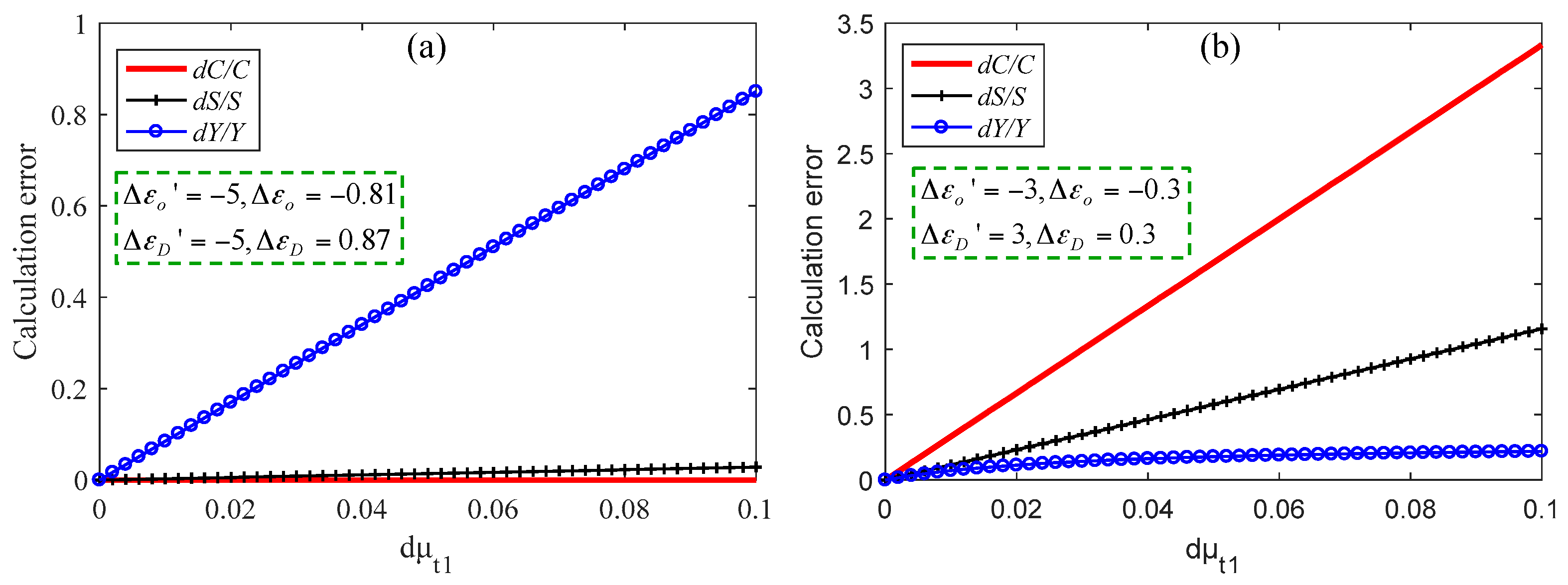
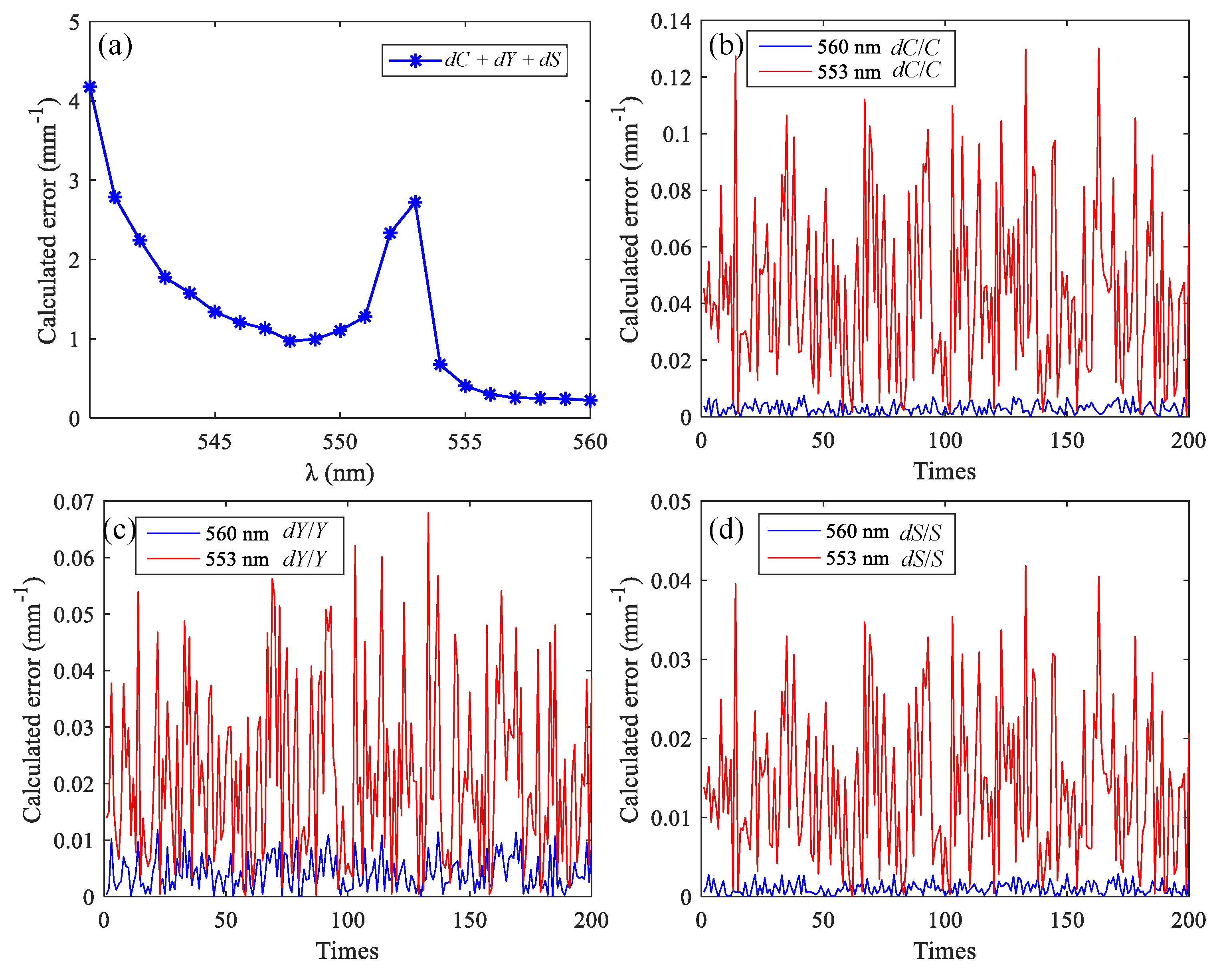
3.2. Simulation Results of Brain Functional Sensing
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xie, Y.; Harsan, L.A.; Bienert, T.; Kirch, R.D.; Von, E.D.; Hofmann, U.G. Qualitative and quantitative evaluation of in vivo SD-OCT measurement of rat brain. Biomed. Opt. Express 2017, 8, 593–607. [Google Scholar] [PubMed]
- Choi, W.J.; Wang, R.K. Optical coherence tomography imaging of cranial meninges post brain injury in vivo. Chin. Opt. Lett. 2017, 15, 16–19. [Google Scholar]
- Tearney, G.J.; Fukumura, D.; Jain, R.K.; Vakoc, B.J.; Lanning, R.M.; Tyrrell, J.A.; Padera, T.P.; Bartlett, L.A.; Stylianopoulos, T.; Munn, L.L. Three-dimensional microscopy of the tumor microenvironment in vivo using optical frequency domain imaging. Nat. Med. 2009, 15, 1219. [Google Scholar]
- Hillman, C.E.M. Optical brain imaging in vivo: Techniques and applications from animal to man. J. Biomed. Opt. 2007, 12, 051402. [Google Scholar] [CrossRef] [PubMed]
- Villringer, A.; Chance, B. Non-invasive optical spectroscopy and imaging of human brain function. Trends Neurosci. 1997, 20, 435–442. [Google Scholar] [PubMed]
- Chong, S.P.; Merkle, C.W.; Leahy, C.; Radhakrishnan, H.; Srinivasan, V.J. Quantitative microvascular hemoglobin mapping using visible light spectroscopic Optical Coherence Tomography. Biomed. Opt. Express 2015, 6, 1429–1450. [Google Scholar] [PubMed]
- Ji, Y.; Vadim, B. Imaging a full set of optical scattering properties of biological tissue by inverse spectroscopic optical coherence tomography. Opt. Lett. 2012, 37, 4443–4445. [Google Scholar]
- Ahn, Y.C.; Jung, W.; Chen, Z. Quantification of a three-dimensional velocity vector using spectral-domain Doppler optical coherence tomography. Opt. Lett. 2007, 32, 1587–1589. [Google Scholar]
- Zhu, C.; Liu, Q. Review of Monte Carlo modeling of light transport in tissues. J. Biomed. Opt. 2013, 18, 50902. [Google Scholar]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML--Monte Carlo modeling of light transport in multi-layered tissues. Comput. Methods Programs Biomed. 1995, 47, 131–146. [Google Scholar]
- Yao, G.; Wang, L.V. Monte Carlo simulation of an optical coherence tomography signal in homogeneous turbid media. Phys. Med. Biol. 1999, 44, 2307–2320. [Google Scholar] [PubMed]
- Shi, B.; Zhuo, M.; Wang, L.; Liu, T. Monte Carlo modeling of human tooth optical coherence tomography imaging. J. Opt. 2013, 15, 075304. [Google Scholar]
- Periyasamy, V.; Pramanik, M. Importance sampling-based Monte Carlo simulation of time-domain optical coherence tomography with embedded objects. Appl. Opt. 2016, 55, 2921–2929. [Google Scholar] [PubMed]
- Hartinger, A.E.; Nam, A.S.; Isabel, C.C.; Vakoc, B.J. Monte Carlo modeling of angiographic optical coherence tomography. Biomed. Opt. Express 2014, 5, 4338–4349. [Google Scholar] [CrossRef] [PubMed]
- Igor, M.; Mikhail, K.; Vladimir, K.; Risto, M. Simulation of polarization-sensitive optical coherence tomography images by a Monte Carlo method. Opt. Lett. 2008, 33, 1581–1583. [Google Scholar]
- Fang, Q. Mesh-based Monte Carlo method using fast ray-tracing in Plücker coordinates. Biomed. Opt. Express 2010, 1, 165–175. [Google Scholar] [PubMed]
- Yao, R.; Intes, X.; Fang, Q. Generalized mesh-based Monte Carlo for wide-field illumination and detection via mesh retessellation. Biomed. Opt. Express 2015, 7, 171–184. [Google Scholar]
- Yi, J.; Chen, S.; Backman, V.; Zhang, H.F. In vivo functional microangiography by visible-light optical coherence tomography. Biomed. Opt. Express 2014, 5, 3603–3612. [Google Scholar] [PubMed]
- Uludag, K.; Kohl, M.; Steinbrink, J.; Obrig, H.; Villringer, A. Cross talk in the Lambert-Beer calculation for near-infrared wavelengths estimated by Monte Carlo simulations. J. Biomed. Opt. 2002, 7, 51–59. [Google Scholar] [PubMed]
- George, M. Optical constants of water in the 200-nm to 200-μm wavelength region. Appl. Opt. 1973, 12, 555–563. [Google Scholar]
- Leitgeb, R.; Wojtkowski, M.; Kowalczyk, A.; Hitzenberger, C.K.; Sticker, M.; Fercher, A.F. Spectral measurement of absorption by spectroscopic frequency-domain optical coherence tomography. Opt. Lett. 2000, 25, 820–822. [Google Scholar] [CrossRef] [PubMed]
- Bosschaart, N.; Edelman, G.J.; Aalders, M.C.G.; Leeuwen, T.G.V.; Faber, D.J. A literature review and novel theoretical approach on the optical properties of whole blood. Laser Med. Sci. 2013, 29, 453–479. [Google Scholar] [CrossRef]
- Smith, M.H.; Denninghoff, K.R.; Hillman, L.W.; Chipman, R.A. Oxygen Saturation Measurements of Blood in Retinal Vessels during Blood Loss. J. Biomed. Opt. 1998, 3, 296–303. [Google Scholar] [PubMed]
- Delori, F.C. Noninvasive technique for oximetry of blood in retinal vessels. Appl. Opt. 1988, 27, 1113–1125. [Google Scholar] [PubMed]
- Hermann, B.; Bizheva, K.; Unterhuber, A.; Povazay, B.; Sattmann, H.; Schmetterer, L.; Fercher, A.; Drexler, W. Precision of extracting absorption profiles from weakly scattering media with spectroscopic time-domain optical coherence tomography. Opt. Express 2004, 12, 1677–1688. [Google Scholar]
- Faber, D.J.; Aalders, M.C.G.; Mik, E.G.; Hooper, B.A.; van Gemert, M.J.C.; van Leeuwen, T.G. Oxygen saturation-dependent absorption and scattering of blood. Phys. Rev. Lett. 2004, 93, 028102. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.V.; Wu, H.I.; Masters, B.R. Biomedical Optics, Principles and Imaging. J. Biomed. Opt. 2008, 13, 049902. [Google Scholar]
- Matcher, S.J.; Cope, M.; Delpy, D.T. In vivo measurements of the wavelength dependence of tissue-scattering coefficients between 760 and 900 nm measured with time-resolved spectroscopy. Appl. Opt. 1997, 36, 386–396. [Google Scholar]
- Hong, G.; Diao, S.; Chang, J.; Antaris, A.L.; Chen, C.; Zhang, B.; Zhao, S.; Atochin, D.N.; Huang, P.L.; Andreasson, K.I. Through-skull fluorescence imaging of the brain in a new near-infrared window. Nat. Photonics 2014, 8, 723–730. [Google Scholar]
- The Program was Downloaded from Open Source Website and Modified. Available online: http://mcx.space/mmc (accessed on 2 November 2018).
- Siavash, M.; Lima, I.T.; Sherif, S.S. Monte Carlo simulation of optical coherence tomography for turbid media with arbitrary spatial distributions. J.Biomed. Opt. 2014, 19, 046001. [Google Scholar]
- Collins, D.L.; Zijdenbos, A.P.; Kollokian, V.; Sled, J.G.; Kabani, N.J.; Holmes, C.J.; Evans, A.C. Design and construction of a realistic digital brain phantom. IEEE Trans. Med. Imaging 1998, 17, 463–468. [Google Scholar] [PubMed]
- Umeyama, S.; Yamada, T. Monte Carlo study of global interference cancellation by multidistance measurement of near-infrared spectroscopy. J.Biomed. Opt. 2009, 14, 064025. [Google Scholar] [PubMed]
- Kholodnykh, A.I.; Petrova, I.Y.; Larin, K.V.; Massoud, M.; Esenaliev, R.O. Precision of measurement of tissue optical properties with optical coherence tomography. Appl. Opt. 2003, 42, 3027–3037. [Google Scholar] [PubMed]
- Yaroslavsky, A.N.; Schulze, P.C.; Yaroslavsky, I.V.; Schober, R.; Ulrich, F.; Schwarzmaier, H.J. Optical properties of selected native and coagulated human brain tissues in vitro in the visible and near infrared spectral range. Phys. Med. Biol. 2002, 47, 2059–2073. [Google Scholar] [CrossRef] [PubMed]
- Ji, Y.; Qing, W.; Liu, W.; Backman, V.; Zhang, H.F. Visible-light optical coherence tomography for retinal oximetry. Opt. Lett. 2013, 38, 1796–1798. [Google Scholar]
- Yin, G.; Yi, Y. Imaging of hemoglobin oxygen saturation using confocal photoacoustic system with three optical wavelengths. In Proceedings of the Seventh International Conference on Photonics and Imaging in Biology and Medicine, Wuhan, China, 24–27 November 2008; Volume 7280. [Google Scholar]
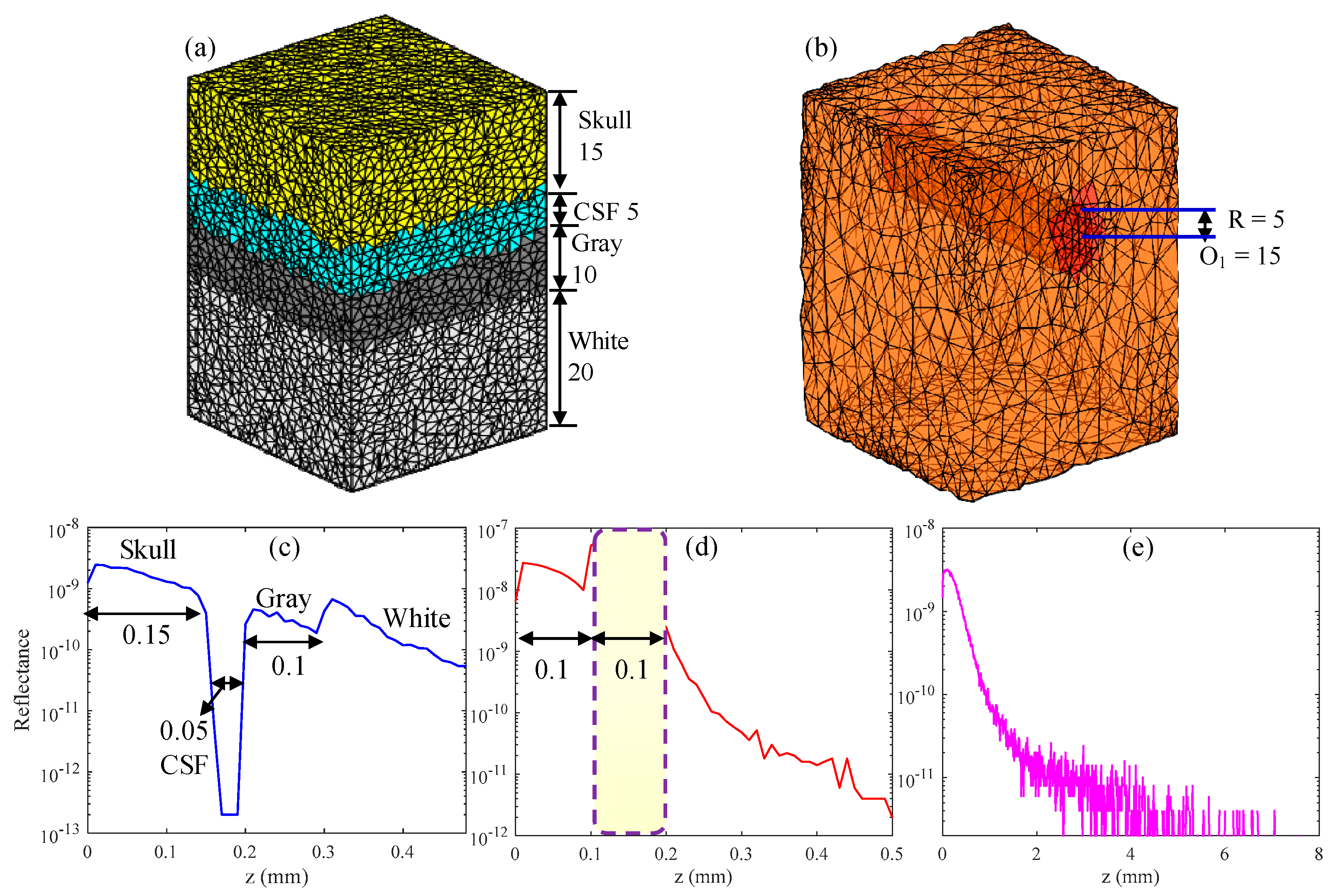
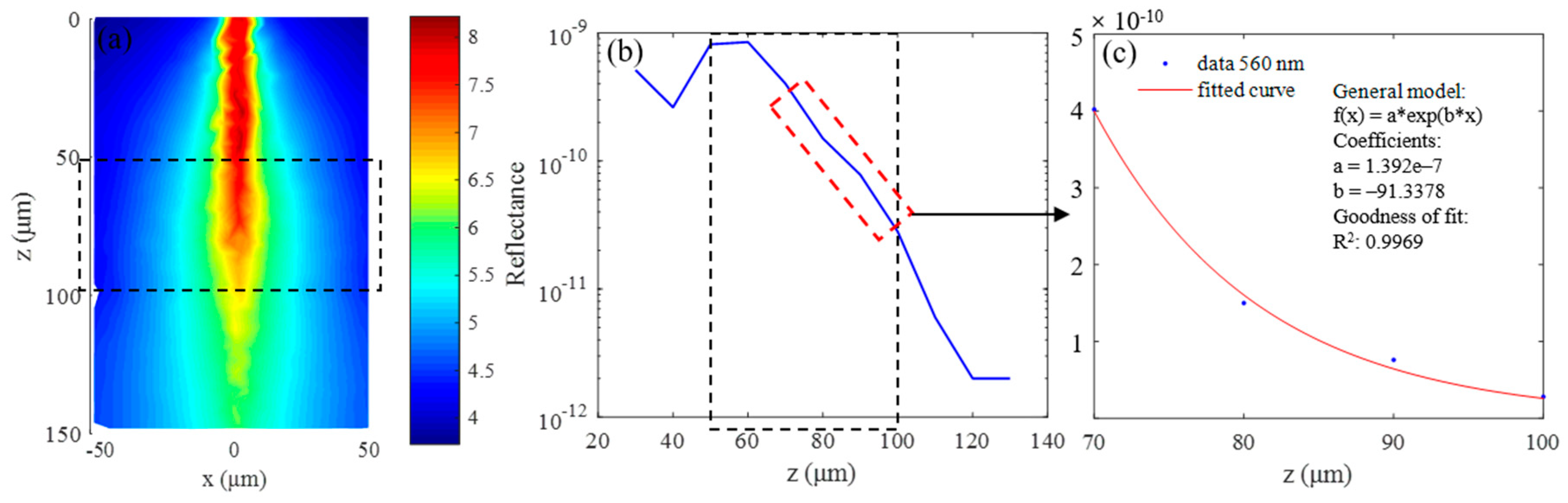
| Tissue Type | Thickness (mm) | μa (mm−1) | μs (mm−1) |
|---|---|---|---|
| Hierarchical Structure | |||
| Skull | 7 (0.15) | 0.019 | 7.8 |
| CSF | 2 (0.05) | 0.004 | 0.009 |
| Gray matter | 4 (0.1) | 0.02 | 9 |
| White matter | 34 (0.2) | 0.08 | 40.9 |
| Vessel Structure | |||
| Medium (Gray matter) | 0.5 | 0.02 | 9 |
| Vessel | 0.1 (Diameter) | 0.28 | 88.55 |
| λ (nm) | εO (mmol−1·mm−1) | εD (mmol−1·mm−1) | S (mm−1) |
|---|---|---|---|
| Optimal Combination | |||
| 560 | 4.1519 | 5.7674 | 70 |
| 575 | 5.8742 | 4.5500 | 70 |
| 590 | 2.1107 | 3.0857 | 70 |
| Worst Combination | |||
| 553 | 4.7611 | 5.7666 | 70 |
| 568 | 4.8988 | 5.2246 | 70 |
| 583 | 4.7178 | 3.8402 | 70 |
| Combinations | The μt1 | The μt2 | The μt3 | Rea μt1 | Rea μt2 | Rea μt3 | C | Y | S1 |
|---|---|---|---|---|---|---|---|---|---|
| 560, 575, 590 | 91.352 | 95.222 | 81.067 | 91.338 | 95.268 | 81.047 | 2.003 | 0.704 | 69.978 |
| 553, 568, 583 | 93.315 | 93.01 | 90.514 | 93.291 | 93.171 | 90.531 | 2.482 | 0.767 | 64.746 |
| λ (nm) | εO (mmol−1·mm−1) | εD (mmol−1·mm−1) | S (mm−1) |
|---|---|---|---|
| 540 | 5.89 | 4.81 | 7.014 |
| 546 | 5.66 | 5.38 | 7.016 |
| 576 | 5.91 | 4.45 | 7.010 |
| λ (nm) | εO (mmol−1·mm−1) | εD (mmol−1·mm−1) | S-Gray (mm−1) | S-Vessel (mm−1) |
|---|---|---|---|---|
| 750 | 0.052 | 0.176 | 7.625 | 76.25 |
| 800 | 0.083 | 0.102 | 7.3 | 73 |
| 900 | 0.122 | 0.1 | 6.65 | 66.5 |
| Tissue | The μt1 | The μt2 | The μt3 | Rea μt1 | Rea μt2 | Rea μt3 | C | Y | S1 |
|---|---|---|---|---|---|---|---|---|---|
| Vessel | 77.072 | 73.814 | 67.56 | 77.084 | 73.785 | 67.524 | 4.14 | 0.65 | 76.18 |
| Gray matter | 7.6661 | 7.3407 | 6.703 | 7.712 | 7.385 | 6.725 | −0.21 | 0.55 | 7.75 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, L.; Sun, L.; Zou, M.; Hou, B. A Mesh-Based Monte Carlo Study for Investigating Structural and Functional Imaging of Brain Tissue Using Optical Coherence Tomography. Appl. Sci. 2019, 9, 4008. https://doi.org/10.3390/app9194008
Yi L, Sun L, Zou M, Hou B. A Mesh-Based Monte Carlo Study for Investigating Structural and Functional Imaging of Brain Tissue Using Optical Coherence Tomography. Applied Sciences. 2019; 9(19):4008. https://doi.org/10.3390/app9194008
Chicago/Turabian StyleYi, Luying, Liqun Sun, Mingli Zou, and Bo Hou. 2019. "A Mesh-Based Monte Carlo Study for Investigating Structural and Functional Imaging of Brain Tissue Using Optical Coherence Tomography" Applied Sciences 9, no. 19: 4008. https://doi.org/10.3390/app9194008
APA StyleYi, L., Sun, L., Zou, M., & Hou, B. (2019). A Mesh-Based Monte Carlo Study for Investigating Structural and Functional Imaging of Brain Tissue Using Optical Coherence Tomography. Applied Sciences, 9(19), 4008. https://doi.org/10.3390/app9194008





