3D Display System Based on Spherical Wave Field Synthesis
Abstract
1. Introduction
2. Principle and Design of Wave Field Synthesis 3D Imaging System
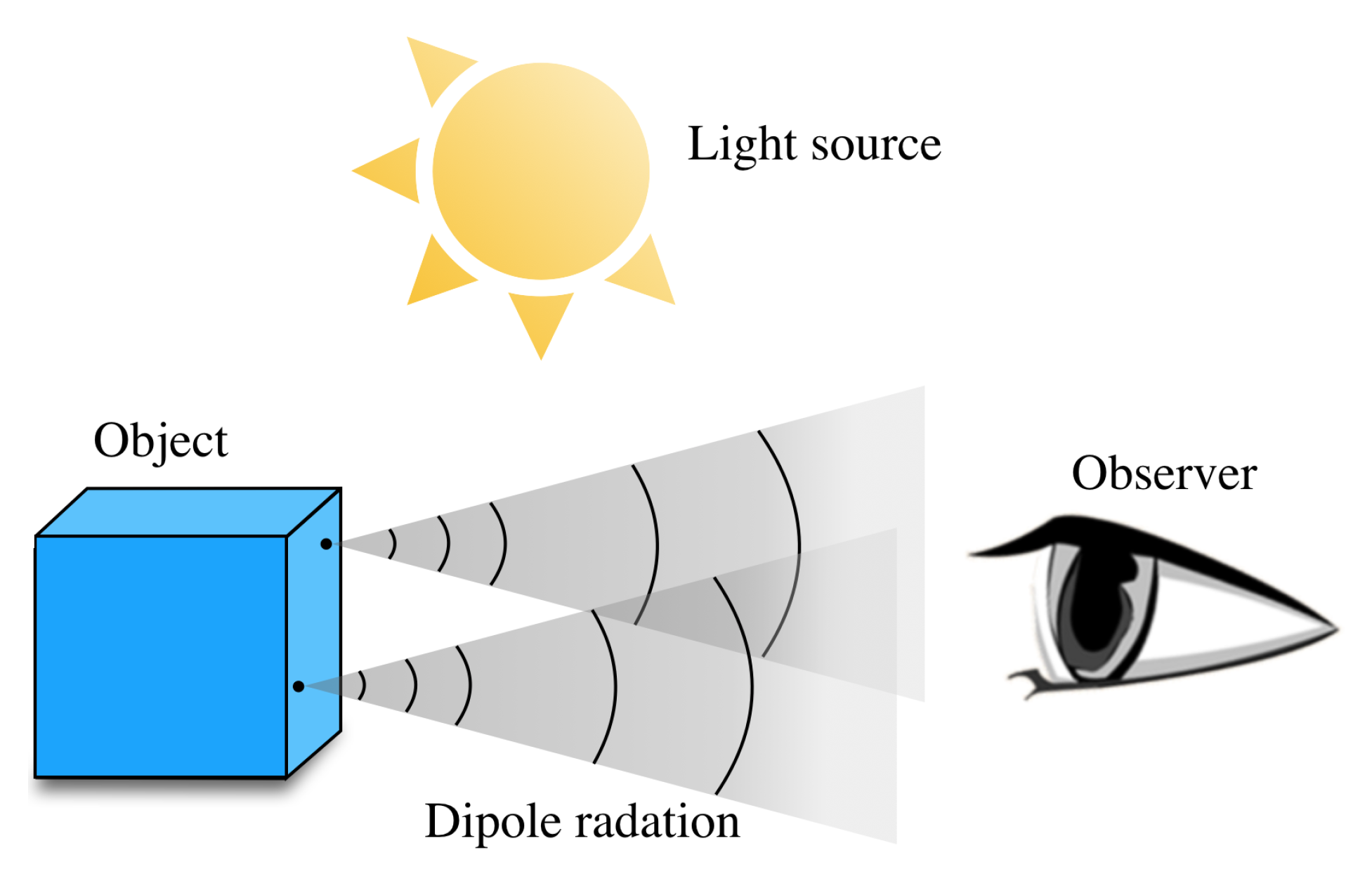
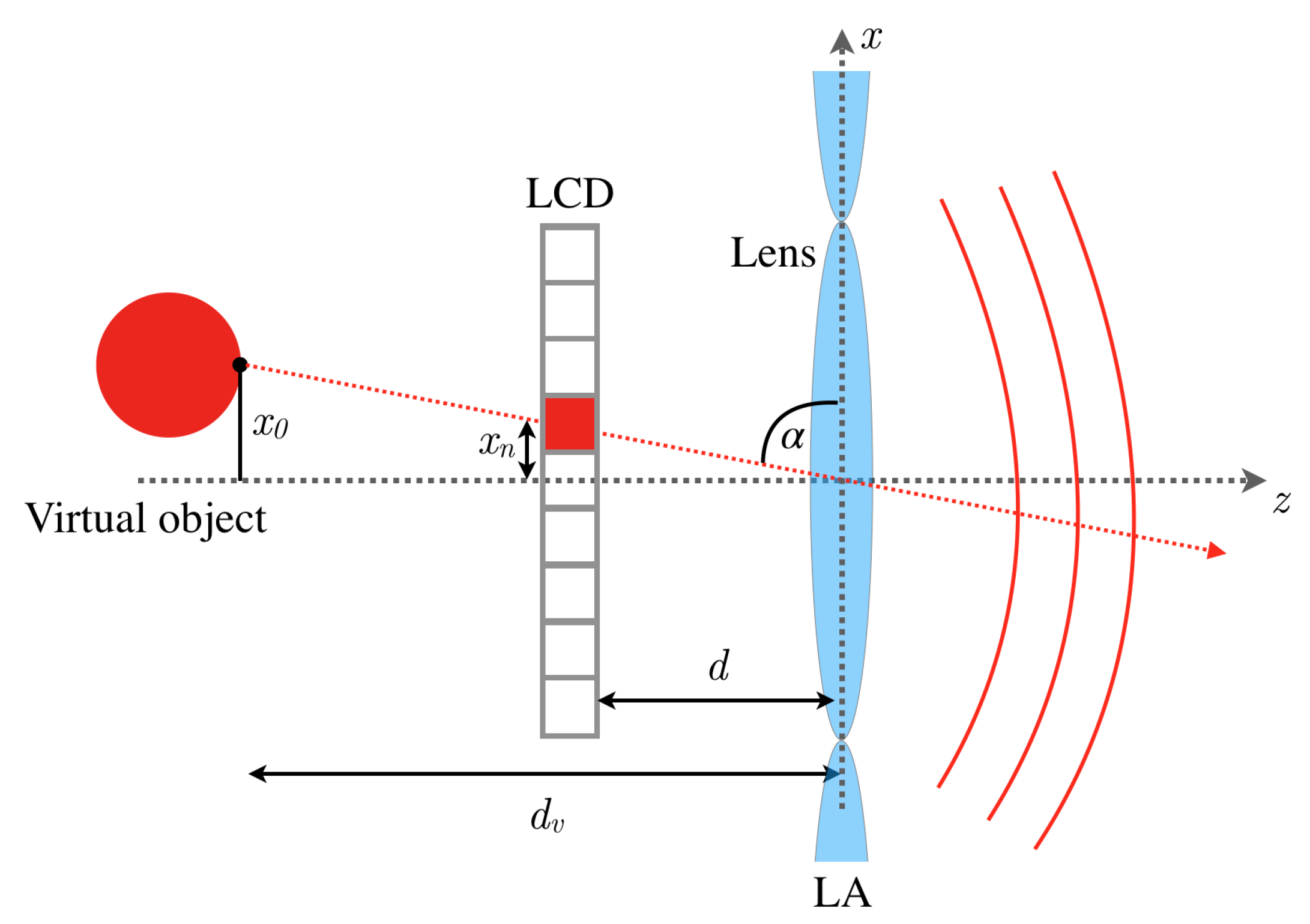
2.1. Optical System Principle
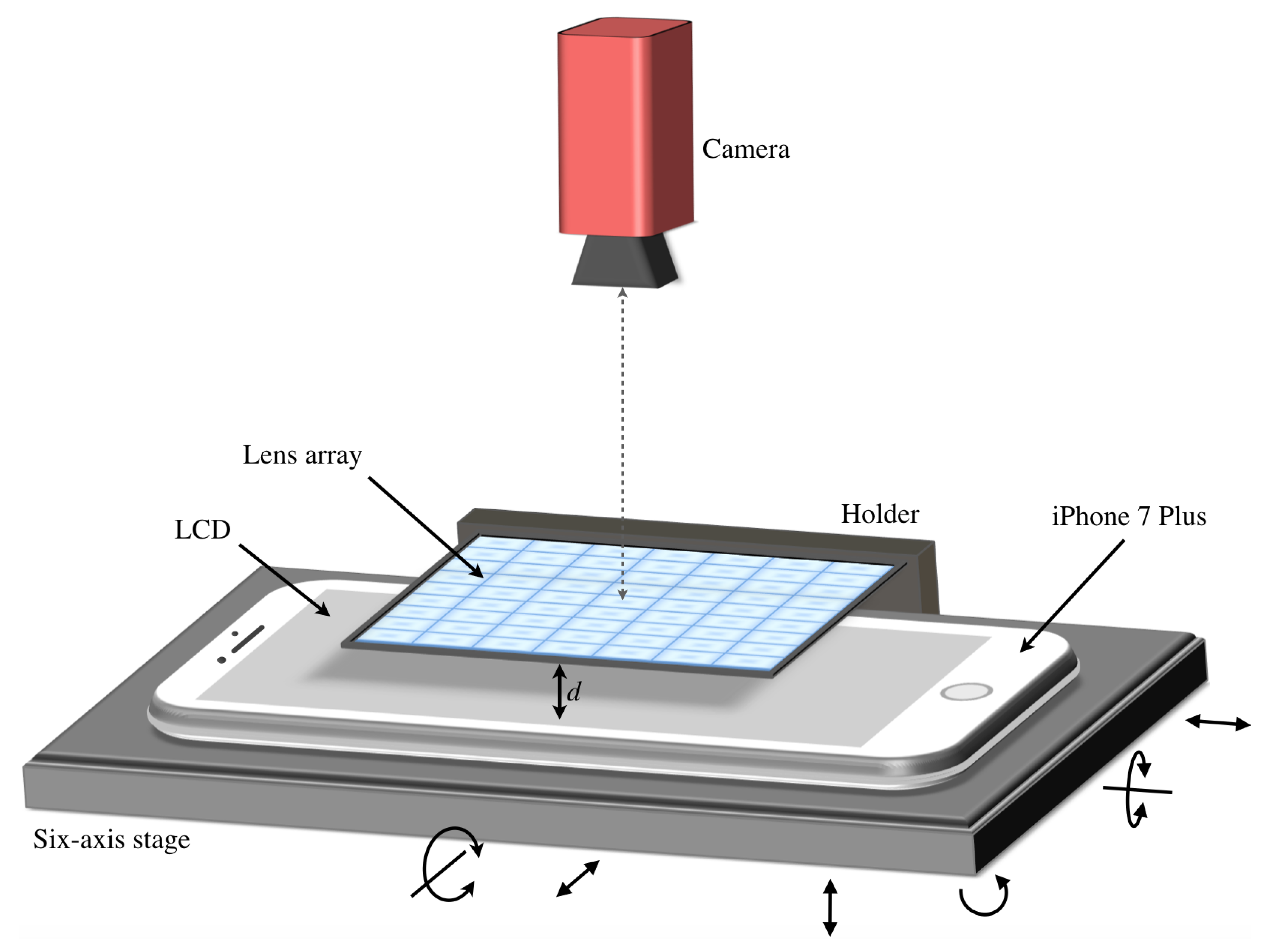
2.2. Optical Components
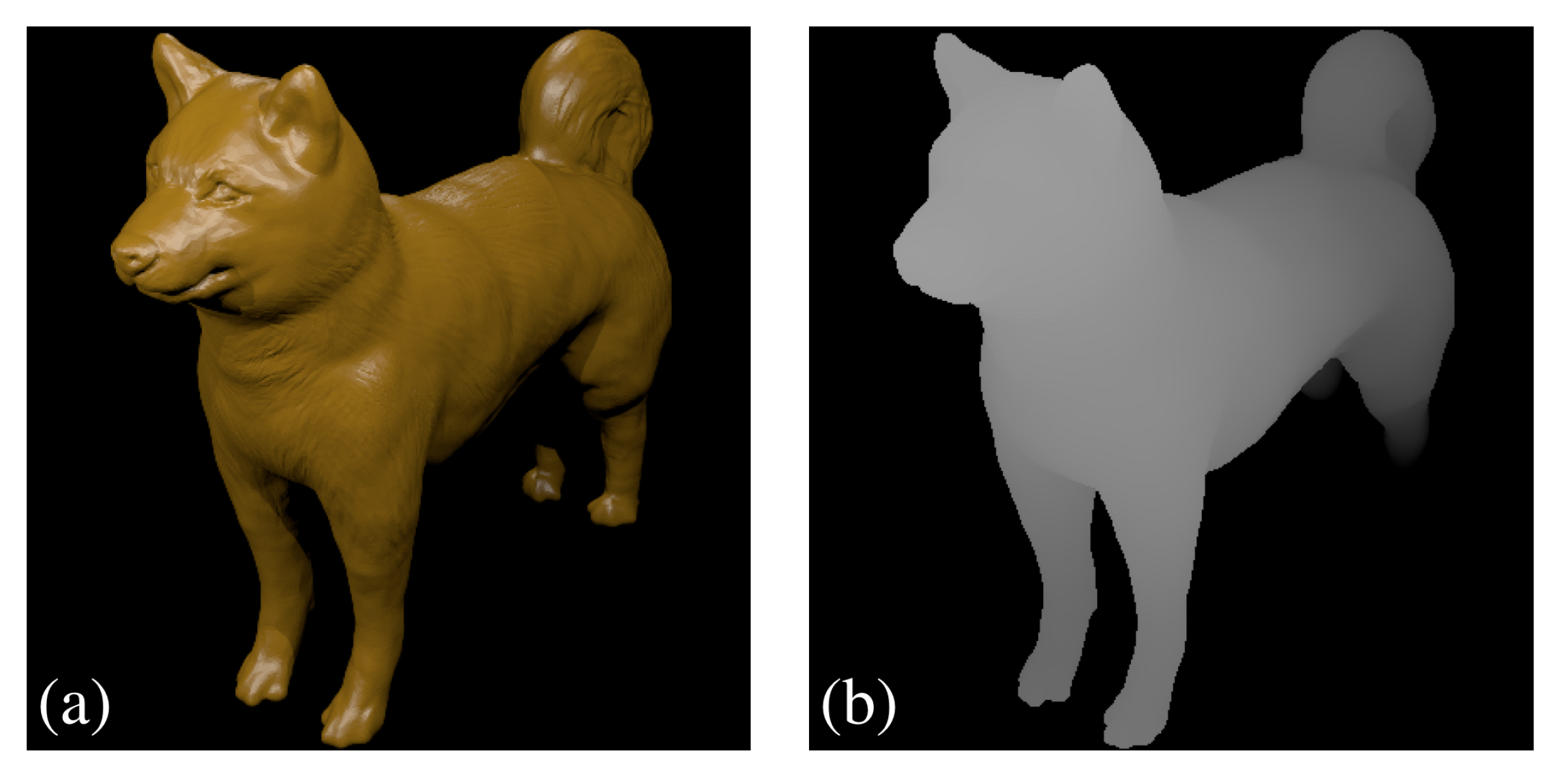
3. Experiments and Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| 3D | Three-dimensional |
| LA | Lens array |
| LCD | Liquid crystal display |
| VAC | Vergence–accommodation conflict |
| LF | Light field |
| MLA | Micro-lens array |
| CDP | Central depth plane |
| CCD | Charge coupled device |
References
- Hainich, R.R.; Bimber, O. Displays–Fundamentals & Applications, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Souk, J. (Ed.) Flat Panel Display Manufacturing; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Geng, J. Three-dimensional display technologies. Adv. Opt. Photonics 2013, 5, 456–535. [Google Scholar] [CrossRef] [PubMed]
- Holliman, N. 3D Display Systems; Department of Computer Science: Durham, UK, 2005; pp. 456–535. [Google Scholar]
- Hill, L.; Jacobs, A. 3-D Liquid Crystal Displays and Their Applications. Proc. IEEE 2006, 94, 575–590. [Google Scholar] [CrossRef]
- Wheatstone, C. Contributions to the physiology of vision.–Part the first. On some remarkable, and hitherto unobserved, phenomena of binocular vision. Phil. Trans. R. Soc. 1838, 128, 371–394. [Google Scholar]
- Lappe, M.; Bremmer, F.; den Berg, A.V. Perception of self-motion from visual flow. Trends Cogn. Sci. 1999, 3, 329–336. [Google Scholar] [CrossRef]
- Kim, J.; Kane, D.; Banks, M.S. The rate of change of vergence-accommodation conflict affects visual discomfort. Vis. Res. 2014, 105, 159–165. [Google Scholar] [CrossRef] [PubMed]
- Burke, R.; Brickson, L. Focus cue enabled head-mounted display via microlens array. TOG 2013, 32, 220. [Google Scholar]
- Agour, M.; Falldorf, C.; Bergmann, R.B. Holographic display system for dynamic synthesis of 3D light fields with increased space bandwidth product. Opt. Express 2016, 24, 14393–14405. [Google Scholar] [CrossRef] [PubMed]
- Blanche, P.A.; Bablumian, A.; Voorakaranam, R.; Christenson, C.; Lin, W.; Gu, T.; Flores, D.; Wang, P.; Hsieh, W.Y.; Kathaperumal, M.; et al. Holographic three-dimensional telepresence using large-area photorefractive polymer. Nature 2010, 458, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Häussler, R.; Gritsai, Y.; Zschau, E.; Missbach, R.; Sahm, H.; Stock, M.; Stolle, H. Large real-time holographic 3d displays: enabling components and results. Appl. Opt. 2017, 56, F45–F52. [Google Scholar] [CrossRef] [PubMed]
- Huang, F.C.; Luebke, D.P.; Wetzstein, G. The light field stereoscope. Acm Trans. Graph. 2015, 34, 60:1–60:12. [Google Scholar] [CrossRef]
- Chou, P.Y.; Wu, J.Y.; Huang, S.H.; Wang, C.P.; Qin, Z.; Huang, C.T.; Hsieh, P.Y.; Lee, H.H.; Lin, T.H.; Huang, Y.P. Hybrid light field head-mounted display using time-multiplexed liquid crystal lens array for resolution enhancement. Opt. Express 2019, 27, 1164–1178. [Google Scholar] [CrossRef] [PubMed]
- Jang, J.S.; Javidi, B. Three-dimensional integral imaging of micro-objects. Opt. Lett. 2004, 29, 1230–1232. [Google Scholar] [CrossRef] [PubMed]
- Levoy, M.; Zhang, Z.; McDowall, I. Recording and controlling the 4D light field in a microscope using microlens arrays. J. Microsc. 2009, 235, 144–162. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Hua, H. Systematic characterization and optimization of 3D light field displays. Opt. Express 2017, 25, 18508–18525. [Google Scholar] [CrossRef] [PubMed]
- Lanman, D.; Luebke, D. Near-eye light field displays. ACM Trans. Graph. 2013, 32, 220.1–220.10. [Google Scholar] [CrossRef]
- Xiao, X.; Javidi, B.; Martinez-Corral, M.; Stern, A. Advances in three-dimensional integral imaging: Sensing, display, and applications. Appl. Opt. 2013, 52, 546–560. [Google Scholar] [CrossRef] [PubMed]
- Balram, N.; Tošić, I. Light-field imaging and display systems. Inf. Display 2019, 32, 6–13. [Google Scholar] [CrossRef]
- Kim, C.J.; Chang, M.H.; Lee, M.Y.; Kim, J.O.; Won, Y.H. Depth plane adaptive integral imaging using a varifocal liquid lens array. Appl. Opt. 2015, 54, 2565–2571. [Google Scholar] [CrossRef] [PubMed]
- Goodmann, J. Introduction to Fourier Optics, 2nd ed.; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Johansson, G. Visual perception of biological motion and a model for its analysis. Percept. Psychophys. 1973, 14, 201–211. [Google Scholar] [CrossRef]



| Dimensions (mm) | 58.0 × 60.0 |
| Size of lenslet (mm) | 5.4 × 7.0 |
| Effective focal length EFL (mm) | 41.90 |
| Radius of lenslet (mm) | 22.0 |
| Substrate | B270 |
| Wavelength range (nm) | 400 … 700 |
| Thickness (mm) | 3.0 |
| Dimensions (mm) | 158.2 × 77.9 |
| Type | IPS LCD |
| Resolution (pixel) | 1920 × 1080 |
| Pixel size (m) | 63.34 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falldorf, C.; Chou, P.-Y.; Prigge, D.; Bergmann, R.B. 3D Display System Based on Spherical Wave Field Synthesis. Appl. Sci. 2019, 9, 3862. https://doi.org/10.3390/app9183862
Falldorf C, Chou P-Y, Prigge D, Bergmann RB. 3D Display System Based on Spherical Wave Field Synthesis. Applied Sciences. 2019; 9(18):3862. https://doi.org/10.3390/app9183862
Chicago/Turabian StyleFalldorf, Claas, Ping-Yen Chou, Daniel Prigge, and Ralf B. Bergmann. 2019. "3D Display System Based on Spherical Wave Field Synthesis" Applied Sciences 9, no. 18: 3862. https://doi.org/10.3390/app9183862
APA StyleFalldorf, C., Chou, P.-Y., Prigge, D., & Bergmann, R. B. (2019). 3D Display System Based on Spherical Wave Field Synthesis. Applied Sciences, 9(18), 3862. https://doi.org/10.3390/app9183862





