Reliable Design for a Network of Networks with Inspiration from Brain Functional Networks
Abstract
:1. Introduction
2. Basic Principles of NoN Models
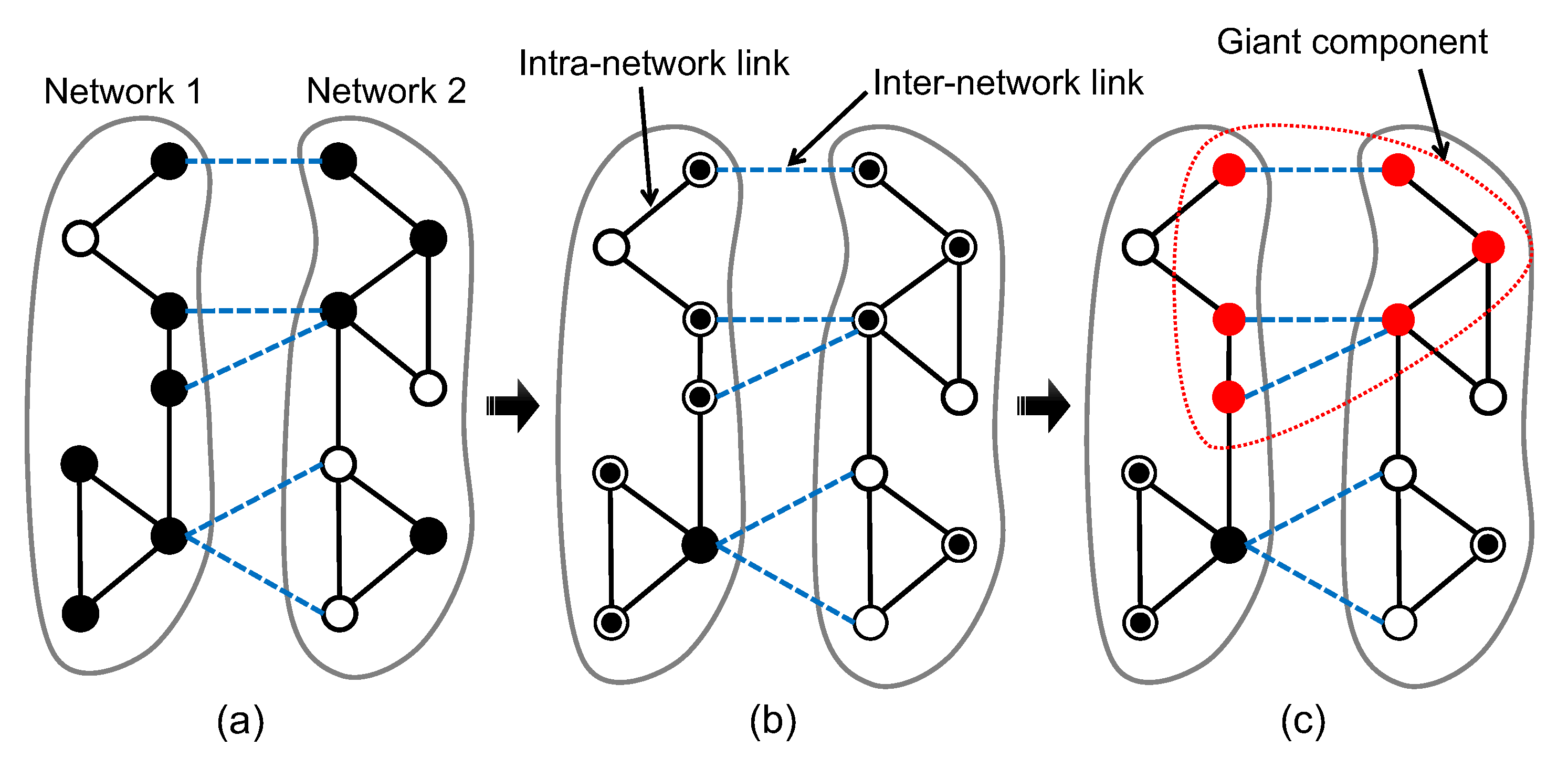
2.1. Network of Networks
2.1.1. Variables in NoN Models
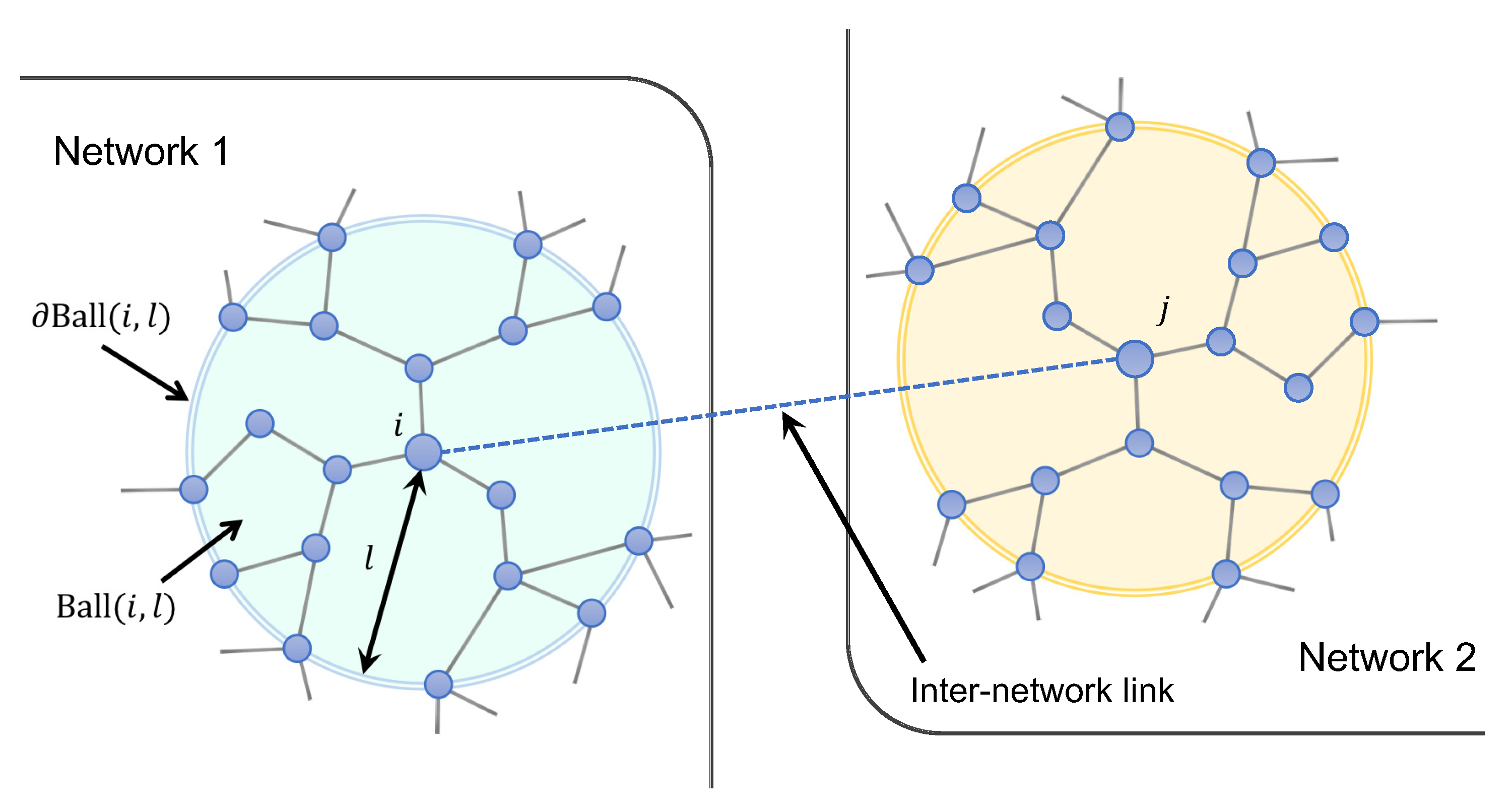
2.1.2. Definition of Local Effectiveness
2.1.3. Definition of Global Effectiveness
B-NoN Model
C-NoN Model
2.2. Influence Identification in a Network of Networks
3. Network of Networks in Virtualized Networks
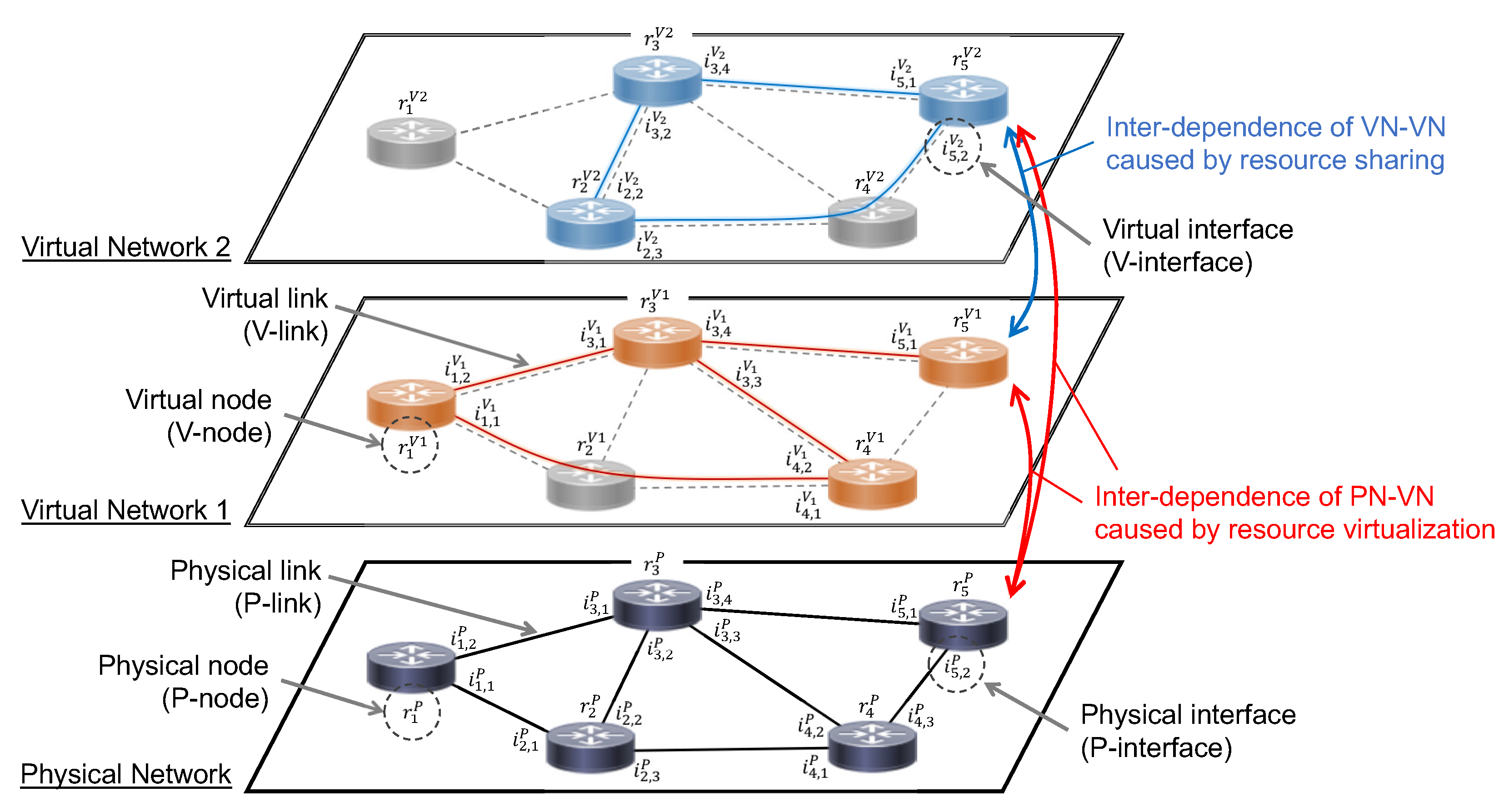
3.1. Interdependence of Virtualized Networks
3.2. Model of Network of Networks with Network Slicing
3.2.1. Input States of Interfaces
3.2.2. Availability States of Interfaces
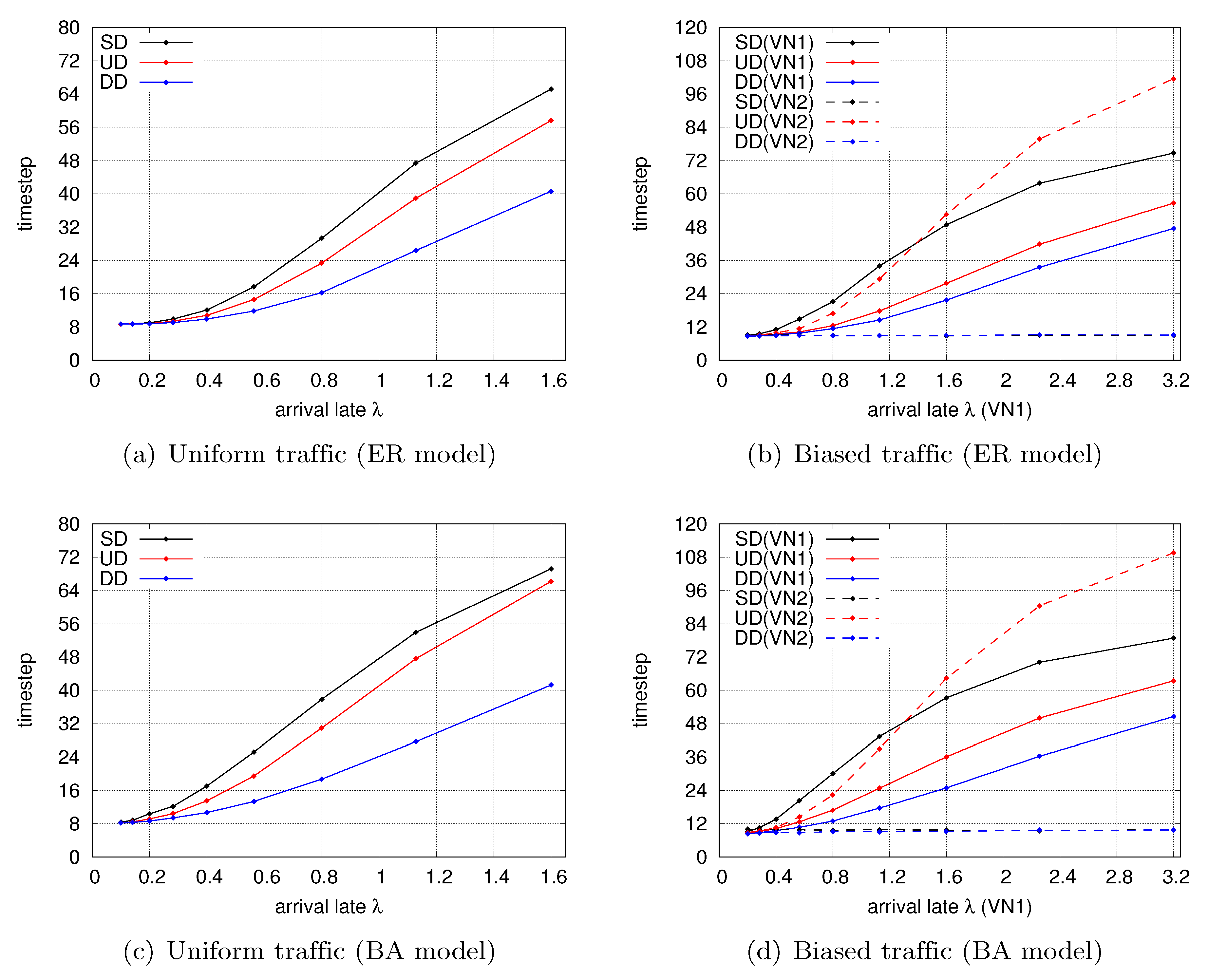
Type-SD
Type-UD
Type-DD
3.3. Influencers in a Network of Networks with Network Slicing
4. Evaluation
4.1. Network Construction
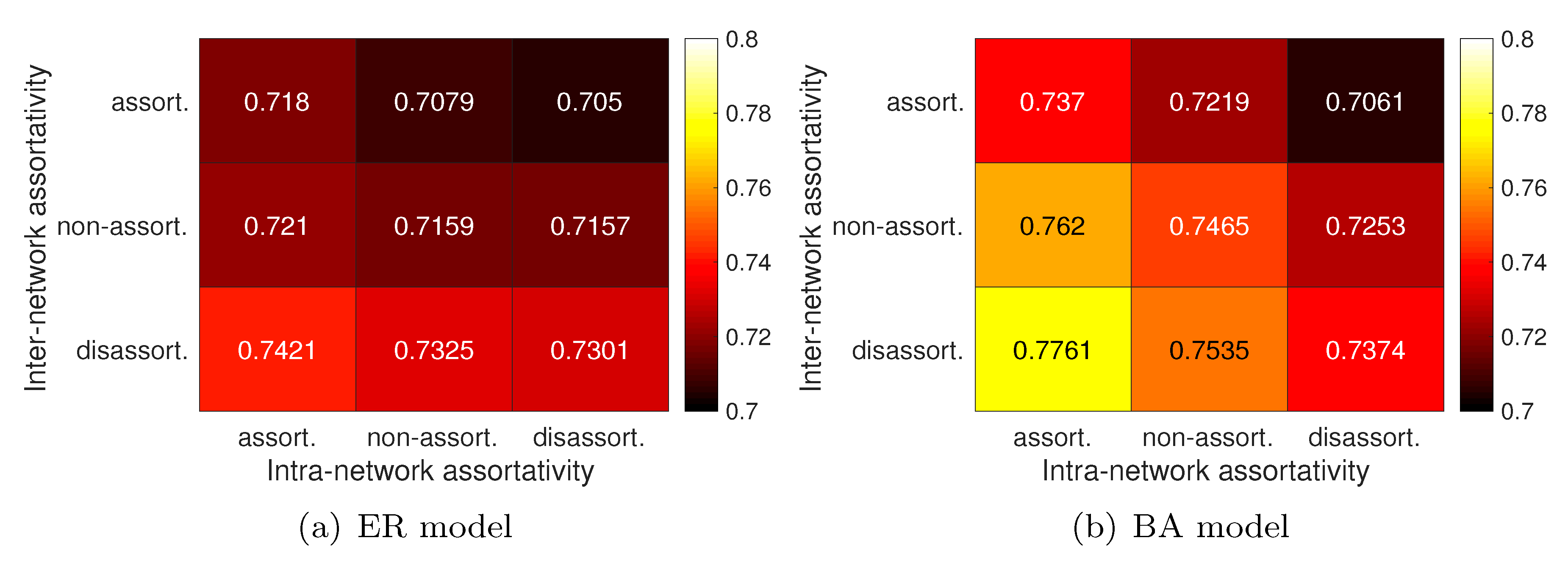
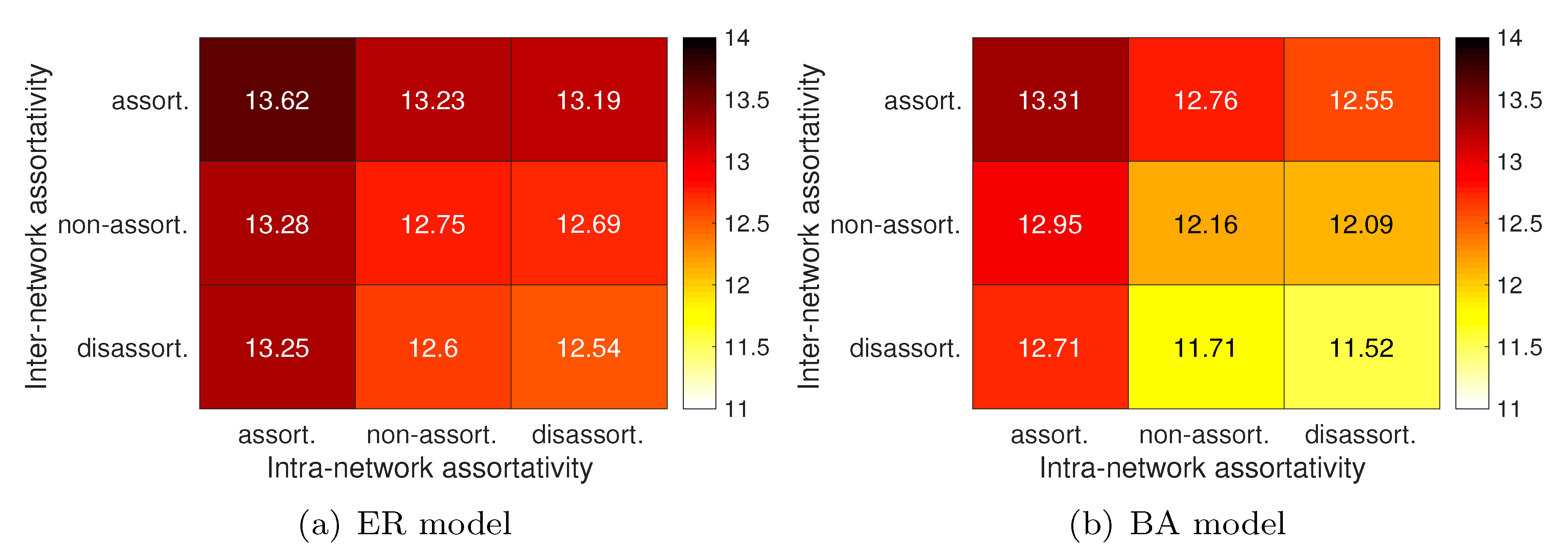
4.1.1. Intranetwork Assortativity
4.1.2. Internetwork Assortativity
4.2. Traffic Model
4.3. Evaluation Results
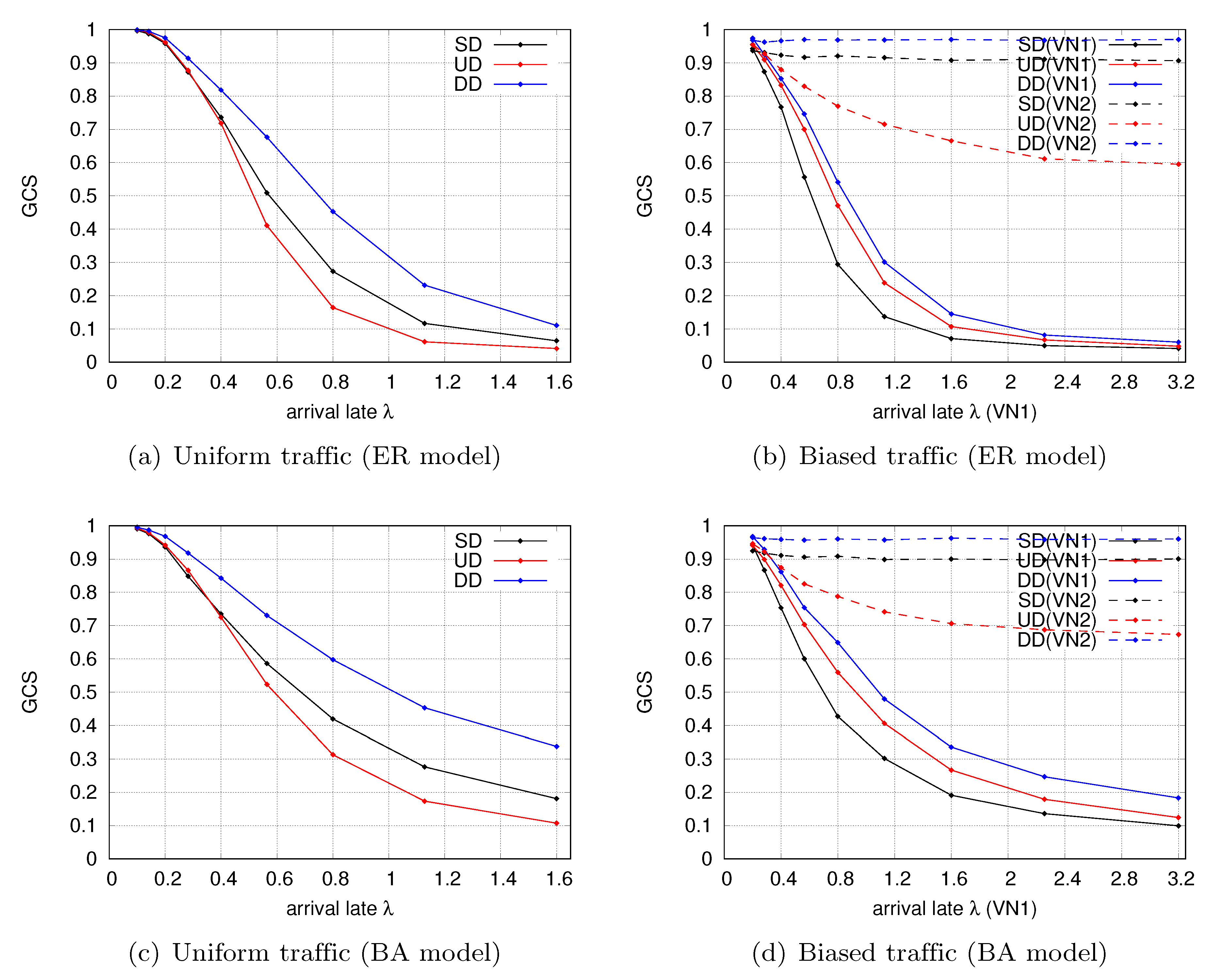
4.3.1. Comparing the Availability of the Three Types of PV-NoN Model
4.3.2. Designing Influencers on the PV-NoN Model
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Arasteh, H.; Hosseinnezhad, V.; Loia, V.; Tommasetti, A.; Troisi, O.; Shafie-khah, M.; Siano, P. Iot-based smart cities: A survey. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC 2016), Florence, Italy, 7–12 June 2016; pp. 1–6. [Google Scholar]
- Whitmore, A.; Agarwal, A.; Da Xu, L. The internet of things—A survey of topics and trends. Inform. Syst. Front. 2015, 17, 261–274. [Google Scholar] [CrossRef]
- Gao, J.; Buldyrev, S.V.; Stanley, H.E.; Havlin, S. Networks formed from interdependent networks. Nat. Phys. 2011, 8. [Google Scholar] [CrossRef]
- Zhou, X.; Li, R.; Chen, T.; Zhang, H. Network slicing as a service: Enabling enterprises’ own software-defined cellular networks. IEEE Commun. Mag. 2016, 54, 146–153. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, N.; Chu, X.; Long, K.; Aghvami, A.H.; Leung, V.C.M. Network slicing based 5G and future mobile networks: Mobility, resource management, and challenges. IEEE Commun. Mag. 2017, 55, 138–145. [Google Scholar] [CrossRef]
- Michalopoulos, D.S.; Doll, M.; Sciancalepore, V.; Bega, D.; Schneider, P.; Rost, P. Network slicing via function decomposition and flexible network design. In Proceedings of the 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017; pp. 1–6. [Google Scholar]
- Yousaf, F.Z.; Gramaglia, M.; Friderikos, V.; Gajic, B.; von Hugo, D.; Sayadi, B.; Sciancalepore, V.; Crippa, M.R. Network slicing with flexible mobility and QoS/QoE support for 5G Networks. In Proceedings of the 2017 IEEE International Conference on Communications Workshops (ICC Workshops), Paris, France, 21–25 May 2017; pp. 1195–1201. [Google Scholar]
- Rost, P.; Mannweiler, C.; Michalopoulos, D.S.; Sartori, C.; Sciancalepore, V.; Sastry, N.; Holland, O.; Tayade, S.; Han, B.; Bega, D.; et al. Network slicing to enable scalability and flexibility in 5G mobile networks. IEEE Commun. Mag. 2017, 55, 72–79. [Google Scholar] [CrossRef]
- Li, X.; Casellas, R.; Landi, G.; de la Oliva, A.; Costa-Perez, X.; Garcia-Saavedra, A.; Deiss, T.; Cominardi, L.; Vilalta, R. 5G-crosshaul network slicing: Enabling multi-tenancy in mobile transport networks. IEEE Commun. Mag. 2017, 55, 128–137. [Google Scholar] [CrossRef]
- Han, B.; Gopalakrishnan, V.; Ji, L.; Lee, S. Network function virtualization: Challenges and opportunities for innovations. IEEE Commun. Mag. 2015, 53, 90–97. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, Z.; Kato, N.; Akashi, O.; Takahara, A. Reliability evaluation for NFV deployment of future mobile broadband networks. IEEE Wirel. Commun. 2016, 23, 90–96. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Parshani, R.; Paul, G.; Stanley, H.E.; Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [Google Scholar] [CrossRef] [Green Version]
- Morone, F.; Roth, K.; Min, B.; Stanley, H.E.; Makse, H.A. Model of brain activation predicts the neural collective influence map of the brain. Proc. Natl. Acad. Sci. USA 2017, 114, 3849–3854. [Google Scholar] [CrossRef] [Green Version]
- Kempe, D.; Kleinberg, J.; Tardos, É. Maximizing the spread of influence through a social network. In Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; pp. 137–146. [Google Scholar]
- Albert, R.; Jeong, H.; Barabási, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cohen, R.; Erez, K.; ben Avraham, D.; Havlin, S. Breakdown of the Internet under intentional attack. Phys. Rev. Lett. 2001, 86, 3682–3685. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. Assortative mixing in networks. Phys. Rev. Lett. 2002, 89, 208701. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhou, W.; Li, R.; Cao, J.; Lin, X. Improving robustness of interdependent networks by a new coupling strategy. Phys. A Stat. Mech. Appl. 2018, 492, 1075–1080. [Google Scholar] [CrossRef]
- Dong, G.; Chen, Y.; Wang, F.; Du, R.; Tian, L.; Stanley, H.E. Robustness on interdependent networks with a multiple-to-multiple dependent relationship. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 073107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Min, B.; Zheng, M. Correlated network of networks enhances robustness against catastrophic failures. PLoS ONE 2018, 13, e0195539. [Google Scholar] [CrossRef] [PubMed]
- Cui, P.; Zhu, P.; Wang, K.; Xun, P.; Xia, Z. Enhancing robustness of interdependent network by adding connectivity and dependence links. Phys. A Stat. Mech. Appl. 2018, 497, 185–197. [Google Scholar] [CrossRef]
- Shekhtman, L.M.; Danziger, M.M.; Vaknin, D.; Havlin, S. Robustness of spatial networks and networks of networks. Comptes Rendus Phys. 2018, 19, 233–243. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Wang, Y.; Yang, S. Efficient influence maximization in social networks. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’09, New York, NY, USA, 28 June–1 July 2009; pp. 199–208. [Google Scholar]
- Chen, Y.; Paul, G.; Havlin, S.; Liljeros, F.; Stanley, H.E. Finding a better immunization strategy. Phys. Rev. Lett. 2008, 101, 058701. [Google Scholar] [CrossRef]
- Newman, M.E.J. Spread of epidemic disease on networks. Phys. Rev. E. 2002, 66, 016128. [Google Scholar] [CrossRef] [Green Version]
- Richardson, M.; Domingos, P. Mining knowledge-sharing sites for viral marketing. In Proceedings of the 8th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002; pp. 61–70. [Google Scholar]
- Kiss, C.; Bichler, M. Identification of influencers–Measuring influence in customer networks. Decis. Support Syst. 2008, 46, 233–253. [Google Scholar] [CrossRef]
- Kitsak, M.; Gallos, L.K.; Havlin, S.; Liljeros, F.; Muchnik, L.; Stanley, H.E.; Makse, H.A. Identification of influential spreaders in complex networks. Nat. Phys. 2010, 6, 888–893. [Google Scholar] [CrossRef] [Green Version]
- Bao, Z.K.; Ma, C.; Xiang, B.B.; Zhang, H.F. Identification of influential nodes in complex networks: Method from spreading probability viewpoint. Phys. A Stat. Mech. Appl. 2017, 468, 391–397. [Google Scholar] [CrossRef]
- Lü, L.; Chen, D.; Ren, X.L.; Zhang, Q.M.; Zhang, Y.C.; Zhou, T. Vital nodes identification in complex networks. Phys. Rep. 2016, 650, 1–63. [Google Scholar] [CrossRef] [Green Version]
- Morone, F.; Makse, H.A. Influence maximization in complex networks through optimal percolation. Nature 2015, 524, 65. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wang, X.; Hou, F.; Luo, Y.; Wang, Z. Dynamic memory balancing for virtualization. ACM Trans. Archit. Code Optim. 2016, 13, 2:1–2:25. [Google Scholar] [CrossRef]
- Beshley, M.; Romanchuk, V.; Chervenets, V.; Masiuk, A. Ensuring the quality of service flows in multiservice infrastructure based on network node virtualization. In Proceedings of the 2016 International Conference Radio Electronics Info Communications (UkrMiCo), Kiev, Ukraine, 11–16 September 2016; pp. 1–3. [Google Scholar]
- Herrera, J.G.; Botero, J.F. Resource allocation in NFV: A comprehensive survey. IEEE Trans. Netw. Serv. Manag. 2016, 13, 518–532. [Google Scholar] [CrossRef]
- Erdös, P.; Rényi, A. On random graphs, I. Publ. Math. (Debr.) 1959, 6, 290–297. [Google Scholar]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Callaway, D.S.; Newman, M.E.J.; Strogatz, S.H.; Watts, D.J. Network robustness and fragility: Percolation on random graphs. Phys. Rev. Lett. 2000, 85, 5468–5471. [Google Scholar] [CrossRef] [PubMed]
- Kawahigashi, H.; Terashima, Y.; Miyauchi, N.; Nakakawaji, T. Modeling ad hoc sensor networks using random graph theory. In Proceedings of the 2nd IEEE Consumer Communications and Networking Conference (CCNC 2005), Las Vegas, NV, USA, 6 January 2005; pp. 104–109. [Google Scholar]
- Onat, F.A.; Stojmenovic, I. Generating random graphs for wireless actuator networks. In Proceedings of the 2007 IEEE International Symposium on a World of Wireless, Mobile and Multimedia Networks, Espoo, Finland, 18–21 June 2007; pp. 1–12. [Google Scholar]
- Ding, L.; Guan, Z.H. Modeling wireless sensor networks using random graph theory. Phys. A Stat. Mech. Appl. 2008, 387, 3008–3016. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440. [Google Scholar] [CrossRef] [PubMed]
- Waxman, B.M. Routing of multipoint connections. IEEE J. Sel. Area Commun. 1988, 6, 1617–1622. [Google Scholar] [CrossRef]
- Dall, J.; Christensen, M. Random geometric graphs. Phys. Rev. E 2002, 66, 016121. [Google Scholar] [CrossRef]
- Ochoa, S.F.; Fortino, G.; Fatta, G.D. Cyber-physical systems, internet of things and big data. Future Gener. Comput. Syst. 2017, 75, 82–84. [Google Scholar] [CrossRef]
- Stankovic, J.A. Research directions for the internet of things. IEEE Internet Things J. 2014, 1, 3–9. [Google Scholar] [CrossRef]
- Xu, L.D.; He, W.; Li, S. Internet of things in industries: A survey. IEEE Trans. Ind. Inform. 2014, 10, 2233–2243. [Google Scholar] [CrossRef]
- Murakami, M.; Ishikura, S.; Kominami, D.; Shimokawa, T.; Murata, M. Robustness and efficiency in interconnected networks with changes in network assortativity. Appl. Netw. Sci. 2017, 2, 6. [Google Scholar] [CrossRef] [PubMed]
- Van Mieghem, P.; Wang, H.; Ge, X.; Tang, S.; Kuipers, F.A. Influence of assortativity and degree-preserving rewiring on the spectra of networks. Eur. Phys. J. B 2010, 76, 643–652. [Google Scholar] [CrossRef] [Green Version]
- Chang, Z.; Zhou, Z.; Zhou, S.; Chen, T.; Ristaniemi, T. Towards service-oriented 5G: virtualizing the networks for everything-as-a-service. IEEE Access 2018, 6, 1480–1489. [Google Scholar] [CrossRef]
- Gupta, A.; Jha, R.K. A survey of 5G network: Architecture and emerging technologies. IEEE Access 2015, 3, 1206–1232. [Google Scholar] [CrossRef]
- Kleinrock, L. Queueing Systems, Volume 2: Computer Applications; Wiley: New York, NY, USA, 1976; Volume 66. [Google Scholar]
- Bullmore, E.; Sporns, O. The economy of brain network organization. Nat. Rev. Neurosci. 2012, 13, 336–349. [Google Scholar] [CrossRef] [PubMed]
- Achard, S.; Salvador, R.; Whitcher, B.; Suckling, J.; Bullmore, E. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J. Neurosci. 2006, 26, 63–72. [Google Scholar] [CrossRef] [PubMed]
| Symbol | Node State | |||
|---|---|---|---|---|
 | removed | 0 | 0 | 0 |
 | exists | 1 | 0 | 0 |
 | locally available | 1 | 1 | 0 |
 | globally available | 1 | 1 | 1 |
| Variable | Value | Description | Equation |
|---|---|---|---|
| {0,1} | Existing state of node i | – | |
| {0,1} | Local effectiveness of node i | Equation (1) | |
| {0,1} | Global effectiveness of node i | Equations (3) and (5) | |
| , | {0,1} | Probability information for message passing sent from node i to j | Equations (2) and (4) |
| [0,∞] | Collective influence of node i | Equations (6) and (7) | |
| , | – | Index for P-node x and V-node x on VN k | – |
| , | – | Index for P-interface y of and V-interface y of | – |
| given | Buffer capacity for P-interface y of | – | |
| {0,1} | Availability state for P-interface y of | – | |
| [0,∞] | Traffic state for V-interface y of at time t | – | |
| {0,1} | Vacancy state for V-interface y of at time t | Equations (8) and (10) | |
| {0,1} | Traffic state for V-interface y of at time t | Equations (9), (11) and (12) | |
| , | [0,∞] | Collective influence of and | Equations (13)–(15) |
| [−1,1] | Assortativity for intra-network connectivity | Equation (17) | |
| [−1,1] | Assortativity for inter-network connectivity | Equation (21) | |
| , | given | Number of P-nodes and V-nodes on VN k | – |
| , | given | Number of P-links and V-links on VN k | – |
| W | given | Bandwidth for P-interfaces | – |
| given | Arrival rate of packets | – | |
| R | given | Number of packet re-transmission | – |
| Type-SD | Type-UD | Type-DD | |
|---|---|---|---|
| Interdependence of PN-VN | yes | yes | yes |
| Interdependence of VN-VN | no | yes | yes |
| Utilization guarantee | yes | no | yes |
| Utilization efficiency | no | yes | yes |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murakami, M.; Kominami, D.; Leibnitz, K.; Murata, M. Reliable Design for a Network of Networks with Inspiration from Brain Functional Networks. Appl. Sci. 2019, 9, 3809. https://doi.org/10.3390/app9183809
Murakami M, Kominami D, Leibnitz K, Murata M. Reliable Design for a Network of Networks with Inspiration from Brain Functional Networks. Applied Sciences. 2019; 9(18):3809. https://doi.org/10.3390/app9183809
Chicago/Turabian StyleMurakami, Masaya, Daichi Kominami, Kenji Leibnitz, and Masayuki Murata. 2019. "Reliable Design for a Network of Networks with Inspiration from Brain Functional Networks" Applied Sciences 9, no. 18: 3809. https://doi.org/10.3390/app9183809
APA StyleMurakami, M., Kominami, D., Leibnitz, K., & Murata, M. (2019). Reliable Design for a Network of Networks with Inspiration from Brain Functional Networks. Applied Sciences, 9(18), 3809. https://doi.org/10.3390/app9183809





