A Method of Ontology Integration for Designing Intelligent Problem Solvers
Abstract
:Featured Application
Abstract
1. Introduction
- Practicality: The method for knowledge integration must be able to represent the real-world knowledge domain in a knowledge base, produce an inference engine that reasons upon the knowledge base, and solve practical problems via a similar reasoning process to that of humans;
- Accuracy: The components of the knowledge domain must be represented precisely and fully using the knowledge integration method, in a way that simulates human acquisition.
2. Related Works
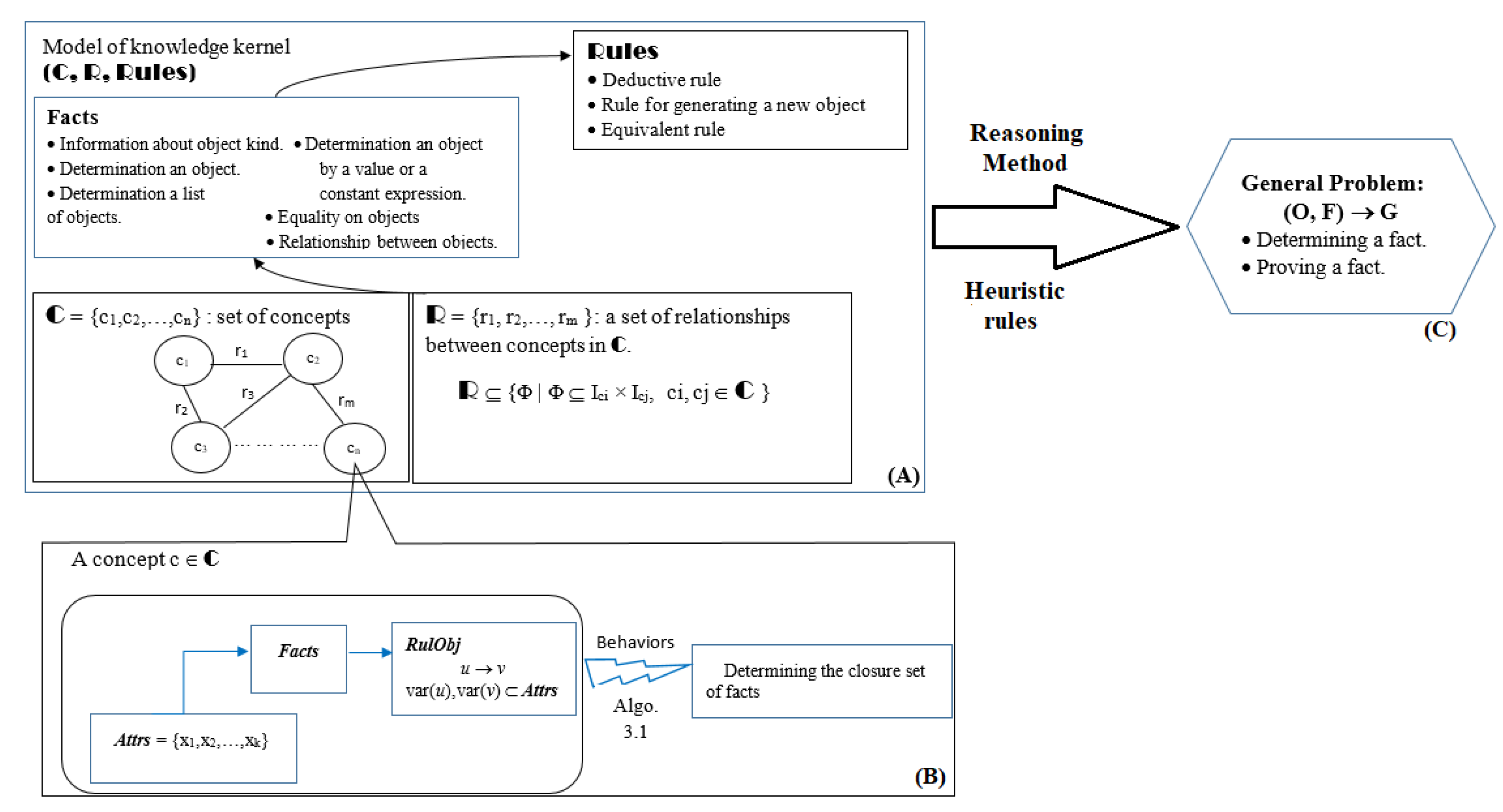
3. The Knowledge Kernel
3.1. Model of Knowledge Kernel
3.1.1. Structure of the Kernel
3.1.2. Unification of Facts
- f1 and f2 have them same kind of k;
- And if k = 1, 2, it means f1 and f2 are facts of information about object kind or determination of an object;
3.1.3. Rules—Set of Rules
- r is a deductive rule, it has the form u(r)→ v(r), where u(r), v(r) are sets of facts;
- r is a deductive rule for generating a new object, it has the form u(r)→ v(r), where u(r) and v(r) are sets of facts, they satisfy the conditions: ∃ object o, o ⊙ v(r) and not(o ⊙ u(r));
- r is an equivalent rule: h(r), u(r) ↔ v(r), where h(r), u(r) and v(r) are sets of facts, they satisfy the conditions: h(r), u(r)→ v(r), and h(r), v(r)→ u(r) are true.
3.2. Problems and Reasoning Methods on the Kernel Model
3.2.1. Problem on an Object
| Algorithm 1. Determine the closure of a set of facts. | |
| Input: Object Obj = (Attrs, Facts, RulObj), F is a set of facts related to Obj; | |
| Output: Obj.Closure(F). | |
| Step 0: Initialize variables flag: = true; KnownFacts: = F ⊔ Obj.Facts; Step 1. Classify the kinds of facts in KnownFacts; Step 2. Determine new facts from facts in KnownFacts by using the reasoning rule; Step 3. Search the closure of facts of kind 2 in KnownFacts; for fact2 in KnownFacts do; if Kind(fact2) = 2 and fact2 ∈ C then # fact2 is a determined object; KnownFacts: = KnownFacts ⊔ fact2. Attrs; end if; end do; Step 4. Search the closure of facts of kind 3 in KnownFacts; for fact3 in KnownFacts do; if Kind(fact3) = 3; then for i from 1 to NumberfElements(fact3) do KnownFacts: = KnownFacts ⊔ fact3[i]; end if; end do; | Step 5. Search the rule r in Obj.RulObj which can be applied on KnownFacts; while (flag! = false) do; 5.1. if (rule r can be found), then for e in v(r) do; KnownFacts: = KnownFacts ⊔ {e}; if (new facts can be determined), then determine new facts from facts in KnownFacts by using deduce rules; end if; if Kind(e) = 2 and e ∈ C, then KnownFacts: = KnownFacts ⊔ e.Closure(v(r)); if (new facts can be determined), then determine new facts from facts in KnownFacts by using deduction rules; end if; end do; # for end if; # 5.1 5.2. if (rule r cannot be found) then flag: = false; end if; end do; # while Step 6. Obj.Closure(F): = KnownFacts. |
3.2.2. General Problem with the Model of the Kernel
- -
- Determine”: to determine the fact f;
- -
- Prove”: to prove the fact f.
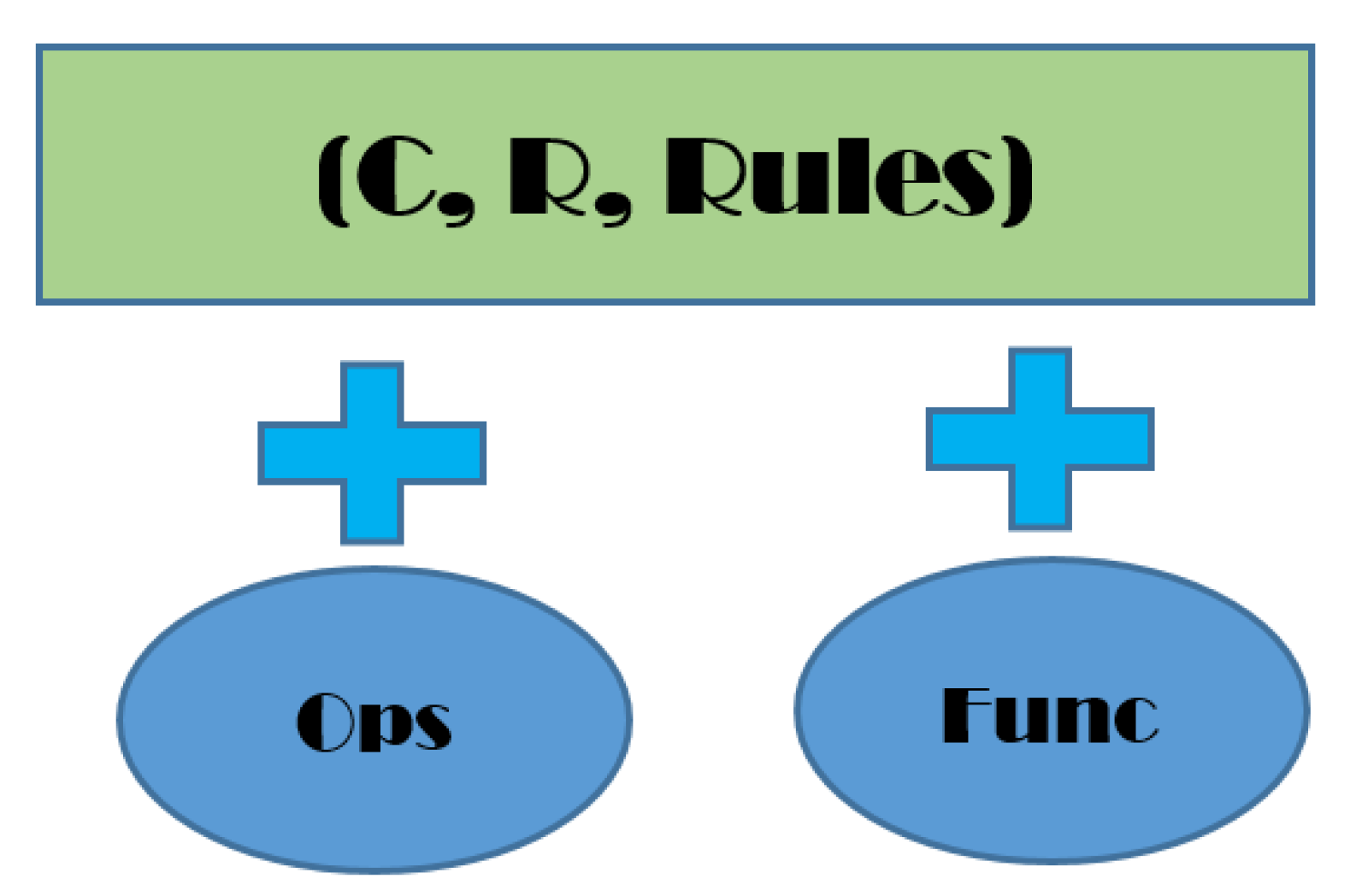
4. Integration Between the Kernel and Other Knowledge
4.1. The Method to Integrate the Kernel and Other Knowledge
4.1.1. Knowledge Components of Operators and Functions
4.1.2. Principle to Integrate the Kernel and Components of Operators and Functions
- Building the structure of the additional component: This structure has to be built upon the kernel such that the integration of new concepts is seamless and consistent. Any additional component should have specification language similar to that of the kernel;
- Adding more kinds of facts: Facts in any additional component need to represent the real knowledge and connect with former kinds of facts in the kernel. This is a study about the unification of facts;
- Adding more kinds of rules from the additional component: More kinds of rules have been studied based on the integrated knowledge and need to be merged into the kernel;
- Proposing the problems with the reasoning by integrating the kernel knowledge and additional knowledge.
4.2. Integration with the Knowledge of Operators—Ops-set
4.2.1. Structure of the Ops-Set
| Operator-def: = OPERATOR <name> |
| ARGUMENT: argument-def+ |
| RETURN: return-def+; |
| PROPERTY: prob-type+ |
| [constraint] |
| [variables] |
| [statements] |
| END OPERATOR. |
| argument-def: = <name>: type |
| return-def: = name: type |
| prob-type: = commutative|associative|identity |
| statement: = name: = <expression>. |
4.2.2. Problems and Reasoning Methods on the Knowledge of Operators
- -
- Compute”: to determine the value of f when f is an expression;
- -
- Transform”: transform an object into an expression between certain objects.
| Algorithm2. Given a knowledge domain combining with operators K = (C, R, Rules) + Ops, and a problem P = (O, F, E) → G on this knowledge domain. This algorithm will solve the problem P though the following steps: | |
| Input: The problem P = (O, F, E) → G | |
| Output: The solution of the problem P. | |
| The idea of the algorithm: Using objects in O, it determines the closure of each object by Algorithm 1. After that, it solves the problem (O, F) → G on the knowledge kernel. Secondly, it uses the knowledge of operators, which was integrated, to process the equations in E for getting new facts. Some new objects may be generated in this reasoning. If the goal G is achieved at any time, this algorithm will stop. | |
| Step 0: Initialize variables; flag: = true; KnownFacts: = F ⊔ E; Sol: = [ ]; # solution of problem; Step 1. Record elements in hypothesis and goal; Classify kinds of facts in F and E. Step 2. Check G; If G is obtained, then go to step 6. Step 3: Use objects in set O and the set of facts in F and E to determine the closure of each object by Algorithm 1; Step 4: Use the equations in E to generate the new facts as relationship form; Use the relationships in F to generate the equations; Update KnownFacts and Sol. Step 5: Select a rule in the set Rules for producing new facts or new objects; While (flag! = false) and not (G is determined) do Search r in the Rules set, which can be applied to KnownFacts. 5.1. Case: r is an equation rule; if (r has form: g = h), then: r can generate a set of new facts. A: = r(KnownFacts) = {f|Kind(f) = 2 ∨ Kind(f) = 3 ∨ Kind(f) = Op.1 ∨ Kind(f) = Op.2} s: = [r, KnownFacts, A]; Sol: = [op(Sol), s]; | if (r generates a new object o) and not (o ⊙ KnownFacts), then: KnownFacts: = KnownFacts ⊔ A; Go to Step 3 with new object o; Or else: KnownFacts: = KnownFacts ⊔ A; continue; end if; end if; #5.1 5.2. Case: r has another kind; Transform equations in E to relationships between objects if possible; Update KnownFacts and Sol; Solve the problem (O, KnownFacts) → G based on the knowledge of the kernel (C, R, Rules) by algorithms in Section 3.2; end if; #5.2 Step 6: Conclusion of the problem; If G is determined, then: Problem (O, F, E) → G is solvable; Sol is a solution of the problem; Reduce the solution found by excluding redundant rules and information in the solution; Or else Problem (O, F, E) → G is unsolvable; end if; |
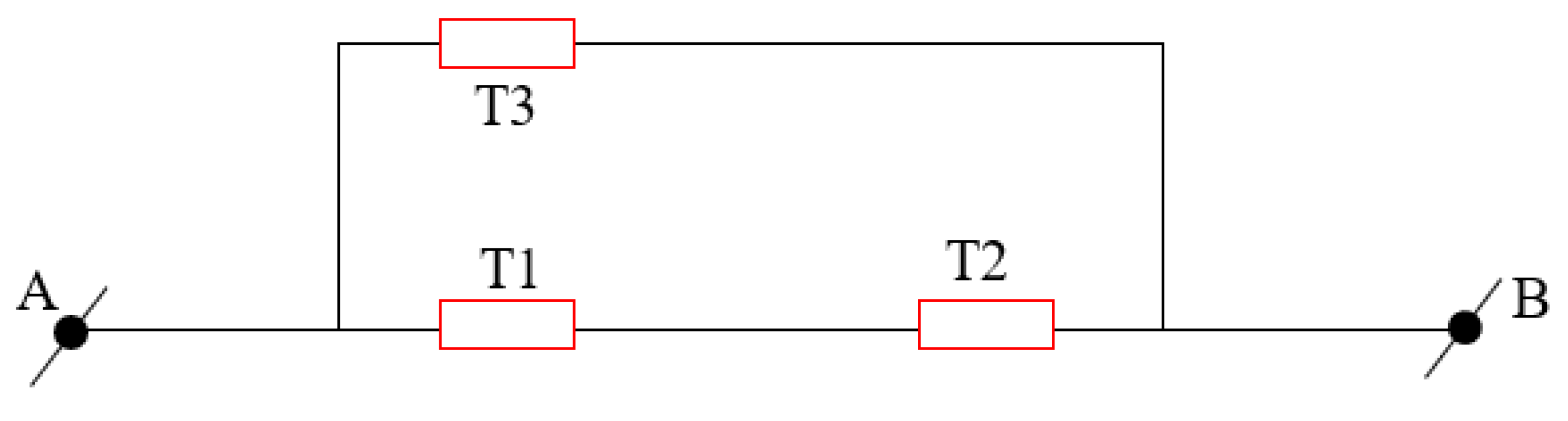
| O: = {T1, T2, T3: RESISTOR; AB: CIRCUIT} |
| F: = {AB = T1 + T2//T3, T1.R = 45, T3.R = 90, T3.I = 0.3, AB.I = 0.5} |
| G: = {T1.I}. |
4.3. Integration with the Knowledge of Functions—Funcs-set
4.3.1. Structure of the Funcs-Set
| function-def: = FUNCTION name; |
| ARGUMENT: argument-def+ |
| RETURN: return-def; |
| [constraint]; |
| [facts]; |
| [variables]; |
| [statements]; |
| ENDFUNCTION; |
| statements: = statement-def+; |
| statement-def: = assign-stmt|if-stmt|for-stmt; |
| asign-stmt: = name: = expr; |
| if-stmt: = IF logic-expr THEN statements+ ENDIF; |
| |IF logic-expr THEN statements+ ELSE statements+ ENDIF; |
| for-stmt: = FOR name IN [range] DO statements+ ENDFOR; |
4.3.2. Problems and Reasoning Methods on the Knowledge of Functions
- -
- Compute”: to determine the value of f when f is a function;
- -
- Prove”: prove the fact f.
| Algorithm 3. Compute the value of a function. | |
| Give a knowledge domain combining functions K = (C, R, Rules) + Funcs, and a problem P = (O, F) → G on this knowledge domain, with G = {“Compute”: g(x1, x2, …, xn)}, where g is a function and xk are objects (k = 1 … n). | |
| Input: The problem P = (O, F) → G | |
| G = {“Compute”: g(x1, x2, …, xn)} with: g: Ic1 × Ic2 … × Icn → Ic | |
| xk ∈ Ick, ck ∈ C (1 ≤ k ≤ n), c ∈ C | |
| Output: The value of g(x1, x2, …, xn). | |
| The idea of the algorithm: The set F is split into two sets: F1—the set of facts in the knowledge kernel, F2—the set of facts about functions. Firstly, using the knowledge kernel, the algorithm uses the objects and facts in the hypothesis (O, F1) to determine new facts by applying the sub-algorithm for solving problems on the kernel model, as in Section 3.2.2. Secondly, combining with the facts in the set F2, the algorithm uses the integrated knowledge of functions to compute the value of g. | |
| Step 0: Initialize variables; KnownFacts: = F; ObjectGoal: = {x1, x2, …, xn}; Sol: = [ ]; # solution of problem. Step 1. Record elements in hypothesis and goal. Classify kinds of facts in F = F1 ∪ F2; F1: = set of facts with kinds in the kernel knowledge model; F2: = set of facts with kinds about functions (Fu.1, Fu.2, Fu.3, Fu.4); Determine the form of the function g in G. Step 2. Check G. If G is obtained, then: Go to step 6. Step 3: Produce new facts based on the hypothesis; Apply objects and facts in the hypothesis (O, F1) to determine new facts by using the algorithm for solving problems on the kernel model, as in Section 3.2.2; Update KnownFacts and Sol. Step 4: If g has form 1, then: Apply facts in F2 and KnownFacts to compute the value of function; Update KnownFacts and Sol. | Apply objects in ObjectGoal and facts in KnownFacts to compute the value of g(x1, x2, …, xn) based on the specification of g; Update KnownFacts and Sol; End if; Go to Step 6. Step 5: If g has form 2, then: Apply objects in ObjectGoal and statements of functions in F2 to produce new facts; Update KnownFacts; Apply facts in KnownFacts and statements of the function g to compute the value of g(x1, …, xn); Update KnownFacts and Sol. end if; Go to Step 6; Step 6: Conclusion of problem; If G is determined, then: Problem (O, F) → G is solvable; Sol is a solution of problem; Reduce the solution found by excluding redundant rules and information in the solution. Or else, problem (O, F) → G is unsolvable; end if; |
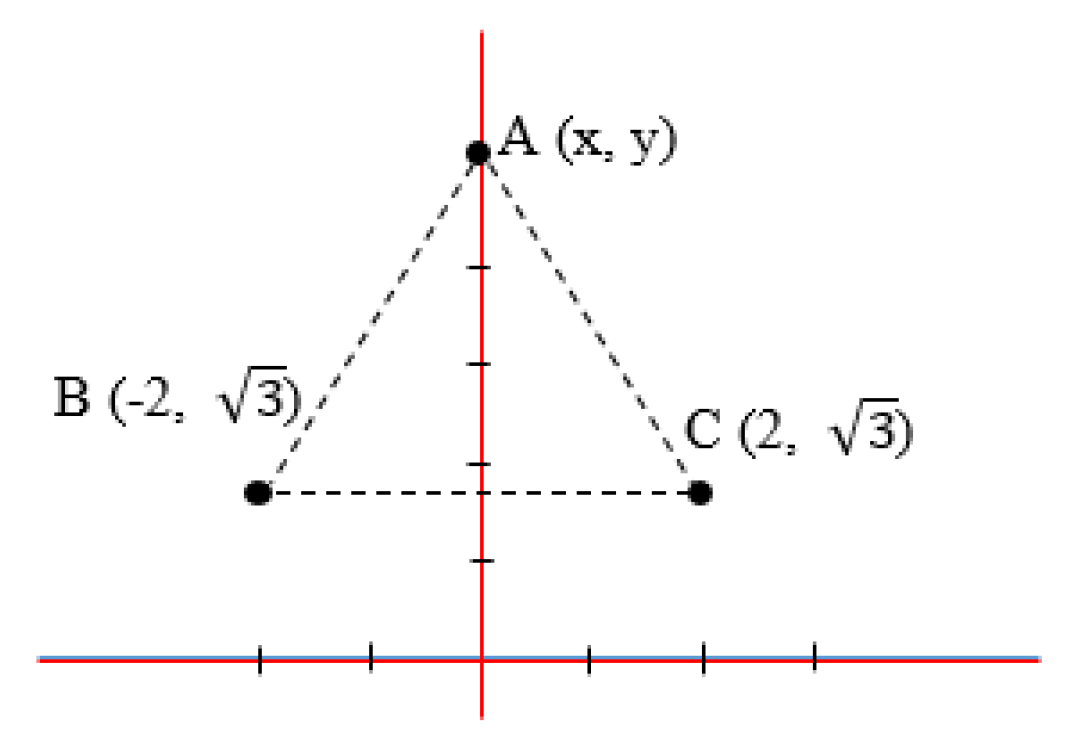
| O:= {A, B, C: POINT, ABC: EquilateralTriangle}; |
| G:= {Compute: Distance(A,B)}. |
| Algorithm 4. Prove the equality between two functions. | |
| Given a knowledge domain combining functions K = (C, R, Rules) + Funcs, and a problem P = (O, F) → G on this knowledge domain, with G = {“Prove”: g(x1, x2, …, xn) = h(y1, y2, …, ym)}, where g, h are functions and xi, yj are objects (i = 1…n, j = 1… m). | |
| Input: The problem P = (O, F) → G. | |
| G = {“Prove”: g(x1, x2, …, xn) = h(y1, y2, …, ym)}, | |
| with: c ∈ C g: Ic1× Ic2… × Icn→ Ic xi ∈ Ici, ci ∈ C (1 ≤ i ≤ n) | h: Ib1 × Ib2 …× Ibm → Ic yk ∈ Ibk, bk ∈ C (1 ≤ k ≤ m) |
| Output: Solution of the proof: g(x1, x2, …, xn) = h(y1, y2, …, ym). | |
| The idea of the algorithm: It uses Algorithm 3 to compute the values of g(x1, x2, …, xn) and h(y1, y2, …, ym) and compare them. In a case where they cannot be computed, from two sets of objects O1 = {x1, …, xn} and O2 = {y1, …, ym}, the algorithm uses the hypothesis (O1, F) and (O2, F) to determine new facts by applying the algorithm for solving problems on the kernel model, as in Section 3.2.2. Based on those results, it concludes the solution to the current problem. | |
| Step 0: Initialize variables; flag: = true; KnownFacts: = F; O1: = {x1, x2, …, xn}; O2: = {y1, y2, …, ym}; Sol: = [ ]; # solution of the problem. Step 1. Record the elements in the hypothesis and goal. Step 2: G1: = {“Compute”: g(x1, x2, …, xn)}; G2: = {“Compute”: h(y1, y2, …, ym)}; If problems (O, F) → G1 and (O, F) → G2 are solvable by using Algorithm 4, then: if the value of g(x1, x2, …, xn) = the value of h(y1, y2, …, ym), then: G is determined, and go to step 5; end if; end if; Step 3: Produce new facts based on the hypothesis; Apply objects and facts in the hypothesis (O, F) to determine new facts by using the algorithm for solving problems on the kernel model, as in Section 3.2; Update KnownFacts and Sol; | Step 4: F1: = set of new facts produced from hypothesis (O1, KnownFacts) by using the algorithm for solving problems on the kernel model as Section 3.2 F2: = set of new facts produced from hypothesis (O2, KnownFacts) by using the algorithm for solving problems on the kernel model as Section 3.2 Update Sol; If (O2 m F1) or (O1 m F2), then: If statements of g are similar to statements of h, then: G is determined and update Sol; Goto step 5; end if; end if; Step 5: Conclusion of problem; If G is determined, then: Problem (O, F) → G is solvable; Sol is a solution of the problem; Reduce the solution found by excluding redundant rules and information in the solution; Or else: Problem (O, F) → G is unsolvable; end if; |
4.4. Heuristic Rules
5. Application for Intelligent Systems in Education
5.1. Representation of the Knowledge of Matrixes Using the Kernel Model
| SquareMatrix: Matrix (A square matrix is a matrix); |
| Attrs: = Matrix.Attrs ∪ {inv, diag, det, sym}; |
| diag: Boolean//the diagonalizable property; |
| inv: Boolean //the invertible property; |
| sym: Boolean//the symmetric property; |
| permutation: Boolean//the property about permutation; |
| Facts: = {m = n}, |
| RulObj: = Matrix.RulObj ∪ {r1: det # 0 → inv = 1, |
| r2: ∀ i, j, 1 ≤ i ≤ n, 1 ≤ j ≤ n: a[i][j] = a[j][i] → sym = 1}. |
5.2. Design Knowledge Base of Linear Algebra Using the Integrating Model (C, R, Rules) + Ops.
5.2.1. Knowledge Base of Linear Algebra
5.2.2. Types of Exercises in Linear Algebra
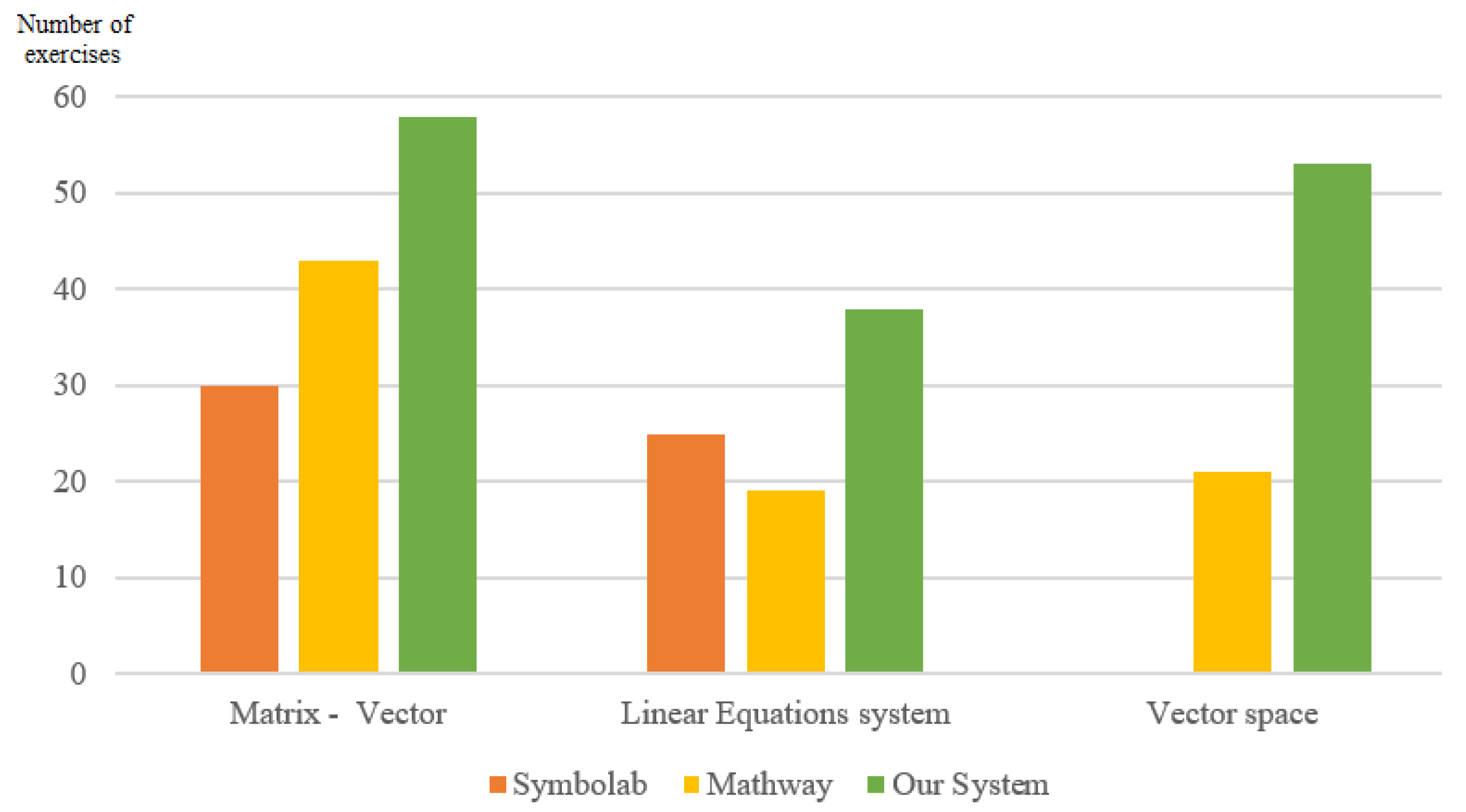
- Problems with the Matrix–Vector: Find the rank of a matrix, find the inverse matrix, find the value of an expression between matrixes.
- Problems with the Linear Equations System: Solve a linear equations system by the Gaussian method and Cramer method.
- Problems with the Vector Space: Determine the independence of vectors, determine the basis of a vector space.
| O: = {W: VectorSpace, x1, x2, x3, x4: Ñ, A: 2Ivector}; |
| F: = {A = {(x1, x2, x3, x4)|x1 = 2x2 , x1 = x3}, A is a spanning-set of W}; |
| G: = {Determine: Based-set of W}. |
| Step 1: From A = {(x1, x2, x3, x4)|x1 = 2x2, x1 = x3}, let u: Vector: u = (x1, x2, x3, x4), u ∈ A. Step 2: From u = (x1, x2, x3, x4), u ∈ A, A = {(x1, x2, x3, x4)|x1 = 2x2, x1 = x3}, then u = (x1, ½.x1, x1, x4). Step 3: From u = (x1, ½.x1, x1, x4), then u = (x1, ½.x1, x1, 0) + (0, 0, 0, x4), u = (1, ½, 1, 0) *x1 + (0, 0, 0, 1) *x4. Step 4: From u = (1, ½, 1, 0) *x1 + (0, 0, 0, 1) *x4, let a1: Vector, a2: Vector, a1 = (1, ½, 1, 0) a2 = (0, 0, 0, 1). | Step 5: Let B = {a1 = (1, ½, 1, 0), a2 = (0, 0, 0, 1)}, then B is linearly independent. Step 6: From u = (1, ½, 1, 0) *x1 + (0, 0, 0, 1) *x4, u ∈ A, x1 ∈ Ñ, x4 ∈ Ñ, a1 = (1, ½, 1, 0), a2 = (0, 0, 0, 1), B = {a1, a2}, A is a spanning-set of W, then B is a spanning-set of W. Step 7: From B is a spanning-set of W, B is linearly independent. Then, B is a based-set of W |
5.3. Design Knowledge Base of Graph Theory Using the Integrating Model (C, R, Rules) + Funcs
5.3.1. Knowledge Base of Graph Theory
5.3.2. Kinds of Exercises in Graph Theory
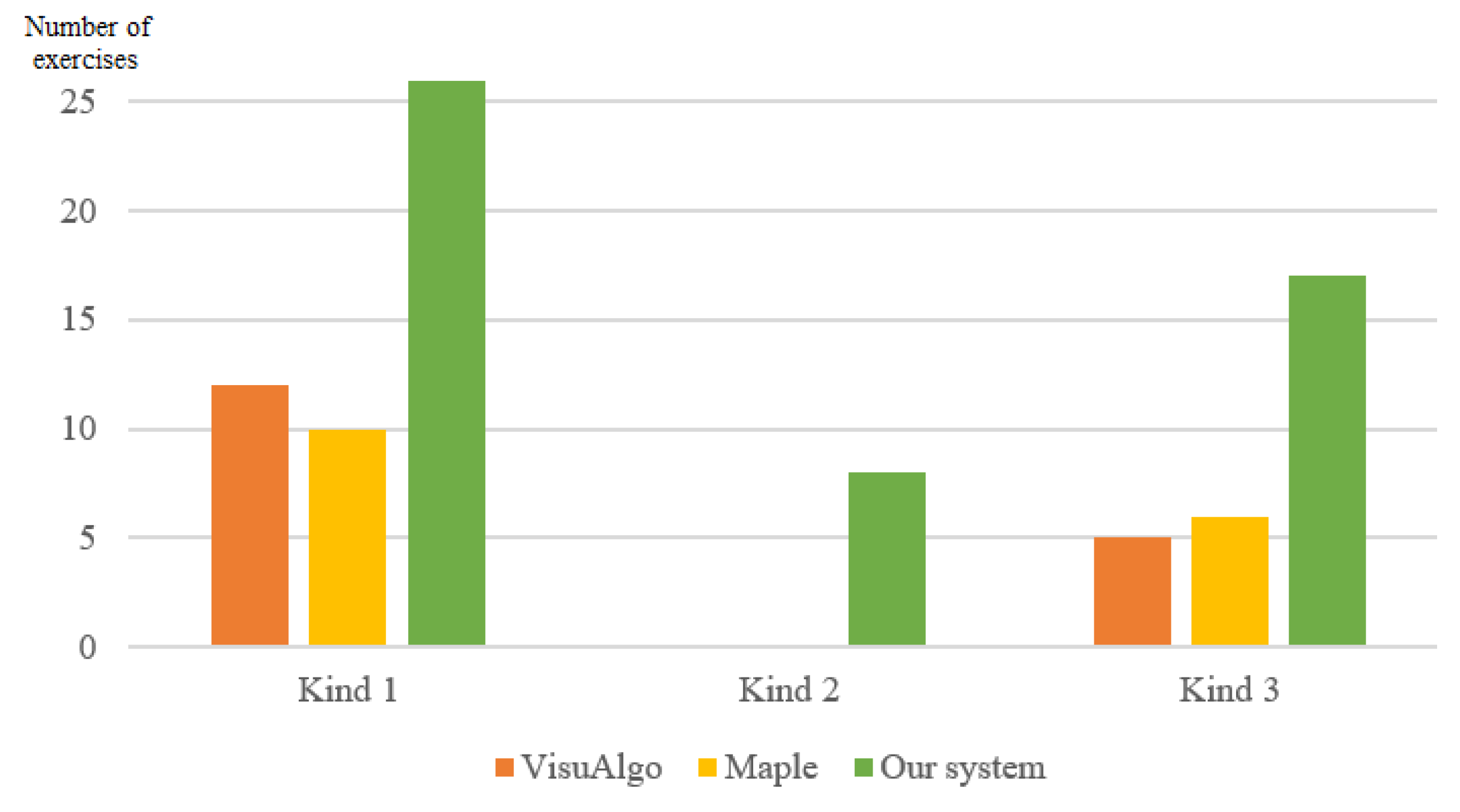
- Type 1: find the shortest paths between nodes in a graph, find a minimum spanning tree for a weighted undirected graph. These problems also have additional conditions;
- Type 2: Determine a graph from an expression of graphs;
- Type 3: Prove a property of a graph or a relationship between two graphs.
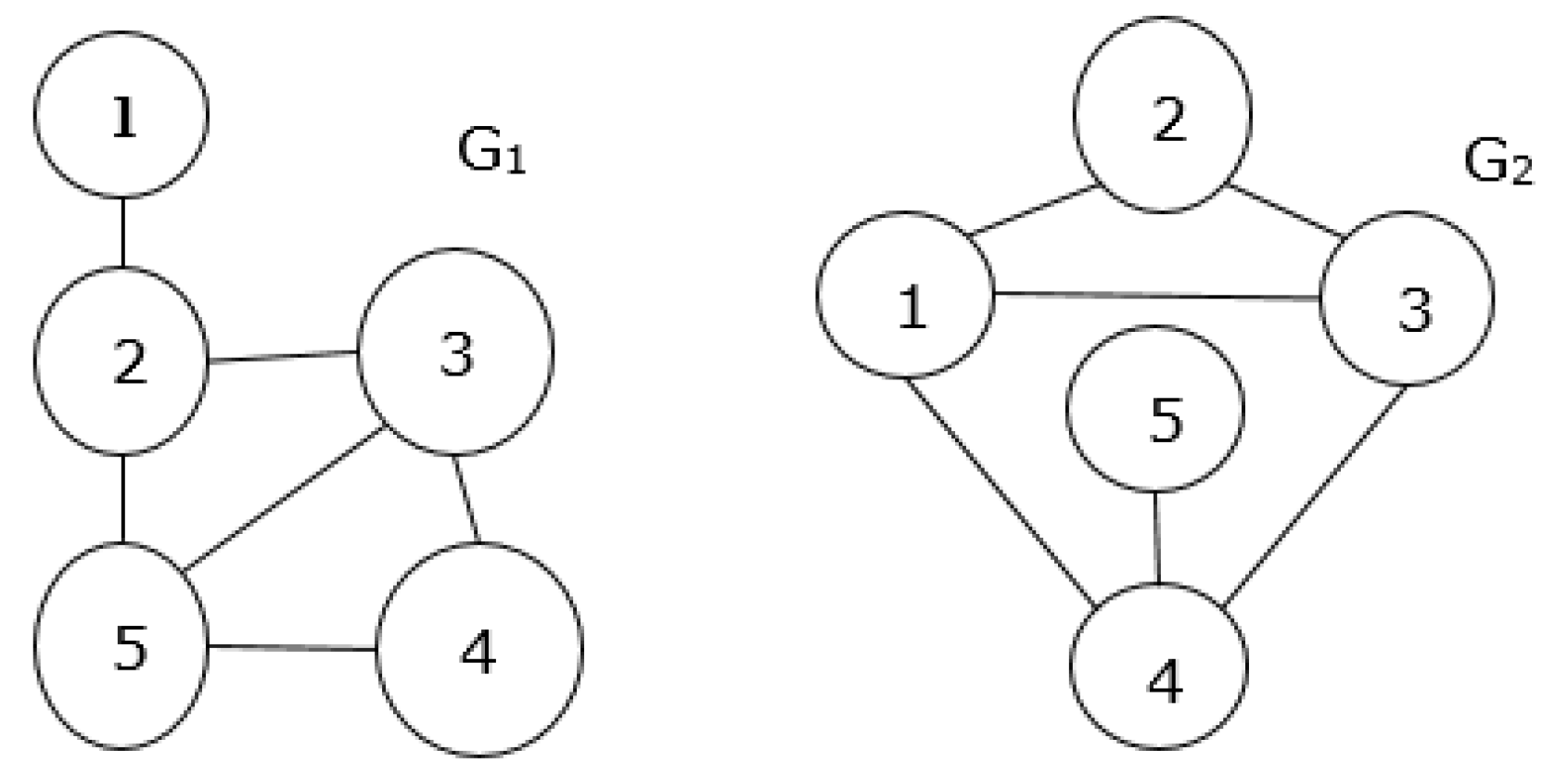
| O: = {G1, G2: Graph}, |
| F: = {G1.Adj = {(0, 1, 0, 0, 0), (1, 0, 1, 0, 1), (0, 1, 0, 1, 1), (0, 0, 1, 0, 1), (0, 1, 1, 1, 0)}, |
| G2.Adj = {(0, 1, 1, 1, 0), (1, 0, 1, 0, 0), (1, 1, 0, 1, 0), (1, 0, 1, 0, 1), (0, 0, 0, 1, 0)}, |
| G: = {“Prove”: G1 and G2 are isomorphic} |
6. Experimental Results
6.1. Intelligent Problem Solver in Linear Algebra
- First-year students (63 students ~72%): students who took this course the first time;
- The other students (24 students ~28%): students who took this course again because they had failed before.
6.2. Intelligent Problem Solver in Graph Theory
7. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Noy, N.; McGuinness, D. Final Report on the 2013 NSF Workshop on Research Challenges and Opportunities in Knowledge Representation; National Science Foundation Workshop Report: Alexandria, VA, USA, 2013. [Google Scholar]
- Mehta, N.; Bharadwaj, A. Knowledge Integration in Outsourced Software Development. J. Manag. Inf. Syst. 2015, 32, 82–115. [Google Scholar] [CrossRef]
- Wolfram|Alpha. Available online: https://www.wolframalpha.com/ (accessed on 7 September 2019).
- IMS Learning Information Services Tools. Available online: https://www.k-int.com/products/ims-learning-information-services-tools/ (accessed on 7 September 2019).
- Bassetta, M.; Fatta, F.; Manti, A. San Pietro di Deca in Torrenova: Integrated Survey Techniques for the Morphological Transformation Analysis. In Handbook of Research on Emerging Technologies for Architectural and Archaeological Heritage; IGI Global: Hershey, PA, USA, 2017. [Google Scholar]
- Sowa, J.F. Knowledge Representation: Logical, Philosophical, and Computational Foundations; Brooks Cole: Pacific Grove, CA, USA, 2000. [Google Scholar]
- Gayathri, R.; Uma, V. Ontology based knowledge representation technique, domain modeling languages and planners for robotic path planning: A survey. ICT Express 2018, 4, 69–74. [Google Scholar]
- Truong, H.B.; Duong, T.H.; Thanh, N.N. A hybrid method for fuzzy ontology integration. Cyber. Syst. Int. J. 2013, 44, 133–154. [Google Scholar] [CrossRef]
- Provine, R.; Schlenoff, C.; Balakirsky, S.; Smith, S.; Uschold, M. Ontology-based methods for enhancing autonomous vehicle path planning. Robot Auton. Syst. 2004, 49, 123–133. [Google Scholar] [CrossRef]
- Fratini, S.; Nogueira, T.; Policella, N. Integrating modeling and knowledge representation for combined task, resource and path planning in robotics. In Proceedings of the Workshop on Knowledge Engineering for Planning and Scheduling—27th International Conference on Automated Planning and Scheduling (ICAPS 2017), Pittsburgh, PA, USA, 18–23 June 2017. [Google Scholar]
- Ong, J.; Remolina, E.; Prompt, A.; Robinson, P.; Sweet, A.; Nishikawa, D. Software testbed for developing and evaluating integrated autonomous systems. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015; pp. 1–12. [Google Scholar]
- Do, N.V. Ontology COKB for Knowledge Representation and Reasoning in Designing Knowledge-Based Systems. In Communications in Computer and Information Science (CCIS); Springer: Berlin/Heidelberg, Germany, 2015; Volume 513, pp. 101–118. [Google Scholar]
- Anton, H.; Rorres, C. Elementary Linear Algebra, 10th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Dumontier, M.; Baker, C.J.; Baran, J.; Callahan, A.; Chepelev, L.; Cruz-Toledo, J.; Del Rio, N.R.; Duck, G.; Furlong, L.I.; Keath, N.; et al. The Semanticscience Integrated Ontology (SIO) for biomedical research and knowledge discovery. J. Biomed. Semant. 2014, 5, 14. [Google Scholar] [CrossRef] [PubMed]
- Chabeb, Y.; Tata, S.; Belaïd, D. Toward an integrated ontology for Web services. In Proceedings of the 2009 Fourth International Conference on Internet and Web Applications and Services, Venice/Mestre, Italy, 24–28 May 2009; pp. 463–467. [Google Scholar]
- Bobillo, F.; Straccia, U. fuzzyDL—An Expressive Fuzzy Description Logic Reasoner. In Proceedings of the 2008 IEEE International Conference on Fuzzy Systems, Hong Kong, China, 1–6 June 2008; pp. 923–930. [Google Scholar]
- Bang, T.H.; Quach, X.H. An Overview of Fuzzy Ontology Integration Methods Based on Consensus Theory. In Advanced Computational Methods for Knowledge Engineering; Van Do, T., Le Thi, H.A., Nguyen, N.T., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 282, pp. 217–227. [Google Scholar]
- Do, N.V.; Nguyen, H.D.; Mai, T.T. Intelligent Educational Software in Discrete Mathematics and Graph Theory. In Proceedings of the 17th International Conference on Intelligent Software Methodologies, Tools, and Techniques (SOMET 2018), Granada, Spain, 26–28 September 2018; Volume 303, pp. 925–938. [Google Scholar]
- Munir, K.; Anjum, M.S. The use of ontologies for effective knowledge modelling and information retrieval. Appl. Comput. Inform. 2018, 14, 116–126. [Google Scholar] [CrossRef]
- Do, N.V.; Nguyen, H.D.; Selamat, A. Knowledge-Based model of Expert Systems using Rela-model. Int. J. Softw. Eng. Knowl. Eng. (IJSEKE) 2018, 28, 1047–1090. [Google Scholar] [CrossRef]
- Do, N.V.; Nguyen, H.D.; Mai, T.T. Designing an Intelligent Problems Solving System based on Knowledge about Sample Problems. In Proceedings of the 5th Asian conference on Intelligent Information and Database Systems (ACIIDS 2013), Kuala Lumpur, Malaysia, 18–20 March 2013; Volume 7802, pp. 465–475. [Google Scholar]
- Nguyen, H.D.; Do, V.; Pham, V.T.; Inoue, K. Solving problems on a knowledge model of operators and application. Int. J. Digit. Enterp. Technol. (IJDET) 2018, 1, 37–59. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Do, N.V.; Tran, N.P.; Pham, X.H. Criteria of a Knowledge model for an Intelligent Problems Solver in Education. In Proceedings of the 10th IEEE International Conference on Knowledge and Systems Engineering (KSE 2018), Ho Chi Minh City, Vietnam, 1–3 November 2018; pp. 288–293. [Google Scholar]
- Lang, S. Linear Algebra, 3rd ed.; Undergraduate Texts in Mathematics; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Fournier, J. Graph Theory and Applications—With Exercises and Problems; Wiley Online Library: Hoboken, NJ, USA, 2010. [Google Scholar]
- Chartrand, G.; Zhang, P. A first Course in Graph Theory; Dover Pub.: Mineola, New York, NY, USA, 2006. [Google Scholar]
- Mier, A.; Maureso, M. Graph Theory: Exercises and Problems; Barcelona School of Informatics: Barcelona, Spain, 2015. [Google Scholar]
- Symbolab. Available online: www.symbolab.com (accessed on 7 September 2019).
- Mathway. Available online: https://www.mathway.com/LinearAlgebra (accessed on 7 September 2019).
- Nguyen, H.D.; Do, N.V. Intelligent Problems Solver in Education for Discrete Mathematics. In Proceedings of the 16th International Conference on Intelligent Software Methodologies, Tools, and Techniques (SOMET_17), Kitakyushu, Japan, 26–28 September 2017; Volume 297, pp. 21–34. [Google Scholar]
- VisuAlgo. Available online: https://visualgo.net/en (accessed on 7 September 2019).
- Maple Software. Available online: https://www.maplesoft.com/ (accessed on 7 September 2019).
| C | R | Facts |
|---|---|---|
| - Each concept c ∈ C is a class of objects, it has an instance set Ic including objects. • Fundamental concepts are the default concepts of the knowledge domain. A set of fundamental concepts is denoted: Co - Set C is a set of concepts, the structure of an object in a concept is a tube: (Attrs, Facts, RulObj), in which: ◊ Attrs is a set of attributes: Attrs = AttrsVar ∪ AttrsList An attribute in AttrsVar is a variable which has the kind in Co: AttrsVar ⊆ {x|x:c, c ∈ Co}. An attribute in AttrsList is a list of variables which have the same kind in Co: AttrsList ⊆ {[x1, …, xn]|n ∈ 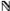 and xi: c, c ∈ Co}. and xi: c, c ∈ Co}.◊ Facts is a set of facts on attributes in Attrs. Facts ⊂ {f|f is a fact, var(f) ⊆ Attrs} ◊ RulObj is a set of deductive rules of the concept: RulObj ⊂ {u → v|u ⊆ Attrs, v ⊆ Attrs, u ⊓ v = Ø} | R ⊂ {Φ|Φ ⊆ Ici × Icj, ci, cj ∈ Co ∪ C, ci ∈ C ∨ cj ∈ C} In the case of ci = cj, the properties of a relationship Φ are considered: reflexive, symmetric, asymmetric, and transitive. * Relationships “is-a” < ∈ R: Let c1, c2 ∈ C: c2 < c1 ⇔ c2 is a sub-concept of c1 | Classify kinds of facts: 1/Information about kind of object Specification: x:c Condition: x ∈ Σ*, c ∈ C 2/Determination an object Specification: o Condition: o ∈ Ic, c ∈ C 3/Determination of a list of objects Specification: [o1, o2, …, on] Condition: n ∈ 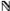 , oi ∈ Ic, , oi ∈ Ic, c ∈ C (1 ≤ i ≤ n) 4/Determination of an object by a value or a constant expression Specification: o = <const> Condition: o ∈ Ic, c ∈ C <const>: constant 5/Equality on objects Specification: x = y Condition: x,y ∈ Ic, c ∈ C or x = [x1, …, xn] and y = [y1, …, yn] with xi, yi ∈ Ic, c ∈ C (1 ≤ i ≤ n) 6/Relationship between objects Specification: x Φ y Condition: Φ ∈ R, x ∈ Icx, y ∈ Icy, cx ∈ C, cy ∈ C * Kind(f): kind of fact f. |
| Structure of the Ops-Set | Additional Facts | Additional Kind of Rules |
|---|---|---|
| Ops = O(1) ∪ O(2) In which: + Set of unary operators O(1): O(1) ⊂ {⊕: Ici → Ick|ci, ck ∈ C} + Set of binary operators O(2): O(2) ⊂ {⊗: Ici × Icj → Ick| ci, cj, ck ∈ C} Each operator is checked for its properties: commutation, association, identity. | Op.1. Dependence of an object by an expression. Specification: x = <expr> Condition: x ∈ Ic, c ∈ C <expr>: expression Op.2. Equality of expressions Specification: <expr1> = <expr2> Condition: <expr1>: expression <expr2>: expression | r is an equation rule, it has the form: g = h where g, h are expressions of objects. Denote: left(r) = g right(r) = h |
| Structure of the Funcs-Set | Additional Facts | Additional Kinds of Rules |
|---|---|---|
| Let F = {f|f is a function}: α: F → N: assigning the number of arguments to a function. Funcs ⊆ {f ∈ F|n = αK(f), f: Ic1 × Ic1 … × Icn → Ic, c1, c2,…, cn, c ∈ C}. Each function is checked for its properties: commutation. | Fu.1. Determination of a function. Specification: f(x1, x2, …, xn); Condition: f ∈ Funcs, n = α(f), f: Ic1 × Ic2 ×…× Icn → Ic, xk ∈ Ick, ck ∈ C (1 ≤ k ≤ n). Fu.2. Dependence of an object on a function. Specification: o = f(x1, x2, …, xn); Condition: f ∈ Funcs, n = α(f), f: Ic1 × Ic2 ×…× Icn → Ic, xk ∈ Ick, ck ∈ C (1 ≤ k ≤ n), o ∈ Ic, c ∈ C. Fu.3. Dependence of a function on an expression. Specification: f(x1, x2, …, xn) = <expr>. Condition: f ∈ Funcs, n = α(f), f: Ic1 × Ic2 ×…× Icn → Ic, xk ∈ Ick, ck ∈ C (1 ≤ k ≤ n), c ∈ C, <expr>: expression. Fu.4. Relationship between functions. Specification: f(x1, x2, …, xn) Φ g(y1, y2, …, ym). Condition: Φ ∈ R, f ∈ Funcs, g ∈ Funcs, n = α(f), m = α(g); c, c’ ∈ C; f: Ic1 × Ic2…× Icn → Ic, xk ∈ Ick, ck ∈ C (1 ≤ k ≤ n), g: Ib1 × Ib2…× Ibm → Ic’, yk ∈ Ibk, bk ∈ C (1 ≤ k ≤ m). | r is an equation rule, it has the form: f = g, where f, g are functions or expressions. Denote: left(r) = f right(r) = g |
| Chapter | Number of Testing Problems | Number of Problems that Can Be Solved | ||
|---|---|---|---|---|
| Symbolab | Mathway | Our System | ||
| Matrix–Vector | 65 | 30 | 43 | 58 |
| Linear Equations system | 39 | 25 | 19 | 38 |
| Vector space | 67 | 0 | 21 | 53 |
| Total | 171 | 55 | 83 | 149 |
| Criterion | Level | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Sufficient knowledge | 25% | 75% | |||
| Ability to solve common exercises | 24% | 76% | |||
| Pedagogy | 32% | 68% | |||
| Usefulness | 31% | 69% | |||
| Kind of Exercises | Number of Testing Exercises | Number of Problems that Can Be Solved | ||
|---|---|---|---|---|
| VisuAlgo | Maple | Our System | ||
| Type 1 | 28 | 12 | 10 | 26 |
| Type 2 | 11 | 0 | 0 | 8 |
| Type 3 | 25 | 5 | 6 | 17 |
| Total | 64 | 17 | 16 | 51 |
| Criterion | Level | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Sufficient Knowledge | 25% | 75% | |||
| Ability to solve common exercises | 24% | 76% | |||
| Pedagogy | 15% | 85% | |||
| Usefulness | 26% | 74% | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Do, N.V.; Nguyen, H.D.; Mai, T.T. A Method of Ontology Integration for Designing Intelligent Problem Solvers. Appl. Sci. 2019, 9, 3793. https://doi.org/10.3390/app9183793
Do NV, Nguyen HD, Mai TT. A Method of Ontology Integration for Designing Intelligent Problem Solvers. Applied Sciences. 2019; 9(18):3793. https://doi.org/10.3390/app9183793
Chicago/Turabian StyleDo, Nhon V., Hien D. Nguyen, and Thanh T. Mai. 2019. "A Method of Ontology Integration for Designing Intelligent Problem Solvers" Applied Sciences 9, no. 18: 3793. https://doi.org/10.3390/app9183793
APA StyleDo, N. V., Nguyen, H. D., & Mai, T. T. (2019). A Method of Ontology Integration for Designing Intelligent Problem Solvers. Applied Sciences, 9(18), 3793. https://doi.org/10.3390/app9183793




