SPICE Model Identification Technique of a Cheap Thermoelectric Cell Applied to DC/DC Design with MPPT Algorithm for Low-Cost, Low-Power Energy Harvesting
Abstract
1. Introduction
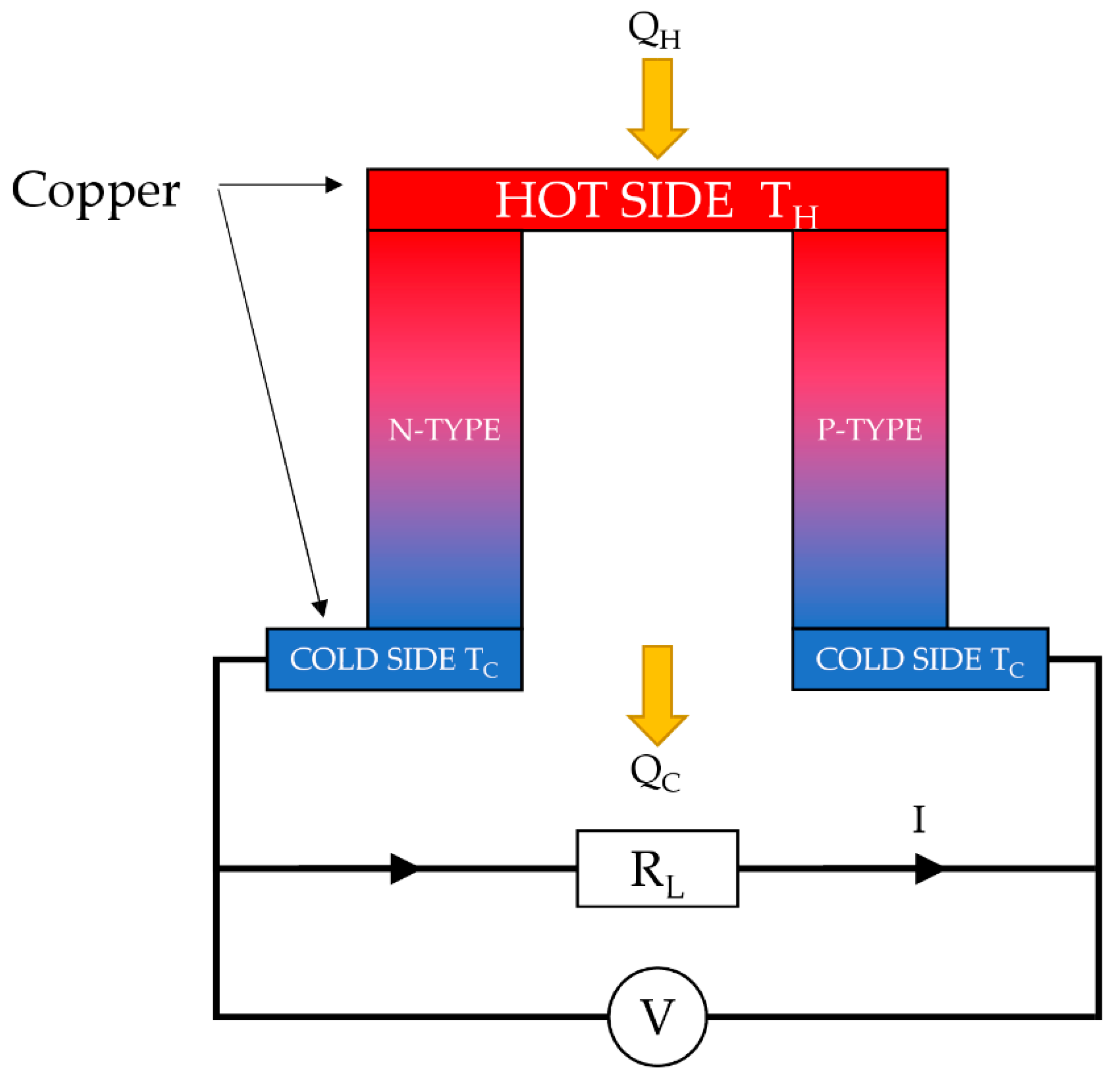
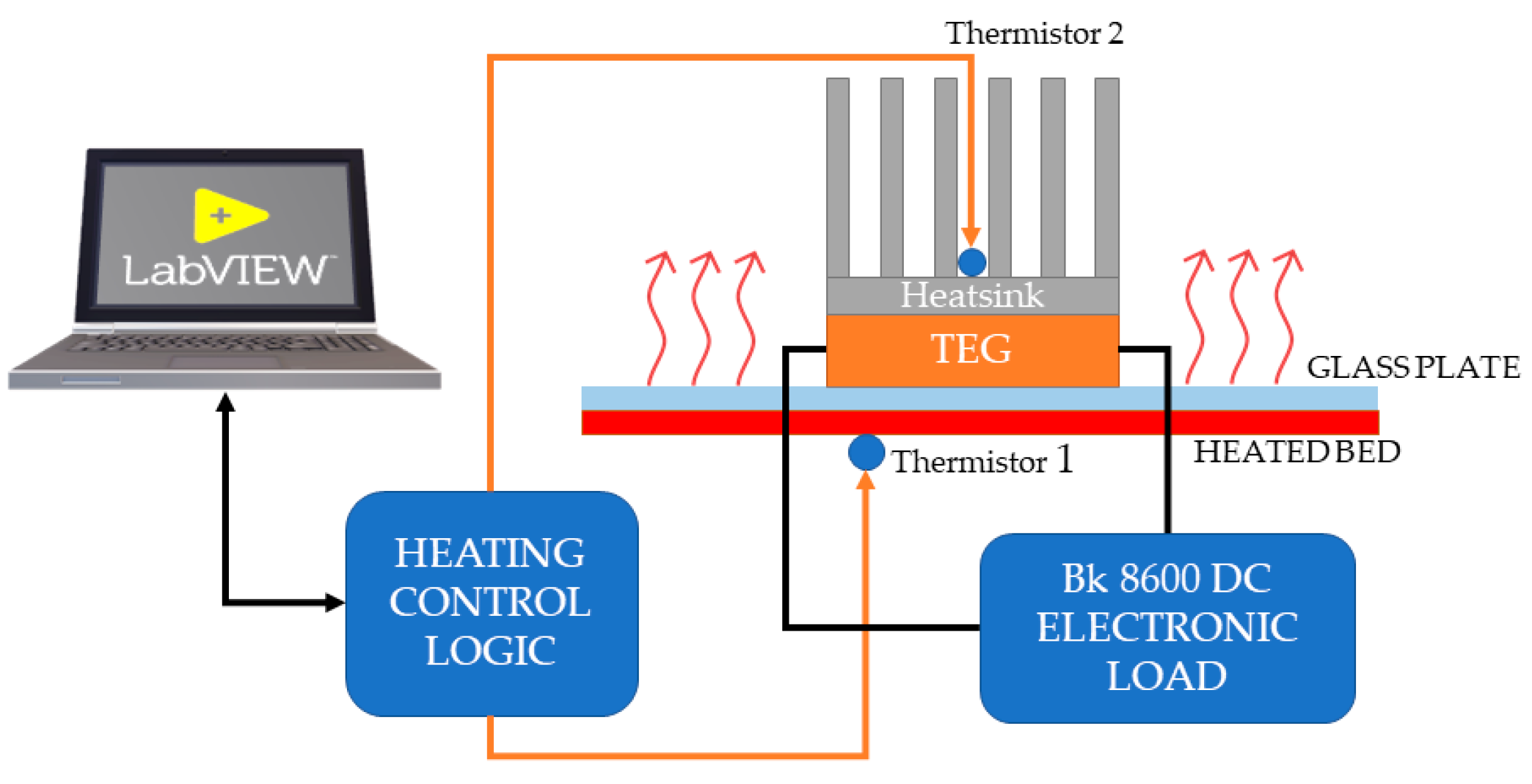
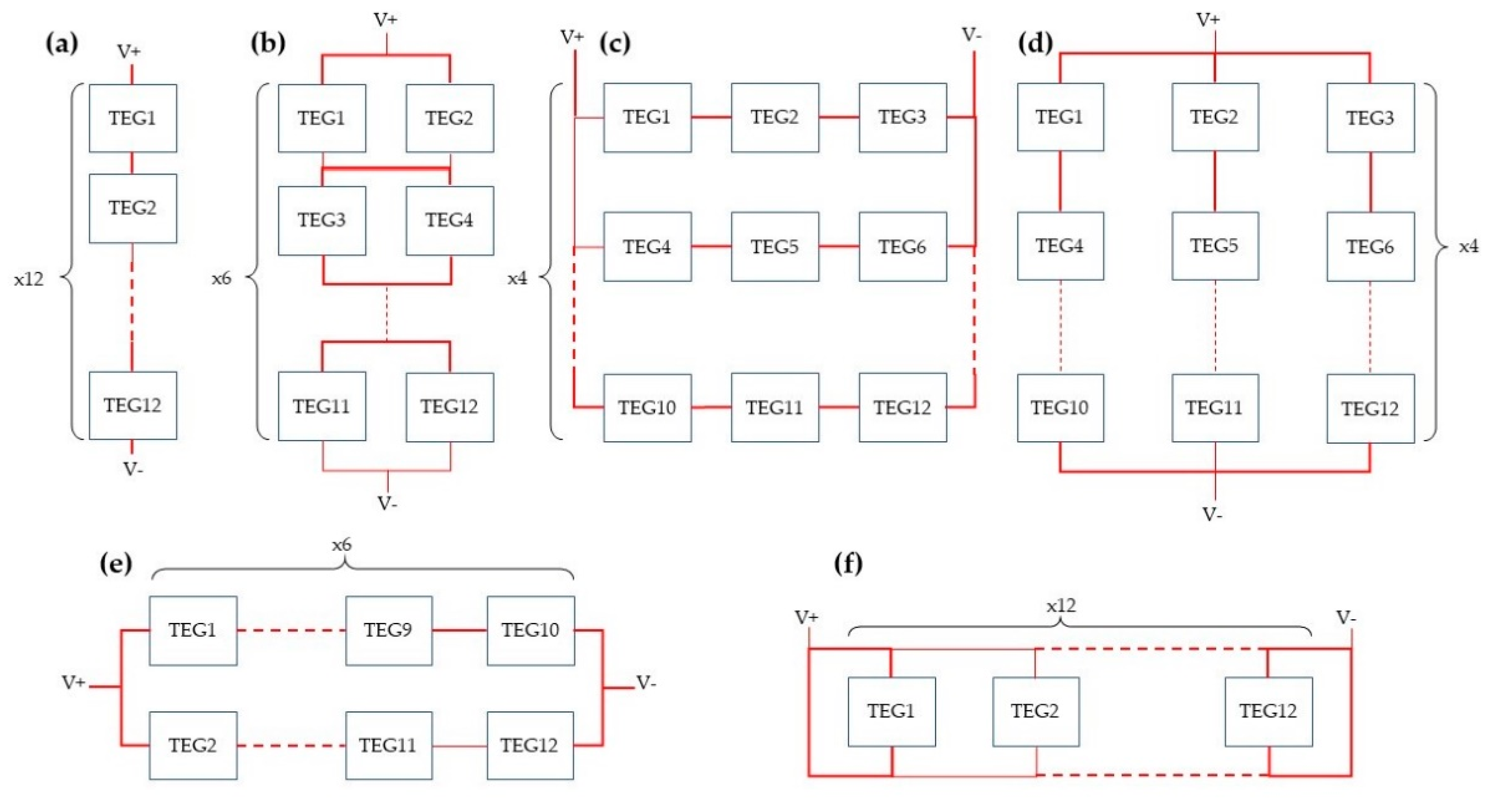
2. Materials and Methods
3. Results and Discussion
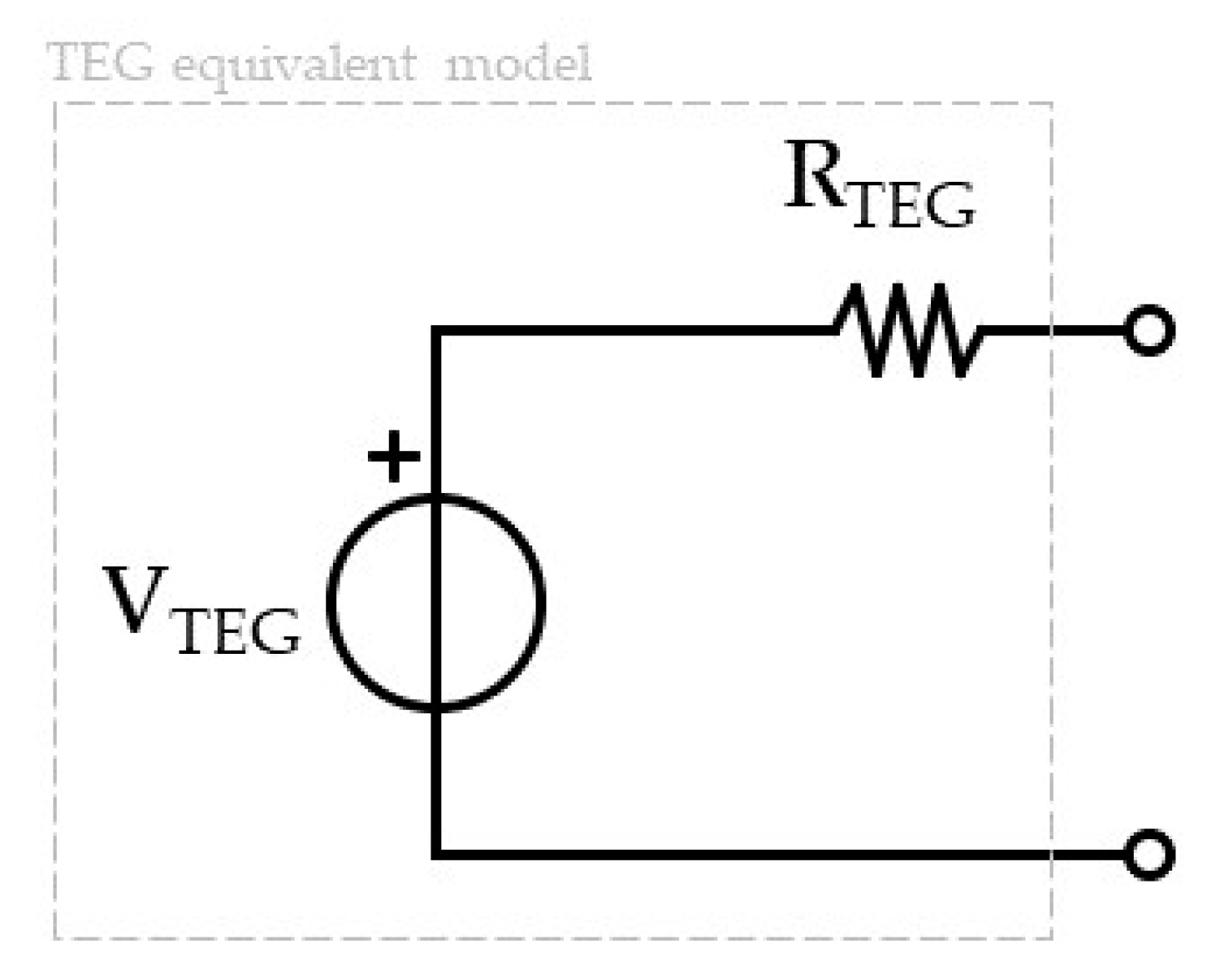
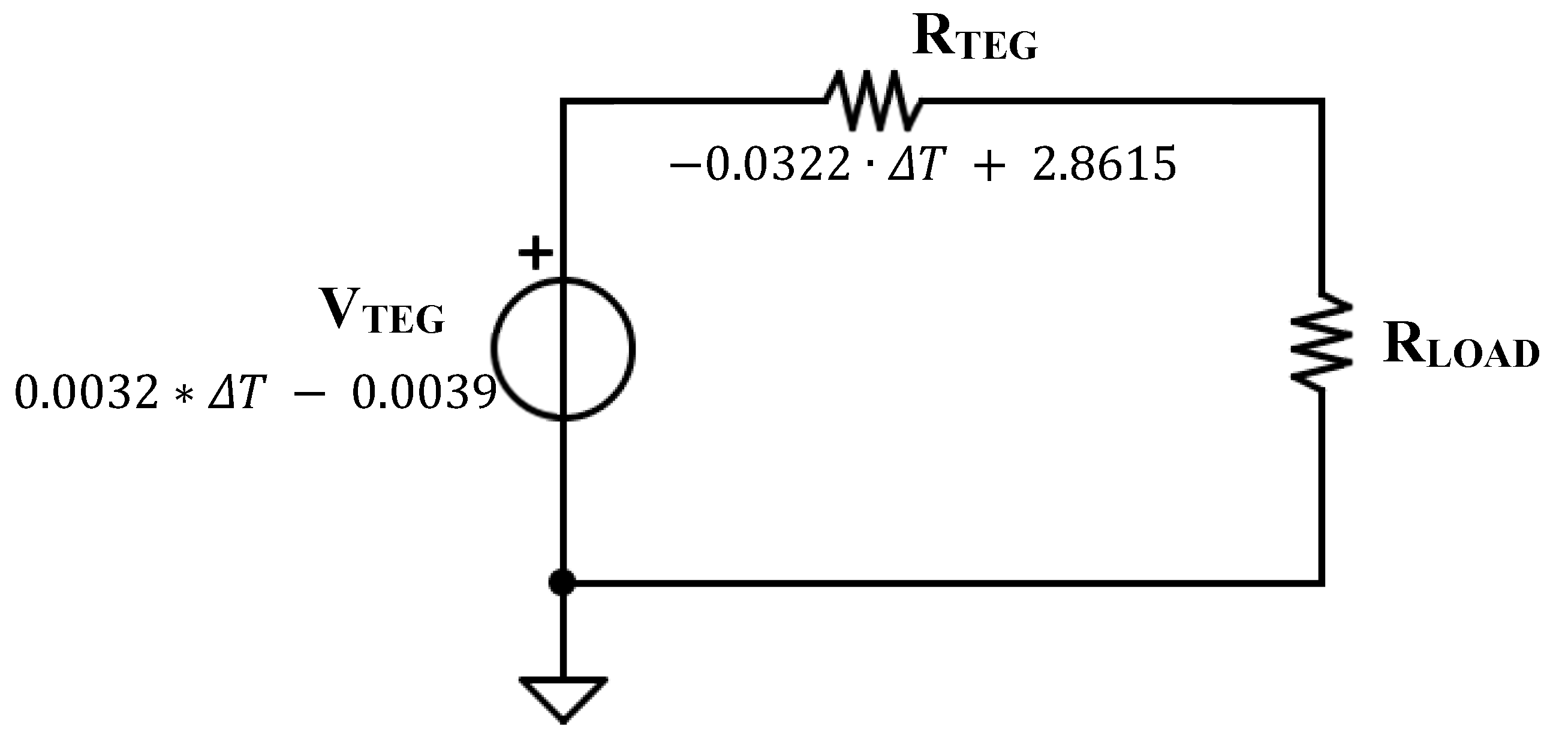
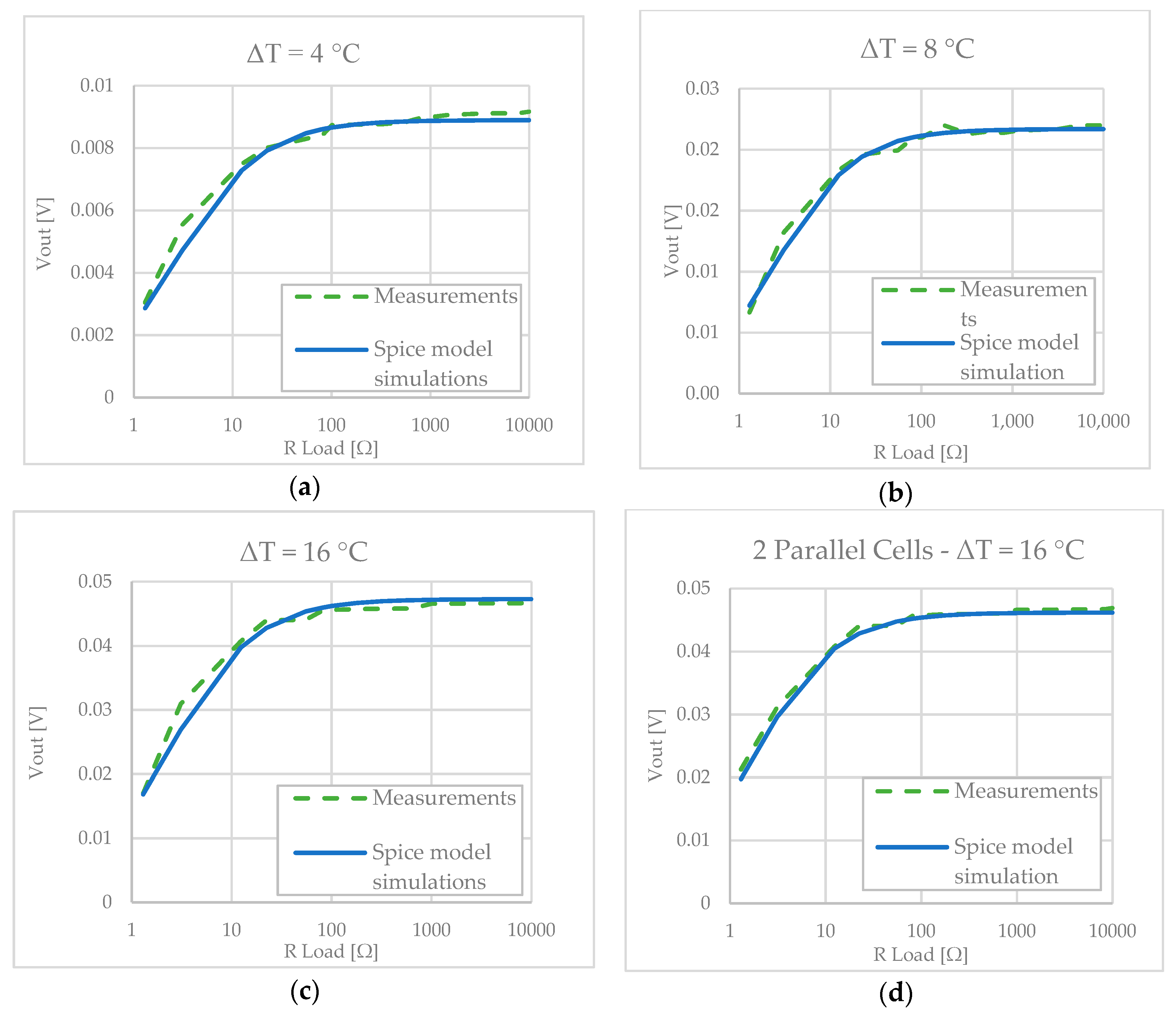
3.1. SPICE Model Identification
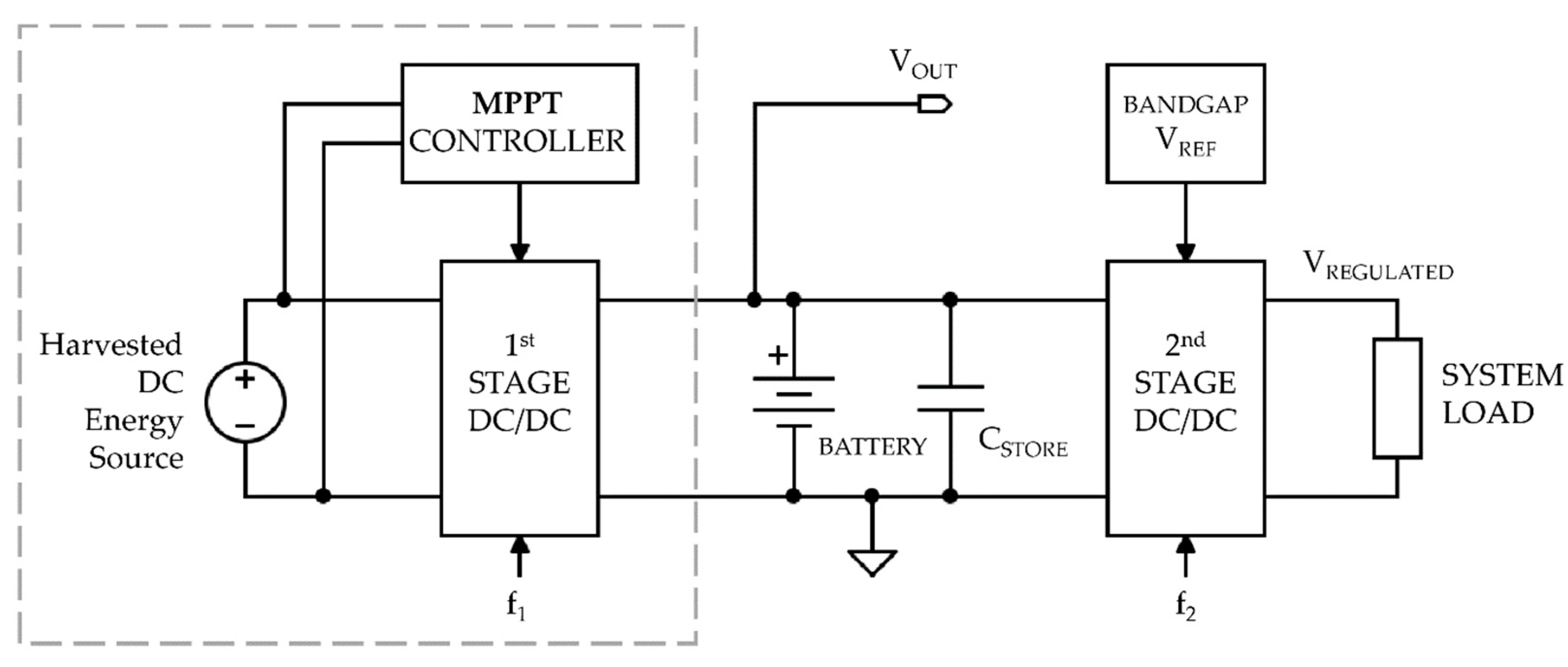
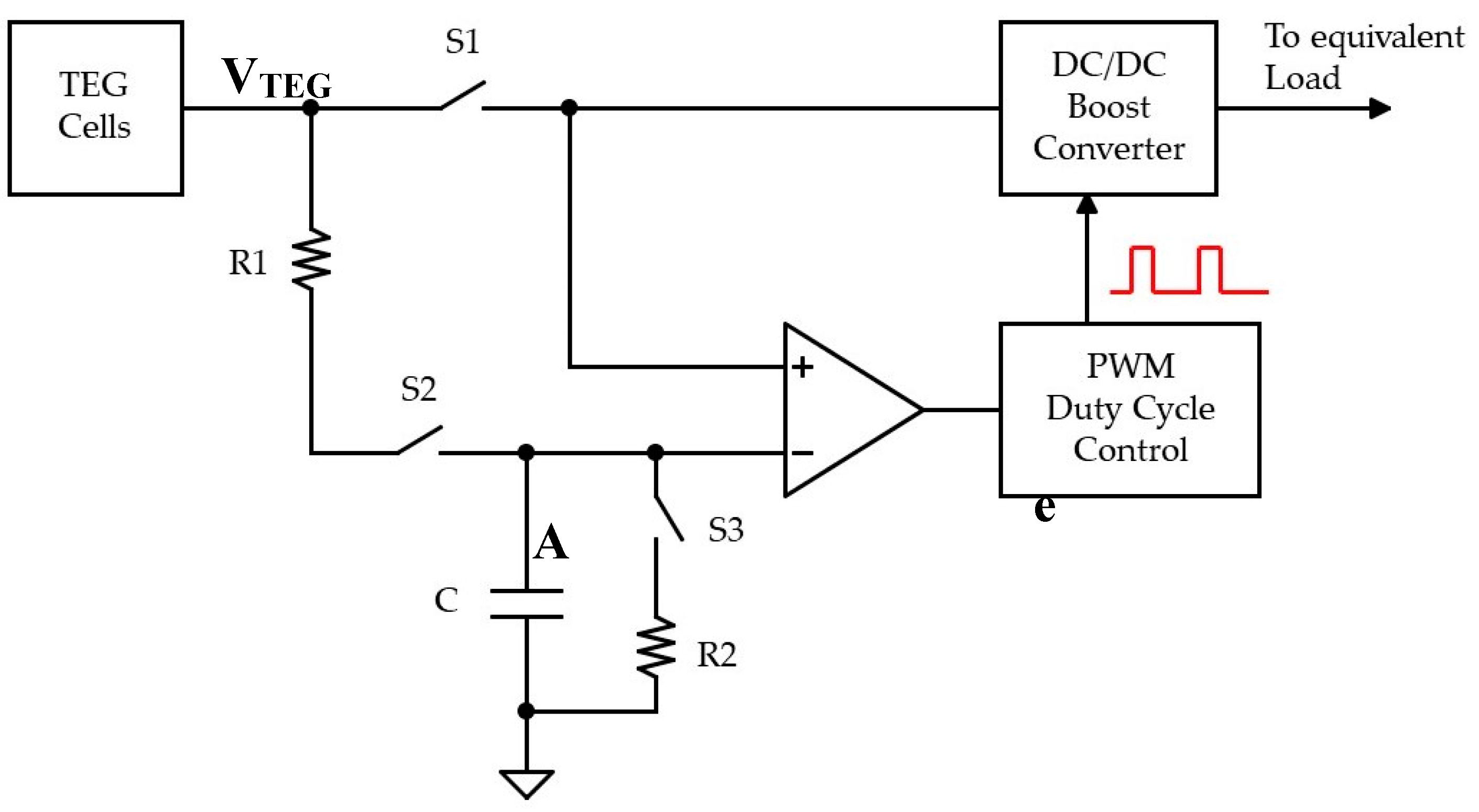
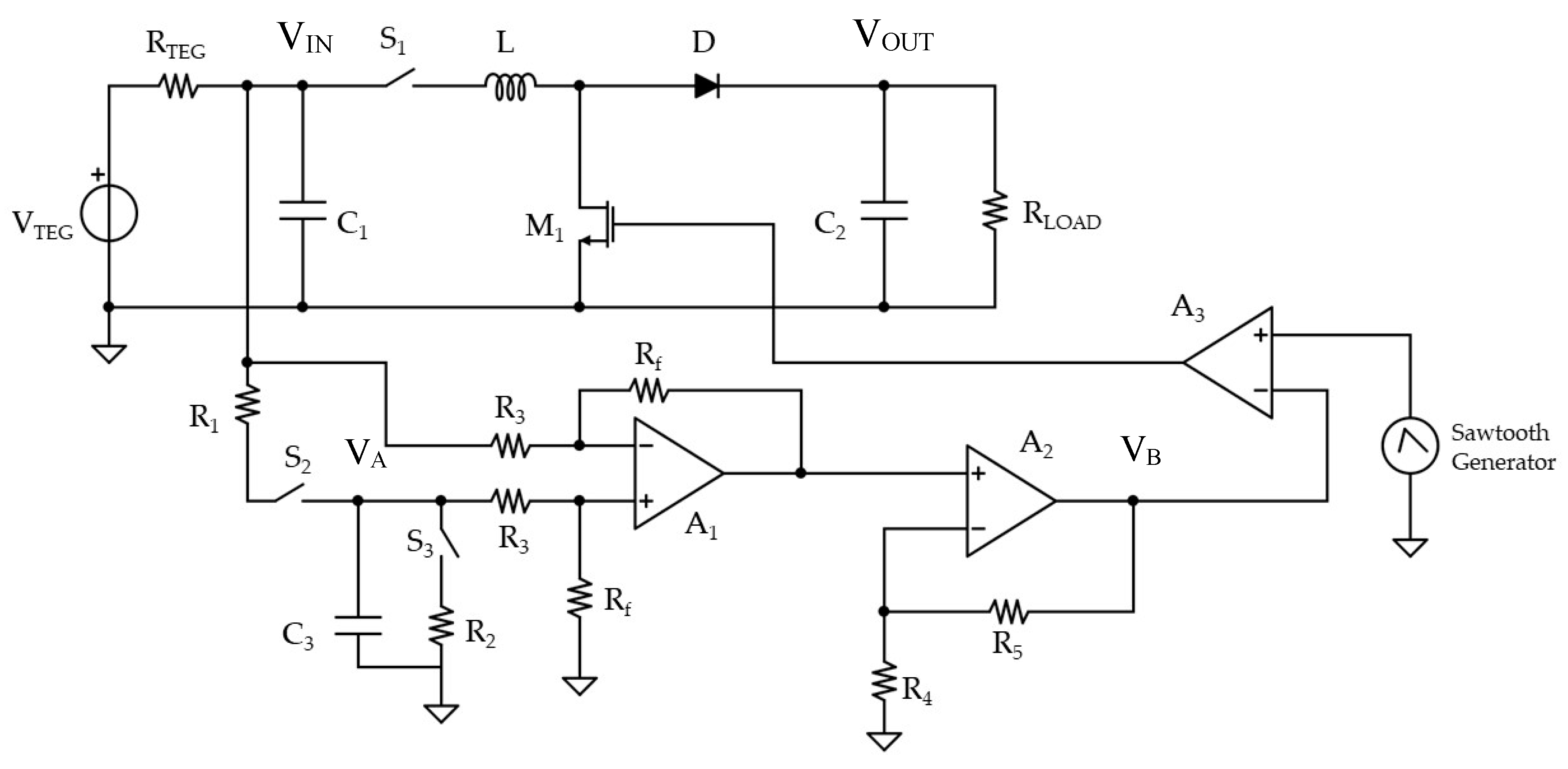
3.2. DC/DC with MPPT Design
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Morales, R.; Badesa, F.J.; García-Aracil, N.; Perez-Vidal, C.; Sabater, J.M. Distributed Smart Device for Monitoring, Control and Management of Electric Loads in Domotic Environments. Sensors 2012, 12, 5212–5224. [Google Scholar] [CrossRef] [PubMed]
- Tejesh, B.S.S.; Neeraja, S. A Smart Home Automation system using IoT and Open Source Hardware. Int. J. Eng. Technol. 2018, 7, 428. [Google Scholar] [CrossRef]
- Piscitelli, G.; Errico, V.; Ricci, M.; Giannini, F.; Saggio, G.; Leoni, A.; Stornelli, V.; Ferri, G.; Pantoli, L.; Ulisse, I. A low-cost energy-harvesting sensory headwear useful for tetraplegic people to drive home automation. AEU. Int. J. Electron. Commun. 2019, 107, 9–14. [Google Scholar] [CrossRef]
- Leoni, A.; Stornelli, V.; Ferri, G.; Errico, V.; Ricci, M.; Pallotti, A.; Saggio, G. A human body powered sensory glove system based on multisource energy harvester. In Proceedings of the 14th Conference on Ph.D. Research in Microelectronics and Electronics (PRIME), Prague, Czech Republic, 2–5 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 113–116. [Google Scholar] [CrossRef]
- Lin, K.-F.; Lin, S.-S.; Hung, M.-H.; Kuo, C.-H.; Chen, P.-N. An Embedded Gateway with Communication Extension and Backup Capabilities for ZigBee-Based Monitoring and Control Systems. Appl. Sci. 2019, 9, 456. [Google Scholar] [CrossRef]
- Pantoli, L.; Leoni, A.; Parente, F.R.; Stornelli, V.; Ferri, G. Integrable autonomous devices for WSNs. In Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2016; Volume 431. [Google Scholar] [CrossRef]
- Di Marco, P.; Stornelli, V.; Ferri, G.; Pantoli, L.; Leoni, A. Dual band harvester architecture for autonomous remote sensors. Sens. Actuators A Phys. 2016, 247, 598–603. [Google Scholar] [CrossRef]
- Banerjee, A.; Hussain, D.M.A. SD-EAR: Energy Aware Routing in Software Defined Wireless Sensor Networks. Appl. Sci. 2018, 8, 1013. [Google Scholar] [CrossRef]
- Leoni, A.; Stornelli, V.; Pantoli, L. A low-cost portable spherical directional anemometer for fixed points measurement. Sens. Actuators A Phys. 2018, 280, 543–551. [Google Scholar] [CrossRef]
- Stornelli, V.; Ferri, G.; Leoni, A.; Pantoli, L. The assessment of wind conditions by means of hot wire sensors and a modifed Wheatstone bridge architecture. Sens. Actuators A Phys. 2017, 262, 130–139. [Google Scholar] [CrossRef]
- Ferri, G.; Parente, F.; Stornelli, V.; Barile, G.; Pantoli, L. Automatic Bridge-based Interface for Differential Capacitive Full Sensing. Procedia Eng. 2016, 168, 1585–1588. [Google Scholar] [CrossRef]
- Wang, C.; Yu, Y.; Niu, J.; Liu, Y.; Bridges, D.; Liu, X.; Pooran, J.; Zhang, Y.; Hu, A. Recent Progress of Metal–Air Batteries—A Mini Review. Appl. Sci. 2019, 9, 2787. [Google Scholar] [CrossRef]
- Hossain, E.; Murtaugh, D.; Mody, J.; Faruque, H.; Haque Sunny, M.; Mohammad, N. A Comprehensive Review on Second-Life Batteries: Current State, Manufacturing Considerations, Applications, Impacts, Barriers & Potential Solutions, Business Strategies, and Policies. IEEE Access 2019, 7, 73215–73252. [Google Scholar]
- Ha, D.-H.; Dong, S.T.C.; Nguyen, T.N.; Trang, T.T.; Voznak, M. Half-Duplex Energy Harvesting Relay Network over Different Fading Environment: System Performance with Effect of Hardware Impairment. Appl. Sci. 2019, 9, 2283. [Google Scholar] [CrossRef]
- Stomelli, V.; Leoni, A.; Ferri, G.; Errico, V.; Ricci, M.; Pallotti, A.; Saggio, G. A Multi-source energy harvesting sensory glove electronic architecture. In Proceedings of the 3rd International Conference on Smart and Sustainable Technologies (SpliTech), Split, Croatia, 26–29 June 2018; pp. 1–4. Available online: http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=8448343&isnumber=8448303.
- Leoni, A.; Pantoli, L.; Stornelli, V.; Ferri, G.; Solic, P.; Russo, M. A Combined 90/900 MHz IC Architecture for Smart Tag Application. J. Commun. Softw. Syst. 2018, 14. [Google Scholar] [CrossRef]
- Leoni, A.; Pantoli, L.; Stornelli, V.; Ferri, G.; Russo, M.; Solic, P. 90/900 MHz IC architecture for autonomous systems. In Proceedings of the 2nd International Multidisciplinary Conference on Computer and Energy Science (SpliTech), Split, Croatia, 12–14 July 2017; pp. 1–4. Available online: http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=8019240&isnumber=8019234.
- Pantoli, L.; Leoni, A.; Stornelli, V.; Ferri, G. Energy harvester for remote sensors systems. In Proceedings of the International Multidisciplinary Conference on Computer and Energy Science (SpliTech), Split, Croatia, 13–15 July 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Di Marco, P.; Leoni, A.; Pantoli, L.; Stornelli, V.; Ferri, G. Remote sensor networks with efficient energy harvesting architecture. In Proceedings of the 12th Conference on Ph.D. Research in Microelectronics and Electronics (PRIME), Lisbon, Portugal, 27–30 June 2016; pp. 1–4. [Google Scholar]
- Bui, N.T.; Vo, T.H.; Kim, B.-G.; Oh, J. Design of a Solar-Powered Portable ECG Device with Optimal Power Consumption and High Accuracy Measurement. Appl. Sci. 2019, 9, 2129. [Google Scholar] [CrossRef]
- Orsetti, C.; Muttillo, M.; Parente, F.; Pantoli, L.; Stornelli, V.; Ferri, G. Reliable and Inexpensive Solar Irradiance Measurement System Design. Procedia Eng. 2016, 168, 1767–1770. [Google Scholar] [CrossRef]
- Salimi, M. Practical implementation of the Lyapunov based nonlinear controller in DC-DC boost converter for MPPT of the PV systems. Sol. Energy 2018, 173, 246–255. [Google Scholar] [CrossRef]
- Dechant, E.; Fedulov, F.; Fetisov, L.Y.; Shamonin, M. Bandwidth Widening of Piezoelectric Cantilever Beam Arrays by Mass-Tip Tuning for Low-Frequency Vibration Energy Harvesting. Appl. Sci. 2017, 7, 1324. [Google Scholar] [CrossRef]
- Chin, W.K.; Ong, Z.C.; Kong, K.K.; Khoo, S.Y.; Huang, Y.-H.; Chong, W.T. Enhancement of Energy Harvesting Performance by a Coupled Bluff Splitter Body and PVEH Plate through Vortex Induced Vibration near Resonance. Appl. Sci. 2017, 7, 921. [Google Scholar] [CrossRef]
- Saida, M.; Zaibi, G.; Samet, M.; Kachouri, A. Design and study of piezoelectric energy harvesting cantilever from human body. In Proceedings of the 15th International Multi-Conference on Systems, Signals & Devices (SSD), Hammamet, Tunisia, 19–22 March 2018; pp. 164–168. [Google Scholar] [CrossRef]
- Li, L.; Zhu, R.; Zhou, Z.; Ren, J. PZT Micro Actuator and Its Application in Robotic Manipulators. In Proceedings of the Second International Symposium on Intelligent Information Technology Application, Shanghai, China, 20–22 December 2008; pp. 598–601. [Google Scholar] [CrossRef]
- Perera, R.; Sevillano, E.; Sun, R.; Arteaga, A.; De Diego, A.; Cisneros, D. Comparison of PZT and FBG sensing technologies for debonding detection on reinforced concrete beams strengthened with external CFRP strips subjected to bending loads. Materiales de Construcción 2016, 66, e088. [Google Scholar] [CrossRef]
- Kim, N.; Jang, S.J.; Shrout, T.R. Relaxor based fine grain piezoelectric materials. In Proceedings of the IEEE 7th International Symposium on Applications of Ferroelectrics, Urbana-Champaign, IL, USA, 6–8 June 1990; pp. 605–609. [Google Scholar] [CrossRef]
- Nesarajah, M.; Frey, G. Optimized Design of Thermoelectric Energy Harvesting Systems for Waste Heat Recovery from Exhaust Pipes. Appl. Sci. 2017, 7, 634. [Google Scholar] [CrossRef]
- Wong, H.; Dahari, Z. Human body parts heat energy harvesting using thermoelectric module. In Proceedings of the IEEE Conference on Energy Conversion (CENCON), Johor Bahru, Malaysia, 19–20 October 2015; pp. 211–214. [Google Scholar] [CrossRef]
- Zhou, S.; Zhuo, C.; Min, Q.; Li, E. Graphene based thermoelectric energy harvesting in 3D ICs. In Proceedings of the IEEE Electrical Design of Advanced Packaging and Systems Symposium (EDAPS), Haining, China, 14–16 December 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Lee, D.G.E. Tunable thermo-triboelectric energy harvesting using human body heat for self-powered applications. In Proceedings of the IEEE Micro Electro Mechanical Systems (MEMS), Belfast, Northern Ireland, 21–25 January 2018; pp. 669–672. [Google Scholar] [CrossRef]
- Uprety, S.; Lee, H. A 93%-power-efficiency photovoltaic energy harvester with irradiance-aware auto-reconfigurable MPPT scheme achieving >95% MPPT efficiency across 650 µW to 1 W and 2.9 ms FOCV MPPT transient time. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 5–9 February 2017; pp. 378–379. [Google Scholar] [CrossRef]
- Morales-Caporal, M.; Rangel-Magdaleno, J.; Morales-Caporal, R. Digital simulation of a predictive current control for photovoltaic system based on the MPPT strategy. In Proceedings of the 13th International Conference on Power Electronics (CIEP), Guanajuato, Mexico, 20–26 June 2016; pp. 295–299. [Google Scholar] [CrossRef]
- Leoni, A.; Ulisse, I.; Pantoli, L.; Errico, V.; Ricci, M.; Orengo, G.; Giannini, F.; Saggio, G. Energy harvesting optimization for built-in power replacement of electronic multisensory architecture. AEU Int. J. Electron. Commun. 2019, 107, 170–176. [Google Scholar] [CrossRef]
- Singkaselit, K.; Sakulkalavek, A.; Sakdanuphab, R. Effects of annealing temperature on the structural, mechanical and electrical properties of flexible bismuth telluride thin films prepared by high-pressure RF magnetron sputtering. Adv. Nat. Sci. Nanosci. Nanotechnol. 2017, 8, 035002. [Google Scholar] [CrossRef]
- Han, M.; Jin, Y.; Lee, D.; Kim, S. Thermoelectric Properties of Bi2Te3: CuI and the Effect of Its Doping with Pb Atoms. Materials 2017, 10, 1235. [Google Scholar] [CrossRef] [PubMed]
- Pei, Y.; Wang, H.; Gibbs, Z.; LaLonde, A.; Snyder, G. Thermopower enhancement. In Proceedings of the Pb1−xMnxTe alloys and its effect on thermoelectric efficiency. NPG Asia Mater. 2012, 4, e28. [Google Scholar] [CrossRef]
- Fujitaka Co. Peltier Guide. Specification. Available online: https://download.siliconexpert.com/pdfs/2008/03/05/c/manual/fujtk/htmls/fph112702ac.pdf? (accessed on 21 August 2019).
- Kubov, V.I.; Dymytrov, Y.Y.; Kubova, R.M. LTSPICE-model of thermoelectric Peltier-Seebeck element. In Proceedings of the IEEE 36th International Conference on Electronics and Nanotechnology (ELNANO), Kiev, Ukraine, 19–21 April 2016; pp. 47–51. [Google Scholar] [CrossRef]
- Liu, X.; Huang, L.; Ravichandran, K.; Sanchez-Sinencio, E. A Highly Efficient Reconfigurable Charge Pump Energy Harvester With Wide Harvesting Range and Two-Dimensional MPPT for Internet of Things. IEEE J. Solid State Circuits 2016, 51, 1302–1312. [Google Scholar] [CrossRef]
- Liu, X.; Sanchez-Sinencio, E. A Highly Efficient Ultralow Photovoltaic Power Harvesting System With MPPT for Internet of Things Smart Nodes. IEEE Trans. Very Large Scale Integr. Syst. 2015, 23, 3065–3075. [Google Scholar] [CrossRef]
- Ram, S.K.; Sahoo, S.R.; Sudeendra, K.; Mahapatra, K. Energy efficient ultra low power solar harvesting system design with MPPT for IOT edge node devices. In Proceedings of the IEEE International Symposium on Smart Electronic Systems (iSES) (Formerly iNiS), Hyderabad, India, 17–19 December 2018; pp. 130–133. [Google Scholar]
- Cheng, Y.; Chao, P.C.; Men, G.; Yang, C.; Wang, T. An 80% effeciency and highly adaptable PV energy harvest circuitry with MPPT for IOT devices. In Proceedings of the IEEE Sensors 2017, Glasgow, Scotland, 30 October–1 November 2017; pp. 1–3. [Google Scholar]
- Alli, S.; Jovanović, S.; Poure, P.; Jamshidpour, E. MPPT and output voltage control of Photovoltaic systems using a Single-Switch DC-DC converter. In Proceedings of the IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Rajendran, M.K.; Kansal, S.; Mantha, A.; Priya, V.; Priyamvada, Y.B.; Dutta, A. Automated environment aware nW FOCV—MPPT controller for self-powered IoT applications. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Montreal, QC, Canada, 22–25 May 2016; pp. 1818–1821. [Google Scholar]
- Selmi, T.; Abdul-Niby, M.; Devis, L.; Davis, A. P&O MPPT implementation using MATLAB/Simulink. In Proceedings of the 9th International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 25–27 March 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Chung, T.M.; Daniyal, H.; Sulaiman, M.; Bakar, M. Comparative study of P&O and modified incremental conductance algorithm in solar maximum power point tracking. In Proceedings of the 4th IET Clean Energy and Technology Conference (CEAT 2016), Kuala Lumpur, Malaysia, 14–15 November 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Motsoeneng, P.; Bamukunde, J.; Chowdhury, S. Comparison of Perturb & Observe and Hill Climbing MPPT schemes for pv plant under cloud cover and varying load. In Proceedings of the 10th International Renewable Energy Congress (IREC), Sousse, Tunisia, 26–28 March 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Baimel, D.; Tapuchi, S.; Levron, Y.; Belikov, J. Improved Fractional Open Circuit Voltage MPPT Methods for PV Systems. Electronics 2019, 8, 321. [Google Scholar] [CrossRef]
- Kollimalla, S.K.; Mishra, M.K. A new adaptive P&O MPPT algorithm based on FSCC method for photovoltaic system. In Proceedings of the International Conference on Circuits, Power and Computing Technologies (ICCPCT), Nagercoil, India, 20–21 March 2013; pp. 406–411. [Google Scholar] [CrossRef]
- Wan, Q.; Teh, Y.; Gao, Y.; Mok, P. Analysis and Design of a Thermoelectric Energy Harvesting System With Reconfigurable Array of Thermoelectric Generators for IoT Applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 2346–2358. [Google Scholar] [CrossRef]
- Wittmann, J.; Wicht, B. A configurable sawtooth based PWM generator with 2 ns on-time for >50 MHz DCDC converters. In Proceedings of the 11th Conference on Ph.D. Research in Microelectronics and Electronics (PRIME), Glasgow, Scotland, 29 June–2 July 2015; pp. 41–44. [Google Scholar] [CrossRef]
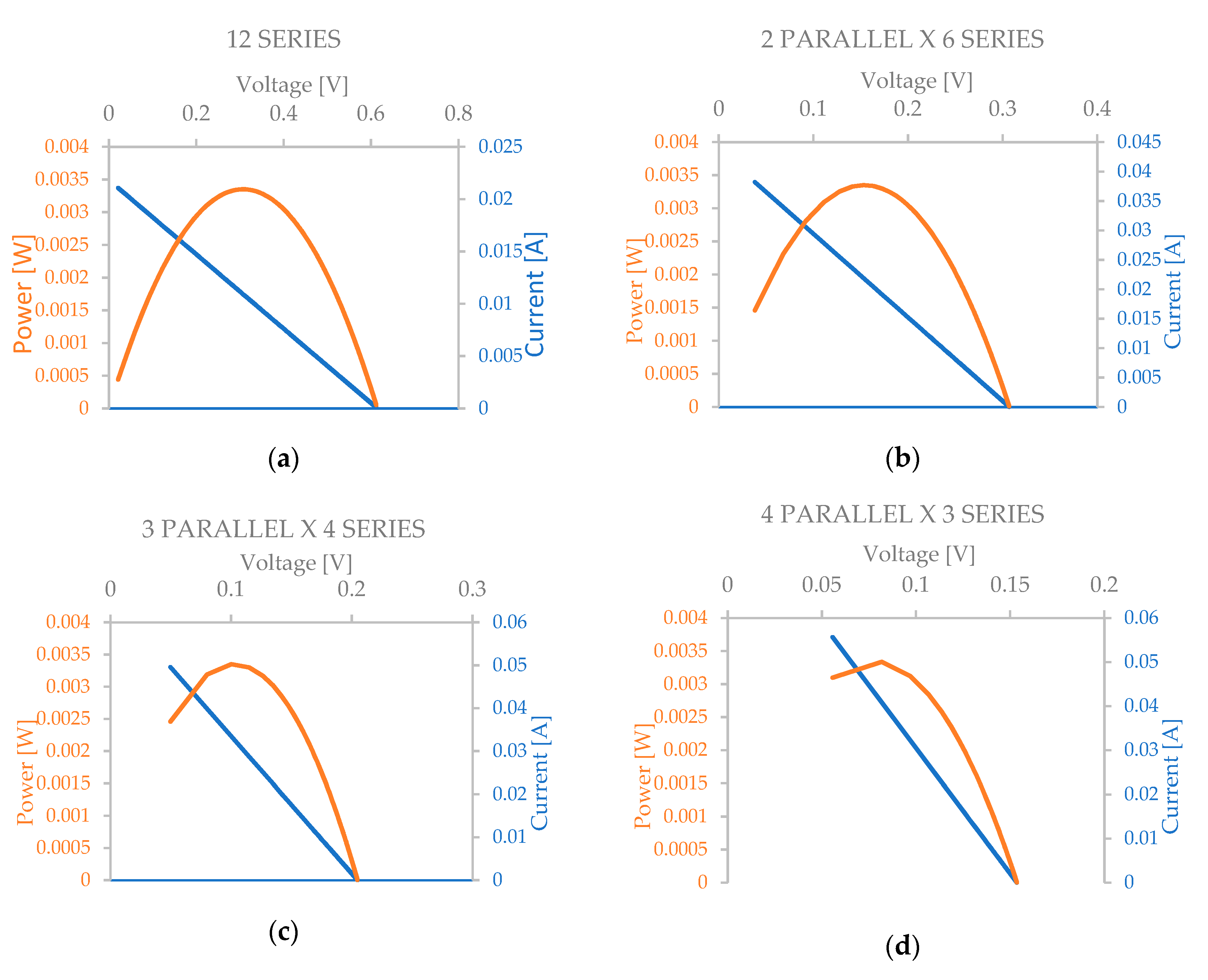
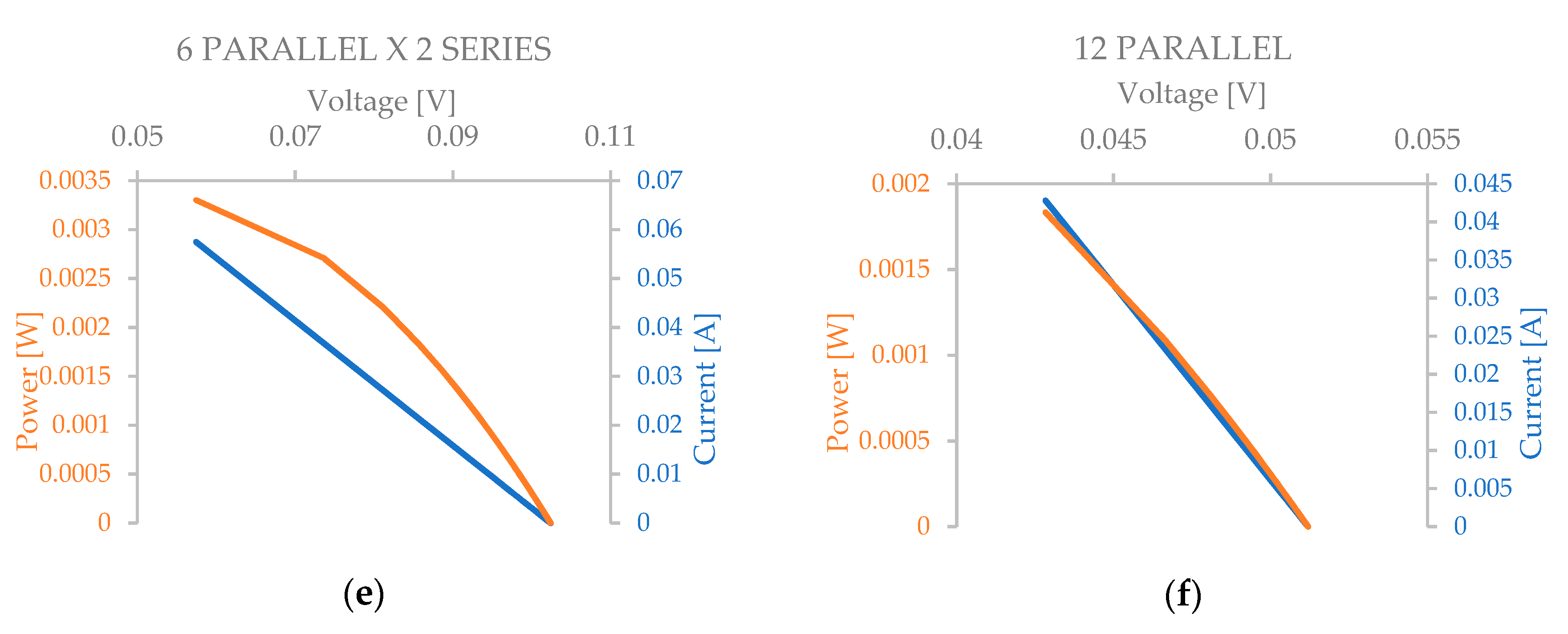
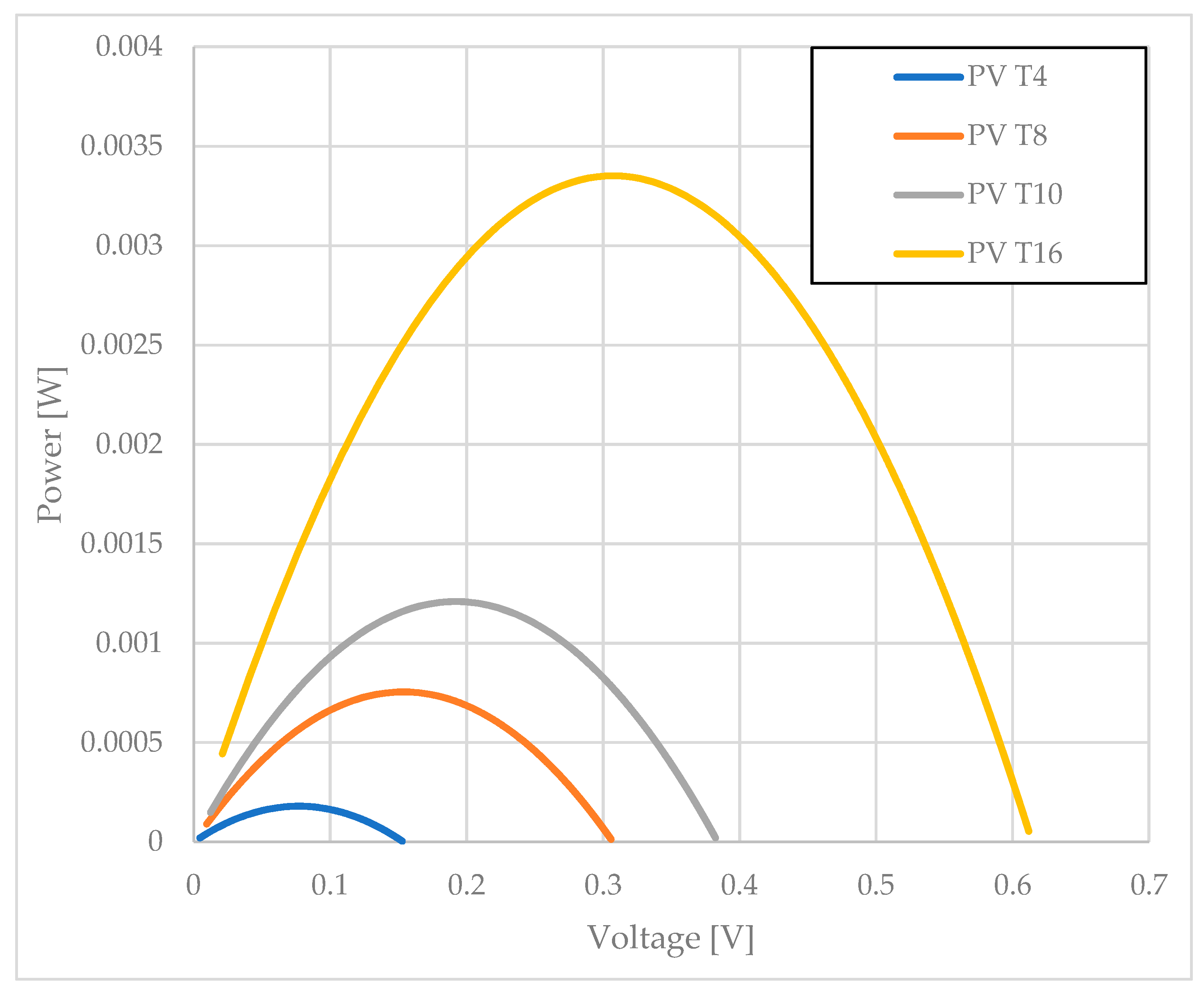
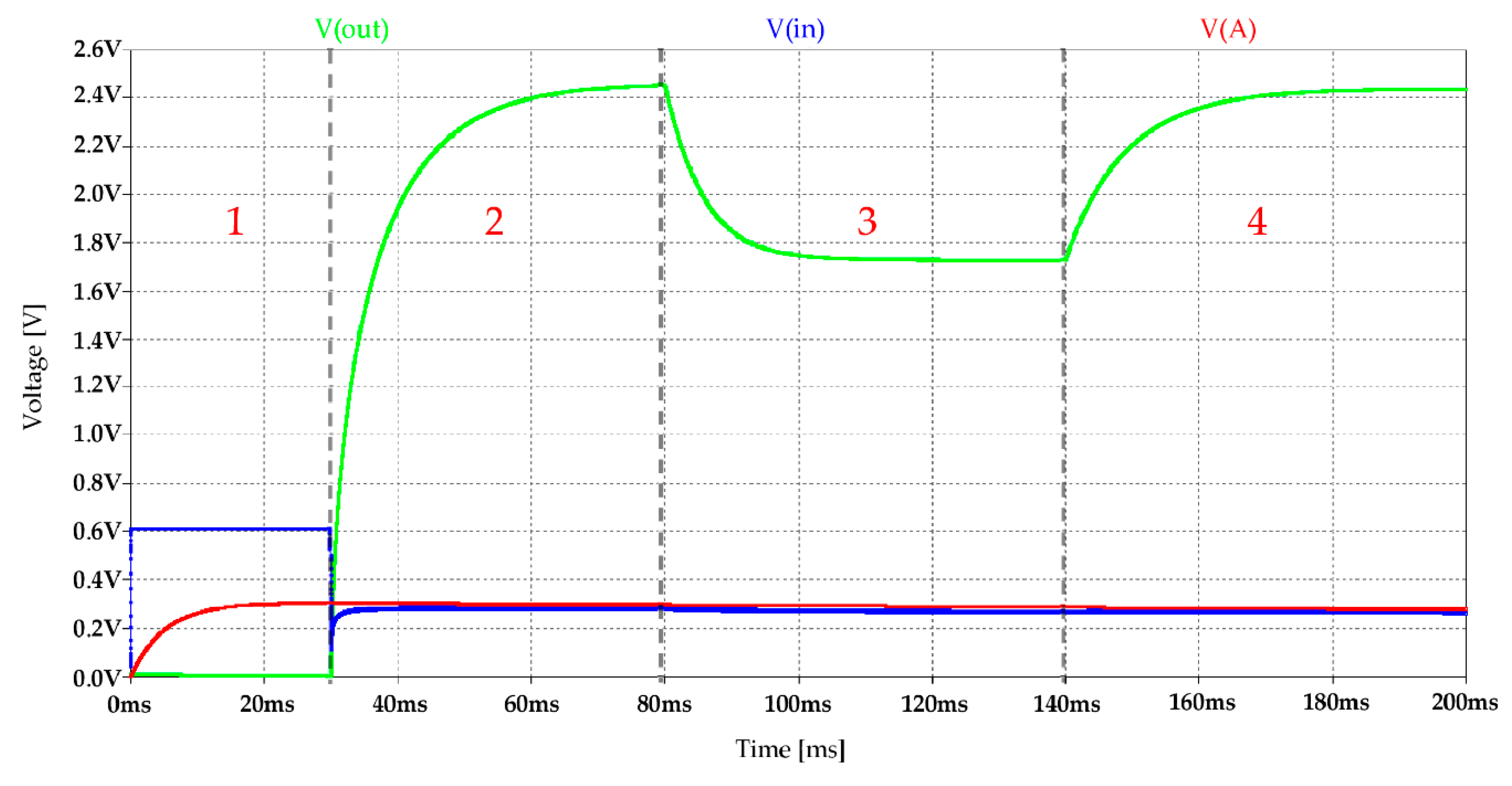
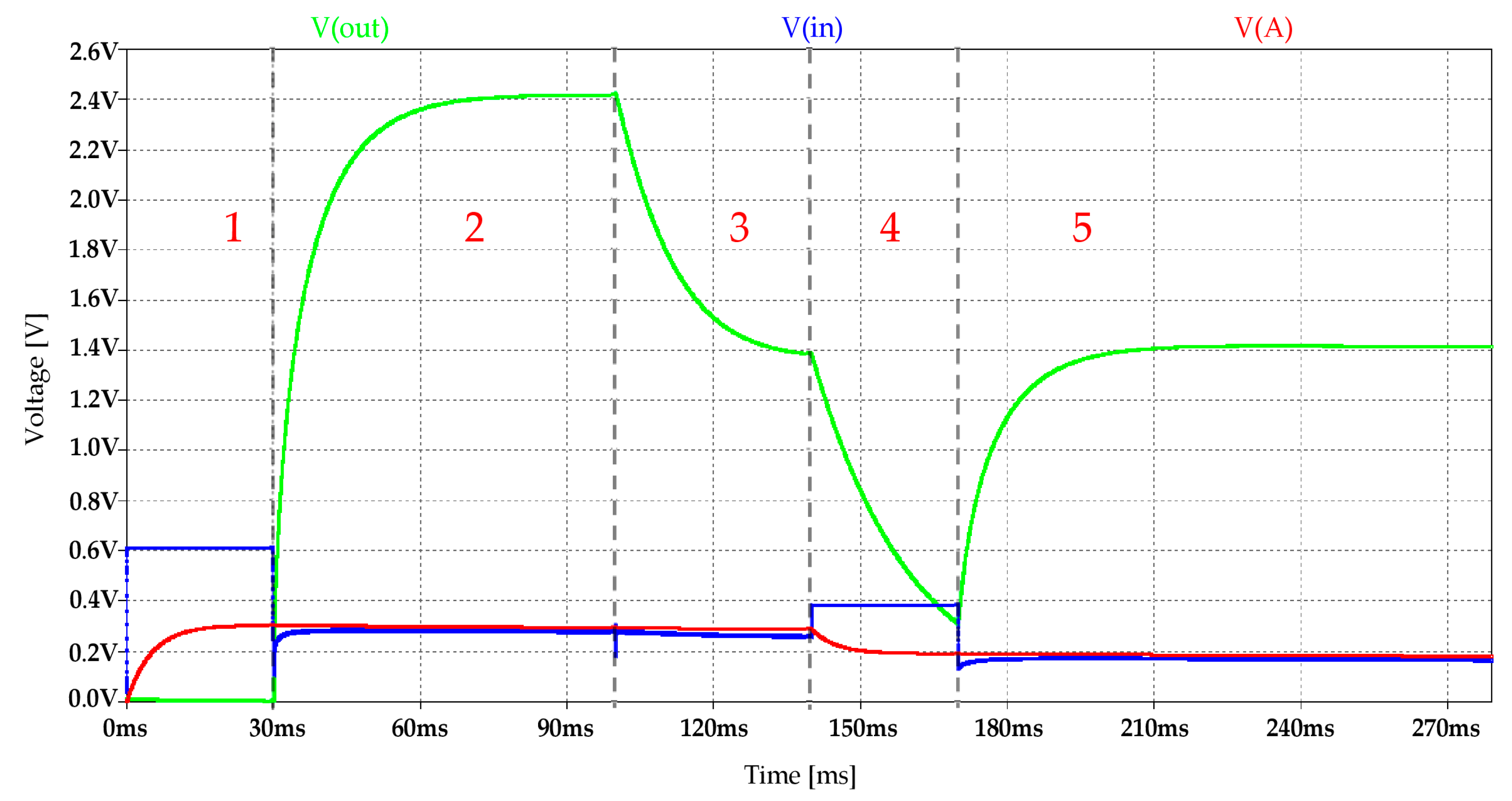
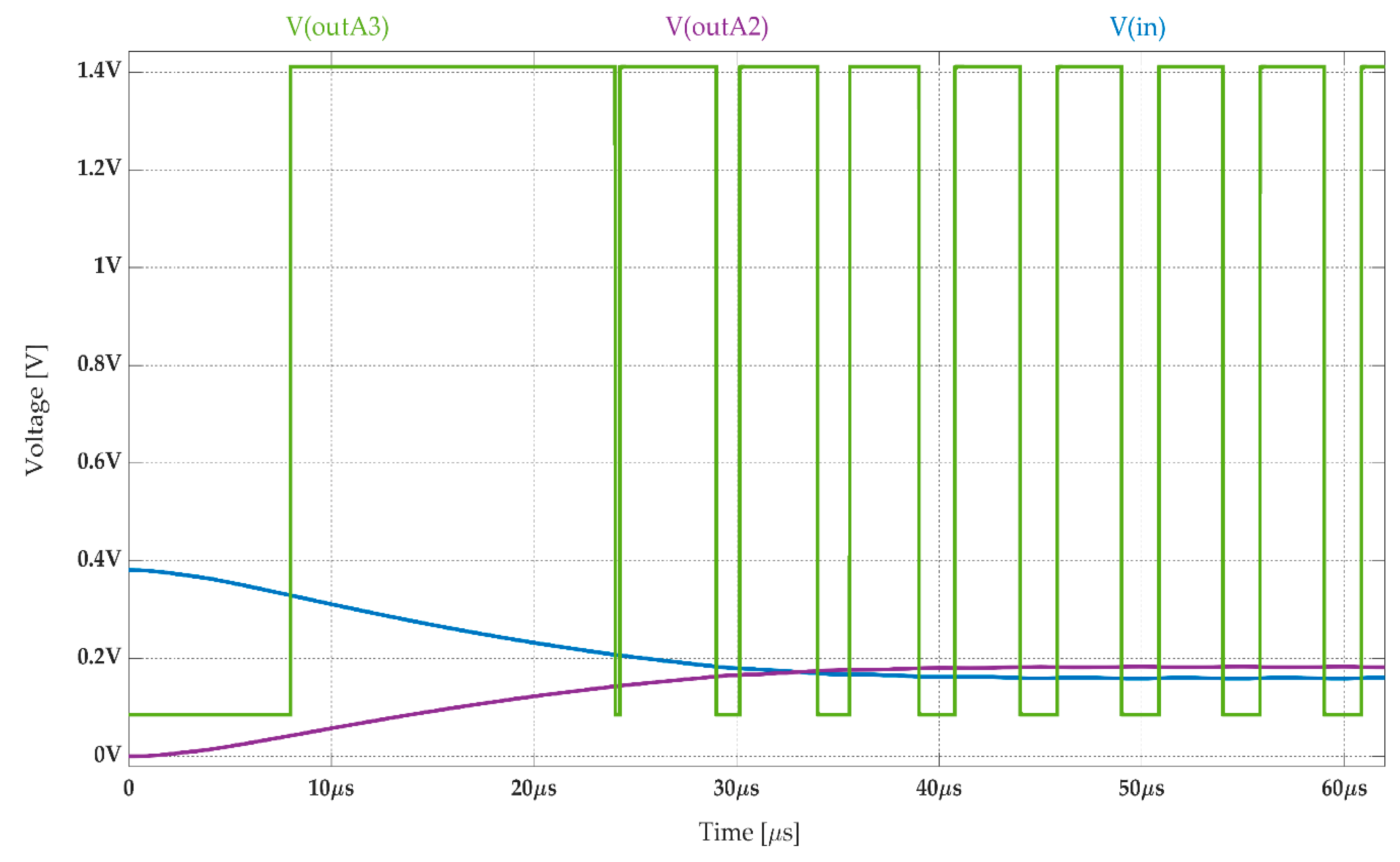
| [°C] | [mV] | [mA] | [μW] |
|---|---|---|---|
| 4 | 9.25 | 2.35 | 9.94 |
| 8 | 20.73 | 5.2 | 48.25 |
| 16 | 47.12 | 13.1 | 309 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leoni, A.; Pantoli, L. SPICE Model Identification Technique of a Cheap Thermoelectric Cell Applied to DC/DC Design with MPPT Algorithm for Low-Cost, Low-Power Energy Harvesting. Appl. Sci. 2019, 9, 3744. https://doi.org/10.3390/app9183744
Leoni A, Pantoli L. SPICE Model Identification Technique of a Cheap Thermoelectric Cell Applied to DC/DC Design with MPPT Algorithm for Low-Cost, Low-Power Energy Harvesting. Applied Sciences. 2019; 9(18):3744. https://doi.org/10.3390/app9183744
Chicago/Turabian StyleLeoni, Alfiero, and Leonardo Pantoli. 2019. "SPICE Model Identification Technique of a Cheap Thermoelectric Cell Applied to DC/DC Design with MPPT Algorithm for Low-Cost, Low-Power Energy Harvesting" Applied Sciences 9, no. 18: 3744. https://doi.org/10.3390/app9183744
APA StyleLeoni, A., & Pantoli, L. (2019). SPICE Model Identification Technique of a Cheap Thermoelectric Cell Applied to DC/DC Design with MPPT Algorithm for Low-Cost, Low-Power Energy Harvesting. Applied Sciences, 9(18), 3744. https://doi.org/10.3390/app9183744






