Abstract
In this work, the nonlocal strain gradient theory is applied to study the free vibration response of a Timoshenko beam made of triclinic material. The governing equations of the problem and the associated boundary conditions are obtained by means of the Hamiltonian principle, whereby the generalized differential quadrature (GDQ) method is implemented as numerical tool to solve the eigenvalue problem in a discrete form. Different combinations of boundary conditions are also considered, which include simply-supports, clamped supports and free edges. Starting with some pioneering works from the literature about isotropic nanobeams, a convergence analysis is first performed, and the accuracy of the proposed size-dependent anisotropic beam model is checked. A large parametric investigation studies the effect of the nonlocal, geometry, and strain gradient parameters, together with the boundary conditions, on the vibration response of the anisotropic nanobeams, as useful for practical engineering applications.
1. Introduction
In the past decades, different analytical and numerical approaches have been applied in literature to study the structural response of even more complicated structures [1,2,3,4,5,6]. Based on the literature, it is well known that many analytical solutions based on the Navier approximations cannot satisfy the governing equations of the problem, such that numerical approaches are usually required. In this context, the differential quadrature method (DQM) has been increasingly applied in several works and demanding applications as a powerful and efficient numerical method [7,8,9,10,11,12], due to its beneficial properties. This method, indeed, is user-friendly for different engineering problems and it features a high accuracy even with few grid points and a reduced computational effort, (see [7,8,9,10,11]). In most cases, the DQM has been used to study the dynamic, static or stability response of structures such as beams, plates, and shells, whereas any application of the DQM in literature has focused to nanostructures made of anisotropic materials, as typically occurs in the actual nature of materials due to their mechanical properties, with different elastic components in each direction. If an isotropic behavior is related to a certain uniformity along all the orientations, on the other hand, anisotropy refers to situations where properties vary systematically. For example, a triclinic material features different properties in different directions, with 21 elastic constants and three components of the propagation vector [13]. Due to the complexity of anisotropic material models, a large amount of simplification in most works in the literature is generally based on isotropic material assumptions. To date, only a few studies have focused on the mechanical response of anisotropic structures. More specifically, in [14,15,16] the authors analyzed the vibration response of square plates made of orthotropic, monoclinic and hexagonal materials for different boundary conditions, whereby the recent works [17,18,19,20] have focused on the wave propagation and buckling response of anisotropic materials at the nanoscale.
The development of nanotechnology has led to significant contributions in the scientific community, due to its advantages for many practical applications, i.e., water purification, medical applications, electronic and mechanical systems, among many. Therefore, the research and development of these novel materials has received special attention in the last decades, especially at a nanoscale level, where classical theories are inapplicable and can fail. Hence, different methods, i.e., experimental tests, molecular dynamics (MD) simulations and non-classical mathematical formulations, have been proposed as alternative ways to predict the behavior of nanomaterials [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35]. In work by Aifantis and Askes [36], a nonlocal strain gradient theory was proposed as an alternative non-classical method to capture both the hardening and softening stiffness mechanisms of nanostructured systems. Moreover, Challamel and Wang [37] proposed the application of a nonlocal strain gradient model to overcome the reported paradox in nonlocal cantilever beams subjected to a point load, whereby in [38] the authors accounted for the effect of three small-scale parameters within the model, while checking for its accuracy with respect to some MD-based results for carbon nanotubes. Further numerical predictions about the size-dependent behavior of functionally graded materials and structures can be found in [39,40,41,42,43,44,45,46], in the presence or not of porosities, in accordance to the nonlocal strain gradient model of elasticity. Based on limitations from the literature, in the current work the free vibrations of triclinic nanobeams with varying thickness along the length are studied for the first time, while applying the Timoshenko beam theory in conjunction with the nonlocal strain gradient model. The Hamiltonian principle is here adopted to drive the governing equations and boundary conditions of the problem, and the DQM is proposed as an efficient numerical tool to discretize and solve the vibrational problem. The influence of some important parameters, e.g., small-scale parameters, geometry and thickness variation, is investigated and discussed in detail. These results could represent some useful benchmark predictions for possible further works on anisotropic nanostructures. The paper is arranged as follows. After this Introduction, in Section 2 the basics of the proposed formulation assumed for the triclinic nanobeam are presented. The problem is solved numerically according to the DQM in Section 3, its efficiency is checked and discussed comparatively in Section 4, together with a large parametric investigation. Finally, the conclusions are drawn in Section 5.
2. Theory and Formulation
In what follows, the nonlocal strain gradient theory [36] is applied to account for both the nonlocal stress field and the strain gradient effects, by means of two small-scale parameters. This theory defines the stress field as
where σij and εij are the stress and strain tensors; Cijkl refers to the elastic properties’ matrix, while l1 and l2 denote the internal length scales to be determined experimentally or numerically by means of microscopic models, e.g., the MD simulations.
A triclinic nanobeam of length L, width b, thickness h is shown in Figure 1. In the current study, it is assumed that the stress components depend on both the longitudinal and transverse shear strains, i.e.,
where εxx, γxz denote the longitudinal and transverse shear strains, respectively, whereas σxx, τxz stand for the axial and shear stress, respectively.
Figure 1.
Geometry of the nanobeam.
In a context where the Timoshenko beam theory has been largely applied to model isotropic structures, herein the theory is extended to handle triclinic beams. According to the proposed continuum model, the displacement field takes the following form
where w refers to the transverse displacements; ψ stands for the rotation of the cross-section and t denotes the time. According to the small deformations assumption, the constitutive relations for the anisotropic nanobeam are defined as follows
cij being the elastic components of the triclinic material, defined as [13]
The governing Equations of the problem are determined through the Hamiltonian principle as follows
U and T being the strain and kinetic energy, respectively. More specifically, the strain energy has the following form
where
And κ is the shear correction factor which depends on the material properties. By using the nonlocal strain gradient theory relations (Equation (1)) and by mathematical manipulation with Equations (13) and (14), the following relations can be obtained
where
In addition, the kinetic energy is expressed as follows
By substituting Equations (12) and (20) into Equation (11), the following equations are obtained, when the coefficients of dw and dψ are assumed to be null, i.e.,
Thus, the introduction of Equations (15) and (16) into Equations (21) and (22), respectively, yields to the following expressions
The governing equations of a nonlocal strain gradient triclinic beam with a continuous variation in thickness, are obtained by substituting Equations (23) and (24) into Equations (21) and (22) as follows,
In the current study, a combination of simply supported, clamped, and free edges is investigated, which satisfy the following conditions
- Simply supported/Simply supported (SS)w(x, t) = 0, M(x, t) = 0 at x = 0, L
- Clamped/Clamped (CC)w(x, t) = 0, ψ(x, t) = 0 at x = 0, L
- Clamped/Simply supported (CS)w(x, t) = 0, ψ(x, t) = 0 at x = 0w(x, t) = 0, M(x, t) = 0 at x = L
- Clamped/Free (CF)w(x, t) = 0, ψ(x, t) = 0 at x = 0M(x, t) = 0, Q (x, t) = 0 at x = L
3. Solution Procure
3.1. Generalized Differential Quadrature Method (GDQM)
In what follows, the GDQM is proposed as a numerical method to solve the equations of motion to free the above-mentioned vibration problem of nanobeams, due to its fast convergence and accuracy as largely demonstrated in the literature for different demanding applications [47,48,49,50,51,52,53]. The GDQM discretizes the partial derivative of a function with respect to a variable by a weighted linear sum of function values at all grid points in that direction. This approximation yields the following relation [7],
for i = 1, 2…, Nζ; j = 1, 2…, Nη; and r = 1, 2…, Nζ − 1.
According to this technique, two important factors should be considered, namely, the appropriate distribution of grid points and weighting coefficients for discretization purposes.
As far as the first key aspect is concerned, different distributions could be selected, involving both uniform or not uniform discretizations, whose numerical performances have been largely discussed and compared in literature [54,55]. In this research the Chebyshev–Gauss–Lobatto sampling point rule is selected, due its high accuracy and fast convergence, and defined by the following relation
for i = 1, 2…, Nζ; j = 1, 2…, Nη; and r = 1, 2…, Nζ − 1.
As far as the weighting coefficients are concerned, the following expressions for the first and second derivatives are considered
where Lζ is the length of the domain along the ζ-direction and
The weighting coefficients of second-forth order derivative can be obtained as follows
Before applying this numerical approach, it is worth mentioning the large variety of versions available in literature. For example, Zhu et al. [56] developed a new Crank–Nicolson type DQM to discretize the 2D space-fractional advection-diffusion equations based on a set of cubic B-splines. Dahiya and Mittal [57] presented a modified cubic B-spline DQM to solve numerically a three-dimensional non-linear diffusion problem, and the pertaining equations. Eftekhari [58] proposed a combined differential quadrature–integral quadrature procedure, to handle singular functions, and possible related drawbacks.
3.2. Implementation of the GDQM
The combination of simply supported, clamped and free triclinic nanobeams are here discretized into N grid points (i = 1, 2…, N). Considering the GDQM, the equations of motion for the nanobeam at the i-th grid point can be discretized as
where µ = l1 and l = l2. To find the unknown frequencies, the above equations can be written in the following form,
where the subscripts d and b represent, respectively, the domain and boundary points related to the stiffness and mass matrices. Considering the eigenvalue and eigenvector system, the natural frequencies will be computed as
where . To obtain a non-trivial solution of Equation (35), the determinant of the coefficient matrix must be enforced equal to zero, namely
After computing the eigenvalues from Equation (36), the system frequencies can be easily obtained.
4. Numerical Results
In this section a triclinic nanobeam is considered with length L = 36.8 nm, and thickness depending on its length. A preliminary convergence analysis is performed between our model and predictions from Ref. [7] based on the application of the DQM (see Table 1). Then, using the present size-dependent model for anisotropic materials, the convergence of the model is studied for triclinic nanobeams with different boundary conditions (see Table 2). Based on these two tables, a fast convergence of the results can be observed, even with a reduced number of grid points. This justifies the selection of the limited number of grid points N = 19, as done henceforth within the numerical investigation.

Table 1.
Convergence analysis of the size-independent Timoshenko beam model.

Table 2.
Convergence analysis of the size-dependent triclinic beam model (L/h = 100, l = µ = 1 nm2).
To validate the numerical size-dependent methodology of the present work, the first-two dimensionless natural frequencies of the nanostructure are compared to predictions by Eltehar [59] for different values of the nonlocal parameter, based on the Euler Bernoulli beam theory (EBBT), see Table 3. A systematic study is performed to check for the sensitivity of the response for different boundary conditions, with a clear good agreement between the two different approaches, and a general increase of the natural frequencies while moving to a clamped nanostructure at both sides.

Table 3.
Sensitivity of the size-dependent natural frequencies for different nonlocal parameters and boundary conditions.
More specifically, in Table 4 the first four non-dimensional frequencies of a simply supported triclinic nanobeam are summarized for a different length-to-thickness ratio (L/h), nonlocal parameter μ, and strain gradient l. The same results are also represented in the 3D plots of Figure 2. An increased mode number enables higher values of the frequency, which, in turn reduce for increasing nonlocal parameters, and increase with the strain gradient parameters. In addition, the small-scale parameter seems to affect the response especially for higher frequencies rather than the lower ones. For lower mode numbers, any meaningful impact can be observed for a varying length-to-thickness ratio, whereas a visible increase of the natural frequency can be observed by changing the length-to-thickness ratio, for higher modes of vibration (see e.g., the results associated to the forth mode of vibration), while keeping fixed the strain gradient and the nonlocal parameter.

Table 4.
Effect of the L/h and small-scale parameters on the natural frequencies for a simply-simply supported triclinic nanobeam.
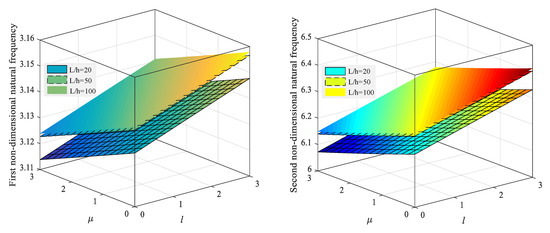
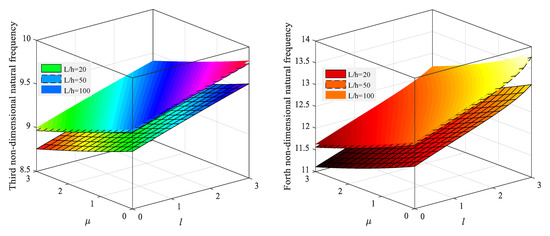
Figure 2.
Variation of the first four natural frequencies for different L/h and small-scale parameters (simply-simply supported nanobeam).
Thus, the same systematic study is repeated for a clamped-simply nanobeam, whose results are listed in Table 5 and are depicted in Figure 3, with the aim of understanding the role of the nonlocal parameter, the strain gradient parameter, and the nondimensional geometrical ratio L/h, in its vibration response. Based on a comparative evaluation of the response between the present case (clamped-simply supports) and the simply-supported case, a general increase in frequency is observed with respect to the previous example, due to the clamped boundary condition enforced on one side, and the general increase in stiffness of the structures. Moreover, an increasing nonlocality μ yields a decreasing structural stiffness, together with a general decrease in the fundamental frequencies. At the same time, an increase in the strain gradient l enables an increase in frequency, independently of the length-to-thickness ratio. Similar considerations can be repeated for the whole vibration modes here analyzed.

Table 5.
Effect of the L/h and small-scale parameters on the natural frequencies for a clamped-simply supported triclinic nanobeam.
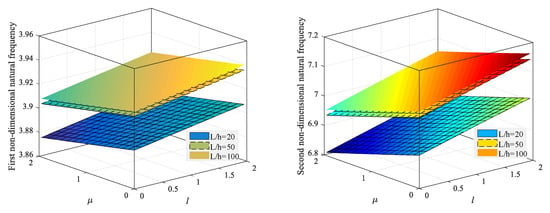
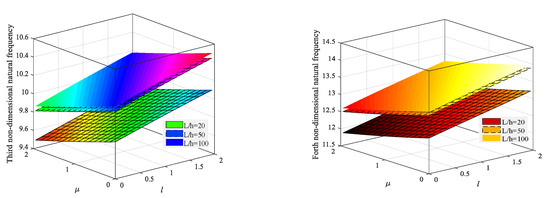
Figure 3.
Variation of the first four natural frequencies for different L/h and small-scale parameters (clamped-simply supported nanobeam).
As a further boundary condition, a fully clamped triclinic nanobeam is analyzed under the same geometry and mechanical assumptions. The results are summarized in Table 6 along with the plots in Figure 4. As expected, an overall increase in stiffness is observed, because of the clamped boundary condition at both sides of the structure. Note also that an increase in the strain gradient parameter l, and nonlocal parameter μ, cause a general increase and decrease of the fundamental frequencies, respectively, in line with the previous examples. As also reported in the pioneering work on the topic [60], the fundamental frequency computed according to the MD is always lower than predictions based on the classical continuum elasticity theory. This behavior is consistent with our findings for nonlocal clamped nanobeams. The last combination of boundary conditions analyzed herein, accounts for a clamped-free triclinic nanobeam, whose parametric vibration response is listed in Table 7 and represented in Figure 5, in terms of the first natural frequencies, while varying the strain gradient parameter l, the nonlocal parameter μ, and the geometrical ratio L/h. Based on the results, note that the clamped-free nanobeam exhibits a different behavior compared to the structural response for the other boundary conditions. Except for the first frequency, the other frequencies reduce for increasing values of μ, and increase for an increasing value of l. The contrary occurs for the first frequency, which decreases for an increasing strain gradient parameter l, and increases by increasing the nonlocal parameter μ. Remarkably, these results are perfectly in line with the findings of Eltaher et al. [59] for a nonlocal cantilever beam. Due to the higher flexibility of the free structure at one side, the lowest values of natural frequencies are registered and compared to all the other examples previously discussed.

Table 6.
Effect of the L/h and small-scale parameters on the natural frequencies for a clamped-clamped triclinic nanobeam.
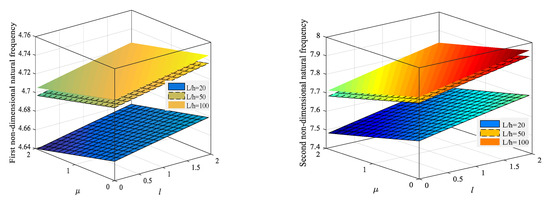
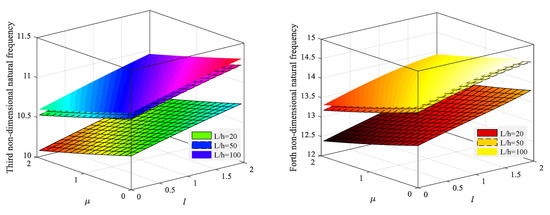
Figure 4.
Variation of the first four natural frequencies for different L/h and small-scale parameters (clamped-clamped nanobeam).

Table 7.
Effect of the L/h and small-scale parameters on the natural frequencies for a clamped-free cantilever triclinic nanobeam.
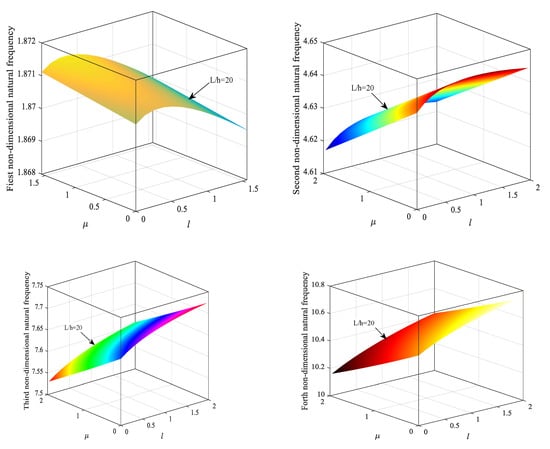
Figure 5.
Variation of the first four natural frequencies for different L/h and small-scale parameters (clamped-free cantilever nanobeam).
Finally, the last parametric investigation compares the response of the triclinic nanobeam under the assumption of constant, linear or quadratic variation in thickness. Table 8 summarizes the results in terms of the first-three non-dimensional natural frequencies, for different nonlocal and strain gradient parameters and boundary conditions. Based on the results in Table 8, a variation in the power-law index q yields a different vibration response. This is clearly affected by the combined values of power-law index and mode numbers. Moreover, it is worth noticing that the small-scale parameters do not affect significantly the response, for different power-law indexes, which is of great interest for design purposes.

Table 8.
Effect of the L/h and thickness variation on the first-three natural frequencies of a triclinic nanobeam for different boundary conditions.
5. Conclusions
In this paper, the free vibration of size-dependent nanobeams made of triclinic material has been investigated. The equations of motion and the associated boundary conditions have been handled by means of the Hamiltonian principle and the Timoshenko beam theory in the context of a nonlocal strain gradient theory. The GDQM has been applied as numerical tool to solve the problem under different boundary conditions assumptions. First, a convergence study verifies successfully the accuracy of the proposed formulation against the available literature. It follows a systematic investigation aimed at checking for the sensitivity of the structural response to small-scale parameters, geometrical dimensions, or possible variations in thickness. According to the parametric results, it is concluded that, the fundamental frequencies increase as the strain gradient parameter increases and nonlocal parameter decreases for all boundary conditions, except for the first mode (in the only case of clamped-free nanobeams). The structural sensitivity to the small-scale parameters becomes much pronounced for higher modes rather than the lower ones. Moreover, the thickness variation impact depends on the vibrational modes and boundary conditions. The highest frequency of the nanobeam is reached always for clamped-clamped boundary conditions, for the same nonlocal parameters and geometrical assumptions. A higher flexibility of the nanostructures is gradually permitted moving from clamped-simply supports, to simply-simply supports, and clamped-free supports. The last combination of boundary conditions yields the lowest values of the vibrational frequency.
Author Contributions
Conceptualization, B.K., R.D. and F.T.; Formal analysis, M.J., R.D. and F.T.; Investigation, B.K. and F.T.; Validation, B.K., M.J., R.D., and F.T.; Writing-original draft, B.K. and M.J.; Writing-review & editing, R.D. and F.T.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mehar, K.; Panda, S.K. Geometrical nonlinear free vibration analysis of FG-CNT reinforced composite flat panel under uniform thermal field. Compos. Struct. 2016, 143, 336–346. [Google Scholar] [CrossRef]
- Kar, V.R.; Mahapatra, T.R.; Panda, S.K. Effect of different temperature load on thermal postbuckling behaviour of functionally graded shallow curved shell panels. Compos. Struct. 2017, 160, 1236–1247. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Strong and weak formulations based on differential and integral quadrature methods for the free vibration analysis of composite plates and shells: Convergence and accuracy. Eng. Anal. Bound. Elem. 2018, 92, 3–37. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D.; Janghorban, M.; Dimitri, R.; Tornabene, F. Wave Propagation of Porous Nanoshells. Nanomaterials 2019, 9, 22. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, M.; Arefi, M.; Dimitri, R.; Tornabene, F. Higher-order thermo-elastic analysis of FG-CNTRC cylindrical vessels surrounded by a pasternak foundation. Nanomaterials 2019, 9, 79. [Google Scholar] [CrossRef] [PubMed]
- Jalaei, M.H.; Dimitri, R.; Tornabene, F. Dynamic stability of temperature-dependent graphene sheet embedded in an elastomeric medium. Appl. Sci. 2019, 9, 887. [Google Scholar] [CrossRef]
- Janghorban, M.; Zare, A. Free vibration analysis of functionally graded carbon nanotubes with variable thickness by differential quadrature method. Phys. E Low Dimens. Syst. Nanostruct. 2011, 43, 1602–1604. [Google Scholar] [CrossRef]
- Ghannadpour, S.A.M.; Karimi, M.; Tornabene, F. Application of plate decomposition technique in nonlinear and post-buckling analysis of functionally graded plates containing crack. Compos. Struct. 2019, 220, 158–167. [Google Scholar] [CrossRef]
- Kandasamy, R.; Dimitri, R.; Tornabene, F. Numerical study on the free vibration and thermal buckling behavior of moderately thick functionally graded structures in thermal environments. Compos. Struct. 2016, 157, 207–221. [Google Scholar] [CrossRef]
- Shafiei, N.; She, G.L. On vibration of functionally graded nano-tubes in the thermal environment. Int. J. Eng. Sci. 2018, 133, 84–98. [Google Scholar] [CrossRef]
- Khaniki, H.B. On vibrations of FG nanobeams. Int. J. Eng. Sci. 2019, 135, 23–36. [Google Scholar] [CrossRef]
- Tornabene, F.; Brischetto, S.; Fantuzzi, N.; Bacciocchi, M. Boundary conditions in 2D numerical and 3D exact models for cylindrical bending analysis of functionally graded structures. Shock Vib. 2016, 2016, 2373862. [Google Scholar] [CrossRef]
- Batra, R.; Qian, L.; Chen, L. Natural frequencies of thick square plates made of orthotropic, trigonal, monoclinic, hexagonal and triclinic materials. J. Sound Vib. 2004, 270, 1074–1086. [Google Scholar] [CrossRef]
- Ferreira, A.; Batra, R. Natural frequencies of orthotropic, monoclinic and hexagonal plates by a meshless method. J. Sound Vib. 2005, 285, 734–742. [Google Scholar] [CrossRef]
- Ferreira, A.; Fasshauer, G.; Batra, R. Natural frequencies of thick plates made of orthotropic, monoclinic, and hexagonal materials by a meshless method. J. Sound Vib. 2009, 319, 984–992. [Google Scholar] [CrossRef]
- Ferreira, A.; Fasshauer, G.; Batra, R.; Rodrigues, J. Static Deformations and Vibration Analysis of Composite and Sandwich Plates Using a LayerwiseTheory and RBF-PS Discretizations with Optimal Shape Parameter. Compos. Struct. 2008, 86, 328–343. [Google Scholar] [CrossRef]
- Karami, B.; Janghorban, M.; Tounsi, A. Nonlocal strain gradient 3D elasticity theory for anisotropic spherical nanoparticles. Steel Compos. Struct. 2018, 27, 201–216. [Google Scholar]
- Karami, B.; Janghorban, M.; Tounsi, A. Effects of triaxial magnetic field on the anisotropic nanoplates. Steel Compos. Struct. 2017, 25, 361–374. [Google Scholar]
- Karami, B.; Janghorban, M.; Tounsi, A. Variational approach for wave dispersion in anisotropic doubly-curved nanoshells based on a new nonlocal strain gradient higher order shell theory. Thin Walled Struct. 2018, 129, 251–264. [Google Scholar] [CrossRef]
- Karami, B.; Janghorban, M.; Tounsi, A. Galerkin’s approach for buckling analysis of functionally graded anisotropic nanoplates/different boundary conditions. Eng. Comput. 2018. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D.; Janghorban, M. Wave propagation analysis in functionally graded (FG) nanoplates under in-plane magnetic field based on nonlocal strain gradient theory and four variable refined plate theory. Mech. Adv. Mater. Struct. 2018, 25, 1047–1057. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D.; Janghorban, M. A comprehensive analytical study on functionally graded carbon nanotube-reinforced composite plates. Aerosp. Sci. Technol. 2018, 82, 499–512. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D.; Li, L. Temperature-dependent flexural wave propagation in nanoplate-type porous heterogenous material subjected to in-plane magnetic field. J. Therm. Stress. 2018, 41, 483–499. [Google Scholar] [CrossRef]
- Ansari, R.; Rouhi, H.; Sahmani, S. Calibration of the analytical nonlocal shell model for vibrations of double-walled carbon nanotubes with arbitrary boundary conditions using molecular dynamics. Int. J. Mech. Sci. 2011, 53, 786–792. [Google Scholar] [CrossRef]
- Han, Y.; Elliott, J. Molecular dynamics simulations of the elastic properties of polymer/carbon nanotube composites. Comput. Mater. Sci. 2007, 39, 315–323. [Google Scholar] [CrossRef]
- Hua, J.; Duan, Z.; Song, C.; Liu, Q. Molecular dynamics study on the tensile properties of graphene/Cu nanocomposite. Int. J. Comput. Mater. Sci. Eng. 2017, 6, 1750021. [Google Scholar] [CrossRef]
- Rahman, R.; Foster, J. A molecular dynamics based investigation of thermally vibrating graphene under different boundary conditions. Phys. E Low Dimens. Syst. Nanostruct. 2015, 72, 25–47. [Google Scholar] [CrossRef]
- Houari, M.S.A.; Bessaim, A.; Bernard, F.; Tounsi, A.; Mahmoud, S. Buckling analysis of new quasi-3D FG nanobeams based on nonlocal strain gradient elasticity theory and variable length scale parameter. Steel Compos. Struct. 2018, 28, 13–24. [Google Scholar]
- Ahouel, M.; Houari, M.S.A.; Bedia, E.; Tounsi, A. Size-dependent mechanical behavior of functionally graded trigonometric shear deformable nanobeams including neutral surface position concept. Steel Compos. Struct. 2016, 20, 963–981. [Google Scholar] [CrossRef]
- Bouadi, A.; Bousahla, A.A.; Houari, M.S.A.; Heireche, H.; Tounsi, A. A new nonlocal HSDT for analysis of stability of single layer graphene sheet. Adv. Nano Res. 2018, 6, 147–162. [Google Scholar]
- Mokhtar, Y.; Heireche, H.; Bousahla, A.A.; Houari, M.S.A.; Tounsi, A.; Mahmoud, S. A novel shear deformation theory for buckling analysis of single layer graphene sheet based on nonlocal elasticity theory. Smart Struct. Syst. 2018, 21, 397–405. [Google Scholar]
- Bouafia, K.; Kaci, A.; Houari, M.S.A.; Benzair, A.; Tounsi, A. A nonlocal quasi-3D theory for bending and free flexural vibration behaviors of functionally graded nanobeams. Smart Struct. Syst. 2017, 19, 115–126. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D.; Li, L. Hygrothermal wave propagation in viscoelastic graphene under in-plane magnetic field based on nonlocal strain gradient theory. Phys. E Low Dimens. Syst. Nanostruct. 2018, 97, 317–327. [Google Scholar] [CrossRef]
- Shahsavari, D.; Karami, B.; Li, L. Damped vibration of a graphene sheet using a higher-order nonlocal strain-gradient Kirchhoff plate model. C. R. Méc. 2018, 346, 1216–1232. [Google Scholar] [CrossRef]
- She, G.L.; Yuan, F.G.; Ren, Y.R.; Xiao, W.S. On buckling and postbuckling behavior of nanotubes. Int. J. Eng. Sci. 2017, 121, 130–142. [Google Scholar] [CrossRef]
- Askes, H.; Aifantis, E.C. Gradient elasticity and flexural wave dispersion in carbon nanotubes. Phys. Rev. B 2009, 80, 195412. [Google Scholar] [CrossRef]
- Challamel, N.; Wang, C. The small length scale effect for a non-local cantilever beam: A paradox solved. Nanotechnology 2008, 19, 345703. [Google Scholar] [CrossRef]
- Lim, C.; Zhang, G.; Reddy, J. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Amabili, M. Nonlinear dynamics of a geometrically imperfect microbeam based on the modified couple stress theory. Int. J. Eng. Sci. 2013, 68, 11–23. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y.; Ling, L. Flexural wave propagation in small-scaled functionally graded beams via a nonlocal strain gradient theory. Compos. Struct. 2015, 133, 1079–1092. [Google Scholar] [CrossRef]
- Li, L.; Li, X.; Hu, Y. Free vibration analysis of nonlocal strain gradient beams made of functionally graded material. Int. J. Eng. Sci. 2016, 102, 77–92. [Google Scholar] [CrossRef]
- Li, L.; Tang, H.; Hu, Y. The effect of thickness on the mechanics of nanobeams. Int. J. Eng. Sci. 2018, 123, 81–91. [Google Scholar] [CrossRef]
- She, G.L.; Yuan, F.G.; Karami, B.; Ren, Y.R.; Xiao, W.S. On nonlinear bending behavior of FG porous curved nanotubes. Int. J. Eng. Sci. 2019, 135, 58–74. [Google Scholar] [CrossRef]
- She, G.L.; Ren, Y.R.; Yuan, F.G.; Xiao, W.S. On vibrations of porous nanotubes. Int. J. Eng. Sci. 2018, 125, 23–35. [Google Scholar] [CrossRef]
- She, G.L.; Yuan, F.G.; Ren, Y.R. On wave propagation of porous nanotubes. Int. J. Eng. Sci. 2018, 130, 62–74. [Google Scholar] [CrossRef]
- She, G.L.; Yan, K.M.; Zhang, Y.L.; Liu, H.B.; Ren, Y.R. Wave propagation of functionally graded porous nanobeams based on non-local strain gradient theory. Eur. Phys. J. Plus 2018, 133, 368. [Google Scholar] [CrossRef]
- Tomasiello, S. Simulating non-linear coupled oscillators by an iterative differential quadrature method. J. Sound Vib. 2003, 265, 507–525. [Google Scholar] [CrossRef]
- Tomasiello, S. A DQ based approach to simulate the vibrations of buckled beams. Nonlinear Dyn. 2007, 50, 37–48. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Ubertini, F.; Viola, E. Strong formulation finite element method based on differential quadrature: A survey. Appl. Mech. Rev. 2015, 67, 1–55. [Google Scholar] [CrossRef]
- Kamarian, S.; Salim, M.; Dimitri, R.; Tornabene, F. Free vibration of conicla shells reinforced witj agglomerated Carbon Nanotubes. Int. J. Mech. Sci. 2016, 108–109, 157–165. [Google Scholar] [CrossRef]
- Tornabene, F.; Dimitri, R.; Viola, E. Transient dynamic response of generally-shaped arches based on a GDQ-time-stepping method. Int. J. Mech. Sci. 2016, 114, 277–314. [Google Scholar] [CrossRef]
- Dimitri, R.; Tornabene, F.; Zavarise, G. Analitical and numerical modeling of the mixed-mode delamination process for composite moment-loaded double cantilever beams. Compos. Struct. 2018, 187, 535–553. [Google Scholar] [CrossRef]
- Tornabene, F.; Dimitri, R. A numerical study of the seismic response of arched and valuted structures made of isotropic or composite materials. Eng. Struct. 2018, 159, 332–366. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer: Berlin, Germany, 2000. [Google Scholar]
- Tornabene, F.; Bacciocchi, M. Anisotropic Doubly-Curved Shells: Higher-Order Strong and Weak Formulations for Arbitrary Shaped Shell Structures; Esculapio: Bologna, Italy, 2018. [Google Scholar]
- Zhu, X.; Nie, Y.; Zhang, W. An efficient differential quadrature method for fractional advection–diffusion equation. Nonlinear Dyn. 2017, 90, 1807–1827. [Google Scholar] [CrossRef]
- Dahiya, S.; Mittal, R.C. A modified cubic B-spline differential quadrature method for three-dimensional non-linear diffusion equations. Open Phys. 2017, 15, 453–463. [Google Scholar] [CrossRef]
- Eftekhari, S. A modified differential quadrature procedure for numerical solution of moving load problem. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 715–731. [Google Scholar] [CrossRef]
- Eltaher, M.; Alshorbagy, A.E.; Mahmoud, F. Vibration analysis of Euler–Bernoulli nanobeams by using finite element method. Appl. Math. Model. 2013, 37, 4787–4797. [Google Scholar] [CrossRef]
- Rudd, R.; Broughton, J. Atomistic simulation of MEMS resonators through the coupling of length scales. J. Model. Simul. Microsyst. 1999, 1, 29–38. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).