Reverse Engineering of Thermoregulatory Cold-Induced Vasoconstriction/Vasodilation during Localized Cooling
Abstract
1. Introduction
2. Materials and Methods
2.1. Controllable Active Cooling Device and Measurements (iGlove-1)
2.2. Experiments
2.2.1. Test Subjects
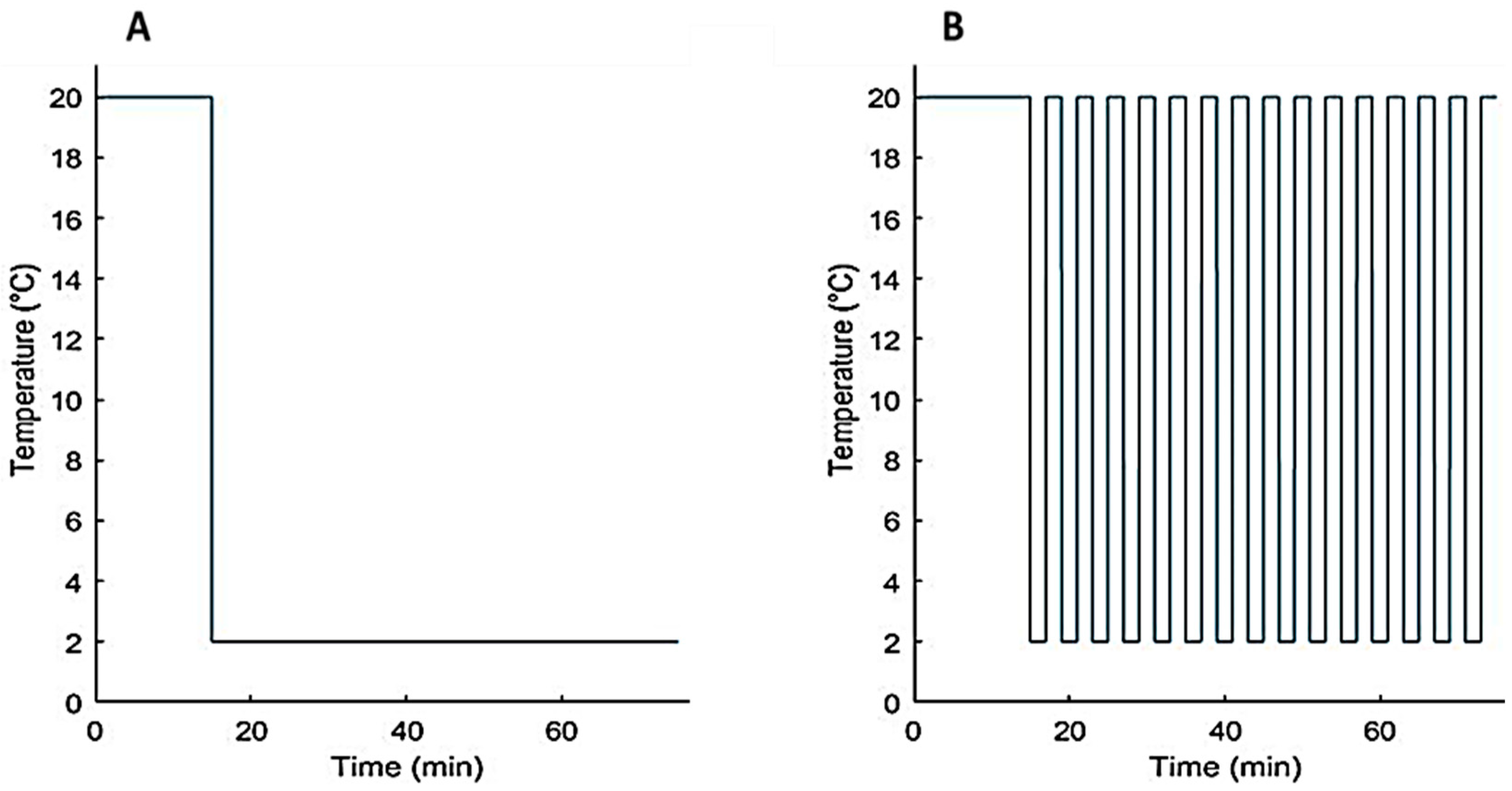
2.2.2. Experimental Protocol
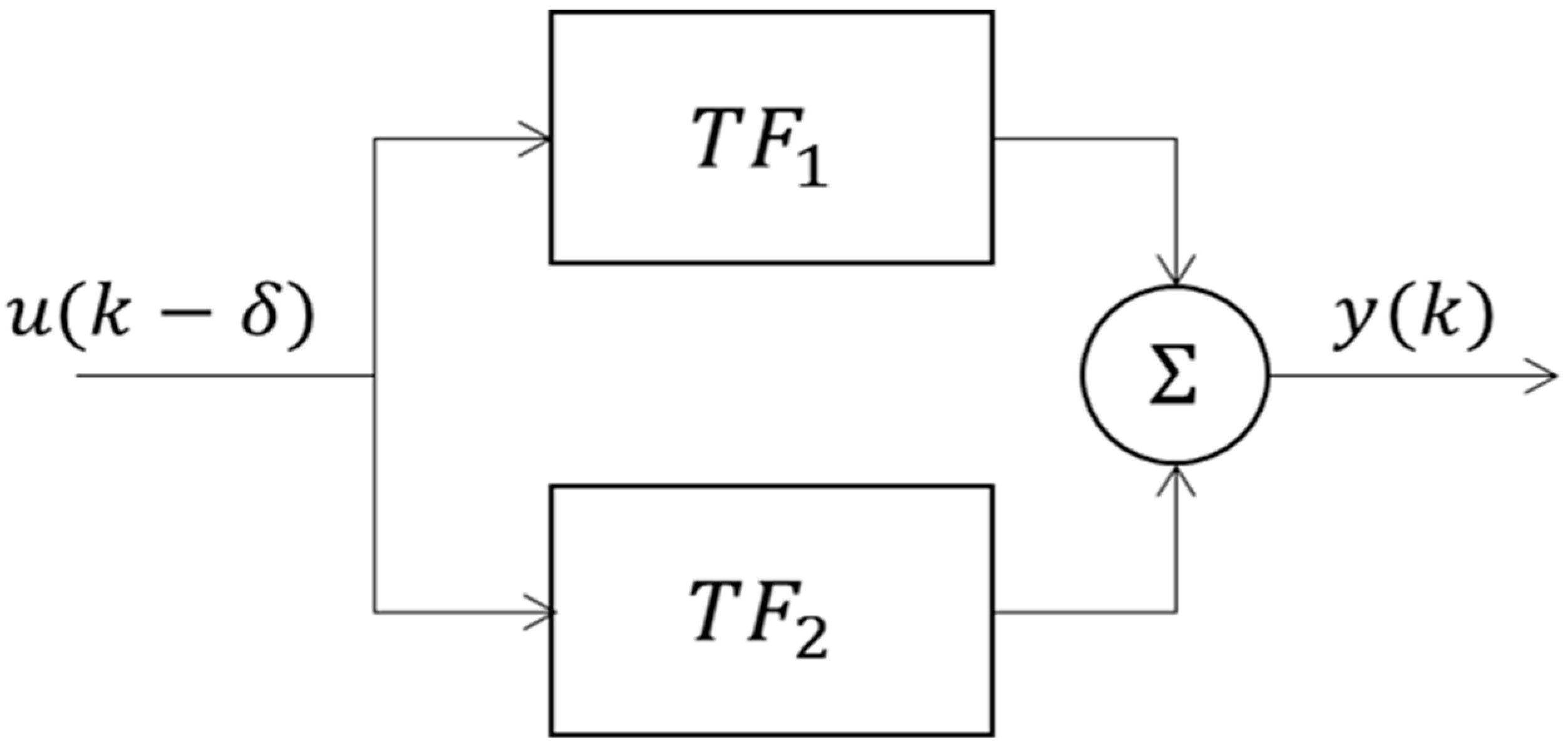
2.3. System Identification and Modelling of CIVC/CIVD
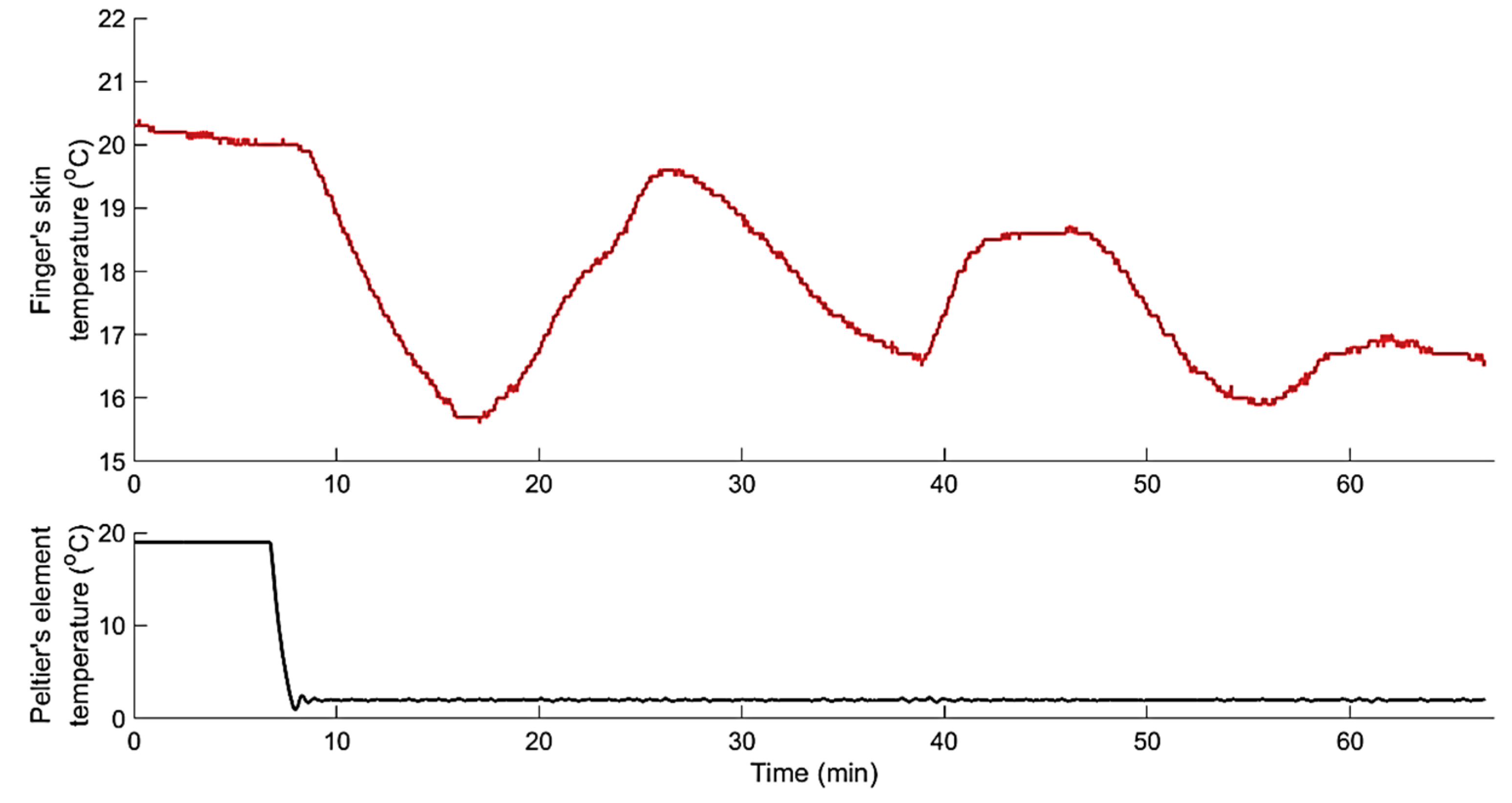
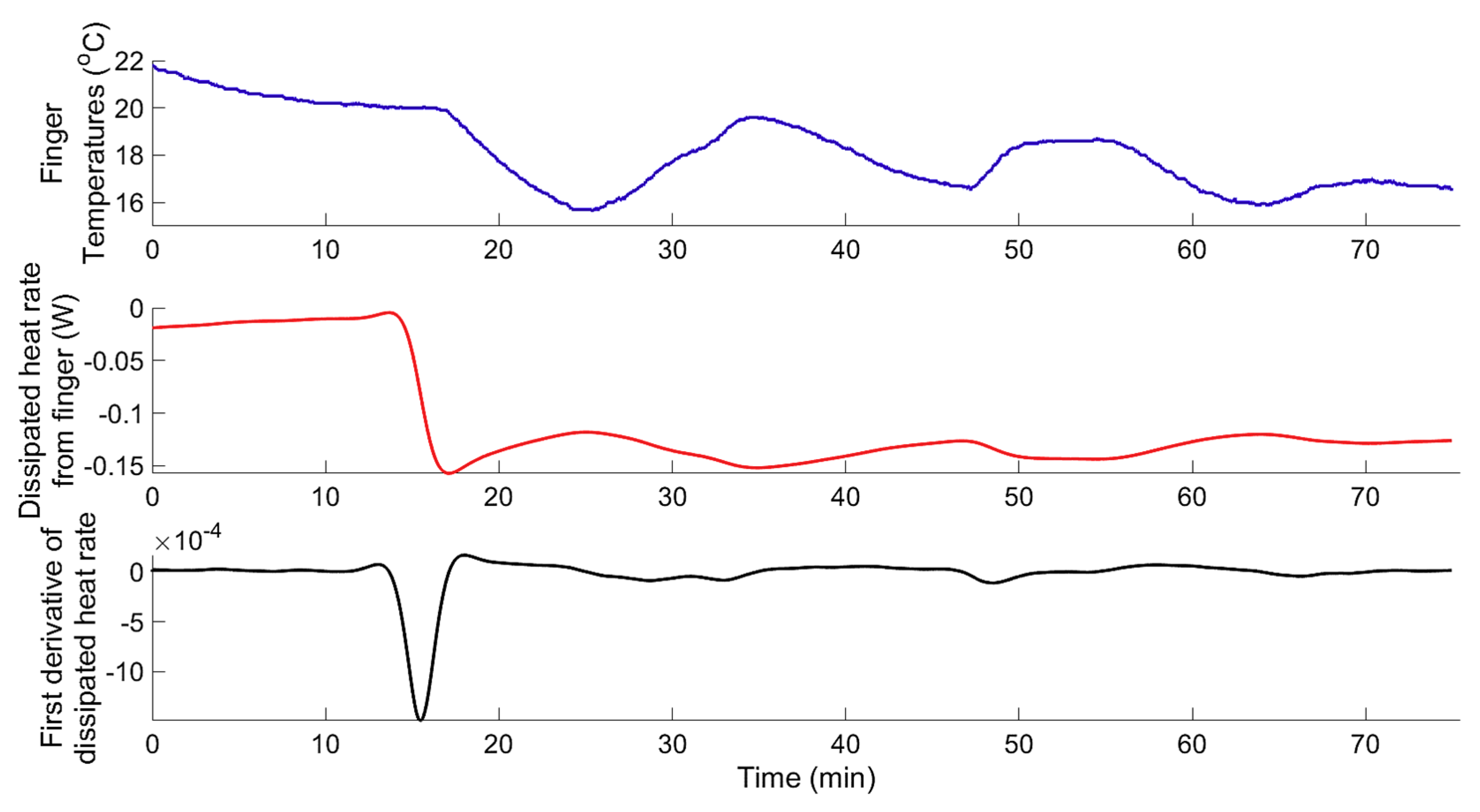
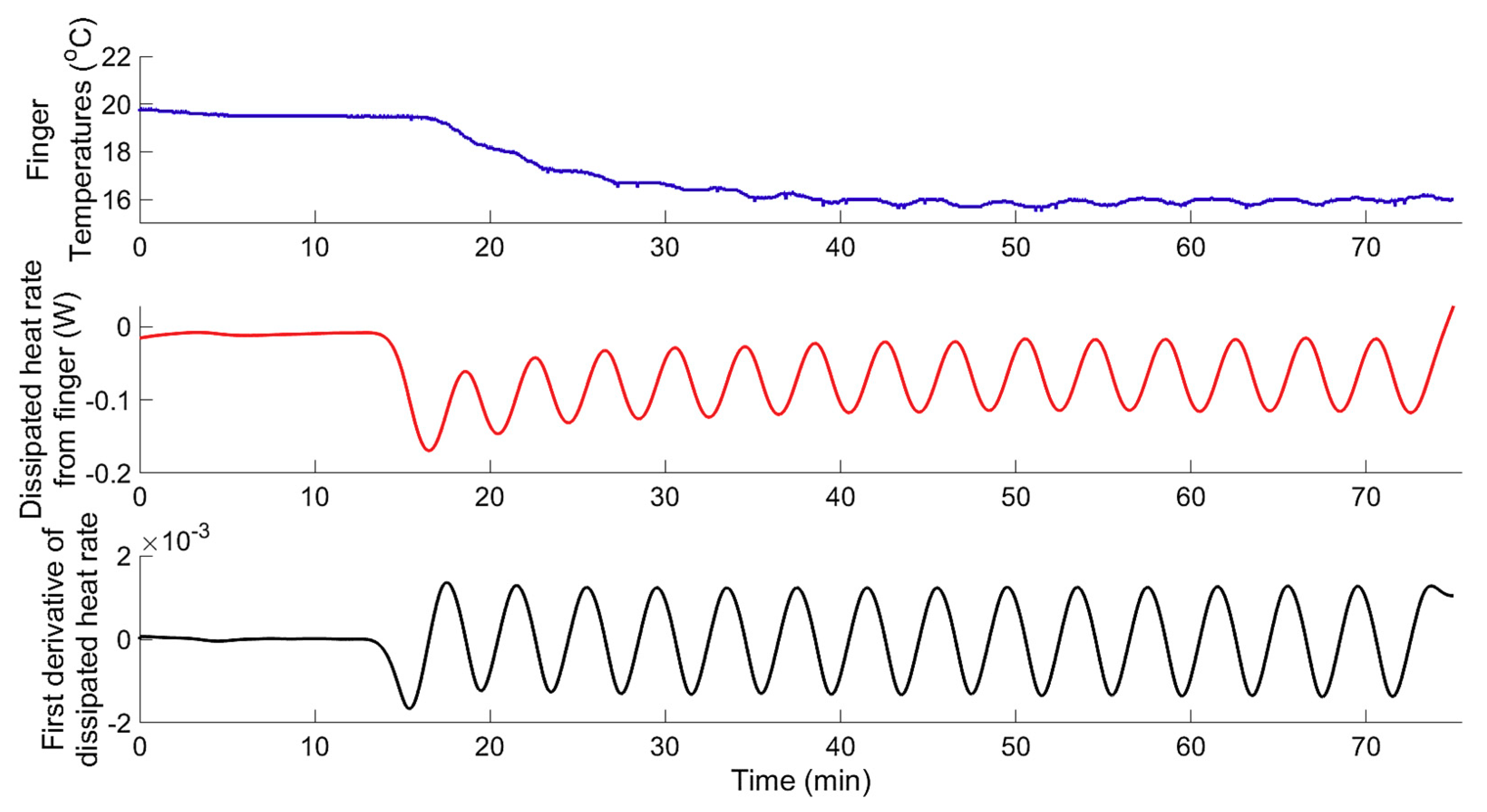
3. Results and Discussion
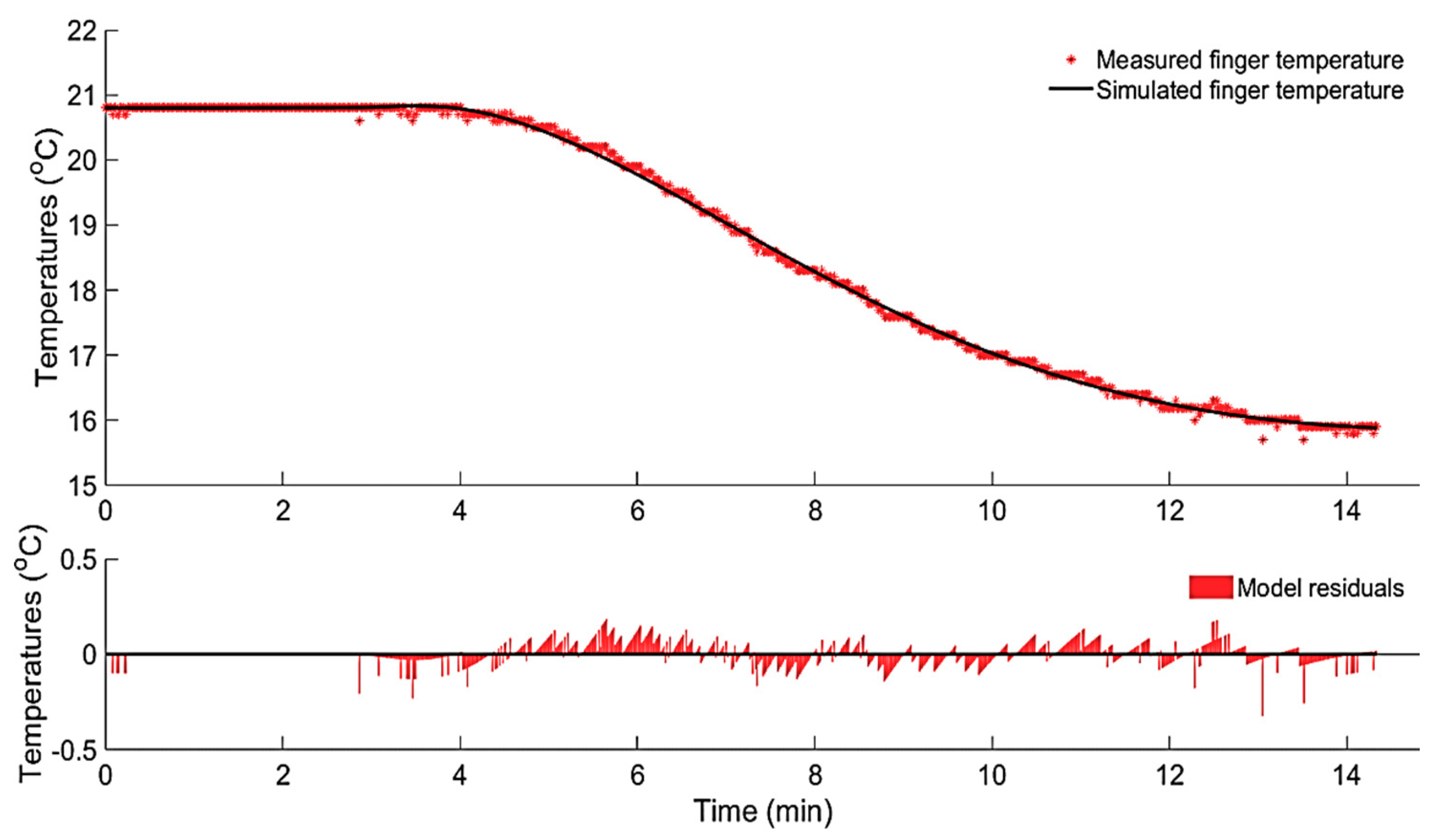
3.1. System Identification
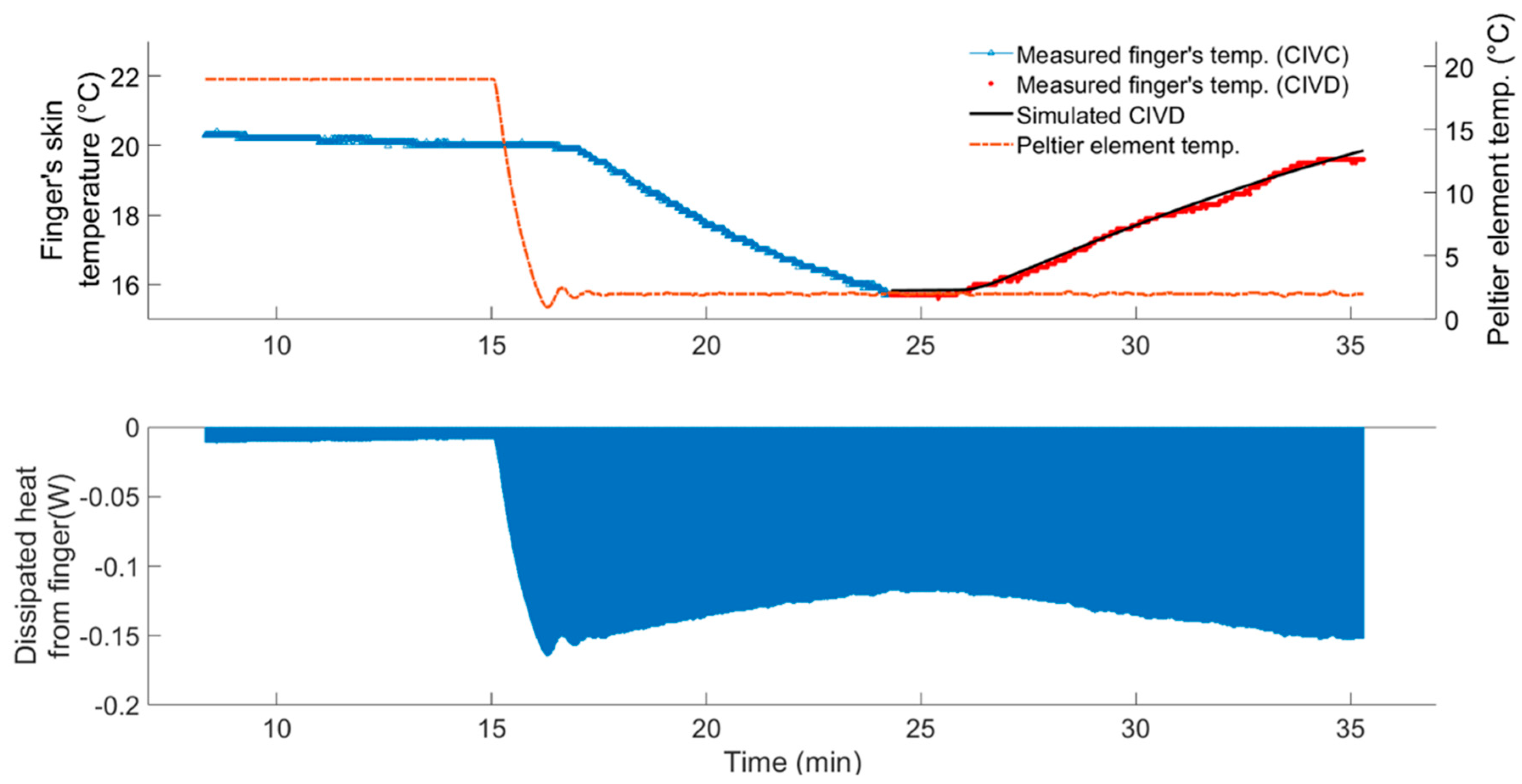
3.1.1. Data-Based Mechanistic Modelling of CIVC
3.1.2. Data-Based Mechanistic Modelling of CIVD
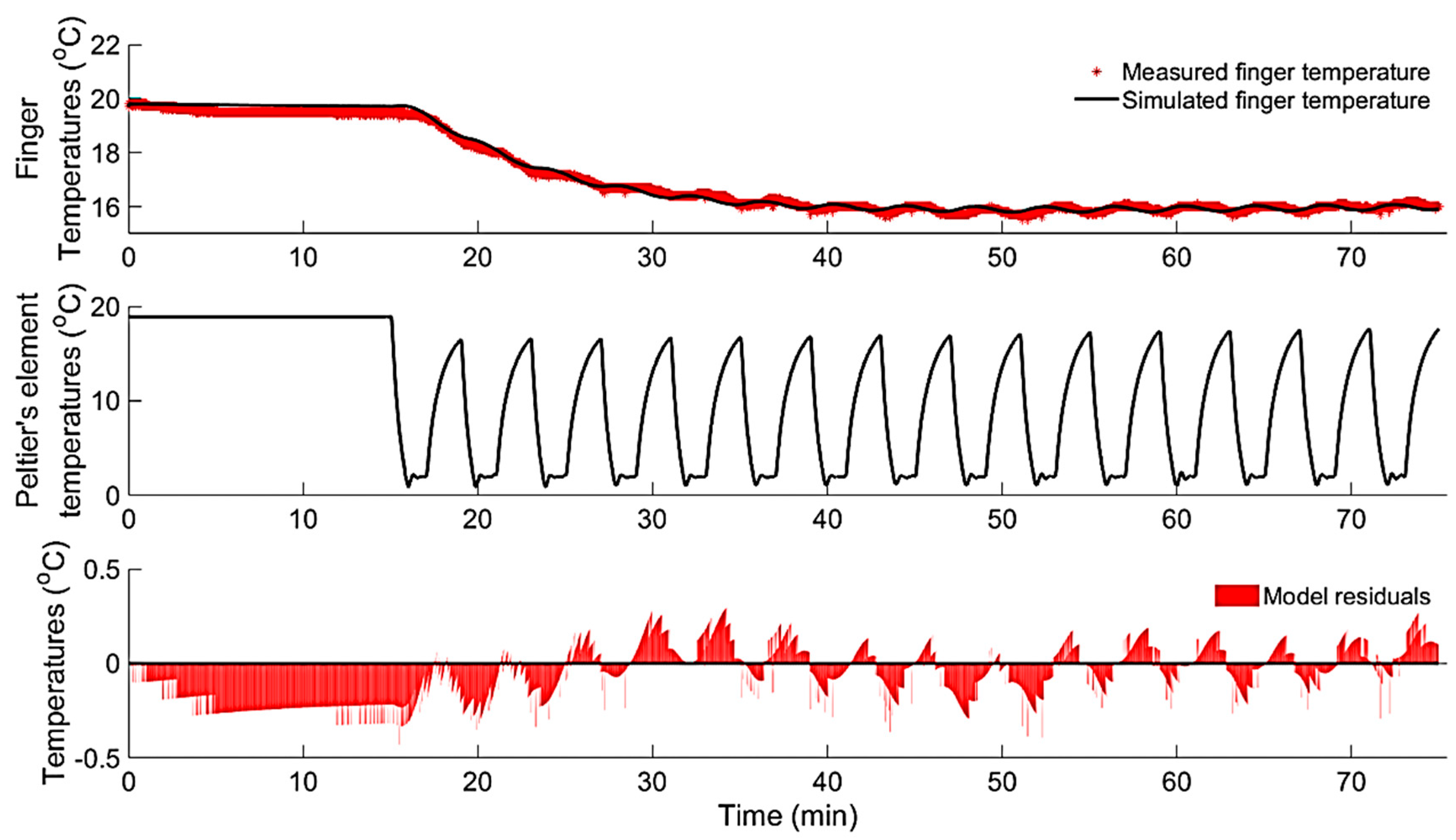
3.1.3. Modelling of Localized Intermittent Cooling Effect
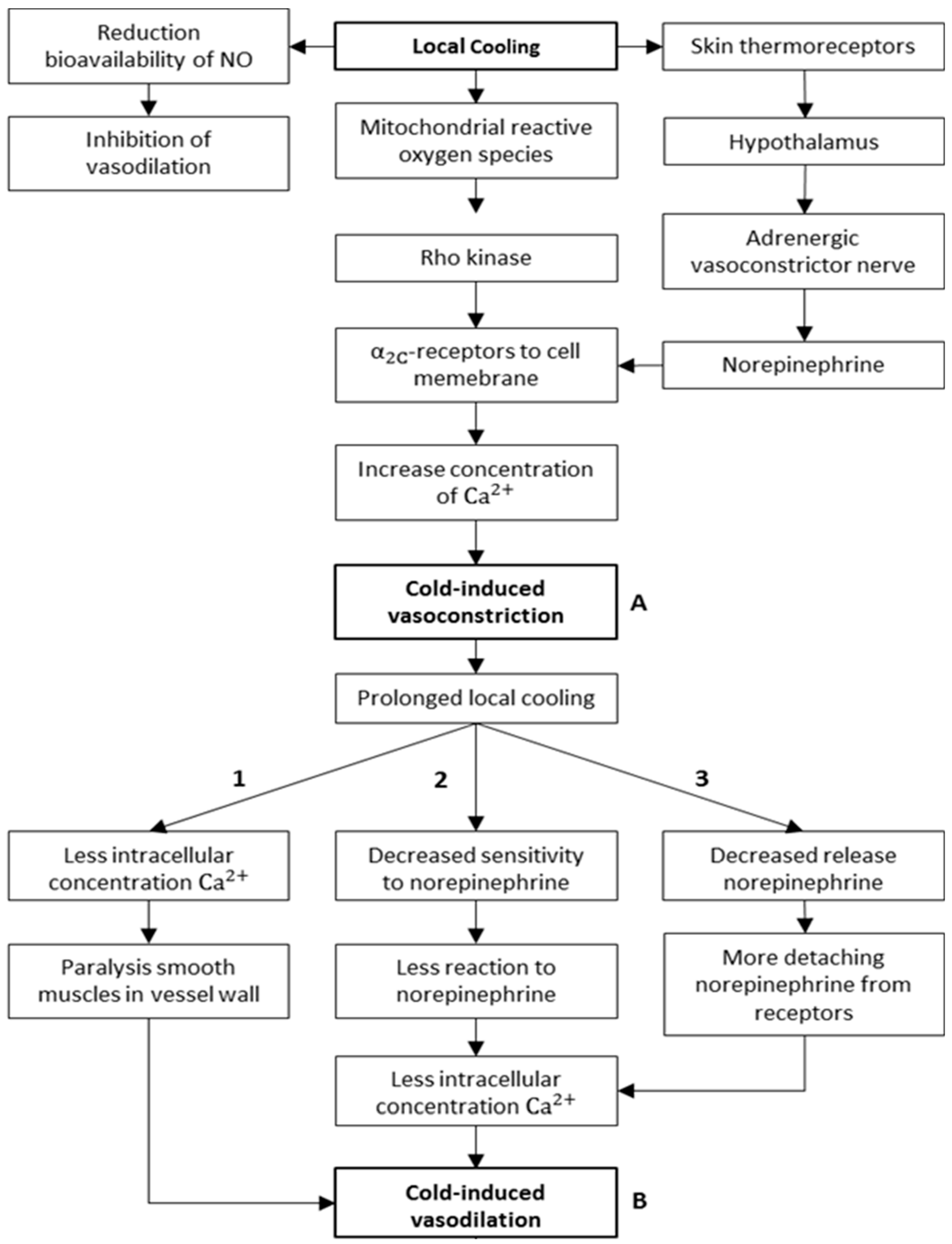
3.2. Physiological/Mechanistic Interpretation of Thermoregulatory CIVC/CIVD Reactions
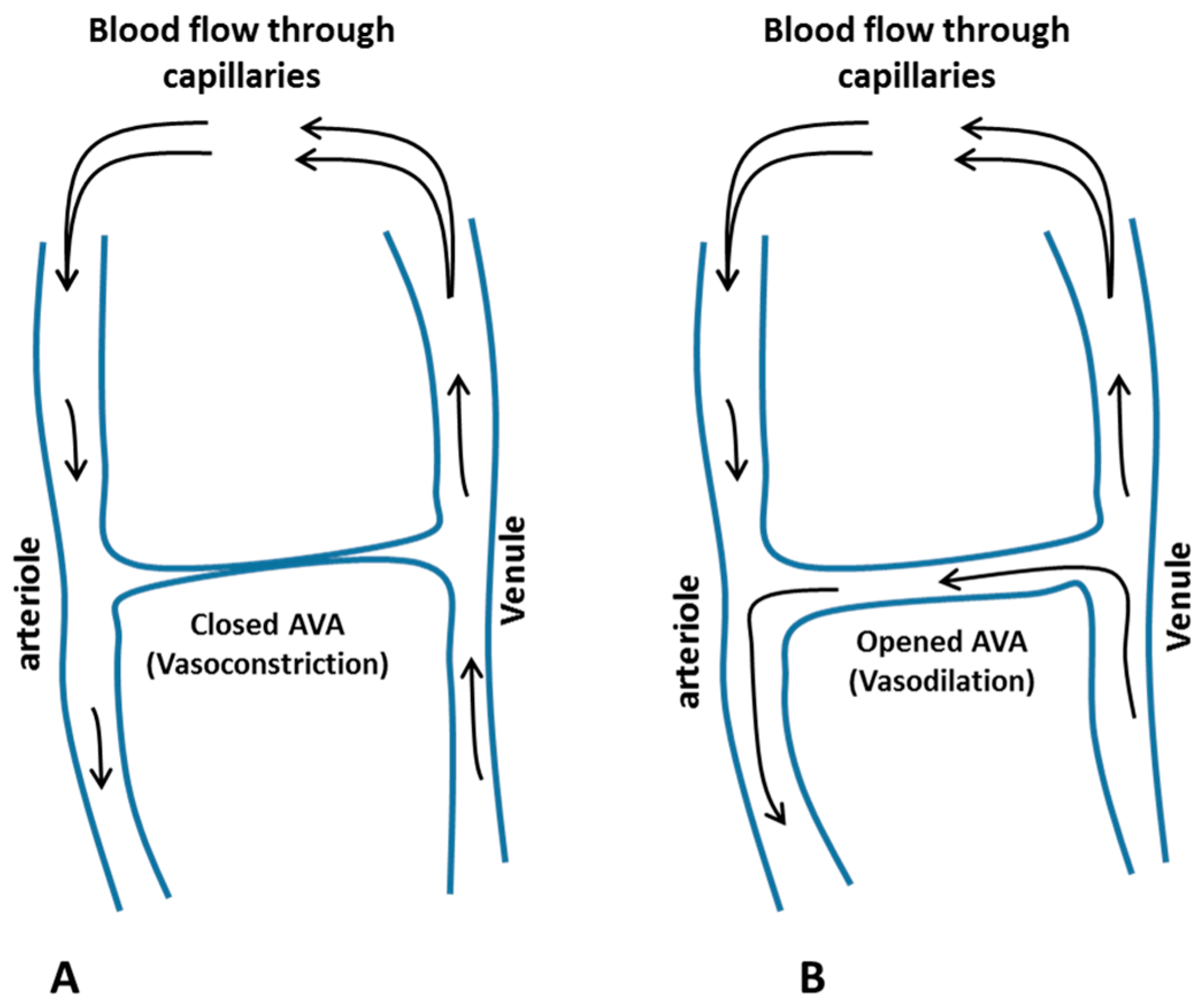
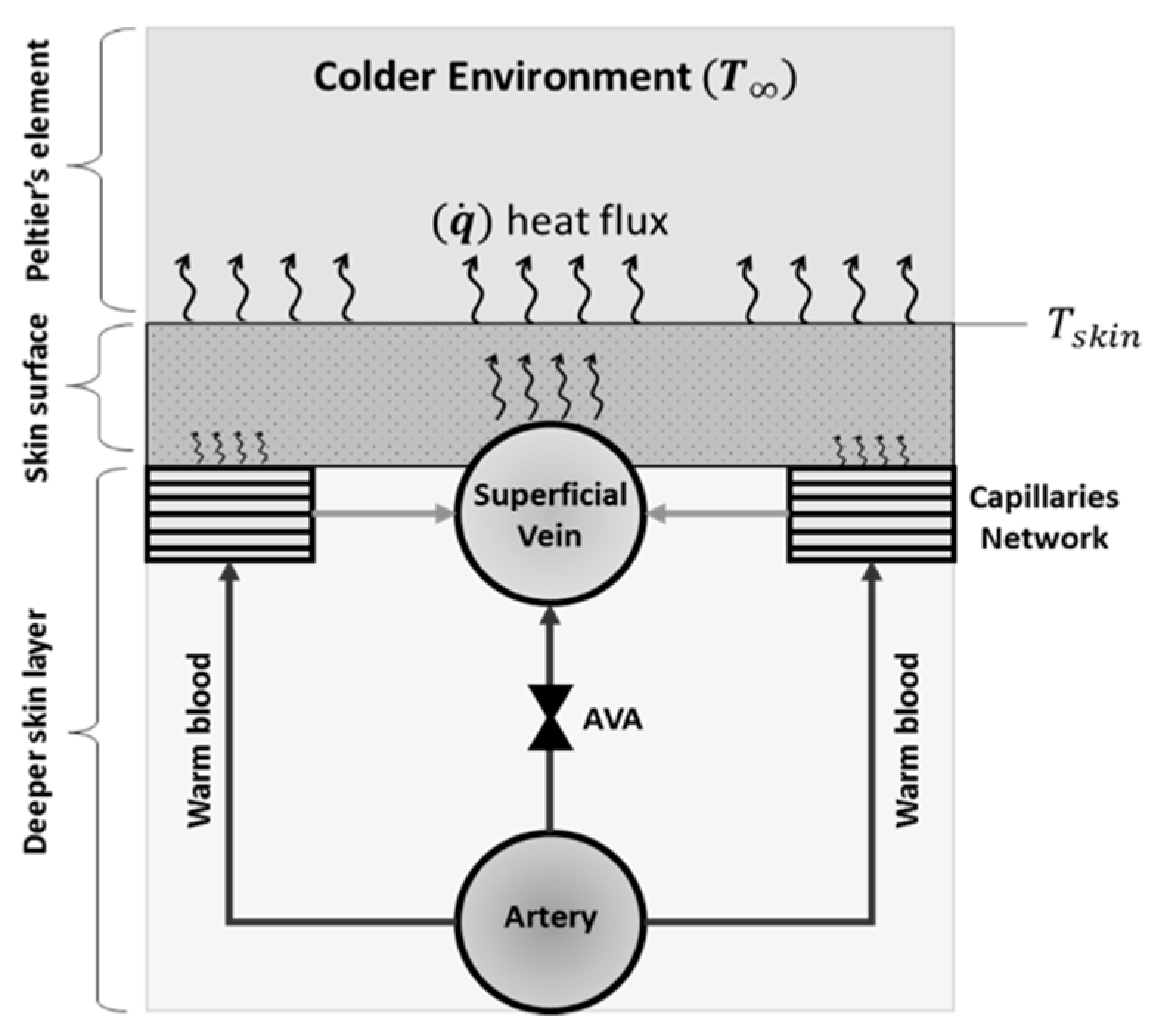
3.2.1. Mechanisms of CIVC/CIVD Reactions during Localised Cooling
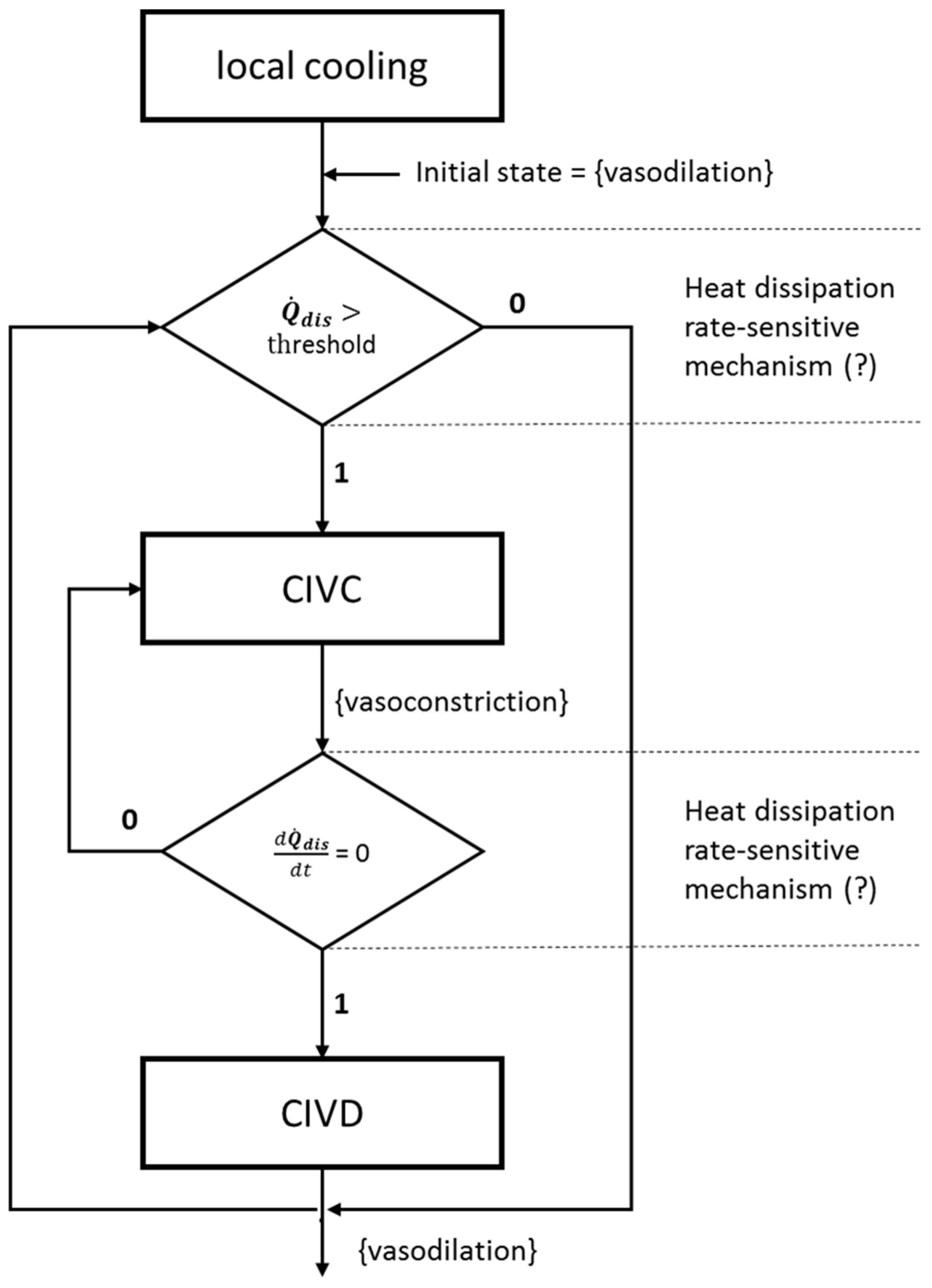
3.2.2. A New Model for Thermoregulatory Localised CIVC/CIVD Reactions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Novosel’tsev, V.N. Homeostasis and health: Analysis from a standpoint of the control theory. Autom. Remote Control 2012, 73, 841–851. [Google Scholar] [CrossRef]
- Bernard, C. De la Physiologie Générale; Librairie Hachette Et: Paris, France, 1872. [Google Scholar]
- Cannon, W.B. The Wisdom of the Body; W.W. Norton: New York, NY, USA, 1939. [Google Scholar]
- Ivanov, K.P. The development of the concepts of homeothermy and thermoregulation. J. Therm. Biol. 2006, 31, 24–29. [Google Scholar] [CrossRef]
- Ivanov, K. Restoration of vital activity of cooled animals without rewarming the body. Eur. J. Appl. Physiol. 2009, 105, 5–12. [Google Scholar] [CrossRef] [PubMed]
- Turner, J.S. On the thermal capacity of a bird’s egg warmed by a brood patch. Physiol. Zool. 1997, 70, 470–480. [Google Scholar] [CrossRef] [PubMed]
- Cheung, S.S. Responses of the hands and feet to cold exposure. Temperature 2015, 2, 105–120. [Google Scholar] [CrossRef] [PubMed]
- Taylor, N.A.S.; Machado-Moreira, C.A.; van den Heuvel, A.M.J.; Caldwell, J.N. Hands and feet: Physiological insulators, radiators and evaporators. Eur. J. Appl. Physiol. 2014, 114, 2037–2060. [Google Scholar] [CrossRef] [PubMed]
- Walløe, L. Arterio-venous anastomoses in the human skin and their role in temperature control. Temp. (Austin. Tex.) 2016, 3, 92–103. [Google Scholar] [CrossRef] [PubMed]
- Grant, R.T.; Bland, E. Observations on arterio venous anastomoses in human skin and in the bird’s foot with special reference to the reaction to cold. Heart 1931, 15, 385–411. [Google Scholar]
- Heus, R.; Daanen, H.A.M.; Havenith, G. Physiological criteria for functioning of hands in the cold. Appl. Ergon. 1995, 26, 5–13. [Google Scholar] [CrossRef]
- Karaki, W.; Ghaddar, N.; Ghali, K.; Kuklane, K.; Holmér, I.; Vanggaard, L. Human thermal response with improved AVA modeling of the digits. Int. J. Therm. Sci. 2013, 67, 41–52. [Google Scholar] [CrossRef]
- Rida, M.; Karaki, W.; Ghaddar, N.; Ghali, K.; Hoballah, J. A new mathematical model to simulate AVA cold-induced vasodilation reaction to local cooling. Int. J. Biometeorol. 2014, 58, 1905–1918. [Google Scholar] [CrossRef] [PubMed]
- Lewis, T. Observations upon the reactions of the vessels of the human skin to cold. Heart 1930, 15, 177–208. [Google Scholar]
- Daanen, H.A.M. Finger cold-induced vasodilation: A review. Eur. J. Appl. Physiol. 2003, 89, 411–426. [Google Scholar] [CrossRef] [PubMed]
- Teichner, W.H. Individual Thermal and Behavioral Factors in Cold-Induced Vasodilation. Psychophysiology 1966, 2, 295–304. [Google Scholar] [CrossRef]
- Bergersen, T.K.; Hisdal, J.; Walløe, L. Perfusion of the human finger during cold-induced vasodilatation. Am. J. Physiol. 1999, 276, R731–R737. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.Y.; Bakri, I.; Matsuo, A.; Tochihara, Y. Cold-induced vasodilation and vasoconstriction in the finger of tropical and temperate indigenes. J. Therm. Biol. 2013, 38, 70–78. [Google Scholar] [CrossRef]
- Cheung, S.S.; Daanen, H.A.M. Dynamic Adaptation of the Peripheral Circulation to Cold Exposure. Microcirculation 2012, 19, 65–77. [Google Scholar] [CrossRef]
- Youssef, A.; D’Haene, M.; Vleugels, J.; de Bruyne, G.; Aerts, J.-M. Localised Model-Based Active Controlling of Blood Flow During Chemotherapy to Prevent Nail Toxicity and Onycholysis. J. Med. Biol. Eng. 2018, 39, 139–150. [Google Scholar] [CrossRef]
- Bladt, L.; De Clercq, J.; Janssens, T.; Van Hulle, J.; Vleugels, J.; Aerts, J.M.; De Bruyne, G. Cold-induced vasoconstriction for preventing onycholysis during cancer treatment. Extrem. Physiol. Med. 2015, 4, A60. [Google Scholar] [CrossRef]
- Steckel, J.; Goethijn, F.; de Bruyne, G. A research platform using active local cooling directed at minimizing the blood flow in human fingers. In Proceedings of the 7th International Conference on Pervasive Computing Technologies for Healthcare and Workshops, Venice, Italy, 5–8 May 2013; pp. 81–84. [Google Scholar]
- Aerts, J.M.; Berckmans, D.; Saevels, P.; Decuypere, E.; Buyse, J. Modelling the static and dynamic responses of total heat production of broiler chickens to step changes in air temperature and light intensity. Br. Poult. Sci. 2000, 41, 651–659. [Google Scholar] [CrossRef]
- Young, P.C. Control and Dynamic Systems: Advances in Theory and Applications; Leondes, C.T., Ed.; New Academic Press Inc Elsevier Science: New York, NY, USA, 1989. [Google Scholar]
- Young, P.C. Data-based mechanistic modelling of environmental, ecological, economic and engineering systems. Environ. Model. Softw. 1998, 13, 105–122. [Google Scholar] [CrossRef]
- Youssef, A.; Dekock, J.; Ozcan, S.E.; Berckmans, D. Data-Based Approach to Model the Dynamic Behaviour of Greenhouse Temperature. Acta Hortic. 2011, 893, 931–938. [Google Scholar] [CrossRef]
- Youssef, A.; Exadaktylos, V.; Berckmans, D. Modelling and quantification of the thermoregulatory responses of the developing avian embryo: Electrical analogies of a physiological system. J. Therm. Biol. 2014, 44, 14–19. [Google Scholar] [CrossRef] [PubMed]
- Youssef, A.; Exadaktylos, V.; Ozcan, S.E.; Berckmans, D. Proportional-Integral-Plus (PIP) Control System for Individual Thermal Zones in a Small Ventilated Space. ASHRAE Trans. 2011, 117, 48–56. [Google Scholar]
- Youssef, A.; Yen, H.; Özcan, S.E.; Berckmans, D. Data-based mechanistic modelling of indoor temperature distributions based on energy input. Energy Build. 2011, 43, 2965–2972. [Google Scholar] [CrossRef]
- Young, P.C.; Jakeman, A. Refined instrumental variable methods of recursive time-series analysis Part III. Extensions. Int. J. Control 1980, 31, 741–764. [Google Scholar] [CrossRef]
- Young, P.C. Recursive Estimation and Time-Series Analysis: An Introduction for the Student and Practitioner; Springer: Heidelberg, Berlin, 2011. [Google Scholar]
- Young, P.C.; Chotai, A.; Tych, W. Identification, Estimation and Control of Continuous-Time Systems Described by Delta Operator Models; Kluwer Academic Publishers: Dordrecht, the Netherlands, 1991. [Google Scholar]
- Tansey, E.A.; Johnson, C.D. Recent advances in thermoregulation. Adv. Physiol. Educ. 2015, 39, 139–148. [Google Scholar] [CrossRef]
- Lienhard, J.H. A Heat Transfer Textbook; Phlogiston Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Yamazaki, F.; Sone, R.; Zhao, K.; Alvarez, G.E.; Kosiba, W.A.; Johnson, J.M. Rate dependency and role of nitric oxide in the vascular response to direct cooling in human skin. J. Appl. Physiol. 2006, 100, 42–50. [Google Scholar] [CrossRef]
- Johnson, J.M.; Yen, T.C.; Zhao, K.; Kosiba, W.A. Sympathetic, sensory, and nonneuronal contributions to the cutaneous vasoconstrictor response to local cooling. Am. J. Physiol. Circ. Physiol. 2005, 288, H1573–H1579. [Google Scholar] [CrossRef]
- Nuzzaci, G.; Evangelisti, A.; Righi, D.; Giannico, G.; Nuzzaci, I. Is There Any Relationship between Cold-Induced Vasodilatation and Vasomotion? Microvasc. Res. 1999, 57, 1–7. [Google Scholar] [CrossRef]
- Sheppard, L.W.; Vuksanović, V.; McClintock, P.V.E.; Stefanovska, A. Oscillatory dynamics of vasoconstriction and vasodilation identified by time-localized phase coherence. Phys. Med. Biol. 2011, 56, 3583–3601. [Google Scholar] [CrossRef] [PubMed]
- Kellogg, D.L. In vivo mechanisms of cutaneous vasodilation and vasoconstriction in humans during thermoregulatory challenges. J. Appl. Physiol. 2006, 100, 1709–1718. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.M.; Minson, C.T.; Kellogg, D.L. Cutaneous vasodilator and vasoconstrictor mechanisms in temperature regulation. Compr. Physiol. 2014, 4, 33–89. [Google Scholar] [PubMed]
- Castellani, J.W.; O’Brien, C. Peripheral Vasodilation Responses to Prevent Local Cold Injuries. In Prevention of Cold Injuries; RTO: Neuilly-sur-Seine, France, 2005; pp. KN2-1–K2-14. [Google Scholar]
- Pérgola, P.E.; Kellogg, D.L.; Johnson, J.M.; Kosiba, W.A.; Solomon, D.E. Role of sympathetic nerves in the vascular effects of local temperature in human forearm skin. Am. J. Physiol. 1993, 265, H785–H792. [Google Scholar] [CrossRef] [PubMed]
- Sendowski, I.; Sarourey, G.; Besnard, Y.; Bittel, J. Cold induced vasodilatation and cardiovascular responses in humans during cold water immersion of various upper limb areas. Eur. J. Appl. Physiol. Occup. Physiol. 1997, 75, 471–477. [Google Scholar] [CrossRef]
- Keramidas, M.E.; Musizza, B.; Kounalakis, S.N.; Mekjavic, I.B. Enhancement of the finger cold-induced vasodilation response with exercise training. Eur. J. Appl. Physiol. 2010, 109, 133–140. [Google Scholar] [CrossRef]
- Flouris, A.D.; Westwood, D.A.; Mekjavic, I.B.; Cheung, S.S. Effect of body temperature on cold induced vasodilation. Eur. J. Appl. Physiol. 2008, 104, 491–499. [Google Scholar] [CrossRef]
- Flouris, A.D.; Cheung, S.S. Thermal Basis of Finger Blood Flow Adaptations During Abrupt Perturbations in Thermal Homeostasis. Microcirculation 2011, 18, 56–62. [Google Scholar] [CrossRef]
- Flouris, A.D.; Cheung, S.S. Influence of thermal balance on cold-induced vasodilation. J. Appl. Physiol. 2009, 106, 1264–1271. [Google Scholar] [CrossRef]
- Daanen, H.A.; Ducharme, M.B. Finger cold-induced vasodilation during mild hypothermia, hyperthermia and at thermoneutrality. Aviat. Space Environ. Med. 1999, 70, 1206–1210. [Google Scholar]
- Mekjavic, I.B.; Dobnikar, U.; Kounalakis, S.N.; Musizza, B.; Cheung, S.S. The trainability and contralateral response of cold-induced vasodilatation in the fingers following repeated cold exposure. Eur. J. Appl. Physiol. 2008, 104, 193–199. [Google Scholar] [CrossRef] [PubMed]
- Ran, C.; Hoon, M.A.; Chen, X. The coding of cutaneous temperature in the spinal cord. Nat. Neurosci. 2016, 19, 1201–1209. [Google Scholar] [CrossRef] [PubMed]
- Vandewauw, I.; Voets, T. Heat is absolute, cold is relative. Nat. Neurosci. 2016, 19, 1188–1189. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, S. Temperature receptors in cutaneous nerve endings are thermostat molecules that induce thermoregulatory behaviors against thermal load. Temp. (Austin. Tex.) 2015, 2, 346–351. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.L.; Cooke, E.K.; Leib, D.E.; Lin, Y.C.; Daly, G.E.; Zimmerman, C.A.; Knight, Z.A. Warm-Sensitive Neurons that Control Body Temperature. Cell 2016, 167, 47–59. [Google Scholar] [CrossRef] [PubMed]
- Romanovsky, A.A. Thermoregulation: Some concepts have changed. Functional architecture of the thermoregulatory system. Am. J. Physiol. Integr. Comp. Physiol. 2007, 292, R37–R46. [Google Scholar] [CrossRef]
- McAllen, R.M.; Tanaka, M.; Ootsuka, Y.; McKinley, M.J. Multiple thermoregulatory effectors with independent central controls. Eur. J. Appl. Physiol. 2010, 109, 27–33. [Google Scholar] [CrossRef] [PubMed]
- Fealey, R.D. Interoception and autonomic nervous system reflexes thermoregulation. Handb. Clin. Neurol. 2013, 117, 79–88. [Google Scholar]

| Experiment | Number of Participants | Age | Gender | |
|---|---|---|---|---|
| M | F | |||
| Exp.1 | 11 | 44.9 (±5.84) | 0 | 11 |
| Exp.2 | 12 | 20.4 (±2.60) | 6 | 6 |
| Mean | 7.34 | 0.73 |
| Standard deviation | 3.2 | 0.56 |
| (min) | |||||||
|---|---|---|---|---|---|---|---|
| −1.989 ±0.005 | 0.980 ±0.002 | 0.0 ±0.0 | −0.0047 ±0.0010 | 0.0045 ±0.0010 | 10.23 ±3.50 | 0.92 ±0.04 | −10.61 ±3.45 |
| Mean | 7.96 | 0.81 |
| Standard deviation | 4.35 | 0.65 |
| (min) | |||||||
|---|---|---|---|---|---|---|---|
| −1.987 ±0.006 | 0.987 ±0.001 | 0.0 ±0.0 | −0.0016 ±0.0010 | 0.0018 ±0.0010 | 2.34 ±1.21 | 0.92 ±0.02 | −11.67 ±3.55 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Youssef, A.; Verachtert, A.; De Bruyne, G.; Aerts, J.-M. Reverse Engineering of Thermoregulatory Cold-Induced Vasoconstriction/Vasodilation during Localized Cooling. Appl. Sci. 2019, 9, 3372. https://doi.org/10.3390/app9163372
Youssef A, Verachtert A, De Bruyne G, Aerts J-M. Reverse Engineering of Thermoregulatory Cold-Induced Vasoconstriction/Vasodilation during Localized Cooling. Applied Sciences. 2019; 9(16):3372. https://doi.org/10.3390/app9163372
Chicago/Turabian StyleYoussef, Ali, Anne Verachtert, Guido De Bruyne, and Jean-Marie Aerts. 2019. "Reverse Engineering of Thermoregulatory Cold-Induced Vasoconstriction/Vasodilation during Localized Cooling" Applied Sciences 9, no. 16: 3372. https://doi.org/10.3390/app9163372
APA StyleYoussef, A., Verachtert, A., De Bruyne, G., & Aerts, J.-M. (2019). Reverse Engineering of Thermoregulatory Cold-Induced Vasoconstriction/Vasodilation during Localized Cooling. Applied Sciences, 9(16), 3372. https://doi.org/10.3390/app9163372







