Experimental and Numerical Study on the Strain Behavior of Buried Pipelines Subjected to an Impact Load
Abstract
1. Introduction
2. Theoretical Research
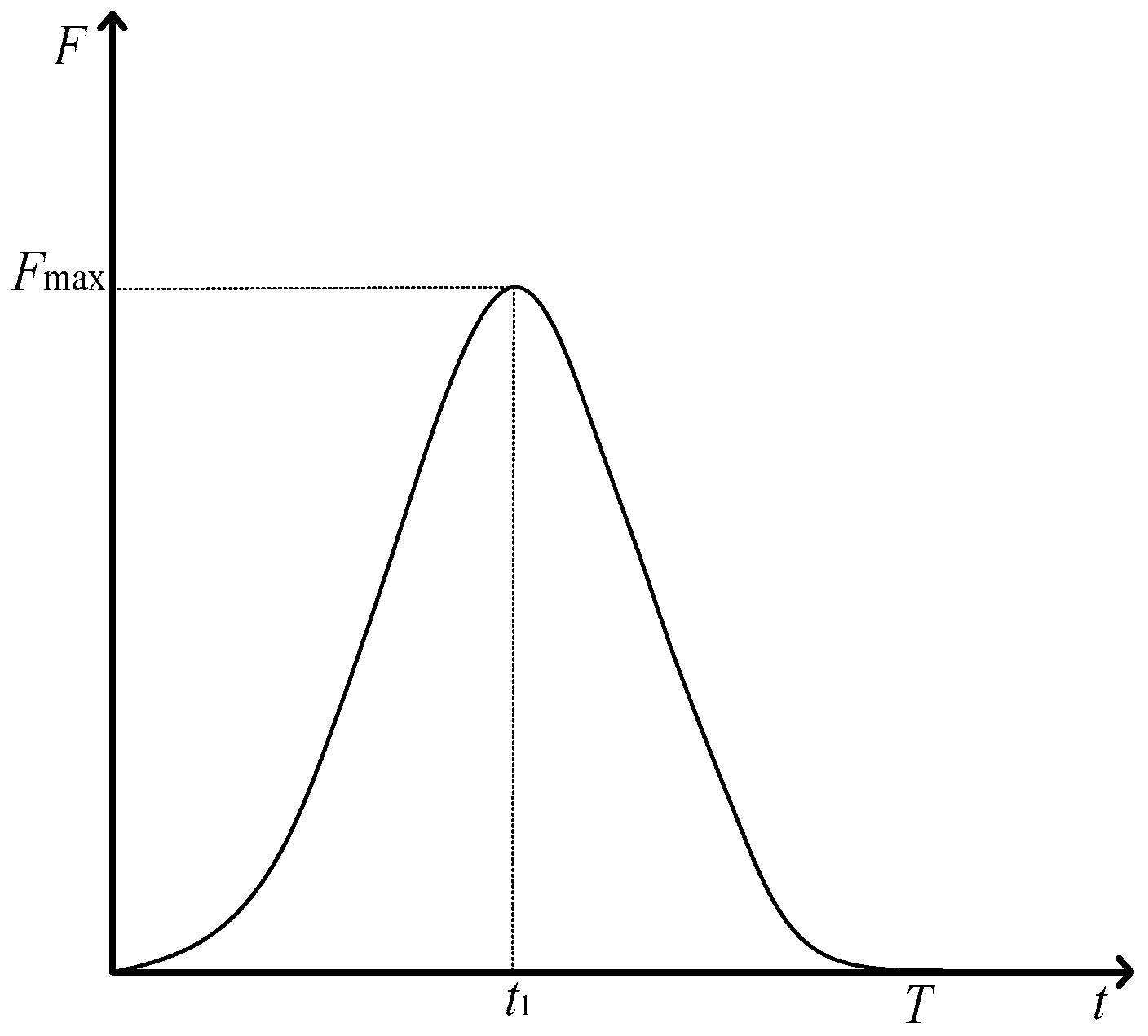
2.1. The Rockfall Impact Force on Soil
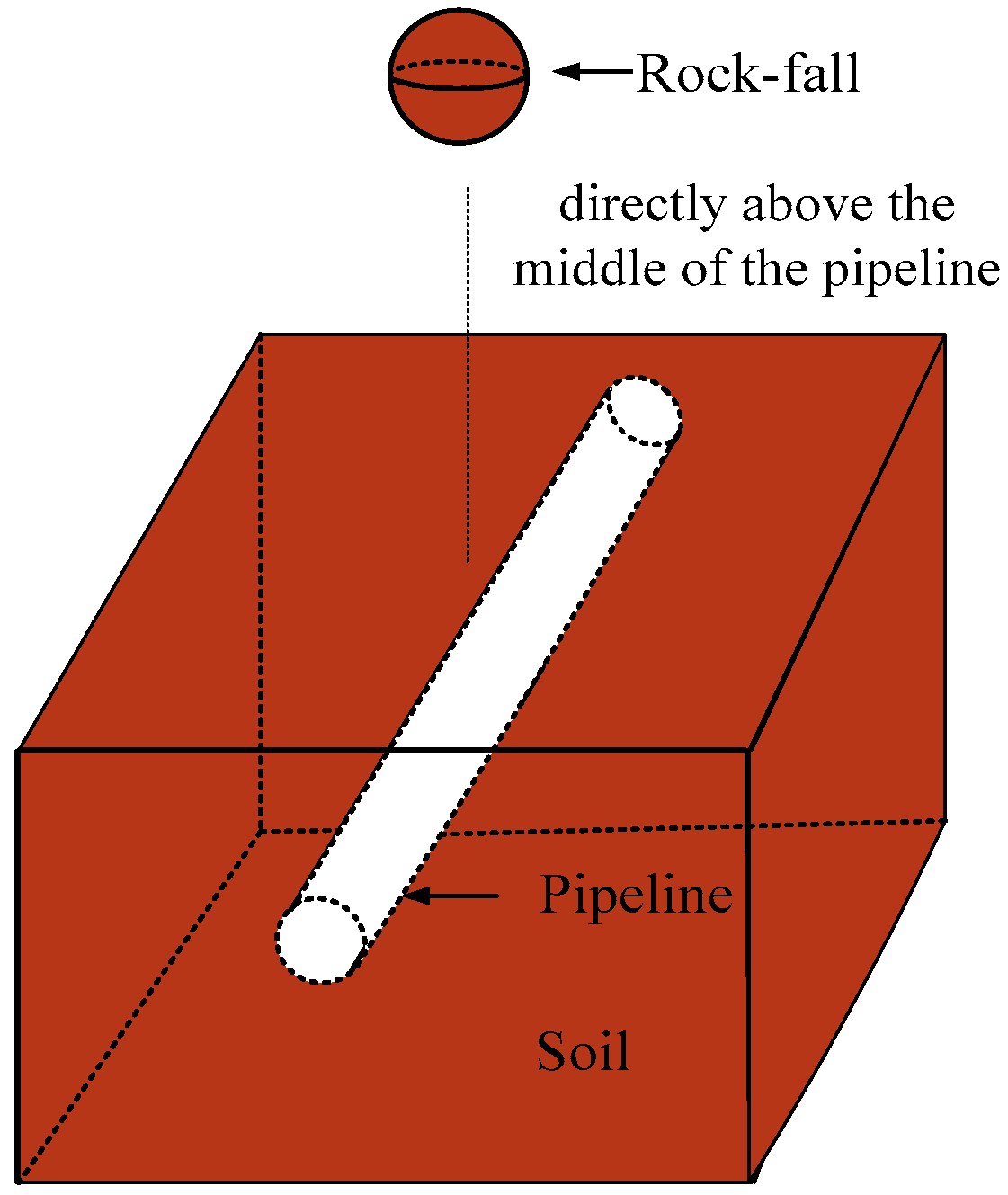
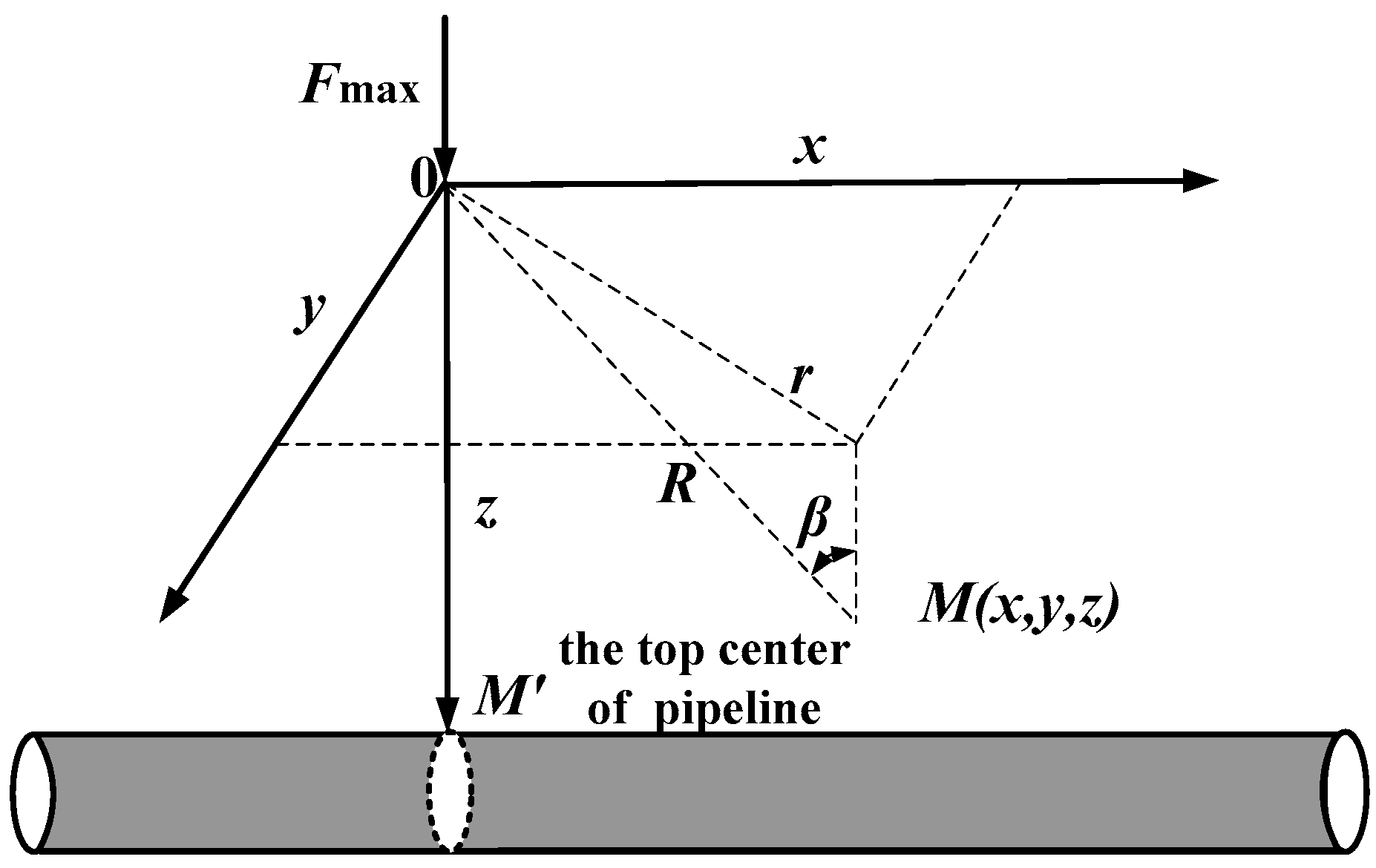
2.2. The Loads on a Buried Long Pipeline
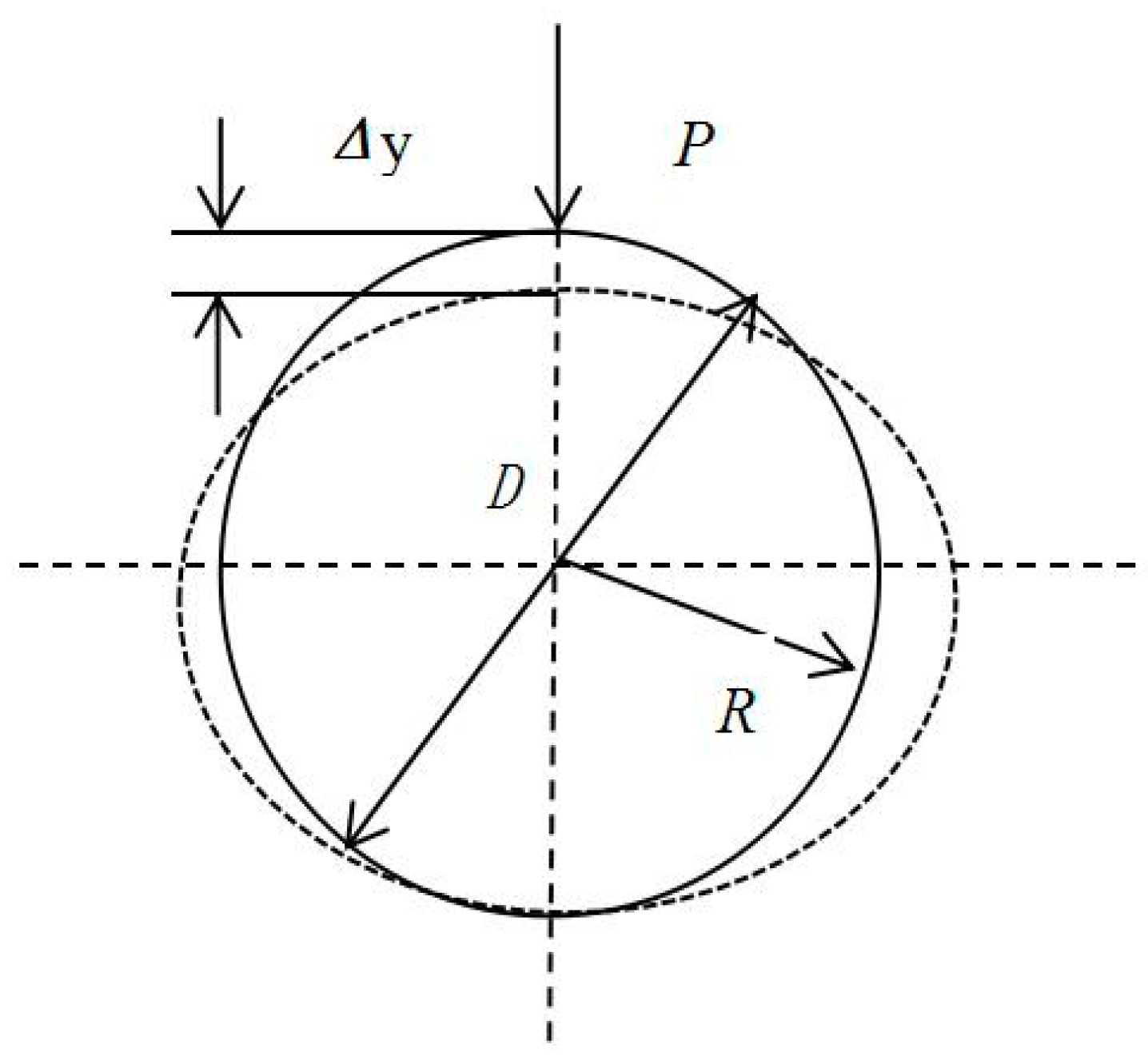
2.2.1. The Vertical Compressive Load
2.2.2. The Horizontal Load
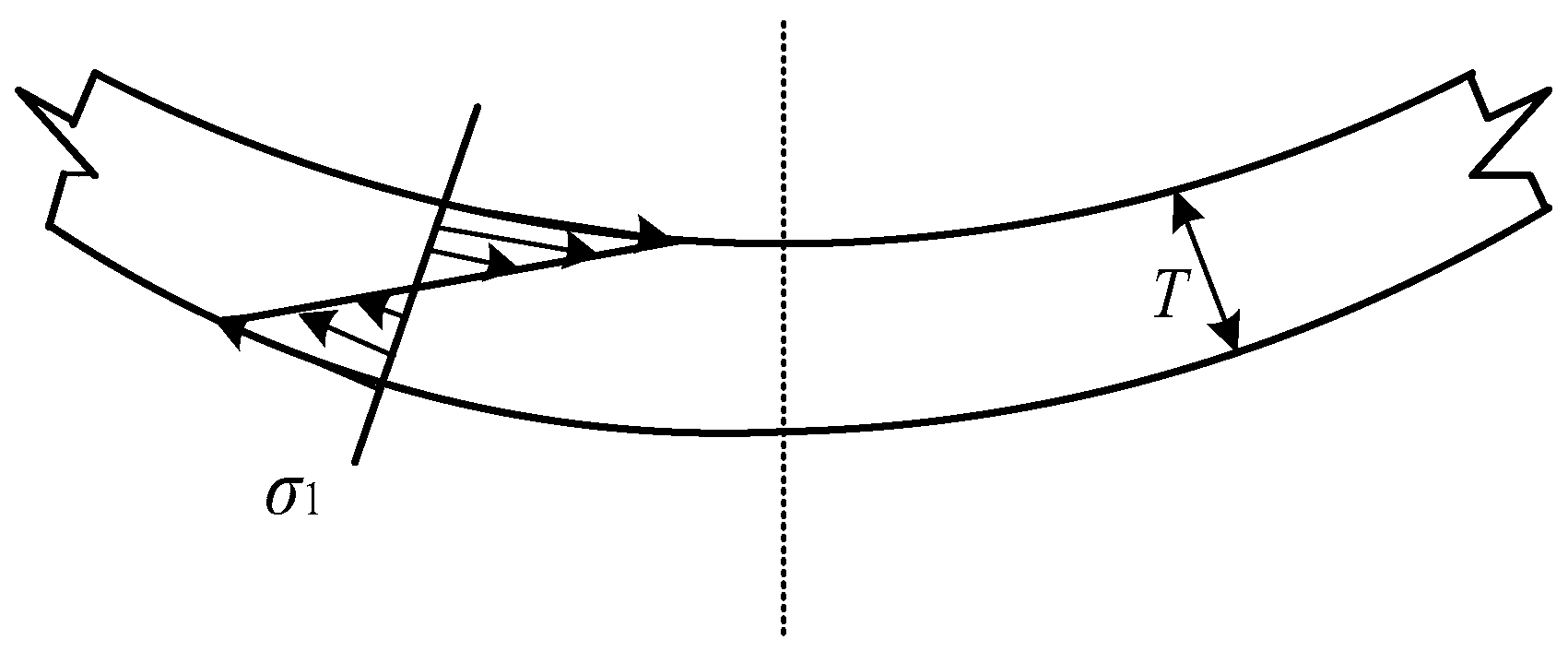
2.3. The Strains on a Buried Long Pipeline
3. Experimental Program
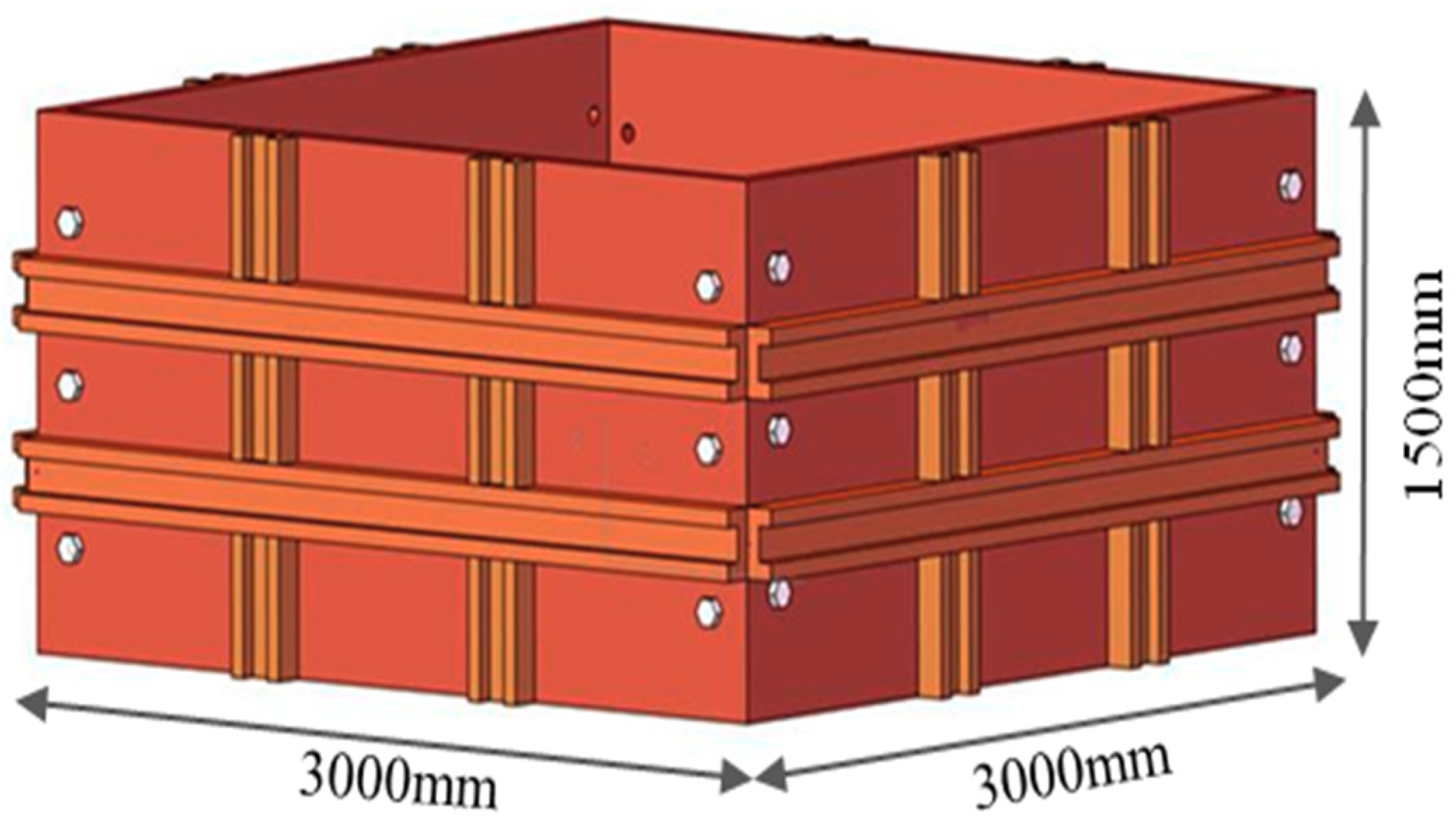
3.1. Experimental Design
3.2. Material Property
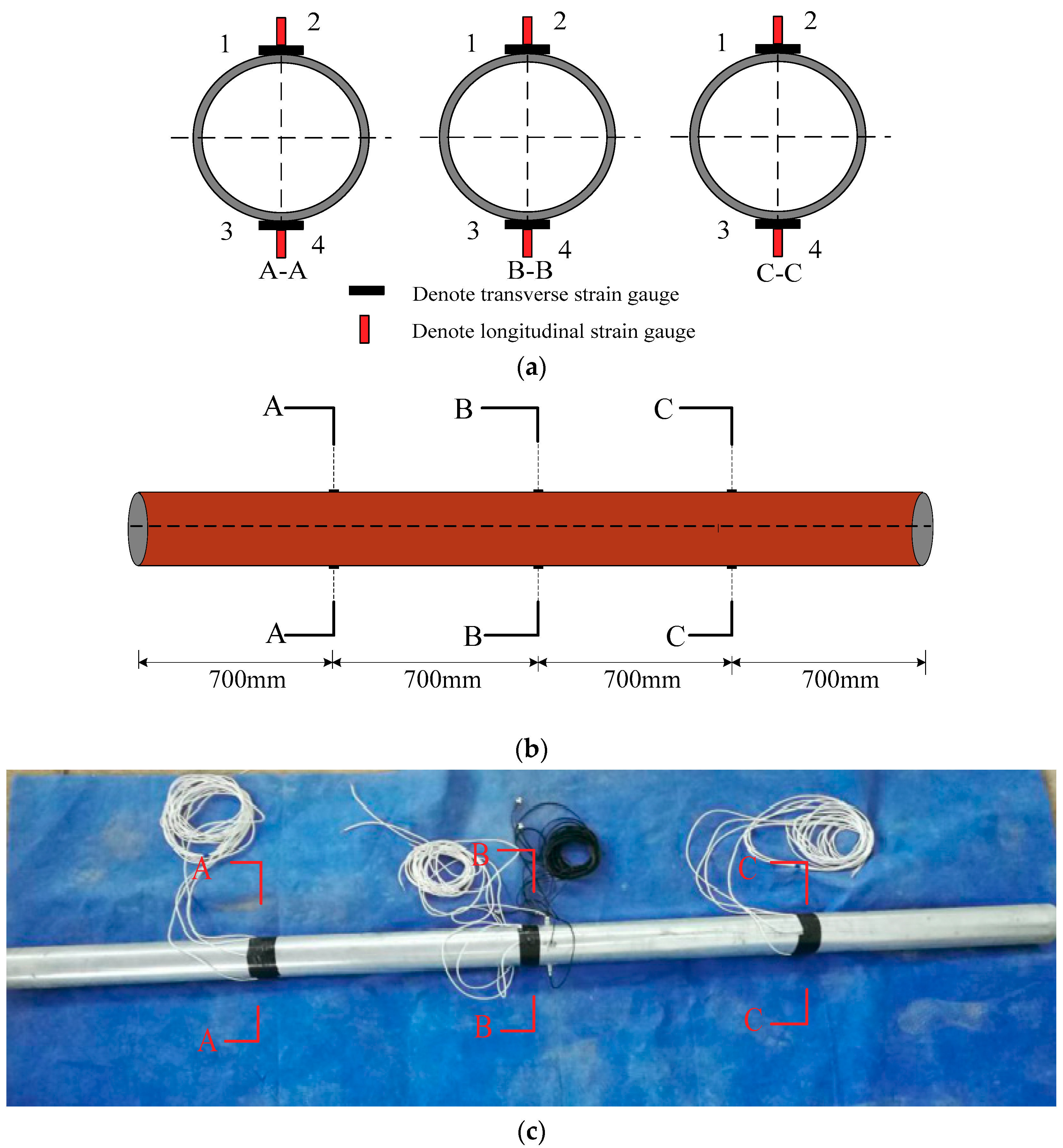
3.3. Layout of Measuring Points
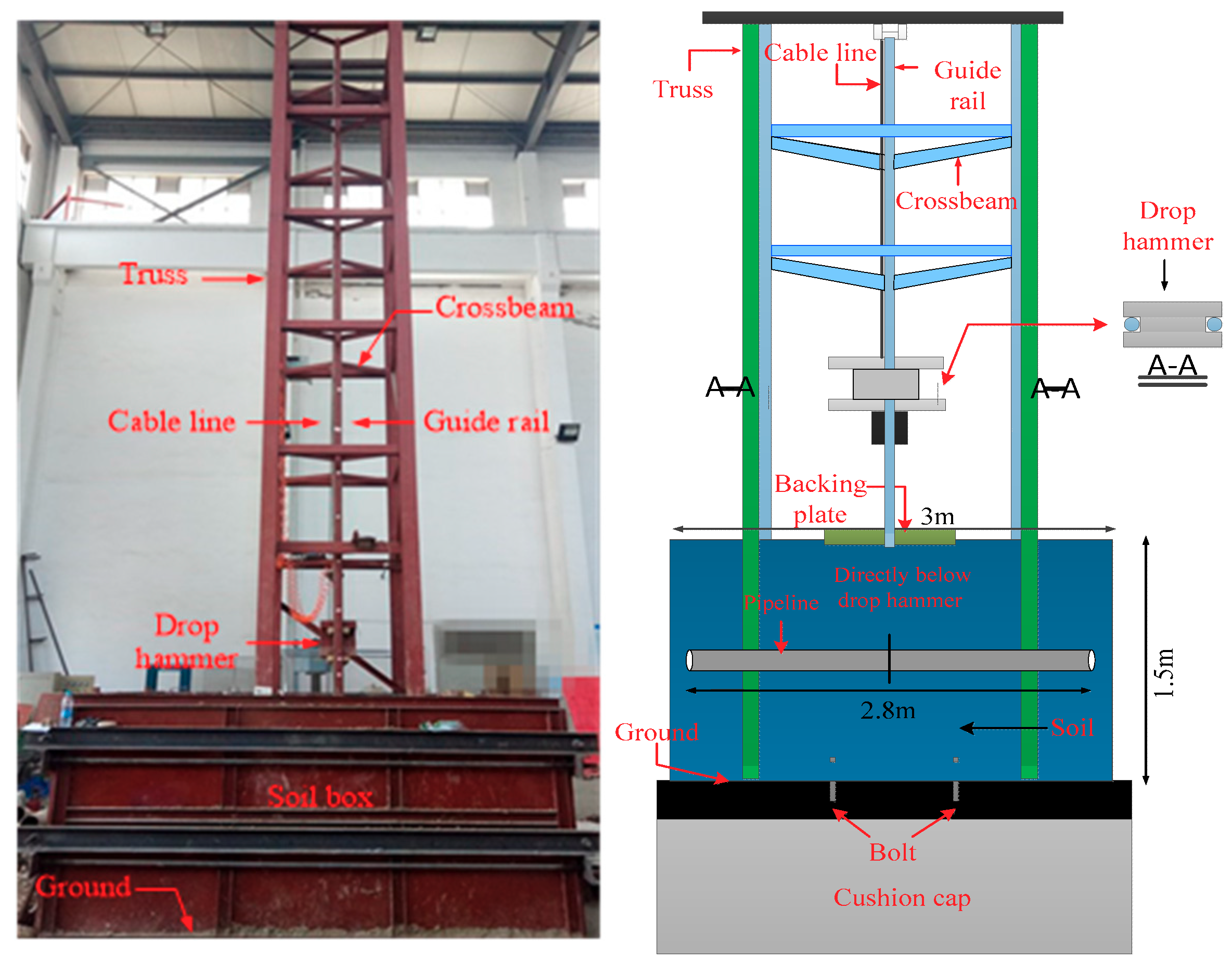
3.4. Test Loading
3.5. Test Results and Discussion
3.5.1. Basic Behavior
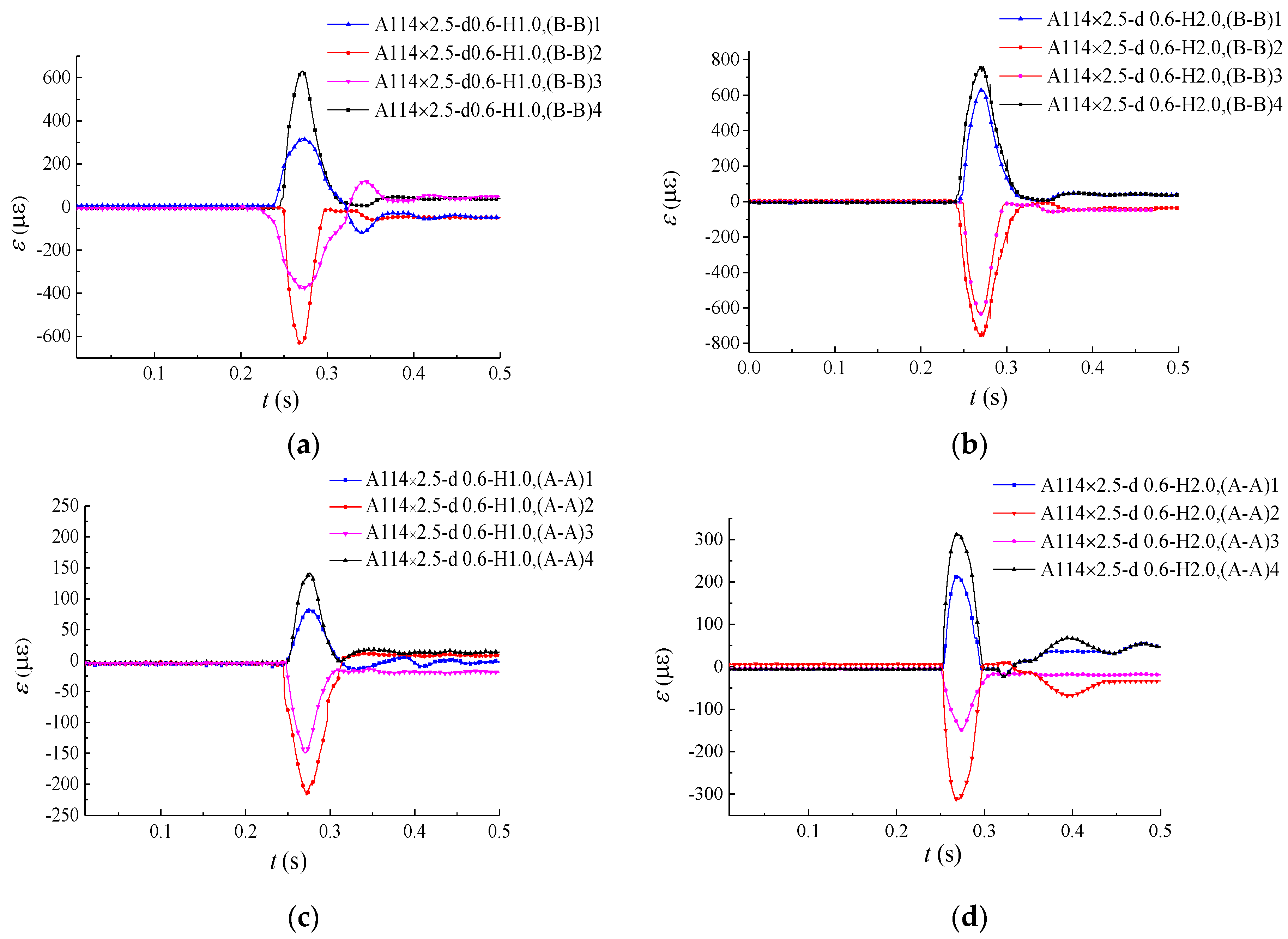
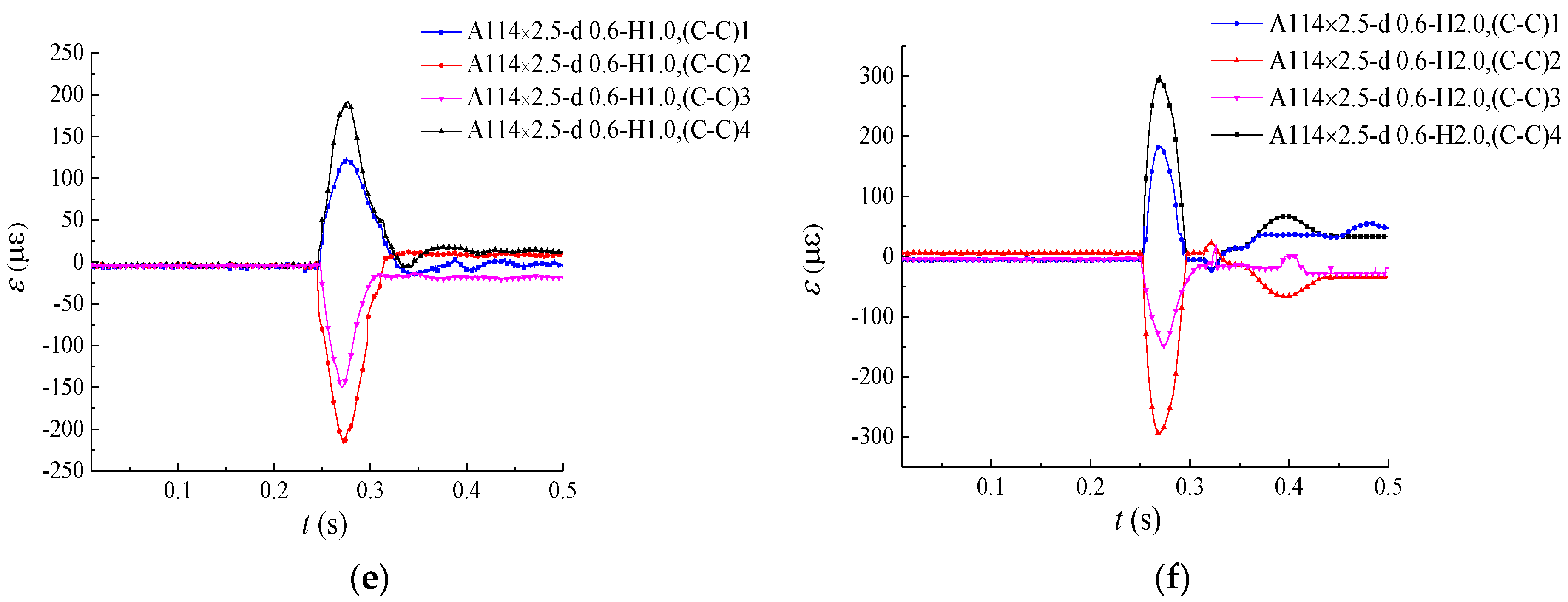
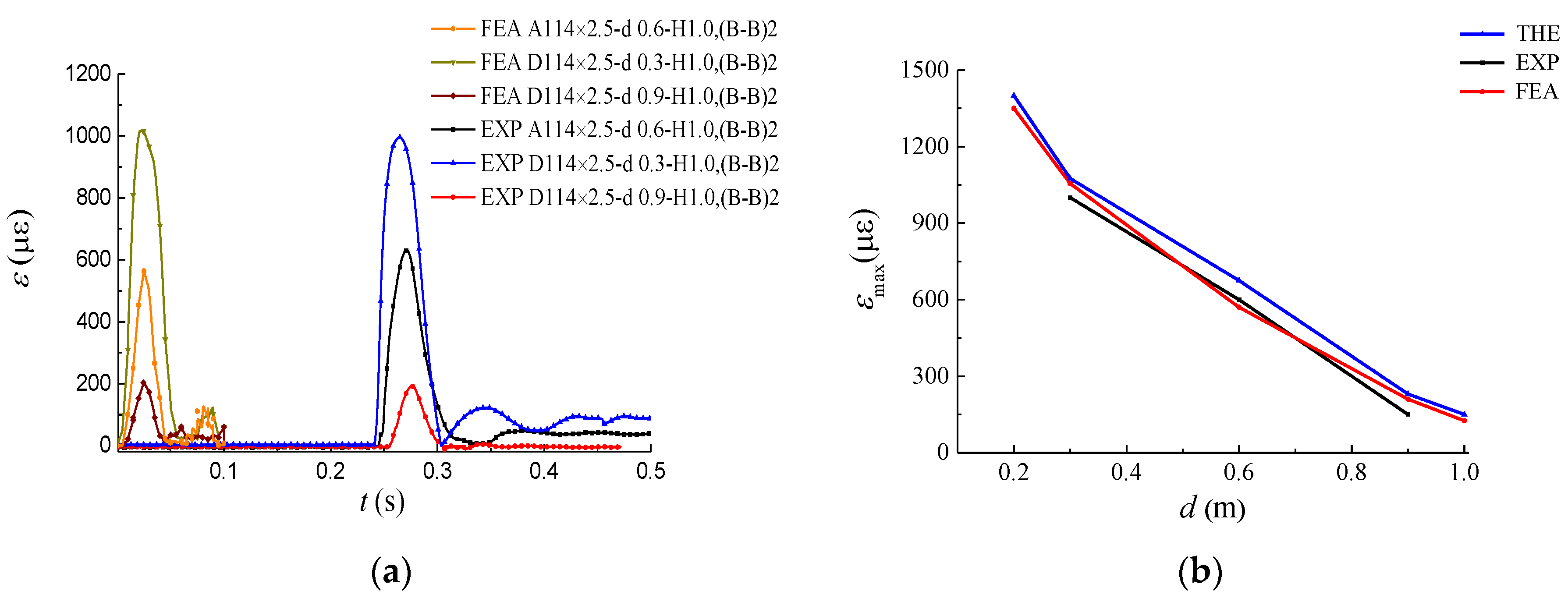
3.5.2. Strain–Time Curves
4. Finite Element Analysis (FEA)
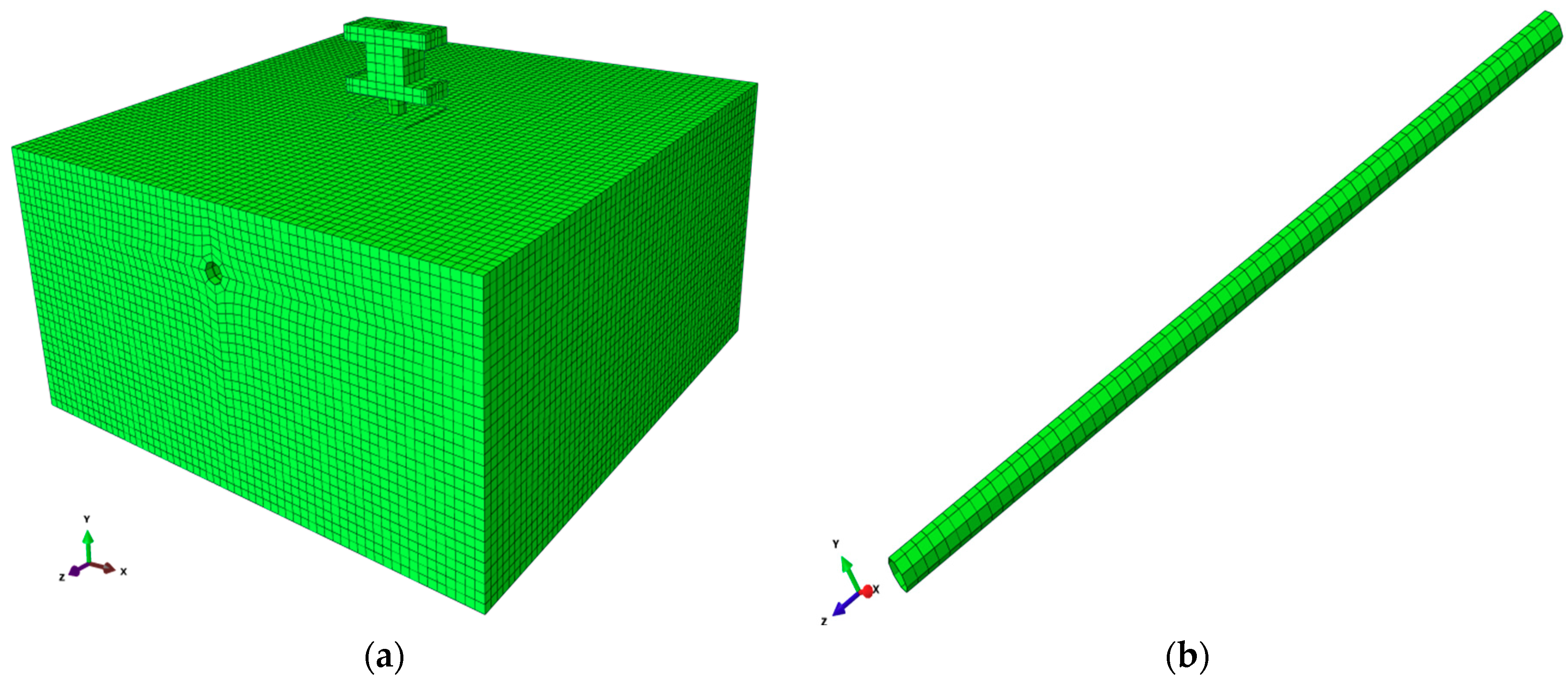
4.1. Finite Element Type and Mesh
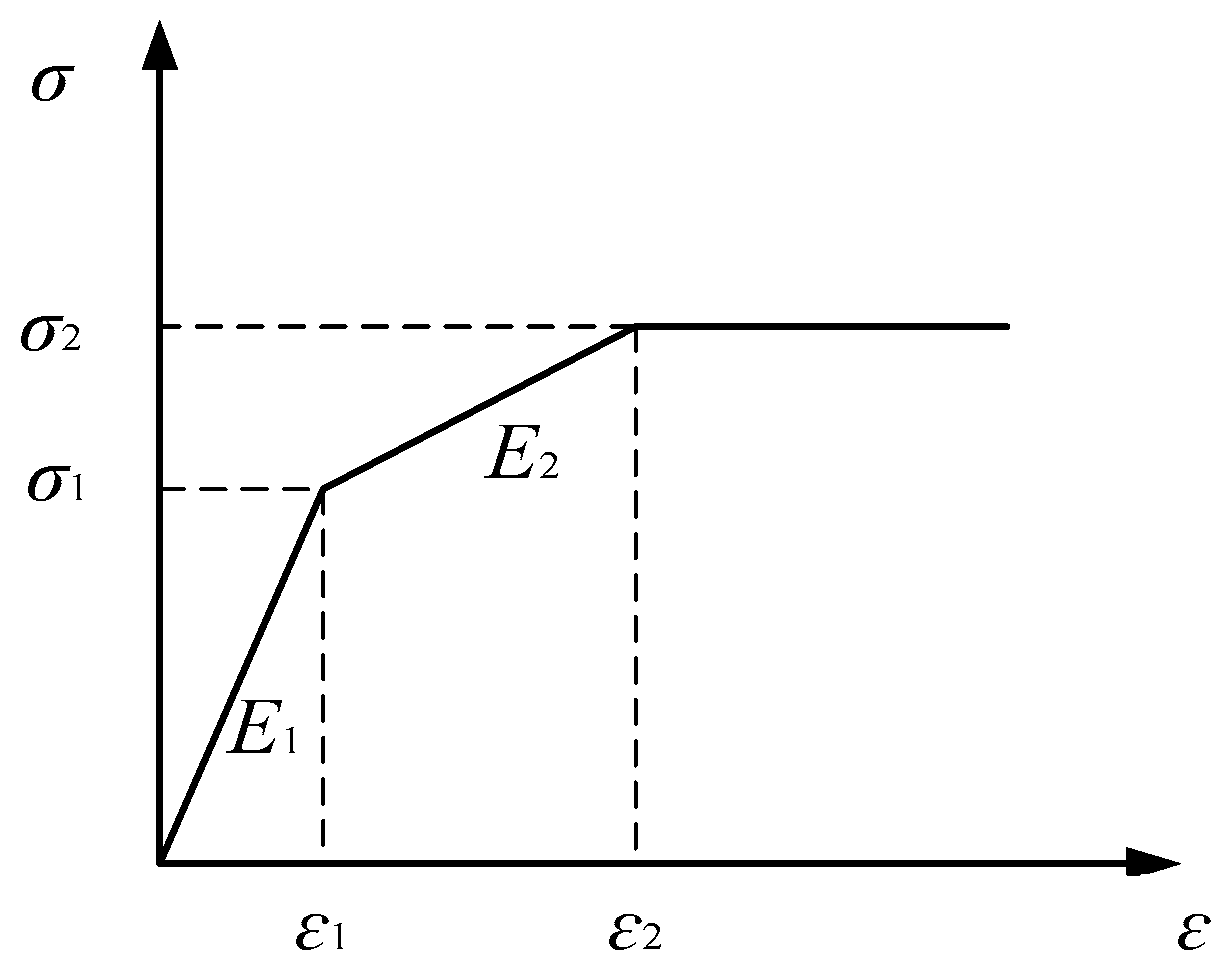
4.2. Material Model
4.3. The Contact between the Soil and Pipeline
4.4. Boundary Conditions and Load Application
5. Results and Discussion
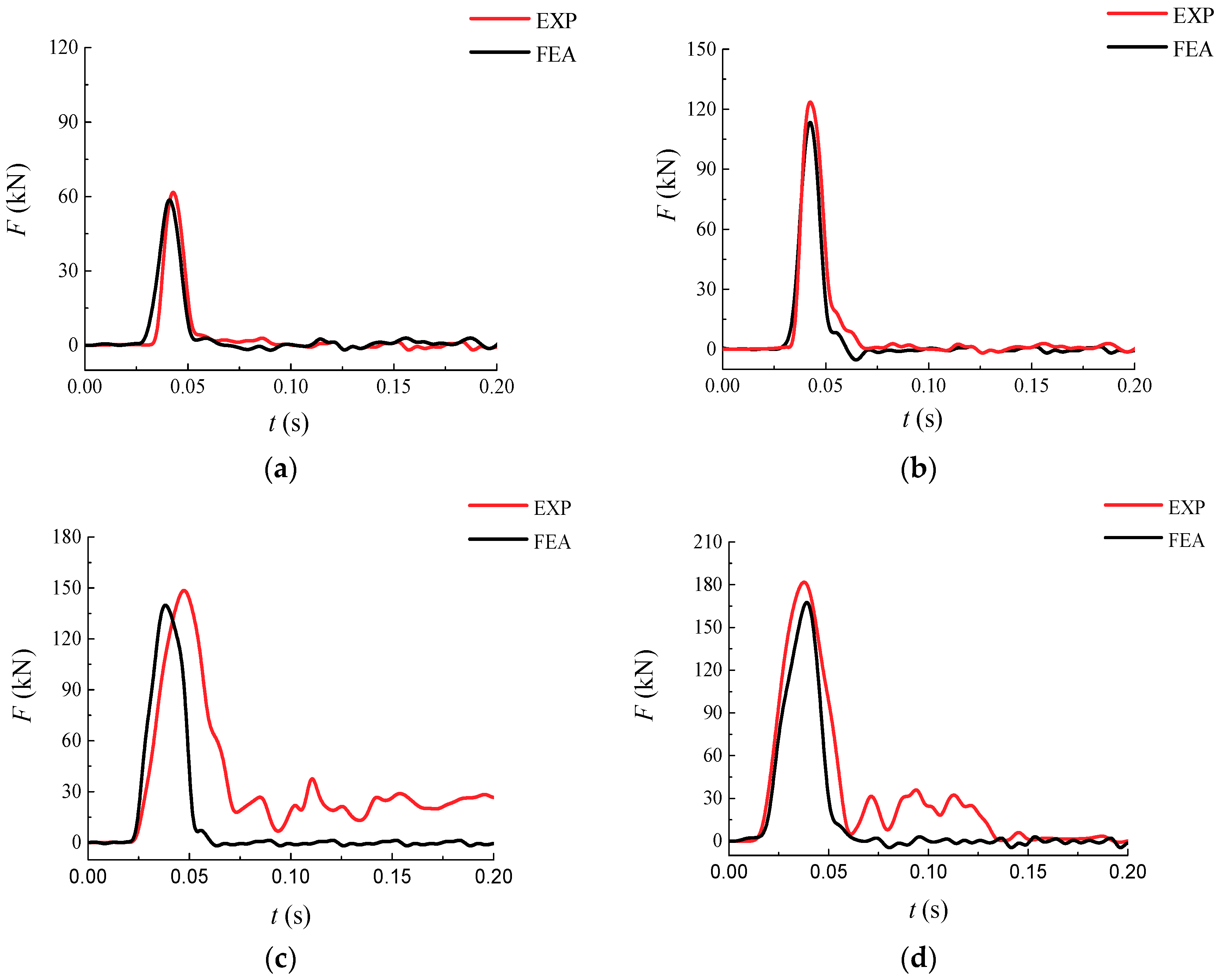
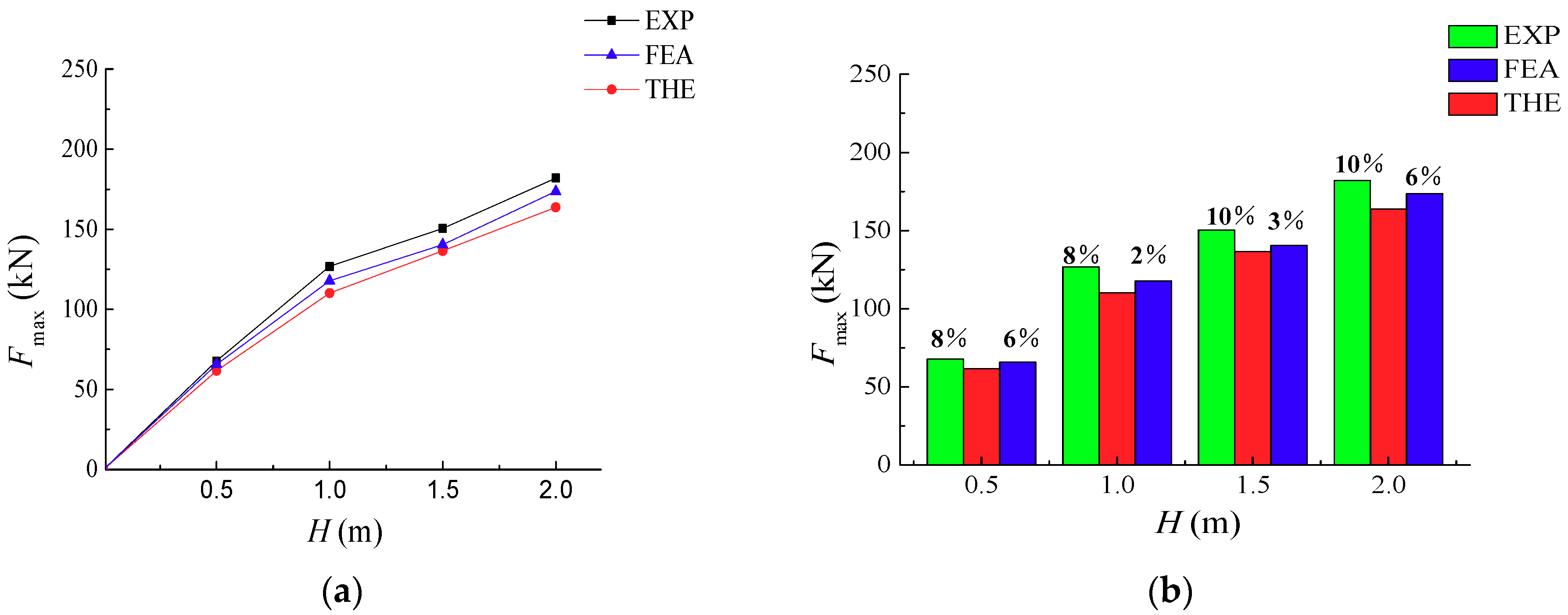
5.1. Impact Force
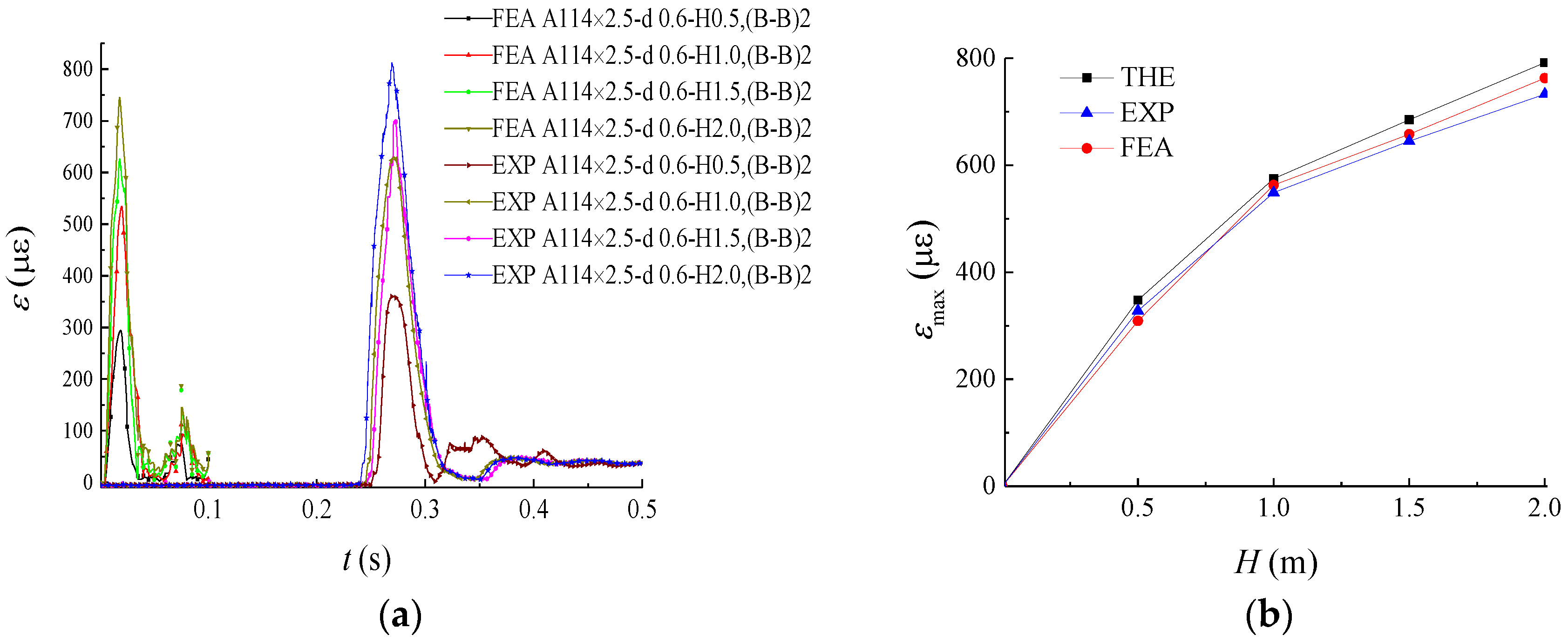
5.2. The Peak Strain
5.3. Strain Distribution
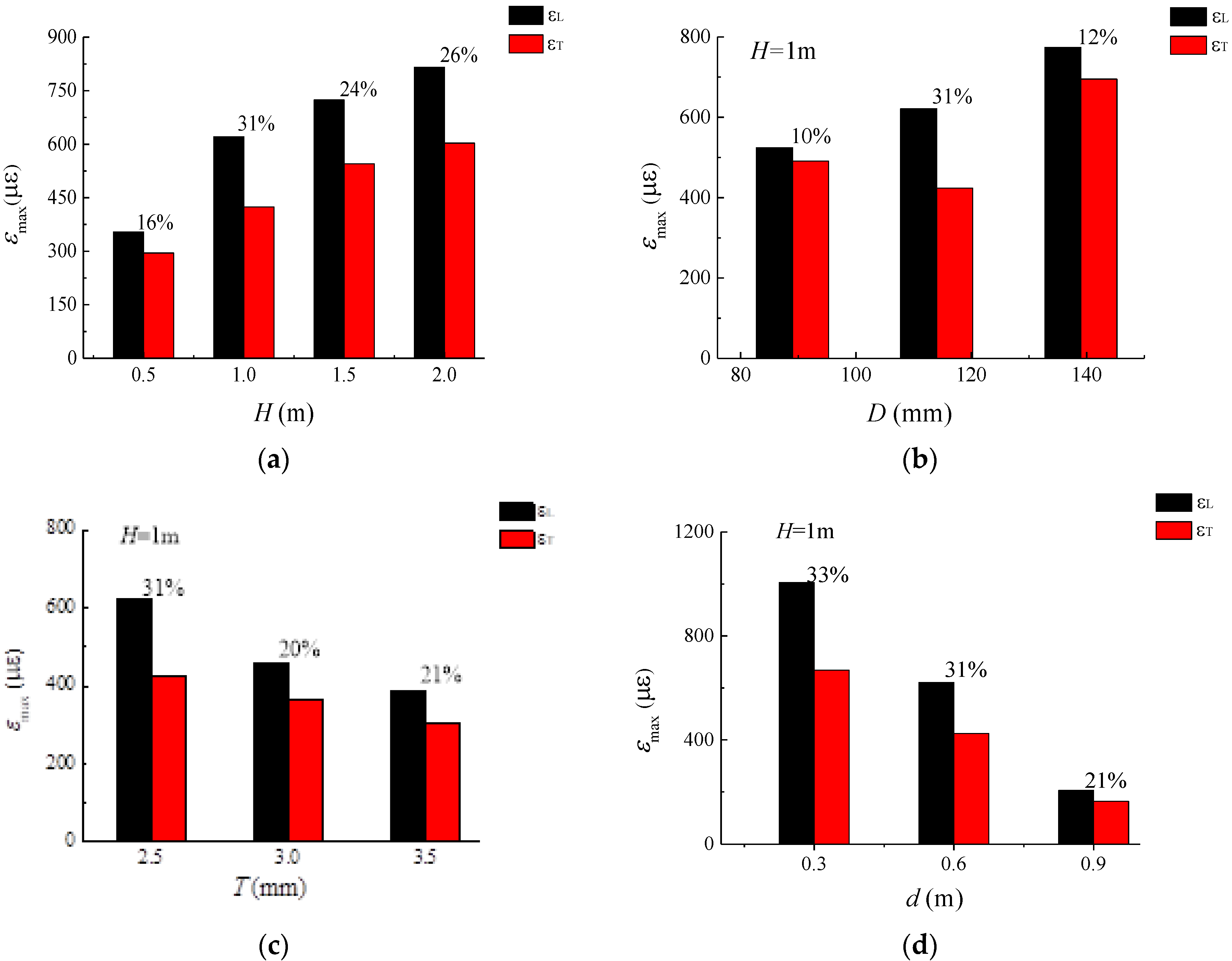
5.3.1. The Influence of Impact Height
5.3.2. The Influence of Pipeline Diameter and Wall Thickness
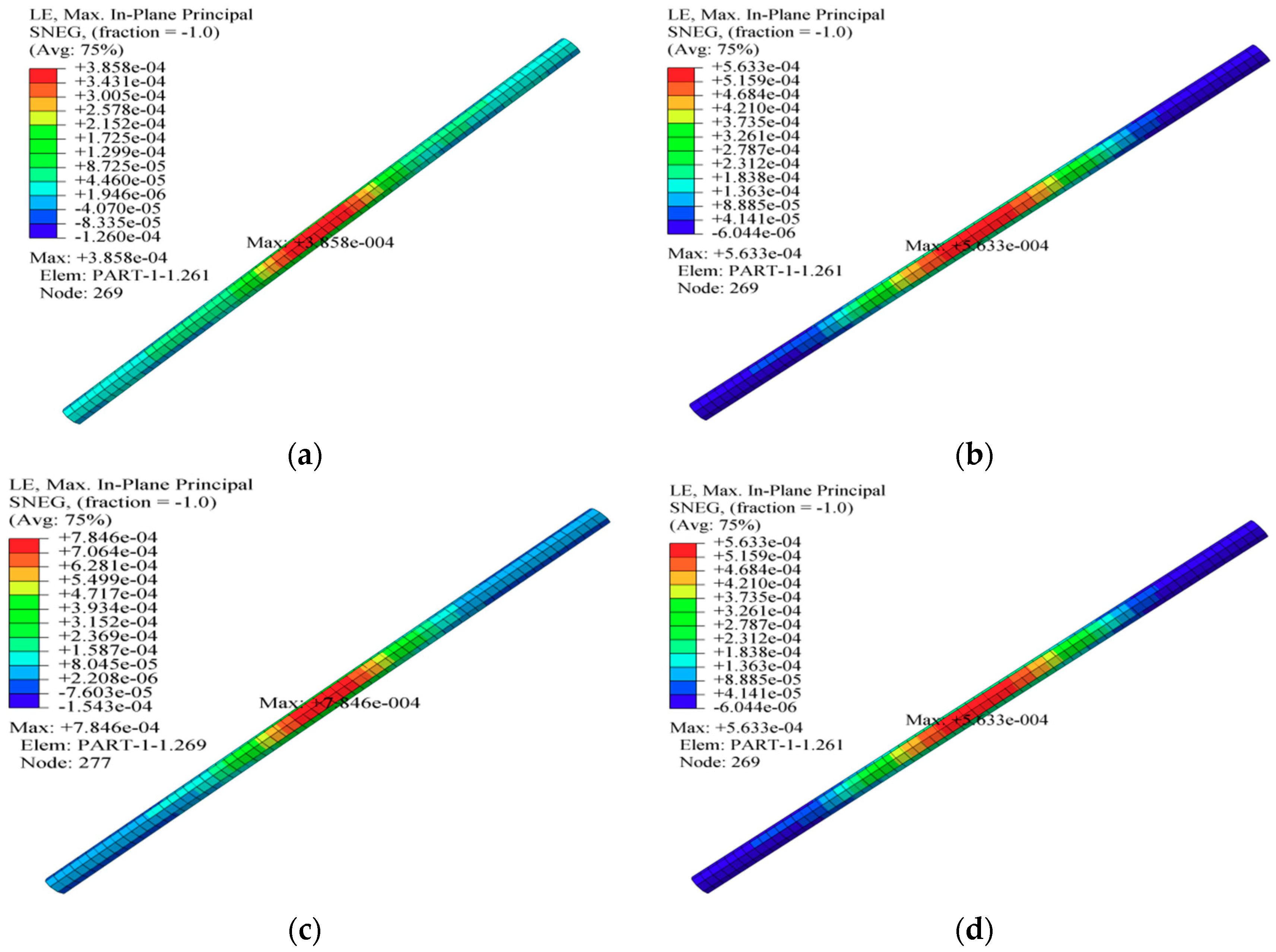
5.3.3. The Influence of Buried Depth
6. Conclusions
- (1)
- For the buried pipeline under an impact load, a generally good agreement was achieved among the FEA results, the EXP results, and THE results in terms of the peak impact force (Fmax) on soil and the peak strain (ɛmax) on pipelines, which indicates that the mathematical formula based on the mechanical model of a buried pipeline and the finite element models are accurate for the prediction of pipeline response under the impact load.
- (2)
- The peak longitudinal strain (ɛL) was much larger than the peak transversal strain (ɛT); thus, longitudinal bending was the main source of deformation for specimens under the impact load.
- (3)
- Under the same impact height (H) of the drop hammer, the diameter (D) had an obvious influence on ɛmax, while the wall thickness (T) had a subtle influence on ɛmax. Furthermore, ɛmax decreased with the increase of T, while it increased with the increase of D and H, which is similar to the distribution of the high-strain area of the pipeline in the experimental results and FEA results. This means that a small diameter and a thick wall thickness are beneficial for the pipeline to resist the impact load.
- (4)
- The ɛmax decreased rapidly with the increase of the buried depth (d) of the pipeline under the same D and T, which indicates that the pipelines cannot be buried shallowly. According to the extension of THE and FEA results, a buried depth of the pipeline from 0.5 m to 0.6 m was more reasonable for the pipeline designed in this paper.
7. Discussion of Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arafah, D.; Madia, M.; Zerbst, U.; Berettaa, S.; Cristea, M. Instability analysis of pressurized pipes with longitudinal surface cracks. Int. J. Press. Vessel. Pip. 2015, 126–127, 48–57. [Google Scholar] [CrossRef]
- Du, G.; Kong, Q.; Zhou, H.; Gu, H. Multiple cracks detection in pipeline using damage index matrix based on piezoceramic transducer-enabled stress wave propagation. Sensors 2017, 17, 1812. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Bai, Y.; Su, C.; Li, M. Effect of interaction between corrosion defects on failure pressure of thin wall steel pipeline. Int. J. Press. Vessel. Pip. 2016, 138, 8–18. [Google Scholar] [CrossRef]
- Kishawy, H.A.; Gabbar, H.A. Review of pipeline integrity management practices. Int. J. Press. Vessel. Pip. 2010, 87, 373–380. [Google Scholar] [CrossRef]
- Kong, Q.; Robert, R.; Silva, P.; Mo, Y. Cyclic crack monitoring of a reinforced concrete column under simulated pseudo-dynamic loading using piezoceramic-based smart aggregates. Appl. Sci. 2016, 6, 341. [Google Scholar] [CrossRef]
- Hong, X.; Liu, Y.; Lin, X.; Luo, Z.; He, Z. Nonlinear ultrasonic detection method for delamination damage of lined anti-corrosion pipes using PZT transducers. Appl. Sci. 2018, 8, 2240. [Google Scholar] [CrossRef]
- Du, G.; Huo, L.; Kong, Q.; Song, G. Damage detection of pipeline multiple cracks using piezoceramic transducers. J. Vibroeng. 2016, 18, 2828–2838. [Google Scholar] [CrossRef]
- Yun, H.; Kyriakides, S. On the beam and shell modes of buckling of buried pipelines. Soil Dyn. Earthq. Eng. 1990, 9, 179–193. [Google Scholar] [CrossRef]
- Chiou, Y.J.; Chi, S.Y. Beam and shell modes of buckling of buried pipes induced by compressive ground failure. Tech. Counc. Lifeline Earthq. Eng. 1995, 6, 176–187. [Google Scholar]
- Takada, S.; Hassani, N.; Fukuda, K. A new proposal for simplified design of buried steel pipes crossing active faults. Earthq. Eng. Struct. Dyn. 2010, 30, 1243–1257. [Google Scholar] [CrossRef]
- Yan, Y.; Shao, B.; Wang, J.; Yan, X. A study on stress of buried oil and gas pipeline crossing a fault based on thin shell FEM model. Tunn. Undergr. Space Technol. 2018, 81, 472–479. [Google Scholar]
- Chavan, K.S.; Wriggers, P. Consistent coupling of beam and shell models for thermo-elastic analysis. Int. J. Numer. Methods Eng. 2010, 59, 1861–1878. [Google Scholar] [CrossRef]
- Liu, A.; Hu, Y.; Li, X.; Zhao, F.; Takada, S. Damage behavior of large-diameter buried steel pipelines under fault movements. Eng. Mech. 2005, 22, 82–87. [Google Scholar]
- Zhang, J.; Liang, Z.; Han, C.; Zhang, H. Buckling behaviour analysis of a buried steel pipeline in rock stratum impacted by a rockfall. Eng. Fail. Anal. 2015, 58, 281–294. [Google Scholar] [CrossRef]
- Liu, M.; Min, Y. Modeling the behavior of natural gas pipeline impacted by falling objects. Eng. Fail. Anal. 2014, 42, 45–59. [Google Scholar] [CrossRef]
- Deng, X.; Xue, S.; Tong, X. Numerical simulation on response of buried pipeline induced by rock-fall transverse impaction. J. China Univ. Pet. 2009, 33, 111–115. [Google Scholar]
- Chen, J.; Wang, Q.; Chen, Y.; Li, J. Amending calculation on impact force of boulders in debris flow based on Hertz theory. J. Harbin Inst. Technol. 2017, 49, 124–129. [Google Scholar]
- Ruta, P.; Szydło, A. Drop-weight test based identification of elastic half-space model parameters. J. Sound Vib. 2005, 282, 411–427. [Google Scholar] [CrossRef]
- Zhao, G.; Li, S.; Xiong, Z.; Gao, W.; Han, Q. A statistical model of elastic-plastic contact between rough surfaces. Trans. Can. Soc. Mech. Eng. 2019, 43, 38–46. [Google Scholar] [CrossRef]
- Gutzwiller, M.C. The impact of a rigid circular cylinder on an elastic solid. Philos. Trans. R. Soc. B Biol. Sci. 1962, 255, 153–191. [Google Scholar] [CrossRef]
- Qi, S.; Zhou, C.; Liu, S.; Song, X. Study on Impact Force of Landfall and Rockfall. Appl. Mech. Mater. 2013, 256–259, 81–85. [Google Scholar] [CrossRef]
- Ye, S.; Chen, H.; Tang, H. The calculation method for the impact force of the rockfall. China Railw. Sci. 2010, 31, 56–62. [Google Scholar]
- Marston, A.; Anderson, A.O. The Theory of Loads on Pipes in Ditch and Tests of Cement and Clay Drain Tile and Sewer Pipe; Iowa State College of Agriculture and Mechanic Arts: Iowa City, IA, USA, 1913; pp. 45–196. [Google Scholar]
- Kang, J.; Parker, F.; Yoo, C. Soil-structure interaction and imperfect trench installations for deeply buried concrete pipes. J. Geotech. Geoenviron. Eng. 2007, 133, 277–285. [Google Scholar] [CrossRef]
- Hindy, A.; Novak, M. Earthquake response of underground pipelines. Earthq. Eng. Struct. Dyn. 1979, 7, 451–476. [Google Scholar] [CrossRef]
- Zheng, J.; Zhao, J.; Chen, B. Vertical earth pressure on culverts under high embankments. Chin. J. Geotech. Eng. 2009, 31, 1009–1013. [Google Scholar]
- Ning, B.K.; Fan, H.; Gong, L.; Liu, G. Study on vertical earth pressure of slab culvert under high embankment. Appl. Mech. Mater. 2013, 256–259, 1898–1902. [Google Scholar] [CrossRef]
- Zhou, S.; Sun, X.; Peng, J.; Lv, J. A study on the earth pressure of top culvert of high embankment. Appl. Mech. Mater. 2012, 178–181, 1104–1111. [Google Scholar] [CrossRef]
- Yun, L.; Kang, L. Reliability analysis of high pressure buried pipeline under landslide. Appl. Mech. Mater. 2014, 501–504, 1081–1086. [Google Scholar] [CrossRef]
- Jing, H.; Deng, Q.; Hao, J.; Han, B.; Li, L. Analysis and numerical simulation on dynamic response of buried pipeline caused by rock fall impaction. Proc. Bienn. Int. Pipeline Conf. 2012, 2, 303–311. [Google Scholar]
- Zhang, H.; Zhang, J.; Liu, S. Mechanical properties of the buried pipeline under impact load caused by adjacent heavy tamping construction. J. Fail. Anal. Prev. 2016, 16, 647–654. [Google Scholar] [CrossRef]
- The American Society of Civil Engineers. Guidelines for the Design of Buried Steel Pipeline; The American Society of Civil Engineers: Reston, VA, USA, 2005. [Google Scholar]
- Wang, G.; Qu, S.; Hou, X.; Zhu, F.; Zhang, J. Preliminary study on vertical subsoil participating mass. Adv. Mater. Res. 2011, 199–200, 1429–1434. [Google Scholar] [CrossRef]
- Terzaghi, K.; Peck, R.B.; Mesri, G. Soil mechanics in engineering practice. In A Wiley-Interscience Publication, 3rd ed.; John Wiley and Sons Inc.: Hoboken, NJ, USA, 1996. [Google Scholar]
- GB 50253-2003 Code for Design of Oil Pipeline Engineering; Planning Press: Beijing, China, 2003.
- Tian, Y.; Liu, H.; Jiang, X.; Yu, R. Analysis of stress and deformation of a positive buried pipe using the improved Spangler model. Soils Found. 2015, 55, 485–492. [Google Scholar] [CrossRef]
- Xiao, J.; Zhang, X.; Chen, J.; Li, Z. Study on 3d Flexible Pipe FEM Analysis by Spangler Theory. Adv. Mater. Res. 2014, 850–851, 821–824. [Google Scholar] [CrossRef]
- She, Y. Study on the effect of vibration loads induced by bridge pile foundation construction on adjacent buried pipeline. Appl. Mech. Mater. 2013, 353–356, 191–197. [Google Scholar] [CrossRef]
- Prisco, C.D.; Andrea, G. Mechanical behavior of geo-encased sand columns: Small scale experimental tests and numerical modeling. Geomech. Geoengin. 2011, 6, 251–263. [Google Scholar] [CrossRef]
- Wijewickreme, D.; Karimian, H.; Honegger, D. Response of buried steel pipelines subjected to relative axial soil movement. Can. Geotech. J. 2009, 46, 735–752. [Google Scholar] [CrossRef]
- Magda, W. Wave-induced uplift force acting on a submarine buried pipeline: Finite element formulation and verification of computations. Comput. Geotech. 1996, 19, 47–73. [Google Scholar] [CrossRef]
- Li, X.; Sun, J.; Li, T. The analysis and comparison of all kinds of buried pipeline model based on seismic effect. Engineering 2016, 8, 365–370. [Google Scholar] [CrossRef][Green Version]
- Robert, D.J. A modified Mohr-Coulomb model to simulate the behavior of pipelines in unsaturated soils. Comput. Geotech. 2017, 91, 146–160. [Google Scholar] [CrossRef]
- Hosseinpour, I.; Mirmoradi, S.H.; Barari, A.; Omidvar, M. Numerical evaluation of sample size effect on the stress-strain behavior of geotextile-reinforced sand. J. Zhe Jiang Univ. Sci. A 2010, 11, 555–562. [Google Scholar] [CrossRef]
- Zeng, X.; Dong, F.; Xie, X.; Du, G. A new analytical method of strain and deformation of pipeline under fault movement. Int. J. Press. Vessel. Pip. 2019, 172, 199–211. [Google Scholar] [CrossRef]
- Daiyan, N.; Kenny, S.; Phillips, R.; Popescu, R. Investigating pipeline-soil interaction under axial-lateral relative movements in sand. Can. Geotech. J. 2011, 48, 1683–1695. [Google Scholar] [CrossRef]
- Roy, K.; Hawlader, B.; Kenny, S.; Moore, I. Finite element modeling of lateral pipeline-soil interactions in dense sand. Can. Geotech. J. 2015, 53, 490–504. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, Z.; Feng, D.; Zhang, C.; Xia, C.; Tu, Y. Response of the buried steel pipeline caused by perilous rock impact: Parametric study. J. Loss Prev. Process Ind. 2016, 43, 385–396. [Google Scholar] [CrossRef]
- Xu, T.; Yao, A.; Jiang, H.; Li, Y.; Zeng, X. Dynamic response of buried gas pipeline under excavator loading: Experimental/numerical study. Eng. Fail. Anal. 2018, 89, 57–73. [Google Scholar] [CrossRef]
- Yao, A.; Xu, T.; Zeng, X.; Jiang, H. Numerical analyses of the stress and limiting load for buried gas pipelines under excavation machine impact. J. Pipeline Syst. Eng. Pract. 2015, 6, A4014003. [Google Scholar] [CrossRef]
- Kong, Q.; Shuang, H.; Ji, Q.; Mo, Y.; Song, G. Very early age concrete hydration characterization monitoring using piezoceramic based smart aggregates. Smart Mater. Struct. 2013, 22, 085025. [Google Scholar] [CrossRef]
- Jia, Z.; Ren, L.; Li, H.; Ho, S.; Song, G. Experimental study of pipeline leak detection based on hoop strain measurement. Struct. Control Health Monit. 2015, 22, 799–812. [Google Scholar] [CrossRef]
- Zhu, J.; Ren, L.; Ho, S.; Jia, Z.; Song, G. Gas pipeline leakage detection based on PZT sensors. Smart Mater. Struct. 2017, 26, 025022. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, J.; Song, Y.; Peng, C.; Song, G. A time reversal based pipeline leakage localization method with the adjustable resolution. IEEE Access 2018, 6, 26993–27000. [Google Scholar] [CrossRef]
- Inaudi, D.; Glisic, B. Long-Range pipeline monitoring by distributed fiber optic sensing. J. Press. Vessel Technol. 2010, 132, 011701. [Google Scholar] [CrossRef]
- Jia, Z.; Ren, L.; Li, H.; Sun, W. Pipeline leak localization based on FBG hoop strain sensors combined with BP neural network. Appl. Sci. 2018, 8, 146. [Google Scholar] [CrossRef]
- Sethi, V.; Song, G. Optimal vibration control of a model frame structure using piezoceramic sensors and actuators. JVC J. Vib. Control 2005, 11, 671–684. [Google Scholar] [CrossRef]
- Du, G.; Kong, Q.; Wu, F.; Ruan, J.; Song, G. An experimental feasibility study of pipeline corrosion pit detection using a piezoceramic time reversal mirror. Smart Mater. Struct. 2016, 25, 037002. [Google Scholar] [CrossRef]
- Wang, F.; Huo, L.; Song, G. A piezoelectric active sensing method for quantitative monitoring of bolt loosening using energy dissipation caused by tangential damping based on the fractal contact theory. Smart Mater. Struct. 2017, 27, 015023. [Google Scholar] [CrossRef]





| The Buried Depth of Pipeline (m) | 0–0.3 | 0.3–0.6 | 0.6–0.9 | >0.9 |
|---|---|---|---|---|
| 1.5 | 1.35 | 1.35 | 1.15 |
| Group | Specimens | D × T (mm) | H (m) | L (mm) | d (m) | Soil Type | ɛL (με) | ɛT (με) |
|---|---|---|---|---|---|---|---|---|
| A | A114 × 2.5-d0.6-H0.5 | 114 × 2.5 | 0.5 | 2800 | 0.6 | Clay | 354 | 295 |
| A114 × 2.5-d0.6-H1.0 | 114 × 2.5 | 1.0 | 2800 | 0.6 | Clay | 621 | 424 | |
| A114 × 2.5-d0.6-H1.5 | 114 × 2.5 | 1.5 | 2800 | 0.6 | Clay | 724 | 545 | |
| A114 × 2.5-d0.6-H2.0 | 114 × 2.5 | 2.0 | 2800 | 0.6 | Clay | 816 | 603 | |
| B | B89 × 2.5-d0.6-H1.0 | 89 × 2.5 | 1.0 | 2800 | 0.6 | Clay | 489 | 321 |
| B139 × 2.5-d0.6-H1.0 | 139 × 2.5 | 1.0 | 2800 | 0.6 | Clay | 774 | 695 | |
| C | C114 × 3.0-d0.6-H1.0 | 114 × 3.0 | 1.0 | 2800 | 0.6 | Clay | 456 | 367 |
| C114 × 3.5-d0.6-H1.0 | 114 × 3.5 | 1.0 | 2800 | 0.6 | Clay | 387 | 204 | |
| D | D114 × 2.5-d0.3-H1.0 | 114 × 2.5 | 1.0 | 2800 | 0.3 | Clay | 1005 | 768 |
| D114 × 2.5-d0.9-H1.0 | 114 × 2.5 | 1.0 | 2800 | 0.9 | Clay | 205 | 165 |
| Soil Type | Cohesive Force (kPa) | Poisson Ratio | Internal Friction Angle (°) | Density (kg∙m−3) |
|---|---|---|---|---|
| Clay | 35.5 | 0.38 | 7.8 | 1880 |
| Yield Strength fy (MPa) | Yield Strain ε1 | Tensile Strength fu (MPa) | Modulus of Elasticity E (MPa) | |
|---|---|---|---|---|
| 89 × 2.5 | 286 | 0.00143 | 426 | 2.01 × 10 5 |
| 114 × 2.5 | 281 | 0.00141 | 420 | 2.01 × 10 5 |
| 139 × 2.5 | 280 | 0.00141 | 418 | 2.01 × 10 5 |
| 114 × 3.0 | 281 | 0.00141 | 420 | 2.01 × 10 5 |
| 114 × 3.5 | 281 | 0.00141 | 420 | 2.01 × 10 5 |
| H (m) | Soil Type | Quality of Drop Hammer (kg) | Test Results (Fmax,EXP) (kN) | Theoretical Results (Fmax,THE) (kN) | FEA Results (Fmax,FEA) (kN) |
|---|---|---|---|---|---|
| 0.5 | Clay | 337 | 67.737 | 61.690 | 65.652 |
| 1.0 | Clay | 337 | 126.817 | 115.186 | 117.841 |
| 1.5 | Clay | 337 | 150.463 | 136.483 | 140.462 |
| 2.0 | Clay | 337 | 181.982 | 163.780 | 173.654 |
| Group | Specimens | The Peak Strain in Test | The Peak Strain in Theory | The Peak Strain in FEA | ||||
|---|---|---|---|---|---|---|---|---|
| εL (με) | εT (με) | εmax,EXP (με) | εmax,THE (με) | The Relative Deviation | εmax,FEA (με) | The Relative Deviation | ||
| A | A114 × 2.5-d0.6-H0.5 | 354 | 295 | 328 | 348 | 6.09% | 309 | 5.79% |
| A114 × 2.5-d0.6-H1.0 | 621 | 424 | 549 | 575 | 4.73% | 563 | 2.10% | |
| A114 × 2.5-d0.6-H1.5 | 724 | 545 | 645 | 685 | 6.20% | 658 | 2.02% | |
| A114 × 2.5-d0.6-H2.0 | 816 | 603 | 733 | 792 | 8.18% | 763 | 4.09% | |
| B | B89 × 2.5-d0.6-H1.0 | 489 | 321 | 425 | – | – | 386 | 9.17% |
| B139 × 2.5-d0.6-H1.0 | 774 | 695 | 737 | – | – | 784 | 6.37% | |
| C | C114 × 3.0-d0.6-H1.0 | 456 | 367 | 418 | – | – | 422 | 1.20% |
| C114 × 3.5-d0.6-H1.0 | 387 | 204 | 232 | – | – | 215 | 7.32% | |
| D | D114 × 2.5-d0.3-H1.0 | 1005 | 768 | 955 | 1032 | 8.06% | 1015 | 7.40% |
| D114 × 2.5-d0.9-H1.0 | 205 | 165 | 190 | 205 | 7.89% | 202 | 5.78% | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, F.; Bie, X.; Tian, J.; Xie, X.; Du, G. Experimental and Numerical Study on the Strain Behavior of Buried Pipelines Subjected to an Impact Load. Appl. Sci. 2019, 9, 3284. https://doi.org/10.3390/app9163284
Dong F, Bie X, Tian J, Xie X, Du G. Experimental and Numerical Study on the Strain Behavior of Buried Pipelines Subjected to an Impact Load. Applied Sciences. 2019; 9(16):3284. https://doi.org/10.3390/app9163284
Chicago/Turabian StyleDong, Feifei, Xuemeng Bie, Jiangping Tian, Xiangdong Xie, and GuoFeng Du. 2019. "Experimental and Numerical Study on the Strain Behavior of Buried Pipelines Subjected to an Impact Load" Applied Sciences 9, no. 16: 3284. https://doi.org/10.3390/app9163284
APA StyleDong, F., Bie, X., Tian, J., Xie, X., & Du, G. (2019). Experimental and Numerical Study on the Strain Behavior of Buried Pipelines Subjected to an Impact Load. Applied Sciences, 9(16), 3284. https://doi.org/10.3390/app9163284




