Heuristics for Spreading Alarm throughout a Network

Featured Application

This study provides heuristics for potential usage in minimizing time steps for fast spreading an alarm or other critical information, for example via satellite, throughout a terrestrial network (e.g., spreading a new routing scheme). It is presumed that the satellite can spread information only sequentially (e.g., by laser beam), but each contacted node (either by a satellite or by its terrestrial neighbor) spreads the information in parallel via Wi-Fi or cable connection to its neighbors.

Abstract

This paper provides heuristic methods for obtaining a burning number, which is a graph parameter measuring the speed of the spread of alarm, information, or contagion. For discrete time steps, the heuristics determine which nodes (centers, hubs, vertices, users) should be alarmed (in other words, burned) and in which order, when afterwards each alarmed node alarms its neighbors in the network at the next time step. The goal is to minimize the number of discrete time steps (i.e., time) it takes for the alarm to reach the entire network, so that all the nodes in the networks are alarmed. The burning number is the minimum number of time steps (i.e., number of centers in a time sequence alarmed “from outside”) the process must take. Since the problem is NP complete, its solution for larger networks or graphs has to use heuristics. The heuristics proposed here were tested on a wide range of networks. The complexity of the heuristics ranges in correspondence to the quality of their solution, but all the proposed methods provided a significantly better solution than the competing heuristic.

1. Introduction

Let us imagine that we want to spread a piece of information (e.g., an alarm) throughout a terrestrial-based network, where the nodes are collected by cables or Wi-Fi and each node can be also reached by a satellite. The satellite, which we control, can reach one node at a time and each node can inform in parallel all its neighboring nodes in one time step. This paper provides a solution to the task, how to spread a piece of information throughout the whole network as fast as possible. In other words, let us suppose that we can send the information (alarm) to any single node in one time step and all the informed nodes can send the information to all their neighboring nodes in one time step. The question therefore is, to which set of nodes we should send the information and in what order, so that after the final time step, all the nodes have the information. The minimum size of such a set is called a “burning number”.

The initial inspiration was taken from a simplified model of contagion or the spread of a belief in a social network, with successful transfer to any neighbor of the already influenced node. The formal definition of this problem was provided in the framework of graph theory by Anthony Bonato et al. [1]. It was proved that computing a “burning number” is NP-complete [2]. The problem was further studied in papers [3,4], where the bounds for the burning number (i.e., the minimum number of time steps, equal to the minimum size of the set of nodes, which are informed or alarmed “from the outside”, not from their neighbor) are analyzed. The papers provided both the lower and the upper bounds, where the upper bound was accompanied by the actual sequence of the set of nodes to be informed from the outside. However, since the authors were graph theorists, they were not primarily concerned about an effective algorithm, how to find a solution close to the optimal one. Bounds for special types of graphs and special cases are also studied as graph theory problems in [5,6,7,8].

A number of different approaches for disseminating information are studied in various areas, like the k center selection, the telephone model in gossiping, or the broadcasting of control or emergency packets in computer networks, viral marketing or influence maximization in social networks, or models of contagion in biology.

In graph theory, the k center selection refers to a related problem, when the message is sent to all k centers (seeds) at once, so no time scheduled sequence is needed, and the parameter k is given in advance. Unlike a burning number problem, heuristic solutions for the k center problem have been studied more extensively [9,10]. Recently the problem has been optimized by stochastic metaheuristics like tabu search or simulated annealing [11], paying for better results with computational time. Instead of spreading an alert through seed hubs, this problem can be interpreted as selecting hubs for sending an alert to a higher level of the network, so that an alert occurring in any node of the network is sent through the closest hub in the shortest time [12]. The alert routing can be employed e.g., in security [13].

In gossiping [14], each node has a unique item of information. By each connection between two nodes, both share all their information. How many connections are needed (a schedule determines, which edges are used in which order; edges may be used repeatedly), until each node has all the pieces of information? In broadcasting, one node has an item of information to be communicated to the rest of the nodes, which is closer to the “burning number” problem than gossiping [14]. In the typically used telephone model of information dissemination [14,15], one node shares or sends information to one of its neighboring nodes. Unlike in k center or in the “burning number” problem, parallel distribution of information to all the neighbors of a node in one time step is not considered. Parallel distribution is allowed in the radio model of information dissemination [14]. However, this model is most often subject to other limitations, which makes it less relevant as an inspiration for the solution of the burning number problem.

The burning number problem is also slightly related to the broadcasting of control or emergency packets to all nodes of a network [16,17]. Such tasks are needed e.g., for route maintenance or critical alert dissemination. However, even though multiple seeds for cluster centers were studied [18], the time schedule for broadcasting to a sequence of cluster centers was not considered in this context. A related problem is also unequal clustering in wireless sensor networks [19].

Related types of problems belong to influence maximization [20,21,22], where the goal is to exploit cascade propagators termed seeds, which are selected in such a way and activated in such times that they maximize the influence spread in a social network. This can be used for viral marketing in politics, or by companies introducing a new product, which pay a set of influencers (each at selected time) to obtain maximum promotion of the product or voting for a party. However, the problem typically differs in the probabilistic nature of the information transfer (the influence probability of each connection), which in the approach in this paper is set to 100 per cent. Moreover, the influencer nodes are informed all at the beginning, while burning sequence nodes are burned one at each time step. The neighborhood of an influencer can be considered as a cluster. A special type of clustering can even be used in studies of brain activities [23,24].

A firefighter problem in graph theory [25] uses somewhat related “burning” terminology, but its similarity is superficial. Like in a burning number problem, a node is initially ignited (burned) and each node burns in each subsequent time steps all its unburned vertices. However, only in the first time step is a node burned from “outside” and a firefighter in each time step can immunize one of the unburned vertices against being burned. The goal is rather different, aiming at prevention of spreading harmful information through the network.

In the following sections, the competing algorithmic approach for finding the burning number [3] is described in more detail, followed by the heuristics designed here, which are then tested on a range of complex networks.

2. Burning Number and Previous Algorithms

In this paper, we only consider finite undirected unweighted simple graphs (aka networks). The problem was originally defined for graphs and therefore the graph theory terminology is retained in this section. Let us have a G = (V, E) where V is a vertex set and E is an edge set. For vertices u, v ∈ V, the distance dist_G(u; v) between them in a graph is the number of edges in a shortest path connecting them. Based on [1], the burning number bn(G) of a graph G is the smallest integer k for which there are vertices x₁, …, x_k such that for every vertex u of G, there is some i ∈ {1, …, k} with dist_G(u; x_i) ≤ k − i.

Sequence x₁, …, x_k of vertices from G from the above definition is called a shortest burning sequence (there may be several such sequences). A burning sequence and burning number are based on a metaphor of a fire spreading among the vertices of a graph. At each discrete time step t_i starting at 1 and terminating at k, a fire starts at a vertex x_i, if it is not already burning. Then the fire starts at all neighboring vertices of the vertices which are already burning (except of the neighbors of the just ignited vertex x_i). The condition ∀u ∈ V(G): ∃i ∈ {1, …, k}: dist_G(u; x_i) ≤ k − i guarantees, that after k steps all the vertices of G are burning. An additional condition ∀i,j ∈ V(G) ∈ {1, …, k}: dist_G(x_i; x_j) ≥ j − i might be included, which means, that in the sequence x₁, …, x_k, one does not try to start a fire at a vertex, which is already burning. However, if the burning sequence is the shortest, this condition is superfluous.

In Figure 1 are presented single time steps (from left to right, top to bottom) of the optimal process of burning an artificially designed graph. The optimum burning number of this graph is seven, since it was burned in seven steps and in no step a greater number of nodes could have been burned. In each time step, one node is painted with a new color, which means, that this node is “burned from the outside” as a part of the burning sequence. All the neighbors of the already burned nodes, which are not yet burned, are also burned (in Figure 1 they are painted with the same color as their painted neighbors). However, the colors only serve to provide an additional piece of information, one non-white color for all burned nodes would be sufficient. In addition, when two or more different colored nodes are neighbors of a white (i.e., not yet burned) node, the decision regarding which of the neighboring colors to choose from would have to be arbitrary. Nevertheless, in Figure 1 such a situation does not occur. Figure 1 presents more clearly the problem of the selection of the vertices in the shortest burning sequence, i.e., which vertices should be colored (aka burned) from outside and in which permutation determining their time schedule.

Until now, the only known approximation algorithm generating a burning sequence for the general graphs was an algorithm by Bonato and Kamali [3]. This algorithm has an approximation ratio of 3, which means, that the optimal, i.e., the shortest possible burning sequence is guaranteed not to be shorter than one third of the burning sequence length provided by the approximation algorithm.

The Bonato algorithm [3] starts with a guess, that the burning number equals 3g − 3. The “shortened” burning sequence is initially empty. Then, starting from an arbitrary node, a randomly selected node is added to the “shortened” burning sequence, if all the nodes already in the burning sequence have a graph distance from the selected node at least 2g − 1. If the resulting sequence has less than g vertices and all vertices have been tried, then the value of burning number is at most 3g − 3 and the guess was good. (The shortened burning sequence can be in time steps from the range of g to 3g − 3 appended by any currently unburned vertex at the given step). If the number of nodes in the prospective “shortened” burning sequence was greater than or equal to g, the guess was bad, and we had to try a bigger g. By binary search, we found the smallest g providing a good guess. This algorithm also provides a lower bound, that the burning number cannot be smaller than g − 1. The complexity of the algorithm for |V| = n, |E| = m is O(mn + n² log n).

In the same paper [3], the authors also present an algorithm, which is optimized for trees with an approximation ratio of 2 and for disjoint paths with an approximation ratio of 1.5. In the results in Section 4 of this paper, we compare our results only to the results of the approximation algorithm for the general graphs [3], even though a few of the tested networks are trees. However, this is consistent with our further described algorithms, which are also intended for general graphs and are not optimized for trees. Our algorithms provide better results for all the tested networks, with the disadvantage, that no approximation ratio is guaranteed.

3. The Proposed Algorithms to Obtain the Shortest Burning Sequence

As already mentioned in the introduction, the burning number problem is NP complete, therefore for larger networks the (likely suboptimum) solution must be obtained by a heuristic. All of the following heuristics start, similarly to the algorithm in [3] with a guess as to what the burning number might be, and then try to build a burning sequence of that length. If any nodes are left unburned afterwards, the guess was bad, and the algorithm must start with a greater burning number. A good guess with a smallest possible burning number should be found by a binary search.

3.1. Maximum Eigenvector Centrality Heuristic

The simplest approach to a burning number sequence seems to be a greedy algorithm. If the value of our guess of the burning number is labelled bg (aka burn guess), then we want to select such a node, which neighborhood up to the graph distance bg − 1 should have the biggest number of nodes (which we then burn). While we could go through all the nodes and find out the one with the maximum neighborhood, such an approach seems to be too computationally demanding. One may guess, that such nodes should be somewhere near the “center” of the network. However, what is the center of a network? There exist various definitions of centrality. The most popular one is a node v with a minimum eccentricity, i.e., a node with the shortest of the maximum graph distance between v and any other node of the network. However, in our pivotal trials we had more success with maximum eigenvector centrality [26], which we further used.

Therefore, for the number of rounds i from bg to 1 we always selected the node x_i with the maximum eigenvector centrality value. The maximum eigenvector centrality value is always evaluated for the remaining reduced network with unburned nodes. Only in the case, when for the number of rounds i the component of the remaining reduced network with maximum diameter has a radius smaller or equal to i, the selected node x_i is the node with minimum eccentricity from that component. The neighborhood subgraph of nodes within the graph distance i − 1 from v is however determined from the original network, which may occasionally burn a few more nodes. Having a series of selected nodes x₁, …, x_i, together with their (diminishing) neighborhood subgraphs, we remove from the original network every edge connecting a couple of nodes from these subgraphs, and then continue to select the next node x_i in the next round.

TG in the Algorithm 1 means a temporary graph with the same nodes as graph G, from which are successively deleted edges between the union of nodes V_e(x_i) from the neighborhood of nodes from the sequence X. The sequence X is successively enlarged. The range of this neighborhood V_e(x_i), is successively diminishing, i.e., in the beginning, the nodes belonging to V_e(x_i) are all the nodes distanced up to bg-1 from the node x₁, while the last vertex set V_e(x_i) contains only the node x_bg.

A component of a graph is a subgraph in which any two nodes are connected by a path, and to which no additional node can be added. The eccentricity of a node v in a connected graph is the maximum graph distance between v and any other node u of G. The graph diameter is the maximum eccentricity. The graph radius is the minimum graph eccentricity. The function eigen_centrality(G) takes a graph G and returns the eigenvector centralities of positions of vertices v within it. The function ego (G, order, x_i) calculates the vertices V_e(x_i) of the neighborhood of the given vertex x_i of graph G within the given graph distance order from x_i. For the graph G = (V, E), let S_i ⊂ V be a subset of vertices of G, such that ${\mathit{S}}_{\mathit{i}}={\cup }_{\mathit{j}=\mathbf{1}}^{\mathit{j}=\mathit{i}}{\mathit{V}}_{\mathit{e}}\left(x_j\right)$. Then the induced subgraph G[S_i] is the graph whose vertex set is S_i and whose edge set consists of all of the edges in E that have both endpoints in S_i. Its edges are removed from TG. Since for |V| = n and |E| = m the bg is bounded from above by n, the largest eigenvalue can be found with complexity O(m log n) which likely dominates the finding ego neighborhood by breath-first search, and the algorithm is called by binary search O(log n) times, the complexity of Algorithm 1 is less than O(m n log² n).

Algorithm 1. Maximum eigenvector centrality heuristic for a shortest burning sequence

Input: A network G = (V, E) and a guess value bg of a burning number

Output: A sequence X= x1, …, xbg of nodes from G

1: X ← ∅; TG ← G;

2: for i = 1, …, bg do

3:  maxDiameterComp $\leftarrow \mathrm{component} \mathrm{of} \mathit{T}\mathit{G} \mathrm{with} \mathrm{maximum} \mathrm{diameter}$

4:  if i ≥ radius of maxDiameterComp

5:  then $x_i\leftarrow v\in \mathit{V}|\underset{v\in V\left(\mathrm{maxDiameterComp}\right)\backslash X}{\min }eccentricity(v,\mathrm{maxDiameterComp}$)]

6:  else $x_i\leftarrow v\in \mathit{V}|\underset{v\in V\left(TG\right)\backslash X}{\max }eigen\_centrality\left(\mathit{v},\mathit{T}\mathit{G}\right)$;

7:  X ← X ∪ $x_i$

8:  Ve(xi) $\leftarrow$ ego(G, bg − i, $x_i$);

9:  ${\mathit{S}}_{\mathit{i}}\leftarrow {\cup }_{\mathit{j}=\mathbf{1}}^{\mathit{j}=\mathit{i}}{\mathit{V}}_{\mathit{e}}\left(x_j\right)$;

10:   TG$\leftarrow \mathit{G}(\mathit{V},\mathit{E}\left(\mathit{T}\mathit{G}\right)\backslash \mathit{E}\left(\mathit{G}\left[{\mathit{S}}_i\right]\right);$

11: if ${\mathit{S}}_{\mathit{i}}$ ≡ V then return X else return FAILED TO BURN

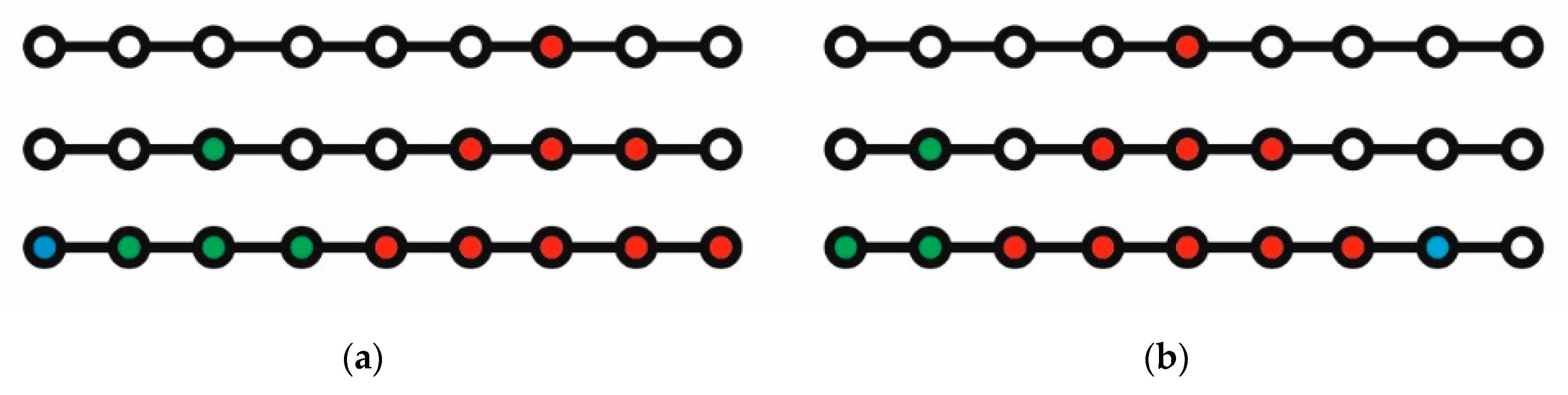
The greedy approach of Algorithm 1 often fails, because by burning the graph from its center, the unburned nodes are likely left in too many unconnected components, when each component spends at least one node in the X sequence to be burned. Algorithm 1 fails to find an optimum even for one of the simplest graphs, a path. This is shown in Figure 2. Its left-hand side (a), going from top to bottom, shows an ideal run with burning number 3. The right hand side (b) of Figure 2 shows the result of Algorithm 1, when, after starting with a central red colored node to be burned, its neighborhood of the nodes distanced bg − 1 = 2 from the initial node is shown with red nodes in the last line of Figure 2. If we remove the lines between the red colored nodes, we are left with two components containing unburned nodes. One component can be burned in two time steps, but the remaining component with two unburned nodes cannot be burned in one time step. One node remains unburned after three rounds. This example shows the necessity of looking for a better algorithm.

3.2. Cutting Corners Heuristic

Firstly, how to characterize a “corner” node? In the path graph in Figure 2, it would be a node of the degree 1, i.e., one of the end nodes. However, no such node exists, e.g., in a square lattice graph. We could select the nodes with smallest degree, but in networks corresponding to a tree graph there may be too many such nodes. Therefore, we chose to select the nodes with the lowest eigenvalues as the “corner” nodes.

If we want to do a local optimization, we should not choose just one such “corner” node, but more, so that we would have a larger selection of “central” nodes within the graph distance bg − i from then. The number was set to ⌈√(|V(G)\Si|)⌉. This means a ceiling of a square root of the number of vertices would remain unburned if the current partial sequence X was in time steps burned and spread the burns up to bg time steps (in the last steps, the new nodes not defined in X yet would not be burned).

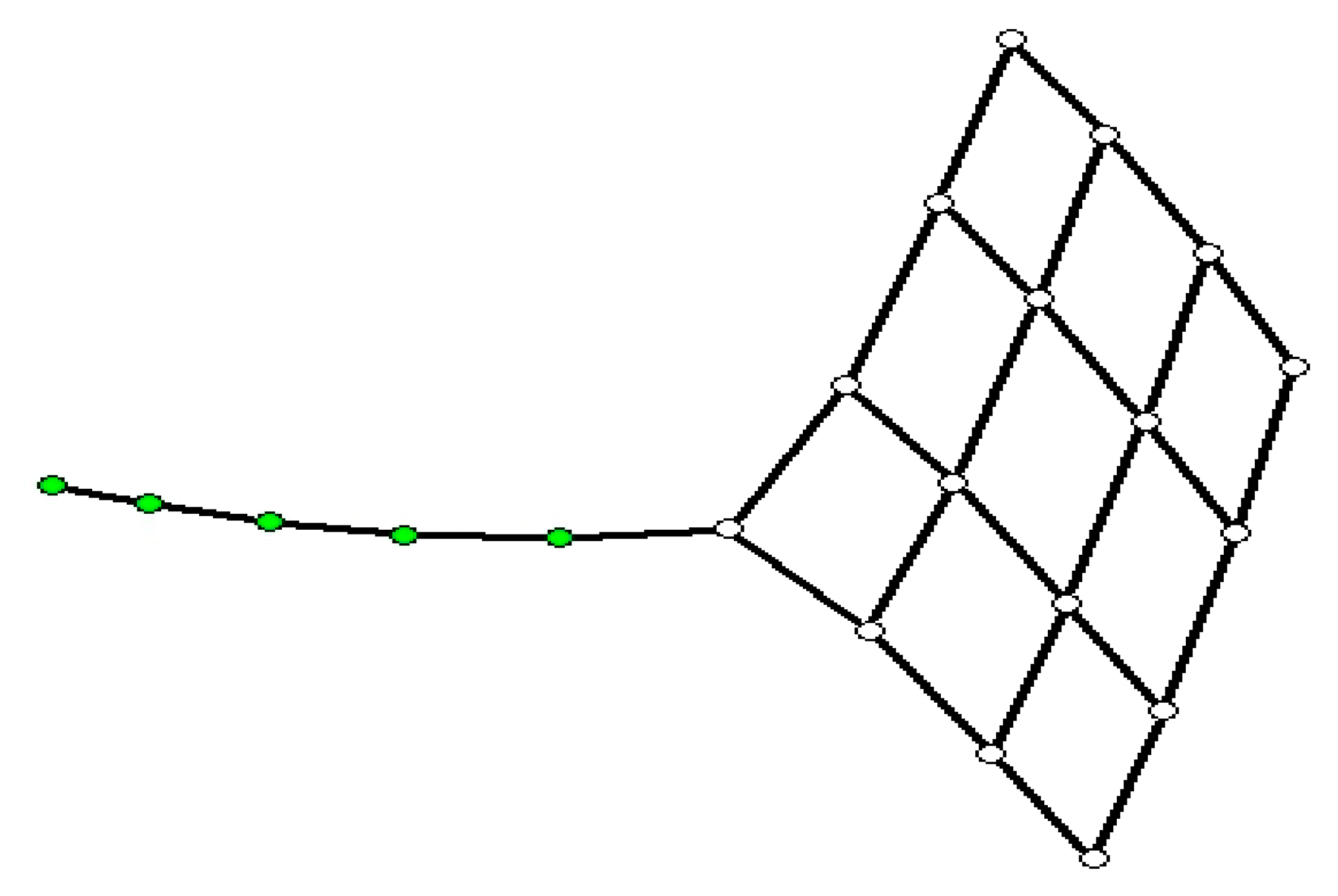
Still, this characterization of “corner” nodes is not satisfactory. Let us take as an example a graph in Figure 3. If we take nodes with minimum eigenvalues, they are all positioned in the “tail”, while we would prefer one node at the end of the tail and the rest in the corners of the square.

This problem has been solved by a sequential selection of the “corner” nodes, when the first one has the minimum eigenvalue, but the next one is one with the minimum eigenvalue of those nodes, which are at least a given minimum distance from any of the already selected nodes. The function minDist(v,CornerNodes) finds the smallest graph distance of v to any of the nodes from the set of CornerNodes. This minimum distance was set to a floor of a half of average path length of the unburned remaining graph, after the partial sequence X would burn and spread the burns up to bg time steps.

For the selected “corner” nodes, the goal is to find the best “center” node ideally in the distance bg − i from the selected corner node. For each “corner” node, a maximum of three potential “center” nodes in the distance bg − i from the current “corner” node and with maximum eigenvalue in the graph with unburned vertices are selected. For each node from this this set of potential central nodes, the number ubn (unburned neighborhood) of unburned nodes in its bg − i neighborhood is evaluated, and nodes with the top quartile of the number of neighboring unburned nodes are selected. These nodes are then evaluated by the apl (average path length) of the remaining unburned graph and by the number of its components, if their neighborhood would be burned.

We then use a weighted aggregated sum product assessment (WASPAS) method to assess the quality of these central nodes. These nodes should have a maximum sized unburned neighborhood ubn (which they would cause to burn in the remaining time steps), a minimum average path length apl of the remaining unburned graph afterwards (more compact graphs burn better than linear paths) and the smallest possible number of the components compNo of the remaining unburned graph. We used practically equal weights w for the normalized values of these parameters, but in general, different weights should be used for different types of graphs.

The cb sequence contains max, if the component is benefit, like ubn, but cb contains min, if the component is cost, like apl and compNo. The best “central” node according to the WASPAS method was then added to the X sequence of nodes to burn.

The Algorithm 2 can find an ideal burning sequence both for a path graph as well as for the artificial test example presented in Figure 1. However, from the NP complexity of the problem, it is clear, that there is still space for improvement. The simplest approach would be to search more candidate nodes to burn.

Algorithm 2. Cutting corners heuristic for a shortest burning sequence

Input: A network G = (V, E) and a guess value bg of a burning number

Output: A sequence X= x1, …, xbg of nodes from G

1: X←∅; TG←G; ${\mathit{S}}_0\leftarrow Ø;$

2: for i = 1, …, bg do

3:  maxSizeComp $\leftarrow \mathrm{component} \mathrm{of} \mathit{T}\mathit{G} \mathrm{with} \mathrm{maximum} \mathrm{number} \mathrm{of} \mathrm{nodes}$

4:  if i ≥ radius of maxSizeComponent

5:  then $x_i\leftarrow v\in \mathit{V}|\underset{v\in V\left(\mathit{maxSizeComp}\right)\backslash X}{\min }eccentricity(v,\mathit{maxSizeComp}$)]

6:  else CentralNodes$\leftarrow Ø;$

7:    CornerNodes ← $v\in \mathit{V}|\underset{v\in V\left(\mathit{maxSizeComponent}\right)}{\min }eigen\_centrality\left(v,\mathit{maxSizeComp}\right)$;

8:    for j = 2, …, $\lceil \sqrt{|\mathit{V}\left(\mathit{G}\right)\backslash {\mathit{S}}_{i-1}|}\rceil$ do

9:      minCornerDist ← $⎣average.path.length\left(\mathit{maxSizeComponent}\right)/2⎦$

10:       distNodes ← $\left\{v\in \mathit{V}\left(\mathit{maxSizeComp}\right)|minDist\left(v,\mathit{CornerNodes}\right)\ge minCornerDist\right\}$

11:       CornerNodes ← CornerNodes ∪ $v\in \mathit{V}|\underset{v\in \mathit{distNodes}}{\min }eigen\_centrality\left(v,\mathit{T}\mathit{G}\right)$;

12:     for k = 1, …, $|\mathit{CornerNodes}|$ do

13:       tempNodes ← $\left\{v\in \mathit{V}\left(\mathit{maxSizeComp}\right)|dist\left(v,\mathit{CornerNode}{\mathit{s}}_{\mathit{i}}\right)\ge bg-i\right\}$

14:       tempNodes ← $\underset{v\in \mathit{tempNodes}}{decreasing\_order(}eige{n}_{centrality\left(v,\mathit{maxSizeComponent}\right)}, 3 nodes)$

15:       CentralNodes ← CentralNodes ∪ tempNodes

16:     for m = 1, …, $|\mathit{CentralNodes}|$ do

17:       Ve($\mathit{CentralNode}{\mathit{s}}_m$) $\leftarrow$ ego(G, bg − i, $\mathit{CentralNode}{s}_m$);

18:       $ub{n}_m=|\mathit{V}e\left(\mathit{CentralNode}{s}_m\right)\backslash {\mathit{S}}_{i-1}|$

19:     CentralNodes $\leftarrow \mathit{CentralNodes} \mathrm{with} \mathrm{top} \mathrm{quartile} \mathrm{values} \mathrm{of} ubn$

20:     ubn$\leftarrow \mathrm{top} \mathrm{quartile} \mathrm{values} \mathrm{of} ubn$

21:     for r = 1, …, $|\mathit{CentralNodes}|$ do

22:       $ap{l}_{\mathit{r}}$ ← average_path_length($\mathit{G}(\mathit{V},\mathit{E}\left(\mathit{T}\mathit{G}\right)\backslash \mathit{E}\left(\mathit{G}\left[{\mathit{S}}_i\cup \mathit{V}e\left(\mathit{CentralNode}{\mathit{s}}_r\right)\right]\right);$

23:       $compN{o}_r\leftarrow \mathrm{number}\_\mathrm{of}\_\mathrm{components}(\mathit{G}(\mathit{V},\mathit{E}\left(\mathit{T}\mathit{G}\right)\backslash \mathit{E}\left(\mathit{G}\left[{\mathit{S}}_i\cup \mathit{V}e\left(\mathit{CentralNode}{\mathit{s}}_r\right)\right]\right);$

24:    w← (0.33,0.33,0.34)

25:     lambda ← 0.5

26:     cb = (max,min,min)

27:     $x_i\leftarrow$best node determined by WASPAS(ubn,apl,compNo,w,cb,lambda);

28:   X ← X ∪ $x_i$

29:   ${\mathit{S}}_{\mathit{i}}\leftarrow {\cup }_{\mathit{j}=\mathbf{1}}^{\mathit{j}=\mathit{i}}{\mathit{V}}_{\mathit{e}}\left(x_j\right)$;

30:   E(TG) $\leftarrow \mathit{E}\left(\mathit{T}\mathit{G}\right)\backslash E\left(G\left[{\mathit{S}}_i\right]\right);$

31: if ${\mathit{S}}_{\mathit{i}}$ ≡ V then return X else return FAILED TO BURN

3.3. Greedy Algorithm with Forward-Looking Search Strategy

Both Algorithm 1 as well as Algorithm 2 select in each time step the currently best looking candidate node to be burned. However, to search the space of solutions more thoroughly, we used an improved greedy algorithm with a forward-looking search strategy, which was originally proposed by Huang et al. [27] and applied to other problems, like packing. In our version of this algorithm, we consider at the first level several candidates for vertices to be burned, so not only the best node determined by a WASPAS method like in Algorithm 2 is used, but also several other less optimal looking candidates (we set the maximum number of candidates in each level to 20). Each of the candidates is used as x₁ in the burning sequence X, and the rest of the sequence X is filled with the best nodes recalculated anew by WASPAS. If the graph is burned at the end of the sequence for any of the candidates, then the algorithm is stopped, and we have our answer. However, if the graph is not burned for burning sequences starting with various candidates, we select the starting node x₁, which left minimum vertices unburned. Then we use this nodes in the next runs as x₁ and start the same procedure with the next node x₂. Again, we select several candidates by WASPAS approach, use each of them as x₂, and fill the x₃ and the remaining sequence X again only by the best new candidates. If for any of the sequences X the graph is burned, we stop. If the algorithm did not stop, we select the x₂ node, which left minimum unburned nodes. In this way we continue with x₃, etc. until the graph is burned, or we tried all the candidates for the last x_bq node. This approach, which we shall refer to as Algorithm 3 in the

Table 1. Burning number results for tested networks and algorithms.

					Burning Number by Tested Algorithms
Name of Network	Description	|V|	|E|	max. degr.	Bonato	Algorithm 1	Algorithm 2	Algorithm 3	Improvement
line of 49 nodes	artificial example	49	48	2	12	8	7	7	42%
squaredIdealBurn7	artificial example	231	418	4	15	10	7	7	53%
Reed98	Facebook	962	18,812	313	9	4	4	4	56%
polblogs	polit. blogosphere	643	2280	165	12	6	7	6	50%
ba-1k-2k	generated graphs	1000	1996	69	9	6	6	6	33%
mahindas	economic problem	1258	7513	206	9	6	6	6	33%
netscience	co-authorship	379	914	34	12	7	7	6	50%
lattice2D	33 × 33 regular lat.	1089	2112	4	24	14	13	13	46%
lattice3D	10 × 10 × 10 reg. lat.	1000	2700	6	15	11	11	10	33%
binary tree	regular	1000	999	3	21	10	10	10	52%
ternary tree	regular	1000	999	4	15	7	7	7	53%
Geometric random	10 generated nets	1000	3764.4	17.9	21	12.8	11.7	11	48%
Erdős-Rényi	10 generated nets	1000	6013.3	24.2	6	5	5	5	17%
Barabási–Albert	10 generated nets	1000	2994	80.1	9	4.9	4.9	4.9	46%
average improvement achieved by the best Algorithm 3 compared to Bonato:									37%

, shares most of the pseudocode with the Algorithm 2, therefore we shall not present it here as a stand-alone code. It searches the solution space slightly more extensively than the entirely greedy approach of Algorithm 2. Theoretically, we could try to use a version of A* algorithm or some other tree search algorithm, however, it would be much more computationally demanding. Improvement can be also found by a parallelization, similar to [28].

4. Testing and Results

For testing purposes, we have selected a wide range of networks, and both real as well as artificial examples. Their resulting burning numbers for all the tested algorithms are given in the Table 1. The first network is a path graph, similar to the one in Figure 2, only with 49 nodes instead of nine nodes. It was used for testing, as it is clear that its optimal burning number is seven (the maximum number of nodes in a path graph for a particular burning number can be calculated as ${\sum }_{i=1}^{bg}\left(2i-1\right)$). The second network, squaredIdealBurn7, is an artificial example with known optimal burning number equal to seven, the network is shown in Figure 1. The Reed98, polblogs, ba-1k-2k, mahindas, and netscience are networks from repository [29]. The 2D and 3D lattices and binary and ternary regular trees were standardly generated and are reproducible. The Geometric random provides averaged results achieved for 10 randomly generated geometric networks, where 1000 random points on a unit square were connected by an undirected edge if they were closer to each other than a given radius 0.05. The Erdős–Rényi provides averaged results achieved for 10 randomly generated networks, each with 1000 nodes, each couple of nodes connected with a probability 0.012. The Barabási–Albert provides averaged results for the networks produced by the Barabási–Albert (BA) preferential attachment model, generated by starting with a triangle and adding each time a node together with three edges. The algorithms as well as the network generation used an igraph module in R [30], which was managed through the RStudio environment. Some of the required functions, like finding eccentricity, radius, eigenvalue centrality, number of components or the largest component, average path length, the vertices of the neighborhood of the given vertex within the given graph distance (EGO), or the weighted aggregated sum product assessment (WASPAS) method are directly available in standard R modules, mostly in the igraph module.

The burning numbers obtained by Algorithms 1–3 were compared with the results by Bonato and Kamali algorithm [3]. The best-obtained results are emphasized by red font. The best-achieved values were obtained by Algorithm 3, which is however also the most complicated. Algorithm 2 was only slightly worse, and Algorithm 1 has the maximum deviations on artificial examples, while on real networks or their models its results were still close to optimum. Compared to the Botato and Kamali algorithm [3], our best Algorithm 3 achieved on average a 37 percent improvement. However, this comparison is slightly unfair, the algorithm in [3] was used mainly to obtain an upper bound value for the burning number and it has the advantage of properly analyzed complexity. Although the complexity of Algorithm 1 is similar to [3], our Algorithm 3 has too many heuristically defined parameters to obtain its complexity easily. From a practical point, run times for the tested networks were comparable (within a minute on PC).

5. Conclusions

In this paper, we have proposed three heuristics to achieve optimal distribution of an alarm in a network during subsequent time steps. The heuristics increase in their complexity as well as in the quality of their results. They were compared on a range of artificial as well as real networks. The best Algorithm 3 achieved, on average, a 37 percent improvement over the algorithm from [3]. In future, slightly better results can be expected from tabu search, simulated annealing or evolutionary heuristics. However, this improvement would likely be paid with an increase of several magnitudes in CPU time. From a practical point of view, the current approach assumes that sending and receiving the critical information from “outside” source, e.g., a satellite, takes the same time as broadcasting the information to neighbors of the already informed node, e.g., within a terrestrial network. Since this assumption may not be correct, the algorithm might require modification due to these technological issues.