1. Introduction
The detection of 1D barcodes has applications in sectors such as production, retailing, logistics, and transportation. Complementary to the traditional human-operated hand-held laser barcode reader, vision-based barcode reading has been gaining much attention in recent years because it allows for automatic object identification, which in turn facilitates a higher degree of automation. The robust automated 1D barcode detection approach aims at detecting a pure 1D barcode region and rotation angle through sensor vision. The right rotation angle ensures the correctness of the decoding result, while accurate region segmentation contributes to faster decoding for barcode decoding tools (such as ZXing library [
1]) and image distortion restoration. However, detecting complete barcodes in harsh visual surroundings with accuracy and speed is still a difficult problem.
Existing approaches to vision-based barcode reading are either geometric-based [
2,
3,
4] or learning-based [
5,
6]. While geometric approaches perform better in terms of accurateness of segmentation, they tend to be weak in the presence of severe distortion or occlusion. Learning-based methods, especially those based on deep neural networks (as Hansen et al. [
6] use an object detection network for location) are gaining attention due to their good generality. However, the lack of interpretation of the detection and the segmentation process limits their practical application. Segmentation neural networks can output the segmentation region quickly, but even a tiny defect in the 1D barcode region can cause a completely different decoding result, which often occurs in real-world scenarios.
Meanwhile, for excellent 1D barcode detection results, existing 1D barcode detection approaches need to tune many thresholds set in the algorithms to apply in different detection conditions. The correctness of the threshold value may directly influence the performance of the algorithm, for example, threshold
T which determines the candidate for the parallel segment detector by Creusot et al. [
3], and the value of threshold ratio
for bar description by Namane et al. [
4].
In this work, we propose a novel 1D barcode detection approach using integrated deep-learning and geometric methods in two-stages: barcode location and region extraction. We design two neural networks for each of the two stages. The outputs of the two networks are then post-processed using geometric methods. The barcode location stage first locates the bounding box region of the 1D barcode quickly, using a you only look once (YOLO) [
7] object detection network. We also predict the rotation angle of the 1D barcode by detecting line segments with the line segment detector (LSD) algorithm [
8] and clustering their angles in the barcode location stage. In the region extraction stage, we estimate the barcode rectangle region where the line segments of the 1D barcode can be extracted. We design a specific neural network, called the region estimation network, to determine this region. The extracted line segments form the clean barcode, which is easy to decode.
Through extensive experiments, we verify the effectiveness of our integrated approach. We also compare our approach to the state-of-the-art methods on the standard benchmarks, showing that our process improves the accuracy by at least 5%. Furthermore, we show that our approach is faster than the existing approaches.
2. Related Work
In recent years, methods focusing on barcode detection have developed rapidly in the computer vision community. Previous approaches required users to manually center and align the camera with the target barcode before detection to achieve a better performance. To improve efficiency, recent works have focused more on an interaction-free solution, enabling barcode detection to be fully automatic. The first barcode detector based on morphological operators was proposed by Katona et al. [
9]. Different approaches based on geometry are widely adopted. Creusot et al. [
3] find a candidate line segment in the barcode which crops the region in orthogonal direction by intensity value. Namane et al. [
4] estimate whether the line segments, transformed from the outer contours, fit the bar description by length and orientation. Li et al. [
10] use maximally stable extremal regions (MSERs) to eliminate the background noise and detect the direction of the barcode. The aforementioned works are all based on the graphic feature that a 1D barcode is composed of, i.e., a series of thin and thick bars, and so detect the line segments and the apparent gradient change in the orthogonal direction.
These methods are accurate in 1D barcode region extraction and perform well in benchmark datasets such as Zamberletti et al. [
5], with the 1D barcodes images captured in a close distance; however, there still exists a localization problem. In various industrial applications, it is necessary to process a high-resolution image where 1D barcodes may appear in a small region, which makes localization of the 1D barcodes difficult especially when the background texture is complex. Increasing the image size also caused a rise in computational cost, which directly influences the speed.
Deep-learning-based approaches deal with localization tasks well. Many methods based on deep learning have been proposed, such as in [
5], where they use a multi-layer perceptron (MLP) neural network in the 2D Hough transform domain to find potential bars. Hansen et al. [
6] use an object detection network to locate the barcodes and another subsequent network to predict the rotation angle of the 1D barcode in the bounding box region. Further segmentation of the 1D barcode is not proposed by Hansen et al. [
6]. With the pure 1D barcode region extracted, many image processes, such as distortion correction [
11], can be applied to help decode the 1D barcode. Although there exist 2D object detection instance segmentation approaches such as Mask-RCNN [
12], a tiny defect in 1D barcode segmentation may cause completely different decoding results; however, the mean average precision (mAP) [
12] is still high. Therefore, we propose to use a geometric approach to solve the segmentation problem and combine it with a deep-learning approach to solve the localization problem. Related methods that we use in this work are the object detection network and line segment algorithm.
The object detection task involves the detection, classification, and localization of one or more target objects in an image; this marks objects with bounding boxes and gives them a category [
13,
14]. Object detection models are mainly built using a deep convolutional neural network, which has excellent performance in graphics processing [
14]. The YOLO detection network [
7,
15,
16] is a representative model famous for its speed, which directly predicts four values to describe a bounding box [
16]. Compared to other detection systems such as RetinaNet [
17] and DSSD513 [
18], YOLO performs faster and better.
The line segment detection algorithm (LSD) [
4] is a fast line segment detector which does not require one to manually tune the parameters for each image. In essence, LSD is a region growing algorithm; each region starts with just one pixel and the region angle set to the level-line angle at that pixel (orthogonal to the gradient angle). Then, the pixels adjacent to the region are tested; the ones with a level-line orientation equal to the region angle up to a certain precision are added to the region. At each iteration, the region angle is updated to the mean level-line orientation of pixels in the region. The process is repeated until no new point can be added. It always starts from seed pixels with a larger gradient magnitude as they likely belong to straight edges [
8].
3. Model Overview
The 1D barcode is usually located on the package surface of a product which can have complex textures, making it difficult for the pure geometric-based methods to locate the region of the barcode. Regions outside 1D barcodes also take unnecessary computational cost, especially when dealing with high-resolution input images, which makes detection hard in real-time applications when using geometric methods, although they perform better in terms of accuracy. Deep-learning-based detection methods can locate the barcode fast using the object detection neural network technique, but the barcode in the bounding box region is still rotated randomly and mixed with background pixels, which makes it hard to decode.
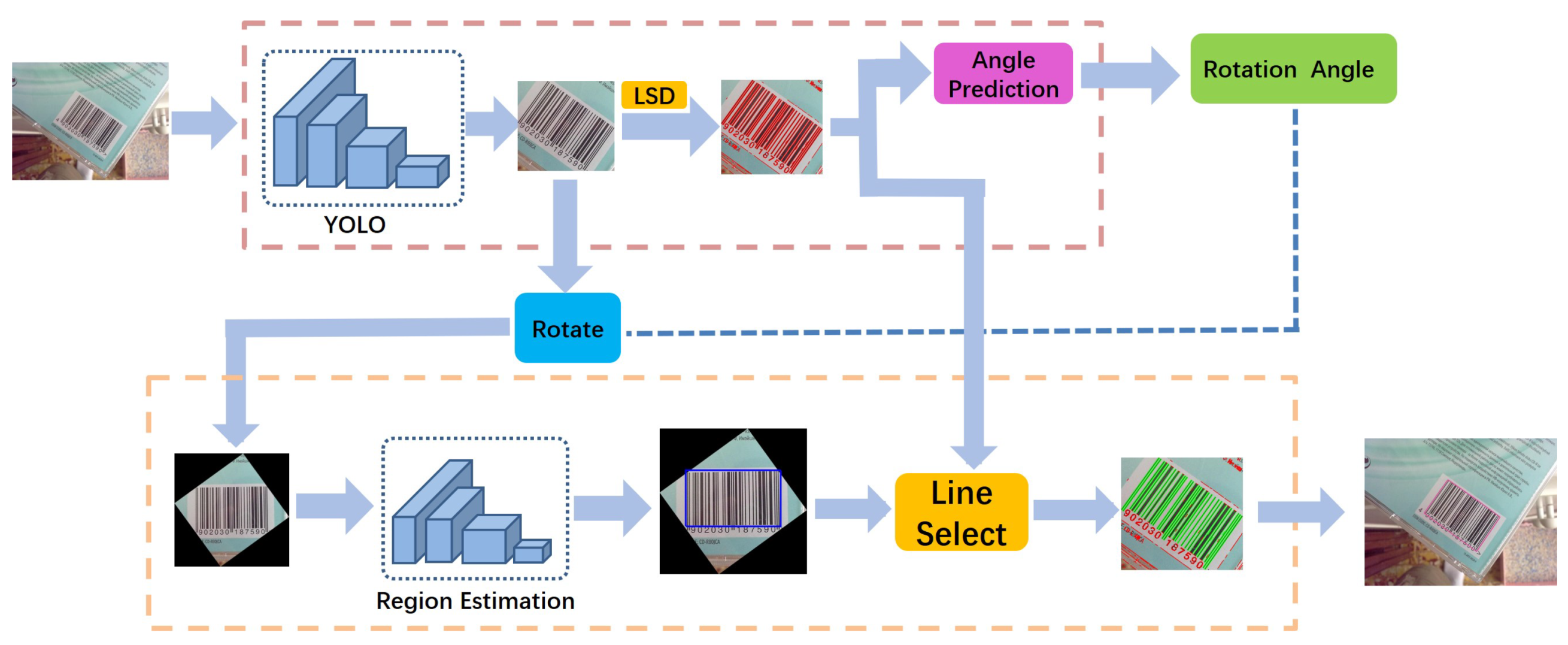
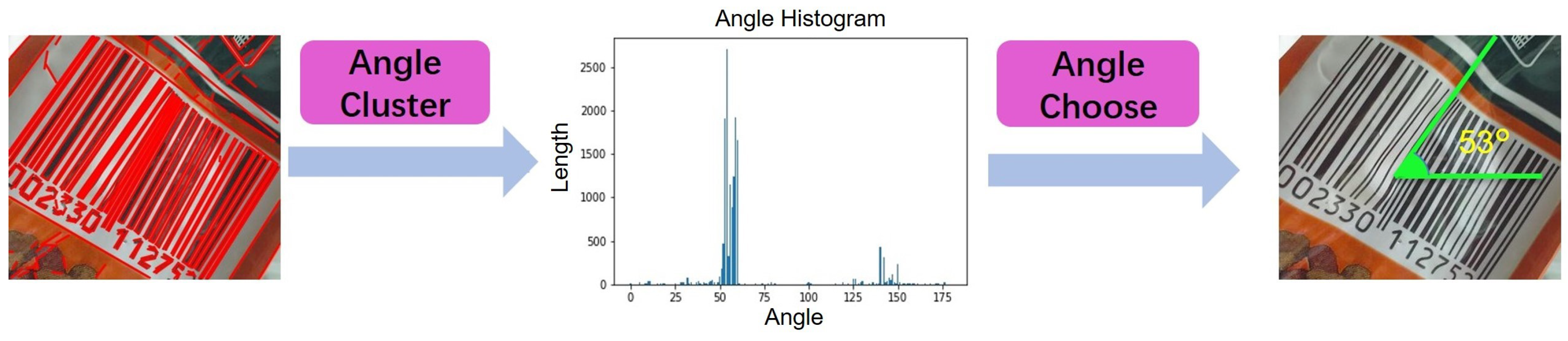
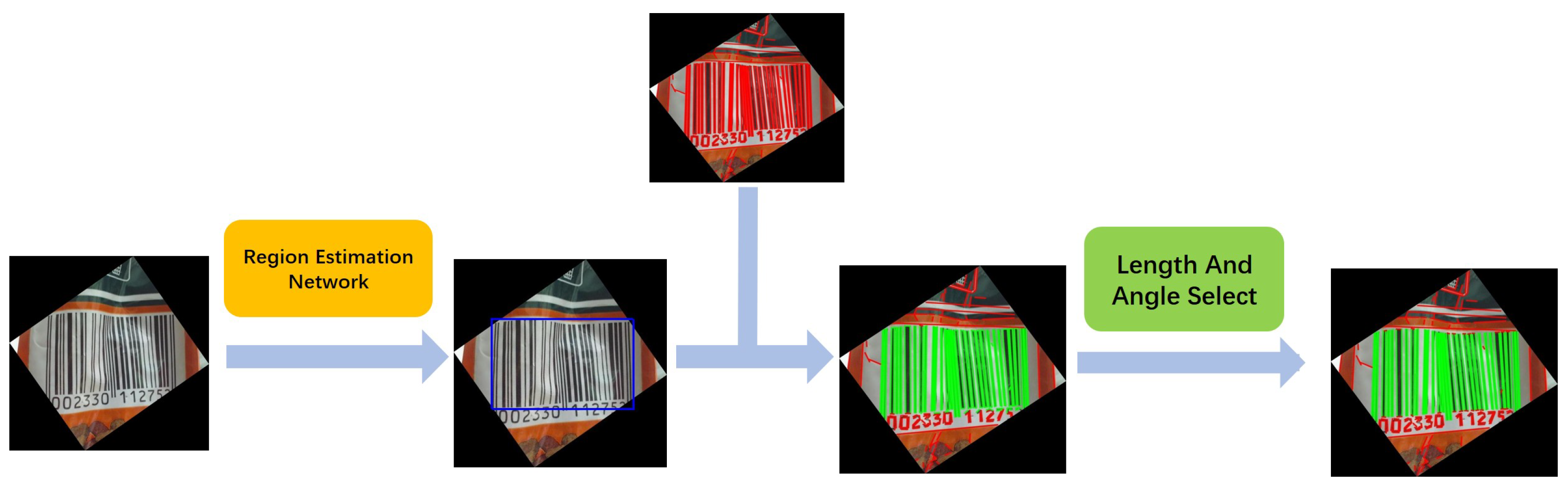
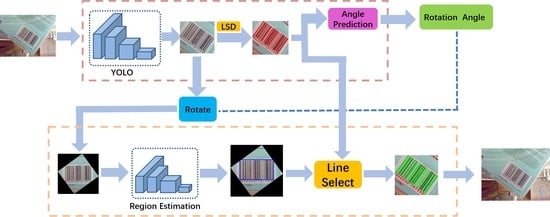
We consider that by incorporating deep-learning and geometric approaches, these problems will become easier to process. Through the fast parallel processing in deep-learning neural networks, geometric approaches help to improve the output accuracy. We propose a novel method in two-stages: barcode location and region extraction. Each stage is composed of a neural network and many geometric processes. The barcode location stage locates the bounding box of the 1D barcode using the YOLO object detection network and detects all line segments in the bounding box region using the LSD algorithm. Because the bars can be considered as a set of parallel line segments in a close distance, the rotation angle of the 1D barcode can be predicted by clustering all of the line segment angles and selecting the angle with the most line segments. Considering any line segments in an image also not belong to the 1D barcode, the region extraction stage processes the images cut from bounding boxes and proposes a selecting range for the line segments using the region estimation network. The final result is generated as a convex hull from the endpoints of the selected line segments. See an overview in
Figure 1.
During the entire process, there is no need to tune any manual parameters. All our approach requires is a standard dataset or some 1D barcode images for network training which can easily be gathered.
6. Experiment and Evaluation
In this section, we show how to process our experimental data, and present the results compared with previous 1D barcode detection methods [
2,
3,
4,
5,
6]. For comparison purposes, the detection rate
and average Jaccard index
are used as in [
2,
5]. A testing computer was used with an Intel Core i7-6600 3.50 GHz processor, 48 GB DDR4 memory, 500 GB SSD hard drive, and Nvidia GeForce Titan V with Ubuntu 16.04.2 LTS as the operating system.
6.1. Dataset and Date Processing
In our experiment, we used two 1D barcode datasets to measure the performance. The first dataset is the ArteLab Rotated Barcode dataset (referred to as Arte-Lab hereafter) with ground-truth provided by Zamberletti et al. [
5]. It contains 365 EAN (European Article Number) barcodes captured with different cellphones. The second dataset is the WWU Muenster Barcode Database (referred to as Muenster hereafter) provided by Wachenfeld et al. [
21]. It consists of 1055 EAN and UPC-A (Universal Product Code) barcodes captured with a Nokia N95 phone. The ground-truth is provided for 595 images [
3]. In this experiment, the image sizes of both datasets are 640 × 480.
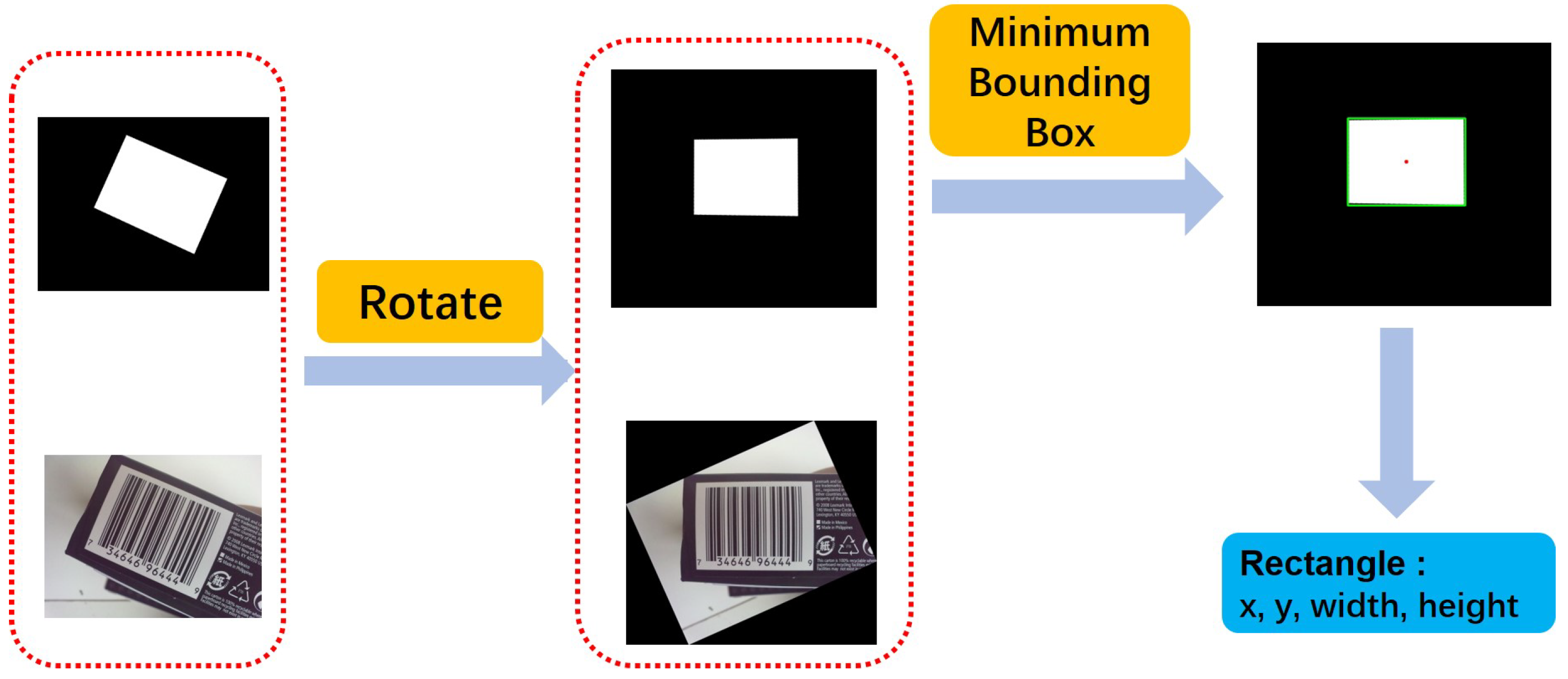
We prepared two kinds of data to train the object detection network and region estimation network. We obtained information about the bounding box from the mask image, which can be used to train the object detection network. The object detection network (YOLO) was modified to only find one class, 1D barcode.
Further data processing was necessary for the region estimation network. We cut the bounding box region individually and estimated the rotation angle of the 1D barcode with the approach in
Section 4. Then, we rotated it and generated a new image. We gathered the 1D barcode rectangle information from the mask image, which also was rotated in the same way as the source image. To train a robust model which can predict the barcode rectangle region in different scales, one-third of the images were not cut from bounding box region, but other processes continued operating.
Figure 4 shows an example. After the above processing, we fed the data to train the region estimation network.
We trained two networks with 80% random data in two datasets as the training set; the remaining data was used to test the training result. As a result of the constraints of GPU memory and the neural network model size, the batch size we set to 64, and the momentum to 0.9. The initial learning rate was set to 0.001, decreasing by 0.5 ratios in every 4000 steps or when the training loss value tended to be stable.
6.2. Evaluation Metrics
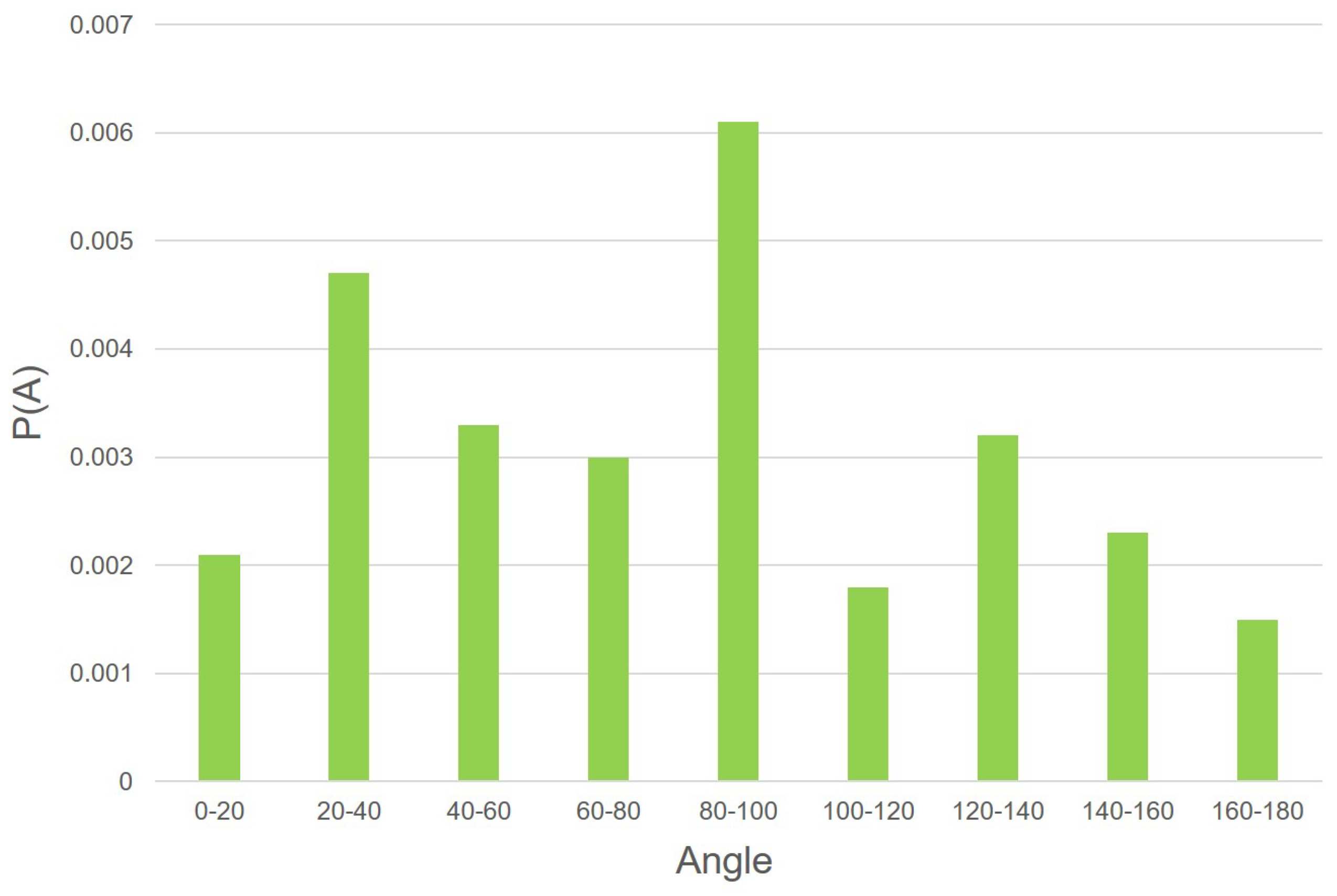
We measured the results of two stages. In the barcode location stage, we propose a novel method to predict the rotation angle. We prepared several images where the 1D barcode rotated with different angles and labeled their rotation angles manually as ground-truth. It was to make sure that the images could be decoded correctly when rotated in a labeled angle. Then, we tested those images in the barcode location stage by measuring the deviation of the predicted angle compared to the ground-truth. The angle deviation is defined as
where
A is the predicted angle,
is the ground-truth, and
is the deviation value. In this work, we measured it with 86 images at different angles, and the results can be seen in
Figure 5. For visual effect, we propose the average angle deviation every 20 degrees.
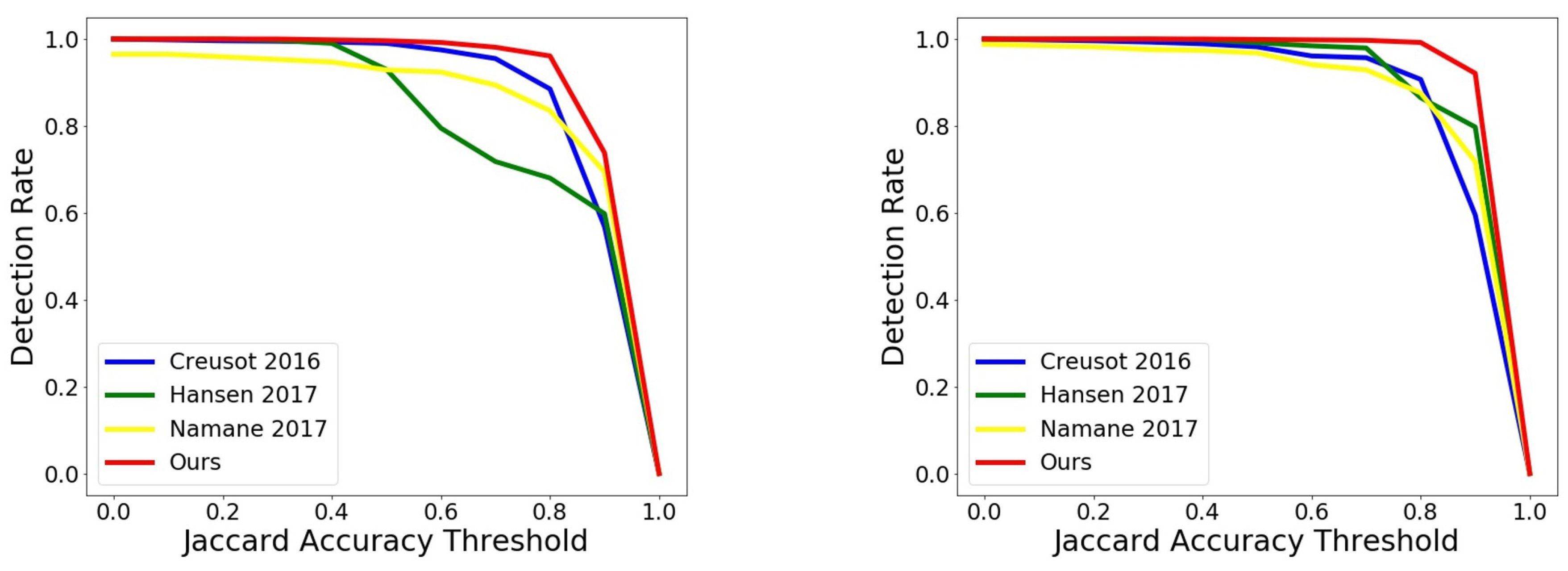
In the region extraction stage, since it gives the final result, we measured it using the same metric for result comparison as in [
5]. The main measurement aims at evaluating the Jaccard index between the ground-truth and the detection. Both the detection result
R and the ground-truth
G are given as binary masks over the whole image [
2]. The Jaccard index is defined as
is the average Jaccard accuracy over the dataset. The overall detection rate
corresponds to the proportion of the files in the dataset achieving at least 0.5 Jaccard accuracy (also called
in [
5]):
where
S is the set of files in the dataset. For completeness, we provide the detection for varying accuracy thresholds in steps of 0.1. The results for the two datasets compared with other methods can be seen in
Figure 6.
6.3. Results and Comparison
We compared the metrics, the accuracy
, and the detection rate
with previous works [
2,
3,
4,
5,
6] using two datasets: the ArteLab Rotated Barcode Dataset and the WWU Muenster Barcode Database. We collected the results that they report in articles and compared them to the results from our approach. The comparison results for the two datasets are shown in
Table 1 and
Table 2 (in [
3], the accuracy
is not reported). It can be seen that our method shows a noticeable improvement both in the accuracy
and the detention rate
. In particular, the accuracy
reaches a score higher than 0.9, which has not been achieved in the previous.
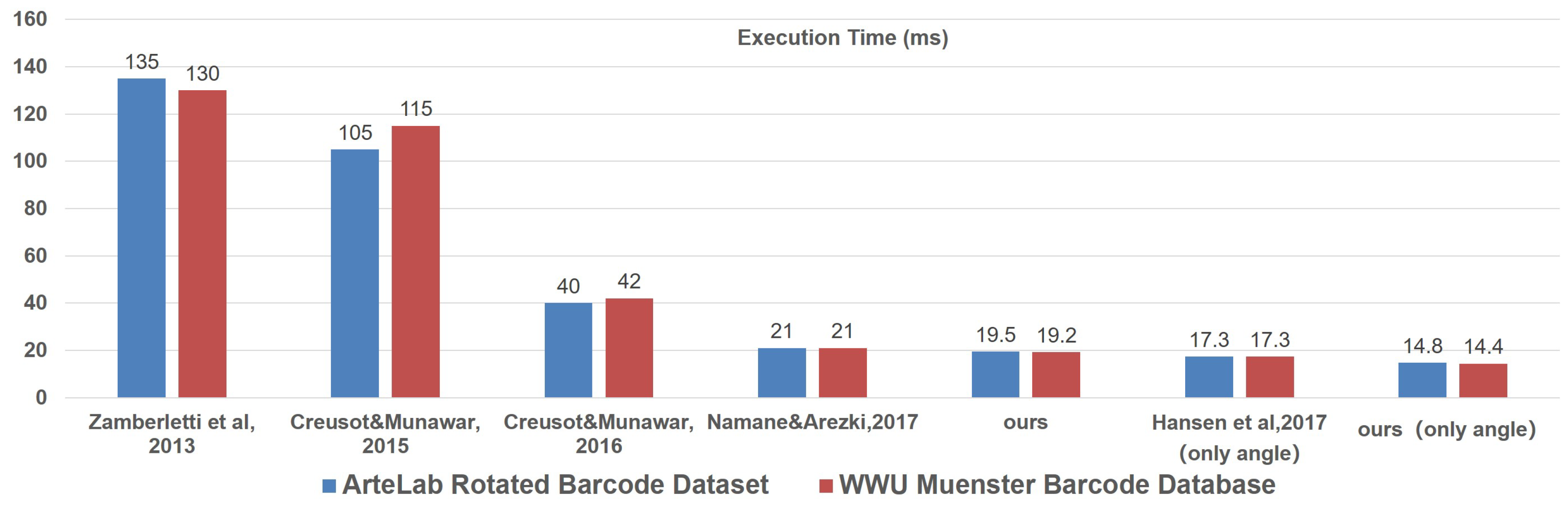
We also compared the speed, which is presented in
Figure 7. The barcode location stage took 14.8 ms for the 1D barcode region location and rotation angle prediction. Note that we performed the same task as Hansen et al. [
6] in terms of the barcode location stage but with a faster speed. The region extraction stage took 4.7 ms to propose an accurate 1D barcode region. The total process took 19.2 ms; this is also faster than the existing approaches mentioned above [
2,
3,
4,
5,
6].
Considering the 1D barcodes may be printed on soft packing surfaces, or packed in plastic film, which brings distortion, occlusion, and reflects light, we collected some images from the retail market using a phone camera to test whether our algorithm can overcome these harsh conditions. The results show that most 1D barcodes can still be captured precisely. The primary purpose of this test in a real-world scenario was to investigate the sensitivity of our approach; some 1D barcodes were not decoded successfully when they were serious distorted and/or occluded. We show some examples in
Figure 8.
7. Conclusions
In this work, we propose a novel two-stage method of 1D barcode detection. In the first stage, we use the YOLO object detection network to locate the position of the 1D barcode and detect all the line segments with the LSD algorithm in the bounding box region, where we predict the rotation angle using clustering line angles. In the second stage, we process the images cut from the bounding boxes and propose a selecting range for the line segments using the region estimation network. Finally, the line segments selected are used to generate a convex hull from the endpoints. We achieved state-of-the-art performance both in terms of accuracy and speed by combining the advantages of both the deep-learning model and geometric method. With no need to manually tune the parameters, this approach enjoys practicability, accuracy, and speed. We believe that our approach would be easily applied in practice and is applicable to all types of 1D barcodes.