Multi-Variable Thermal Modeling of Power Devices Considering Mutual Coupling
Abstract
:1. Introduction
2. Thermal Models in a Boost Converter System
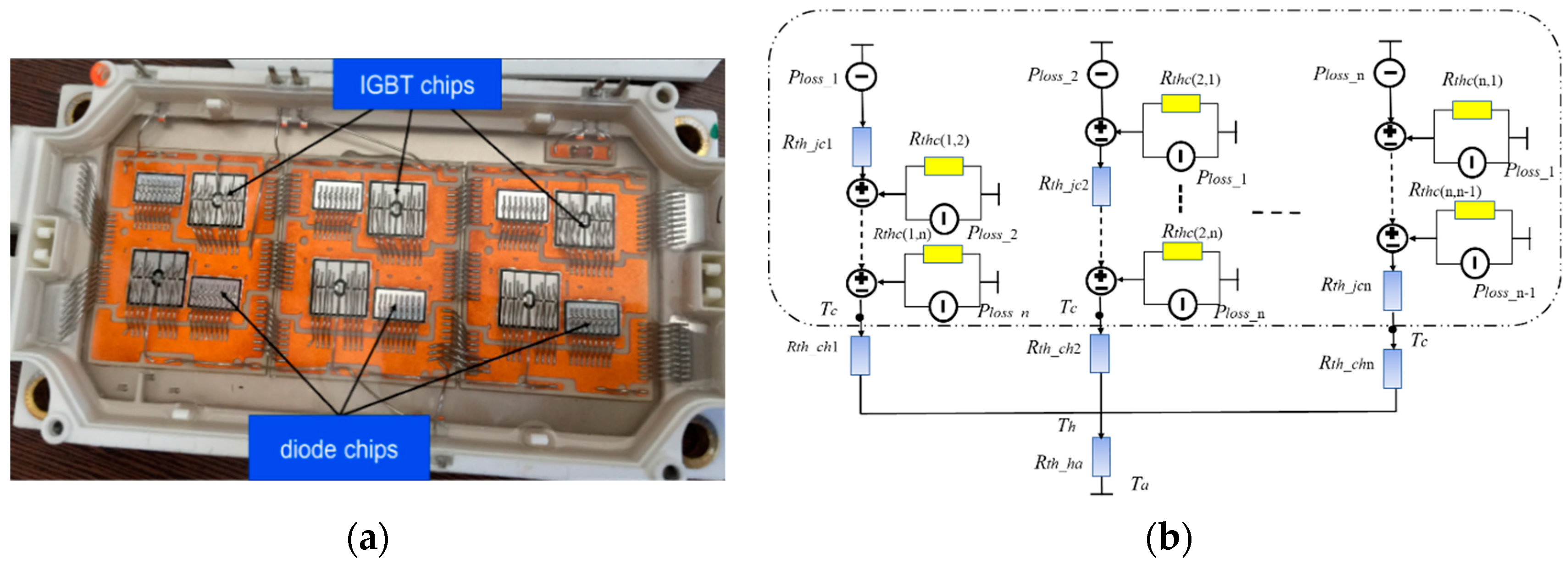
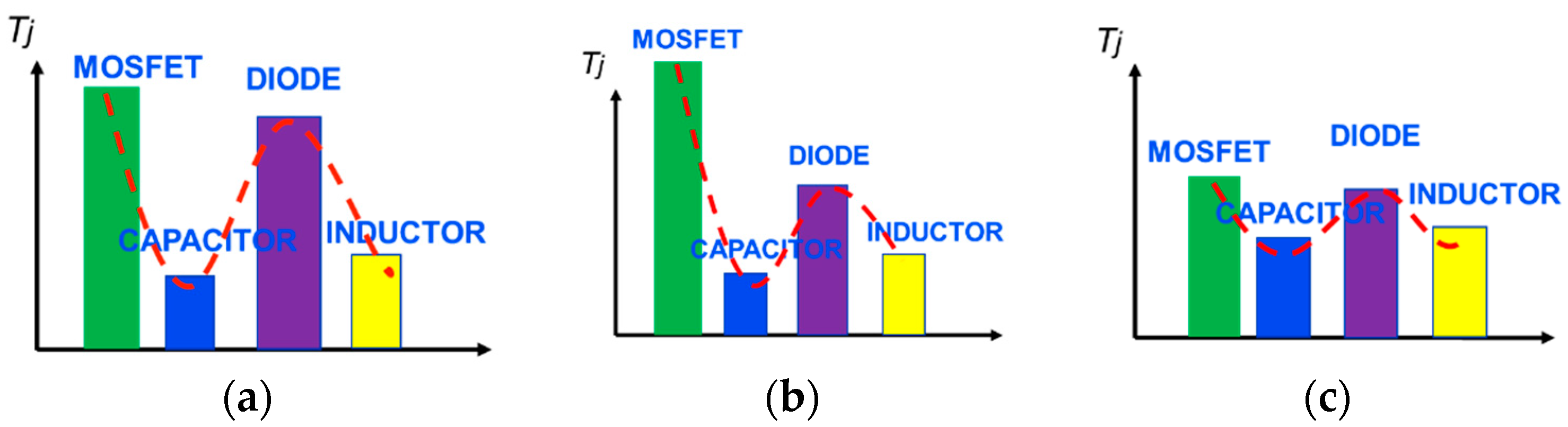
3. Thermal Coupling of Power Components
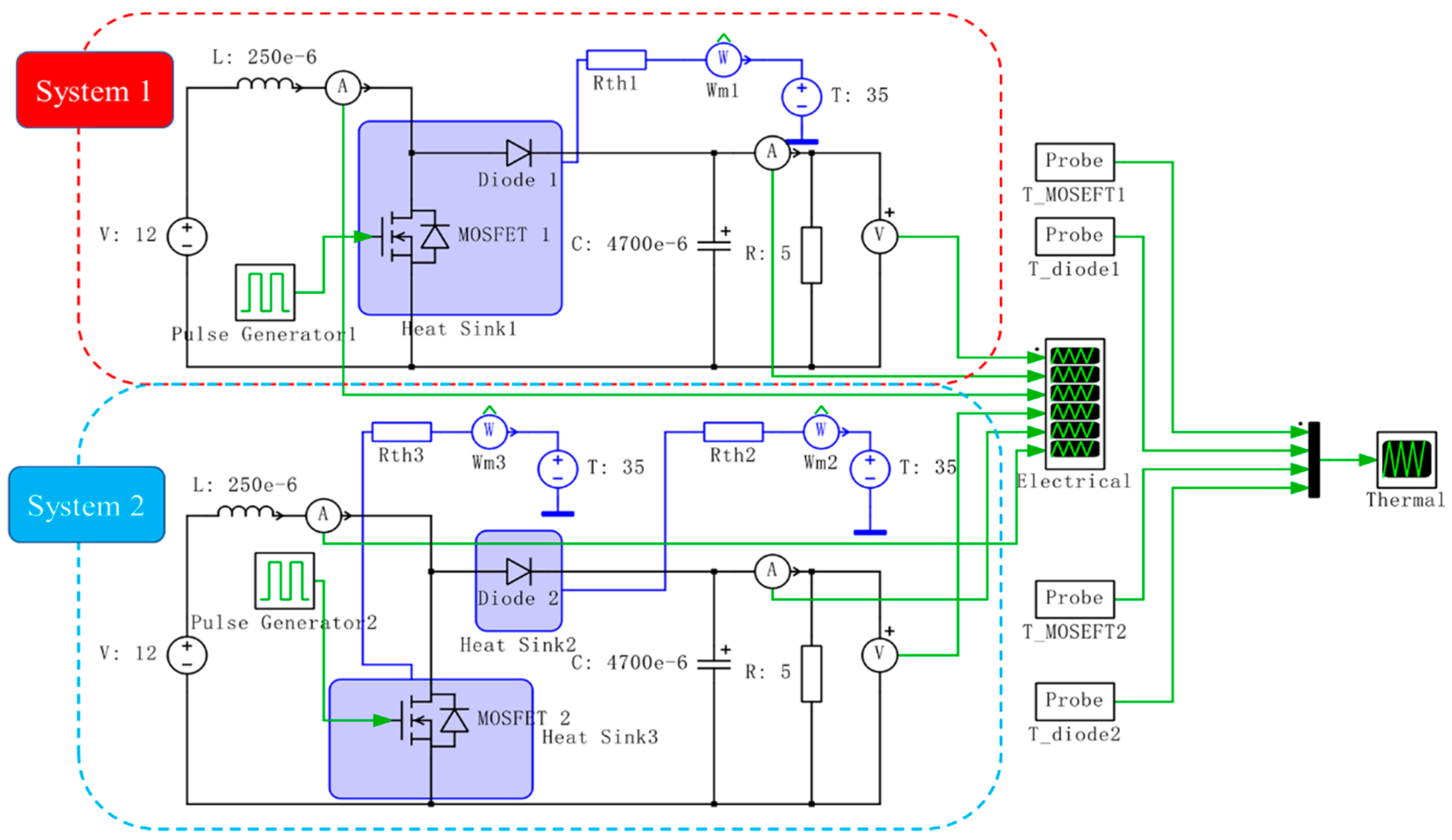
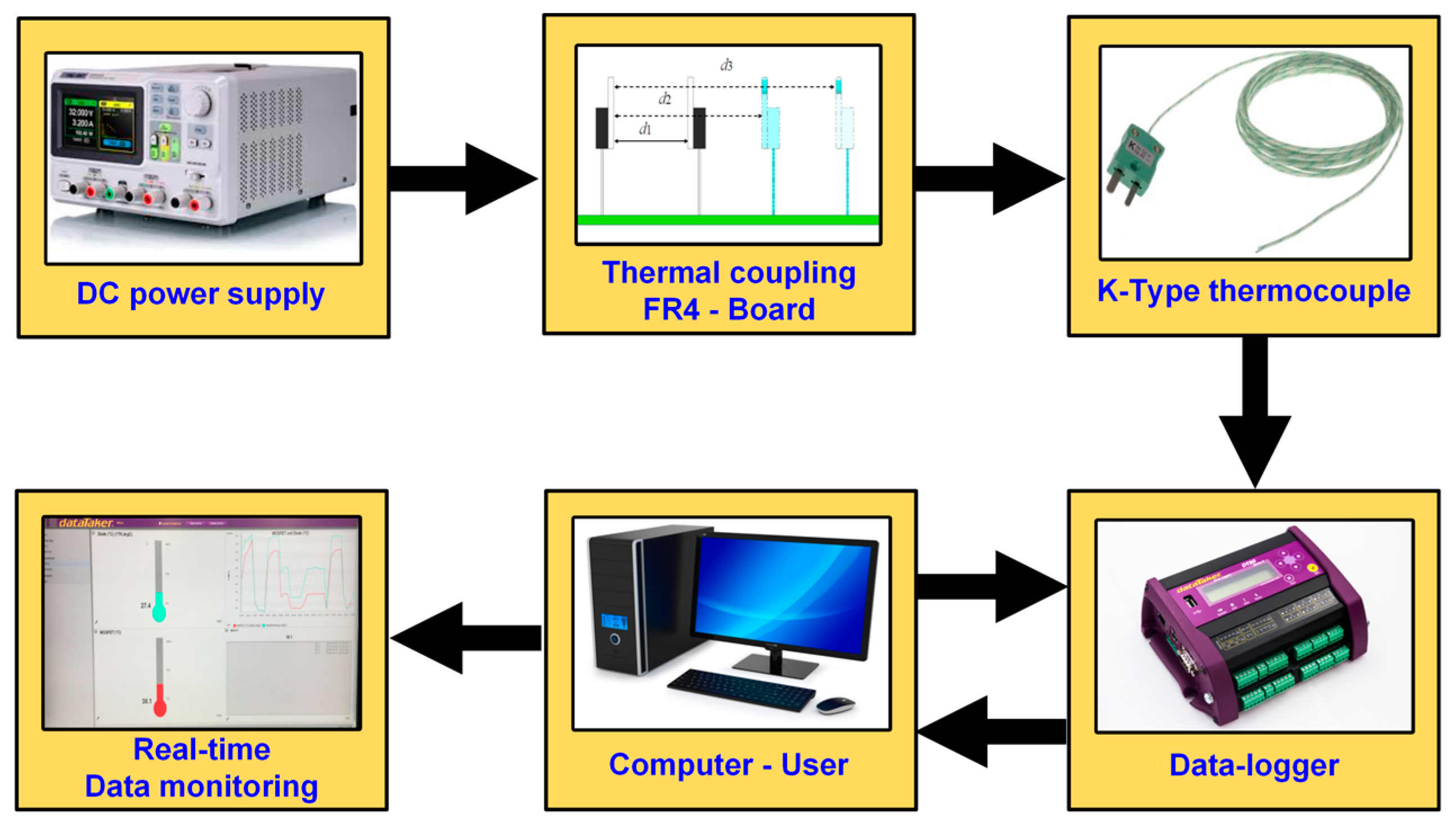
3.1. The Experimental Platform
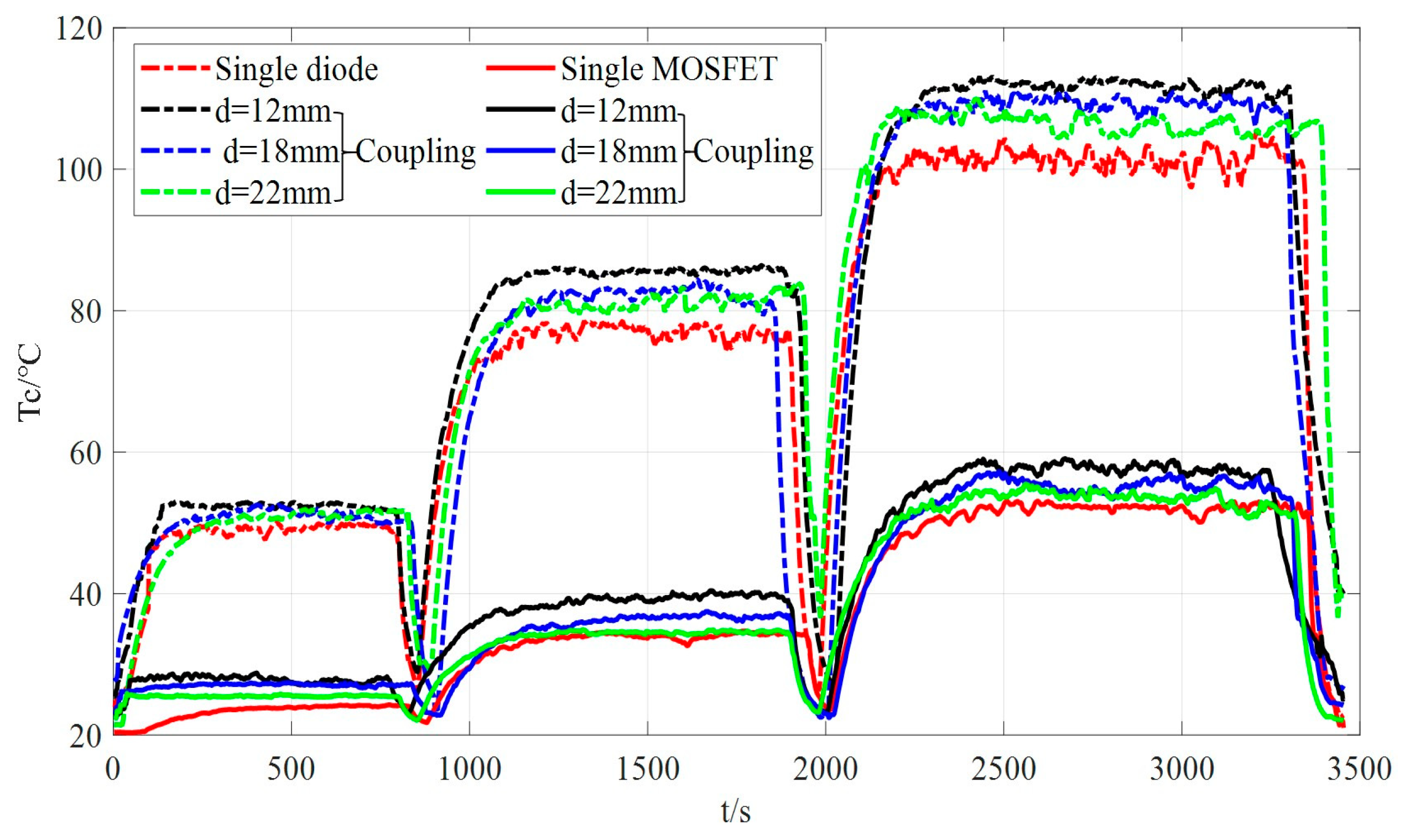
3.2. Losses Calculation and Tc Comparisons
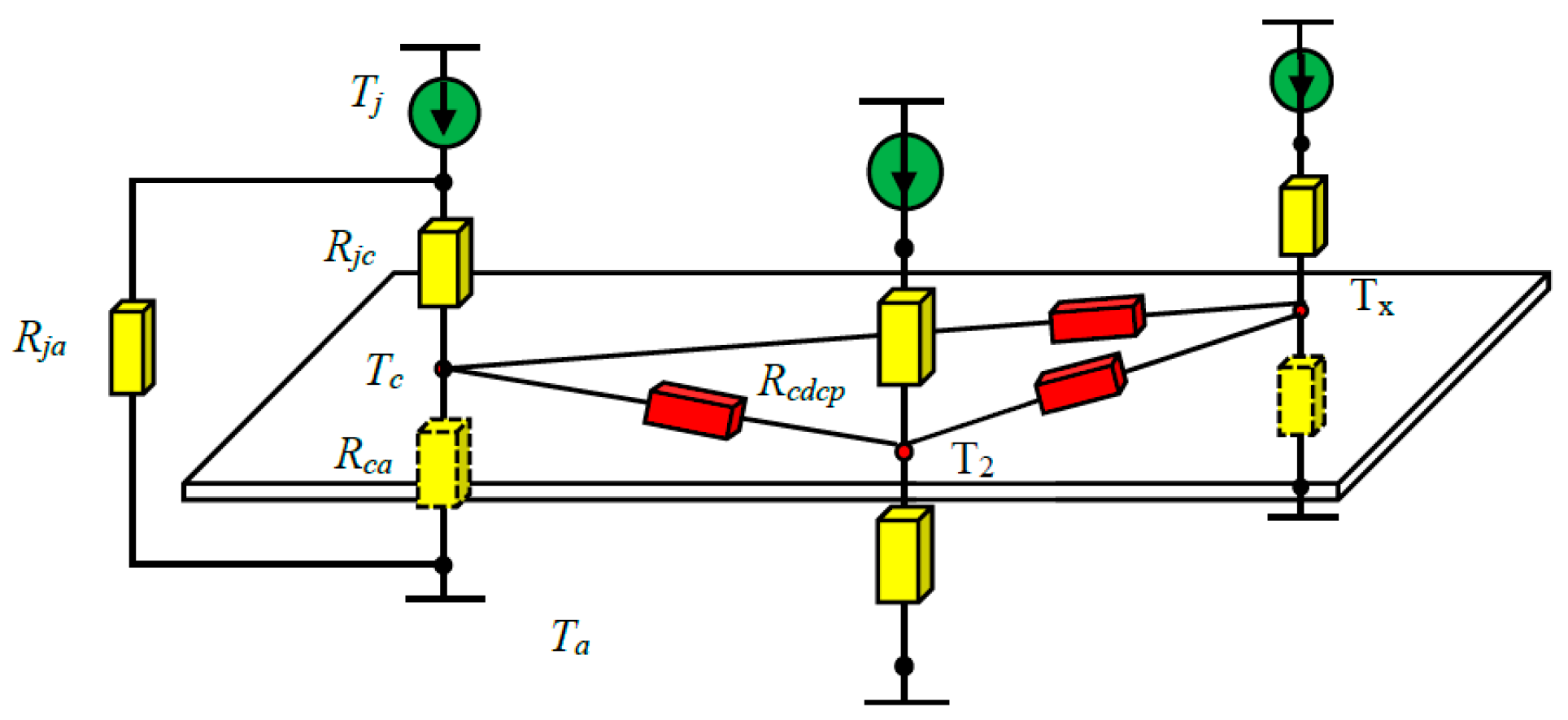
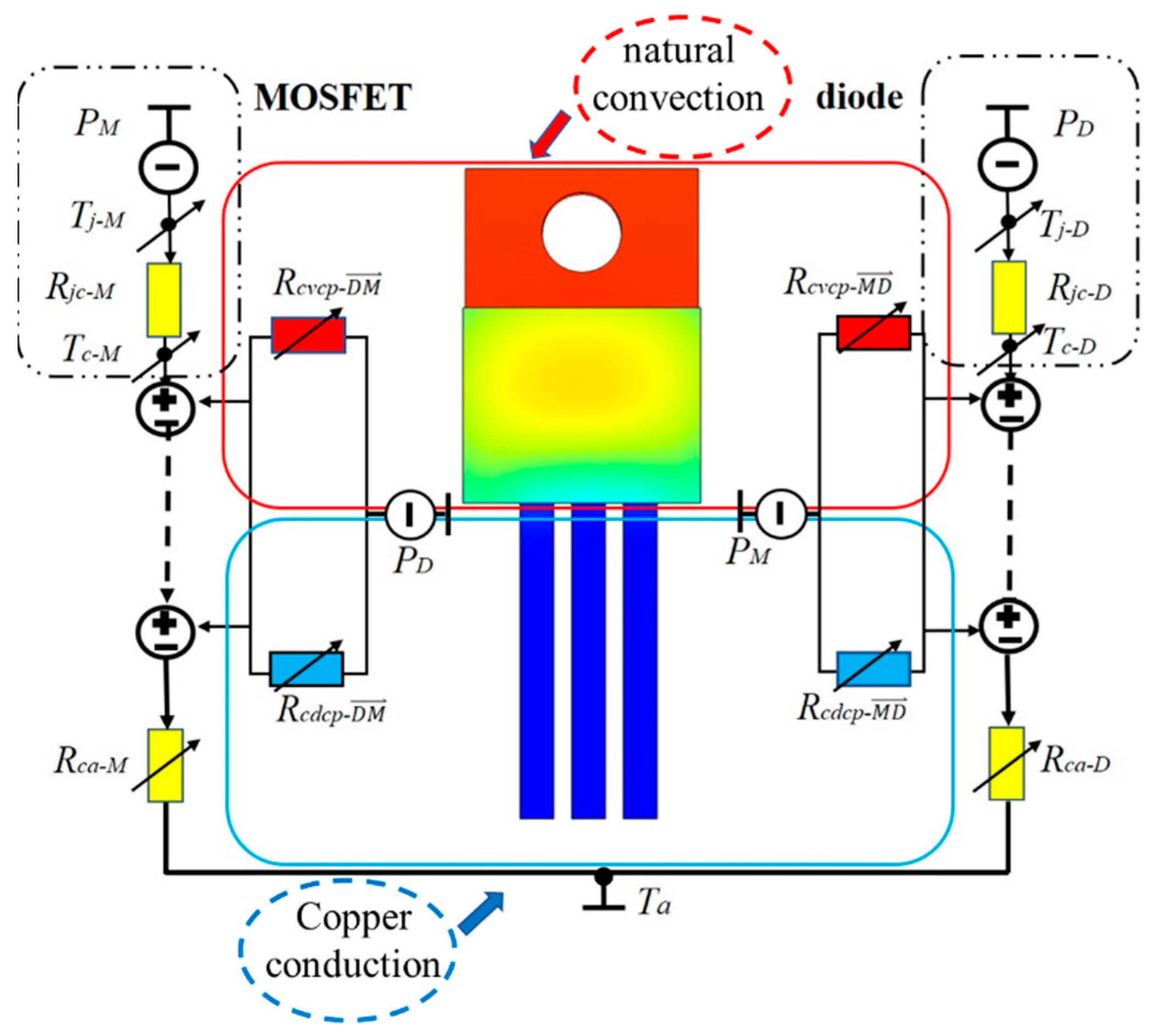
4. Multi-Variable Thermal Resistances Network Modeling
4.1. Thermal Resistances Network
4.2. Self-Resistances Calculation
4.3. Thermal Coupling Resistances Calculation
4.4. Relationships
- (1)
- The values of and increase when the distance between power components increases, which means the coupling effect decreases when the separation distances increase, and vice versa.
- (2)
- The values of and decrease when the working currents increase, which means the coupling effect increases when the currents increase, and vice versa.
- (3)
- and have decreasing trends when the currents increase and the distances decrease, which means the coupling effect increases when the devices are brought closer with higher current magnitude, and vice versa.
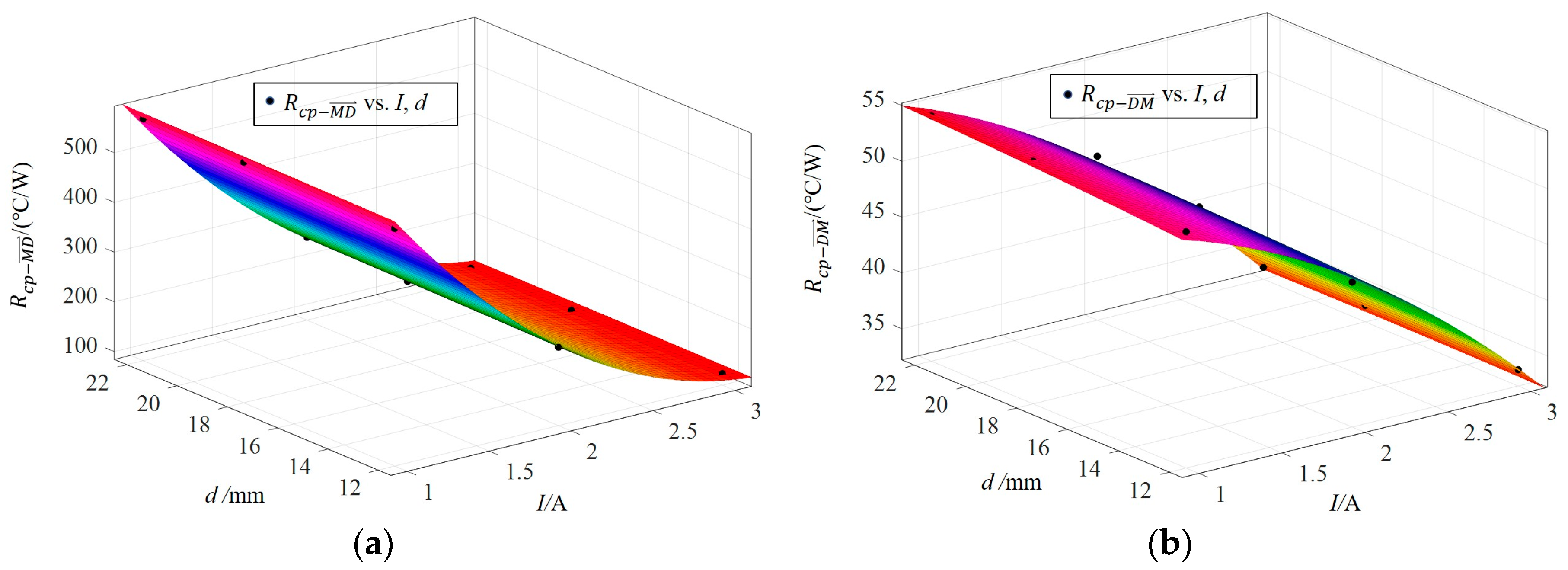
4.5. Rcp Calculation
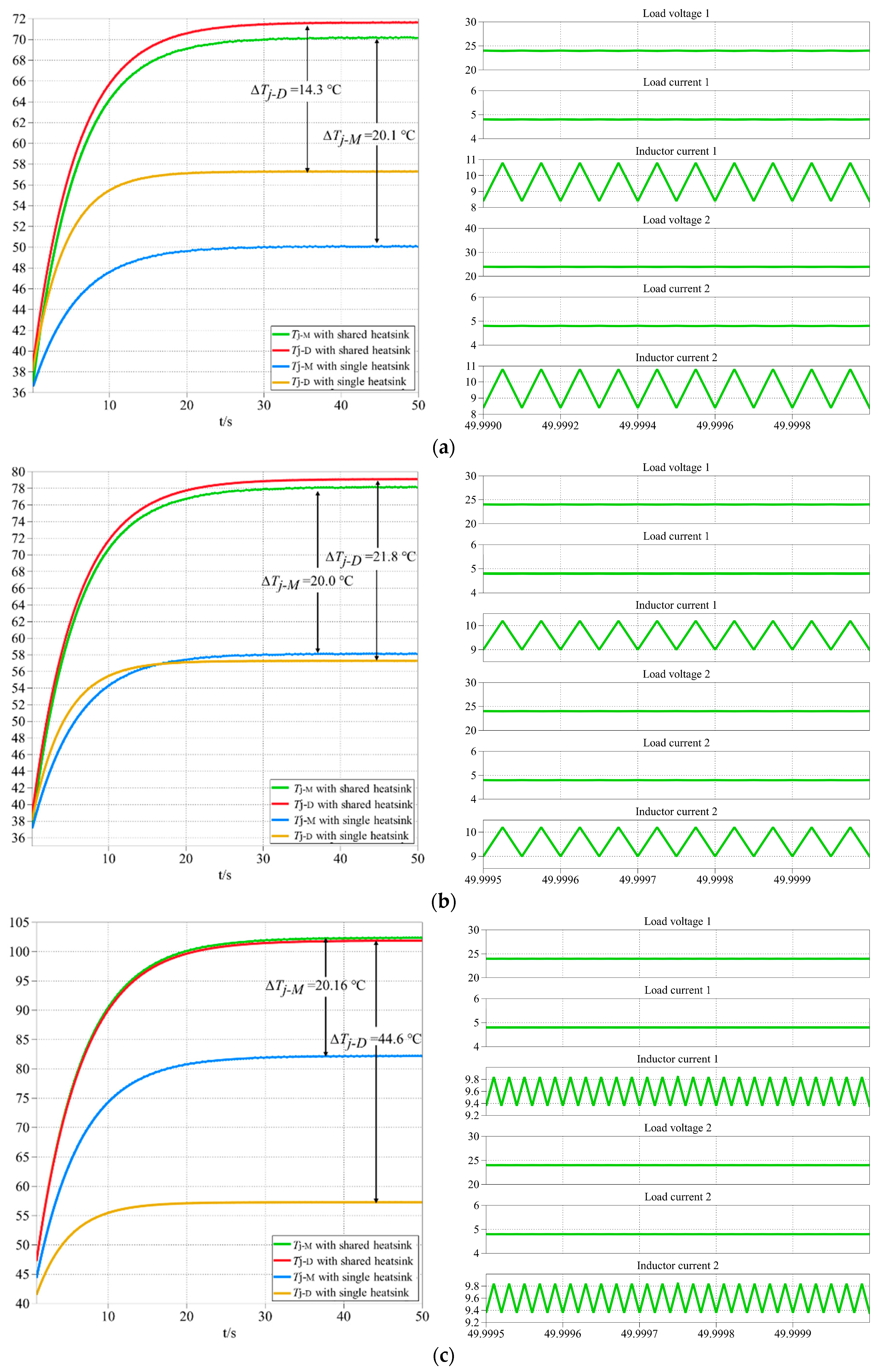
5. Verifications
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gautam, D.; Wager, D.; Musavi, F.; Edington, M.; Eberle, W.; Dunford, W.G. A review of thermal management in power converters with thermal vias. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013. [Google Scholar]
- Hasan, A.; Hejase, H.; Abdelbaqi, S.; Assi, A.; Hamdan, M. Comparative effectiveness of different phase change materials to improve cooling performance of heat sinks for electronic devices. Appl. Sci. 2016, 6, 226. [Google Scholar] [CrossRef]
- Natarajan, S.; Ha, M.; Graham, S. Measuring the thermal resistance in light emitting diodes using a transient thermal analysis technique. IEEE Trans. Electron Devices 2013, 60, 2548–2555. [Google Scholar] [CrossRef]
- Wei, K.; Wang, W.; Hu, Z.; Du, M. Condition Monitoring of IGBT Modules Based on Changes of Thermal Characteristics. IEEE Access 2019, 7, 47525–47534. [Google Scholar] [CrossRef]
- Hanini, W.; Ayadi, M. Electro thermal modeling of the power diode using Pspice. Microelectron. Reliab. 2018, 86, 82–91. [Google Scholar] [CrossRef]
- Davidson, J.; Stone, D.; Foster, M. Required Cauer network order for Modeling of thermal transfer impedance. Electron. Lett. 2014, 50, 260–262. [Google Scholar] [CrossRef]
- Luo, Z.; Ahn, H.; Nokali, M. A thermal model for insulated gate bipolar transistor module. IEEE Trans. Power Electron. 2004, 19, 902–907. [Google Scholar] [CrossRef]
- Li, H.; Liao, X.; Zeng, Z.; Hu, Y.; Li, Y.; Liu, S.; Ran, L. Thermal Coupling Analysis in a Multichip Paralleled IGBT Module for a DFIG Wind Turbine Power Converter. IEEE Trans. Energy Convers. 2017, 32, 80–90. [Google Scholar] [CrossRef]
- Reichl, J.; Ortiz-Rodriguez, J.M.; Hefner, A.; Lai, J.S. 3-D thermal component model for electrothermal analysis of multichip power modules with experimental validation. IEEE Trans. Power Electron. 2015, 30, 3300–3308. [Google Scholar] [CrossRef]
- Bernardoni, M.; Cova, P.; Delmonte, N.; Menozzi, R. Heat management for power converters in sealed enclosures: A numerical study. Microelectron. Reliab. 2009, 49, 1293–1298. [Google Scholar] [CrossRef]
- Lu, H.L.; Lu, Y.J.; Zhu, L.H.; Lin, Y.; Guo, Z.Q.; Liu, T.; Chen, Z. Efficient measurement of thermal coupling effects on multichip light-emitting diodes. IEEE Trans. Power Electron. 2017, 32, 9280–9292. [Google Scholar] [CrossRef]
- Bahman, S.A.; Ma, K.; Blaabjerg, F. A Lumped Thermal Model Including Thermal Coupling and Thermal Boundary Conditions for High-Power IGBT Modules. IEEE Trans. Power Electron. 2018, 33, 2518–2530. [Google Scholar] [CrossRef]
- Pepper, D. The Intermediate Finite Element Method: Fluid Flow and Heat Transfer Applications; Routledge: Abingdon-on-Thames, UK; London, UK, 2017. [Google Scholar]
- De Jong, W.C.E.; Ferreira, J.A.; Bauer, P. Thermal design based on surface temperature mapping. IEEE Power Electron. Lett. 2005, 3, 125–129. [Google Scholar] [CrossRef]
- De Jong, W.C.E.; Ferreira, J.A.; Bauer, P. Design techniques for thermal management in switch mode converters. IEEE Trans. Ind. Appl. 2006, 42, 1375–1386. [Google Scholar] [CrossRef]
- Marz, M. Thermal management in high-density power converters. IEEE Int. Conf. Ind. Technol. 2003, 2, 1196–1201. [Google Scholar]
- Wanes, J. A novel integrated packaging technique for high density DC-DC converters providing enhanced efficiency and thermal management. In Proceedings of the Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 22–26 February 2004. [Google Scholar]
- Haque, S.; Xing, K.; Suchicital, C.; Nelson, D.J.; Lu, G.Q.; Borojevic, D.; Lee, F.C. Thermal management of high-power electronics modules packaged with interconnected parallel plates. Fourteenth Annu. IEEE Semicond. Therm. Meas. Manag. Symp. 1998, 1195, 111–119. [Google Scholar]
- Vermeersch, B.; De Mey, G. Dependency of thermal spreading resistance on convective heat transfer coefficient. Microelectron. Reliab. 2008, 48, 734–738. [Google Scholar] [CrossRef]
- Laloya, E.; Lucia, O.; Sarnago, H.; Burdio, J.M. Heat management in power converters: From state of the art to future ultrahigh efficiency systems. IEEE Trans. Power Electron. 2016, 31, 7896–7908. [Google Scholar] [CrossRef]
- De Jong, W.C.E.; Ferreira, B.J.; Bauer, P. Toward the next level of PCB usage in power electronic converters. IEEE Trans. Power Electron. 2008, 23, 3151–3163. [Google Scholar] [CrossRef]
- Bulut, Y.; Pandya, K. Thermal modeling for power MOSFETs in DC/DC applications. In Proceedings of the 5th International Conference on Thermal and Mechanical Simulation and Experiments in Microelectronics and Microsystems, Brussels, Belgium, 10–12 May 2004. [Google Scholar]
- Biweta, M.; Mamo, M. Closed loop control strategy of back to back PWM converter fed by PMSG using PLECS toolbox on Matlab/Simulink for wind energy application. In Proceedings of the 2017 IEEE AFRICON, Cape Town, South Africa, 18–20 September 2017. [Google Scholar]
- Lai, W.; Zhao, Y.; Chen, M.; Wang, Y.; Ding, X.; Xu, S.; Pan, L. Condition Monitoring in a Power Module Using On-State Resistance and Case Temperature. IEEE Access 2018, 6, 67108–67117. [Google Scholar] [CrossRef]
- Rodriguez, R.; Alizadeh, M.; Bauman, J.; Ravi, P.S.; Emadi, A. Performance Evaluation of Thermal Management for a 3-Phase Interleaved DC-DC Boost Converter. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo (ITEC), Long Beach, CA, USA, 13–15 June 2018. [Google Scholar]
- Kulkarni, A.; John, V. Thermal model for paralleled surface-mount power MOSFETs. In Proceedings of the 2014 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Mumbai, India, 16–19 December 2014. [Google Scholar]
- Kim, T.; Jang, M.; Agelidis, V.G. Practical implementation of a silicon carbide-based 300 kHz, 1.2 kW hard-switching boost-converter and comparative thermal performance evaluation. IET Power Electron. 2014, 8, 333–341. [Google Scholar] [CrossRef]
- Graovac, D.; Purschel, M.; Kiep, A. MOSFET Power Losses Calculation Using the Data-Sheet Parameters, Infineon application note; Neubiberg, Germany, 2006.
- Ren, Y.; Xu, M.; Zhou, J.; Lee, F.C. Analytical loss model of power MOSFET. IEEE Trans. Power Electron. 2006, 21, 310–319. [Google Scholar]
- Semiconductor, F. IRF540N Datasheet; IR World Headquarters: El Segundo, CA, USA, 2002. [Google Scholar]
- Wang, Y.; Ao, J.; Liu, S.; Hao, Y. Thermal Modeling of the GaN-based Gunn Diode at Terahertz Frequencies. Appl. Sci. 2019, 9, 75. [Google Scholar] [CrossRef]
- Taler, J. Superposition method for multidimensional heat conduction problems. Encycl. Therm. Stresses 2014, 4708–4718. [Google Scholar] [CrossRef]
- Cheng, J.; He, X.; Li, X.; Zhou, B.; Bao, H.; Zhou, L.; Wang, Z. Thermal coupling effects and thermal resistance matrix research of multi-heat sources MCM. In Proceedings of the 2014 International Conference on Reliability, Maintainability and Safety (ICRMS), Guangzhou, China, 6–8 August 2014. [Google Scholar]
- Sofia, J.W. Electrical Thermal Resistance Measurements for Hybrids and Multi-Chip Packages; Application notes; Analysis Tech.: Wakefield, MA, USA, 1990. [Google Scholar]




| d [mm] | I [A] | Tc-M [°C] | Tc-D [°C] |
|---|---|---|---|
| 12 | 1 | 28.22 | 52.94 |
| 2 | 39.72 | 84.91 | |
| 3 | 58.27 | 111.45 | |
| 18 | 1 | 26.87 | 51.85 |
| 2 | 36.39 | 82.57 | |
| 3 | 55.21 | 108.42 | |
| 22 | 1 | 25.81 | 50.89 |
| 2 | 34.56 | 81.45 | |
| 3 | 53.71 | 106.95 |
| d [mm] | I [A] | Rca-M [°C/W] | Rca-D [°C/W] |
|---|---|---|---|
| 12 | 1 | 69.32 | 60.39 |
| 2 | 62.73 | 58.89 | |
| 3 | 61.76 | 54.35 | |
| 18 | 1 | 69.32 | 60.39 |
| 2 | 62.73 | 58.89 | |
| 3 | 61.76 | 54.35 | |
| 22 | 1 | 69.32 | 60.39 |
| 2 | 62.73 | 58.89 | |
| 3 | 61.76 | 54.35 |
| d [mm] | I [A] | [°C/W] | [°C/W] |
|---|---|---|---|
| 12 | 1 | 53.39 | 561.82 |
| 2 | 45.19 | 241.66 | |
| 3 | 33.66 | 107.43 | |
| 18 | 1 | 53.95 | 567.73 |
| 2 | 46.18 | 246.95 | |
| 3 | 33.68 | 107.50 | |
| 22 | 1 | 54.17 | 570.00 |
| 2 | 46.89 | 250.75 | |
| 3 | 33.25 | 107.56 |
| d | I | Coupling Effect | ||
|---|---|---|---|---|
| ↑ | - | ↑ | ↑ | ↓ |
| ↓ | - | ↓ | ↓ | ↑ |
| - | ↑ | ↓ | ↓ | ↑ |
| - | ↓ | ↑ | ↑ | ↓ |
| ↓ | ↑ | ↓ | ↓ | ↑ |
| ↑ | ↓ | ↑ | ↑ | ↓ |
| I (A) | Tc-M (°C) | (°C/W) (Calculation) | (°C/W) (Experimental Data) | Error (%) |
|---|---|---|---|---|
| 1 | 27.32 | 563.97 | 542.95 | 3.87 |
| 2 | 37.66 | 244.88 | 241.50 | 1.40 |
| 3 | 56.85 | 106.90 | 107.54 | 0.60 |
| I (A) | Tc-D (°C) | (°C/W) (Calculation) | (°C/W) (Experimental Data) | Error (%) |
|---|---|---|---|---|
| 1 | 51.21 | 53.50 | 51.60 | 3.68 |
| 2 | 82.82 | 45.90 | 45.16 | 1.64 |
| 3 | 110.08 | 33.50 | 34.79 | 3.71 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, K.; Cheng, T.; Lu, D.D.-C.; Siwakoti, Y.P.; Zhang, C. Multi-Variable Thermal Modeling of Power Devices Considering Mutual Coupling. Appl. Sci. 2019, 9, 3240. https://doi.org/10.3390/app9163240
Wei K, Cheng T, Lu DD-C, Siwakoti YP, Zhang C. Multi-Variable Thermal Modeling of Power Devices Considering Mutual Coupling. Applied Sciences. 2019; 9(16):3240. https://doi.org/10.3390/app9163240
Chicago/Turabian StyleWei, Kaixin, Tian Cheng, Dylan Dah-Chuan Lu, Yam P. Siwakoti, and Chengning Zhang. 2019. "Multi-Variable Thermal Modeling of Power Devices Considering Mutual Coupling" Applied Sciences 9, no. 16: 3240. https://doi.org/10.3390/app9163240
APA StyleWei, K., Cheng, T., Lu, D. D.-C., Siwakoti, Y. P., & Zhang, C. (2019). Multi-Variable Thermal Modeling of Power Devices Considering Mutual Coupling. Applied Sciences, 9(16), 3240. https://doi.org/10.3390/app9163240






