Reinforced Concrete Slab Optimization with Simulated Annealing
Abstract
Featured Application
Abstract
1. Introduction
2. Structural Model
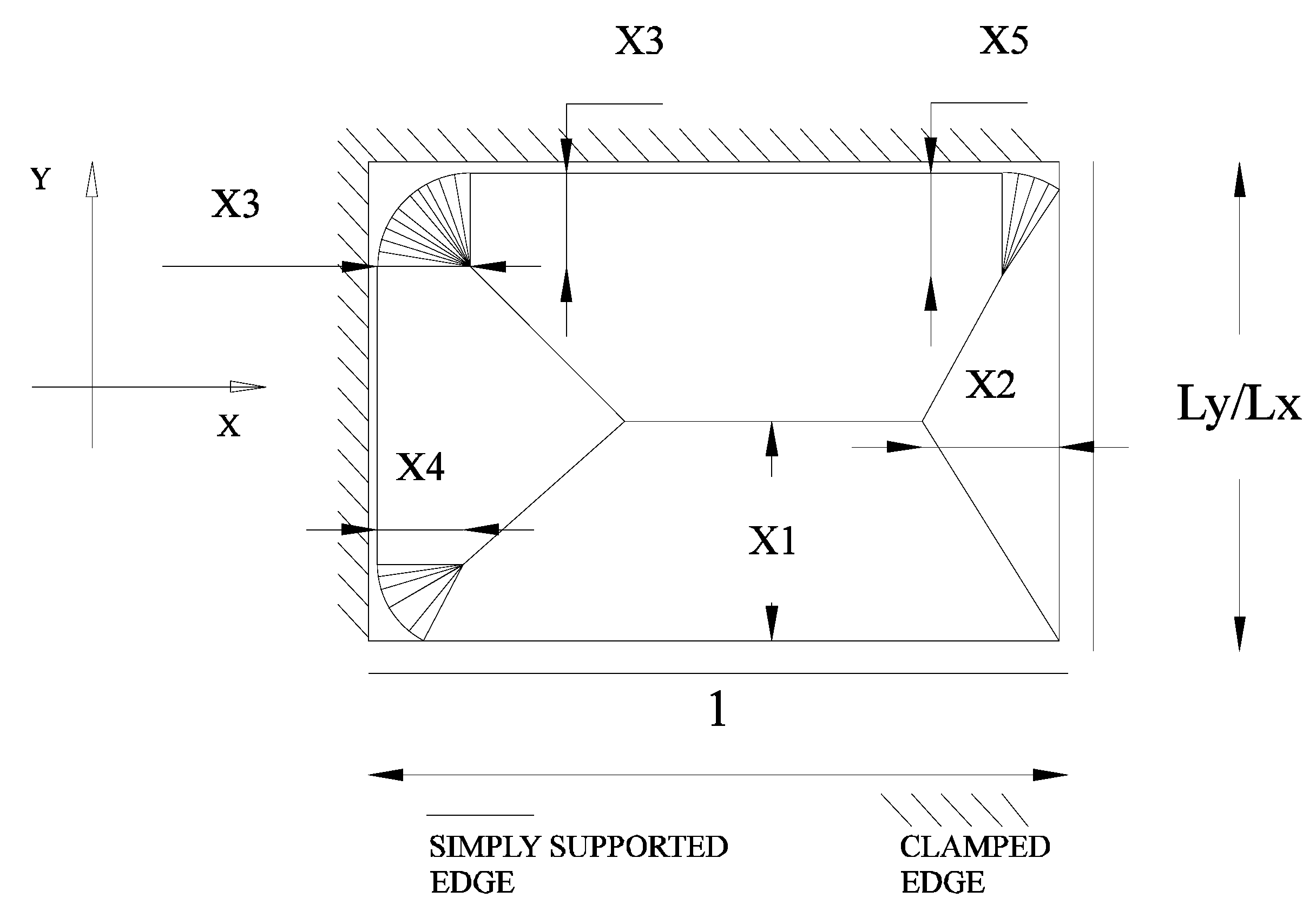
2.1. Problem Definition
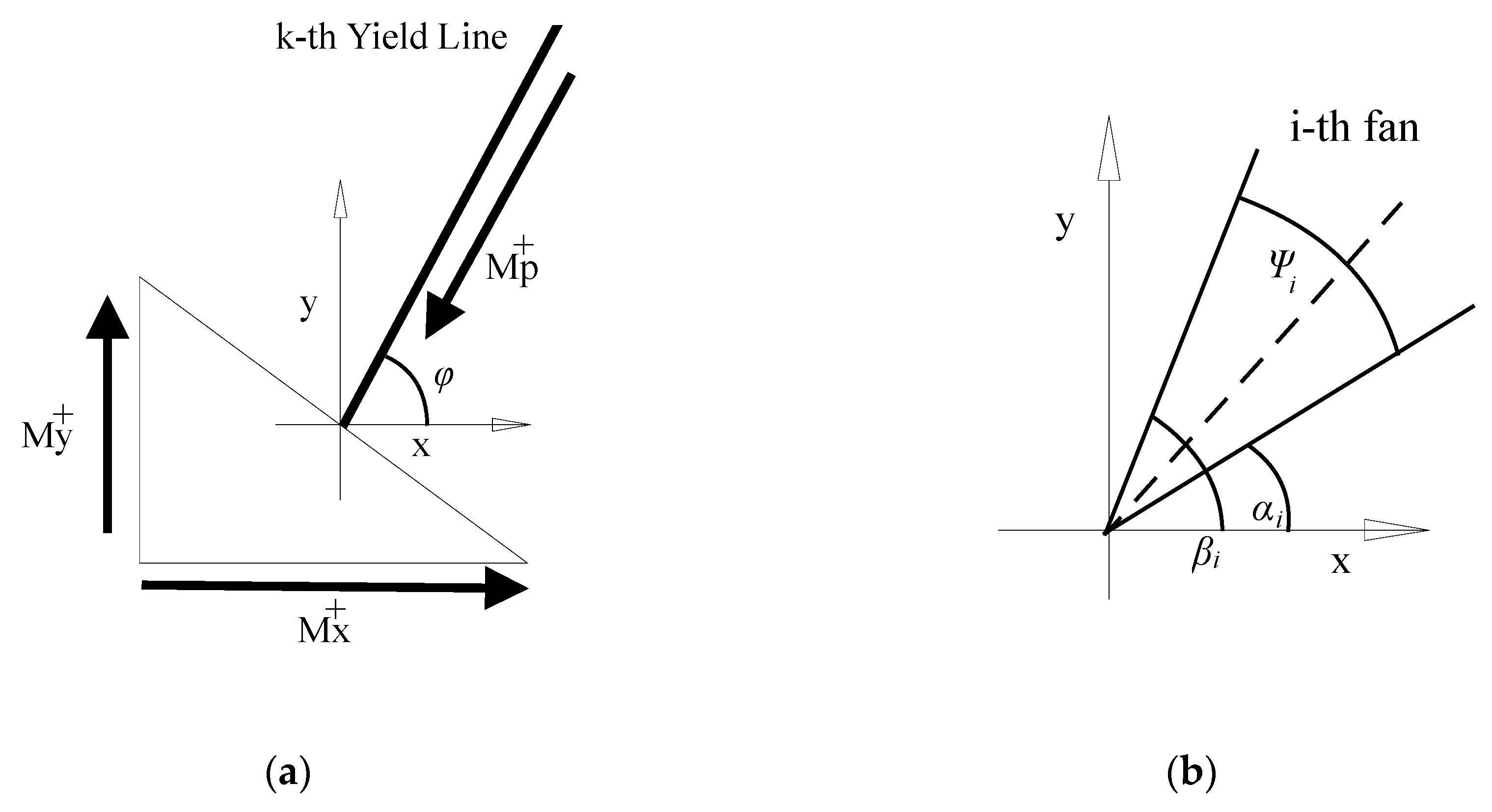
2.2. Yield Line Method
- The materials present a plastic constitutive law.
- Plastic deformations are located only along hinge lines.
- Hinge lines are always straight lines.
- (1)
- Taking into account the geometrical, constraint and load characteristics of the slab, one or more families of possible failure mechanisms are determined. Each family is defined by a certain number of geometric parameters that can express the ultimate load as a scalar function of the same parameters .
- (2)
- Enforcing the kinematic limit analysis theorem, the failure mechanism corresponding to the smallest limit load is identified for each mechanism family. The smallest value among the loads of each family will be the collapse load of the slab.
2.3. Internal Work
2.3.1. Yield Line Internal Work
2.3.2. Fan Internal Work
2.4. External Work
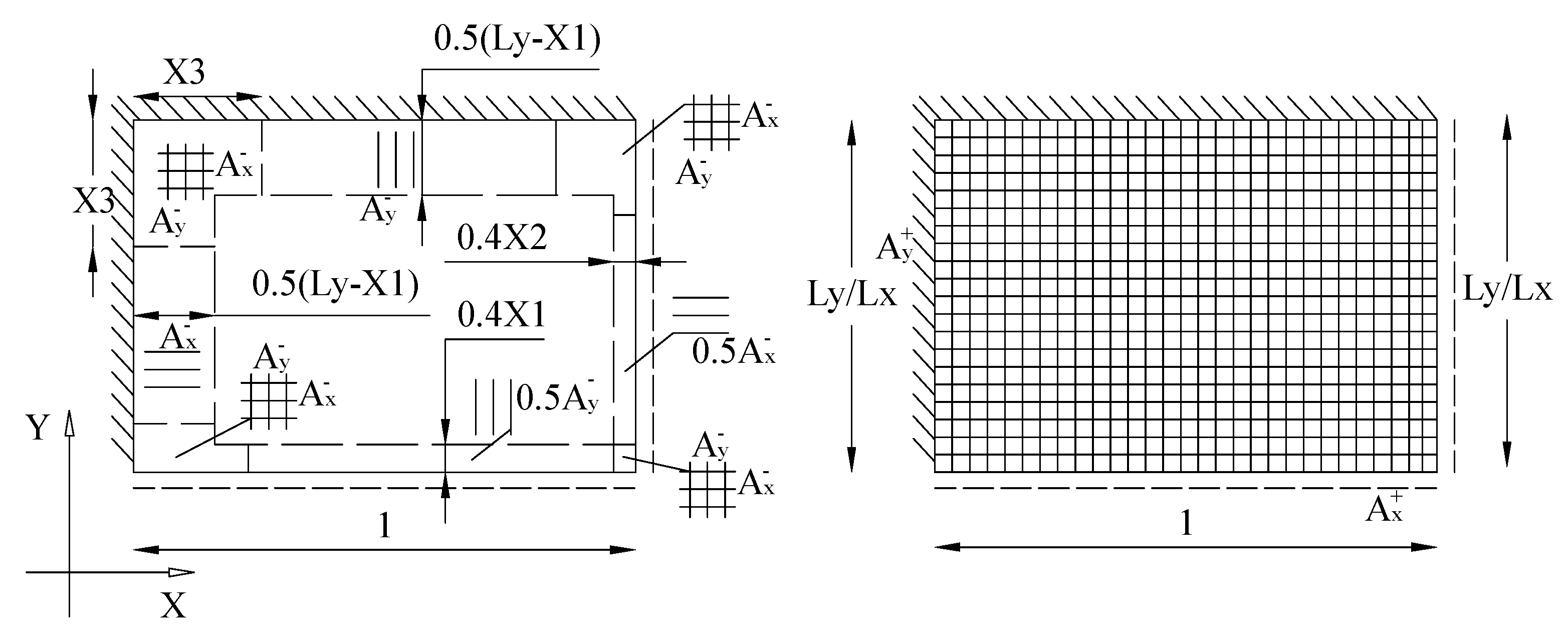
2.5. Reinforcement Arrangement Optimization
2.6. Slab Cost Optimization
- Input of geometrical characteristics and boundary conditions.
- Expression of the collapse mechanism and definition of collapse load (Equation (20)) as a function of the mechanism parameters:
- Optimization of varying anystropic and orthotropy coefficients (g, k) in order to find the reinforcement distribution that minimizes Equation (20) by means of the SA algorithm.
- Optimization of slab thickness (Equation (23)) given the reinforcement distribution by means of the SA algorithm.
3. Simulated Annealing
- c0 = 1 initial value of the control parameter;
- cmin = 10−8 final value of the control parameter; and
- kB = 1 Boltzmann constant.
4. Results
4.1. Test Case
4.2. Reinforcement Arrangement Optimization
4.3. Slab Thickness Optimization
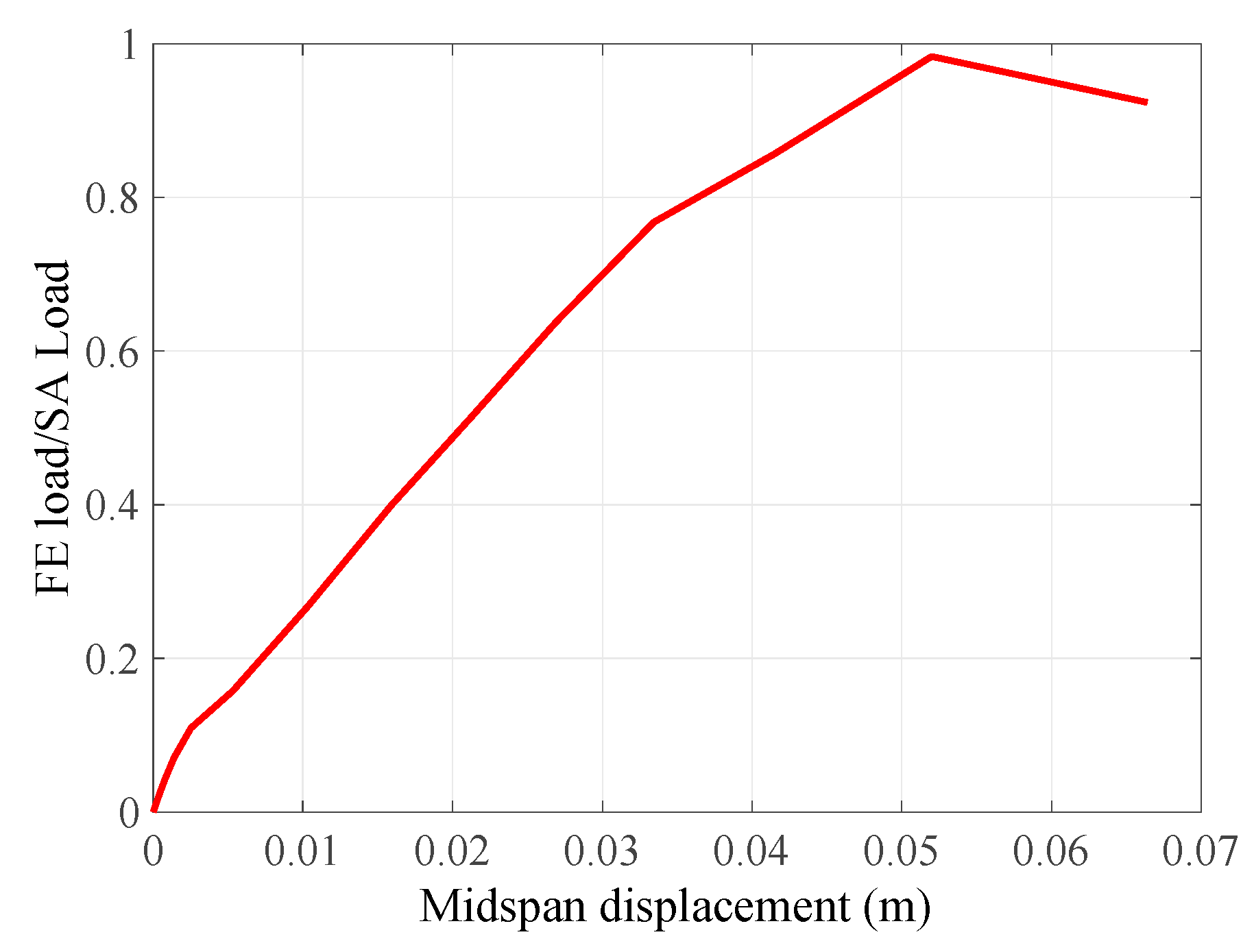
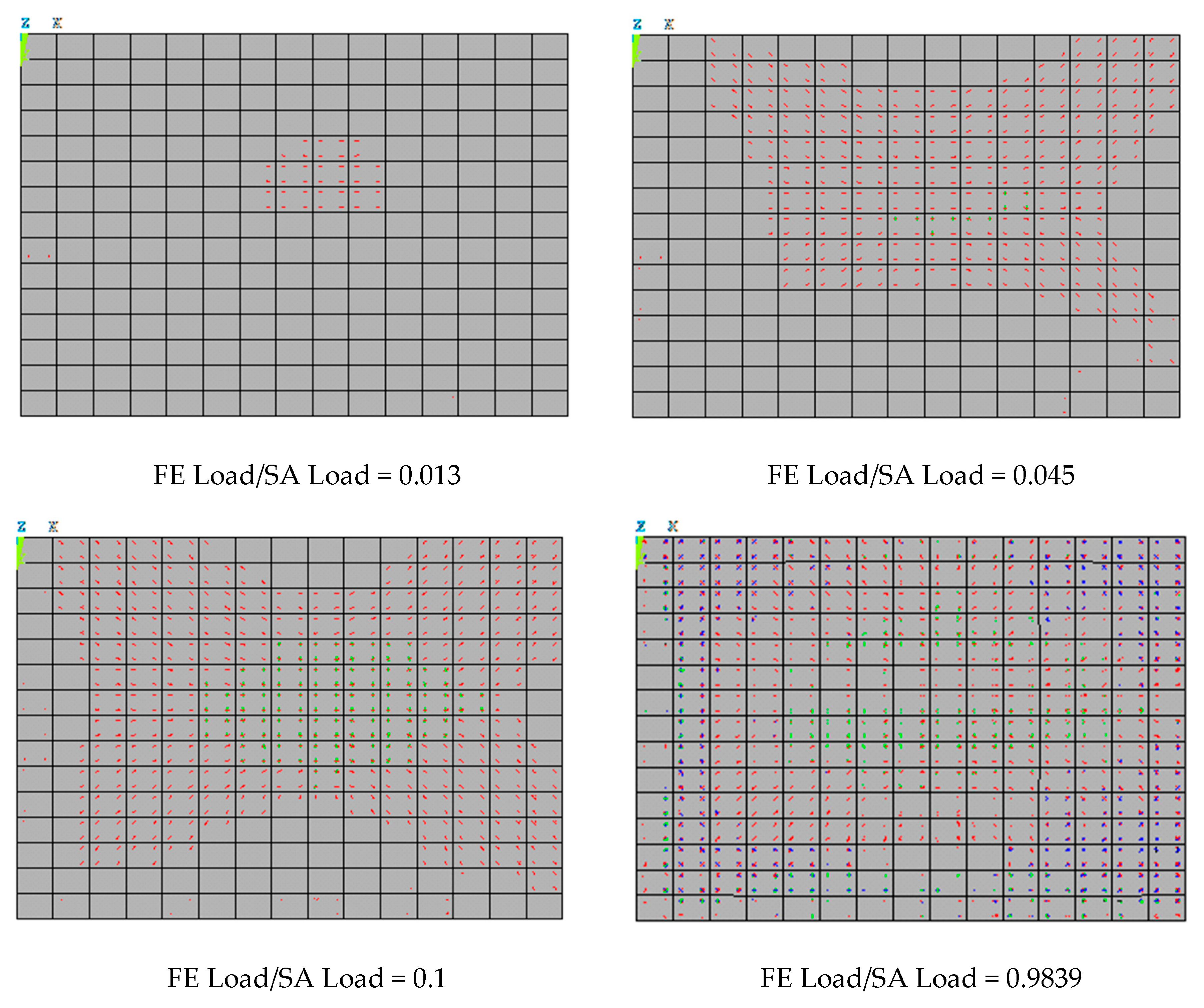
4.4. Finite Element Method Comparison
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Grierson, D.E. Practical optimization of structural steel frameworks. In Advances Design Optimization; Adeli, H., Ed.; Chapman & Hall: London, UK, 1994; pp. 451–491. [Google Scholar]
- Maxwell, C. Scientific Papers; Dover Publications: New York, NY, USA, 1952; Volume 2. [Google Scholar]
- Schmit, L.A. Structural Design by Systematic Synthesis. In Proceedings 2nd Conference on Electronic Computation; ASCE: New York, NY, USA, 1960; pp. 105–132. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Hansen, N.; Arnold, D.V.; Auger, A. Evolution strategies. In Springer Handbook of Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2015; pp. 871–898. [Google Scholar]
- Kicinger, R.; Arciszewski, T.; De Jong, K. Evolutionary computation and structural design: A survey of the state-of-the-art. Comp. Struct. 2005, 83, 1943–1978. [Google Scholar] [CrossRef]
- Chisari, C.; Bedon, C. Multi-objective optimization of FRP jackets for improving the seismic response of reinforced concrete frames. Am. J. Eng. App. Sci. 2016, 9, 669–679. [Google Scholar] [CrossRef]
- Tran, B.; Xue, B.; Zhang, M. Genetic programming for feature construction and selection in classification on high-dimensional data. Memet. Comput. 2016, 8, 3–15. [Google Scholar] [CrossRef]
- Lee, K.S.; Geem, Z.W. A new structural optimization method based on the harmony search algorithm. Comp. Struct. 2004, 82, 781–798. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y.M. Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method. Finite Elem. Anal. Des. 2007, 43, 1039–1049. [Google Scholar] [CrossRef]
- Liu, X.; Yi, W.J.; Li, Q.S.; Shen, P.S. Genetic evolutionary structural optimization. J. Constr. Steel Res. 2008, 64, 305–311. [Google Scholar] [CrossRef]
- Quaranta, G.; Fiore, A.; Marano, G.C. Optimum design of prestressed concrete beams using constrained differential evolution algorithm. Struct. Multidiscip. Optim. 2014, 49, 441–453. [Google Scholar] [CrossRef]
- Scodeggio, A.; Quaranta, G.; Marano, G.C.; Monti, G.; Fleischman, R.B. Optimization of force-limiting seismic devices connecting structural subsystems. Comput. Struct. 2016, 162, 16–27. [Google Scholar] [CrossRef]
- Chatterjee, S.; Sarkar, S.; Hore, S.; Dey, N.; Ashour, A.S.; Balas, V.E. Particle swarm optimization trained neural network for structural failure prediction of multistoried RC buildings. Neural Comput. App. 2017, 28, 2005–2016. [Google Scholar] [CrossRef]
- Quaranta, G.; Monti, G.; Marano, G.C. Parameters identification of Van der Pol–Duffing oscillators via particle swarm optimization and differential evolution. Mech. Syst. Signal Process. 2010, 24, 2076–2095. [Google Scholar] [CrossRef]
- Sarma, K.C.; Adeli, H. Cost optimization of concrete structures. J. Struct. Eng. 1998, 124, 570–578. [Google Scholar] [CrossRef]
- Sassu, M.; Puppio, M.L.; Mannari, E. Seismic reinforcement of a RC school structure with strength irregularities throughout external bracing walls. Buildings 2017, 7, 58. [Google Scholar] [CrossRef]
- Puppio, M.; Pellegrino, M.; Giresini, L.; Sassu, M. Effect of material variability and mechanical eccentricity on the seismic vulnerability assessment of reinforced concrete buildings. Buildings 2017, 7, 66. [Google Scholar] [CrossRef]
- Giresini, L.; Solarino, F.; Paganelli, O.; Oliveira, D.V.; Froli, M. One-sided rocking analysis of corner mechanisms in masonry structures: Influence of geometry, energy dissipation, boundary conditions. Soil Dyn. Earthq. Eng. 2019, 123, 357–370. [Google Scholar] [CrossRef]
- Bruggi, M.; Milani, G.; Taliercio, A. Design of the optimal fiber-reinforcement for masonry structures via topology optimization. Int. J. Solids Struct. 2013, 50, 2087–2106. [Google Scholar] [CrossRef]
- Kouris, L.A.S.; Triantafillou, T.C. State-of-the-art on strengthening of masonry structures with textile reinforced mortar (TRM). Constr. Build. Mater. 2018, 188, 1221–1233. [Google Scholar] [CrossRef]
- Gautier, P.E. Slab track: Review of existing systems and optimization potentials including very high speed. Constr. Build. Mater. 2015, 92, 9–15. [Google Scholar] [CrossRef]
- Hejazi, F.; Toloue, I.; Jaafar, M.S.; Noorzaei, J. Optimization of earthquake energy dissipation system by genetic algorithm. Comput. Aided Civ. Infrastruct. Eng. 2013, 28, 796–810. [Google Scholar] [CrossRef]
- Martins, A.M.; Simões, L.M.; Negrão, J.H. Optimization of concrete cable-stayed bridges under seismic action. Comp. Struct. 2019, 222, 36–47. [Google Scholar] [CrossRef]
- Xu, G.H. Dynamic Parameter Optimization and Experimental Study of Tuned Slab Damper on Metro Systems. Shock Vib. 2019, 2019, 1–14. [Google Scholar] [CrossRef]
- Huang, M. Integrated Structural Optimization and Vibration Control for Improving Dynamic Performance of Tall Buildings. In High-Rise Buildings under Multi-Hazard Environment; Springer: Singapore, 2017; pp. 133–156. [Google Scholar]
- Engle, T.; Mahmoud, H.; Chulahwat, A. Hybrid tuned mass damper and isolation floor slab system optimized for vibration control. J. Earthq. Eng. 2015, 19, 1197–1221. [Google Scholar] [CrossRef]
- Setareh, M.; Ritchey, J.K.; Baxter, A.J.; Murray, T.M. Pendulum tuned mass dampers for floor vibration control. J. Perform. Constr. Fac. 2006, 20, 64–73. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L.; Koekkoek, R.; van der Veen, C.; Sliedrecht, H. Fatigue Assessment of Prestressed Concrete Slab-Between-Girder Bridges. Appl. Sci. 2019, 9, 2312. [Google Scholar] [CrossRef]
- Bielak, J.; Adam, V.; Hegger, J.; Classen, M. Shear Capacity of Textile-Reinforced Concrete Slabs without Shear Reinforcement. Appl. Sci. 2019, 9, 1382. [Google Scholar] [CrossRef]
- Mashrei, M.A.; Mahdi, A.M. An Adaptive Neuro-Fuzzy Inference Model to Predict Punching Shear Strength of Flat Concrete Slabs. Appl. Sci. 2019, 9, 809. [Google Scholar] [CrossRef]
- Francesconi, L.; Pani, L.; Stochino, F. Punching shear strength of reinforced recycled concrete slabs. Constr. Build. Mater. 2016, 127, 248–263. [Google Scholar] [CrossRef]
- Fang, J.; Ishida, T.; Yamazaki, T. Quantitative Evaluation of Risk Factors Affecting the Deterioration of RC Deck Slab Components in East Japan and Tokyo Regions Using Survival Analysis. Appl. Sci. 2018, 8, 1470. [Google Scholar] [CrossRef]
- Ishida, T.; Pen, K.; Tanaka, Y.; Kashimura, K.; Iwaki, I. Numerical Simulation of Early Age Cracking of Reinforced Concrete Bridge Decks with a Full-3D Multiscale and Multi-Chemo-Physical Integrated Analysis. Appl. Sci. 2018, 8, 394. [Google Scholar] [CrossRef]
- Stochino, F.; Pani, L.; Francesconi, L.; Mistretta, F. Cracking of Reinforced Recycled Concrete Slabs. Int. J. Struct. Glass Adv. Mater. Res. 2017, 1, 3–9. [Google Scholar] [CrossRef]
- Aldwaik, M.; Adeli, H. Cost optimization of reinforced concrete flat slabs of arbitrary configuration in irregular highrise building structures. Struct. Multidiscip. Optim. 2016, 54, 151–164. [Google Scholar] [CrossRef]
- He, L.; Gilbert, M.; Shepherd, M. Automatic yield-line analysis of practical slab configurations via discontinuity layout optimization. J. Struct. Eng. 2017, 143, 04017036. [Google Scholar] [CrossRef]
- Sahab, M.G.; Ashour, A.F.; Toropov, V.V. A hybrid genetic algorithm for reinforced concrete flat slab buildings. Comput. Struct. 2005, 83, 551–559. [Google Scholar] [CrossRef]
- Hossain, K.M.A.; Olufemi, O.O. Design optimization of simply supported concrete slabs by finite element modelling. Struct. Multidiscip. Optim. 2005, 30, 76–88. [Google Scholar] [CrossRef]
- Fraile-Garcia, E.; Ferreiro-Cabello, J.; Martinez-Camara, E.; Jimenez-Macias, E. Optimization based on life cycle analysis for reinforced concrete structures with one-way slabs. Eng. Struct. 2016, 109, 126–138. [Google Scholar] [CrossRef]
- Ferreiro-Cabello, J.; Fraile-Garcia, E.; Martinez-Camara, E.; Perez-de-la-Parte, M. Sensitivity analysis of Life Cycle Assessment to select reinforced concrete structures with one-way slabs. Eng. Struct. 2017, 132, 586–596. [Google Scholar] [CrossRef]
- Ferreiro-Cabello, J.; Fraile-Garcia, E.; de Pison Ascacibar, E.M.; de Pison Ascacibar, F.J.M. Minimizing greenhouse gas emissions and costs for structures with flat slabs. J. Clean. Prod. 2016, 137, 922–930. [Google Scholar] [CrossRef]
- Paya-Zaforteza, I.; Yepes, V.; Hospitaler, A.; Gonzalez-Vidosa, F. CO2-optimization of reinforced concrete frames by simulated annealing. Eng. Struct. 2009, 31, 1501–1508. [Google Scholar] [CrossRef]
- Ferreiro-Cabello, J.; Fraile-Garcia, E.; de Pison Ascacibar, E.M.; Martinez-de-Pison, F.J. Metamodel-based design optimization of structural one-way slabs based on deep learning neural networks to reduce environmental impact. Eng. Struct. 2018, 155, 91–101. [Google Scholar] [CrossRef]
- Mistretta, F.; Stochino, F.; Sassu, M. Structural and thermal retrofitting of masonry walls: An integrated cost-analysis approach for the Italian context. Build. Environ. 2019, 155, 127–136. [Google Scholar] [CrossRef]
- Sassu, M.; Stochino, F.; Mistretta, F. Assessment method for combined structural and energy retrofitting in masonry buildings. Buildings 2017, 7, 71. [Google Scholar] [CrossRef]
- Johansen, K.W. Yield-Line Formulae for Slabs; Cement and Concrete Association: London, UK, 1972; p. 106. [Google Scholar]
- European Committee for Standardization. EN-1992-1-1, Eurocode 2–Design of Concrete Structures; Part 1-1: General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2008. [Google Scholar]
- Oldenhuis, R.P. Trajectory Optimization for a Mission to the Solar Bow Shock and Minor Planets. Master’s Thesis, University of Delft, Delft, The Netherlands, 2010. [Google Scholar]
- Bailey, C.G. Membrane action of unrestrained lightly reinforced concrete slabs at large displacements. Eng. Struct. 2001, 23, 470–483. [Google Scholar] [CrossRef]
- Foster, S.J.; Bailey, C.G.; Burgess, I.W.; Plank, R.J. Experimental behaviour of concrete floor slabs at large displacements. Eng. Struct. 2004, 26, 1231–1247. [Google Scholar] [CrossRef]
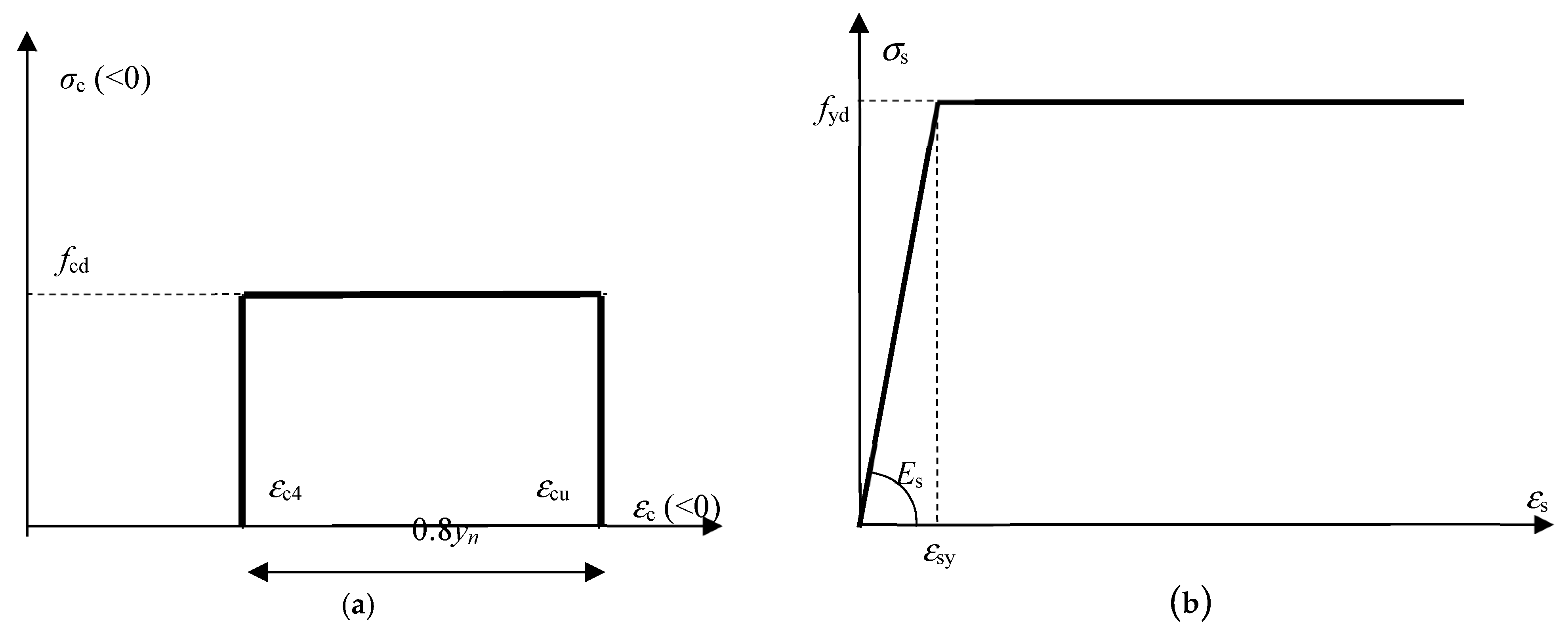

| fcd (MPa) | εc4 ‰ | εcu ‰ | fyd (MPa) | εsy ‰ | ps €/m3 | pc €/m3 |
|---|---|---|---|---|---|---|
| 14 | 0.7 | 3.5 | 391 | 2.2 | 10,822 | 200 |
| Parameters | Value |
|---|---|
| x1 | 0.28667 |
| x2 | 0.14872 |
| x3 | 0.27574 |
| x4 | 0.21739 |
| x5 | 0.36519 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stochino, F.; Lopez Gayarre, F. Reinforced Concrete Slab Optimization with Simulated Annealing. Appl. Sci. 2019, 9, 3161. https://doi.org/10.3390/app9153161
Stochino F, Lopez Gayarre F. Reinforced Concrete Slab Optimization with Simulated Annealing. Applied Sciences. 2019; 9(15):3161. https://doi.org/10.3390/app9153161
Chicago/Turabian StyleStochino, Flavio, and Fernando Lopez Gayarre. 2019. "Reinforced Concrete Slab Optimization with Simulated Annealing" Applied Sciences 9, no. 15: 3161. https://doi.org/10.3390/app9153161
APA StyleStochino, F., & Lopez Gayarre, F. (2019). Reinforced Concrete Slab Optimization with Simulated Annealing. Applied Sciences, 9(15), 3161. https://doi.org/10.3390/app9153161






