Abstract
We review the progress in the investigation of the Verdet constant of new magneto-active materials for the Faraday-effect-based devices used in high-power laser systems. A practical methodology for advanced characterization of the Verdet constant of these materials is presented, providing a useful tool for benchmarking the new materials. The experimental setup used for the characterization is a flexible and robust tool for evaluating the Faraday rotation angle induced in the magneto-active material, from which the Verdet constant is calculated based on the knowledge of the magnetic field and the material sample parameters. A general model for describing the measured Verdet constant data as a function of wavelength and temperature is given. In the final part of this review, we present a brief overview of several magneto-active materials, which have been to-date reported as promising candidates for utilization in the Faraday devices. This overview covers room-temperature investigations of the Verdet constant of several materials, which could be used for the ultraviolet, visible, near-infrared and mid-infrared wavelengths.
1. Introduction
1.1. Faraday Effect and Its Applications
The Faraday effect (or magnetic circular birefringence) is one of the fundamental magneto-optical phenomena emerging from the interaction of light and matter subjected to a magnetic field. This effect manifests itself in the magnetized medium as a circular anisotropy, which is an outcome of the longitudinal Zeeman effect–splitting of the ground and excited states of the medium in the magnetic field [1]. A linearly polarized light beam (which may be represented as a superposition of the right-hand(+) and the left-hand(−) circularly polarized waves with a definite phase difference) undergoes rotation of the polarization plane as it propagates through the medium because of the different propagation velocities of the +/− waves. This phenomenon may be conveniently described by assuming a ray coordinate system travelling along the ray’s path in the medium, with the unit vector in the direction of ray propagation. Considering linear (far from saturation) Faraday effect, the rotation angle distribution over the beam’s cross-section may be described using the following expression
where is the magnetic field, denotes the dot product of and vectors and V is the Verdet constant, a material parameter depending on wavelength and temperature T. The sign of the rotation angle is determined by the projection of the magnetic field into the beam’s propagation direction and by the sign of the Verdet constant. According to the convention, the Verdet constant is considered negative if the medium rotates the polarization clockwise and if the laser beam propagation is parallel to the magnetic field. By assuming constant temperature, constant magnetic field parallel to the beam of monochromatic light, Equation (1) simplifies into the familiar expression , where L is the distance travelled in the medium.
There are vast possibilities for utilization of the Faraday rotation in technological and scientific applications. For instance, it can be used for magneto-optical devices for polarization-manipulation-based processing of an optical signal (e.g., modulators, switches, rotators or optical isolators [1,2,3,4,5]), magneto-optical current sensors [6], gravitational wave detection experiments [7] or magnetic splitting of ultrashort laser pulses in plasmas [8]. Within this broad scientific community dealing with the development of the Faraday devices (FDs), a great effort is dedicated to the investigation of the FDs for high-power laser systems. The high-power lasers have made several remarkable advancements in the recent years [9,10,11], leading to highly demanding criteria on new architectures, materials, and other related laser technologies. The FDs are used in the laser systems particularly for the multi-pass amplification and regenerative amplifiers as well as for optical isolation of one part of the system from another by eliminating possible harmful back-reflections. This makes the FDs indispensable components of any high-power laser system.
1.2. Thermal Effects in High-Power Faraday Devices
One of the main factors limiting the performance of the laser components are the thermal effects arising due to the always-present absorption of a small portion of the incident laser power [9,12,13,14]. Among all of the components of a laser system, the FDs are particularly affected: the absorption of the vast majority of the magneto-active media is much higher (∼) than that of the common optical elements. A full description of the physical phenomena involved in the heating of magneto-active medium and their impact on the FD performance is a very complex topic. There are, however, several sources in the available literature dealing with the detailed description [15,16]. Within the scope of this review, we consider only a simplified cause-and-effect diagram of the physical phenomena involved in the absorption-induced thermal effects in magneto-active media (see Figure 1). When a magneto-active medium is exposed to high power laser radiation, a nonuniform temperature distribution is generated as a result of absorption and nonuniform cooling of the medium. This nonuniformity in the temperature results in a nonuniform distribution of the polarization-plane rotation angle over the cross-section in Equation (1) (polarization distortions) due to the temperature dependence of the Verdet constant, as well as due to the induced nonuniform polarization state changes, because of the thermal-stress-induced birefringence (via the photo-elastic effect). Consequently, the performance of a FD strongly deteriorates. As an example, we may mention the case of a Faraday isolator, in which the polarization distortions decrease the isolation ratio, leading to output power losses in the permeable direction, backward power leakage in the opaque direction, and to a beam quality degradation. Furthermore, the nonuniform temperature distribution leads to the thermal lensing, due to the thermal bulging and changes in the refractive index, causing wavefront distortions of the passing laser beam.
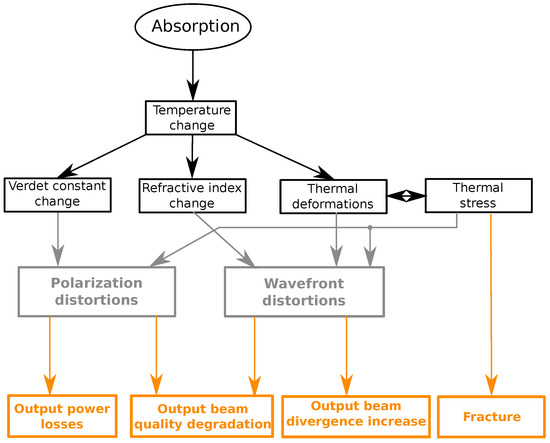
Figure 1.
A simplified scheme of the physical phenomena involved in the absorption-induced thermal effects in magneto-active media.
1.3. Methods for the Thermal Effects Compensation or Reduction
Many techniques and methods for a partial reduction or compensation of the arising thermal effects have been reported in recent years. To satisfy the high demands on the high-power FDs, it is essential to take into consideration an appropriate optical layout for compensation of the thermally-induced polarization and wavefront distortions [17,18,19,20]. The needed length L for achieving the desired rotation angle by a magneto-optical element (MOE) may be reduced by enhancement of the applied magnetic field [21,22,23,24,25,26]. This leads to a reduced amount of generated heat as well as to a reduced optical path travelled through a distorted medium. Another aspect which needs to be taken into account is the optimal design of the geometry and cooling of the MOE [27,28,29]. One possibility is to consider the cryogenic cooling [30,31,32], which, on the one hand, greatly enhances both Verdet constant and thermal properties of the medium, but, on the other hand, increases the cost and technological complexity of the FD and makes the system more sensitive to temperature fluctuations.
The degrading impact of the thermal effects may be substantially reduced by a careful choice of the magneto-active material used as a magneto-optical element in the FD. The common materials used for the laser FDs incorporate solid-state crystals, transparent ceramics or glass [33,34]. Possession of a high Verdet constant and transparency at the desired wavelength are the fundamental criteria for selection of a magneto-active material as a highly promising for utilization in FDs. Historically, for the purpose of comparison between the magneto-active materials, a parameter called a magneto-optical figure of merit (FOM) was introduced as a ratio between the Verdet constant and absorption – . However, in the context of the high-power FDs, it is more convenient to include the material thermal properties for more accurate benchmarking. The “extended” FOM may have the following forms [16]
where k denotes the thermal conductivity; Q and P are the so-called thermo-optical constants evaluating the polarization and wavefront distortions, respectfully; and is the optical anisotropy parameter. Media with a negative parameter of optical anisotropy allow compensating the thermally-induced depolarization without using a reciprocal rotator in the optically-compensating layout [35,36,37,38]. The parameters are dependent on a large set of material parameters incorporating optical, thermo-optical, thermo-mechanical and elasto-optical properties [16,17,18]. However, it was reported multiple times, how these constants may be evaluated indirectly using different measurement methods (see, e.g., [39,40,41,42,43]).
Within the scope of this manuscript, we cover in detail:
- A method for simultaneous characterization of the Verdet constant wavelength and temperature dependence.
- A brief summary of the reported room-temperature investigations of the Verdet constant for several magneto-active materials suitable for the high-power FDs.
The measurement of the Verdet constant dispersion at room temperature usually represents an initial step in the benchmarking process of new magneto-active materials by the FOM parameters in Equations (2)–(4). The knowledge of the temperature dependence of the Verdet constant is useful for the investigation of the FDs performance under thermal loading by a high-power laser. Therefore, an advanced method for the characterization of the Verdet constant temperature-wavelength dependence represents a very important tool for the scientific community devoted to the development of the high-power FDs. In the final section, we review the results of the room-temperature investigations of the Verdet constant of several yet-reported magneto-active materials for FDs. A similar review was given already in Ref. [33], which is, however, relatively out-dated. A comparison of several magneto-active media employed in various Faraday isolator devices was given in Refs. [15,16]. The main goal of this paper is to update the available reviews and to provide the needed summary of several recently reported Verdet constant investigations of magneto-active materials developed for the high-power FDs operating from the ultraviolet to mid-infrared wavelengths. The material summary will be useful for further evaluation of the FOM parameters of the covered materials, for additional high-power testing, for construction of real devices as well as for giving directions in the future research of the magneto-active materials for high-power FDs.
2. Characterization of the Verdet Constant as a Function of Wavelength and Temperature
This review presents the characterization method based upon a modified version of the polarization-stepping technique [44], which has been systematically developed in the recent years [45,46,47,48]. One of the main advantages of this method is that the rotation angle induced in the examined material sample is analyzed based on a large number of angular positions (typically a few hundred) of the analyzing polarization-sensitive element of the experimental detection system. This makes the method more robust, i.e., less sensitive to the fluctuations of the detected signal, as compared with the other commonly used characterization methods, which usually rely only on a smaller number of steps/measurements [33,44,49,50]. Further, the presented method takes advantage of the utilization of a broadband radiation source as a probe beam, allowing an advanced analysis of the Verdet constant wavelength dependence based on a larger number of detected values distributed across the investigated spectral range. When using a broadband source, the presence of the material resonance regions is more easily detected and it is possible to study their impact on the examined Verdet constant dispersion.
The main drawback of the method then lies within the time demanding data analysis, as compared with the methods which rely only on a smaller number of measurements. From these techniques, which benefit from a relatively simple and quick measurement, we may mention the procedure in which the examined material sample is put between the crossed polarizers and then, after applying the magnetic field, the induced Faraday rotation angle is detected by finding the new mutual polarizers’ angular position ensuring the maximal extinction of the detected signal. This procedure or its variations has been frequently reported in several Verdet constant investigation studies (see, e.g., [49,50,51]).
Another drawback of the method discussed here is that it is not suitable for investigation of the Faraday effect in the media with a non-negligible co-occurrence of the other phenomena altering the polarization state of the probe beam (e.g., the linear birefringence). In such cases, it is advantageous to use more general ellipsometric methods allowing to filter the parasitic influences of the other phenomena. A suitable procedure for such cases was described, for instance, by Majeed et al. [52].
2.1. Experimental Setup for the Characterization
A simplified scheme of the experimental setup used for the characterization of the Verdet constant is depicted in Figure 2. In the experiment, a probe beam from the broadband radiation source is linearly polarized by an input high-contrast Glan polarizer (P) and propagates through the measured material sample, which is thermally coupled to a cryostat ledge. An external magnetic field is applied on the sample, inducing a Faraday rotation of the propagating probe beam. The beam then enters the detection system, which may be realized in different configurations, as depicted in Figure 2. The reason for consideration of different detection systems is the following: the transmission ranges of the employed optical elements and the wavelengths provided by the utilized broadband source will eventually limit the effective spectral range of the measurement. The first depicted configuration for the detection system consists of another Glan polarizer (an analyzer), which could be arbitrarily rotated around the optical axis and a diffuser. The latter may be either transmissive or reflective and its purpose is to suppress the polarization dependence of the fiber couplings delivering the optical signal to the spectrometers. This configuration was used in the investigations in Refs. [45,46,47], and its main advantage is the relative simplicity of the setup, compared with the other configurations. Furthermore, assuming we measure the Verdet constant on a single wavelength only (we use a laser probe beam except the broadband source), the spectrometers may be exchanged with a power meter, which even more simplifies the measurement and data analysis. The other depicted configurations take advantage of using an arbitrarily rotated achromatic wave plate, half (No. 2) or quarter-wave plate (No. 3) or of an arbitrarily rotated polarizer (No. 4) in a combination with a static analyser. The latter three configurations practically cancel the problem of the polarization-sensitive fiber couplings and allow to construct different spectral ranges of the measurement, based on the availability of the listed components. The configuration with the rotating half-wave plate was quite recently demonstrated [48] (a 3D overview of the experimental setup is depicted in Figure 3a), with the effective range of the measurement covering visible, near-infrared and mid-infrared wavelengths. The other configurations are planned to be investigated in the near future.
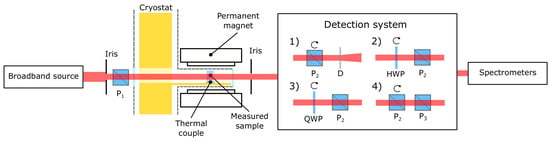
Figure 2.
Experimental setup for the Verdet constant characterization.
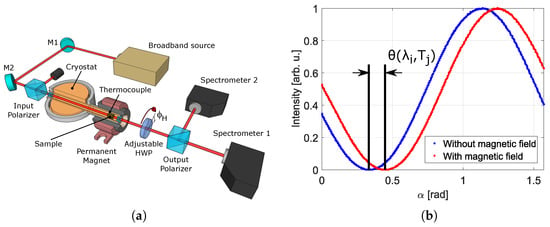
Figure 3.
Experimental setup for the Verdet constant characterization, detection system with an arbitrarily rotated half-wave plate [48]: (a) a 3D overview of the experimental setup; and (b) an example of data obtained at a single wavelength and temperature.
Regardless of the what type of detection system is used, the measurement is taken twice (at each of the measured temperatures), i.e., with and without applying the magnetic field. The spectra are gathered in a large number of angular steps of the rotating element of the detection system, making the measurement more robust, as compared with taking only three angular steps in the original method [44]. According to the Jones calculus, the detected intensity data need to be proportional to the angular position of the rotating element of the depicted detection systems (Nos. 1–4) as follows
where denotes the measured intensity data gathered at each of the detectable wavelengths and temperatures . corresponds to the initial mutual angular position of the input polarizer and the rotating element in the detection system. represents the induced polarization rotation angle, which occurs only in the measurement with the magnetic field, and, hence, it may be easily calculated as a subtraction of the respective fitting parameters values (the initial phase shifts) obtained for the measurement with the magnetic field from the values obtained for the measurement without it. Example data are shown in Figure 3b obtained at a single wavelength and temperature for the -configuration [48]. The Verdet constant data are calculated from the rotation angles using the expression . The effective value of the magnetic field is obtained by a numeric integration of the known longitudinal distribution of the axial magnetic field magnitude over the length L of the sample. It is assumed that the sample is placed in the maximum of the magnetic field, i.e., (the maximum is located at ).
Using a standard error calculus, the uncertainty of the obtained Verdet constant data is given by
is the uncertainty of the obtained rotation angles , caused by small deviations of the intensity data from the cosine-squared functions in Equations (5)–(8). represents the uncertainty of the effective magnetic field value given by both measurement error of the magnetic field longitudinal distribution as well as by an undesired displacement of the material sample from the maximum of the magnetic field. is the uncertainty of the sample length L.
2.2. Model Function for the Verdet Constant Temperature-Wavelength Dependence
In the next step, after obtaining the Verdet constant data , we need to find a model function for describing the Verdet constant temperature-wavelength dependence . A general model for the Verdet constant may be written as follows [1,45,48,53,54,55,56]
The model was derived for solid-state compounds containing rare-earth paramagnetic ions, assuming that: (a) the described spectral range is sufficiently far from any resonance line; and (b) only the contribution of N dominant transitions at wavelengths are considered. It consists of four different contributions (associated with the , , and D-terms), arising from various phenomena associated with the Zeeman splitting of the ground and excited states of a material subjected to a magnetic field. A full description of these individual contributions is beyond the scope of this paper, however, a brief explanation of the individual terms is given with the corresponding references to additional literature. The -terms refers to the so-called diamagnetic contributions of the material lattice. This contribution, as well as its mathematical formulation, is discussed in Refs. [1,53,55]. The second bracketed -terms stand for the mixing term derived by Van Vleck and Hebb based on quantum mechanical considerations [1,54,55]. This contribution comes from the overlap of wavefunctions of ground and neighboring excited states which causes the perturbation of the amplitude elements of the electric moment by the magnetic field. The next terms, proportional to , are the paramagnetic terms, arising from the different occupation of energy sublevels of the magneto-active ion ground states [1,55]. The D-term is called the gyromagnetic contribution, which is the only wavelength-independent term of the model [1,55]. The origin of this contribution is associated with the magnetic dipole transitions. The influence of this contribution becomes more prominent at longer wavelengths. All contributions except for the mixing terms are temperature-dependent according to the Curie–Weiss law, i.e., , for the temperatures above the magnetic state phase transition characterized by the Néel temperature [57]. It should be noted that the diamagnetic contributions are often referred as temperature-independent, which is, however, a valid assumption only for higher temperatures (e.g., around the room temperature) or for a narrow range of temperatures.
The model in Equation (10) may be easily transformed into a single-variable function of either wavelength (for a fixed temperature ) or temperature (at a given wavelength ) to get
When performing a full temperature-wavelength analysis of the Verdet constant, it is often advantageous to fit the data first with the single-variable functions in Equations (11) and (12) to obtain initial estimations of the fitting parameters of the general model in Equation (10).
Note that the model in Equation (10) may be considerably simplified. For instance, the contribution of the diamagnetic terms is usually very weak compared to the paramagnetic and mixing terms if the described spectral region is sufficiently far from any resonance line. Therefore, the diamagnetic contributions may be neglected in these cases. Furthermore, assuming that only one dominant transition is contributing to the Verdet constant, together with neglecting the diamagnetic term and considering the temperature is fixed, Equation (10) will reduce to the widely-used single-transition model
Equation (13) is used in the vast majority of the reported Verdet constant investigations at room temperature since the needed criteria for its use are usually very well met (e.g., [41,46,58,59,60]). However, when the investigated spectral range contains additional resonance lines, they should be included in the model function, especially when the resonance strongly affect the overall Verdet constant dependence. Careful analysis of the measured data, as well as knowledge of the spectroscopic characteristics of the investigated compound, may provide valuable insight into the considerations about the selection of the lines which need to be taken into account [48].
3. Verdet Constant Investigations of Magneto-Active Materials Developed for High-Power Faraday Devices
In this section, a brief overview of the reported Verdet constant investigations at the room temperature is given. The overview is divided into three subsections, corresponding to different spectral regions: (1) UV region (); (2) VIS-NIR region (); and (3) NIR-MIR region (). This allows us to discuss the current status and possible future development of the covered materials more conveniently. In each of the subsections, the historical development of the reported materials is briefly discussed along with a table providing:
- Fitting parameters () of the single-transition model in Equation (13), which could be used for the description of the listed materials’ Verdet constant wavelength dependence within the discussed spectral region.
- Values of the Verdet constant at two wavelengths selected from the spectral region.
- Additional references leading to further investigations of the parameters related to the high-power benchmarking (e.g., Verdet constant temperature dependence, Q and P constants, optical anisotropy parameter, thermal properties or LIDT tests) or to studies dealing with the optimization of the fabrication process of the listed materials.
The following Table 1, Table 2 and Table 3 list only the absolute values of the Verdet constant to make the comparison of the listed materials more convenient.

Table 1.
A brief overview of magneto-active materials for the UV FDs ( < 400 nm). The Verdet constant dispersion is given by the single-transition model in Equation (13) with the specified ()-parameters; the G-parameter is equal to 0 for all materials. The listed V-values are the absolute values of the Verdet constant, specified in .

Table 2.
A brief overview of magneto-active materials for the VIS-NIR FDs (). The Verdet constant dispersion is given by the single-transition model in Equation (13) with the specified ()-parameters. The listed V-values are the absolute values of the Verdet constant, specified in . Some of the listed values were measured * at 600 nm, ** at 635 nm, *** at 1060 nm or **** at 1075 nm. A function different from the model in Equation (13) for the Verdet constant dispersion may be found in the listed reference.

Table 3.
A brief overview of magneto-active materials for the NIR-MIR FDs ( > 1100 nm). The Verdet constant dispersion is given by the single-transition model in Equation (13) with the specified ()-parameters; the G-parameter is equal to 0 for all materials. The listed V-values are the absolute values of the Verdet constant, specified in . For the YIG crystal, the saturated Verdet constant is specified in . A function different from the model in Equation (13) for the Verdet constant dispersion may be found in the listed reference.
3.1. UV Region ( < 400 nm)
The historical development of magneto-active materials for the UV region has already been very well summarized in Refs. [59,61]. The very first investigations were performed on the commonly used solids and liquids (e.g., quartz, water, etc.), which, however, exhibit only very small values of the Verdet constant because of their diamagnetic character. The following research was therefore focused more on various materials containing rare-earth (RE) paramagnetic ions, which were reported to have high magneto-optical characteristics [62,63,64,65]. In this manner, several RE-containing glasses were investigated as possible magneto-active materials for the UV FDs, with the cut-off wavelengths equal to ∼200–300 nm [66,67,68]. It was observed that the Verdet constant in these glasses is directly proportional to the concentration of the RE ions. Unfortunately, the increase in the concentration (and the Verdet constant) was found to be constricted by the composition of the glass and, furthermore, it is counterbalanced by increased absorption losses [67,69]. Phosphates (KDP, DKDP, ADP, etc.) and arsenates (ADA, KDA or DKDA) were studied as possible material candidates for deeper UV ( < 200 nm) [70,71]. Nevertheless, these compounds exhibit serious drawbacks for their further utilization in the FDs because they are relatively soft and hygroscopic. The focus of attention was then switched to fluoride crystals, which were already studied in Refs. [72,73,74], but more comprehensively, with a focus on the UV region, in Refs. [59,61]. In the latter, magneto-optical characteristics of CeF, PrF [61] and of LiREF (RE = Tb, Dy, Ho, Er and Yb) [59] crystals were reported and studied in detail. The conclusion is that these fluorides exhibit high Verdet constant values and low absorption in the UV (inside their local transmission windows), with the cut-off wavelengths >158 nm. To the best of our knowledge, only the CeF crystal has been more extensively studied in the following years. These investigations were focused mainly on the magneto-optical characteristics of the CeF in the VIS-NIR region, which we discuss in the following subsection. The reason is the higher FOM parameter of CeF as compared to the most commonly used magneto-active material in the VIS-NIR—the terbium gallium garnet crystal. A successful design and construction of CeF-based UV Faraday isolators was reported in Ref. [75].
3.2. VIS-NIR Region ( < 1100 nm)
For the specified VIS-NIR region, terbium gallium garnet (TGG) crystal represents the most commonly used magneto-active material used in the FDs. One of the first investigations of this material dates back to 1970s, in which the TGG was proved to have higher Verdet constant [77] and higher thermal conductivity [78] than the often used Tb-doped magneto-optical glasses. Properties of the TGG crystal and its performance in the Faraday devices have been later investigated in many papers (e.g., in [17,18,49,56,79,80]). However, the TGG crystal exhibits two major disadvantages: (a) its use in the VIS region is struggling with increasing absorption losses towards the shorter wavelengths [59,61]; and (b) growth of large-aperture TGG crystals is difficult and expensive [59,61,81,82]. Although the manufacturing process was greatly improved during the last decades, the largest aperture TGG-crystal-based FD (to the best of our knowledge) was reported in 2015 by Mironov et al. [83], having a 40-mm clear aperture. For a larger-aperture FD, the magneto-active glasses still represent a viable option for a non-repetitive high-power operation. Because of this advantage, the glass-based magneto-active materials are still being actively developed [67,68,69,84,85,86,87,88,89]. More and more attention is being put into the investigation of magneto-active transparent ceramics in the recent years [34].
A considerable amount of scientific effort has been put into the investigation of magneto-active materials, which could supersede the TGG crystal in the thermo-optical or magneto-optical characteristics or in the large-aperture scalability. One of the materials, which has been frequently co-investigated along with the TGG crystal ever since the 1960s, is the terbium aluminium garnet (TAG) crystal [56,63]. The main advantage of TAG is its ∼30% higher Verdet constant [56,90] and > higher thermal conductivity [91] as compared with the TGG. Nevertheless, TAG crystals are difficult to grow in dimensions suitable for practical applications because of their incongruent melting properties [90,92]. The solution to this drawback has brought the development of the transparent ceramics technology, which enabled production of TAG in the form of ceramics [93]. A distinct enhancement of the magneto-optical properties of the TAG ceramics has been obtained by doping with: Ce [94,95,96,97], Si [98], Ti [98,99], Ho [100], Pr [101], Tm [102] or TbO [103,104]. A TGG transparent ceramics [105], with the properties similar to those of the <111>-cut of the single crystal [45,106], has been also successfully manufactured and investigated in detail in the recent years [29,51,58,107,108,109,110]. The largest piece of the TGG ceramics, a 100 mm × 100 mm slab, was reported in [111], greatly overcoming the manufacturing limits of the TGG crystal. Another material, which could be used as an advantageous alternative to the TGG crystal, is the terbium scandium aluminium crystal (TSAG) [112,113], which possesses ∼25% higher Verdet constant [114,115], lower thermo-optical constant Q and negative optical anisotropy parameter [41]. All of these properties ensure that the TSAG scores much higher in the FOM parameter than TGG, which has marked this material as one of the prime candidates of several other scientific investigations [37,116,117,118]. The sodium terbium fluoride (NTF) [50,119] and the potassium terbium fluoride (KTF) crystals [72,120,121] also deserve attention: although they possess ∼20% lower Verdet constant, they exhibit a higher FOM parameter than the TGG crystal. Notable characteristics were recently reported for the rare-earth (RE) sesquioxide ceramics (REO; RE = Tb [122,123,124,125,126,127], Dy [48,128,129,130] or Ho [47,131,132,133]), which possess high concentrations of the magnetically-active RE ions. Among these, TbO holds the record Verdet constant (∼3.5 times higher than TGG), followed by the DyO (∼2 times higher (at 633 nm wavelength)) and HoO (∼1.4 times higher (at 1064 nm wavelength)). The manufacturing process of the REO-based ceramic materials still needs to be optimized before the ceramics will be obtained in a high optical grade and in larger dimensions. Nevertheless, these structures represent one of the most promising options for the large-aperture VIS-NIR FDs. The fluorides mentioned in the UV region, i.e., LiREF [59], PrF and CeF [61] could be used as Faraday rotators in the VIS region as well. The latter one, CeF, has been extensively studied over the VIS-NIR region (), since it exhibits higher FOM than TGG crystal [46,60,134,135].
There are many more reports on promising magneto-active materials for the VIS-NIR region, which offer properties superior to the TGG crystal, most of them targeting on the enhancement of the Verdet constant. From the vast number of these materials, we may mention, e.g., NaTb(WO) [136], TSLAG [81,137], NaTb(MoO) [138], LiCaTb(BO) [139], RE:TGG (RE= Ce [140], Pr [141], Ho [142], Tm [143] or Dy [144]), TbVO [145], Nd:TbVO [146], NaCe(MoO) [147], TCZ [148,149], TbHfO [150] or CeAlO [151].
3.3. NIR-MIR Region ( > 1100 nm)
Above 1100 nm, a ferrimagnetic material yttrium iron garnet (YIG) crystal and its RE-substituted compositions represent the established materials for the FDs, as they have been investigated since the 1960s [65,152]. The RE-substituted iron garnets possess very high Verdet constant [153,154,155,156] and low saturation magnetization [157], which is the main reason for its wide utilization for low-power applications in telecommunications, medical field or integrated magneto-optical devices [4]. Moreover, a high-grade YIG ceramics has been very recently reported [158], possibly enabling fabrication of large-aperture YIG elements in the near future.
Recently, there have been a few reports on MIR paramagnetic materials as well. The main advantage of using a paramagnetic material is the possibility of fine adjustment of the desired rotation angle by changing the magnetic field applied on the magneto-optical element [129]. This can be done either by moving the element to a stronger/weaker magnetic field (if a permanent magnetic system is used) or by changing the input current to the electromagnet. The majority of materials used for the NIR wavelengths contain Tb ions (see the Table 2), which have strong absorption in the MIR, and, therefore, it is needed to search for materials with different compositions. The fluorides CeF, PrF and LiREF (RE = Dy, Ho or Er) [59] have several transparency windows in the MIR; nevertheless, their magneto-optical characteristics in this region are unknown. The only exception is the CeF crystal, for which the Verdet constant was reported up to 1950 nm in Ref. [46]. The CeAlO material [151] is also transparent up to ∼ and its Verdet constant is about twice as high as the one of CeF at the 633 and 1064 nm wavelengths. Apart from these cerium-based materials, Verdet constant investigations of (DyYLa)O (with variable doping = 0.7, 0.8 and 0.9) ceramics [129,130], EuF crystal [42,159] and DyO ceramics [48] were recently reported. Although further optimization of the fabrication process is needed, all of them exhibit very promising magneto-optical characteristics for their future utilization in high-power MIR FDs. All of these materials, however, have the Verdet constant in the range of ∼, which implies a requirement for a relatively strong magnetic field > (for a ∼ long MOE to achieve the desired 45-degree polarization rotation in a Faraday isolator). Although some permanent magnets with the needed peak magnetic field magnitudes were already reported [24,26], it is still challenging to construct such magnets with the desired field distributed homogeneously over the whole MOE. Searching for other paramagnetic materials with higher magneto-optical characteristics in MIR is therefore still very topical.
4. Conclusions
In this review, we deal with the development of magneto-active materials for Faraday-effect-based magneto-optical devices for high-power lasers. The major task to be solved in the area of high-power FDs is the compensation and reduction of the absorption-induced thermal effects which seriously deteriorate the performance of these devices. In the Section 1.3, we mention several methods on how to mitigate the thermal effects:
- Optical layout for compensation of the thermally-induced polarization and wavefront distortions
- Enhancement of the applied magnetic field
- Design of optimal geometry and cooling of the magneto-optical elements
- Development of new magneto-active materials
The desirable properties of a magneto-active material for high-power FD are: possession of high Verdet constant and transparency, high thermal conductivity and low value of thermo-optical constants Q and P (evaluating the thermally induced polarization and wavefront distortions).
In the following Section 2, we describe an advanced method for characterization of the Verdet constant dependence on wavelength and temperature. The presented experimental setup is an easily-adjustable and robust tool for the measurement of the Faraday rotation angle induced in the magneto-active material. The Verdet constant is calculated based on the knowledge of the magnetic field and the material sample parameters. Due to the utilization of a broadband source, the wavelength dependence of the Verdet constant may be studied at a higher level of detail. For the purpose of this analysis, a general model function for describing the Verdet constant as a function of wavelength and temperature is introduced.
In the final part Section 3, we review the room-temperature investigations of the Verdet constant for several magneto-active materials developed for the high-power FDs. The overview covers several materials, which could be used for the UV, VIS, NIR and MIR wavelengths. For the UV wavelengths, the fluorides CeF, PrF and LiREF (RE = Tb, Dy, Ho, Er and Yb) represent promising materials for the high-power FDs: they possess high Verdet constant and local windows of high transparency. Nevertheless, reports on the construction of UV FDs based on these materials are still rare. The by far most intensively studied magneto-active materials for FDs are those for the VIS-NIR region . These studies often aim at achieving the higher value of the Verdet constant as compared with the TGG crystal—an established material for this wavelength range, which, however, has insufficient properties to be employed in the great number of the newly developed high-power laser systems. Most of these new successors of the TGG crystal are also Tb-based, having a higher concentration of the Tb ions. The other commonly investigated materials contain Ce, Pr, Ho or Dy ions, in a combination with the Tb ions. From these, we may mention TAG, TSAG, RE:TGG, or RE:TAG, all of them having approximately a few tenths of percent higher Verdet constant than the TGG. The record holds the TbO ceramics with more than three times higher Verdet constant than that of the TGG crystal. Reports of Tb-less compounds are less common, but, among those, materials such as DyO, HoO, CeF, CeAlO or NaCe(MoO) show promising magneto-optical characteristics. The extended FOM parameters in Equations (2)–(4), which offer a much more realistic comparison of these materials under high-power operation, are, unfortunately, for the vast majority of these materials unknown. It is, therefore, one of the main tasks for future research to evaluate the performance of these promising materials under the thermal loading by a high-power laser. A comparison of some of these materials was already reported by the authors of [16,38] based on a maximum achievable power in a Faraday isolator ensuring a 30 dB isolation ratio.
The last spectral region reviewed is the NIR-MIR region (), for which the ferrimagnetic YIG crystal represents the most commonly used material for low-power laser applications. Most recently, magneto-optical characteristics of a few paramagnetic materials were reported, i.e., Dy-based sesquioxide ceramics or EuF crystal, which could be used as an alternative to the YIG. However, due to the low values of the Verdet constant, their utilization in a FD would demand relatively strong magnetic fields >2 T for achieving standard rotation angles. Therefore, it is crucial to continue the investigation of new materials with higher magneto-optical activity.
Author Contributions
Conceptualization, D.V., O.S. and A.L.; methodology, D.V. and O.S.; software, D.V. and O.S.; validation, D.V. and O.S.; formal analysis, D.V. and O.S.; investigation, D.V. and O.S.; resources, A.L. and T.M.; data curation, D.V. and O.S.; writing—original draft preparation, D.V.; writing—review and editing, O.S. and A.L.; visualization, D.V. and O.S.; supervision, O.S., A.L. and T.M.; project administration, D.V., O.S., A.L. and T.M.; and funding acquisition, A.L. and T.M.
Funding
This article was co-financed by the European Regional Development Fund and the state budget of the Czech Republic (project HiLASE CoE: Grant No. CZ.02.1.01/0.0/0.0/15_006/0000674) and by the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 739573. This work was also supported by the Ministry of Education, Youth and Sports of the Czech Republic (Programmes NPU I Project No. LO1602, and Large Research Infrastructure Project No. LM2015086).
Acknowledgments
The authors would like to express their gratitude to Ryo Yasuhara from the National Institute for Fusion Science, Japan, for the fruitful collaboration on the characterization experiments of new magneto-active materials for the high-power Faraday devices.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Zvezdin, A.K.; Kotov, V.A. Modern Magnetooptics and Magnetooptical Materials, 1 ed.; Taylor & Francis Group: New York, NY, USA, 1997; pp. 1–109. [Google Scholar]
- Scott, G.; Lacklison, D. Magnetooptic properties and applications of bismuth substituted iron garnets. IEEE Trans. Magn. 1976, 12, 292–311. [Google Scholar] [CrossRef]
- Dötsch, H.; Bahlmann, N.; Zhuromskyy, O.; Hammer, M.; Wilkens, L.; Gerhardt, R.; Hertel, P.; Popkov, A.F. Applications of magneto-optical waveguides in integrated optics: review. J. Opt. Soc. Am. B 2005, 22, 240–253. [Google Scholar] [CrossRef]
- Stadler, B.J.H.; Mizumoto, T. Integrated Magneto-Optical Materials and Isolators: A Review. IEEE Photonics J. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Shoji, Y.; Mizumoto, T.; Shoji, Y.; Mizumoto, T. Silicon Waveguide Optical Isolator with Directly Bonded Magneto-Optical Garnet. Appl. Sci. 2019, 9, 609. [Google Scholar] [CrossRef]
- Kumari, S.; Chakraborty, S. Study of different magneto-optic materials for current sensing applications. J. Sens. Sens. Syst. 2018, 7, 421–431. [Google Scholar] [CrossRef]
- Palashov, O.V.; Zheleznov, D.S.; Voitovich, A.V.; Zelenogorsky, V.V.; Kamenetsky, E.E.; Khazanov, E.A.; Martin, R.M.; Dooley, K.L.; Williams, L.; Lucianetti, A.; et al. High-vacuum-compatible high-power Faraday isolators for gravitational-wave interferometers. J. Opt. Soc. Am. B 2012, 29, 1784–1792. [Google Scholar] [CrossRef]
- Weng, S.; Zhao, Q.; Sheng, Z.; Yu, W.; Luan, S.; Chen, M.; Yu, L.; Murakami, M.; Mori, W.B.; Zhang, J. Extreme case of Faraday effect: Magnetic splitting of ultrashort laser pulses in plasmas. Optica 2017, 4, 1086–1091. [Google Scholar] [CrossRef]
- Kiriyama, H.; Mori, M.; Pirozhkov, A.S.; Ogura, K.; Sagisaka, A.; Kon, A.; Esirkepov, T.Z.; Hayashi, Y.; Kotaki, H.; Kanasaki, M.; et al. High-contrast, high-intensity petawatt-class laser and applications. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 232–249. [Google Scholar] [CrossRef]
- Danson, C.; Hillier, D.; Hopps, N.; Neely, D. Petawatt class lasers worldwide. High Power Laser Sci. Eng. 2015, 3, e3. [Google Scholar] [CrossRef]
- Mason, P.; Divoký, M.; Ertel, K.; Pilař, J.; Butcher, T.; Hanuš, M.; Banerjee, S.; Phillips, J.; Smith, J.; De Vido, M.; et al. Kilowatt average power 100 J-level diode pumped solid state laser. Optica 2017, 4, 438–439. [Google Scholar] [CrossRef]
- Fujioka, K.; Mochida, T.; Fujimoto, Y.; Tokita, S.; Kawanaka, J.; Maruyama, M.; Sugiyama, A.; Miyanaga, N. Heat treatment of transparent Yb:YAG and YAG ceramics and its influence on laser performance. Opt. Mater. 2018, 79, 353–357. [Google Scholar] [CrossRef]
- Chi, H.; Dehne, K.A.; Baumgarten, C.M.; Wang, H.; Yin, L.; Reagan, B.A.; Rocca, J.J. In situ 3-D temperature mapping of high average power cryogenic laser amplifiers. Opt. Express 2018, 26, 5240–5252. [Google Scholar] [CrossRef] [PubMed]
- Furuse, H.; Koike, Y.; Yasuhara, R. Sapphire/Nd:YAG composite by pulsed electric current bonding for high-average-power lasers. Opt. Lett. 2018, 43, 3065–3068. [Google Scholar] [CrossRef] [PubMed]
- Snetkov, I.L.; Voitovich, A.V.; Palashov, O.V.; Khazanov, E.A. Review of faraday isolators for kilowatt average power lasers. IEEE J. Quantum Electron. 2014, 50, 434–443. [Google Scholar] [CrossRef]
- Khazanov, E. Thermooptics of magnetoactive medium: Faraday isolators for high average power lasers. Uspekhi Fiz. Nauk 2016, 186, 975–1000. [Google Scholar] [CrossRef]
- Khazanov, E.A. Compensation of thermally induced polarization distortions in Faraday isolators. Quantum Electron. 1999, 29, 59–64. [Google Scholar] [CrossRef]
- Khazanov, E.; Andreev, N.F.; Mal’shakov, A.; Palashov, O.; Poteomkin, A.K.; Sergeev, A.; Shaykin, A.A.; Zelenogorsky, V.; Ivanov, I.A.; Amin, R.; et al. Compensation of thermally induced modal distortions in Faraday isolators. IEEE J. Quantum Electron. 2004, 40, 1500–1510. [Google Scholar] [CrossRef]
- Snetkov, I.; Mukhin, I.; Palashov, O.; Khazanov, E. Compensation of thermally induced depolarization in Faraday isolators for high average power lasers. Opt. Express 2011, 19, 6366–6376. [Google Scholar] [CrossRef]
- Snetkov, I.L.; Palashov, O.V. Compensation of thermal effects in Faraday isolator for high average power lasers. Appl. Phys. B Lasers Opt. 2012, 109, 239–247. [Google Scholar] [CrossRef]
- Shiraishi, K.; Tajima, F.; Kawakami, S. Compact Faraday rotator for an optical isolator using magnets arranged with alternating polarities. Opt. Lett. 1986, 11, 82–84. [Google Scholar] [CrossRef]
- Gauthier, D.J.; Narum, P.; Boyd, R.W. Simple, compact, high-performance permanent-magnet Faraday isolator. Opt. Lett. 1986, 11, 623–625. [Google Scholar] [CrossRef]
- Fischer, G.L.; Moore, T.R.; Boyd, R.W. Enhancement of the Uniformity and Rotation of Large Aperture, Permanent Magnet, Tunable Faraday Rotators. J. Mod. Opt. 1995, 42, 1137–1143. [Google Scholar] [CrossRef]
- Mukhin, I.; Voitovich, A.; Palashov, O.; Khazanov, E. 2.1 Tesla permanent-magnet Faraday isolator for subkilowatt average power lasers. Opt. Commun. 2009, 282, 1969–1972. [Google Scholar] [CrossRef]
- Trénec, G.; Volondat, W.; Cugat, O.; Vigué, J. Permanent magnets for Faraday rotators inspired by the design of the magic sphere. Appl. Opt. 2011, 50, 4788–4797. [Google Scholar] [CrossRef]
- Mironov, E.A.; Snetkov, I.L.; Voitovich, A.V.; Palashov, O.V. Permanent-magnet Faraday isolator with the field intensity of 25 kOe. Quantum Electron. 2013, 43, 740–743. [Google Scholar] [CrossRef]
- Mukhin, I.B.; Khazanov, E.A. Use of thin discs in Faraday isolators for high-average-power lasers. Quantum Electron. 2004, 34, 973–978. [Google Scholar] [CrossRef]
- Palashov, O.V.; Ievlev, I.B.; Perevezentsev, E.A.; Katin, E.V.; Khazanov, E.A. Cooling and thermal stabilisation of Faraday rotators in the temperature range 300-200 K using Peltier elements. Quantum Electron. 2011, 41, 858–861. [Google Scholar] [CrossRef]
- Slezak, O.; Yasuhara, R.; Lucianetti, A.; Vojna, D.; Mocek, T. Thermally induced depolarization in terbium gallium garnet ceramics rod with natural convection cooling. J. Opt. 2015, 17. [Google Scholar] [CrossRef]
- Zheleznov, D.S.; Mukhin, I.B.; Palashov, O.V.; Khazanov, E.A.; Voitovich, A.V. Faraday Rotators with Short Magneto-Optical Elements for 50-kW Laser Power. IEEE J. Quantum Electron. 2007, 43, 451–457. [Google Scholar] [CrossRef]
- Zheleznov, D.S.; Zelenogorskii, V.V.; Katin, E.V.; Mukhin, I.B.; Palashov, O.V.; Khazanov, E.A. Cryogenic Faraday isolator. Quantum Electron. 2010, 40, 276–281. [Google Scholar] [CrossRef]
- Starobor, A.V.; Zheleznov, D.S.; Palashov, O.V.; Khazanov, E.A. Magnetoactive media for cryogenic Faraday isolators. J. Opt. Soc. Am. B 2011, 28, 1409–1415. [Google Scholar] [CrossRef]
- Weber, M.J. Faraday Rotator Materials For Laser Systems. Proc. SPIE 1987, 681, 75–90. [Google Scholar] [CrossRef]
- Dai, J.; Li, J. Promising magneto-optical ceramics for high power Faraday isolators. Scr. Mater. 2018, 155, 78–84. [Google Scholar] [CrossRef]
- Mukhin, I.B.; Palashov, O.V.; Khazanov, E.A.; Ivanov, I.A. Influence of the orientation of a crystal on thermal polarization effects in high-power solid-state lasers. J. Exp. Theor. Phys. Lett. 2005, 81, 90–94. [Google Scholar] [CrossRef]
- Snetkov, I.; Vyatkin, A.; Palashov, O.; Khazanov, E. Drastic reduction of thermally induced depolarization in CaF_2 crystals with [111] orientation. Opt. Express 2012, 20, 13357–13367. [Google Scholar] [CrossRef]
- Yasuhara, R.; Snetkov, I.; Starobor, A.; Mironov, E.; Palashov, O. Faraday rotator based on TSAG crystal with <001> orientation. Opt. Express 2016, 24, 15486–15493. [Google Scholar] [CrossRef]
- Snetkov, I.L. Features of Thermally Induced Depolarization in Magneto-Active Media With Negative Optical Anisotropy Parameter. IEEE J. Quantum Electron. 2018, 54, 1–8. [Google Scholar] [CrossRef]
- Snetkov, I.L.; Mukhin, I.B.; Palashov, O.V.; Khazanov, E.A. Properties of a thermal lens in laser ceramics. Quantum Electron. 2007, 37, 633–638. [Google Scholar] [CrossRef]
- Snetkov, I.L.; Silin, D.E.; Palashov, O.V.; Khazanov, E.A.; Yagi, H.; Yanagitani, T.; Yoneda, H.; Shirakawa, A.; Ueda, K.i.; Kaminskii, A.A. Study of the thermo-optical constants of Yb doped Y2O3, Lu2O3 and Sc2O3 ceramic materials. Opt. Express 2013, 21, 21254–21263. [Google Scholar] [CrossRef]
- Snetkov, I.L.; Yasuhara, R.; Starobor, A.V.; Mironov, E.A.; Palashov, O.V. Thermo-Optical and Magneto-Optical Characteristics of Terbium Scandium Aluminum Garnet Crystals. IEEE J. Quantum Electron. 2015, 51, 1–7. [Google Scholar] [CrossRef]
- Mironov, E.A.; Volkov, M.R.; Palashov, O.V.; Karimov, D.N.; Khaydukov, E.V.; Ivanov, I.A. Thermo-optical properties of EuF2-based crystals. Appl. Phys. Lett. 2019, 114, 073506. [Google Scholar] [CrossRef]
- Yakovlev, A.; Snetkov, I.; Palashov, O. The dependence of optical anisotropy parameter on dopant concentration in Yb:CaF2 and Tb:CaF2 crystals. Opt. Mater. 2018, 77, 127–131. [Google Scholar] [CrossRef]
- Flores, J.L.; Ferrari, J.A. Verdet constant dispersion measurement using polarization-stepping techniques. Appl. Opt. 2008, 47, 4396–4399. [Google Scholar] [CrossRef]
- Slezák, O.; Yasuhara, R.; Lucianetti, A.; Mocek, T. Temperature-wavelength dependence of terbium gallium garnet ceramics Verdet constant. Opt. Mater. Express 2016, 6, 3683–3691. [Google Scholar] [CrossRef]
- Vojna, D.; Yasuhara, R.; Slezák, O.; Mužík, J.; Lucianetti, A.; Mocek, T. Verdet constant dispersion of CeF3 in the visible and near-infrared spectral range. Opt. Eng. 2017, 56, 067105. [Google Scholar] [CrossRef]
- Vojna, D.; Yasuhara, R.; Furuse, H.; Slezak, O.; Hutchinson, S.; Lucianetti, A.; Mocek, T.; Cech, M. Faraday effect measurements of holmium oxide (Ho2O2) ceramics-based magneto-optical materials. High Power Laser Sci. Eng. 2018, 6, e2. [Google Scholar] [CrossRef]
- Slezák, O.; Yasuhara, R.; Vojna, D.; Furuse, H.; Lucianetti, A.; Mocek, T. Temperature-wavelength dependence of Verdet constant of Dy2O3 ceramics. Opt. Mater. Express 2019, 9, 2971–2981. [Google Scholar] [CrossRef]
- Barnes, N.P.; Petway, L.B. Variation of the Verdet constant with temperature of terbium gallium garnet. J. Opt. Soc. Am. B 1992, 9, 1912–1915. [Google Scholar] [CrossRef]
- Karimov, D.N.; Sobolev, B.P.; Ivanov, I.A.; Kanorsky, S.I.; Masalov, A.V. Growth and magneto-optical properties of Na0.37Tb0.63F2.26 cubic single crystal. Crystallogr. Rep. 2014, 59, 718–723. [Google Scholar] [CrossRef]
- Yasuhara, R.; Tokita, S.; Kawanaka, J.; Kawashima, T.; Kan, H.; Yagi, H.; Nozawa, H.; Yanagitani, T.; Fujimoto, Y.; Yoshida, H.; et al. Cryogenic temperature characteristics of Verdet constant on terbium gallium garnet ceramics. Opt. Express 2007, 15, 11255–11261. [Google Scholar] [CrossRef]
- Majeed, H.; Shaheen, A.; Anwar, M.S. Complete Stokes polarimetry of magneto-optical Faraday effect in a terbium gallium garnet crystal at cryogenic temperatures. Opt. Express 2013, 21, 25148–25158. [Google Scholar] [CrossRef]
- Serber, R. The Theory of the Faraday Effect in Molecules. Phys. Rev. 1932, 41, 489–506. [Google Scholar] [CrossRef]
- Van Vleck, J.H.; Hebb, M.H. On the paramagnetic rotation of tysonite. Phys. Rev. 1934, 46, 17–32. [Google Scholar] [CrossRef]
- Buckingham, A.D.; Stephens, P.J. Magnetic Optical Activity. Annu. Rev. Phys. Chem. 1966, 17, 399–432. [Google Scholar] [CrossRef]
- Mukimov, K.M.; Sokolov, B.Y.; Valiev, U.V. The Faraday Effect of Rare-Earth Ions in Garnets. Phys. Status Solidi (a) 1990, 119, 307–315. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2005; pp. 297–361. [Google Scholar]
- Slezak, O.; Yasuhara, R.; Lucianetti, A.; Mocek, T. Wavelength dependence of magneto-optic properties of terbium gallium garnet ceramics. Opt. Express 2015, 23, 13641–13647. [Google Scholar] [CrossRef]
- Vasyliev, V.; Villora, E.G.; Nakamura, M.; Sugahara, Y.; Shimamura, K. UV-visible Faraday rotators based on rare-earth fluoride single crystals: LiREF4 (RE = Tb, Dy, Ho, Er and Yb), PrF3 and CeF3. Opt. Express 2012, 20, 14460–14470. [Google Scholar] [CrossRef]
- Mironov, E.A.; Starobor, A.V.; Snetkov, I.L.; Palashov, O.V.; Furuse, H.; Tokita, S.; Yasuhara, R. Thermo-optical and magneto-optical characteristics of CeF3 crystal. Opt. Mater. 2017, 69, 196–201. [Google Scholar] [CrossRef]
- Molina, P.; Vasyliev, V.; Víllora, E.G.; Shimamura, K. CeF3 and PrF3 as UV-Visible Faraday rotators. Opt. Express 2011, 19, 11786–11791. [Google Scholar] [CrossRef]
- Berger, S.B.; Rubinstein, C.B.; Kurkjian, C.R.; Treptow, A.W. Faraday Rotation of Rare-Earth (III) Phosphate Glasses. Phys. Rev. 1964, 133, A723–A727. [Google Scholar] [CrossRef]
- Rubinstein, C.B.; Van Uitert, L.G.; Grodkiewicz, W.H. Magneto-Optical Properties of Rare Earth (III) Aluminum Garnets. J. Appl. Phys. 1964, 35, 3069–3070. [Google Scholar] [CrossRef]
- Rubinstein, C.B.; Berger, S.B.; Van Uitert, L.G.; Bonner, W.A. Faraday Rotation of Rare-Earth (III) Borate Glasses. J. Appl. Phys. 1964, 35, 2338–2340. [Google Scholar] [CrossRef]
- Crossley, W.A.; Cooper, R.W.; Page, J.L.; van Stapele, R.P. Faraday Rotation in Rare-Earth Iron Garnets. Phys. Rev. 1969, 181, 896–904. [Google Scholar] [CrossRef]
- Potseluyko, A.; Edelman, I.; Malakhovskii, A.; Yeshurun, Y.; Zarubina, T.; Zamkov, A.; Zaitsev, A. RE containing glasses as effective magneto-optical materials for 200–400 nm range. Microelectron. Eng. 2003, 69, 216–220. [Google Scholar] [CrossRef]
- Tanaka, K.; Tatehata, N.; Fujita, K.; Hirao, K.; Soga, N. The Faraday effect and magneto-optical figure of merit in the visible region for lithium borate glasses containing. J. Phys. D Appl. Phys. 1998, 31, 2622–2627. [Google Scholar] [CrossRef]
- Qiu, J.; Tanaka, K.; Sugimoto, N.; Hirao, K. Faraday effect in Tb3+-containing borate, fluoride and fluorophosphate glasses. J. Non-Cryst. Solids 1997, 213-214, 193–198. [Google Scholar] [CrossRef]
- Petrovskii, G.; Edelman, I.; Zarubina, T.; Malakhovskii, A.; Zabluda, V.; Ivanov, M. Faraday effect and spectral properties of high-concentrated rare earth oxide glasses in visible and near UV region. J. Non-Cryst. Solids 1991, 130, 35–40. [Google Scholar] [CrossRef]
- Koralewski, M. Dispersion of the faraday rotation in KDP-type crystals by pulse high magnetic field. Phys. Status Solidi (a) 1981, 65, K49–K53. [Google Scholar] [CrossRef]
- Dexter, J.; Landry, J.; Cooper, D.; Reintjes, J. Ultraviolet optical isolators utilizing KDP-isomorphs. Opt. Commun. 1990, 80, 115–118. [Google Scholar] [CrossRef]
- Weber, M.J.; Morgret, R.; Leung, S.Y.; Griffin, J.A.; Gabbe, D.; Linz, A. Magneto-optical properties of KTb3F10 and LiTbF4 crystals. J. Appl. Phys. 1978, 49, 3464–3469. [Google Scholar] [CrossRef]
- Leycuras, C.; Le Gall, H.; Guillot, M.; Marchand, A. Magnetic susceptibility and Verdet constant in rare earth trifluorides. J. Appl. Phys. 1984, 55, 2161–2163. [Google Scholar] [CrossRef]
- Xu, Y.; Duan, M. Theory of Faraday rotation and susceptibility of rare-earth trifluorides. Phys. Rev. B 1992, 46, 11636–11641. [Google Scholar] [CrossRef]
- Víllora, E.G.; Shimamura, K.; Plaza, G.R. Ultraviolet-visible optical isolators based on CeF3 Faraday rotator. J. Appl. Phys. 2015, 117, 8–12. [Google Scholar] [CrossRef]
- Zelmon, D.E.; Erdman, E.C.; Stevens, K.T.; Foundos, G.; Kim, J.R.; Brady, A. Optical properties of lithium terbium fluoride and implications for performance in high power lasers. Appl. Opt. 2016, 55, 834–837. [Google Scholar] [CrossRef]
- Villaverde, A.B.; Donatti, D.A.; Bozinis, D.G. Terbium gallium garnet Verdet constant measurements with pulsed magnetic field. J. Phys. C: Solid State Phys. 1978, 11, L495–L498. [Google Scholar] [CrossRef]
- Slack, G.A.; Oliver, D.W. Thermal Conductivity of Garnets and Phonon Scattering by Rare-Earth Ions. Phys. Rev. B 1971, 4, 592–609. [Google Scholar] [CrossRef]
- Wynands, R.; Diedrich, F.; Meschede, D.; Telle, H.R. A compact tunable 60-dB Faraday optical isolator for the near infrared. Rev. Sci. Instrum. 1992, 63, 5586–5590. [Google Scholar] [CrossRef]
- Khazanov, E.; Kulagin, O.; Yoshida, S.; Tanner, D.; Reitze, D. Investigation of self-induced depolarization of laser radiation in terbium gallium garnet. IEEE J. Quantum Electron. 1999, 35, 1116–1122. [Google Scholar] [CrossRef]
- Víllora, E.G.; Molina, P.; Nakamura, M.; Shimamura, K.; Hatanaka, T.; Funaki, A.; Naoe, K. Faraday rotator properties of {Tb3}Sc1.95Lu0.05(Al3)O12, a highly transparent terbium-garnet for visible-infrared optical isolators. Appl. Phys. Lett. 2011, 99, 1–4. [Google Scholar] [CrossRef]
- Linares, R.C. Growth of garnet laser crystals. Solid State Commun. 1964, 2, 229–231. [Google Scholar] [CrossRef]
- Mironov, E.A.; Zheleznov, D.S.; Starobor, A.V.; Voitovich, A.V.; Palashov, O.V.; Bulkanov, A.M.; Demidenko, A.G. Large-aperture Faraday isolator based on a terbium gallium garnet crystal. Opt. Lett. 2015, 40, 2794–2797. [Google Scholar] [CrossRef]
- Malshakov, A.N.; Pasmanik, G.A.; Potemkin, A.K. Comparative characteristics of magneto-optical materials. Appl. Opt. 1997, 36, 6403–6410. [Google Scholar] [CrossRef]
- Hayakawa, T.; Nogami, M.; Nishi, N.; Sawanobori, N. Faraday Rotation Effect of Highly Tb2O3/Dy2O3- Concentrated B2O3-Ga2O3-SiO2-P2O5 Glasses. Chem. Mater. 2002, 14, 3223–3225. [Google Scholar] [CrossRef]
- Gao, G.; Winterstein-Beckmann, A.; Surzhenko, O.; Dubs, C.; Dellith, J.; Schmidt, M.A.; Wondraczek, L. Faraday rotation and photoluminescence in heavily Tb3+-doped GeO2-B2O3-Al2O3-Ga2O3 glasses for fiber-integrated magneto-optics. Sci. Rep. 2015, 5, 8942. [Google Scholar] [CrossRef]
- Ding, J.; Man, P.; Chen, Q.; Guo, L.; Hu, X.; Xiao, Y.; Su, L.; Wu, A.; Zhou, Y.; Zeng, F. Influence of Tb3+ concentration on the optical properties and Verdet constant of magneto-optic ABS-PZZ glass. Opt. Mater. 2017, 69, 202–206. [Google Scholar] [CrossRef]
- Yin, H.; Gao, Y.; Guo, H.; Wang, C.; Yang, C. Effect of B2O3 Content and Microstructure on Verdet Constant of Tb2O3-Doped GBSG Magneto-Optical Glass. J. Phys. Chem. C 2018, 122, 16894–16900. [Google Scholar] [CrossRef]
- Yakovlev, A.; Snetkov, I.; Dorofeev, V.; Motorin, S. Magneto-optical properties of high-purity zinc-tellurite glasses. J. Non-Cryst. Solids 2018, 480, 90–94. [Google Scholar] [CrossRef]
- Geho, M.; Sekijima, T.; Fujii, T. Growth of terbium aluminum garnet (Tb3Al5O12; TAG) single crystals by the hybrid laser floating zone machine. J. Cryst. Growth 2004, 267, 188–193. [Google Scholar] [CrossRef]
- Liu, H.; Zhan, G.; Wu, G.; Song, C.; Wu, X.; Xu, Q.; Chen, X.; Hu, X.; Zhuang, N.; Chen, J. Improved Edge-defined film-fed growth of incongruent-melting Tb3Al5O12 crystal with high magneto-optical and thermal performances. Cryst. Growth Des. 2019, 19, 1525–1531. [Google Scholar] [CrossRef]
- Ganschow, S.; Klimm, D.; Reiche, P.; Uecker, R. On the Crystallization of Terbium Aluminium Garnet. Cryst. Res. Technol. 1999, 34, 615–619. [Google Scholar] [CrossRef]
- Lin, H.; Zhou, S.; Teng, H. Synthesis of Tb3Al5O12 (TAG) transparent ceramics for potential magneto-optical applications. Opt. Mater. 2011, 33, 1833–1836. [Google Scholar] [CrossRef]
- Zheleznov, D.; Starobor, A.; Palashov, O.; Chen, C.; Zhou, S. High-power Faraday isolators based on TAG ceramics. Opt. Express 2014, 22, 2578–2583. [Google Scholar] [CrossRef]
- Zheleznov, D.; Starobor, A.; Palashov, O.; Lin, H.; Zhou, S. Improving characteristics of Faraday isolators based on TAG ceramics by cerium doping. Opt. Lett. 2014, 39, 2183–2186. [Google Scholar] [CrossRef]
- Starobor, A.; Zheleznov, D.; Palashov, O.; Chen, C.; Zhou, S.; Yasuhara, R. Study of the properties and prospects of Ce:TAG and TGG magnetooptical ceramics for optical isolators for lasers with high average power. Opt. Mater. Express 2014, 4, 2127–2132. [Google Scholar] [CrossRef]
- Dai, J.; Pan, Y.; Li, X.; Xie, T.; Yang, Z.; Li, J. Fabrication and properties of (Tb1 - xCex)3Al5O12 magneto-optical ceramics with different doping concentrations. Scr. Mater. 2018, 155, 46–49. [Google Scholar] [CrossRef]
- Starobor, A.; Palashov, O.; Zhou, S. Thermo-optical properties of terbium-aluminum garnet ceramics doped with silicon and titanium. Opt. Lett. 2016, 41, 1510–1513. [Google Scholar] [CrossRef]
- Furuse, H.; Yasuhara, R.; Hiraga, K.; Zhou, S. High Verdet constant of Ti-doped terbium aluminum garnet (TAG) ceramics. Opt. Mater. Express 2016, 6, 191–196. [Google Scholar] [CrossRef]
- Dai, J.; Pan, Y.; Xie, T.; Kou, H.; Li, J. A novel (Tb0.995Ho0.005)3Al5O12 magneto-optical ceramic with high transparency and Verdet constant. Scr. Mater. 2018, 150, 160–163. [Google Scholar] [CrossRef]
- Liu, Q.; Li, X.; Dai, J.; Yang, Z.; Xie, T.; Li, J. Fabrication and characterizations of (Tb1 - xPrx)3Al5O12 magneto-optical ceramics for Faraday isolators. Opt. Mater. 2018, 84, 330–334. [Google Scholar] [CrossRef]
- Hao, D.; Chen, J.; Ao, G.; Tian, Y.; Tang, Y.; Yi, X.; Zhou, S. Fabrication and performance investigation of Thulium-doped TAG transparent ceramics with high magneto-optical properties. Opt. Mater. 2019, 94, 311–315. [Google Scholar] [CrossRef]
- Dai, J.; Pan, Y.; Chen, H.; Xie, T.; Kou, H.; Li, J. Synthesis of Tb4O7 nanopowders by the carbonate-precipitation method for Tb3Al5O12 magneto-optical ceramics. Opt. Mater. 2017, 73, 706–711. [Google Scholar] [CrossRef]
- Hao, D.; Chen, J.; Ao, G.; Tian, Y.; Tang, Y.; Yi, X.; Zhou, S. Effect of Tb4O7 excess on the microstructure and magneto-optical properties of TAG transparent ceramic. Opt. Mater. 2019, 94, 47–52. [Google Scholar] [CrossRef]
- Khazanov, E.A. Investigation of Faraday isolator and Faraday mirror designs for multi-kilowatt power lasers. Proc. SPIE 2003, 4968, 115–126. [Google Scholar] [CrossRef]
- Kagan, M.A.; Khazanov, E.A. Thermally induced birefringence in Faraday devices made from terbium gallium garnet-polycrystalline ceramics. Appl. Opt. 2004, 43, 6030–6039. [Google Scholar] [CrossRef]
- Yoshida, H.; Tsubakimoto, K.; Fujimoto, Y.; Mikami, K.; Fujita, H.; Miyanaga, N.; Nozawa, H.; Yagi, H.; Yanagitani, T.; Nagata, Y.; et al. Optical properties and Faraday effect of ceramic terbium gallium garnet for a room temperature Faraday rotator. Opt. Express 2011, 19, 15181–15187. [Google Scholar] [CrossRef]
- Snetkov, I.L.; Yasuhara, R.; Starobor, A.V.; Palashov, O.V. TGG ceramics based Faraday isolator with external compensation of thermally induced depolarization. Opt. Express 2014, 22, 4144–4151. [Google Scholar] [CrossRef]
- Yasuhara, R.; Snetkov, I.; Starobor, A.; Zheleznov, D.; Palashov, O.; Khazanov, E.; Nozawa, H.; Yanagitani, T. Terbium gallium garnet ceramic Faraday rotator for high-power laser application. Opt. Lett. 2014, 39, 1145–1148. [Google Scholar] [CrossRef]
- Li, X.; Liu, Q.; Jiang, N.; Hu, Z.; Feng, Y.; Pan, H.; Liu, X.; Yang, Z.; Xie, T.; Li, J. Fabrication and characterizations of highly transparent Tb3Ga5O12 magneto-optical ceramics. Opt. Mater. 2019, 88, 238–243. [Google Scholar] [CrossRef]
- Yasuhara, R.; Snetkov, I.; Starobor, A.; Palashov, O. Terbium gallium garnet ceramic-based Faraday isolator with compensation of thermally induced depolarization for high-energy pulsed lasers with kilowatt average power. Appl. Phys. Lett. 2014, 105, 241104. [Google Scholar] [CrossRef]
- Yoshikawa, A.; Kagamitani, Y.; Pawlak, D.; Sato, H.; Machida, H.; Fukuda, T. Czochralski growth of Tb3Sc2Al3O12 single crystal for Faraday rotator. Mater. Res. Bull. 2002, 37, 1–10. [Google Scholar] [CrossRef]
- Kagamitani, Y.; Pawlak, D.; Sato, H.; Yoshikawa, A.; Martinek, J.; Machida, H.; Fukuda, T. Dependence of Faraday effect on the orientation of terbium–scandium–aluminum garnet single crystal. J. Mater. Res. 2004, 19, 579–583. [Google Scholar] [CrossRef]
- Valiev, U.V.; Gruber, J.B.; Burdick, G.W.; Ivanov, I.A.; Fu, D.; Pelenovich, V.O.; Juraeva, N.I. Optical and magnetooptical properties of terbium–scandium–aluminum and terbium-containing (gallates and aluminates) garnets. J. Lumin. 2016, 176, 86–94. [Google Scholar] [CrossRef]
- Ivanov, I.; Karimov, D.; Snetkov, I.; Palashov, O.; Kochurikhin, V.; Masalov, A.; Fedorov, V.; Ksenofontov, D.; Kabalov, Y. Study of the influence of Tb-Sc-Al garnet crystal composition on Verdet constant. Opt. Mater. 2017, 66, 106–109. [Google Scholar] [CrossRef]
- Mironov, E.A.; Palashov, O.V. Faraday isolator based on TSAG crystal for high power lasers. Opt. Express 2014, 22, 23226–23230. [Google Scholar] [CrossRef]
- Starobor, A.; Yasyhara, R.; Snetkov, I.; Mironov, E.; Palashov, O. TSAG-based cryogenic Faraday isolator. Opt. Mater. 2015, 47, 112–117. [Google Scholar] [CrossRef]
- Starobor, A.V.; Snetkov, I.L.; Palashov, O.V. TSAG-based Faraday isolator with depolarization compensation using a counterrotation scheme. Opt. Lett. 2018, 43, 3774–3777. [Google Scholar] [CrossRef]
- Mironov, E.A.; Palashov, O.V.; Voitovich, A.V.; Karimov, D.N.; Ivanov, I.A. Investigation of thermo-optical characteristics of magneto-active crystal Na0.37Tb0.63F2.26. Opt. Lett. 2015, 40, 4919–4922. [Google Scholar] [CrossRef]
- Jalali, A.A.; Rogers, E.; Stevens, K. Characterization and extinction measurement of potassium terbium fluoride single crystal for high laser power applications. Opt. Lett. 2017, 42, 899–902. [Google Scholar] [CrossRef]
- Zelmon, D.E.; Foundos, G.; Stevens, K.T. Magneto-optical properties of potassium terbium fluoride. Proc. SPIE 2018, 10553, 105530E1–105530E8. [Google Scholar] [CrossRef]
- Veber, P.; Velázquez, M.; Gadret, G.; Rytz, D.; Peltz, M.; Decourt, R. Flux growth at 1230 ∘C of cubic Tb2O3 single crystals and characterization of their optical and magnetic properties. CrystEngComm 2015, 17, 492–497. [Google Scholar] [CrossRef]
- Snetkov, I.; Palashov, O. Cryogenic temperature characteristics of Verdet constant of terbium sesquioxide ceramics. Opt. Mater. 2016, 62, 697–700. [Google Scholar] [CrossRef]
- Snetkov, I.L.; Permin, D.A.; Balabanov, S.S.; Palashov, O.V. Wavelength dependence of Verdet constant of Tb3+:Y2O3 ceramics. Appl. Phys. Lett. 2016, 108, 161905. [Google Scholar] [CrossRef]
- Ikesue, A.; Aung, Y.L.; Makikawa, S.; Yahagi, A. Polycrystalline (TbXY1 - X)2O3 Faraday rotator. Opt. Lett. 2017, 42, 4399–4401. [Google Scholar] [CrossRef]
- Ikesue, A.; Aung, Y.; Makikawa, S.; Yahagi, A.; Ikesue, A.; Aung, Y.L.; Makikawa, S.; Yahagi, A. Total Performance of Magneto-Optical Ceramics with a Bixbyite Structure. Materials 2019, 12, 421. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, H.; Wang, J.; Wang, D.; Han, D.; Zhang, J.; Wang, S. Phase transformation process of Tb2O3 at elevated temperature. Scr. Mater. 2019, 171, 108–111. [Google Scholar] [CrossRef]
- Morales, J.R.; Amos, N.; Khizroev, S.; Garay, J.E. Magneto-optical Faraday effect in nanocrystalline oxides. J. Appl. Phys. 2011, 109, 093110. [Google Scholar] [CrossRef]
- Snetkov, I.L.; Yakovlev, A.I.; Permin, D.A.; Balabanov, S.S.; Palashov, O.V. Magneto-optical Faraday effect in dysprosium oxide (Dy2O3) based ceramics obtained by vacuum sintering. Opt. Lett. 2018, 43, 4041–4044. [Google Scholar] [CrossRef]
- Yakovlev, A.; Snetkov, I.; Permin, D.; Balabanov, S.; Palashov, O. Faraday rotation in cryogenically cooled dysprosium based (Dy2O3) ceramics. Scr. Mater. 2019, 161, 32–35. [Google Scholar] [CrossRef]
- Furuse, H.; Yasuhara, R. Magneto-optical characteristics of holmium oxide (Ho2O3) ceramics. Opt. Mater. Express 2017, 7, 827–833. [Google Scholar] [CrossRef]
- Lu, B.; Cheng, H.; Xu, X.; Chen, H. Preparation and characterization of transparent magneto-optical Ho2O3 ceramics. J. Am. Ceram. Soc. 2018, 102, 118–122. [Google Scholar] [CrossRef]
- Cheng, H.; Lu, B.; Liu, Y.; Zhao, Y.; Sakka, Y.; Li, J.G. Transparent magneto-optical Ho2O3 ceramics: Role of self-reactive resultant oxyfluoride additive and investigation of vacuum sintering kinetics. Ceram. Int. 2019, 45, 14761–14767. [Google Scholar] [CrossRef]
- Starobor, A.; Palashov, O. Peculiarity of the thermally induced depolarization and methods of depolarization compensation in square-shaped Yb:YAG active elements. Opt. Commun. 2017, 402, 468–471. [Google Scholar] [CrossRef]
- Starobor, A.; Mironov, E.; Palashov, O. High-power Faraday isolator on a uniaxial CeF3 crystal. Opt. Lett. 2019, 44, 1297–1299. [Google Scholar] [CrossRef]
- Liu, J.; Guo, F.; Zhao, B.; Zhuang, N.; Chen, Y.; Gao, Z.; Chen, J. Growth and magneto-optical properties of NaTb(WO4)2. J. Cryst. Growth 2008, 310, 2613–2616. [Google Scholar] [CrossRef]
- Hu, Q.; Jia, Z.; Yin, Y.; Mu, W.; Zhang, J.; Tao, X. Crystal growth, thermal and optical properties of TSLAG magneto-optical crystals. J. Alloys Compd. 2019, 805, 496–501. [Google Scholar] [CrossRef]
- Chen, X.; Ruan, M.; Guo, F.; Chen, J. Czochralski growth, magnetic and magneto-optical properties of Na2Tb4(MoO4)7 crystal. J. Cryst. Growth 2015, 421, 8–12. [Google Scholar] [CrossRef]
- Li, R.K.; Wu, C.C.; Xia, M.J. LiCaTb5(BO3)6: A new magneto-optical crystal promising as Faraday rotator. Opt. Mater. 2016, 62, 452–457. [Google Scholar] [CrossRef]
- Chen, Z.; Hang, Y.; Yang, L.; Wang, J.; Wang, X.; Hong, J.; Zhang, P.; Shi, C.; Wang, Y. Fabrication and characterization of cerium-doped terbium gallium garnet with high magneto-optical properties. Opt. Lett. 2015, 40, 820–822. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, L.; Wang, X.; Hang, Y. Wavelength dependence of Verdet constant of Pr doped terbium gallium garnet crystal. Opt. Mater. 2016, 62, 475–478. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, L.; Wang, X.; Yin, H. High magneto-optical characteristics of Holmium-doped terbium gallium garnet crystal. Opt. Lett. 2016, 41, 2580–2583. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, L.; Hang, Y.; Wang, X. Improving characteristic of Faraday effect based on the Tm3+doped terbium gallium garnet single crystal. J. Alloys Compd. 2016, 661, 62–65. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, L.; Hang, Y.; Wang, X. Faraday effect improvement by Dy3+-doping of terbium gallium garnet single crystal. J. Solid State Chem. 2016, 233, 277–281. [Google Scholar] [CrossRef]
- Zhu, Y.; Tu, H.; Jia, L.; Yue, Y.; Zhao, Y.; Hu, Z. Growth and thermophysical properties of magneto-optical crystal TbVO4. Opt. Mater. 2017, 65, 106–111. [Google Scholar] [CrossRef]
- Zhu, X.; Tu, H.; Hu, Z.; Zhuang, N. Preparation and characterization of Tb1-xNdxVO4 single crystals for optical isolators. Opt. Mater. 2019, 89, 549–553. [Google Scholar] [CrossRef]
- Guo, F.; Gui, X.; Tao, Z.; Sun, Y.; Chen, X.; Chen, J. Growth, magnetic anisotropy and Faraday characteristics of NaCe(MoO4)2 crystal. Opt. Mater. 2018, 84, 658–662. [Google Scholar] [CrossRef]
- Mironov, E.A.; Palashov, O.V. Spectral, magneto-optical and thermo-optical properties of terbium containing cubic zirconia crystal. Appl. Phys. Lett. 2018, 113, 063504. [Google Scholar] [CrossRef]
- Mironov, E.A.; Palashov, O.V. Characterization of terbium containing cubic zirconia crystal for high power laser applications. Opt. Quantum Electron. 2019, 51, 46. [Google Scholar] [CrossRef]
- Yasuhara, R.; Ikesue, A. Magneto-optic pyrochlore ceramics of Tb2Hf2O7 for Faraday rotator. Opt. Express 2019, 27, 7485–7490. [Google Scholar] [CrossRef]
- Guo, F.; Li, Q.; Zhang, H.; Yang, X.; Tao, Z.; Chen, X.; Chen, J.; Guo, F.; Li, Q.; Zhang, H.; et al. Czochralski Growth, Magnetic Properties and Faraday Characteristics of CeAlO3 Crystals. Crystals 2019, 9, 245. [Google Scholar] [CrossRef]
- Cooper, R.W.; Crossley, W.A.; Page, J.L.; Pearson, R.F. Faraday Rotation in YIG and TbIG. J. Appl. Phys. 1968, 39, 565–567. [Google Scholar] [CrossRef]
- Booth, R.C.; White, E.A.D. Magneto-optic properties of rare earth iron garnet crystals in the wavelength range 1.1–1.7 μm and their use in device fabrication. J. Phys. D Appl. Phys. 1984, 17, 579–587. [Google Scholar] [CrossRef]
- Zhao, W. Magneto-optic properties and sensing performance of garnet YbBi:YIG. Sens. Actuators A Phys. 2001, 89, 250–254. [Google Scholar] [CrossRef]
- Huang, M.; Zhang, S.Y. Growth and characterization of cerium-substituted yttrium iron garnet single crystals for magneto-optical applications. Appl. Phys. A Mater. Sci. Process. 2002, 74, 177–180. [Google Scholar] [CrossRef]
- Stevens, G.; Legg, T.; Shardlow, P. Integrated disruptive components for 2μm fibre lasers (ISLA): project overview and passive component development. Proc. SPIE 2016, 9730, 973001. [Google Scholar] [CrossRef]
- Sekijima, T.; Kishimoto, H.; Fujii, T.; Wakino, K.; Okada, M. Magnetic, Optical and Microwave Properties of Rare-Earth-Substituted Fibrous Yttrium Iron Garnet Single Crystals Grown by Floating Zone Method. Jpn. J. Appl. Phys. 1999, 38, 5874–5878. [Google Scholar] [CrossRef]
- Ikesue, A.; Aung, Y.L. Development of optical grade polycrystalline YIG ceramics for faraday rotator. J. Am. Ceram. Soc. 2018, 101, 5120–5126. [Google Scholar] [CrossRef]
- Mironov, E.; Palashov, O.; Karimov, D. EuF2-based crystals as media for high-power mid-infrared Faraday isolators. Scr. Mater. 2019, 162, 54–57. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).