Temperature-Activated Change of Permeable Material Properties for Low-Noise Trailing Edge Applications
Abstract
1. Introduction
2. Materials and Methods
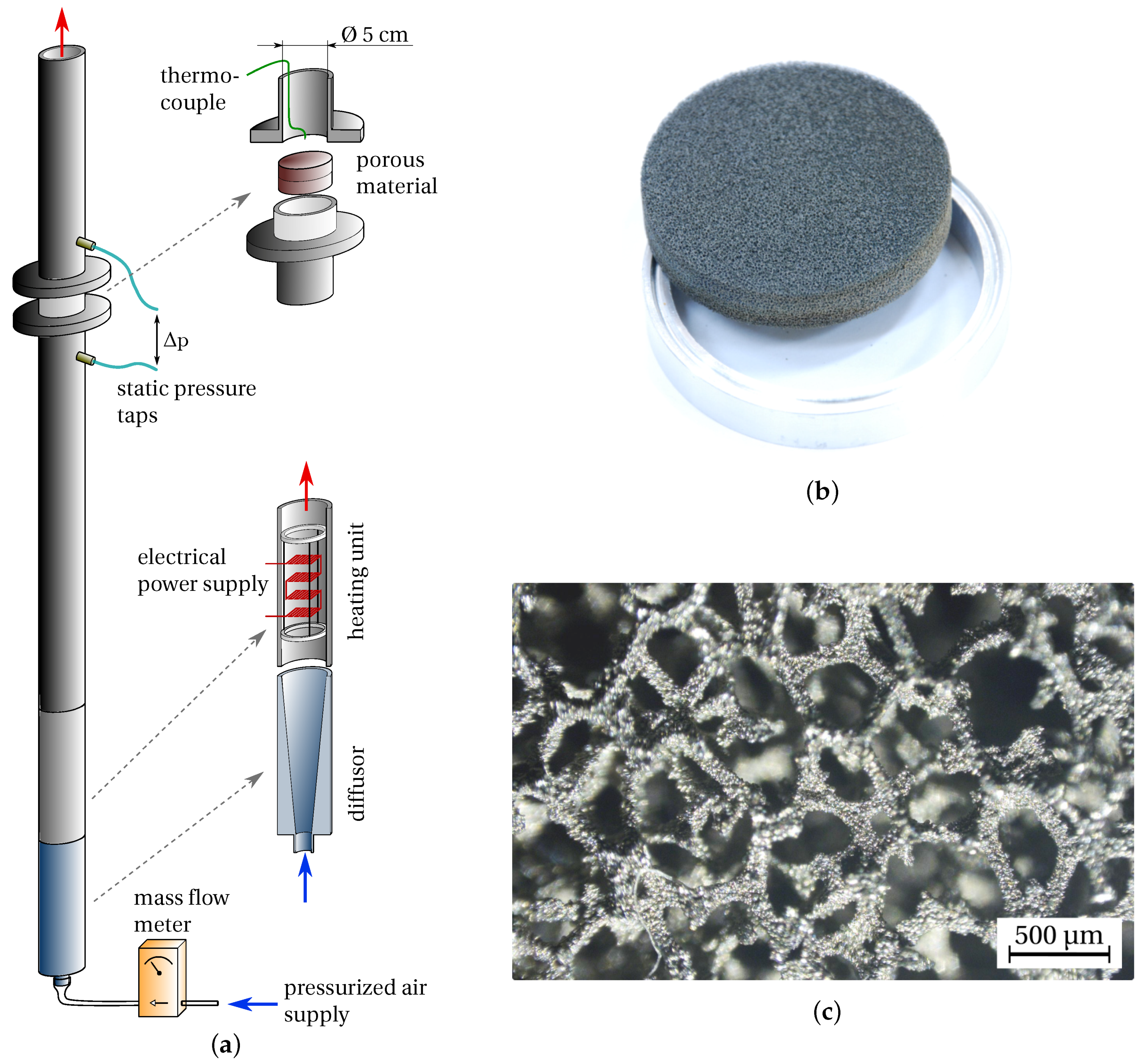
2.1. Flow Resistivity
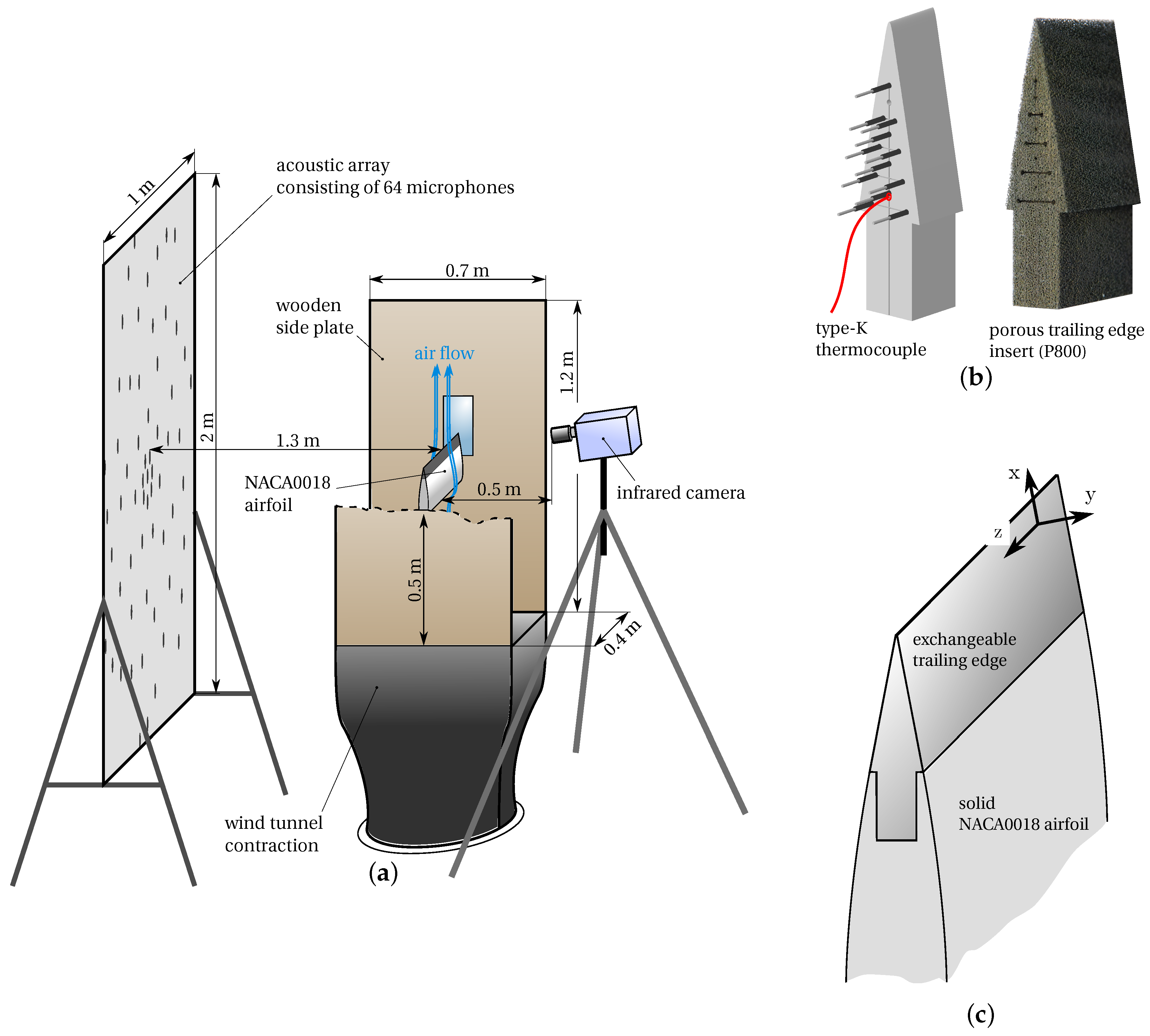
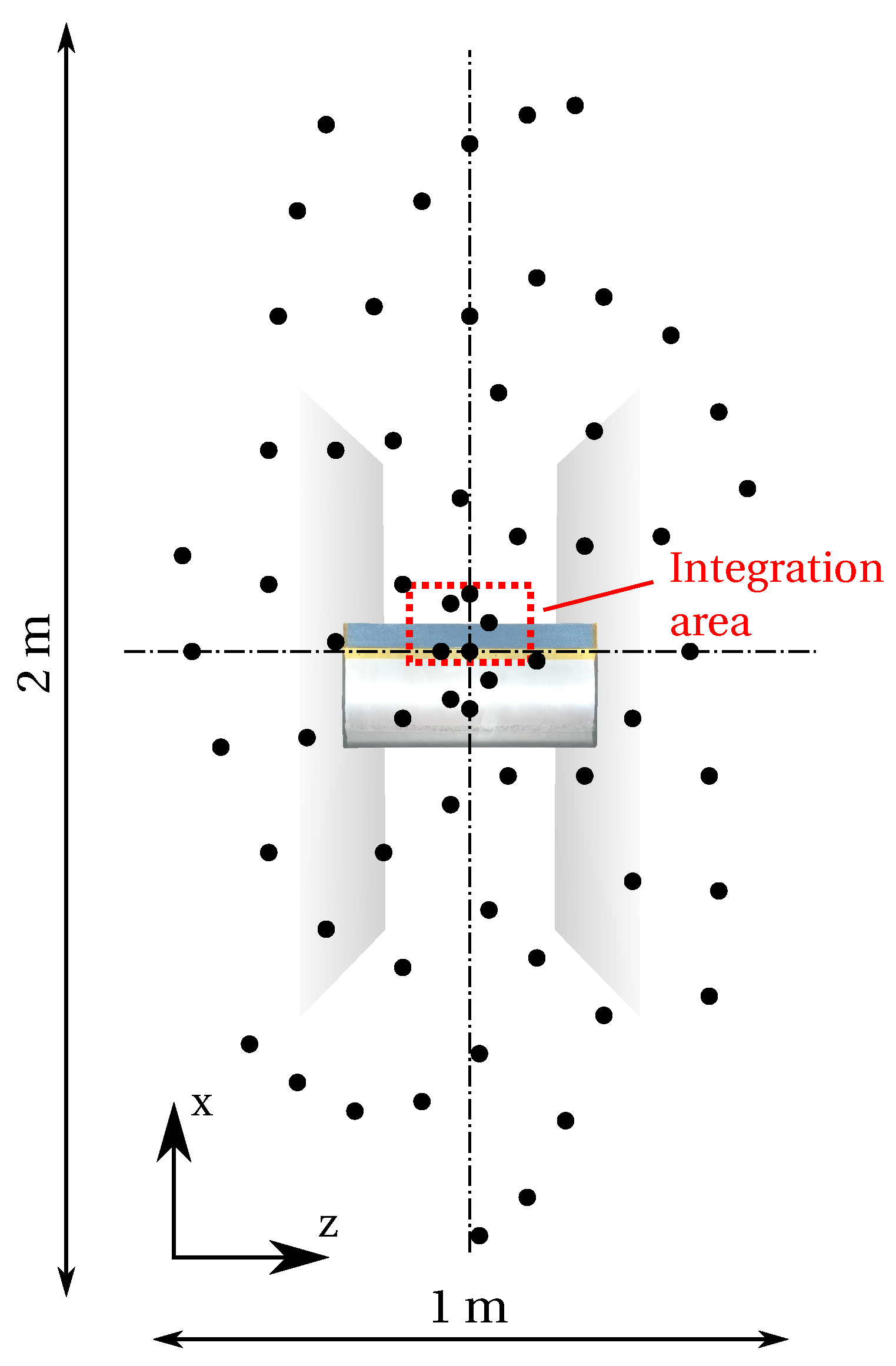
2.2. Aeroacoustic Measurements
3. Results and Discussion
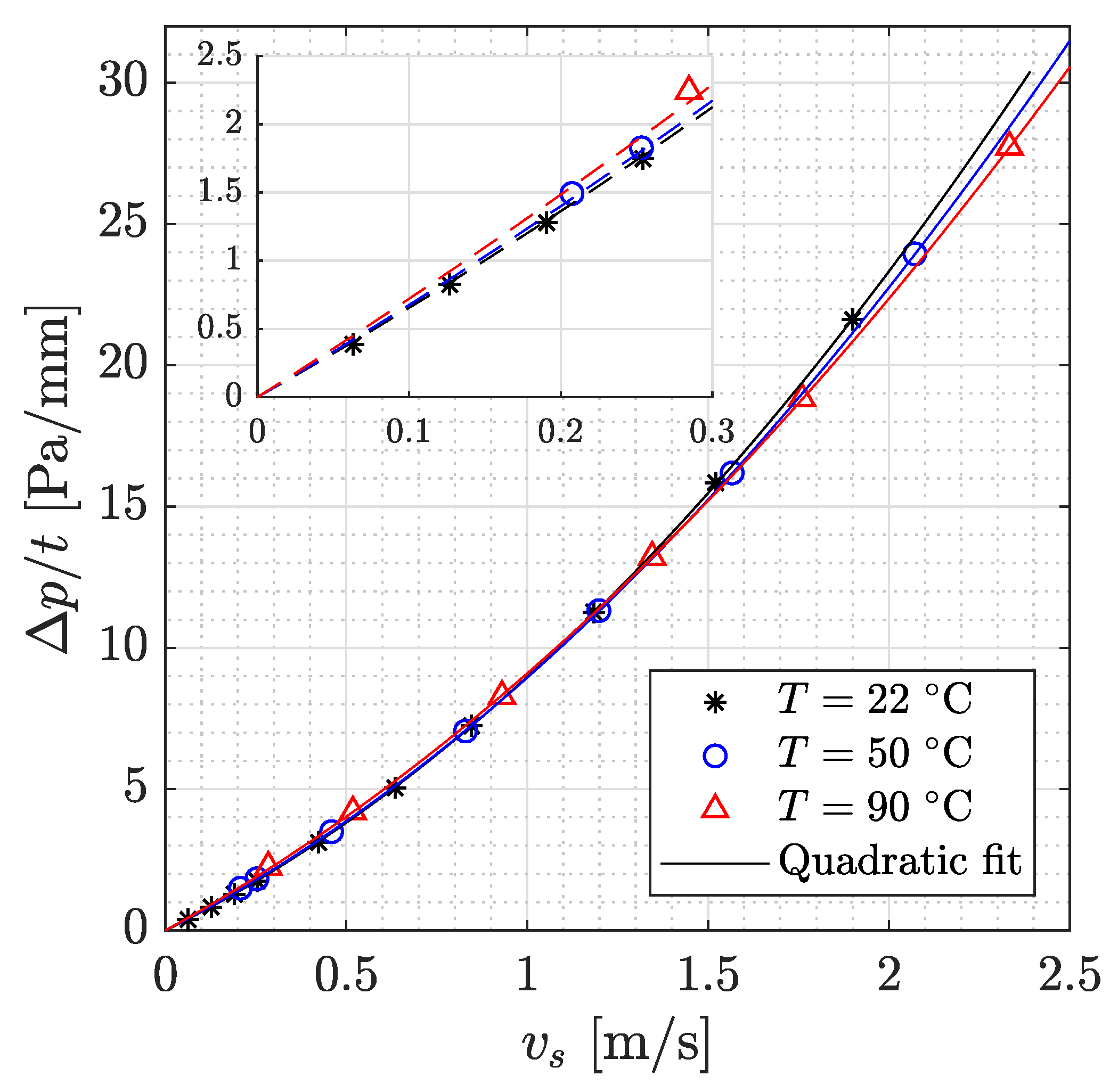
3.1. Heated Flow through Porous Materials
3.2. Far-Field Noise
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| CSM | Cross Spectral Matrix |
| EDM | Electrical Discharge Machining |
| FS | Full Scale |
| IR | Infrared |
| P800 | Porous metal foam with nominal pore size of |
| SPI | Source Power Integration |
| SPL | Sound Pressure Level |
| TBL-TE noise | Turbulent Boundary Layer Trailing Edge noise |
References
- Ruijgrok, G. Elements of Aviation Acoustics; Delft University Press: Delft, The Netherlands, 1993. [Google Scholar]
- Chow, L.; Mau, K.; Remy, H. Landing Gears and High Lift Devices Airframe Noise Research. In Proceedings of the 8th AIAA/CEAS Aeroacoustics Conference, Breckenridge, Colorado, 17–19 June 2002. [Google Scholar] [CrossRef]
- Dobrzynski, W. Almost 40 Years of Airframe Noise Research: What Did We Achieve? J. Aircr. 2010, 47, 353–367. [Google Scholar] [CrossRef]
- Oerlemans, S.; Sijtsma, P.; López, B.M. Location and quantification of noise sources on a wind turbine. J. Sound Vib. 2007, 299, 869–883. [Google Scholar] [CrossRef]
- Merino-Martínez, R. Microphone Arrays for Imaging of Aerospace Noise Sources. Ph.D. Thesis, Technische Universiteit Delft, Delft, The Netherlands, 2018. [Google Scholar] [CrossRef]
- Ffowcs Williams, J.; Hall, L. Aerodynamic sound generation by turbulent flow in the vicinity of a scattering half plane. J. Fluid Mech. 1970, 40, 657–670. [Google Scholar] [CrossRef]
- Hayden, R.E. Exploratory Investigation of Aeroacoustic Optimization of the Variable Impedance Edge Concept Applied to Upper Surface Blown Configurations. In NASA Contractor Report 145072; Bolt Beranek and Newman Inc.: Cambridge, MA, USA, 1976. [Google Scholar]
- Howe, M.S. On the added mass of a perforated shell, with application to the generation of aerodynamic sound by a perforated trailing edge. Proc. R. Soc. Lond. 1979, 365, 209–233. [Google Scholar] [CrossRef]
- Lee, S. Reduction of Blade-Vortex Interaction Noise Through Porous Leading Edge. AIAA J. 1994, 32, 480–488. [Google Scholar] [CrossRef]
- Revell, J.; Kuntz, H.; Balena, F.; Horne, C.; Storms, B.; Dougherty, R. Trailing-edge flap noise reduction by porous acoustic treatment. In Proceedings of the 3rd AIAA/CEAS Aeroacoustics Conference, Atlanta, Georgia, USA, 12–14 May 1997. [Google Scholar] [CrossRef]
- Kisil, A.; Ayton, L. Aerodynamic noise from rigid trailing edges with finite porous extensions. J. Fluid Mech. 2018, 836, 117–144. [Google Scholar] [CrossRef]
- Moreau, S.; Laffay, P.; Idier, A.; Atalla, N. Several noise controls of the trailing-edge noise of a Controlled-Diffusion airfoil. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016. [Google Scholar] [CrossRef]
- Moreau, S.; Dignou, B.; Jaiswal, P.; Yakhina, G.; Pasco, Y.; Sanjose, M.; Alstrom, B.; Atalla, N. Trailing-Edge Noise of a Flat Plate with Several Liner-Type Porous Appendices. 2018 AIAA/CEAS Aeroacoust. Conf. 2018. [Google Scholar] [CrossRef]
- Geyer, T.; Sarradj, E.; Fritzsche, C. Porous airfoils: noise reduction and boundary layer effects. In Proceedings of the 15th AIAA/CEAS Aeroacoustics Conference, Miami, FL, USA, 11–13 May 2009. [Google Scholar] [CrossRef]
- Herr, M.; Rossignol, K.S.; Delfs, J.; Lippitz, N.; Mößner, M. Specification of Porous Materials for Low-Noise Trailing-Edge Applications. In Proceedings of the 20th AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar] [CrossRef]
- Rubio Carpio, A.; Avallone, F.; Ragni, D. On the Role of the Flow Permeability of Metal Foams on Trailing Edge Noise Reduction. In Proceedings of the 2018 AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Vathylakis, A.; Chong, T.P.; Joseph, P.F. Poro-Serrated Trailing-Edge Devices for Airfoil Self-Noise Reduction. AIAA J. 2015, 53, 3379–3394. [Google Scholar] [CrossRef]
- Geyer, T.F.; Sarradj, E. Noise reduction and aerodynamics of airfoils with porous trailing edges. In Proceedings of the 2018 Inter-Noise, Chicago, IL, USA, 26–29 August 2018. [Google Scholar]
- Aldheeb, M.; Asrar, W.; Sulaeman, E.; Omar, A.A. Aerodynamics of porous airfoils and wings. Acta Mech. 2018, 229, 3915–3933. [Google Scholar] [CrossRef]
- Lage, J.L. The Fundamental Theory of Flow through Permeable Media. In Transport Phenomena in Porous Media; Ingham, D.B., Pop, I., Eds.; Elsevier Ltd.: Edinburgh, UK, 1998; pp. 1–30. [Google Scholar] [CrossRef]
- Schewe, G. On the structure and resolution of wall-pressure fluctuations associated with turbulent boundary-layer flow. J. Fluid Mech. 1983, 134, 311–328. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow, 2nd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Mensor Corporation. Operation Manual Digital Pressure Gauge, Series 2100; Mensor Corporation: San Marcos, TX, USA, 2006. [Google Scholar]
- Baril, E.; Mostafid, A.; Lefebvre, L.P.; Medraj, M. Experimental Demonstration of Entrance/Exit Effects on the Permeability Measurements of Porous Materials. Adv. Eng. Mater. 2008, 10, 889–894. [Google Scholar] [CrossRef]
- Bronkhorst. Instruction Manual EL-FLOW Select Series, Thermal Mass Flow Meters and Controllers; Bronkhorst High-Tech B.V.: Ruurlo, The Netherlands, 2018. [Google Scholar]
- Underbrink, J.R. Circulary Symmetric, Zero Redundancy, Planar Array Having Broad Frequency Range Applications. U.S. Patent 6,205,224 B1, 20 March 2001. [Google Scholar]
- Allen, C.S.; Blake, W.K.; Dougherty, R.P.; Lynch, D.; Soderman, P.T.; Underbrink, J.R. Aeroacoustic Measurements; Springer: Berlin, Germany, 2002. [Google Scholar]
- Merino-Martínez, R.; Snellen, M.; Simons, D.G. Functional Beamforming Applied to Imaging of Flyover Noise on Landing Aircraft. J. Aircr. 2016, 53, 1830–1843. [Google Scholar] [CrossRef]
- Sijtsma, P. Phased Array Beamforming Applied to Wind Tunnel and Fly-Over Tests; Report no.: NLR-TP-2010-549; National Aerospace Laboratory NLR: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Merino-Martínez, R.; Sijtsma, P.; Snellen, M. Inverse Integration Method for Distributed Sound Sources. In Proceedings of the 7th Berlin Beamforming Conference, Berlin, Germany, 5–6 March 2018. [Google Scholar]
- Geyer, T.; Sarradj, E. Trailing edge noise of partially porous airfoils. In Proceedings of the 20th AIAA/CEAS Aeroacoustics Conference, AIAA Aviation Forum, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar] [CrossRef]
- Sarradj, E.; Geyer, T. Noise Generation by Porous Airfoils. In Proceedings of the 13th AIAA/CEAS Aeroacoustics Conference, Rome, Italy, 21–23 May 2007; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2007. [Google Scholar] [CrossRef]
- Rubio Carpio, A.; Merino-Martínez, R.; Avallone, F.; Ragni, D.; Snellen, M.; van der Zwaag, S. Broadband Trailing Edge Noise Reduction Using Permeable Metal Foams. In Proceedings of the 46th International Congress and Exposition on Noise Control Engineering Taming Noise and Moving Quiet, Hong Kong, China, 27–30 August 2017; pp. 4373–4383. [Google Scholar]

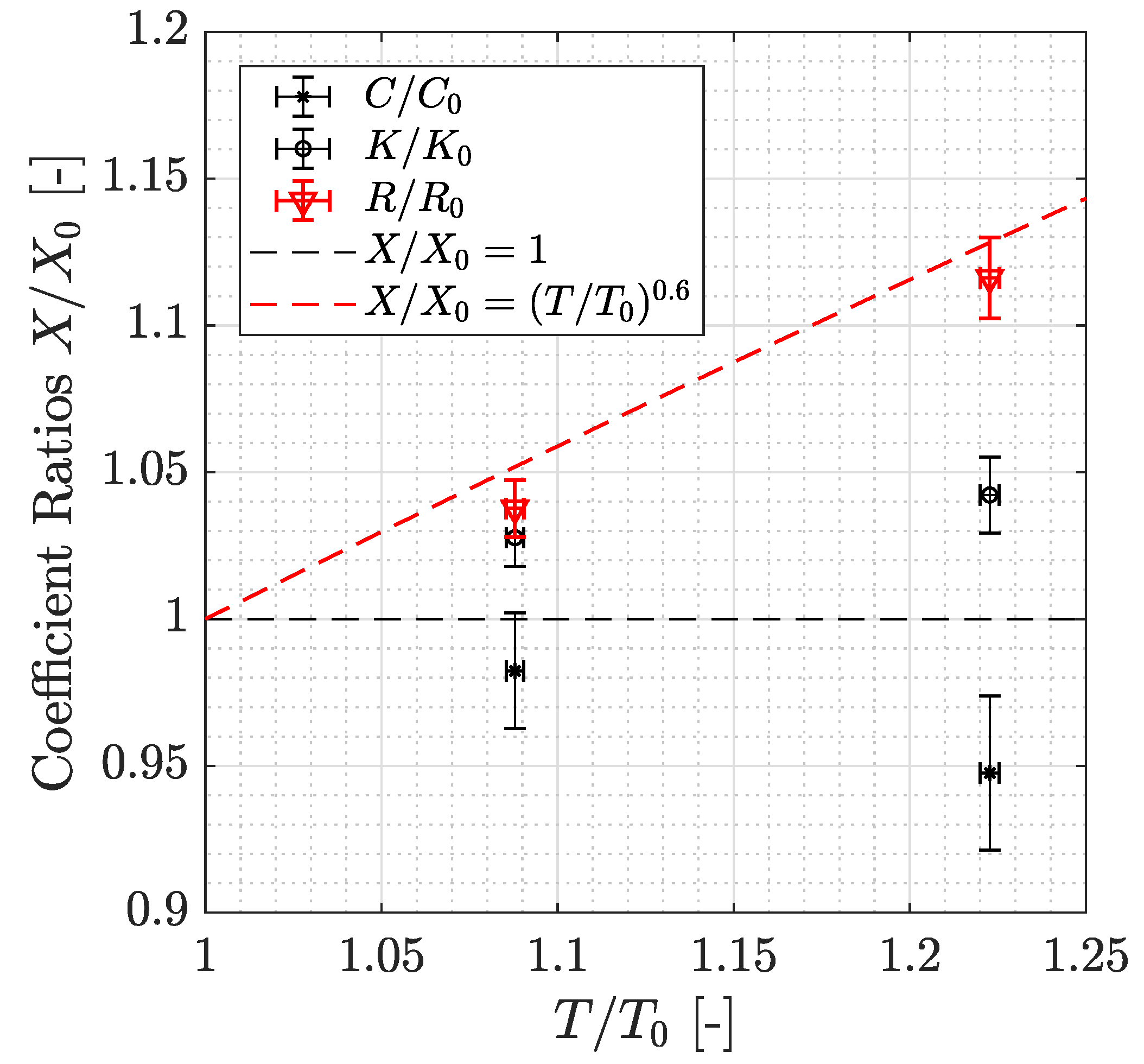
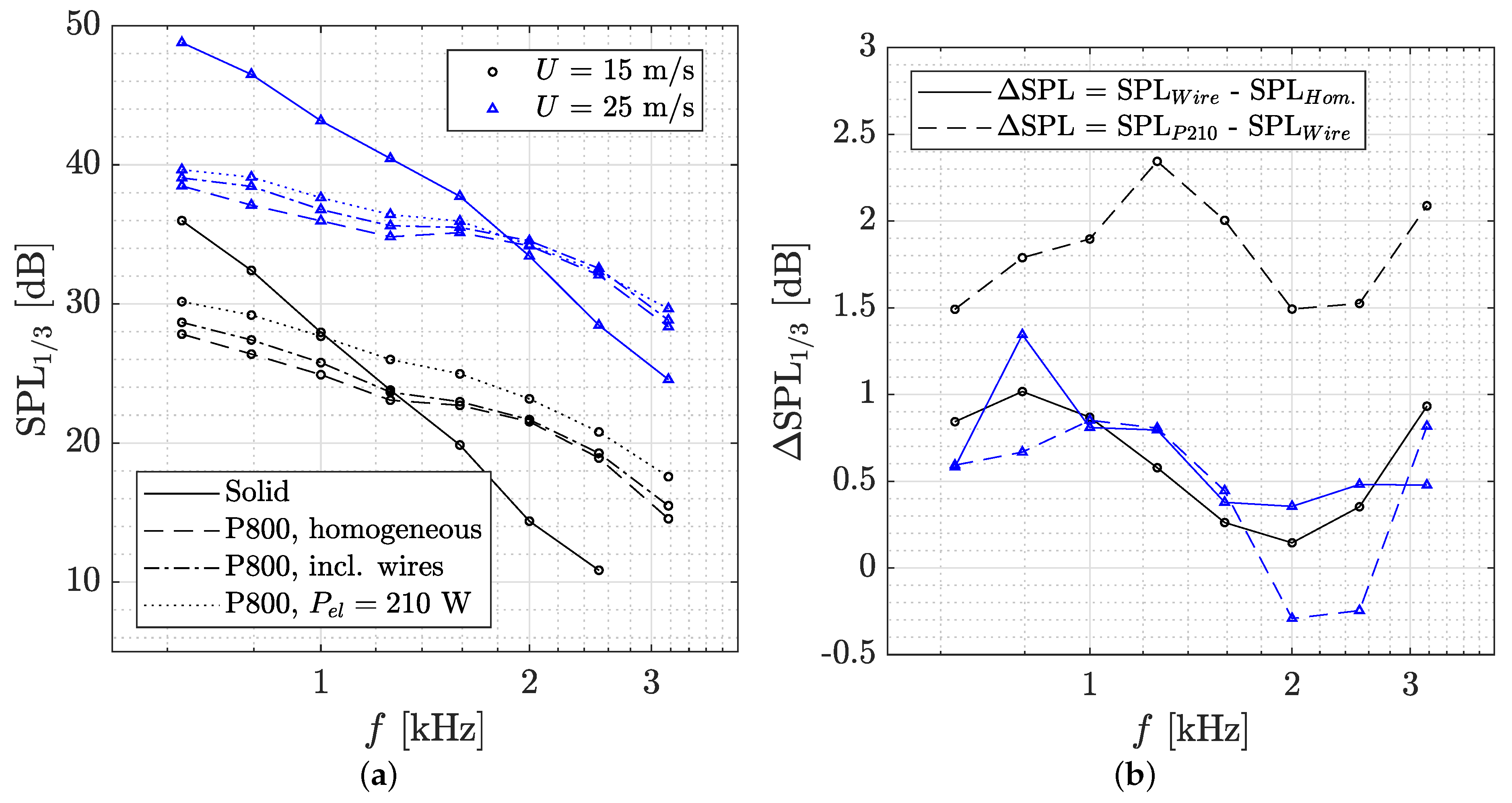
| Nominal Pore Size | Porosity | Resistivity R | Permeability K | form Coefficient C |
|---|---|---|---|---|
| [] | 6274 | 6511 | 7003 |
| [] | |||
| [] | 2242 | 2202 | 2124 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mayer, J.; Rubio Carpio, A.; Ragni, D. Temperature-Activated Change of Permeable Material Properties for Low-Noise Trailing Edge Applications. Appl. Sci. 2019, 9, 3119. https://doi.org/10.3390/app9153119
Mayer J, Rubio Carpio A, Ragni D. Temperature-Activated Change of Permeable Material Properties for Low-Noise Trailing Edge Applications. Applied Sciences. 2019; 9(15):3119. https://doi.org/10.3390/app9153119
Chicago/Turabian StyleMayer, Jonathan, Alejandro Rubio Carpio, and Daniele Ragni. 2019. "Temperature-Activated Change of Permeable Material Properties for Low-Noise Trailing Edge Applications" Applied Sciences 9, no. 15: 3119. https://doi.org/10.3390/app9153119
APA StyleMayer, J., Rubio Carpio, A., & Ragni, D. (2019). Temperature-Activated Change of Permeable Material Properties for Low-Noise Trailing Edge Applications. Applied Sciences, 9(15), 3119. https://doi.org/10.3390/app9153119




