On Data Protection Regulations, Big Data and Sledgehammers in Higher Education

Abstract

Universities in Latin America commonly gather much more information about their students than allowed by data protection regulations in other parts of the world. We have tackled the question of whether abundant socio-economic data can be harnessed for the purpose of predicting academic outcomes and, thereby, taking proactive actions in student attention, course planning and resource management. A study was conducted to analyze the data gathered by a private university in Ecuador over more than 20 years, to normalize them and to parameterize a Multi-Layer Perceptron neural network, whose best-performing configuration would be used as a benchmark for the comparison of more recent and sophisticated Artificial Intelligence techniques. However, an extensive scan of hyperparameters for the perceptron—exploring more than 12,000 configurations—revealed no significant relationships between the input variables and the chosen metrics, suggesting that there is no gain from processing the extensive socio-economic data. This finding contradicts the expectations raised by previous works in the related literature and in some cases highlights important methodological flaws.

1. Introduction

Many countries are implementing data protection regulations by which any personal data collected by public or private entities must be handled according to two general principles:

• Data must be collected for specified, explicit and legitimate purposes and not further processed in a manner that is incompatible with those purposes. Archiving purposes in the public interest, just like scientific or historical research purposes or statistical purposes, are not considered incompatible.
• Data must be adequate, relevant and limited to what is necessary in relation to the purposes for which they are processed.

These requirements on purpose and data minimization have been part of the global debate about data protection rights for years [1], with some stances criticizing the fact that they may create unnecessary/unwanted barriers to trade or to unforeseen uses of the information that would be beneficial for the data subjects [2,3]. Higher Education institutions have not been alien to the discussions, as some scholars argued that gathering as much information as possible about university students, professors and administration staff could enable deep analysis and, thereby, proactive actions in student attention, course planning and resource management [4,5,6]. In this line, there have been numerous studies in the recent past about predicting student outcomes using Artificial Intelligence (AI) techniques [7,8,9,10,11,12,13,14,15,16,17] and it is generally assumed that the more abundant the data, the more accurate the predictions.

We have tackled this question in a context that is not up to the highest standards of fair data use, namely that of Ecuadorean universities, which are representative of common practices held throughout the whole of Latin America. In particular, we have worked with the data gathered by Universidad Politécnica Salesiana (henceforth, UPS) over more than 20 years in the campuses of Cuenca, Guayaquil and Quito, containing profuse information about more than 6000 students. The managers of this institution—motivated by the positive findings of the studies cited above—were interested in analyzing the data, with the expectation of detecting useful relationships among socio-economic variables (e.g., familiar income, health-related conditions, places of origin/residence, …) and metrics of academic performance. Whereas the previous works always fed academic data to the AI (in some cases, along with other data like personality traits [10] or demographic features [13]), we made an experiment to assess the predictive value of socio-economic data alone, in order to better inform the theory in this area of research.

Our experiment consisted in performing a scan of hyperparameters for a Multi-Layer Perceptron (MLP) neural network, in search for the configuration that attained the greater accuracy in predicting academic outcomes from the socio-economic data. We chose the MLP for being one of the best understood machine learning models, commonly used in the related literature [18,19]; its best configuration would be used as a benchmark for the comparison of other techniques, including the ones used in References [7,8,9,10,11,12,13,14,15,16,17] and more advanced neural network schemes. However, the scan of hyperparameters revealed no correlations or dependencies between the input variables and the chosen metrics in any case, showing that—at least for the UPS and alike settings—there is no actual gain from applying machine learning techniques on extensive socio-economic data. This finding yields valuable observations in relation to the hype about AI in Higher Education management and the convenience of modern data management policies.

The paper is organized as follows. First, Section 2 explains how the UPS data were processed, to be fed into the MLP or to assess its outputs. Section 3 describes the criteria for the preparation of the scan of hyperparameters. The results of its execution are presented in Section 4, followed by a discussion with regard to the previous works in Section 5. Our final conclusions are given in Section 6.

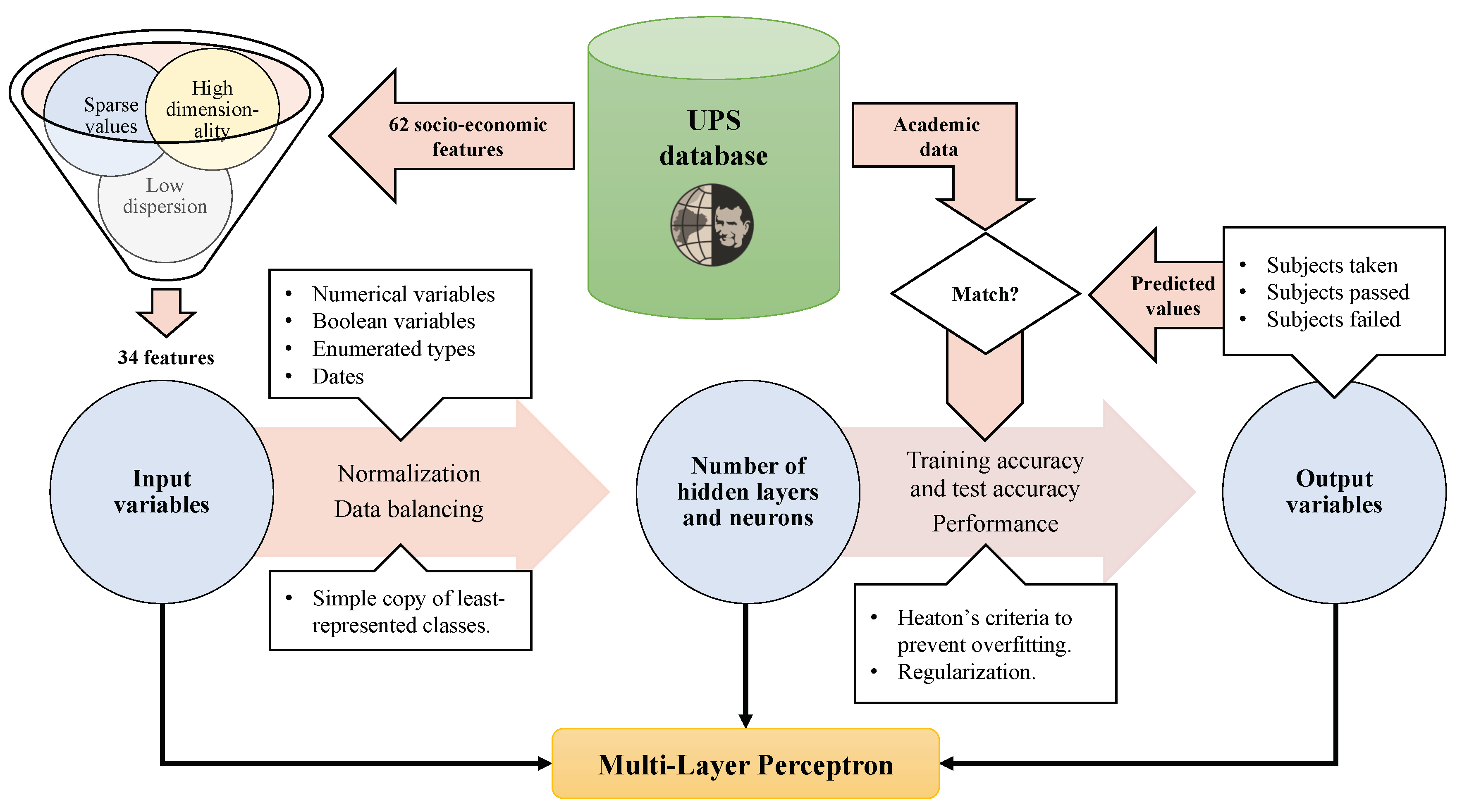
2. Selecting Inputs and Outputs to/from the MLP

Table 1. The data fields captured in the Universidad Politécnica Salesiana (UPS) records.

Field	Type	Values
Gender	Enum	Male/female.
Birthdate	Date	Dates from 1970 to 1996.
Marital status	Enum	Single/married/divorced/widow/domestic partnership.
Country of birth	Enum	Several countries—most commonly, Ecuador.
City of birth	Enum	City names
Nationality	Enum	Several nationalities—most commonly, Ecuadorean.
Race	Enum	White/indigenous/mestizo/black/Afro-Ecuadorean/unknown.
Blood type	Enum	Includes ‘unknown’.
Mobile operator	Enum	Claro/CNT/Movistar/Others.
Country of origin	Enum	Several countries—most commonly, Ecuador.
High school of origin	Enum	Names of many different high schools.
Type of high school	Enum	Foreign/fiscal/fiscommisional/particular.
Province of high school	Enum	Province names.
City of high school	Enum	City names.
High school diploma	Enum	Many official denominations.
High school graduation year	Enum	Dates from 1984 to 2018
High school grade	Float	From 0 to 20, except for foreign students.
Has another diploma?	Boolean	Yes/no.
Diploma level	Enum	Several values, if the above is ‘yes’.
Is currently studying another degree?	Boolean	Yes/no.
Country of residence	Enum	Ecuador.
Province of residence	Enum	Province names.
City of residence	Enum	City names.
Parish of residence	Enum	Parish names.
Type of parish	Enum	Rural/urban/marginal urban.
Neighborhood	Enum	Neighborhood names.
Area of residence	Enum	Center/north/south/valleys/rural/suburbs.
Country of origin	Enum	Several countries—most commonly, Ecuador.
Province of origin	Enum	Province names.
City of origin	Enum	City names.
Parish of origin	Enum	Parish names.
Type of parish	Enum	Rural/urban/marginal urban.
Neighborhood	Enum	Neighborhood names.
Area of origin	Enum	Center/north/south/valleys/rural/suburbs.
Head of family	Boolean	Yes/no.
Economically dependent	Boolean	Yes/no.
Who covers expenses	Enum	Self/parents/siblings/NGO/…
Has health problems?	Boolean	Yes/no.
Has any disability?	Boolean	Yes/no.
Type of disability	Enum	Disability denomination from taxonomy.
Member of CONADIS	Boolean	Yes/no.
Housing	Enum	Own/leased/rented/…
Type of housing	Enum	House/apartment/residence/…
Housing structure	Enum	Bricks/blocks/concrete/wood/substandard/…
Potable water	Boolean	Yes/no.
Sewage system	Boolean	Yes/no.
Electricity supply	Boolean	Yes/no.
Landline phone	Boolean	Yes/no.
Internet	Boolean	Yes/no.
Cable TV	Boolean	Yes/no.
Additional real estate properties	Integer	0/1/2/…
Value of additional properties	Float	Value in USD.
Number of family-owned vehicles	Integer	0/1/2/…
Value of vehicles	Float	Value in USD.
Monthly expenses in housing	Float	Value in USD.
Monthly expenses in food	Float	Value in USD.
Monthly expenses in education	Float	Value in USD.
Monthly expenses in transport	Float	Value in USD.
Monthly expenses in health	Float	Value in USD.
Monthly expenses in commodity services	Float	Value in USD.
Other monthly expenses	Float	Value in USD.
Overall monthly expenses	Float	Sum of the above.

lists the data fields contained in the UPS student records, including demographic information (including aspects like race, that could be controversial in other contexts), data reflecting some peculiarities of Latin American societies (e.g., marginal settings), high school studies, health condition, home economics and some other fields whose pertinence would be questionable elsewhere too (e.g., mobile operator). These 62 parameters appear in the record of each student, along with the academic information related to his/her outcomes in the courses taught at the UPS, such as the grades obtained and the numbers of attempts needed to pass each subject.

To start our study, as shown on the top-left corner of Figure 1, we made a selection of the variables that would be input to the MLP. While we could have taken all of them into account, removing the ones that looked less interesting allowed to reduce the dimensionality of the neural network in the first iterations of the experiment. The following criteria were applied:

• Low dispersion parameters. Some parameters—such as nationality, country of birth or country of residence—were treated separately, because the number of records with values other than ‘Ecuadorean’ or ‘Ecuador’ was very low. While it was interesting to study the differences between nationalities, the convergence of the neural network would be hindered both in terms of speed and quality, while the majority of the estimations to make in the future would be for Ecuadorean students anyway. Besides, the choice of a given mobile operator was not considered relevant, even though it did exhibit some correlation with economic variables.
• Dependent parameters. In a first approach, we decided to use the overall monthly expenses as the only indicator of economic level. Individual items of expenditure were considered in a second stage. Likewise, we did not consider at first the ‘Diploma level’ field, which only gets values when ‘Has another diploma?’ stores ‘Yes’.
• Missing or sparse values. We noticed that several fields about the students’ origin (e.g., province or city) were not systematically filled in, which was not the case for residence data. We thought it was undesirable to handle fields with too many gaps, because we would have to assign some value during the normalization and there would be no clear policies to follow.
• Dates. In general, temporal variables ought to be treated carefully before being used as input to a neural network, because their magnitude and range hampers normalization. Incorrect treatment can lead to overfitting and, thereby, to nullifying the informative value of the variables. (Overfitting happens when a neural network models the training data very accurately but fails to provide proper outputs for unknown data.) We used the normalized datum of the student’s age at high school graduation. A categorization of dates, corresponding to different generations, would be of little interest because, obviously, all the intended predictions would be made for new records, corresponding to posterior dates.
• High dimensionality parameters. Fields like ‘High school of origin’, ‘Parish of residence’ or ‘Neighborhood of residence’ take tens of different values. We did not consider them at first, if there were less granular fields conveying similar information. Thus, for example, in the first stages we used ‘Type of high school’, ‘Province of high school’ and ‘City of residence’ to assess the influence of the locations of pre-University studies and residence on the predictions. Likewise, ‘Type of disability’ was not considered because it took too many different values and the Boolean ‘Has any disability’ was used instead.
• Infrastructure services. The students’ enjoyment of potable water, sewage system, electricity supply, landline phone, Internet and cable TV was treated as an accumulated numerical value, from 0 to 6, instead of managing the 64 different combinations. We tried configurations in which the six variables were given the same weight and others in which water, sewage and electricity got double importance.

As for the normalization methods, we applied the following criteria:

• Enumerated types: in general, the method that adds the lowest topological dispersion to the inputs of a neural network for enumerated types is one-to-K. As a shortcoming, the dimensionality of the network grows exponentially with each possible value.
• Binary variables: for simplicity, we chose to encode Boolean variables as enumerated types of 2 values.
• Numerical variables: we decided to use Gaussian normalization for the numerical fields, preprocessing the data (based on normalized median) in order to remove out-of-range values and false zeros that could have detrimental effects.

For each record at the input, we had output data comprising the following numerical fields for each academic year:

• Number of subjects taken.
• Average qualification.
• Number of subjects passed.
• Number of subjects failed.

We defined prediction metrics as a function of these parameters, plus the count of the number of years that each student stayed with the UPS. More granular data, such as the qualifications obtained in each subject or the number of attempts until passing each, were not used in the first stage.

Initial analysis of the data showed that the data were largely unbalanced. For example, if we used a classifier on the results of individual students passing any given subject, then 81.5% of the samples fell in the class pass, whereas the remaining 18.5% were put in fail. Such distributions pose a problem to machine learning models, due to the overfitting trend on the most represented class. In order to avoid this, we resorted to the simplest technique: multiplying the samples of the least-represented class by means of simple copies.

3. Configuration of the MLP

For the setup of the Multi-Layer Perceptron, we assumed (i) that the different input data would have different influence over the network, (ii) that the best configuration of its hyperparameters is not straightforward to find and (iii) that there would be a point of equilibrium between the number of input data fields, the dimensionality of the network and the values of other hyperparameters, which would yield a good balance in terms of performance and prediction capabilities. Our scan of hyperparameters sought to get as close as possible to that point, exhaustively trying combinations over the ranges of values indicated in

Table 2. Ranges of values for the Multi-Layer Perceptron (MLP) hyperparameters.

Hyperparameter	Effect	Range
Learning rate	Rate of change of the internal weights of the neural network.	{constant, inverse, adaptive}
Penalty factor ($\alpha$)	Used in regularization, to prevent excessive variations in the internal weights of the network.	0.001–125
Optimizer	Functions that decide the direction and gradient size to minimize the chosen error metrics.	{BFGS, Adam, Adadelta, SGD}
Activation functions	Shape of the output of any neuron, given an input or set of inputs.	{ReLu, cReLu, tanh}
Hidden layers and neurons	General architecture of the network.	1 or 2 hidden layers, their numbers of neurons equal to 0.7 or 0.8 times the number of neurons at the input layer.
Momentum	It helps stabilize the neural network, controlling the impact of feedback information. If it takes an excessively low value, the internal weights of the network vary too much and the convergence process takes longer. In contrast, if its value is too high, the network may converge too far from the best point.	0.05, 0.1, … 0.9

.

To begin with, we had to make a decision on the number of hidden layers and the number of perceptrons in each. For many years, the numerical techniques available allowed a maximum of one fully-connected hidden layer. However, since the advent of deep neural networks [20], new learning and feedback techniques allow handling an arbitrary number of layers, each one representing different functions that allow solving much more complex learning problems. In general (see Reference [21]), one layer can be used to approximate any continuous function, whereas two layers can represent any function with arbitrary precision. Uses of more than two layers typically have to do with specialized solutions for very complex domains (e.g., computer vision) featuring not fully-connected layers, convolutional layers and so forth. For the problem we were facing, we chose to explore configurations with one or two hidden layers, because the complexity of the variables did not justify the use of more.

In general, a high number of neurons in the intermediate layers makes the neural network prone to overfitting. Besides, having too many neurons increases the time needed to train the network, to the point of rendering it unusable in practical scenarios. On the other hand, too few neurons lead to low accuracy too, because there are not enough elements to capture the function that maps inputs to outputs. In our study, we initially applied the criteria of Reference [22]:

• It should fall between the numbers of neurons at the input and output layers.
• It should be close to $\frac{2}{3}$ of the size of the inputs plus the size of the outputs.
• It should be lower than twice the number of input neurons.

We used these criteria as a starting point but—as is frequently done in practice,—we sought further optimization of the number of neurons for our particular problem by trial and error, iterating over different ranges to find the right balance between overfitting and prediction accuracy.

Finally, also aiming to fight overfitting, we implemented the regularization strategy proposed in Reference [23], with a penalty factor $\alpha$ taking values in the range indicated in Table 2. When overfitting occurs, the neural network implements overly complex functions that fit exactly the points it interpolates—defined by the training data,—but that change enormously when a new intermediate point is added. Regularization, as explained thoroughly in Reference [24], helps flattening the model.

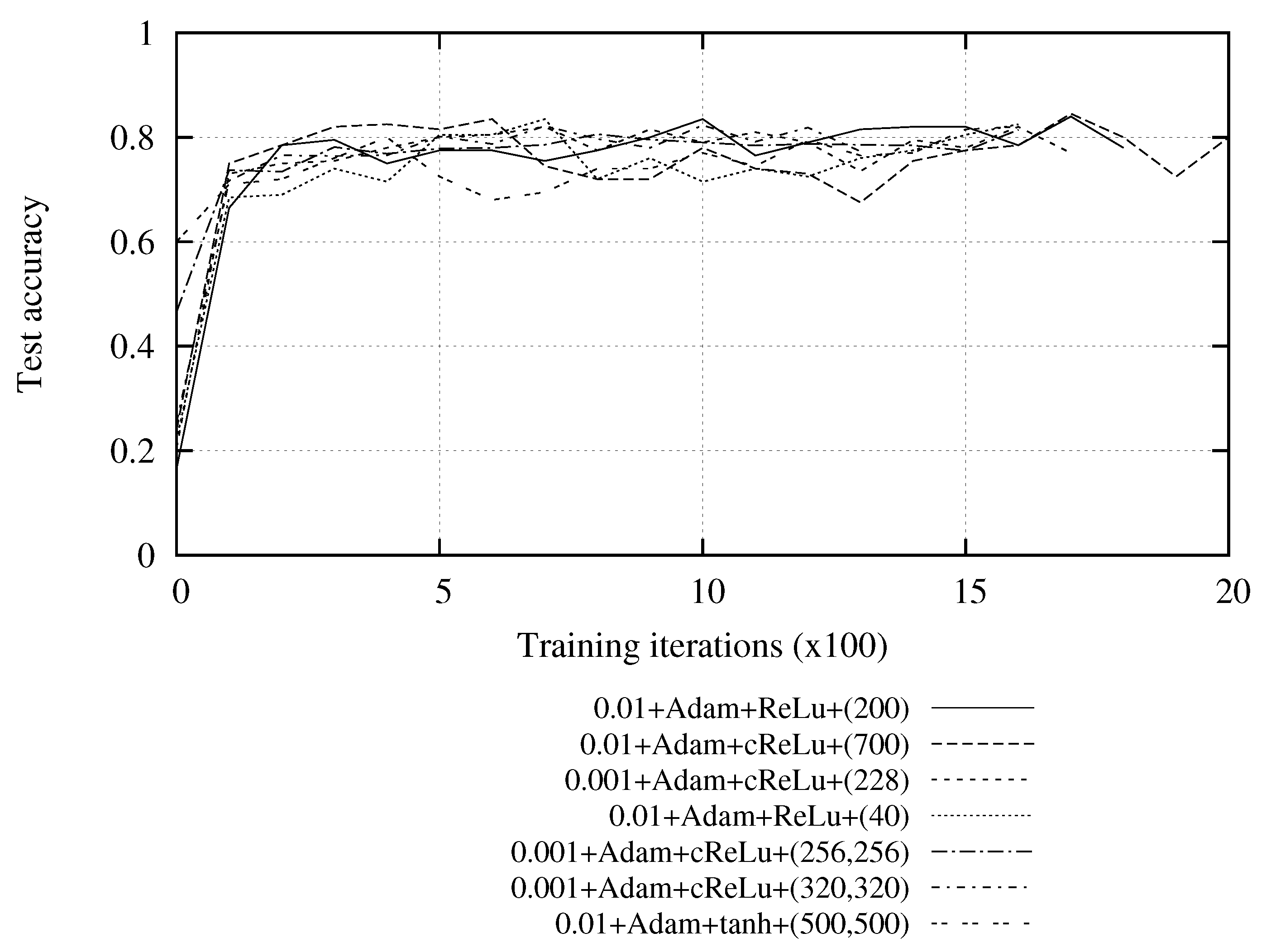
4. Results

We implemented the MLP using the scikit-learn toolkit (https://scikit-learn.org/), which offers a comprehensive set of tools for machine learning that can be fully customized. We did not use GPU-based solutions because the amount of data was manageable by simpler means. Our implementation supervised the convergence of two parameters:

• Training accuracy monitors the speed at which the neural network adjusts to the training data; the value must tend to 1.
• Test accuracy monitors the speed at which the neural network learns to predict the correct outputs for a set of input data for which it has not been trained.

If the value of training accuracy is greater than test accuracy, then it can be asssumed that the neural network has overfitted. Any network that is big enough and has been trained sufficiently must converge to total precision on the training data, whereas for the test data it will only get close to 1 if there exists a mathematical relationship between inputs and outputs. Therefore, our algorithm would adjust the $\alpha$ value and the numbers of neurons automatically whenever it detected signs of overfitting.

The scan tested more than 12,000 configurations. Figure 2 shows, for a selected subset of them, that the MLP quickly converges to a level of accuracy around 80% after providing successive batches of training data at the input, considering the output metrics of predicting whether a new student will pass or fail a given subject. All of the other metrics yield similar graphs if we discard the MLP configurations that fail to converge or incur overfitting.

A level of accuracy around 80% may seem good at first but, as we said at the end of Section 2, we could successfully guess the pass/fail outcome for any new student in a given subject with an accuracy of 81.5% by always choosing pass, regardless of any data about the student. Therefore, Figure 2 does not represent any improvement over the null hypothesis. Contrary to the expectations raised by previous works in the literature, this happened to be the case for all of our metrics and all the MLP configurations we tried: at the best, we were in the case of what some authors call the natural or null point of the data, since it was possible to guess the values of the metrics of interest, with the highest possible accuracy, just by properly weighing the outputs, regardless of the input values.

It is worth noting that precision peaks beyond the null point were obtained in many cases (e.g., in the configurations listed in

Table 3. Details of the MLP configurations represented in Figure 2.

Learning Rate	$\mathit{\alpha }$	Optimizer	Activation Function	Hidden Layers	Training Accuracy	Test Accuracy
0.01	0.48	Adam	cReLu	(560)	1	0.825
0.01	0.12	Adam	ReLu	(160)	1	0.815
0.01	0.576	Adam	ReLu	(128)	0.965	0.83
0.1	0.01	SGD	tanh	(200)	0.785	0.81
0.1	0.1	SGD	tanh	(200)	0.734	0.82
0.001	0.01	Adadelta	ReLu	(200,200)	0.5225	0.832
0.01	0.21	Adam	cReLu	(81,81)	1	0.81
0.01	0.4	SGD	cReLu	(320)	0.87	0.82
0.1	0.025	SGD	cReLu	(104)	0.955	0.825
0.001	0.358	Adam	ReLu	(104)	0.99	0.825
0.01	0.0358	Adam	ReLu	(104)	1	0.81
0.1	0.25	SGD	ReLu	(163,163)	1	0.82

) but these were due to oscillations of the neural network weights, which in turn led to oscillations in the outputs. The long-term averages remained always below the null point.

The null hypothesis, by the way, gives us an orientation on the quality of our neural network. A divergent or poorly-designed network would not conform to the null hypothesis; rather, its accuracy would have significant oscillations or attain systematically lower values than expected through simple analysis of the outputs.

5. Discussion vs. Related Work

As noted in the introduction, the challenge of predicting students’ performance in Higher Education institutions has been addressed by many authors in the recent past, using more or less abundant and fine-grained data of different types (always including, at least, academic data) and employing different machine learning techniques. The following are the most relevant highlights from the literature:

• The authors of Reference [7] ran a comparative study on a dataset of 257 student records, showing that Bayesian networks (76.8% accuracy) outperformed decision trees (73.9%) and these in turn outperformed the Multi-Layer Perceptron (71.2%).
• Similarly, a study was presented in Reference [8] with data about 280 students, making predictions with 10 off-the-shelf algorithms implemented in the Weka data mining framework (https://www.cs.waikato.ac.nz/ml/weka/). The Naive Bayes classifier was found to be the best predictor (65% accuracy).
• Another comparison was made in Reference [9] on a dataset containing 225 student records, with 10 attributes of academic performance each. Once again, a Bayesian network (92% accuracy) turned out to be slightly better than other classifiers (Naive Bayes, ID3 and J48) and than the Multi-Layer Perceptron.
• Mishra et al. conducted a study including some social and emotional parameters in the students’ profiles, which the evaluation showed to be much less relevant to the predictions than the records of previous academic results. Random Tree happened to be the most accurate algorithm [10].
• Some socio-economic data—a small subset of the fields than ours (Table 1)—were used in Reference [11] to make predictions from only 165 student records by using several techniques. The Multi-Layer Perceptron (74.8% accuracy) stood out above NBTree (73%), REPTree (71%) and others.
• The authors of Reference [12] applied a range of classifiers and clustering methods on the academic results of 480 students in order to predict the outcomes of 25 others in new subjects, taking as input the recent grades obtained by the latter in the preceding semesters too. They attained an accuracy of 80% in classifying the students’ performance as low, medium or high.
• Alsheddy and Habib [13] used the J48 classifier to predict (with 85.8% accuracy) the students’ probability of abandoning the University at the end of the year, working with some demographic variables as well as from the results of preceding semesters. This study used—to the best of our knowledge—the most extensive dataset in the literature to date, with records of 1980 students.

In relation to these precedents, plus those of References [14,15,16,17], our work involves the most extensive and fine-grained dataset of student records (30 times as many as the average from above). Besides, whereas many others have focused on comparing different algorithms and techniques with single configurations or, at the most, a few tens of combinations of hyperparameters, we are the first to conduct an extensive scan (more than 12,000 configurations) to make the most of one technique that ranked well in the literature, namely the Multi-Layer Perceptron. Without such an exploration and faced with limited training data, we may wonder whether the positive results claimed by the previous studies can indeed be taken as evidence that advanced AI techniques have a role to play in the proactive management of Higher Education institutions and whether the configurations of the techniques that turned out to be most advantageous would work just as well in other contexts and with other datasets. At this point, we wonder whether the idea that educational success can be explained in this way may be overly enthusiastic.

Finally, it is important to highlight that most of the papers cited above do not explain whether the studies pass the null hypothesis; that is, they do not address the essential question of whether the prediction techniques were actually providing valuable information that could not be attained by much simpler means, such as rolling a properly-weighed die. It might be the case, then, that researchers and practitioners in this area have been trying to crack nuts using a sledgehammer, as we suggest in the title of this paper.

6. Conclusions and Future Work

We have run one experiment on the potential use of neural networks for the detection of correlations and dependencies among the diverse data fields stored in databases with thousands of records of Higher Education students, specifically focusing on whether socio-economic variables, familiar and health-related conditions and places of origin/residence could influence metrics of academic performance to a statistically-significant extent. The context of Universidad Politécnica Salesiana was considered a propitious one because, in line with common practice throughout Latin America, the records contain fields that would raise concerns under the scrutiny of the most advanced data protection regulations. Our experiment was set up in a way that would bring to light, at least, the most noticeable relationships between a selection of input variables—presumably, the ones entailing greater opportunities to find something—and the chosen metrics, which looked at academic performance with coarse granularity. From those findings, we would move on to refined neural network designs and more detailed metrics, aiming to make predictions about new students coming every year from the experience accumulated with many others in the past.

Contrary to the initial expectations, however, the scan of hyperparameters for the multi-layer network of perceptrons (including settings that fall within the denomination of deep learning) showed that there was no correlation or dependency between the many input variables of socio-economic nature and any of the chosen metrics of academic performance. Given the space of possibilities we explored and the size of the dataset, this finding is not about the particular tool provided by the MLP but rather about the nature of the data: there is no additional knowledge to be extracted from the abundant socio-economic data and no other technique would get to find a function mapping inputs to outputs, that could underpin some decision-making at the University.

Still, before rushing into the conclusion that this might be the case for all universities in the region—which would extrapolate almost directly to other countries where universities do not gather so extensive data about their students,—we must consider the hypothesis that there might be an implicit pre-filters in place, by which the records of students in the UPS databases conform a uniform population in socio-economical and academic terms: on the one hand, UPS is a private university with a cost of enrollment, tuition and fees that ranges from USD 1765 to USD 2432, which are significant amounts of money for families in Ecuador; on the other, the teaching staff systematically strive to help students pass their subjects. The more uniform the population, the lower the probability of finding meaningful correlations or dependencies among data fields. Accordingly, we have started negotiations in order to check this hypothesis by performing a similar study in the context of an Ecuadorean public university, where the costs and the pass/fail rations are lower. If we got the same results, the study would further inform the theory in this area of research and reinforce the fact that the widespread adoption of advanced data protection regulations is not hampering potential uses of AI to improve the Higher Education systems but just preventing misuses of personal data as intended.

For future research, we also hypothesize that the data fields currently handled by UPS (listed in Table 1) could be supplemented with the students’ history in secondary education. It could be valuable to match fine-grained info about related subjects (e.g., on different branches of science) or even specific topics within them. For instance, a student who was skillful with trigonometry but had difficulties with derivatives would be likely to do better in Algebra-related courses than in Physics. However, the idea faces three significant challenges: (i) the need to match multiple sources of data, with different formats and levels of granularity, (ii) the fact that we would be partitioning the data available for training and (iii) the severe limits set by data protection regulations to the merging of databases in the hands of different institutions.

In any case, it is worth noting that the negative findings reported in this paper do not imply that there is no purpose in gathering the extensive data about the students. They do highlight, however, the fact that not all the data we have access to are useful and that researchers need to make theory-based decisions regarding which variables to feed into the AI systems. Thus far, the literature suggests that prior academic history is more relevant than socio-economic data and personality traits for the purposes of making predictions on academic performance. But the opposite might happen for other activities, such as the ones that the UPS Department of Student Welfare is conducting to promote equity, psychological well-being, health and employability among the students. Empirical evidence in such areas is still scarce, as when AI is used to advice students by means of course recommendations, career path options, … as in the works in References [25,26,27].