Entanglement, and Unsorted Database Search in Noise-Based Logic
Featured Application
Abstract
1. Introduction: On Noise-Based Logic
1.1. Instantaneous Noise-Based Logic
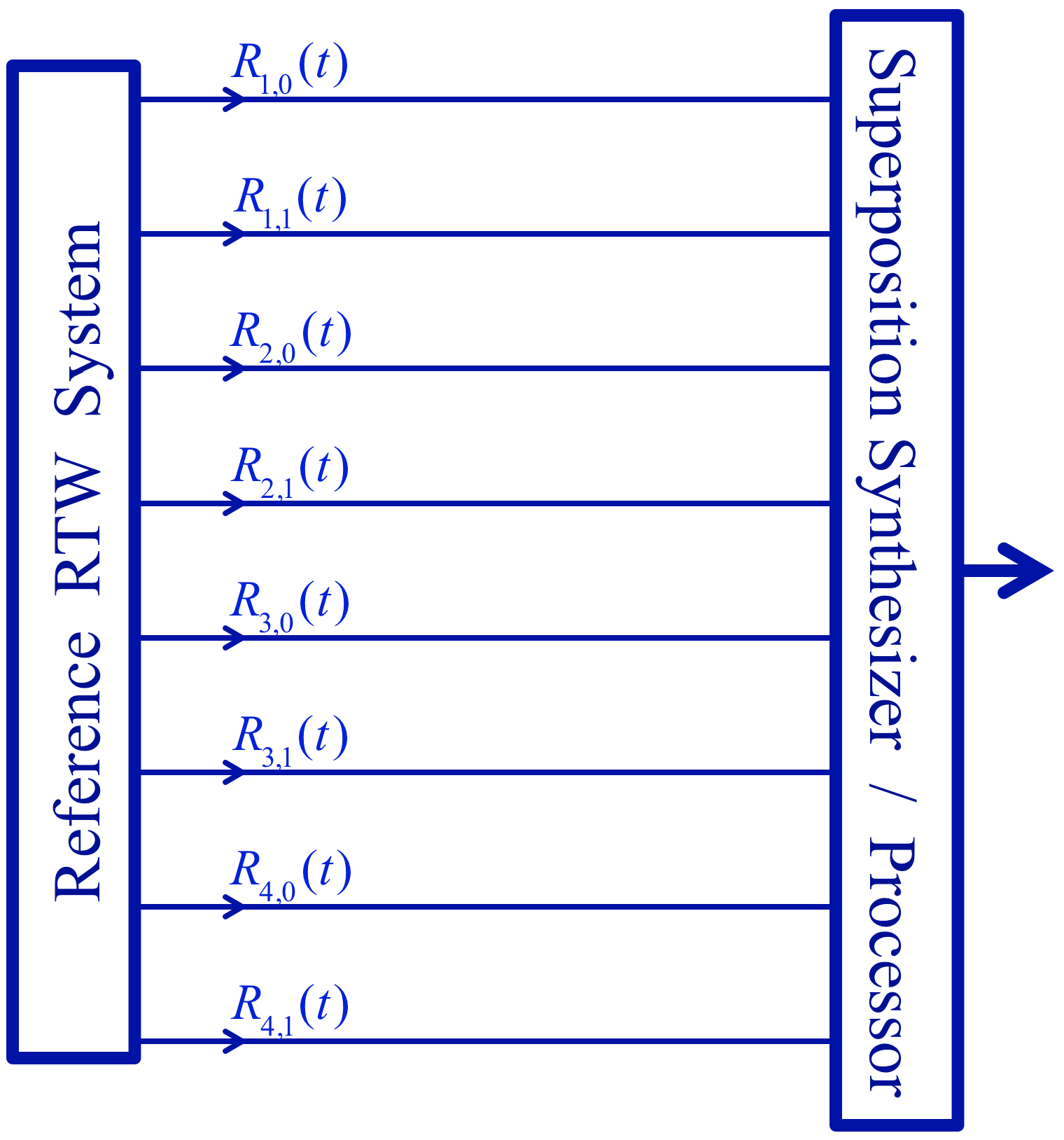
1.2. Hyperspace (Hilbert Space) Vectors: Product-Strings
Exponentially Large Superpositions with Polynomial Complexity
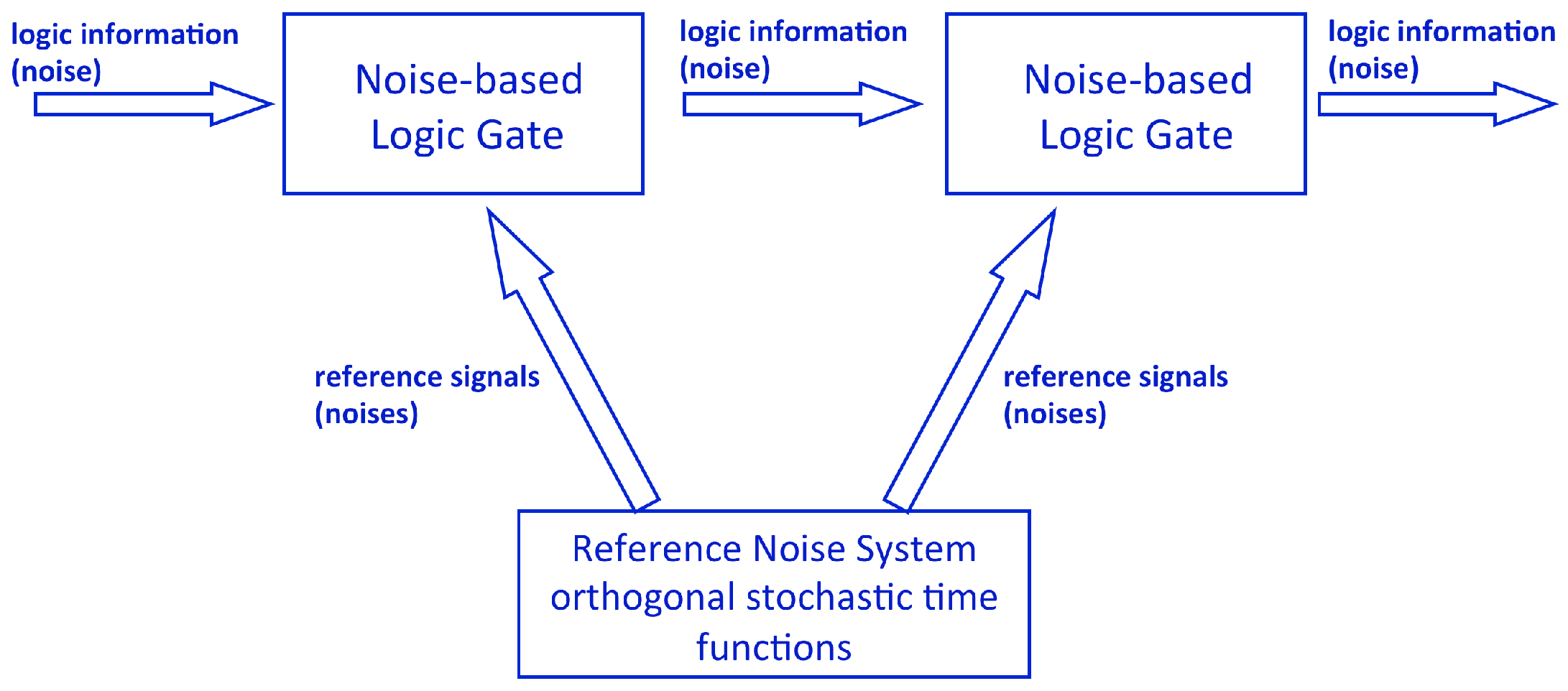
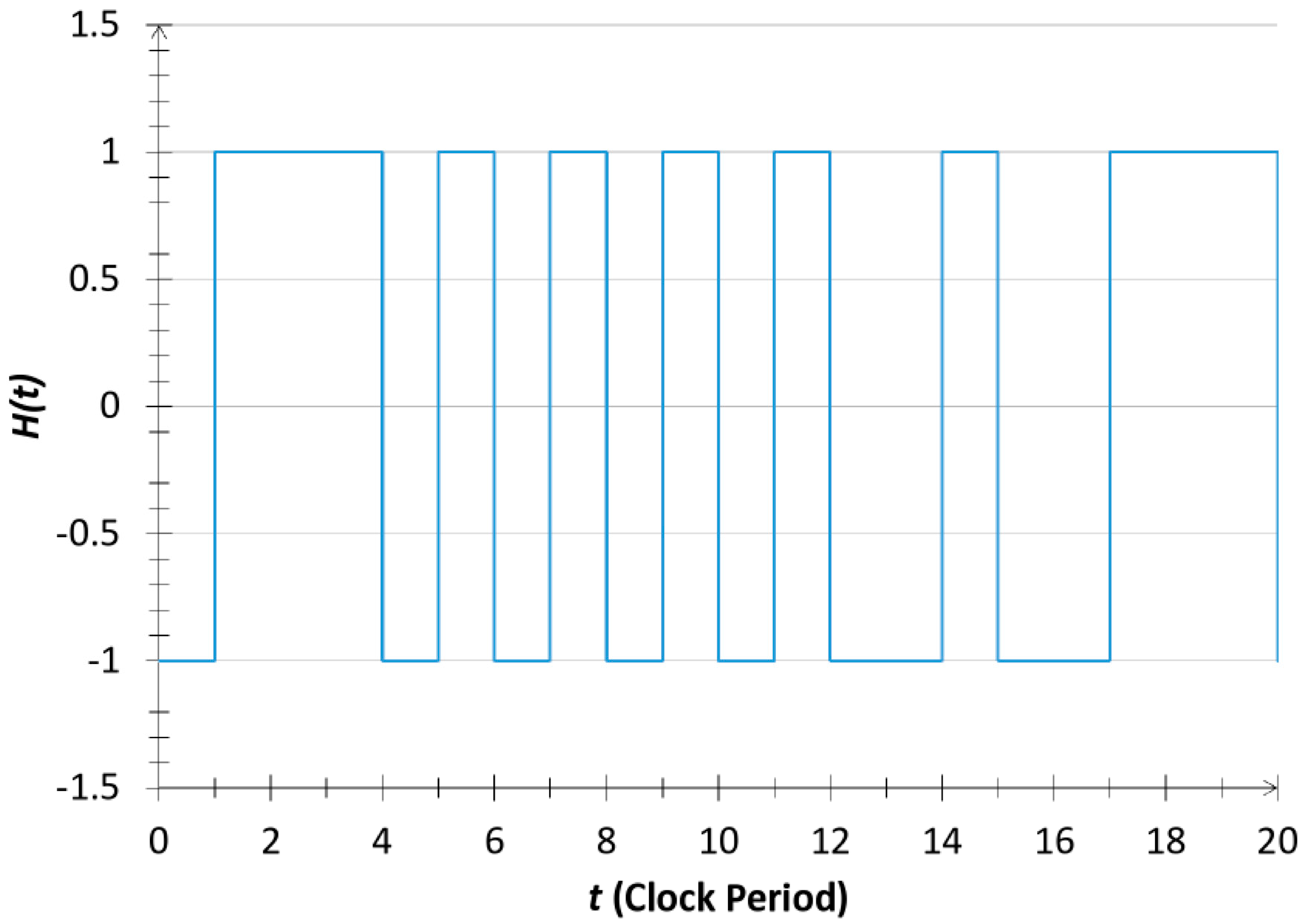
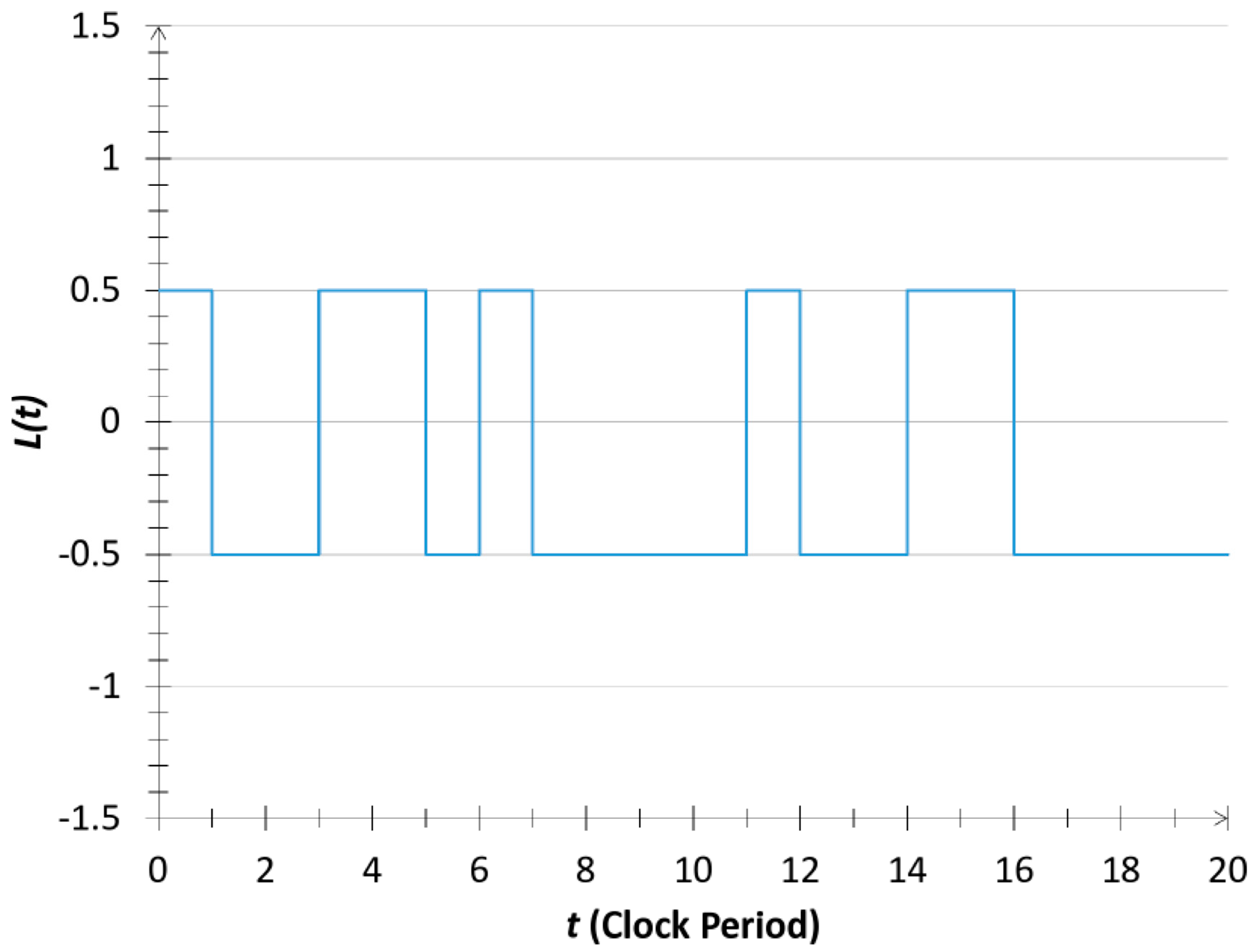
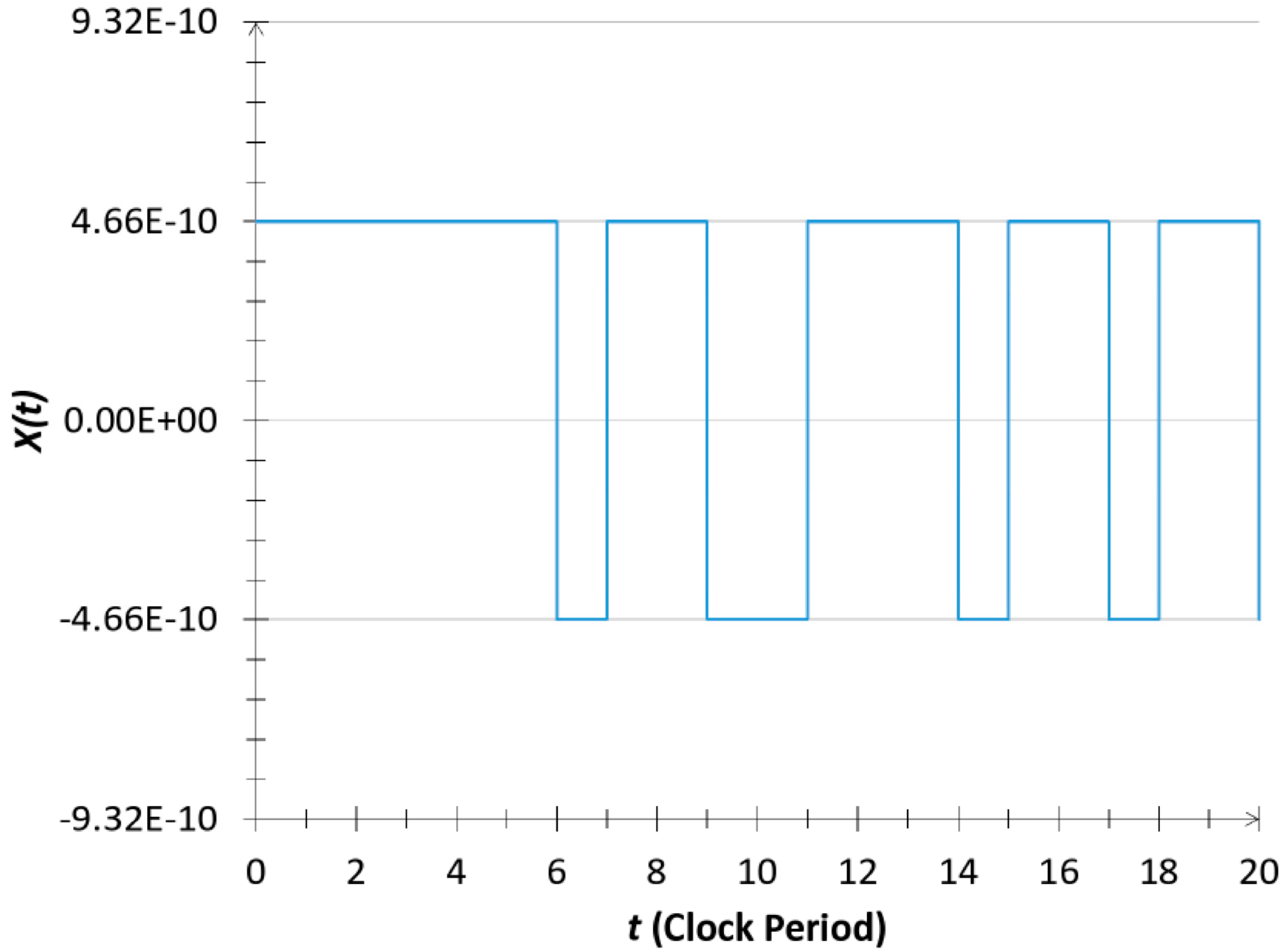
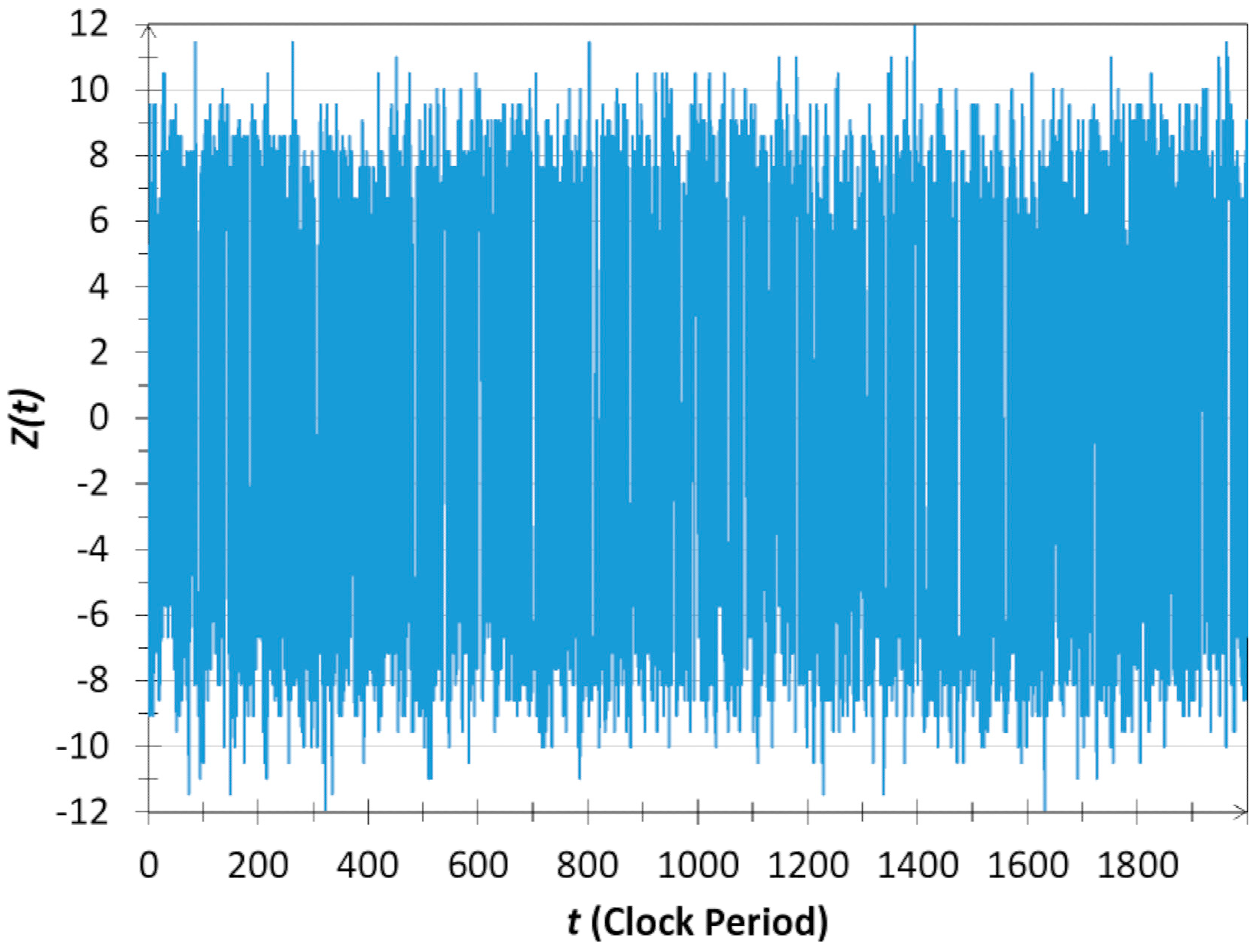
1.3. Random Telegraph Waves as a Reference System
2. New Measurement Tools Involving the Reference Wires
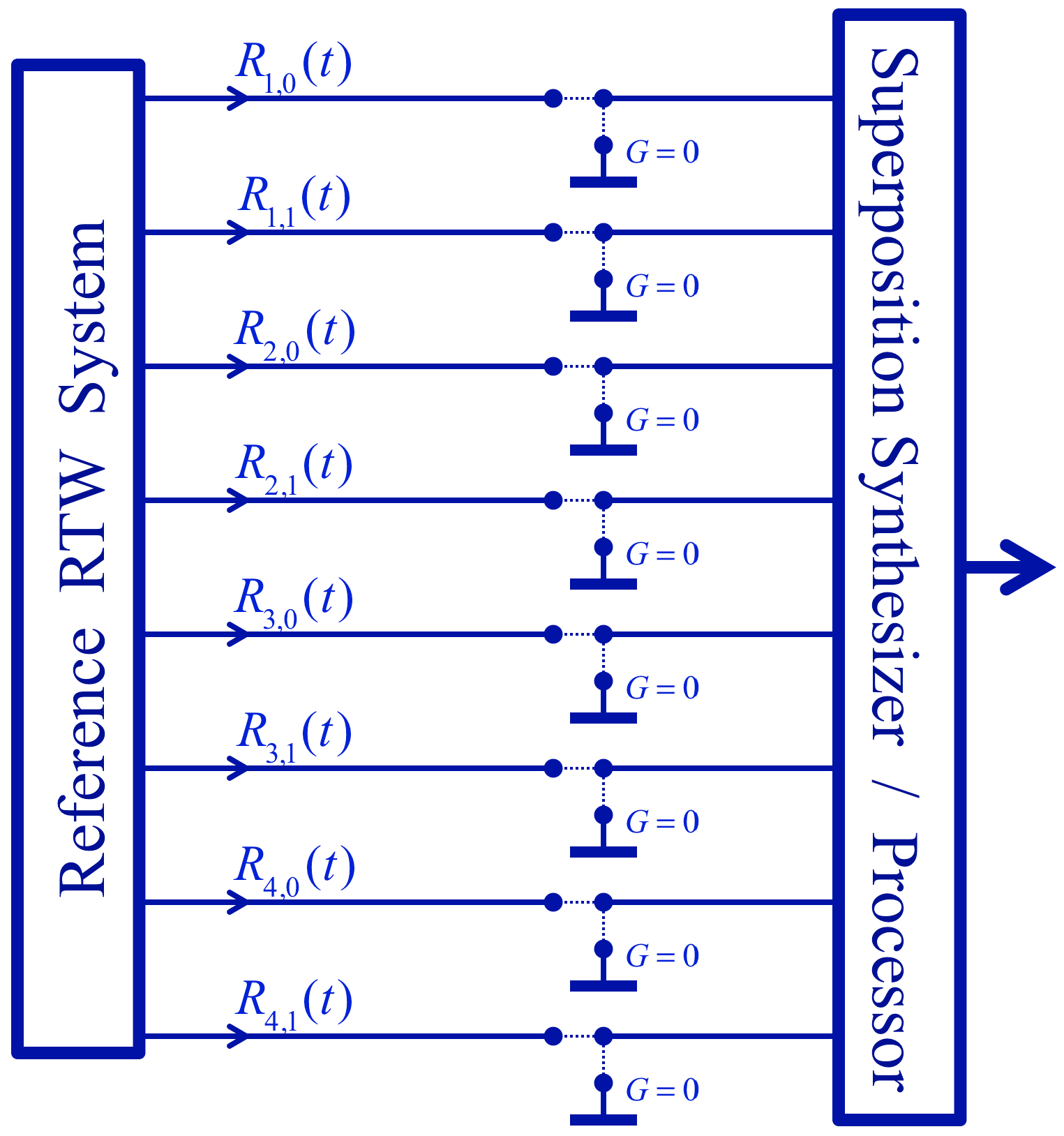
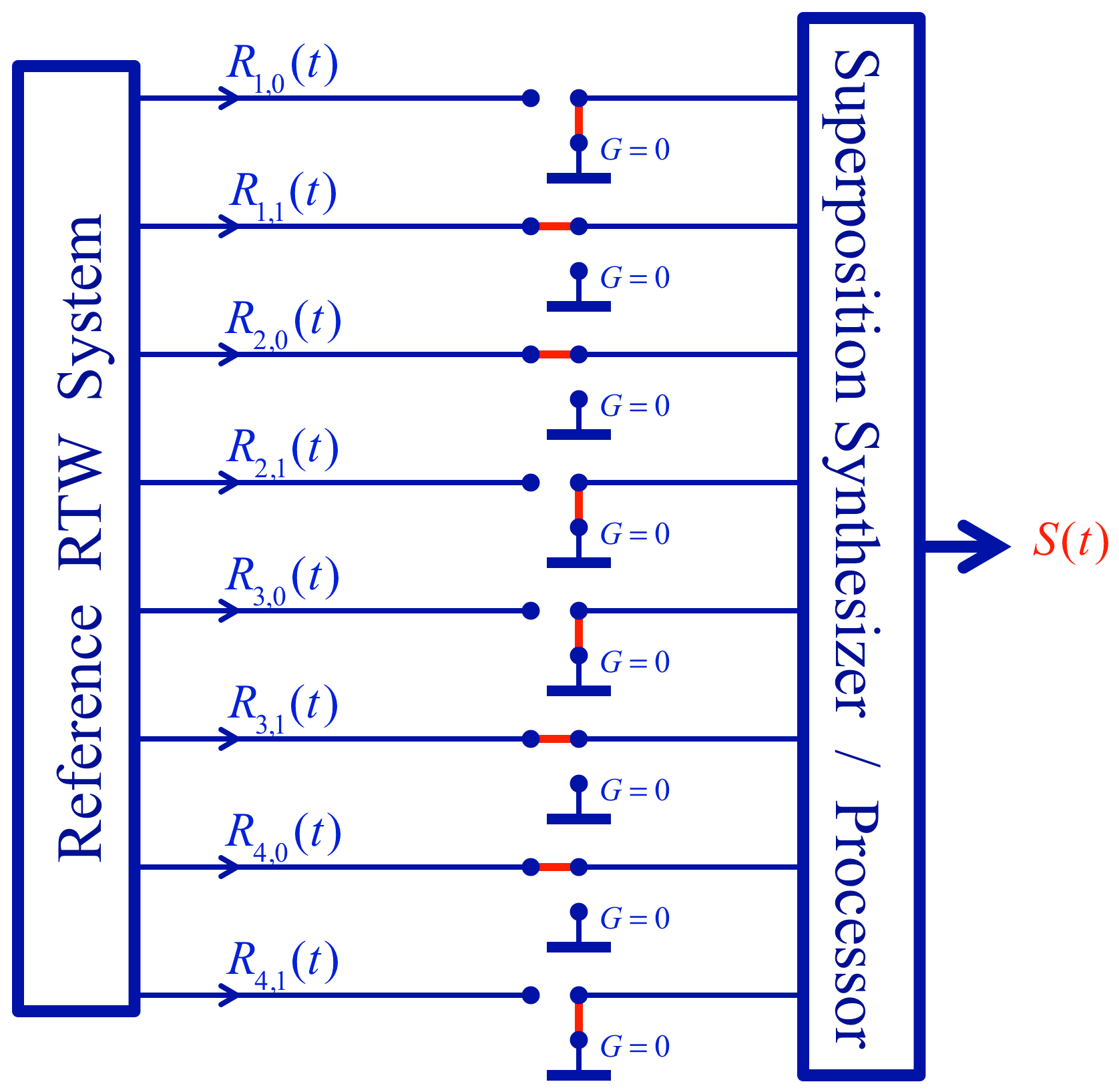
2.1. “Quantum” Measurement of a Given String within a Superposition: “Collapse of the System Wavefunction”
2.2. Deterministic Measurement and Evaluation of Entangled States and Their Superposition in INBL
2.3. Essential Differences between Measuring Entanglement in INBL and Quantum Systems
3. The Two Search Algorithms
3.1. Search for the Existence of a String or String-Fragment in an Unknown, Unsorted Superposition
3.2. Phonebook Search
- ➢
- Search for the existence of the string-fragment that is identical to , that is, ground the reference wires of the inverse bit values of . Then the original superposition wave collapses into the single string, the product. This operation requires N switching operations (N groundings).
- ➢
- Then, while keeping those N references wires grounded, ground one by one the 2S reference wires of the phone number database and record which bit value groundings result in . These bit values constitute the phone number string .
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Kish, L.B. Noise-based logic: Binary, multi-valued, or fuzzy, with optional superposition of logic states. Phys. Lett. A 2009, 373, 911–918. [Google Scholar] [CrossRef]
- Kish, L.B.; Khatri, S.; Sethuraman, S. Noise-based logic hyperspace with the superposition of 2N states in a single wire. Phys. Lett. A 2009, 373, 1928–1934. [Google Scholar] [CrossRef]
- Kish, L.B.; Khatri, S.; Peper, F. Instantaneous noise-based logic. Fluct. Noise Lett. 2010, 9, 323–330. [Google Scholar] [CrossRef]
- Peper, F.; Kish, L.B. Instantaneous, non-squeezed, noise-based logic. Fluct. Noise Lett. 2011, 10, 231–237, Open access. [Google Scholar] [CrossRef]
- Bezrukov, S.M.; Kish, L.B. Deterministic multivalued logic scheme for information processing and routing in the brain. Phys. Lett. A 2009, 373, 2338–2342. [Google Scholar] [CrossRef]
- Kish, L.B.; Granqvist, C.G.; Bezrukov, S.M.; Horvath, T. Brain: Biological Noise-Based Logic. In Advances in Cognitive Neurodynamics (IV), Proceedings of the 4th International Conference on Cognitive Neurodynamics, Sigtuna, Sweden, 23 June 2013; Liljenström, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 319–322. [Google Scholar]
- Wen, H.; Kish, L.B. Noise-Based logic: Why noise? A comparative study of the necessity of randomness out of orthogonality. Fluct. Noise Lett. 2012, 11, 1250021. [Google Scholar] [CrossRef]
- Wen, H.; Kish, L.B.; Klappenecker, A.; Peper, F. New noise-based logic representations to avoid some problems with time complexity. Fluct. Noise Lett. 2012, 11, 1250003. [Google Scholar] [CrossRef]
- Wen, H.; Kish, L.B.; Klappenecker, A. Complex noise-bits and large-scale instantaneous parallel operations with low complexity. Fluct. Noise Lett. 2013, 12, 1350002. [Google Scholar] [CrossRef]
- Stachó, L.L. Fast measurement of hyperspace vectors in noise-based logic. Fluct. Noise Lett. 2012, 11, 1250001. [Google Scholar] [CrossRef]
- Kish, L.B.; Khatri, S.; Horvath, T. Computation using noise-based logic: Efficient string verification over a slow communication channel. Eur. J. Phys. B 2011, 79, 85–90. [Google Scholar] [CrossRef]
- Kish, L.B.; Granqvist, C.G.; Horvath, T.; Klappenecker, A.; Wen, H.; Bezrukov, S.M. Bird’s-eye view on noise-based logic. Int. J. Mod. Phys. Conf. Ser. 2014, 33, 1460363. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Kish, L.B.; Granqvist, C.G. Drawing from hats by noise-based logic. Intern. J. Parallel Emergent Distrib. Syst. 2017, 32, 244–251. [Google Scholar] [CrossRef][Green Version]
- Kish, L.B.; Daugherity, W.C. Noise-Based Logic Gates by Operations on the Reference System. Fluct. Noise Lett. 2018, 17, 1850033. [Google Scholar] [CrossRef]
- Tang, E. Quantum-inspired Classical Algorithms for Principal Component Analysis and Supervised Clustering. Available online: https://arxiv.org/abs/1811.00414 2018 (accessed on 31 October 2018).
- Tang, E. A Quantum-Inspired Classical Algorithm for Recommendation Systems 2018. Available online: https://arxiv.org/abs/1807.04271 (accessed on 10 July 2018).
- Kish, L.B. The Kish Cypher. The Story of Kljn for Unconditional Security; World Scientific: Singapore, 2017. [Google Scholar]
- Dyakonov, M. The Case Against Quantum Computing. IEEE Spectrum, 15 November 2019. Available online: https://spectrum.ieee.org/computing/hardware/the-case-against-quantum-computing (accessed on 15 July 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kish, L.B.; Daugherity, W.C. Entanglement, and Unsorted Database Search in Noise-Based Logic. Appl. Sci. 2019, 9, 3029. https://doi.org/10.3390/app9153029
Kish LB, Daugherity WC. Entanglement, and Unsorted Database Search in Noise-Based Logic. Applied Sciences. 2019; 9(15):3029. https://doi.org/10.3390/app9153029
Chicago/Turabian StyleKish, Laszlo B., and Walter C. Daugherity. 2019. "Entanglement, and Unsorted Database Search in Noise-Based Logic" Applied Sciences 9, no. 15: 3029. https://doi.org/10.3390/app9153029
APA StyleKish, L. B., & Daugherity, W. C. (2019). Entanglement, and Unsorted Database Search in Noise-Based Logic. Applied Sciences, 9(15), 3029. https://doi.org/10.3390/app9153029




