Surrogate Models for Estimating Failure in Brittle and Quasi-Brittle Materials
Abstract
1. Introduction
2. HOSS Simulations and FDEM Model for Dynamic Fracture
3. An Algorithm to Estimate Failure Paths
| Algorithm 1 Failure paths prediction algorithm for many-crack geometries using weighted graphs. |
| 1: INPUT: Domain length; Initial coordinates of the crack tips; : Total number of regions the domain is divided into (in-order to estimate zone of failure); Length of FPZ. |
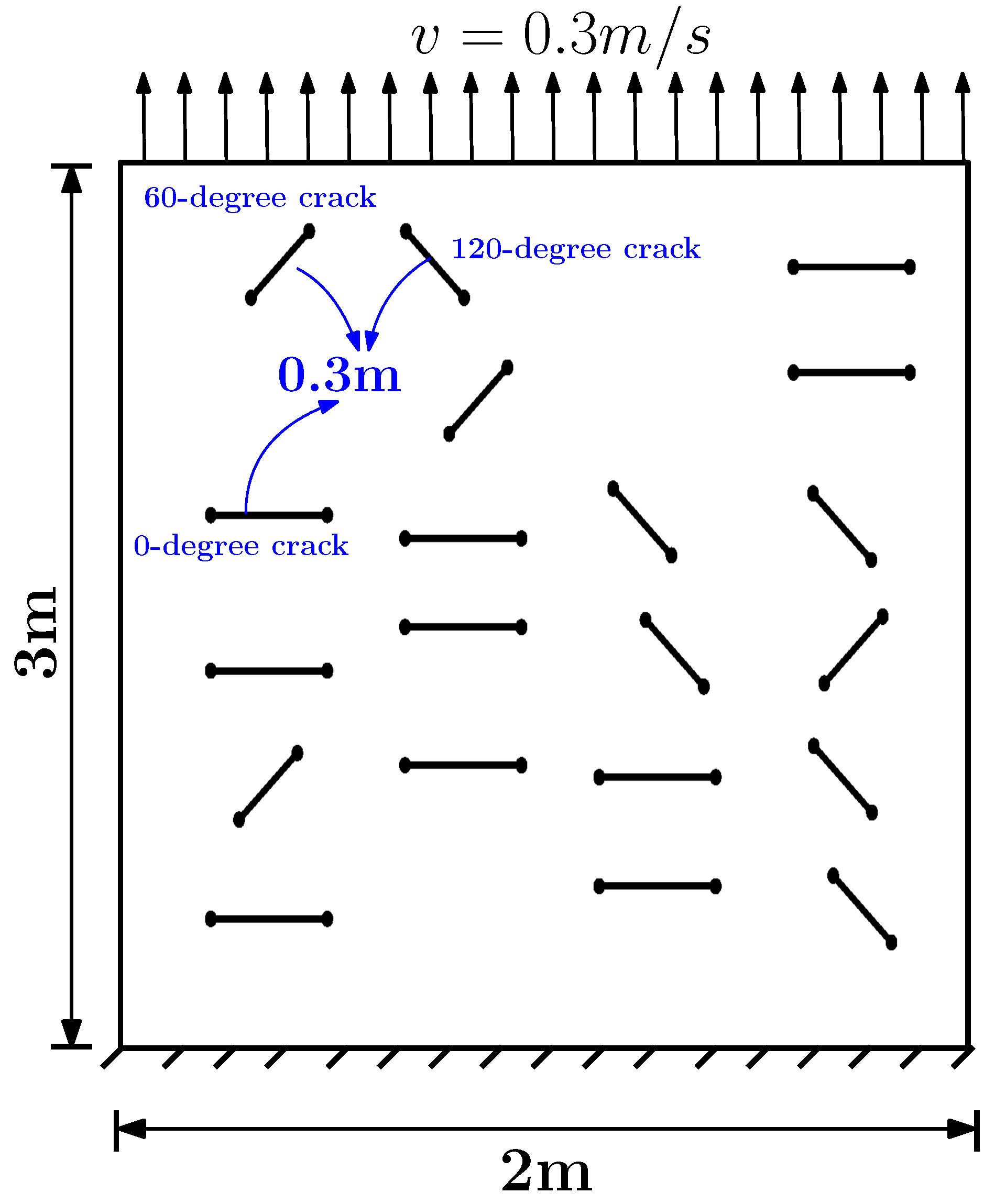
| 2: Identify the 0-degree angle cracks that are perpendicular to tensile loading. |
| 3: for Each crack tip in the set of all 0-degree angle cracks: do |
| 4: Calculate ten nearest crack tip neighbors using kNN algorithm with and their respective Euclidean distances. |
| 5: Among these ten nearest crack tip neighbors, identify the ones that fall within the FPZ. These are determined as follows: |
| 6: for : do |
| 7: if The Euclidean distance of an -nearest neighbor ≤ Length of FPZ: then |
| 8: Mark and store the -crack tip and the corresponding Euclidean distance. |
| 9: end if |
| 10: end for |
| 11: end for |
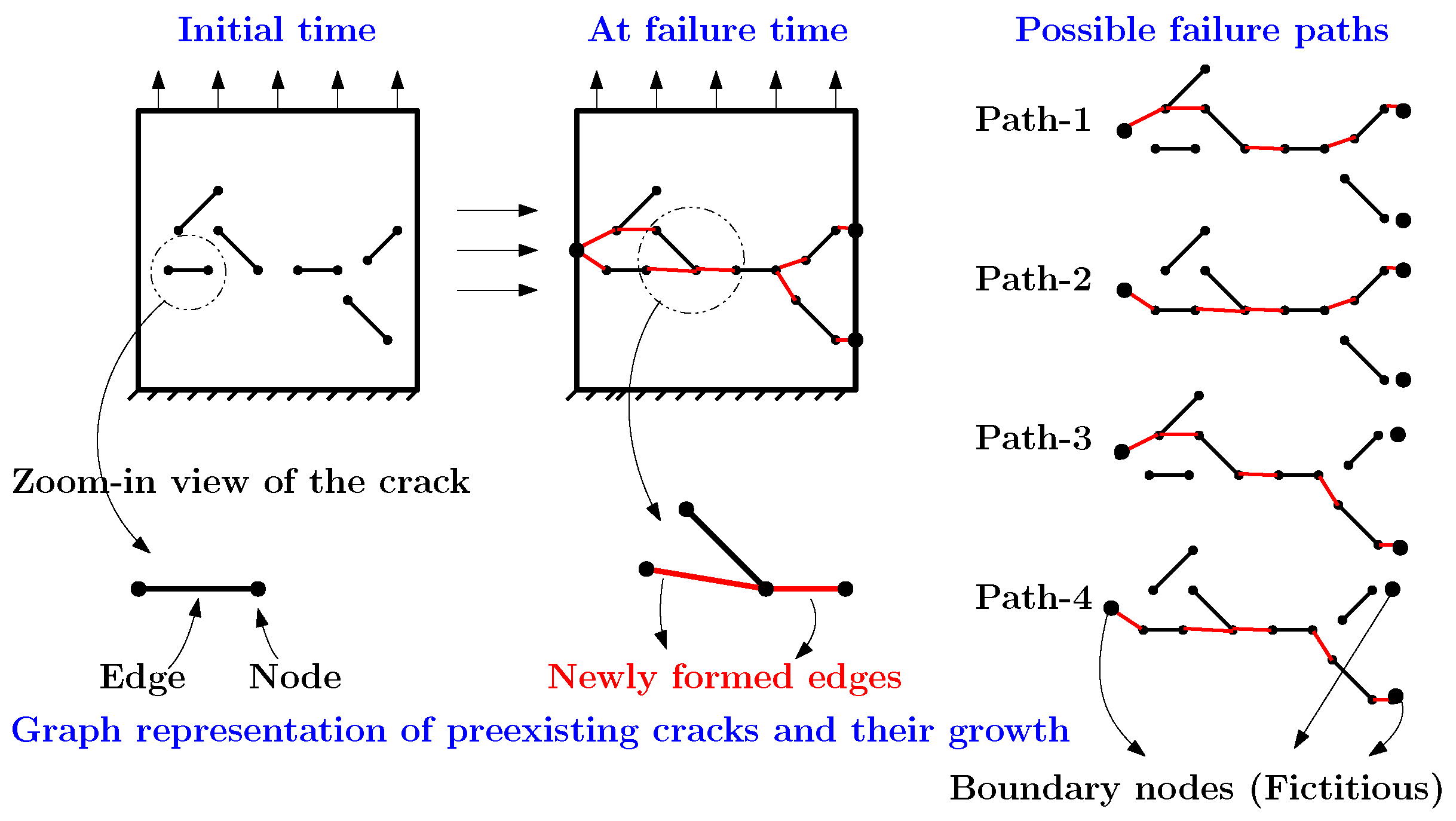
| 12: Form new edges by joining the crack tips that fall within the fracture process zone. |
| 13: for : do |
| 14: Get and store the connected components in -zone. |
| 15: Get the total number of connected components, size of each connected component, and its length. |
| 16: Identify and store the 0-degree cracks present in these connected components. |
| 17: end for |
18: Identify the failure zone. This is accomplished as follows:
|
19: The goal is to detect failure paths along the length of sample, we introduce boundary nodes in the failure zone. Their location is given as follows:
|
20: Create a weighted graph within the failure zone. To achieve this we do the following:
|
| 21: Next, we compute shortest paths within this weighted graph using Dijkstra’s method. The weighted shortest paths are calculated in two ways, both with and without the constraint that the path has to traverse through the identified connected component in the failure zone. |
4. An Algorithm to Estimate Damage
5. Results
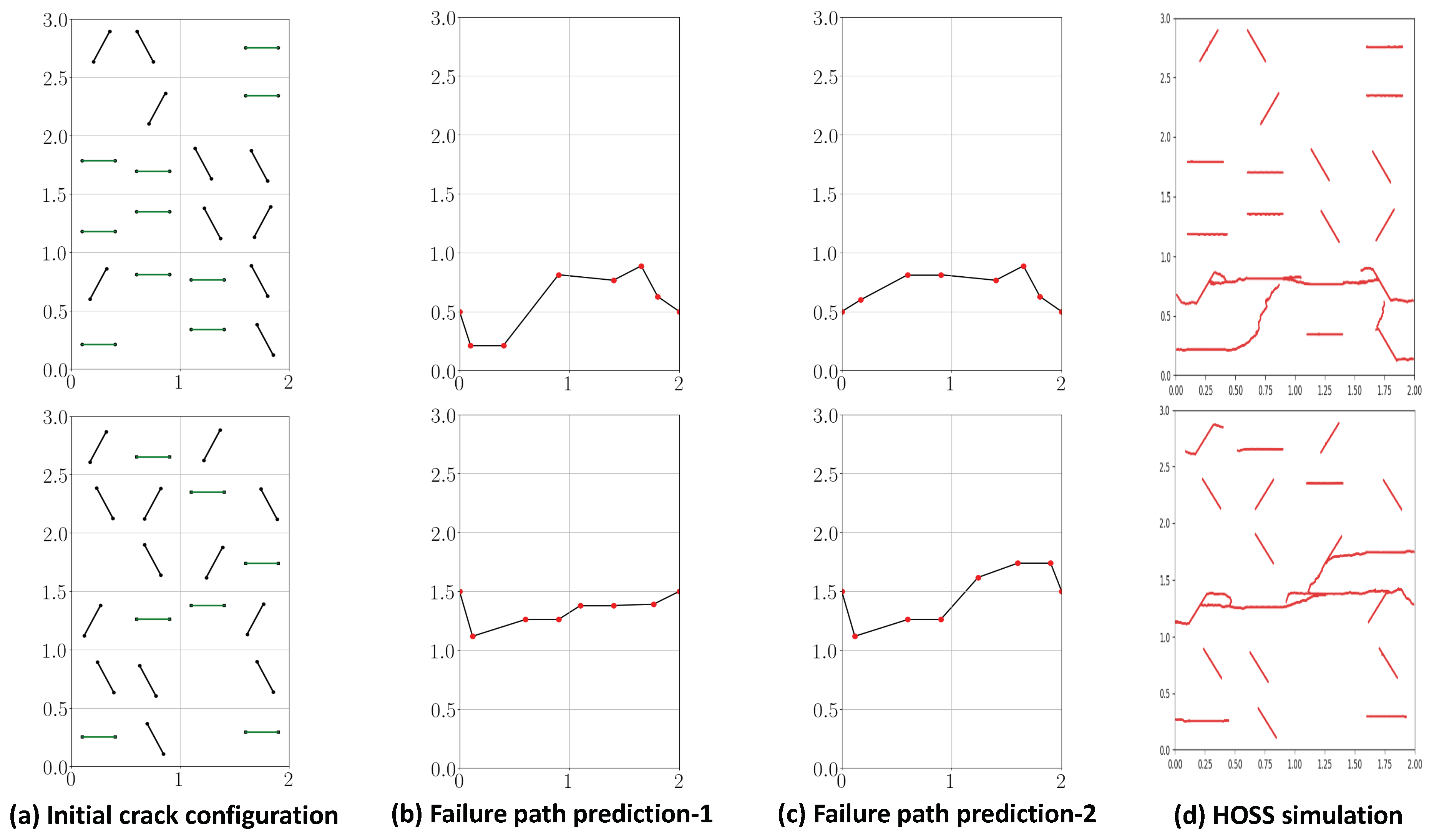
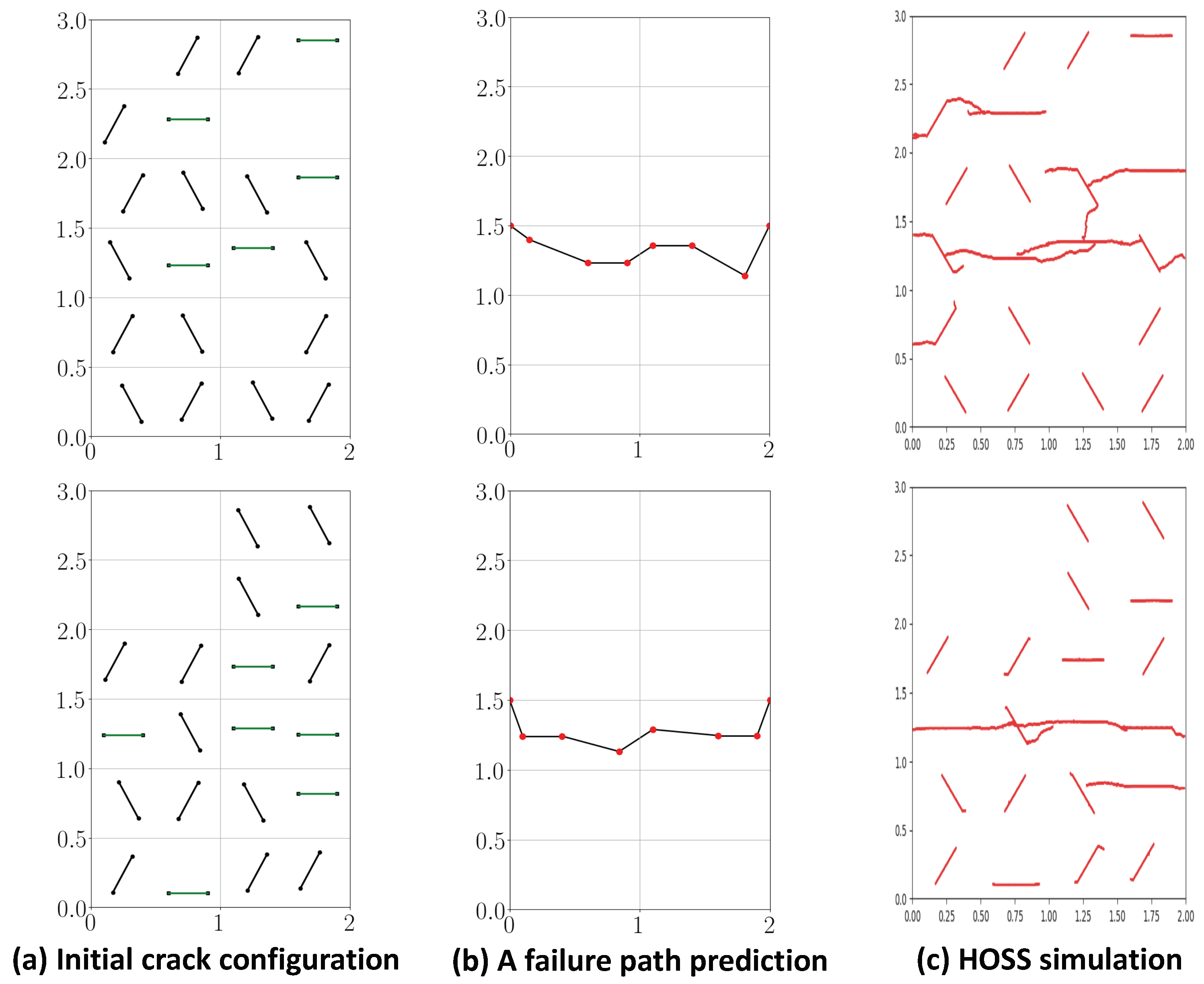
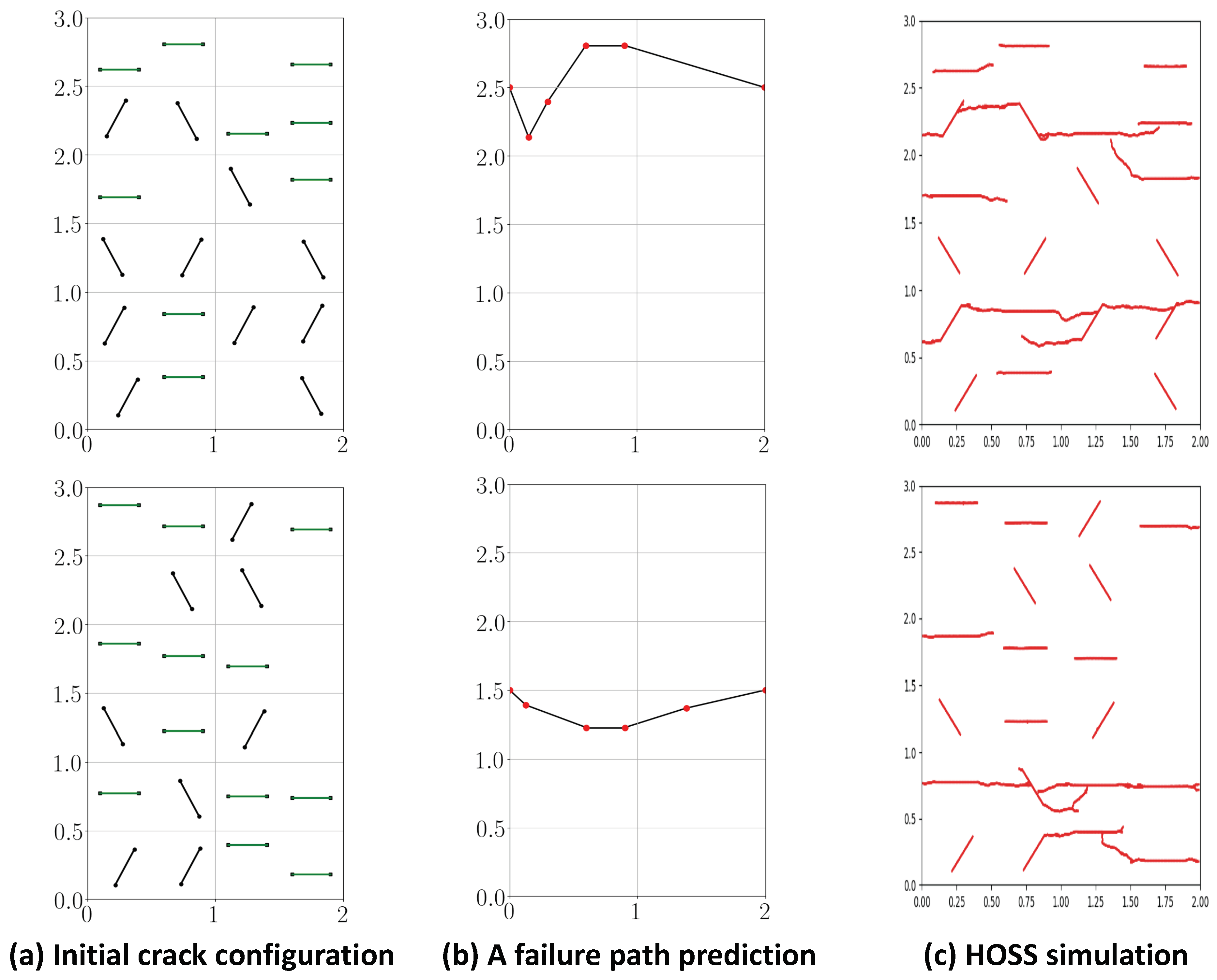
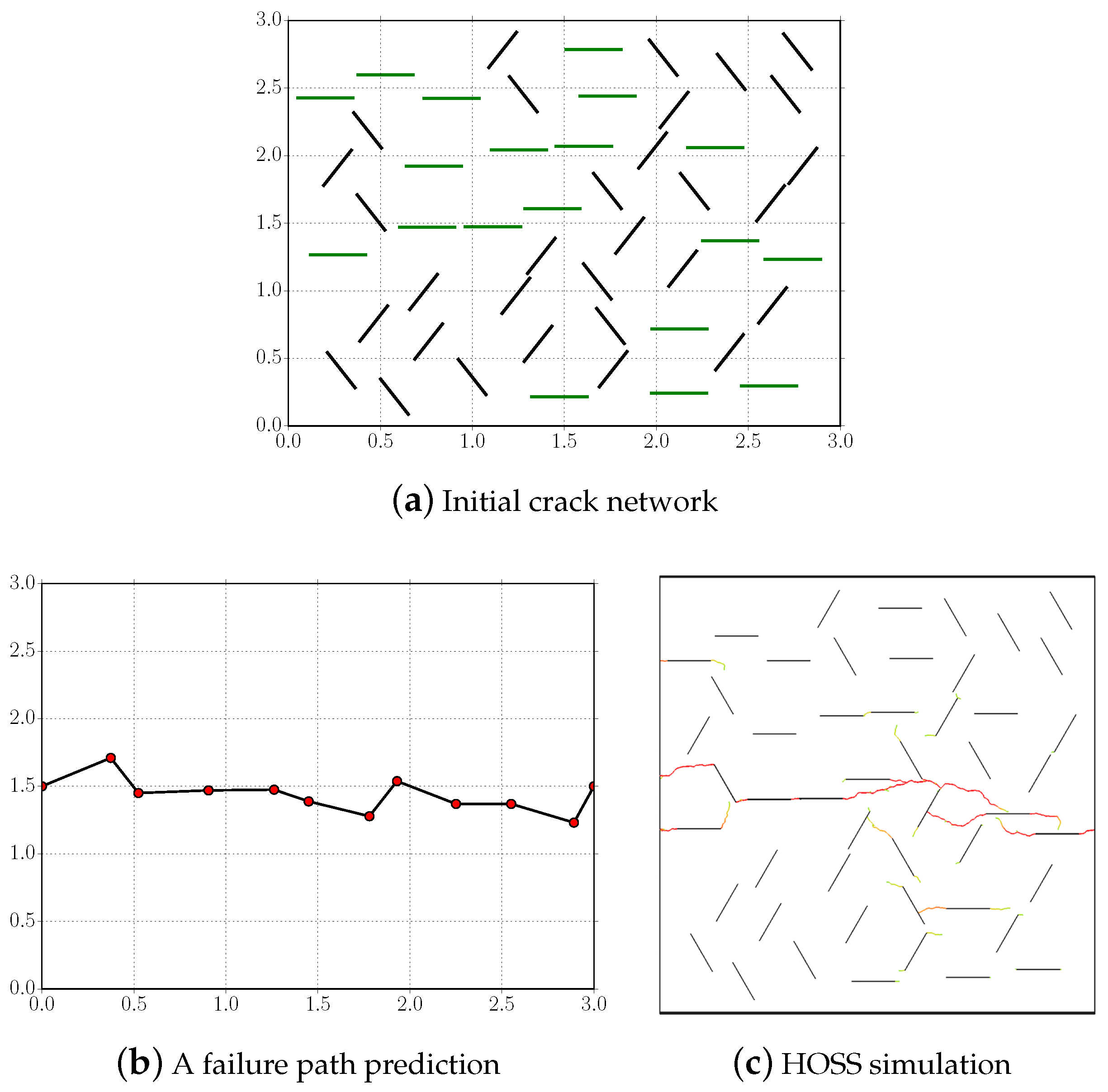
5.1. Estimating Failure Paths
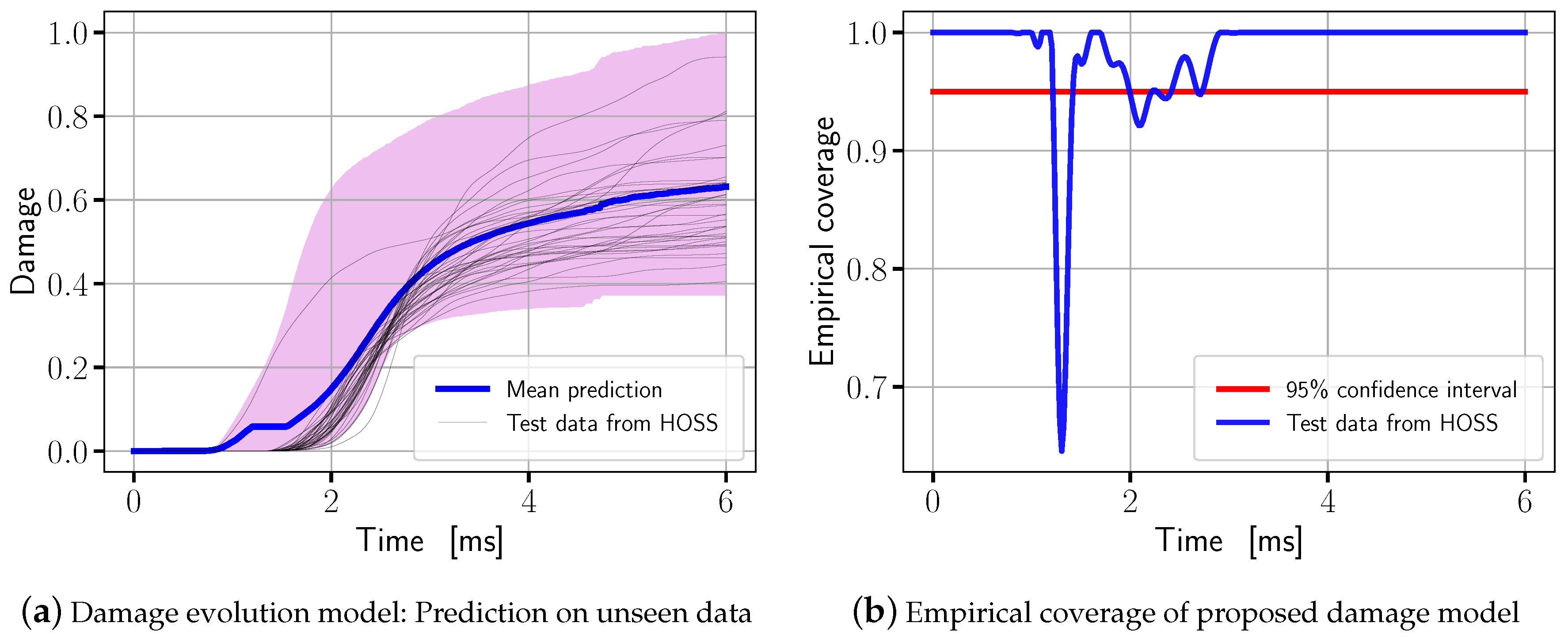
5.2. Estimating Damage Along the Failure Paths
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bažant, Z.P.; Planas, J. Fracture and Size Effect in Concrete and Other Quasibrittle Materials; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Petersson, P.-E. Crack Growth and Development of Fracture Zones in Plain-Concrete and Similar Materials. Ph.D. Thesis, Lund Institute of Technology, Lund, Sweden, 1981. [Google Scholar]
- Brooks, Z. Fracture Process Zone: Microstructure and Nanomechanics in Quasi-Brittle Materials. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2013. [Google Scholar]
- Veselý, V.; Rǒutil, L.; Keršner, Z. Structural geometry, fracture process zone and fracture energy. In Proceedings of the Fracture Mechanics of Concrete and Concrete Structures, Catania, Italy, 17–22 June 2007. [Google Scholar]
- Freiman, S.W.; Mecholsky, J.J., Jr. The Fracture of Brittle Materials: Testing and Analysis; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Lamon, J. Brittle Fracture and Damage of Brittle Materials and Composites: Statistical-Probabilistic Approaches; Elsevier: Oxford, UK, 2016. [Google Scholar]
- Hyman, J.D.; Martínez, J.J.; Viswanathan, H.S.; Carey, J.W.; Porter, M.L.; Rougier, E.; Karra, S.; Kang, Q.; Frash, L.; Chen, L.; et al. Understanding hydraulic fracturing: A multi-scale problem. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 2016, 374, 20150426. [Google Scholar] [CrossRef] [PubMed]
- Mudunuru, M.K.; Karra, S.; Makedonska, N.; Chen, T. Sequential geophysical and flow inversion to characterize fracture networks in subsurface systems. Stat. Anal. Data Min. ASA Data Sci. 2017, 10, 326–342. [Google Scholar] [CrossRef]
- Mudunuru, M.K.; Karra, S.; Harp, D.R.; Guthrie, G.D.; Viswanathan, H.S. Regression-based reduced-order models to predict transient thermal output for enhanced geothermal systems. Geothermics 2017, 70, 192–205. [Google Scholar] [CrossRef]
- Noor, A.K.; Zarchan, P. (Eds.) Structures Technology for Future Aerospace Systems, Volume 188 of Progress in Astronautics and Aeronautics; Aerospace Press: Los Angeles, CA, USA, 2000. [Google Scholar]
- Rice, J.R. Mathematical analysis in the mechanics of fracture. Fract. Adv. Treatise 1968, 2, 191–311. [Google Scholar]
- Rice, J.R.; Thomson, R. Ductile versus brittle behaviour of crystals. Philos. Mag. A J. Theor. Appl. Phys. 1974, 29, 73–97. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Plastic stress and strain fields at a crack tip. J. Mech. Phys. Solids 1968, 16, 337–342. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Singular behaviour at the end of a tensile crack in a hardening material. J. Mech. Phys. Solids 1968, 16, 13–31. [Google Scholar] [CrossRef]
- Hutchinson, J.W.; Suo, Z. Mixed mode cracking in layered materials. In Advances in Applied Mechanics; Academic Press Inc.: San Diego, CA, USA, 1991; Volume 29, pp. 63–191. [Google Scholar]
- Xu, X.-P.; Needleman, A. Numerical simulations of fast crack growth in brittle solids. J. Mech. Phys. Solids 1994, 42, 1397–1434. [Google Scholar] [CrossRef]
- Li, F.Z.; Shih, C.F.; Needleman, A. A comparison of methods for calculating energy release rates. Eng. Fract. Mech. 1985, 21, 405–421. [Google Scholar] [CrossRef]
- Buehler, M.J.; Abraham, F.F.; Gao, H. Hyperelasticity governs dynamic fracture at a critical length scale. Nature 2003, 426, 141. [Google Scholar] [CrossRef]
- Ravi-Chandar, K.; Yang, B. On the role of microcracks in the dynamic fracture of brittle materials. J. Mech. Phys. Solids 1997, 45, 535–563. [Google Scholar] [CrossRef]
- Desroches, J.; Detournay, E.; Lenoach, B.; Papanastasiou, P.; Pearson, J.R.A.; Thiercelin, M.; Cheng, A. The crack tip region in hydraulic fracturing. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1994, 447, 39–48. [Google Scholar] [CrossRef]
- Griffith, A.A. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond. A 1921, 221, 163–198. [Google Scholar] [CrossRef]
- Irwin, G.R. Analysis of stresses and strains near the ends of a crack traversing a plate. J. Appl. Mech. 1957, 24, 361–364. [Google Scholar]
- Barenblatt, G.I. The mathematical theory of equilibrium cracks in brittle fracture. Adv. Appl. Mech. 1962, 7, 55–129. [Google Scholar]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Needleman, A. An analysis of tensile decohesion along an interface. J. Mech. Phys. Solids 1990, 38, 289–324. [Google Scholar] [CrossRef]
- Beltz, G.E.; Rice, J.R. Dislocation nucleation versus cleavage decohesion at crack tips. In Modeling the Deformation of Crystalline Solids; Metallurgical Society of AIME: Englewood, CO, USA, 1991; pp. 457–480. [Google Scholar]
- Xu, X.-P.; Needleman, A. Void nucleation by inclusion debonding in a crystal matrix. Model. Simul. Mater. Sci. Eng. 1993, 1, 111. [Google Scholar] [CrossRef]
- Pandolfi, A.; Krysl, P.; Ortiz, M. Finite element simulation of ring expansion and fragmentation: The capturing of length and time scales through cohesive models of fracture. Int. J. Fract. 1999, 95, 279–297. [Google Scholar] [CrossRef]
- Freed, Y.; Banks-Sills, L. A new cohesive zone model for mixed mode interface fracture in bimaterials. Eng. Fract. Mech. 2008, 75, 4583–4593. [Google Scholar] [CrossRef]
- Park, K.; Paulino, G.H.; Roesler, J.R. A unified potential-based cohesive model of mixed-mode fracture. J. Mech. Phys. Solids 2009, 57, 891–908. [Google Scholar] [CrossRef]
- De Borst, R. Fracture in quasi-brittle materials: A review of continuum damage-based approaches. Eng. Fract. Mech. 2002, 69, 95–112. [Google Scholar] [CrossRef]
- Lisjak, A.; Grasselli, G. A review of discrete modeling techniques for fracturing processes in discontinuous rock masses. J. Rock Mech. Geotech. Eng. 2014, 6, 301–314. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Ambati, M.; Gerasimov, T.; DeLorenzis, L. A review on phase-field models of brittle fracture and a new fast hybrid formulation. Comput. Mech. 2015, 55, 383–405. [Google Scholar] [CrossRef]
- Verhoosel, C.V.; deBorst, R. A phase-field model for cohesive fracture. Int. J. Numer. Methods Eng. 2013, 96, 43–62. [Google Scholar] [CrossRef]
- Borden, M.J.; Verhoosel, C.V.; Scott, M.A.; Hughes, T.J.R.; Landis, C.M. A phase-field description of dynamic brittle fracture. Comput. Methods Appl. Mech. Eng. 2012, 217, 77–95. [Google Scholar] [CrossRef]
- Hakim, V.; Karma, A. Laws of crack motion and phase-field models of fracture. J. Mech. Phys. Solids 2009, 57, 342–368. [Google Scholar] [CrossRef]
- Kuhn, C.; Müller, R. A continuum phase field model for fracture. Eng. Fract. Mech. 2010, 77, 3625–3634. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 7th ed.; Butterworth-Heinemann, Elsevier Ltd.: Oxford, UK, 2013. [Google Scholar]
- Mudunuru, M.K.; Nakshatrala, K.B. A framework for coupled deformation-diffusion analysis with application to degradation/healing. Int. J. Numer. Methods Eng. 2011, 89, 1144–1170. [Google Scholar] [CrossRef]
- Munjiza, A.; Rougier, E.; Knight, E.E. Large Strain Finite Element Method: A Practical Course; John Wiley & Sons, Inc.: West Sussex, UK, 2015. [Google Scholar]
- Portela, A.; Aliabadi, M.H.; Rooke, D.P. The dual boundary element method: Effective implementation for crack problems. Int. J. Numer. Methods Eng. 1992, 33, 1269–1287. [Google Scholar] [CrossRef]
- Blandford, G.E.; Ingraffea, A.R.; Liggett, J.A. Two dimensional stress intensity factor computations using the boundary element method. Int. J. Numer. Methods Eng. 1981, 17, 387–404. [Google Scholar] [CrossRef]
- Xu, C.; Mudunuru, M.K.; Nakshatrala, K.B. Material degradation due to moisture and temperature. Part 1, Mathematical model, analysis, and analytical solutions. Contin. Mech. Thermodyn. 2016, 28, 1847–1885. [Google Scholar] [CrossRef]
- De Borst, R.; Sluys, L.J.; Muhlhaus, B.-H.; Pamin, J. Fundamental issues in finite elements analyses of localization of deformation. Eng. Comput. 1993, 10, 99–121. [Google Scholar] [CrossRef]
- Belytschko, T.; Gracie, R.; Ventura, G. A review of extended/generalized finite element methods for material modeling. Model. Simul. Mater. Sci. Eng. 2009, 17, 043001. [Google Scholar] [CrossRef]
- Emden, H.K.; Simsek, E.; Rickelt, S.; Wirtz, S.; Scherer, V. Review and extension of normal force models for the discrete element method. Powder Technol. 2007, 171, 157–173. [Google Scholar] [CrossRef]
- Munjiza, A.; Andrews, K.R.F.; White, J.K. Combined single and smeared crack model in combined finite-discrete element analysis. Int. J. Numer. Methods Eng. 1999, 44, 41–57. [Google Scholar] [CrossRef]
- Munjiza, A. The Combined Finite Discrete Element Method; John Wiley & Sons, Inc.: West Sussex, UK, 2004. [Google Scholar]
- Munjiza, A.; E, E.; Rougier, E. Computational Mechanics of Discontinua; John Wiley & Sons, Inc.: West Sussex, UK, 2011. [Google Scholar]
- Lei, Z.; Rougier, E.; Knight, E.E.; Munjiza, A.; Viswanathan, H. A generalized anisotropic deformation formulation for geomaterials. Comput. Part. Mech. 2016, 3, 215–228. [Google Scholar] [CrossRef]
- Osthus, D.; Godinez, H.C.; Rougier, E.; Srinivasan, G. Calibrating the stress-time curve of a combined finite-discrete element method to a Split Hopkinson pressure bar experiment. Int. J. Rock Mech. Min. Sci. 2018, 106, 278–288. [Google Scholar] [CrossRef]
- Knight, E.E.; Rougier, E.; Lei, Z.; Munjiza, A. User’s Manual for Los Alamos National Laboratory Hybrid Optimization Software Suite (HOSS)—Educational Version; Technical Report LA-UR-16-23118; Los Alamos National Laboratory: Washington, DC, USA, 2016.
- Knight, E.E.; Rougier, E.; Lei, Z. Hybrid Optimization Software Suite (HOSS)–Educational Version; Technical Report LA-UR-15-27013; Los Alamos National Laboratory: Washington, DC, USA, 2015. [Google Scholar]
- Jordan, A.B.; Stauffer, P.H.; Knight, E.E.; Rougier, E.; Anderson, D.N. Radionuclide gas transport through nuclear explosion-generated fracture networks. Sci. Rep. 2015, 5, 18383. [Google Scholar] [CrossRef] [PubMed]
- Brady, L.G.; Huq, F. Upscaling crack propagation and random interactions in brittle materials under dynamic loading. Procedia IUTAM 2013, 6, 108–113. [Google Scholar] [CrossRef]
- Kachanov, L. Introduction to Continuum Damage Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 10. [Google Scholar]
- Cady, C.M.; Adams, C.D.; Hull, L.M.; Gray, G.T.; Prime, M.B.; Addessio, F.L.; Wynn, T.A.; Papin, P.A.; Brown, E.N. Characterization of shocked beryllium. In EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2012; Volume 26, p. 01009. [Google Scholar]
- Escobedo, J.P.; Trujillo, C.P.; Cerreta, E.K.; Gray, G.T., III; Brown, E.N. Effect of shock wave duration on dynamic failure of tungsten heavy alloy. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2014; Volume 500, p. 112012. [Google Scholar]
- Moore, B.A.; Rougier, E.; O’Malley, D.; Srinivasan, G.; Hunter, A.; Viswanathan, H.S. Predictive modeling of dynamic fracture growth in brittle materials with machine learning. Comput. Mater. Sci. 2018, 148, 46–53. [Google Scholar] [CrossRef]
- Schwarzer, M.; Rogan, B.; Ruan, Y.; Song, Z.; Lee, D.Y.; Percus, A.G.; Chau, V.T.; Moore, B.A.; Rougier, E.; Viswanathan, H.S.; et al. Learning to fail: Predicting fracture evolution in brittle material models using recurrent graph convolutional neural networks. Comput. Mater. Sci. 2019, 162, 322–332. [Google Scholar] [CrossRef]
- Fung, J.; Harrison, A.K.; Chitanvis, S.; Margulies, J. Ejecta source and transport modeling in the FLAG hydrocode. Comput. Fluids 2013, 83, 177–186. [Google Scholar] [CrossRef]
- Tonks, D.L.; Bingert, J.; Livescu, V.; Luo, S.; Bronkhorst, C. Mesoscale polycrystal calculations of damage in spallation in metals. In EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2010; Volume 10, p. 00006. [Google Scholar]
- Tonks, D.; Bronkhorst, C.A.; Bingert, J. A comparison of calculated damage from square waves and triangular waves. In AIP Conference Proceedings; AIP: Melville, NY, USA, 2012; Volume 1426, pp. 1045–1048. [Google Scholar]
- Krajcinovic, D.; Sumarac, D. Micromechanics of the damage processes. In Continuum Damage Mechanics Theory and Application; Springer: Berlin/Heidelberg, Germany, 1987; pp. 135–194. [Google Scholar]
- Krajcinovic, D.; Mastilovic, S. Some fundamental issues of damage mechanics. Mech. Mater. 1995, 21, 217–230. [Google Scholar] [CrossRef]
- Labuz, J.F.; Zang, A. Mohr–Coulomb failure criterion. Rock Mech. Rock Eng. 2012, 45, 975–979. [Google Scholar] [CrossRef]
- Rougier, E.; Knight, E.E.; Broome, S.T.; Sussman, A.J.; Munjiza, A. Validation of a three-dimensional finite-discrete element method using experimental results of the split Hopkinson pressure bar test. Int. J. Rock Mech. Min. Sci. 2014, 70, 101–108. [Google Scholar] [CrossRef]
- Carey, J.W.; Lei, Z.; Rougier, E.; Mori, H.; Viswanathan, H. Fracture-permeability behavior of shale. J. Unconv. Oil Gas Resour. 2015, 11, 27–43. [Google Scholar] [CrossRef]
- Euser, B.; Rougier, E.; Lei, Z.; Knight, E.E.; Frash, L.P.; Carey, J.W.; Viswanathan, H.; Munjiza, A. Simulation of fracture coalescence in granite via the combined finite–discrete element method. In Rock Mechanics and Rock Engineering; Springer: Vienna, Austria, 2018; pp. 1–15. [Google Scholar]
- Jungnickel, D. Graphs, Networks, and Algorithms, volume 5 of Algorithms and Computation in Mathematics, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Freund, L.B. Dynamic Fracture Mechanics; Cambridge Monographs on Mechanics and Applied Mathematics; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Unger, D.J. Analytical Fracture Mechanics; Dover Publications: San Diego, CA, USA, 1995. [Google Scholar]
- Krajcinovic, D.; Vujosevic, M. Intrinsic failure modes of brittle materials. Int. J. Solids Struct. 1998, 35, 2487–2503. [Google Scholar] [CrossRef]
- Hu, X.Z.; Wittmann, F.H. Fracture energy and fracture process zone. Mater. Struct. 1992, 25, 319–326. [Google Scholar] [CrossRef]
- Wang, Y.-Z.; Atkinson, J.D.; Akid, R.; Parkins, R.N. Crack interaction, coalescence, and mixed mode fracture mechanics. Fatigue Fract. Eng. Mater. Struct. 1995, 19, 427–439. [Google Scholar] [CrossRef]
- Kamaya, M. Growth evaluation of multiple interacting surface cracks.Part I: Experiments and simulation of coalesced crack. Eng. Fract. Mech. 2008, 75, 1336–1349. [Google Scholar] [CrossRef]
- Kamaya, M. Growth evaluation of multiple interacting surface cracks. Part II: Growth evaluation of parallel cracks. Eng. Fract. Mech. 2008, 75, 1350–1366. [Google Scholar] [CrossRef]
- Kamaya, M.; Miyokawa, E.; Kikuchi, M. Growth prediction of two interacting surface cracks of dissimilar sizes. Eng. Fract. Mech. 2010, 77, 3120–3131. [Google Scholar] [CrossRef]
- Bidokhti, A.A.; Shahani, A.R. Interaction analysis of non-aligned cracks using extended finite element method. Lat. Am. J. Solids Struct. 2015, 12, 2439–2459. [Google Scholar] [CrossRef]
- Keller, J.M.; Gray, M.R.; Givens, J.A. A fuzzy k-nearest neighbor algorithm. IEEE Trans. Syst. Man Cybern. 1985, 4, 580–585. [Google Scholar] [CrossRef]
- Forsyth, P.J.E. A unified description of micro and macroscopic fatigue crack behaviour. Int. J. Fatigue 1983, 5, 3–14. [Google Scholar] [CrossRef]
- Ochi, Y.; Ishii, A.; Sasaki, S.K. An experimental and statistical investigation of surface fatigue crack initiation and growth. Fatigue Fract. Eng. Mater. Struct. 1985, 8, 327–339. [Google Scholar] [CrossRef]
- Suh, C.M.; Lee, J.J.; Kang, Y.G.; Ahn, H.J.; Woo, B.C. A simulation of the fatigue crack process in type 304 stainless steel at 538 C. Fatigue Fract. Eng. Mater. Struct. 1992, 15, 671–684. [Google Scholar] [CrossRef]
- Argence, D.; Weiss, J.; Pineau, A. Observation and modelling of transgranular and intergranular multiaxial low-cycle fatigue damage of austenitic stainless steels. In ICBFF4 Conference; Mechanical Engineering Publication: Paris, France, 1994. [Google Scholar]
- Hagberg, A.; Swart, P.; Chult, D. Exploring Network Structure, Dynamics, and Function Using NetworkX; Technical Report LA-UR-08-05495; Los Alamos National Laboratory: Washington, DC, USA, 2008.
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and their Application; Cambridge University Press: New York, NY, USA, 1997; Volume 1. [Google Scholar]
- Paliwal, B.; Ramesh, K.T. An interacting micro-crack damage model for failure of brittle materials under compression. J. Mech. Phys. Solids 2008, 56, 896–923. [Google Scholar] [CrossRef]
- Vaughn, N.; Kononov, A.; Moore, B.; Rougier, E.; Viswanathan, H.; Hunter, A. Statistically informed upscaling of damage evolution in brittle materials. Theor. Appl. Fract. Mech. 2019, 102, 210–221. [Google Scholar] [CrossRef]
- Sundararaghavan, V.; Srivastava, S. Microfract: An image based code for microstructural crack path prediction. SoftwareX 2017, 6, 94–97. [Google Scholar] [CrossRef]
- Hunter, A.; Moore, B.A.; Mudunuru, M.; Chau, V.; Tchoua, R.; Nyshadham, C.; Karra, S.; O’Malley, D.; Rougier, E.; Viswanathan, H.; et al. Reduced-order modeling through machine learning and graph-theoretic approaches for brittle fracture applications. Comput. Mater. Sci. 2019, 157, 87–98. [Google Scholar] [CrossRef]
- Khodabakhshi, P.; Reddy, J.N.; Srinivasa, A. GraFEA: A graph-based finite element approach for the study of damage and fracture in brittle materials. Meccanica 2016, 51, 3129–3147. [Google Scholar] [CrossRef]
- Lü, L.; Zhou, T. Link prediction in complex networks: A survey. Phys. A: Stat. Mech. Appl. 2011, 390, 1150–1170. [Google Scholar] [CrossRef]



| Scenario Description | Number of Simulations | % of Failure Path Match |
|---|---|---|
| Accurate prediction of failure path | 43 | 100% match |
| Reasonable prediction of failure path | 75 | >50% match |
| Non-matching failure paths | 72 | <50% match |
| Total | 190 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mudunuru, M.K.; Panda, N.; Karra, S.; Srinivasan, G.; Chau, V.T.; Rougier, E.; Hunter, A.; Viswanathan, H.S. Surrogate Models for Estimating Failure in Brittle and Quasi-Brittle Materials. Appl. Sci. 2019, 9, 2706. https://doi.org/10.3390/app9132706
Mudunuru MK, Panda N, Karra S, Srinivasan G, Chau VT, Rougier E, Hunter A, Viswanathan HS. Surrogate Models for Estimating Failure in Brittle and Quasi-Brittle Materials. Applied Sciences. 2019; 9(13):2706. https://doi.org/10.3390/app9132706
Chicago/Turabian StyleMudunuru, Maruti Kumar, Nishant Panda, Satish Karra, Gowri Srinivasan, Viet T. Chau, Esteban Rougier, Abigail Hunter, and Hari S. Viswanathan. 2019. "Surrogate Models for Estimating Failure in Brittle and Quasi-Brittle Materials" Applied Sciences 9, no. 13: 2706. https://doi.org/10.3390/app9132706
APA StyleMudunuru, M. K., Panda, N., Karra, S., Srinivasan, G., Chau, V. T., Rougier, E., Hunter, A., & Viswanathan, H. S. (2019). Surrogate Models for Estimating Failure in Brittle and Quasi-Brittle Materials. Applied Sciences, 9(13), 2706. https://doi.org/10.3390/app9132706








