Analytical Model for the Structural Behavior of Pipelines During Lowering-In
Abstract
:1. Introduction
2. Modeling of a Pipeline During Lowering-in
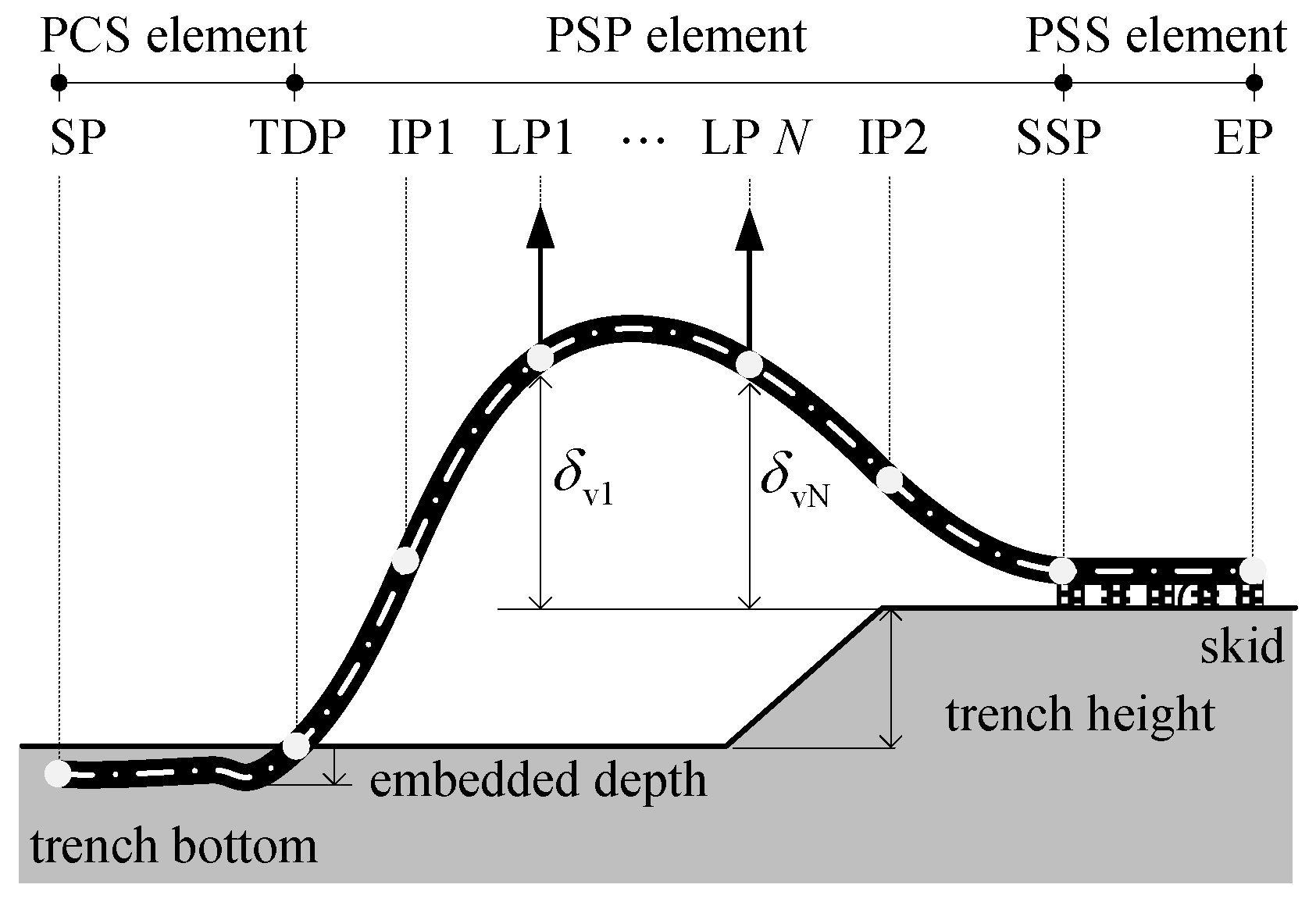
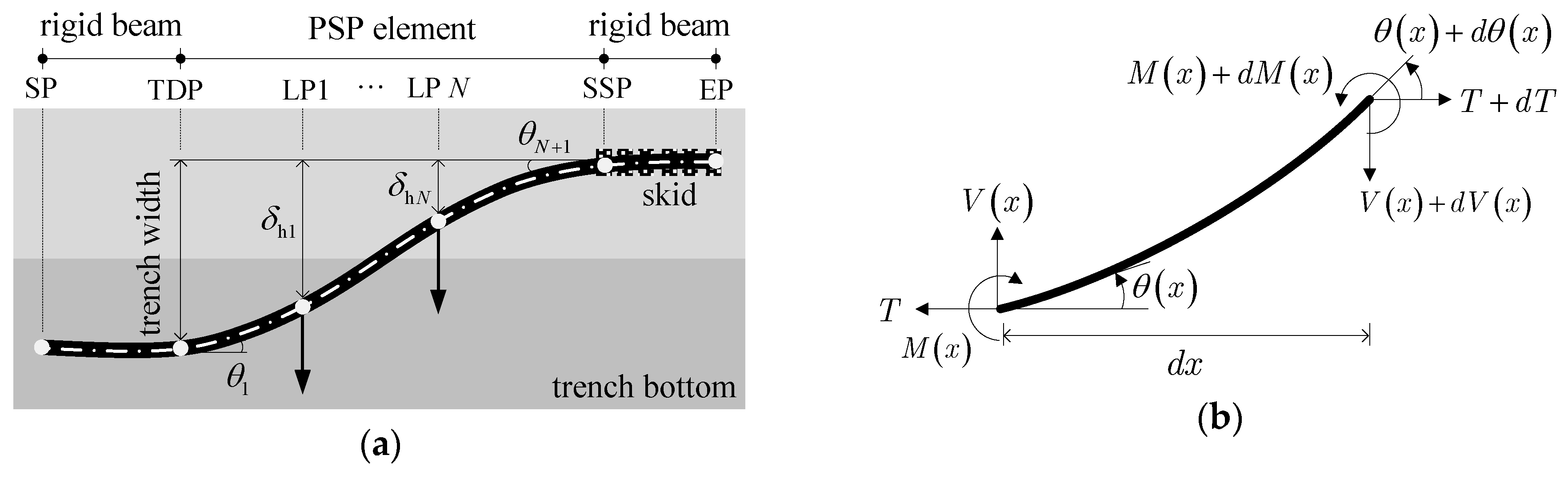
2.1. Segmental Pipeline Model Elements
2.2. Mathematical Formulations for Segmental Pipeline Models
3. Validation of Segmental Pipeline Models
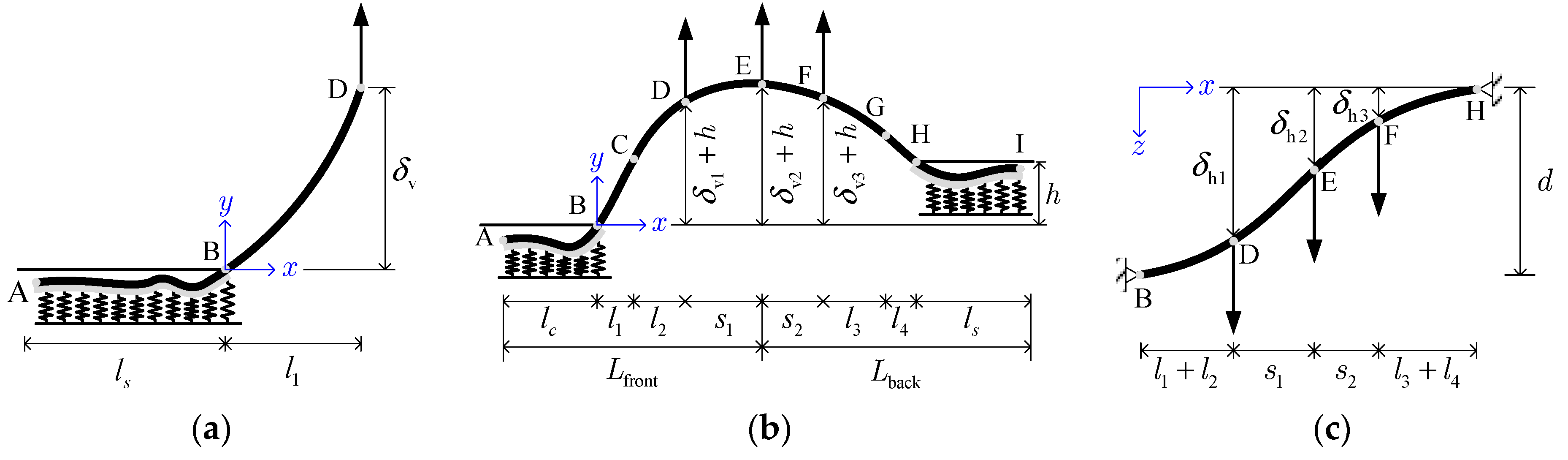
3.1. Lowering-in Process and Configuration of Pipeline
3.2. Model 1 and 2 for the Lowering-in Phase
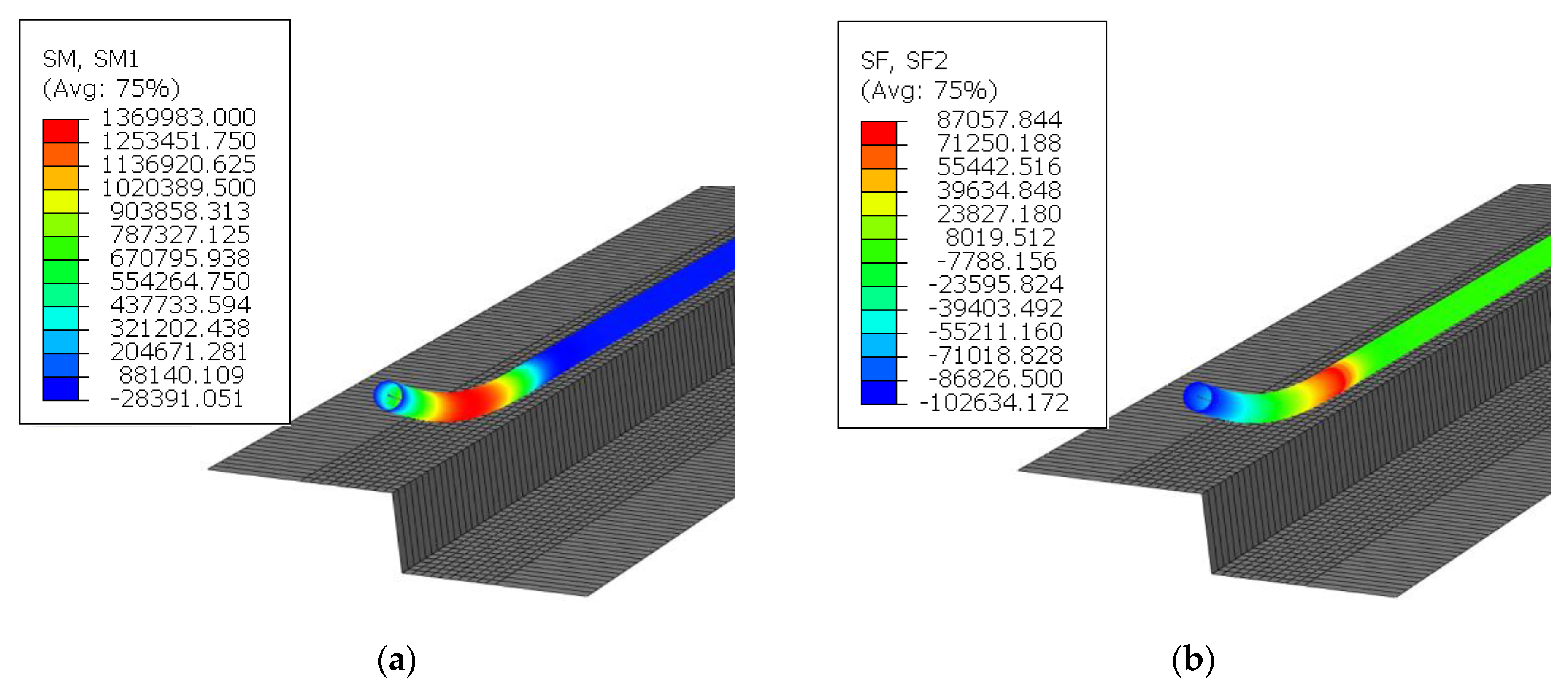
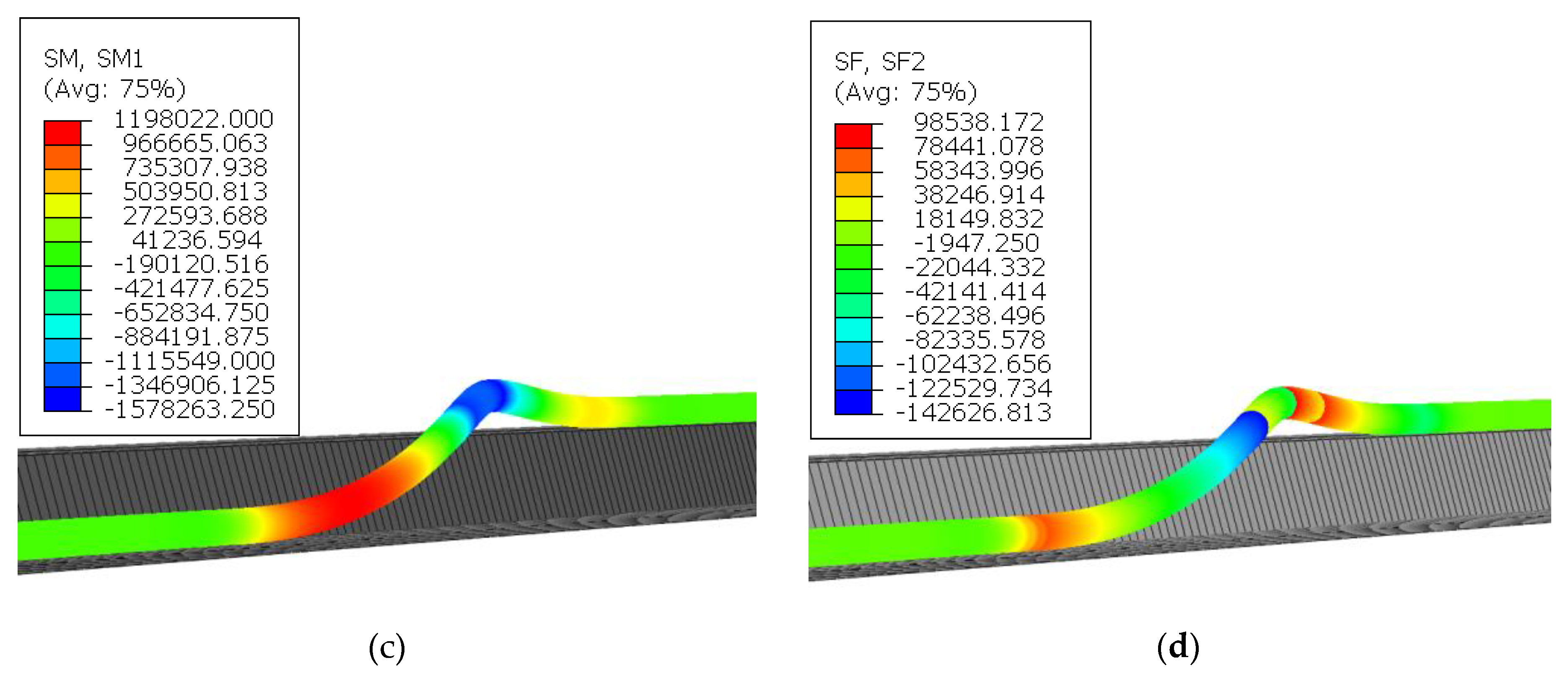
3.3. Finite Element Analysis for the Lowering-in Phase
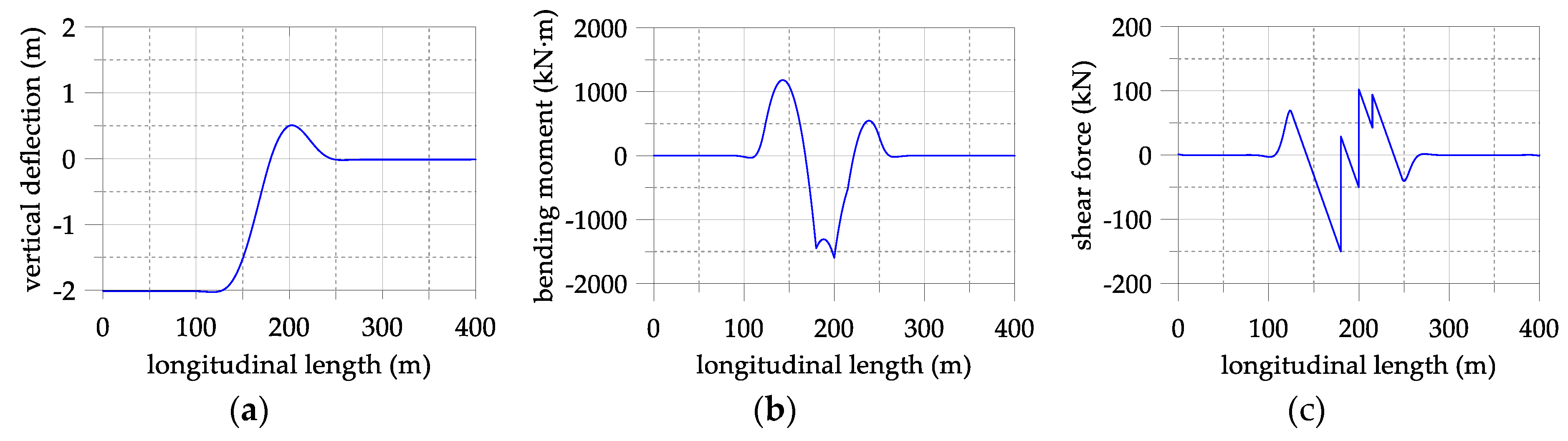
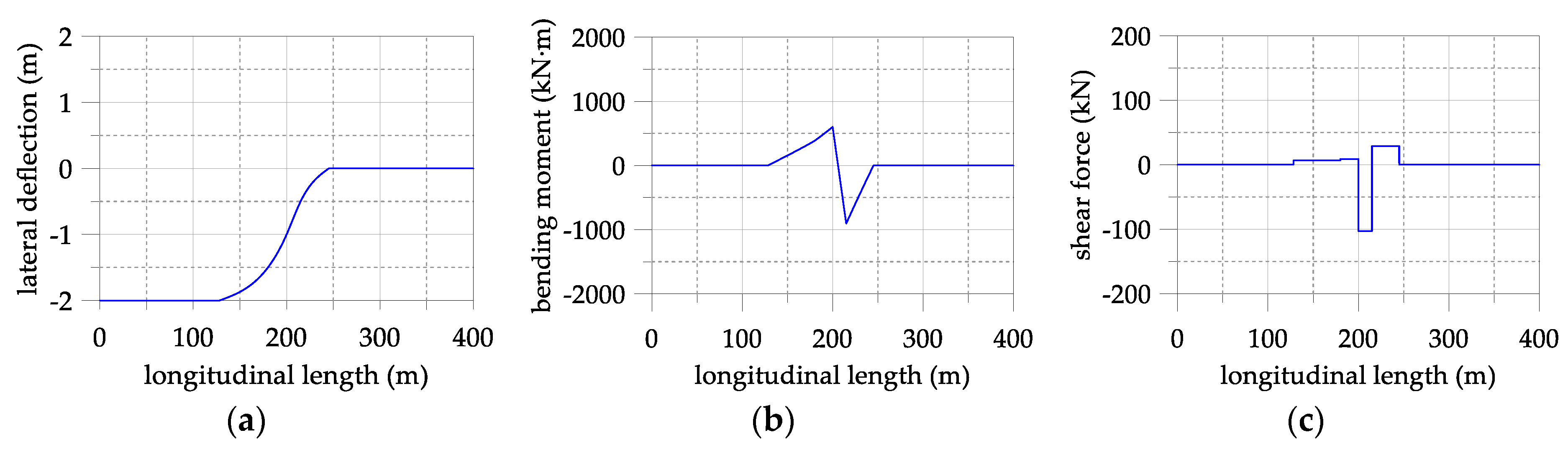
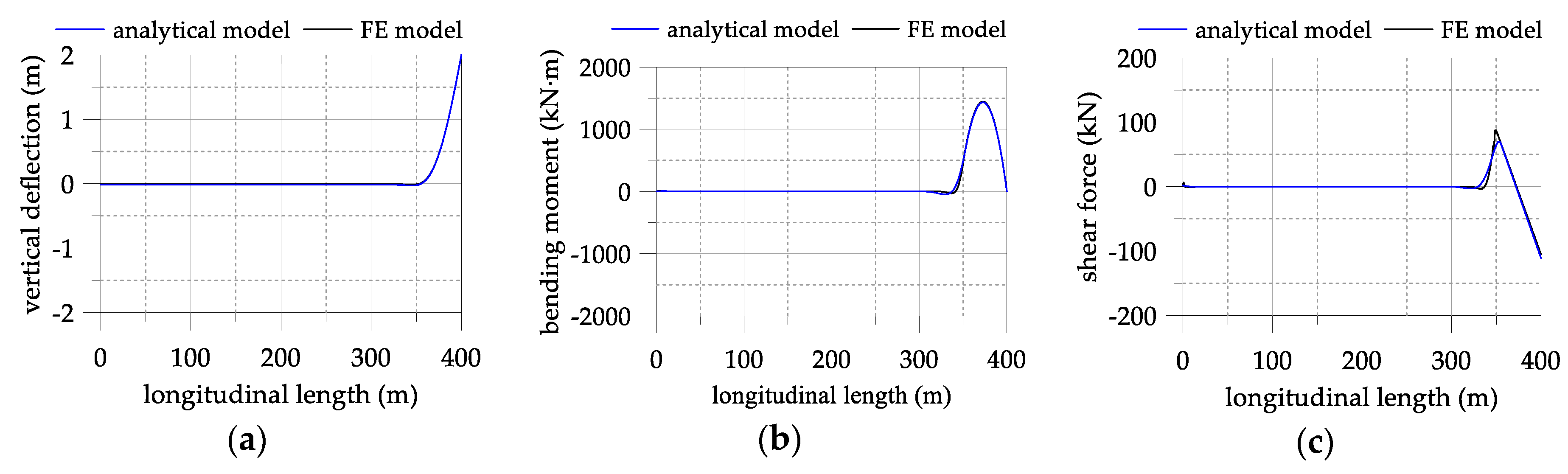
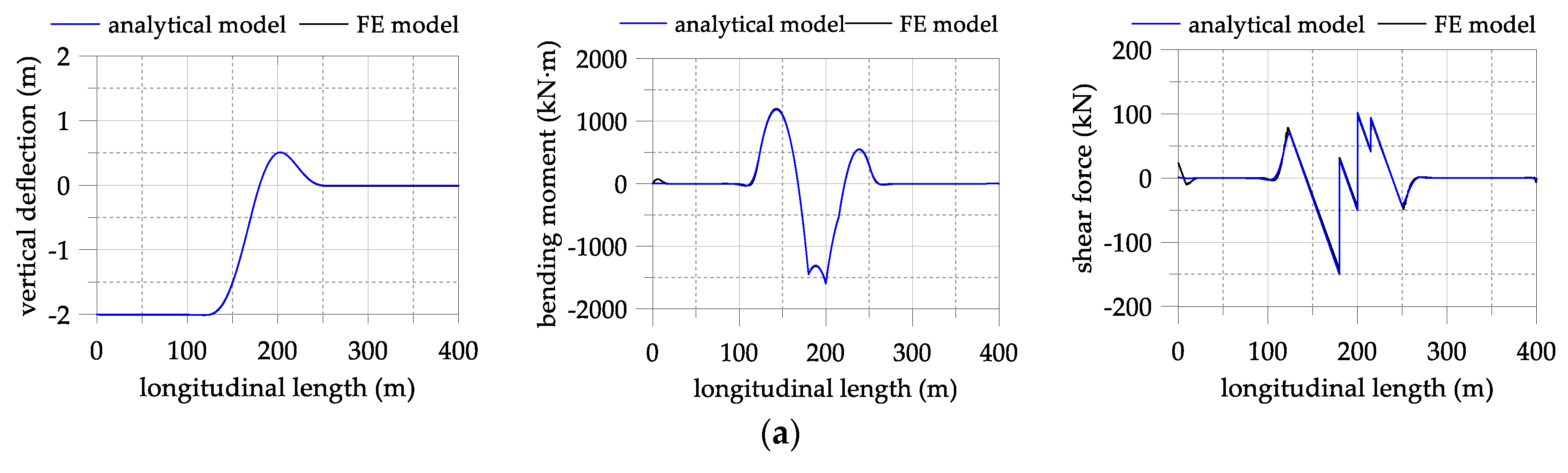
3.4. Comparison of the Analytical and FE Analysis Results
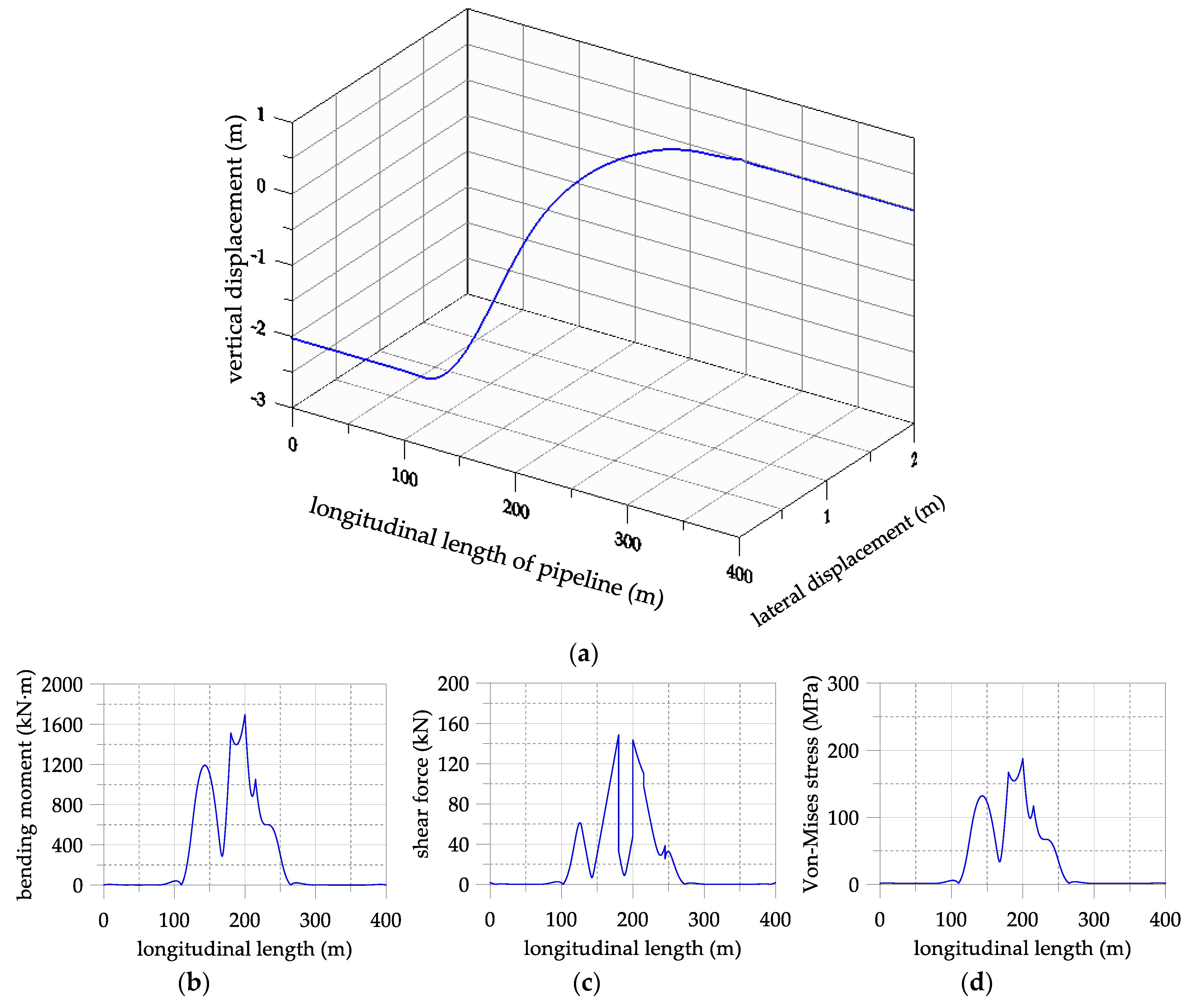
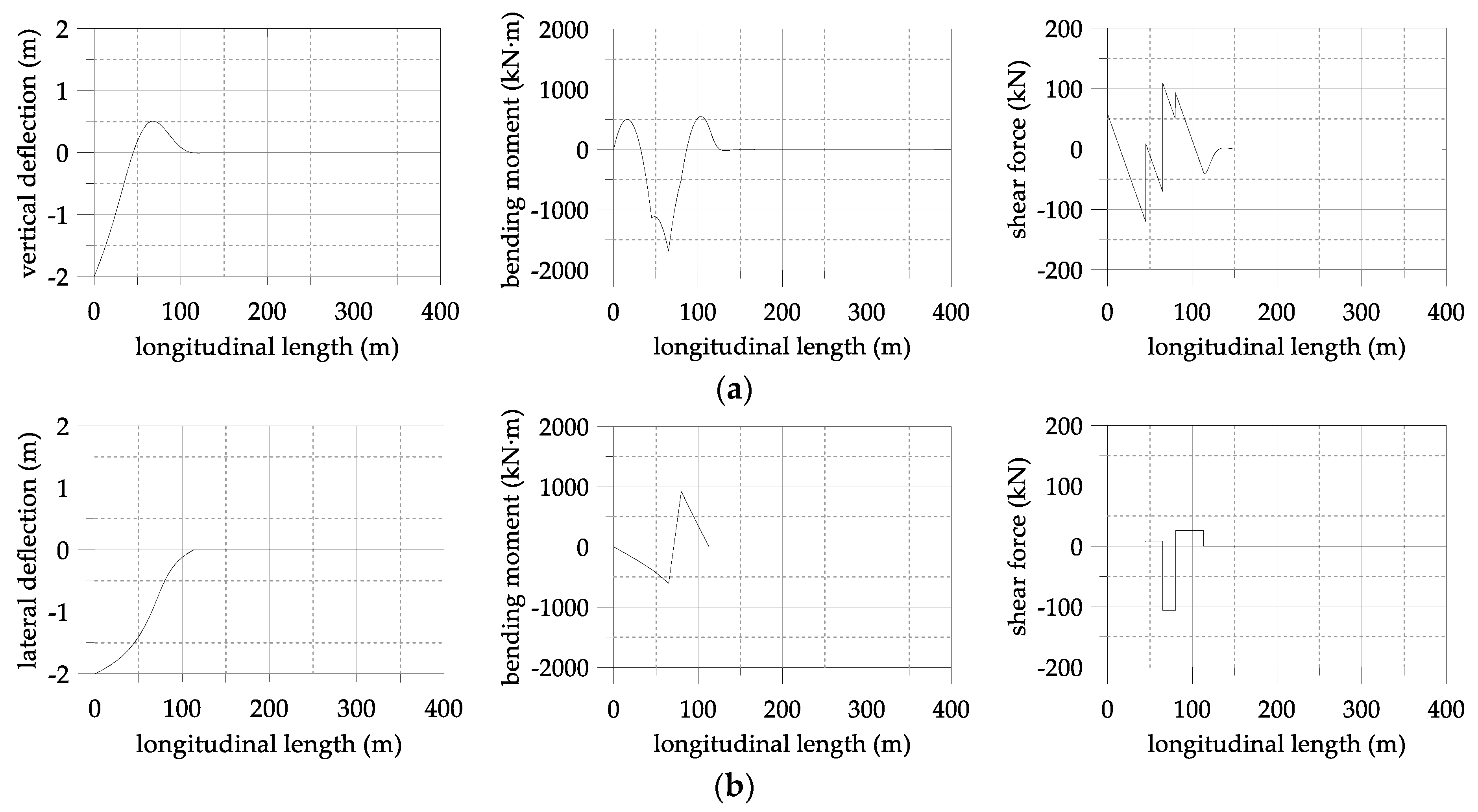
4. Application of the Segmental Pipeline Model
5. Discussion
6. Conclusions
- The structural behavior resulting from the segmental pipeline model and the FE analysis showed good agreement, except for being slightly different in terms of the bending moments and shear forces near the TDP and SSP positions. The small difference is caused due to the limitation of applicable boundary conditions and simplification of the modeling of pipeline-soil interaction.
- During lowering-in, the boundary conditions of the pipeline are continuously changed due to the use of pipelayers. The segmental pipeline model can simulate variable boundary conditions, combining several PCS, PSP and PSS elements. This makes it more convenient to expand the segmental model to cover various construction sequences during lowering-in.
- The necessary elements in the modeling process can be intuitively selected by considering the geometric deformations and boundary conditions. The segmental pipeline model is built by combining the necessary elements and the final system equations of the segmental model are nonlinear, which can be solved easily through a numerical approach.
- The ratios of the absolute maximum bending moment and shear force in Case 2 to Case 1 were about 0.91 and about 1.17, respectively. Additionally, the ratios of the absolute maximum bending moment and shear force in the transverse direction to the vertical direction were about 0.56 and 0.68, respectively. This indicates that it is necessary to consider the sectional forces of pipeline in the lateral direction and the shear forces for an increase of pipelayers when analyzing the structural behavior of pipelines.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

| Equations for Each Element | ||
|---|---|---|
| shear layer of PCS | ||
| SP to TDP | PCS | |
| TDP to IP1 | PSP 1 | |
| IP1 to LP1 | PSP 2 | |
| LP1 to LP2 | PSP 3 | |
| LP2 to LP3 | PSP 4 | |
| LP3 to IP2 | PSP 5 | |
| IP2 to SSP | PSP 6 | |
| SSP to EP | PSS | |
| shear layer of PSS | ||
| Front Side of LP2 | Back Side of LP2 | ||
|---|---|---|---|
| elements | Length of elements | elements | Length of elements |
| PCS () | 128.249 m | PSP 4 () | 15 m |
| PSP 1 () | 39.606 m | PSP 5 () | 23.223 m |
| PSP 2 () | 12.145 m | PSP 6 () | 6.855 m |
| PSP 3 () | 20 m | PSS () | 154.922 m |

| Equations for Each Element | Elemental Length | ||
|---|---|---|---|
| TDP to LP1 | PSP 1 | 51.752 m | |
| LP1 to LP2 | PSP 2 | 20 m | |
| LP2 to LP3 | PSP 3 | 15 m | |
| LP3 to SSP | PSP 4 | 30.078 m | |
References
- Pipeline Research Council International, Inc. Best Practices in Applying API 1104 Appendix A; API Publishing Services: Washington, DC, USA, 2014. [Google Scholar]
- Scott, C.; Etheridge, B.; Vieth, P. An analysis of the stresses incurred in pipe during laying operations. In Proceedings of the 7th International Pipeline Conference (IPC 2008), Calgary, AB, Canada, 29 September–3 October 2008. [Google Scholar]
- Duan, D.M.; Jurca, T.; Zhou, C. A stress check procedure for pipe lowering-in process during pipeline construction. In Proceedings of the IPC, 10th International Pipeline Conference, Calgary, AB, Canada, 29 September–3 October 2014. [Google Scholar]
- Newmark, N.M.; Rosenblueth, E. Fundamentals of Earthquake Engineering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1971. [Google Scholar]
- Hall, W.J.; Newmark, N.M. Seismic design criteria for pipelines and facilities, the current state of knowledge of lifeline Earthquake engineering. J. Struct. Eng. ASCE 1977, 103, 18–34. [Google Scholar]
- Wang, L.R.L.; O’Rourke, M.J.; Pikul, R.R. Seismic response behavior of buried pipelines. J. Press. Vessel Technol. ASME 1979, 101, 21–30. [Google Scholar] [CrossRef]
- Nelson, I.; Weidlinger, P. Dynamic seismic analysis of long segmented lifelines. J. Press. Vessel Technol. ASME 1979, 101, 10–20. [Google Scholar] [CrossRef]
- Muleski, G.E.; Ariman, T.; Aumen, C.P. A shell model for buried pipes in earthquakes. Int. J. Soil Dyn. Earthq. Eng. 1985, 4, 43–51. [Google Scholar] [CrossRef]
- O’Leary, P.M.; Datta, S.K. Dynamics of buried pipelines. Int. J. Soil Dyn. Earthq. Eng. 1985, 4, 151–159. [Google Scholar]
- Luco, J.E.; Barnes, F.C.P. Seismic response of cylindrical shell embedded in layered visco elastic half space. Earthq. Eng. Struct. Dyn. 1994, 23, 553–580. [Google Scholar] [CrossRef]
- Wong, K.C.; Shah, A.H.; Datta, S.K. Three dimensional motion of buried pipeline. J. Eng. Mech. ASME 1986, 112, 1319–1348. [Google Scholar] [CrossRef]
- Datta, S.K.; Shah, A.H.; Wong, K.C. Dynamic stresses and displacements in buried pipe. J. Eng. Mech. ASME 1984, 110, 1451–1465. [Google Scholar] [CrossRef]
- Takada, S.; Tanabe, K. Three dimensional seismic response analysis of buried continuous or jointed pipelines. J. Press. Vessel Technol. ASME 1987, 109, 80–87. [Google Scholar] [CrossRef]
- Lee, D.H.; Kim, B.H.; Lee, H.; Kong, J.S. Seismic behavior of a buried gas pipeline under earthquake excitations. Eng. Struct. 2009, 31, 1011–1023. [Google Scholar] [CrossRef]
- Kennedy, R.P.; Chow, A.W.; Williamson, R.A. Fault movement effects on buried oil pipeline. Transp. Eng. J. ASCE 1977, 103, 617–633. [Google Scholar]
- Wang, L.R.L.; Yeh, Y. A refined seismic analysis and design of buried pipeline for fault movement. Earthq. Eng. Struct. Dyn. 1985, 13, 75–96. [Google Scholar] [CrossRef]
- Karamitros, D.K.; Bouckovalas, G.D.; Kouretzis, G.P. Stress analysis of buried steel pipelines at strike-slip fault crossings. Soil Dyn. Earthq. Eng. 2007, 27, 200–211. [Google Scholar] [CrossRef]
- Trifonov, O.V.; Cherniy, V.P. A semi-analytical approach to a nonlinear stress–strain analysis of buried steel pipelines crossing active faults. Earthq. Eng. Struct. Dyn. 2010, 30, 1298–1308. [Google Scholar] [CrossRef]
- Dixon, D.A.; Rutledge, D.R. Stiffened catenary calculations in pipeline laying problem. J. Eng. Ind. ASME 1968, 90, 153–160. [Google Scholar] [CrossRef]
- Lenci, S.; Callegari, M. Simple analytical models for the J-lay problem. Acta Mech. 2005, 178, 23–39. [Google Scholar] [CrossRef]
- Maats Pipeline Professionals. Available online: https://www. maats.com/higher-lifting-capacity-roller-cradles (accessed on 3 December 2018).
- Sen, M.; Zhou, J. Evaluation of pipeline stresses during line lowering. In Proceedings of the 7th International Pipeline Conference (IPC 2008), Calgary, AB, Canada, 29 September–3 October 2008. [Google Scholar]
- Hetenyi, M. Beams on Elastic Foundation; University of Michigan Press: Ann Arbor, MI, USA, 1946. [Google Scholar]
- Filonenko-Borodich, M.M. Some Approximate Theories of the Elastic Foundation; No. 46; Uchenyie Zapiski Moskovskogo Gosudarstuennogo Universiteta Mechanika: Moscow, Russia, 1940; pp. 3–18. (In Russian) [Google Scholar]
- Pasternak, P.L. On a New Method of Analysis of an Elastic Foundation by Means of Two Foundation Constants; Gosudarsrvennoe Izdatelstvo Literaturi po Stroitelstvu i Arkhitekture: Moscow, Russia, 1954. (In Russian) [Google Scholar]
- Reissner, E. A note on deflection of plates on a viscoelastic foundation. J. Appl. Mech. 1958, 25, 144–145. [Google Scholar]
- Kerr, A.D. Elastic and viscoelastic foundation models. J. Appl. Mech. 1964, 31, 491–498. [Google Scholar] [CrossRef]
- Vlasov, V.Z.; Leont’ev, U.N. Beams, Plates and Shells on Elastic Foundations; Israel Program for Scientific Translation: Jerusalem, Israel, 1966; (Translated from Russian). [Google Scholar]
- Scott, R.F. Foundation Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1981. [Google Scholar]
- Zhaohua, F.; Cook, R.D. Beam element on two-parameter elastic foundations. J. Eng. Mech. ASCE 1986, 109, 1390–140220. [Google Scholar] [CrossRef]
- Simulia, D.S. Abaqus 6.16 Theory Manual; DS Simulia Corp: Providence, RI, USA, 2015. [Google Scholar]
- The Ministry of Fuel and Power Industry of the Russian Federation. Design and Construction of Gas Pipelines from Metal Pipes SP 42-102-2004; The Ministry of Fuel and Power Industry of the Russian Federation: Moscow, Russia, 2004.


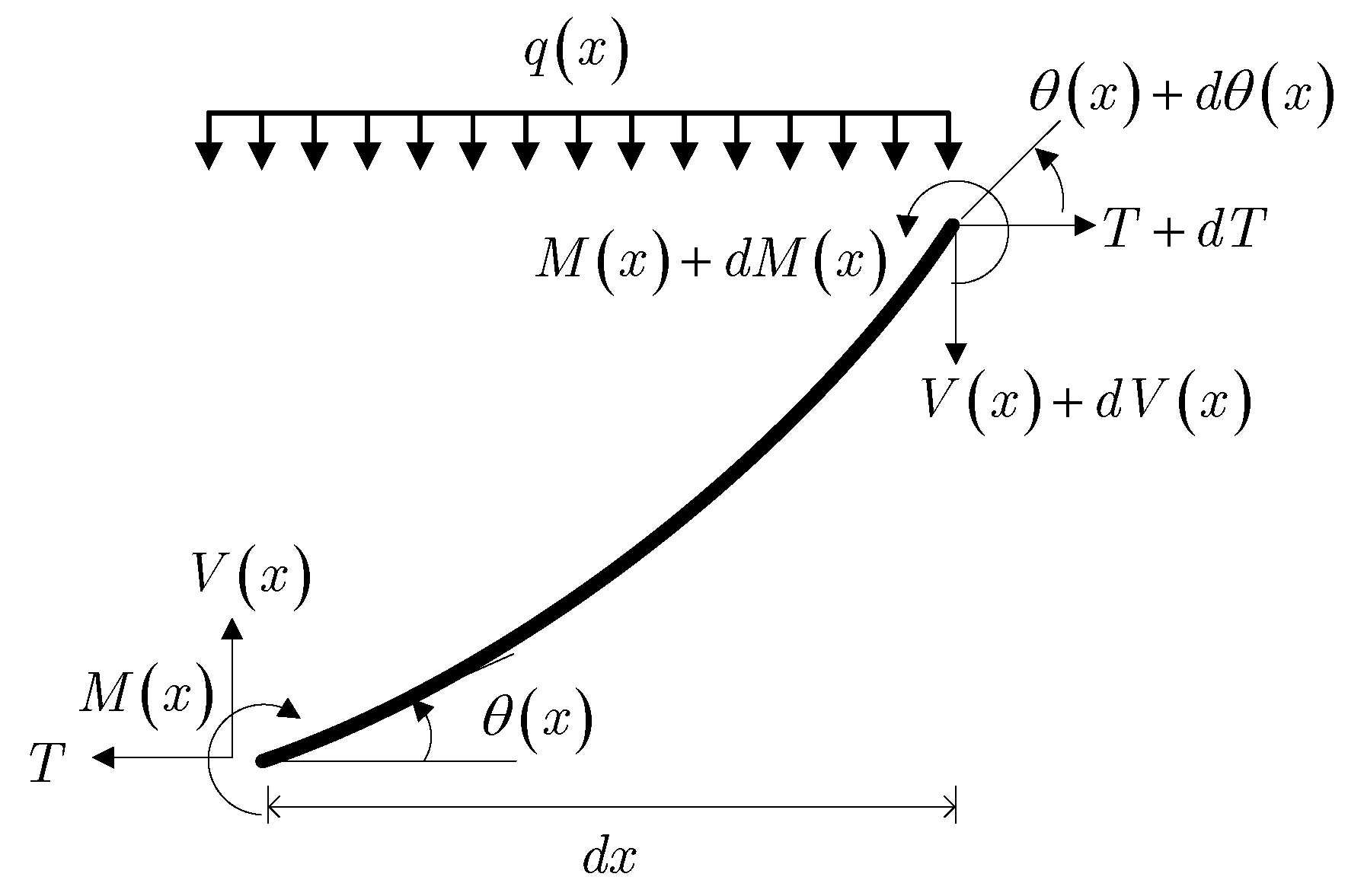


| Classification | Pipeline | Trench | |
|---|---|---|---|
| material properties | density | 7850 kg/m3 | 1520 kg/m3 |
| elastic modulus | 210 GPa | 50MPa | |
| Poisson’s ratio | 0.3 | 0.32 | |
| geometric properties | section property |  |  |
| length | 400 m | 400 m | |
| Case | LP1 (Location of First Pipelayer) | LP2 (Location of Second Pipelayer) | LP3 (Location of Third Pipelayer) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Location | Displacement | Location | Displacement | Location | Displacement | ||||
| Vertical | Lateral | Vertical | Lateral | Vertical | Lateral | ||||
| 1 | 380 | 1.5 | - | 400 | 1.8 | - | - | - | - |
| 2 | 365 | 2.4 | - | 385 | 2.5 | - | 400 | 2.4 | - |
| 3 | 45 | 0.0 | 0.5 | 65 | 0.5 | 1.5 | 80 | 0.4 | 2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, W.; Lee, J.S. Analytical Model for the Structural Behavior of Pipelines During Lowering-In. Appl. Sci. 2019, 9, 2595. https://doi.org/10.3390/app9132595
Hwang W, Lee JS. Analytical Model for the Structural Behavior of Pipelines During Lowering-In. Applied Sciences. 2019; 9(13):2595. https://doi.org/10.3390/app9132595
Chicago/Turabian StyleHwang, Woongik, and Jong Seh Lee. 2019. "Analytical Model for the Structural Behavior of Pipelines During Lowering-In" Applied Sciences 9, no. 13: 2595. https://doi.org/10.3390/app9132595
APA StyleHwang, W., & Lee, J. S. (2019). Analytical Model for the Structural Behavior of Pipelines During Lowering-In. Applied Sciences, 9(13), 2595. https://doi.org/10.3390/app9132595





