Abstract
This paper studies the combined effects of viscous dissipation, first and second-order slip and variable transport properties on phase-change hydromagnetic bio-nanofluid convection flow from a stretching sheet. Nanoscale materials possess a much larger surface to volume ratio than bulk materials, significantly modifying their thermodynamic and thermal properties and substantially lowering the melting point. Gyrotactic non-magnetic micro-organisms are present in the nanofluid. The transport properties are assumed to be dependent on concentration and temperature. Via appropriate similarity variables, the governing equation with boundary conditions are converted to nonlinear ordinary differential equations and are solved using the BVP4C subroutine in the symbolic software MATLAB. The non-dimensional boundary value features a melting (phase change) parameter, temperature-dependent thermal conductive parameter, first as well as second-order slip parameters, mass diffusivity parameter, Schmidt number, microorganism diffusivity parameter, bioconvection Schmidt number, magnetic body force parameter, Brownian motion and thermophoresis parameters. Extensive computations are visualized for the influence of these parameters. The present simulation is of relevance in the fabrication of bio-nanomaterials for bio-inspired fuel cells.
1. Introduction
Melting fluid dynamics and heat transfer constitute an interesting sub-section of thermo-physics. They relate to phase change problems which arise in many manufacturing processes. These include laser ablation [1], polymer synthesis [2], metallic processing [3] and electromagnetic crucible systems [4] and glass treatment [5]. Simulation of melting processes is very complex since; in general, engineers must correctly model thermally-driven flow which is coupled with a moving interface. The latent heat of the processes is either absorbed or released. There is a very sophisticated interplay between the fluid flow and the moving boundary which is largely associated with the fact that the location of the solid—liquid interface emerges as an unknown, as elaborated by Gau and Viskanta [6]. Important variables in melting heat transfer computation include the melting front position and Nusselt number. In the most general case, the melting heat transfer problem is a moving boundary problem, and powerful computational methods are necessary for a solution (adaptive grid methods, volume-of-fluid methods, front tracking methods, phase field approaches etc.). An alternative approach is, however, to focus on boundary-layer flow in melting phase-change problems in which the melting effect can be simulated as a boundary condition which circumvents the need to solve the full field equations in real time. Although less accurate, this approach has its merits since it does provide a reasonable approximation for the wall heat transfer rates. Tien and Yen [7] theoretically determined the effect of melting on heat transfer via convection between a body which is melting and the surrounding fluid. It was shown that melting has the effect of retarding heat transfer rate. Epstein and Cho [8] investigated steady laminar flow over a flat plate in the case of melting heat transfer. They found that melting has the effect of inhibiting the rate of heat transfer and reducing the local Nusselt number. The Chebyshev spectral method was used by Mahmoud and Waheed [9] to compute solutions for melting stagnation point flow of a micropolar fluid in a permeable material with heat absorption effect, noting a reduction in surface shear stress with stronger melting effect and the reverse response in the local Nusselt number. Karimipour [10] employed the lattice Boltzmann method to solve the problem of slip flow in a microchannel of a copper, silver and aluminium oxide with water-based nanofluid. Kazmierczak et al. [11] investigated phase-change forced convection flow from a metal plate in porous regime, noting the strong influence of melting parameter on the local heat transfer rate at the melt interface with the solid. Wang [12] obtained perturbation solutions for phase-change convection in swirling flow from a disk, observing a significant modification in temperature, velocity, torque and wall heat transfer with the ratio of injection (melt) rate and viscosity parameter. Andersson et al. [13] computed solutions for magnetohydrodynamic melting flow and convection from a planar spinning disk, identifying that the melt rate for which a steady state solution exists is reduced with stronger magnetic field. Yao et al. [14] used the D2Q9 Lattice Boltzmann method (LBM) to study numerically the free convection melting with radiative heat transfer applied to solve the coupled heat transfer during phase change process involving natural convection and radiation.
Nanofluids are a relatively new class of nanoscale materials which are synthesized by doping conventional fluids (water, oils, polymers and gels) with nanoparticles. The nanoparticles generally comprise either metals, oxides, carbides, nitrides, or non-metal in which the particles have diameter size between 1 and 100 nm. Das et al. [15] among others have confirmed that nanofluids achieve demonstrably greater thermal performance via augmented heat transfer properties than the base fluids (water, kerosene, ethylene glycol, methanol, polymeric solutions etc.). Numerous studies of nanofluid transport phenomena have been communicated. Tripathi and Bég [16] have conducted an extensive review of applications in medicine, fuel cells, biopolymers and other emerging fields including peristaltic nano-pumps and nano-bioreactor systems. However, in most computational investigations the nanofluids have been assumed to be in one state, i.e., they do not undergo a phase change. Melting of nano-materials and nanofluids, however, constitutes a major branch of nanoscience. Experimental studies in this regard have shown there is a substantial reduction in the melting point of a material when the particle size of the material approaches to the nanoscale ranges. Nanoscale materials change phase at temperatures hundreds of degrees lower than bulk materials. This phenomenon has been observed in many manifestations of nanomaterials, including base materials doped with nanowires, nanotubes and nanoparticles. The engineered nanomaterials consistently melt at lower temperatures than the bulk form of the same material; this has been attributed to the radically greater surface to volume ratio achieved compared to purely bulk materials. This serves to modify the thermodynamic and thermal properties [17]. Other important studies in this regard include one by Kumaresan et al. [18], who reported on the fabrication of an advanced class of nanofluid phase change materials which were synthesized by dispersing carbon nanotubes in water. Barlak et al. [19] investigated viscosity and thermal conductivity modifications in nano-encapsulated phase change materials. They observed that the viscosity of the nanofluids is lowered with greater temperature whereas it is enhanced with increasing solid nanoparticle concentration. Thermal conductivity of nanofluids is however elevated with increasing temperature. Han et al. [20] developed hybrid nanofluids by deploying nanoparticles made of phase-change materials. Guisbiers and Buchaillot [21] have presented a detailed thermodynamic analysis of the melting enthalpy of nanofluids. Boundary layer melting convection flows of nanofluids have recently stimulated some interest. Kumar Ch and Bandari [22] presented numerical quadrature solutions for two-dimensional stagnation-point thermal convection of a nanofluid towards a melting stretching sheet of copper and silver nanoparticles in a water-based fluid. Kumari and Gorla [23] studied laminar nano-liquid flow to a melting vertical plate surface in a moving nano-liquid, noting an elevation in both wall heat transfer and mass transfer rate with melting effect, and furthermore an enhancement in heat transfer rate (Nusselt number) at the solid/fluid interface. Chieruzzi et al. [24] quantified thermal properties of hybrid nanofluids by mixing a molten salt base fluid (NaNO3–KNO3 (60:40 ratio) binary salt selected as phase change material) with nanoparticles using the direct-synthesis method as a possible working medium for concentrating solar plants. Sheikholeslami and Rokni [25] simulated the nanofluid flow over a stretching plate in the presence of a magnetic field, strong radiative heat transfer and melting, computing elevation in both nanofluid velocity and concentration with melting parameter. Mastiani et al. [26] analyzed the melting of paraffin-based copper nanoparticle-doped nanofluids in an annulus using an unstructured finite volume method to track the solid and liquid interface. They noted that heat transfer rate and melting time are respectively increased and reduced with a rise in nanoparticle volume fraction.
Magnetized nanofluids constitute yet another development in nanoscale fluidics. These nanomaterials exploit suspended magnetite nanoparticles which effectively render the nanofluid to be electrically-conducting. To simulate the dynamics of magnetic nanofluids, magnetohydrodynamic (MHD) models are required. The nanofluid is therefore more intelligent and operates more as a smart fluid allowing the manipulation of flow and thermal characteristics with externally applied magnetic fields Shima et al. [27]. The fusion of nanofluid and magnetohydrodynamics produces many interesting combined effects including Lorentzian drag effects, secondary flow (Hall currents), electromagnetic induction, damping, ferrofluidics, levitation phenomena, Ohmic dissipation, magnetic torque, ionslip and Maxwell displacement currents. Numerous studies of magnetized nanofluids have been communicated in manufacturing, biomedical, energy and chemical engineering systems. Rajesh et al. [28] used the Crank-Nicholson finite difference technique to study transient mixed convection MHD nanofluid flow from an exponentially stretching sheet in permeable materials. Beg et al. [29] obtained MAPLE quadrature solutions for time-dependent slip hydromagnetic nanofluid flow in porous media. Uddin et al. [30] computed chemical reaction effects on natural convection magnetized nanofluid boundary layer flows. Akbar et al. [31] investigated nanoparticle shape (brick, cylinder and platelet) effects on hydromagnetic pumping and heat transfer in nanofluids in a deformable conduit as a model of magnetic-targeted drug delivery. Further studies include Thumma et al. [32] who employed a finite element code for simulating dissipative magnetic nanofluid inclined Sakiadis flows; Bég et al. [33], who used a B-spline collocation algorithm for unsteady nanofluid orthopedic lubrication flows; and Daniel et al. [34] who evaluated both chemical reaction and viscous heating effects in hydromagnetic nanofluid Sakiadis flow. Several authors have also examined melting effects in magneto-nanofluid transport. Gireesha et al. [35] computed magnetohydrodynamic effects on melting heat transfer for the case of boundary layer stagnation-point. This study was for an electrically conducting nanofluid moving toward a stretching surface as well as heat source/sink. Other melting magneto-nanofluid dynamics investigations include Hayat et al. [36] with non-Newtonian and radiative effects and Hayat et al. [37] with radiation and stagnation point flow effects in carbon-water nanofluid.
Bioconvection involves the motion of micro-organisms under special conditions [38]. For such flows, as heavier micro-organisms sink, they are replaced by up swimming micro-organisms. The process causes a macroscopic motion (convection). The mechanism driving up-swimming is closely linked to the species of micro-organisms [39]. Common micro-organisms include oxytactic bacteria and gyrotactic algae. Oxytactic bacteria are an oxygen-consuming microorganism, and gyrotactic algae are linked to gravitational torque. It is only in the past three decades that bioconvection has gained much attention [40]. The current focus on “green technologies” is a major impetus behind the idea of using bioconvection micro-organism mechanisms in certain engineering systems. Bioconvection is interesting since the driving up-swimming is known to be associated with the microorganism species. Nano-bioconvection fuel cells are, in particular, stimulating great interest in recent years [41,42]. Many studies have confirmed that the accumulation of microorganisms in the upper portion of the fluid layer causes a top-heavy density stratification, instability then sets in and causes the microorganism to fall. “Return up” swimming microorganisms maintain this pattern. The addition of gyrotactic microorganisms, for example, in nanofluids has been shown to increases the stability of the suspension [43]. A state-of-the-art review of progress in nano-bioconvection flows has recently been presented by Beg [44] and includes Von Karman swirling, helical and peristaltic flows. Magnetic nanofluid bioconvection flows have also been addressed recently. Relevant studies include Alsaedi et al. [45] who also considered stratification effects, Zohra et al. [46] who considered slip, swirl and wall transpiration effects, and Rana et al. [47] who investigated stagnation-point flow from a stretching sheet with Stefan blowing effect. This study also involved the entropy generated flow of magnetized reactive nano-bioconvection fluids.
All previous researchers use constant fluid properties. The aim of the present article is to extend the magneto-nanofluid dissipative slip melting model of Mabood and Mastroberardino [48] to include gyrotactic bioconvection with variable transport properties. Using suitable similarity transformations, the governing boundary layer equations are converted into ordinary differential equations. The equations are then solved numerically using the BVP4C quadrature sub-routine in MATLAB. Variables transport properties such as Brownian diffusion, microorganism diffusivity, thermal conductivity and temperature dependent viscosity are considered. Validation is carried out. Further validation of the new solutions is also presented via the Variational Iteration Method (VIM) [49,50].
2. Problem Formulation
Steady two-dimensional, nonlinear, laminar magnetohydrodynamic convective flow of incompressible viscous nanofluid over a stretching sheet with variable viscosity and variable thermal conductivity are considered. Gyrotactic micro-organisms are suspended in the nanofluid. The -axis is along the stretching surface while -axis is normal to it. It is assumed that the stretching velocity where a is a constant. The fluid is electrically-conducting owing to the presence of magnetic nanoparticles. A constant transverse magnetic field is imposed normal to the stretching sheet. Since magnetic Reynolds number is small, the induced magnetic field is thereby deemed to have been negated. The assumption is made that the temperature of the melting surface is while the temperature in the free stream is such that . The nanoparticle volume fraction, , is assumed constant at the stretching surface and at the free stream is denoted as . Motile microorganisms are assumed to be at the wall. is assumed as microorganism at ambient values. The physical model and associated Cartesian coordinate system are illustrated in Figure 1.
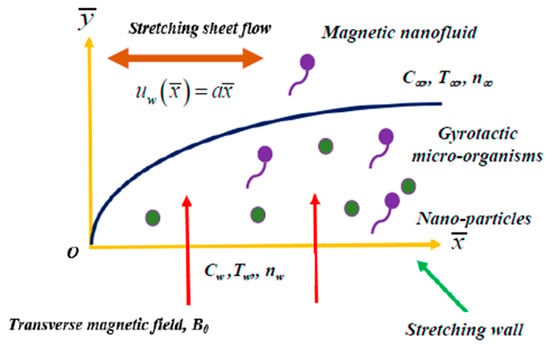
Figure 1.
Physical configuration and coordinate system [48,51].
The governing equations for continuity, momentum, energy, nanoparticle volume fraction (concentration) and microorganism may be stated following Mabood, Mastroberardino [48] and Animasaun [51] with modifications for bioconvection species conservation and variable properties as:
Continuity:
Momentum:
Energy:
Concentration:
Microorganism:
The relevant boundary condition is
Following studies by Amirsom et al. [52] and Animasaun [51], the variation in viscosity, thermal conductivity and nanoparticle and micro-organism diffusivities are modelled with the following mathematical functions:
where and denote the velocity components in the and directions; respectively. is the density of the base fluid; is the chemotaxis constant; is the maximum cell swimming speed; is the variable diffusivity of Brownian motion; is thermophoretic diffusion coefficient; is the variable diffusivity of microorganisms; is the variable thermal conductivity of nanofluids; is the variable temperature dependent viscosity; is electrical conductivity of the magnetic nanofluid; is the specific heat at constant pressure; is the temperature dependent viscous parameter; is the temperature dependent thermal conductive parameter; is the mass diffusivity parameter; microorganism diffusivity parameter; is velocity slip. The nonlinear two-dimensional steady-state boundary value problem defined by Equations (1)–(7) may be solved in primitive form. However, it is judicious to normalize the problem via the following group of similarity transformations:
The equation of continuity is satisfied if we select a stream function such that
Here all symbolism with units is defined in the nomenclature. Using Equation (8), the continuity Equation (1) is identically satisfied, and the governing conservation Equations (2)–(6) emerge as a ninth order system of coupled, nonlinear, multi-degree, ordinary differential equations (ODEs):
The associated transformed boundary conditions become:
The parameters present in Equations (10)–(14) are:
- : Prandtl number,
- : Brownian motion parameter,
- : thermophoresis parameter,
- : Schmidt number,
- : bioconvection Péclet number,
- : bioconvection Schmidt number,
- : magnetic body force parameter,
- : melting (phase change) parameter,
- : Eckert number,
- : first-order hydrodynamic slip parameter,
- : second-order hydrodynamic slip parameter.
We further note that is a combination of the Stefan numbers and for the liquid and solid phases, respectively. Important parameters of engineering interest are local skin friction factors , local Nusselt numbers , local Sherwood number and local density number of motile microorganisms, . These quantify the transfer rates of momentum, heat, nanoparticle species and motile micro-organisms at the sheet surface. They are defined respectively as:
where are the skin friction, surface heat flux, surface mass flux and surface motile microorganism flux which are defined by:
Substitute Equations (8) and (16) into (15), yields:
3. Numerical Computations with MATLAB BVP4C Code
The set of nonlinear ordinary differential equations, Equations (10)–(13) with boundary conditions (14) are solved numerically by using BVP4C numerical method under MATLAB for various values of the flow controlling parameters. In order to apply the BVP4C routine, we must rewrite the coupled non-linear differential equations as systems of first-order ODEs. The function BVP4C is a finite difference code that implements the three stages of Lobatto IIIa formula. It is a collocation formula, and the collocation polynomial provide us with a C1-continuous solution, which is fourth-order accurate uniformly in the interval where the function is integrated. In this solving approach, we have chosen a finite value of and fixing the relative tolerance to 10−5 produces every numerical solution in this problem. Mesh selection and error control are based on the residual of the continuous solution. The range of parameters are: and To validate the present solution, comparison has been made with previously published data from the literature for the skin friction in Table 1 and Table 2, and favourable agreement is achieved.

Table 1.
Comparison of skin friction for different values of when

Table 2.
Comparison of skin friction for when
4. Further Validation with Variational Iteration Method (VIM)
The MATLAB code has been validated against limited published results in Table 1. The case benchmarked used the data: . Therefore melting, slip, nanoscale and bioconvection effects are not validated against. In order to further validate the model, an alternative algorithm was used to solve the boundary value problem. The variational iteration method [56] has been used in several related studies [49,50,57,58] and is now used. The comparison with the benchmark case is shown in the last column of Table 1 and correlation is excellent. Further validations with the general model are illustrated in Figure 2a–d where the influence of temperature dependent viscous parameter, , and Eckert number, Ec, on velocity, temperature, nanoparticle volume fraction and micro-organism density number function are visualized.
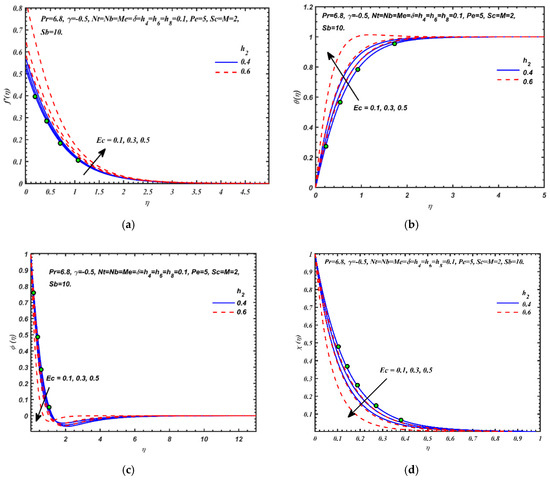
Figure 2.
Influences of and on the dimensionless: (a) velocity, (b) temperature, (c) nanoparticle volume fraction, (d) micro-organism density number function.
The circles correspond to the VIM solution and the lines to the BVP4C computations. The comparison cases are for Ec = 0.1 and = 0.4 in Figure 2a–d and very close agreement is attained. Confidence in the MATLAB BVP4C code is therefore justifiably high. Both velocity and temperature profile increase as both Ec and increase in Figure 2a,b. A significant temperature enhancement is obtained with an increase in both temperature dependent viscous parameter, , and Eckert number, Ec, on temperature and nanoparticle volume fraction. However, increasing Eckert number and temperature dependent viscous parameter are observed to suppress the volume fraction of nanoparticles throughout the boundary layer. Thermal boundary layer thickness is therefore elevated with greater viscous heating effect owing to the conversion of kinetic energy into heat (thermal energy) in the boundary layer. With increasing values of temperature dependent viscous parameter , nanofluid viscosity increases (based on the formulae in Equation (7)), which exacerbates thermal diffusion in the regime manifesting in temperature elevation. However, this simultaneously reduces the species diffusion of nanoparticles in the boundary layer and results in a decrease in nanoparticle species boundary layer thickness.
5. Results and Discussion
Selected computations based on the BVP4C code are presented in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10.
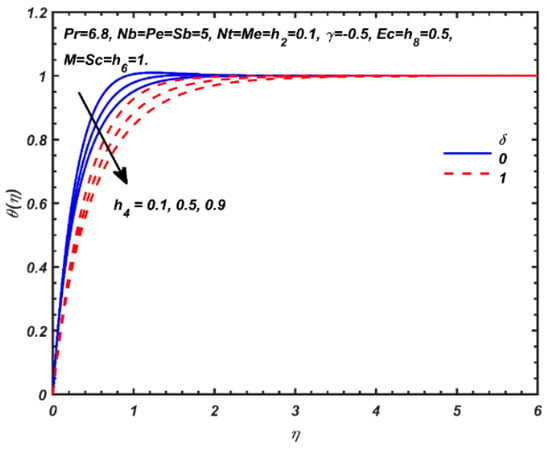
Figure 3.
Effects and on the dimensionless temperature.
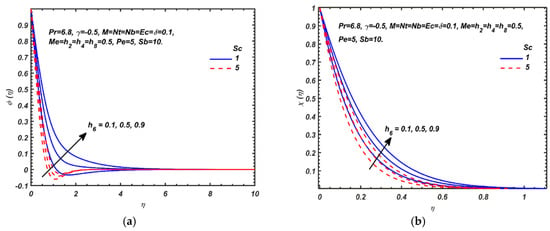
Figure 4.
Effects and on the dimensionless (a) nanoparticle volume fraction and (b) micro-organism density number function.
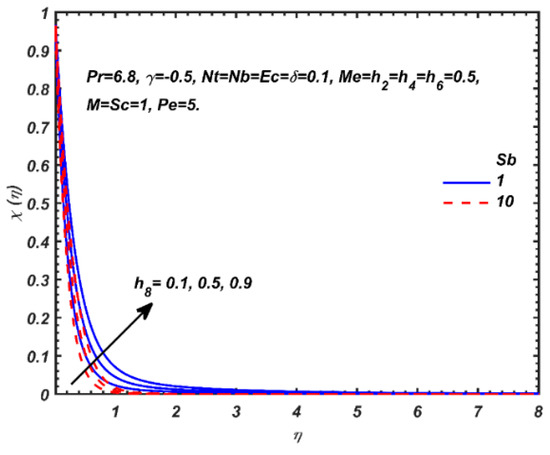
Figure 5.
Effects and on the dimensionless micro-organism density number function.
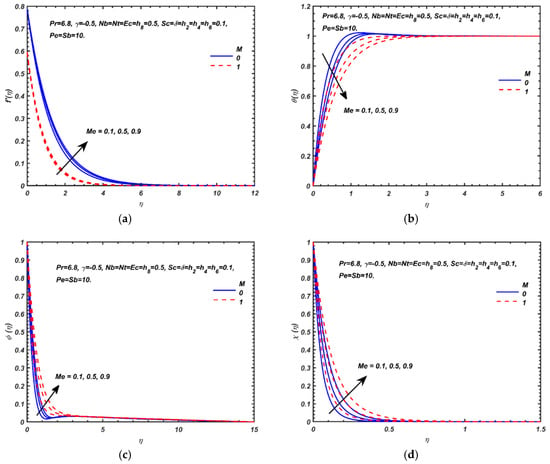
Figure 6.
Effects M and Me on the dimensionless (a) velocity, (b) temperature, (c) nanoparticle volume fraction and (d) micro-organism density number function.
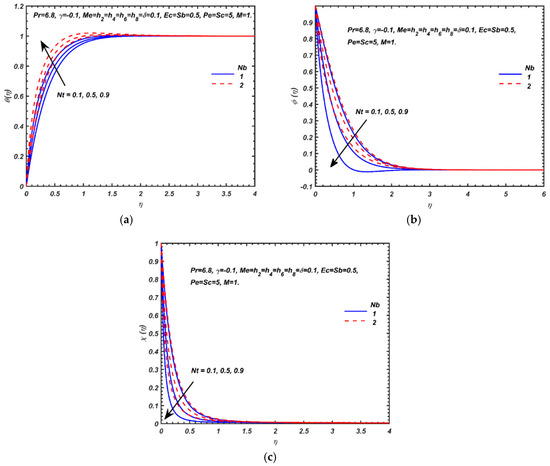
Figure 7.
Effects of Nb and Nt on the dimensionless (a) temperature, (b) nanoparticle volume fraction and (c) micro-organism density number function.
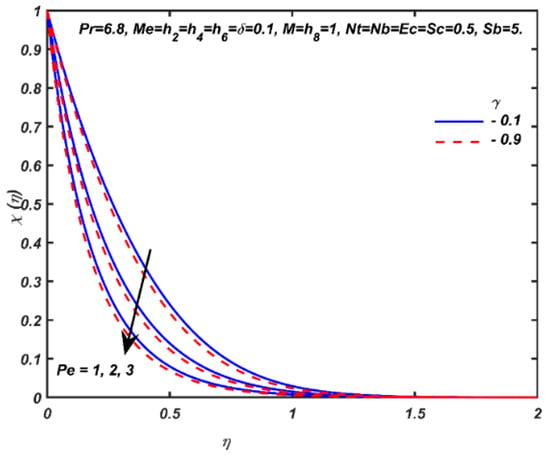
Figure 8.
Effects and Pe on the dimensionless micro-organism density number function.
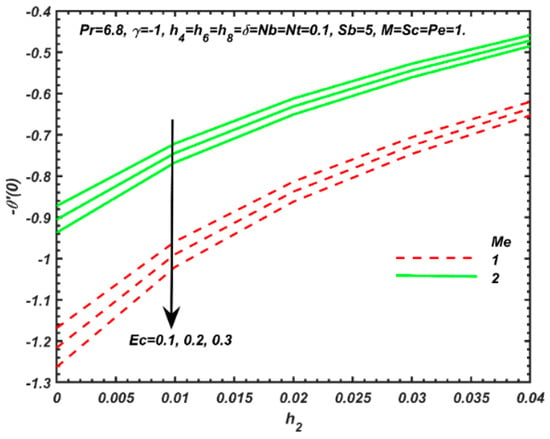
Figure 9.
Local Nusselt number, versus and Me for different values of Ec.
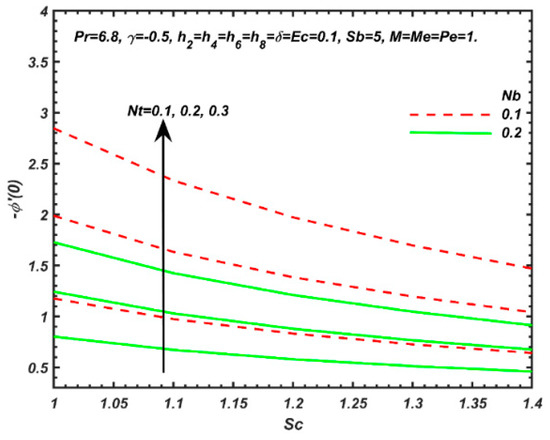
Figure 10.
Local Sherwood number, versus Sc and Nb for different values of Nt.
Figure 3 illustrates the collective impact of the temperature-dependent thermal conductive parameter and first-order slip parameter The former parameter , based on the original definition in Equation (7) arises in two key terms in the energy conservation Equation (11), via in the augmented thermal diffusion term, , and the thermophoretic term, . It also features in the melting interface wall boundary condition (14). It therefore plays a prominent role in heat diffusion in the regime. The latter parameter , only features in the wall velocity boundary condition. A strong decrease in temperature is associated with an increase in both and . Hydrodynamic slip increases momentum diffusion near the wall, and this impedes thermal diffusion leading to a reduction in thermal boundary layer thickness. The non-inclusion of slip effects will clearly lead to erroneous computations which will diverge from results of relevance to practical applications. With increasing thermal conductivity there will be a faster diffusion of heat from the nanofluid to the wall which will effectively reduce temperatures in the medium. In other words, greater thermal conductivity will serve to cool the medium more efficiently. Asymptotically smooth solutions are achieved in the free stream indicating (as in Figure 2a–d) that enough infinity boundary conditions have been imposed in the MATLAB BVP4C code.
Figure 4a,b depict the impact of nanoparticle mass diffusivity parameter, , and Schmidt number, Sc, on nanoparticle volume fraction and microorganism density number function. A strong enhancement in both nanoparticle volume fraction and motile microorganism density is induced with greater . The converse response is generated with greater Schmidt number. Both nanoparticle species and motile microorganism species boundary layer thicknesses are enhanced with accentuation in mass diffusivity. Increasing Schmidt number, however, corresponds to a decrease in nanoparticle species diffusivity which results in a reduction in both nanoparticle species and motile microorganism species boundary layer thicknesses. Monotonic decays from the wall (sheet surface) to the free stream are observed in both plots, although the trend is more consistent for the micro-organism density function (Figure 4b).
Figure 5 visualizes the response in motile microorganism density number with a variation in both microorganism diffusivity parameter, , and bioconvection Schmidt number, Sb. A rise in value of clearly shows that micro-organism profile increases with greater Sb but decreases when the value of Sb increases. is an important parameter controlling the bioconvection propulsion phenomenon. When both viscous diffusivity and micro-organism diffusivity are equivalent, i.e., viscous and micro-organisms diffuse at the same rate and both velocity (hydrodynamic) and micro-organism boundary layer thicknesses are the same. When Sb = 10 clearly the viscous diffusivity exceeds the micro-organism diffusivity by a factor of ten and this results in a substantial reduction in diffusion rate of micro-organisms relative to the viscous diffusion. Micro-organism species concentration boundary layer thickness will therefore be considerably reduced.
Figure 6a–d displays the influence of the magnetic body force parameter (M) and melting parameter (Me) on velocity, temperature, nanoparticle volume fraction and motile microorganism density number. As both magnetic field and melting heat transfer parameter increase, it is evident from Figure 6a, that the flow is accelerated strongly. Although in conventional stationary wall magnetohydrodynamics, the Lorentz body force decelerates flow, the presence of a stretching wall reverses this effect, as observed in various studies including Zueco et al. [59]. The motion of the wall drags the magnetic field with the free stream, and this results in flow acceleration. Momentum boundary layer thickness is therefore effectively decreased. The intensification in melting effect also imparts significant momentum to the nanofluid which results in flow acceleration and thinning of the momentum boundary layer. The electrically non-conducting scenario (M = 0) therefore produces deceleration compared with the magnetic case. Conversely, Figure 6b shows that temperatures are reduced with increasing melting parameter, Me. Again, this is associated with the boost in momentum with greater melting effect which is enhanced relative to the heat diffusion rate. Thermal boundary layer thickness is therefore decreased. However, although the magnetic field accelerates the flow, it generates a similar effect to that encountered in stationary wall magnetohydrodynamics, namely an elevation in temperature. This is associated with the dissipation in supplementary work expended in dragging the nanofluid against the action of the magnetic field which manifests as thermal energy. The boundary layer regime is therefore heated, and thermal boundary layer thickness is enhanced. Figure 6c indicates that the nanoparticle species is elevated with increasing melting effect whereas it is strongly suppressed with increasing magnetic body force effect. Nanoparticle species diffusion is therefore assisted with phase change whereas it is impeded with a stronger magnetic field. The implication is that melting encourages better distribution of nanoparticles in the nanomaterial whereas a transverse magnetic field stifles dispersion of nanoparticles leading to less homogenous distributions. Figure 6d shows that micro-organism species concentration (number density function) is affected in a similar fashion to the nanoparticle volume fraction (concentration). It is consistently elevated by larger melting parameter values and reduced with greater magnetic field strengths. Micro-organism species boundary layer thickness is therefore respectively increased and decreased with a rise in melting heat transfer and magnetic body force parameter.
Figure 7a–c presents the evolution in temperature, nanoparticle volume fraction and microorganism density number, with variation in Brownian motion parameter (Nb) and thermophoresis parameter (Nt). The impact of Brownian motion is strongly related to the size of nanoparticles. Physically smaller nanoparticles yield higher Nb values, which assist in thermal diffusion in the boundary layer via increased thermal conduction. On the contrary, larger nanoparticles show lower Nb values, and this depresses thermal conduction to the fluid and encourages heat diffusion to the wall. Higher Nb values will conversely stifle the diffusion of nanoparticles towards the sheet surface and enhance thermal diffusion into the nanofluid. This results in an escalation in temperatures as observed in Figure 7a. Increasing values of Nt indicate a stronger thermophoretic force (due to the temperature gradient) which draws the nanoparticles from the nanofluid towards the sheet surface and produces a depletion in nanoparticle volume fraction (concentration) and an associated decrease in nanoparticle species boundary layer thickness (Figure 7b). Increasing thermophoresis effect also elevates temperatures significantly as witnessed in Figure 7a and this trend is sustained throughout the boundary layer. Thermal boundary layer thickness is therefore enhanced consistently with greater thermophoresis. Brownian diffusion (Nb), however, enhances nanoparticle species volume fraction (Figure 7b), and this is related to molecular agitation of the nanoparticles. Nb quantifies the random motion of small colloidal particles suspended in a fluid, caused by the collision of the fluid molecules with the particles [60]. Figure 7c shows that increasing the Brownian motion parameter weakly increases the micro-organism density number, whereas increasing thermophoresis parameter strongly reduces it. Thicker micro-organism species boundary layers are produced with higher Nb, whereas the converse effect is induced with increasing Nt. The distribution of heat, nanoparticles and micro-organisms in the boundary layer regime can be successfully manipulated with both nanoscale effects, i.e., the Brownian motion mechanism (higher Nb values) and thermophoresis effect. The influence of Brownian motion on the velocity fields was found to be inconsequential, and these plots are therefore excluded here.
Figure 8 presents the impact of second-order slip and bioconvection Péclet number Pe on the motile micro-organism density number. Higher Pe and smaller generally result in a decrease in microorganism density number magnitudes. Bioconvection Péclet numbers relate the rate of advection of micro-organisms driven by the flow to the rate of diffusion of micro-organisms under gyrotaxis. This parameter is often used in mathematical models of micro-organism propulsion as an alternative to bioconvection Rayleigh number (Rab) and bioconvection Lewis number (Leb). Ordinary Péclet number is associated with convective heat transfer processes. In bioconvection, the Péclet number when sufficiently high has been shown to significantly change patterns of the motile micro-organism flow. Bioconvection is due to the internal energy of the microorganisms. With greater swimming speed (higher Péclet number), the micro-organisms move faster, which reduces their concentrations. At lower Péclet numbers the effect is reversed, i.e., motility of the micro-organisms is inhibited and move slower. This then leads to higher and more homogenous concentrations. The second-order slip parameter also arises in the velocity wall boundary condition but induces a lesser effect than first-order slip. It weakly decreases motile micro-organism species boundary layer thickness whereas the bioconvection Péclet number generates a strong reduction.
Figure 9 exhibits the variation of the local Nusselt number, versus temperature dependent viscous parameter, and melting parameter, Me for a different value of Eckert number, Ec. The results show that decreases with increasing of , Ec and Me. Greater nanomaterial viscosity, viscous dissipation and melting heat transfer therefore all impede diffusion of heat from the nanofluid to the sheet surface.
Figure 10 depicts the variation of the local Sherwood number, , versus Schmidt number, Sc, and Brownian motion, Nb, for a different value of thermophoresis parameter, Nt. Results show that increases with increasing of Nt, but decreases with Nb. Nanoparticles species diffusion to the sheet (wall) is therefore stifled with greater Brownian motion whereas it is encouraged with stronger thermophoretic body force effect. The values of Schmidt number are selected between 1 and 1.4, and these correspond to common metallic nanoparticles (e.g., titanium, copper, silver) diffusing in water as the base fluid [15]. Smaller values of the Schmidt number, , are equivalent to increasing chemical molecular diffusivity of the nanoparticle species. Sc also represents the relative thickness of the velocity (hydrodynamic) boundary layer to the concentration (nanoparticle species) boundary layer. Larger Sc fluids have lower mass diffusion characteristics. Evidently, Sc significantly modifies the nanoparticle mass transfer rate at the wall and produces a gradual decay in local Sherwood number, .
6. Conclusions
A mathematical model has been developed to simulate the influence of viscous dissipation, second-order slip and variable transport properties (viscosity, thermal conductivity, nanoparticle mass and micro-organism species diffusivity) in melting magneto-nanofluid bioconvection heat transfer from a stretching sheet. Via a group of similarity transformations, the governing partial differential equations, wall and free stream boundary conditions have been rendered into ordinary differential form. The emerging nonlinear two-point ordinary differential boundary value problem has been solved with the BVP4C MATLAB numerical code. The velocity, temperature, concentration and microorganism profiles have been plotted for various values of parameters. The computations have shown that:
- Increasing magnetic body force parameter reduces velocity, nanoparticle concentration and motile microorganism species number density, whereas hydrodynamic boundary layer thickness is increased as are temperatures.
- Increasing Brownian motion and thermophoresis effect lead to an enhancement in temperatures. Increasing melting effect accelerates the flow (via momentum diffusion assistance) whereas it decreases temperatures. Increasing first-order slip and temperature-dependent thermal conductivity parameters significantly cool the boundary layer regime.
- Nanoparticle volume fraction and motile microorganism density number are both elevated with increasing mass diffusivity parameter whereas they are depressed with greater Schmidt number.
- Motile microorganism density number is boosted with increasing microorganism diffusivity parameter, whereas the converse response is induced with increasing bioconvection Schmidt number.
- Increasing temperature-dependent viscous parameter and Eckert number increases temperatures but reduce nanoparticle volume fraction.
- Local Sherwood number is depressed with Brownian motion parameter and Schmidt number, whereas it is enhanced with thermophoresis parameter.
- Increasing nanomaterial viscosity, viscous dissipation and melting heat transfer reduce local Nusselt number at the sheet surface.
The present study has ignored electrical field effects which are also relevant to nanofluid materials processing [61,62]. Furthermore, field simulation with computational fluid dynamics software is required for fully three-dimensional flow modelling; these aspects are also being explored [63].
Author Contributions
All authors were jointly involved in the formulation of the problem, numerical solution and writing up the paper. N.A.A. and M.F.M.B. conceived and designed the experiments; M.J.U. performed the experiments; O.A.B. and A.K. analyzed the data; A.I.M.I. contributed reagents/materials/analysis tools; M.F.M.B. wrote the paper.
Funding
This research was funded by Universiti Sains Malaysia, grant number 1001/PMATHS/8011013 and the APC was funded by Universiti Sains Malaysia, grant number 1001/PMATHS/8011013.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| dimensional positive constant | |
| dimensional positive constant | |
| chemotaxis constant | |
| positive constant | |
| magnetic field and strength | |
| specific heat at constant pressure | |
| specific heat of the solid particle at constant pressure | |
| specific heat of the base fluid at constant pressure | |
| wall nanoparticle volume fraction | |
| ambient nanoparticle volume fraction | |
| skin friction coefficient | |
| variable Brownian diffusion coefficient | |
| constant Brownian diffusion coefficient | |
| variable diffusivity of microorganisms | |
| constant diffusivity of microorganisms | |
| dimensionless velocity | |
| dimensional positive constant | |
| temperature dependent viscous parameter | |
| dimensional positive constant | |
| temperature dependent thermal conductive parameter | |
| positive constant | |
| mass diffusivity parameter | |
| microorganism diffusivity parameter | |
| variable thermal conductivity of nanofluid | |
| constant thermal conductivity of nanofluid | |
| melting (phase change) parameter | |
| density of motile microorganism | |
| Brownian motion parameter | |
| local density number of motile microorganisms | |
| thermophoresis parameter | |
| local Nusselt number | |
| bioconvection Péclet number | |
| Pr | Prandtl number |
| surface mass flux | |
| surface motile microorganism flux | |
| Surface heat flux | |
| Sb | bioconvection Schmidt number |
| Schmidt number | |
| local Sherwood number | |
| Stefan numbers | |
| nanofluid temperature | |
| solid surface temperature | |
| solid surface temperature | |
| velocity slip | |
| velocity along stretching surface | |
| velocity component along the direction | |
| non-dimensional velocity component along the direction | |
| velocity components along the direction | |
| non-dimensional velocity component along the direction | |
| maximum cell swimming speed | |
| coordinate along the surface | |
| non-dimensional coordinate along the surface | |
| coordinate along the surface | |
| non-dimensional coordinate along the surface | |
| Greek Letters | |
| thermal diffusivity | |
| second-order slip parameter | |
| first-order slip parameter | |
| similarity independent variable | |
| dimensionless temperature | |
| latent heat of diffusion | |
| variable temperature dependent viscosity | |
| constant temperature dependent viscosity | |
| density of the base fluid | |
| ratio of effective heat capacity of the nanoparticle material to the fluid heat capacity | |
| wall skin friction in | |
| constant kinematic viscosity of nanofluid | |
| rescaled nanoparticle volume fraction | |
| rescaled number of motile microorganisms | |
| Subscripts/Superscripts | |
| condition at the wall | |
| free stream condition | |
| differentiation with respect to | |
References
- Pocorni, J.; Powell, J.; Deichsel, E.; Frostevarg, J.; Kaplan, A.F. Fibre laser cutting stainless steel: Fluid dynamics and cut front morphology. Opt. Laser Technol. 2017, 87, 87–93. [Google Scholar] [CrossRef]
- Chen, H.; Sundararaj, U.; Nandakumar, K. Modeling of polymer melting, drop deformation, and breakup under shear flow. Polym. Eng. Sci. 2004, 44, 1258–1266. [Google Scholar] [CrossRef]
- Bergman, T.; Webb, B. Simulation of pure metal melting with buoyancy and surface tension forces in the liquid phase. Int. J. Heat Mass Transf. 1990, 33, 139–149. [Google Scholar] [CrossRef]
- Song, J.; Min, B.; Kim, J.; Kim, H.; Hong, S.; Chung, S. An electromagnetic and thermal analysis of a cold crucible melting. Int. Commun. Heat Mass Transf. 2005, 32, 1325–1336. [Google Scholar] [CrossRef]
- Mcneil, T.J.; Cole, R.; Subramanian, R.S. Surface-Tension-Driven Flow in a Glass Melt. J. Am. Ceram. Soc. 1985, 68, 254–259. [Google Scholar] [CrossRef]
- Gau, C.; Viskanta, R. Melting and solidification of a pure metal on a vertical wall. J. Heat Transf. 1986, 108, 174–181. [Google Scholar] [CrossRef]
- Tien, C.; Yen, Y.-C. The effect of melting on forced convection heat transfer. J. Appl. Meteorol. 1965, 4, 523–527. [Google Scholar] [CrossRef]
- Epstein, M.; Cho, D. Melting heat transfer in steady laminar flow over a flat plate. J. Heat Transf. 1976, 98, 531–533. [Google Scholar] [CrossRef]
- Mahmoud, M.; Waheed, S. Melting heat transfer effects on stagnation point flow of micropolar fluid saturated in porous medium with internal heat generation (absorption). Appl. Math. Mech. 2014, 35, 979–992. [Google Scholar] [CrossRef]
- Karimipour, A. New correlation for Nusselt number of nanofluid with Ag/Al2O3/Cu nanoparticles in a microchannel considering slip velocity and temperature jump by using lattice Boltzmann method. Int. J. Therm. Sci. 2015, 91, 146–156. [Google Scholar] [CrossRef]
- Kazmierczak, M.; Poulikakos, D.; Sadowski, D. Melting of a vertical plate in porous medium controlled by forced convection of a dissimilar fluid. Int. Commun. Heat Mass Transf. 1987, 14, 507–517. [Google Scholar] [CrossRef]
- Wang, C. Melting from a horizontal rotating disk. J. Appl. Mech. 1989, 56, 47–50. [Google Scholar] [CrossRef]
- Andersson, H.; Holmedal, B.; Dandapat, B.; Gupta, A. Magnetohydrodynamic melting flow from a horizontal rotating disk. Math. Models Methods Appl. Sci. 1993, 3, 373–393. [Google Scholar] [CrossRef]
- Yao, F.-J.; Luo, K.; Yi, H.-L.; Xie, M. Analysis of melting with natural convection and volumetric radiation using lattice Boltzmann method. Int. J. Heat Mass Transf. 2017, 112, 413–426. [Google Scholar] [CrossRef]
- Das, S.K.; Choi, S.U.; Yu, W.; Pradeep, T. Nanofluids: Science and Technology; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Tripathi, D.; Bég, O.A. A study on peristaltic flow of nanofluids: Application in drug delivery systems. Int. J. Heat Mass Transf. 2014, 70, 61–70. [Google Scholar] [CrossRef]
- Zhu, J.; Fu, Q.; Xue, Y.; Cui, Z. Comparison of different models of melting transformation of nanoparticles. J. Mater. Sci. 2016, 51, 4462–4469. [Google Scholar] [CrossRef]
- Kumaresan, V.; Velraj, R.; Nanda, M.; Maini, A. Phase change material-based nanofluids for heat transfer enhancement in latent heat thermal energy storage system. Int. J. Green Nanotechnol. 2012, 4, 541–546. [Google Scholar] [CrossRef]
- Barlak, S.; Sara, O.N.; Karaipekli, A.; Yapıcı, S. Thermal conductivity and viscosity of nanofluids having nanoencapsulated phase change material. Nanoscale Microscale Thermophys. Eng. 2016, 20, 85–96. [Google Scholar] [CrossRef]
- Han, Z.; Yang, B.; Liu, Y.Y. Phase-Change Nanofluids with Enhanced Thermophysical Properties. In Proceedings of the ASME 2009 Second International Conference on Micro/Nanoscale Heat and Mass Transfer, Shanghai, China, 18–21 December 2009; pp. 441–447. [Google Scholar]
- Guisbiers, G.; Buchaillot, L. Modeling the melting enthalpy of nanomaterials. J. Phys. Chem. C 2009, 113, 3566–3568. [Google Scholar] [CrossRef]
- Kumar, C.K.; Bandari, S. Melting heat transfer in boundary layer stagnation-point flow of a nanofluid towards a stretching–shrinking sheet. Can. J. Phys. 2014, 92, 1703–1708. [Google Scholar] [CrossRef]
- Kumari Ch, M.; Gorla, R.S.R. Effect of Melting on Mixed Convective Boundary Layer Flow Over a Vertical Plate Embedded in a Porous Medium Saturated with a Nanofluid. J. Nanofluids 2015, 4, 82–90. [Google Scholar] [CrossRef]
- Chieruzzi, M.; Cerritelli, G.F.; Miliozzi, A.; Kenny, J.M. Effect of nanoparticles on heat capacity of nanofluids based on molten salts as PCM for thermal energy storage. Nanoscale Res. Lett. 2013, 8, 448. [Google Scholar] [CrossRef] [PubMed]
- Sheikholeslami, M.; Rokni, H.B. Effect of melting heat transfer on nanofluid flow in existence of magnetic field considering Buongiorno Model. Chin. J. Phys. 2017, 55, 1115–1126. [Google Scholar] [CrossRef]
- Mastiani, M.; Sebti, S.S.; Mirzaei, H.; Kashani, S.; Sohrabi, A. Numerical study of melting in an annular enclosure filled with nanoenhanced phase change material. Therm. Sci. 2015, 19, 1067–1076. [Google Scholar]
- Shima, P.; Philip, J.; Raj, B. Magnetically controllable nanofluid with tunable thermal conductivity and viscosity. Appl. Phys. Lett. 2009, 95, 133112. [Google Scholar] [CrossRef]
- Rajesh, V.; Beg, O.A.; Mallesh, M. Transient nanofluid flow and heat transfer from a moving vertical cylinder in the presence of thermal radiation: Numerical study. Proc. Inst. Mech. Eng. Part N J. Nanomater. Nanoeng. Nanosyst. 2016, 230, 3–16. [Google Scholar] [CrossRef]
- Beg, O.A.; Khan, W.A.; Uddin, M.J. Multiple slip effects on unsteady magnetohydrodynamic nanofluid transport with heat generation/absorption effects in temperature dependent porous media. J. Porous Media 2015, 18, 907–922. [Google Scholar] [CrossRef]
- Uddin, M.; Bég, O.A.; Aziz, A.; Ismail, A. Group analysis of free convection flow of a magnetic nanofluid with chemical reaction. Math. Probl. Eng. 2015, 2015, 621503. [Google Scholar] [CrossRef]
- Akbar, N.S.; Tripathi, D.; Bég, O.A. Modeling nanoparticle geometry effects on peristaltic pumping of medical magnetohydrodynamic nanofluids with heat transfer. J. Mech. Med. Biol. 2016, 16, 1650088. [Google Scholar] [CrossRef]
- Thumma, T.; Bég, O.A.; Kadir, A. Numerical study of heat source/sink effects on dissipative magnetic nanofluid flow from a non-linear inclined stretching/shrinking sheet. J. Mol. Liq. 2017, 232, 159–173. [Google Scholar] [CrossRef]
- Bég, O.A.; Sohail, A.; Kadir, A.; Bég, T.A. B-spline collocation simulation of non-linear transient magnetic nanobio-tribological squeeze-film flow. J. Mech. Med. Biol. 2018, 18, 1850007. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Salah, F. Entropy analysis in electrical magnetohydrodynamic (MHD) flow of nanofluid with effects of thermal radiation, viscous dissipation, and chemical reaction. Theor. Appl. Mech. Lett. 2017, 7, 235–242. [Google Scholar] [CrossRef]
- Gireesha, B.; Mahanthesh, B.; Shivakumara, I.; Eshwarappa, K. Melting heat transfer in boundary layer stagnation-point flow of nanofluid toward a stretching sheet with induced magnetic field. Eng. Sci. Technol. Int. J. 2016, 19, 313–321. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Alsaedi, A.; Alhuthali, M. Magnetohydrodynamic three-dimensional flow of viscoelastic nanofluid in the presence of nonlinear thermal radiation. J. Magn. Magn. Mater. 2015, 385, 222–229. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Waqas, M.; Alsaedi, A.; Farooq, M. Numerical simulation for melting heat transfer and radiation effects in stagnation point flow of carbon–water nanofluid. Comput. Methods Appl. Mech. Eng. 2017, 315, 1011–1024. [Google Scholar] [CrossRef]
- Platt, J.R. “Bioconvection Patterns” in Cultures of Free-Swimming Organisms. Science 1961, 133, 1766–1767. [Google Scholar] [CrossRef] [PubMed]
- Keller, E.F.; Segel, L.A. Traveling bands of chemotactic bacteria: A theoretical analysis. J. Theor. Biol. 1971, 30, 235–248. [Google Scholar] [CrossRef]
- Pedley, T.; Kessler, J. Hydrodynamic phenomena in suspensions of swimming microorganisms. Annu. Rev. Fluid Mech. 1992, 24, 313–358. [Google Scholar] [CrossRef]
- Janicek, A.; Fan, Y.; Liu, H. Design of microbial fuel cells for practical application: A review and analysis of scale-up studies. Biofuels 2014, 5, 79–92. [Google Scholar] [CrossRef]
- Uddin, M.; Khan, W.; Qureshi, S.; Bég, O.A. Bioconvection nanofluid slip flow past a wavy surface with applications in nano-biofuel cells. Chin. J. Phys. 2017, 55, 2048–2063. [Google Scholar] [CrossRef]
- Shafiq, A.; Hammouch, Z.; Sindhu, T. Bioconvective MHD flow of tangent hyperbolic nanofluid with newtonian heating. Int. J. Mech. Sci. 2017, 133, 759–766. [Google Scholar] [CrossRef]
- Beg, O. Nonlinear multiphysical laminar nanofluid bioconvection flows: Models and computation. In Computational Approaches in Biomedical Nano-Engineering; Sohail, A., Li, Z., Eds.; Wiley: Weinheim, Germany, 2018; pp. 113–145. [Google Scholar]
- Alsaedi, A.; Khan, M.I.; Farooq, M.; Gull, N.; Hayat, T. Magnetohydrodynamic (MHD) stratified bioconvective flow of nanofluid due to gyrotactic microorganisms. Adv. Powder Technol. 2017, 28, 288–298. [Google Scholar] [CrossRef]
- Zohra, F.; Uddin, M.; Ismail, A.; Bég, O.A.; Kadir, A. Anisotropic slip magneto-bioconvection flow from a rotating cone to a nanofluid with Stefan blowing effects. Chin. J. Phys. 2018, 56, 432–448. [Google Scholar] [CrossRef]
- Rana, P.; Shukla, N.; Bég, O.A.; Kadir, A.; Singh, B. Unsteady electromagnetic radiative nanofluid stagnation-point flow from a stretching sheet with chemically reactive nanoparticles, Stefan blowing effect and entropy generation. Proc. Inst. Mech. Eng. Part N J. Nanomater. Nanoeng. Nanosyst. 2018, 232, 69–82. [Google Scholar] [CrossRef]
- Mabood, F.; Mastroberardino, A. Melting heat transfer on MHD convective flow of a nanofluid over a stretching sheet with viscous dissipation and second order slip. J. Taiwan Inst. Chem. Eng. 2015, 57, 62–68. [Google Scholar] [CrossRef]
- Beg, O.A.; Motsa, S.S.; Islam, M.N.; Lockwood, M. Pseudo-spectral and variational iteration simulation of exothermically-reacting Rivlin-Ericksen viscoelastic flow and heat transfer in a rocket propulsion duct. Comput. Therm. Sci. Int. J. 2014, 6, 91–102. [Google Scholar] [CrossRef]
- Elsayed, A.F.; Bég, O.A. New computational approaches for biophysical heat transfer in tissue under ultrasonic waves: The variational iteration and Chebyschev spectral simulations. J. Mech. Med. Biol. 2014, 14, 1450043. [Google Scholar] [CrossRef]
- Animasaun, I.L. Melting heat and mass transfer in stagnation point micropolar fluid flow of temperature dependent fluid viscosity and thermal conductivity at constant vortex viscosity. J. Egypt. Math. Soc. 2017, 25, 79–85. [Google Scholar] [CrossRef]
- Amirsom, N.; Uddin, M.; Ismail, A. Three dimensional stagnation point flow of bionanofluid with variable transport properties. Alex. Eng. J. 2016, 55, 1983–1993. [Google Scholar] [CrossRef]
- Hayat, T.; Hussain, Q.; Javed, T. The modified decomposition method and Padé approximants for the MHD flow over a non-linear stretching sheet. Nonlinear Anal. Real World Appl. 2009, 10, 966–973. [Google Scholar] [CrossRef]
- Andersson, H.I. Slip flow past a stretching surface. Acta Mech. 2002, 158, 121–125. [Google Scholar] [CrossRef]
- Hamad, M.A.A.; Uddin, M.J.; Ismail, A.I.M. Investigation of combined heat and mass transfer by Lie group analysis with variable diffusivity taking into account hydrodynamic slip and thermal convective boundary conditions. Int. J. Heat Mass Transf. 2012, 55, 1355–1362. [Google Scholar] [CrossRef]
- He, J.-H. Variational iteration method–a kind of non-linear analytical technique: Some examples. Int. J. Non-Linear Mech. 1999, 34, 699–708. [Google Scholar] [CrossRef]
- El-Wakil, S.; Abulwafa, E. Variational-iterative method for conductive-radiative heat transfer in spherical inhomogeneous medium. J. Thermophys. Heat Transf. 2000, 14, 612–615. [Google Scholar] [CrossRef]
- Kim, J.-Y.; Jang, K.; Yang, S.-J.; Baek, J.-H.; Park, J.-R.; Yeom, D.-I.; Kim, J.-S.; Kim, H.-S.; Jun, J.-H.; Chung, S.-C. Simulation study of the thermal and the thermoelastic effects induced by pulsed laser absorption in human skin. J. Korean Phys. Soc. 2016, 68, 979–988. [Google Scholar] [CrossRef]
- Zueco, J.; Bég, O.A.; Takhar, H.; Prasad, V. Thermophoretic hydromagnetic dissipative heat and mass transfer with lateral mass flux, heat source, Ohmic heating and thermal conductivity effects: Network simulation numerical study. Appl. Therm. Eng. 2009, 29, 2808–2815. [Google Scholar] [CrossRef]
- Khan, J.A.; Mustafa, M.; Hayat, T.; Alsaedi, A. Three-dimensional flow of nanofluid over a non-linearly stretching sheet: An application to solar energy. Int. J. Heat Mass Transf. 2015, 86, 158–164. [Google Scholar] [CrossRef]
- Tripathi, D.; Sharma, A.; Bég, O.A. Electrothermal transport of nanofluids via peristaltic pumping in a finite micro-channel: Effects of Joule heating and Helmholtz-Smoluchowski velocity. Int. J. Heat Mass Transf. 2017, 111, 138–149. [Google Scholar] [CrossRef]
- Tripathi, D.; Yadav, A.; Bég, O.A.; Kumar, R. Study of microvascular non-Newtonian blood flow modulated by electroosmosis. Microvasc. Res. 2018, 117, 28–36. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Chapter 11—Electrohydrodynamic Nanofluid Natural Convection Using CVFEM. In Application of Control Volume Based Finite Element Method (CVFEM) for Nanofluid Flow and Heat Transfer; Sheikholeslami, M., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 373–398. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).