Adaptive Fuzzy-Based Fault-Tolerant Control of a Continuum Robotic System for Maxillary Sinus Surgery
Abstract
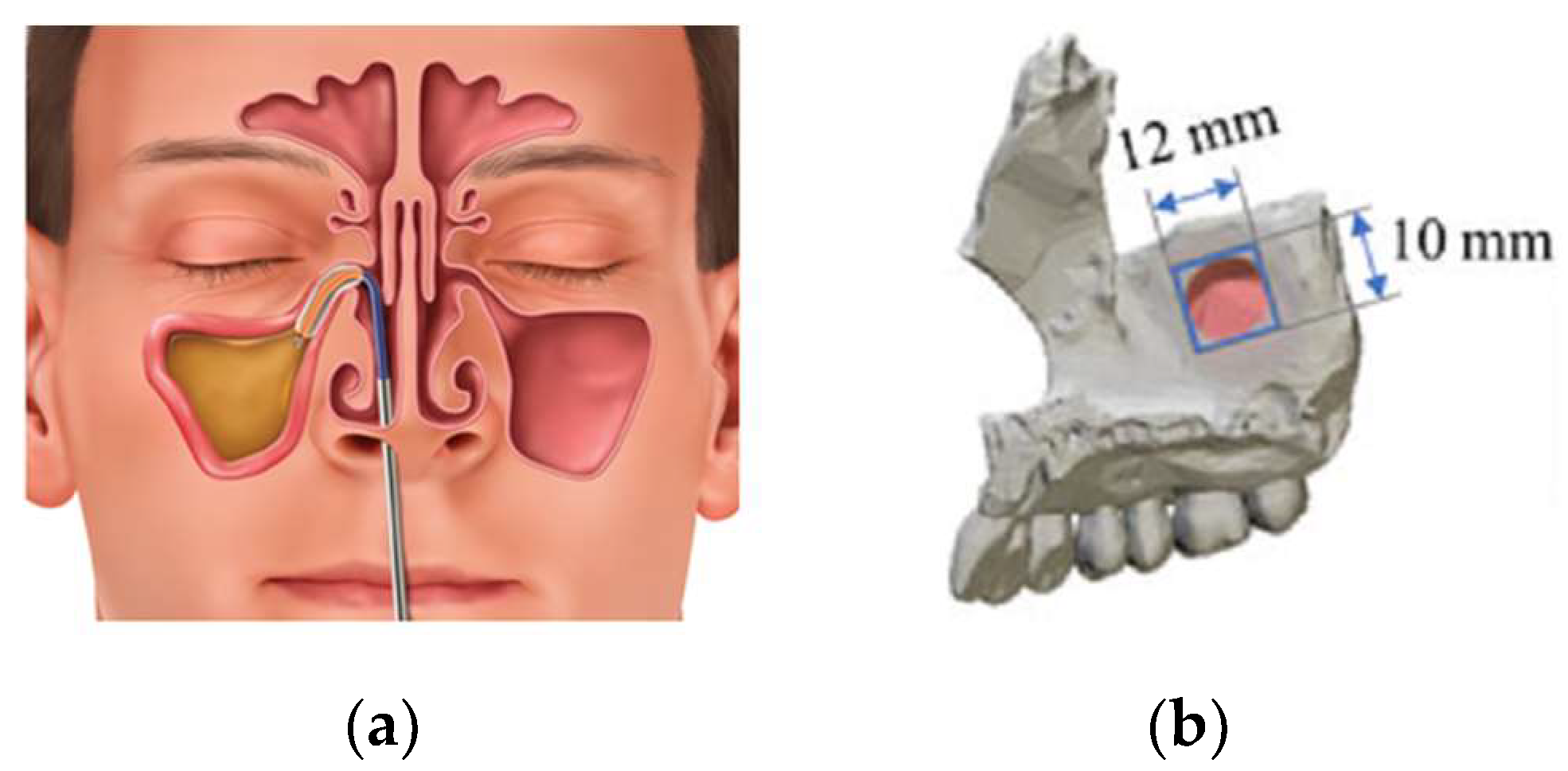
1. Introduction
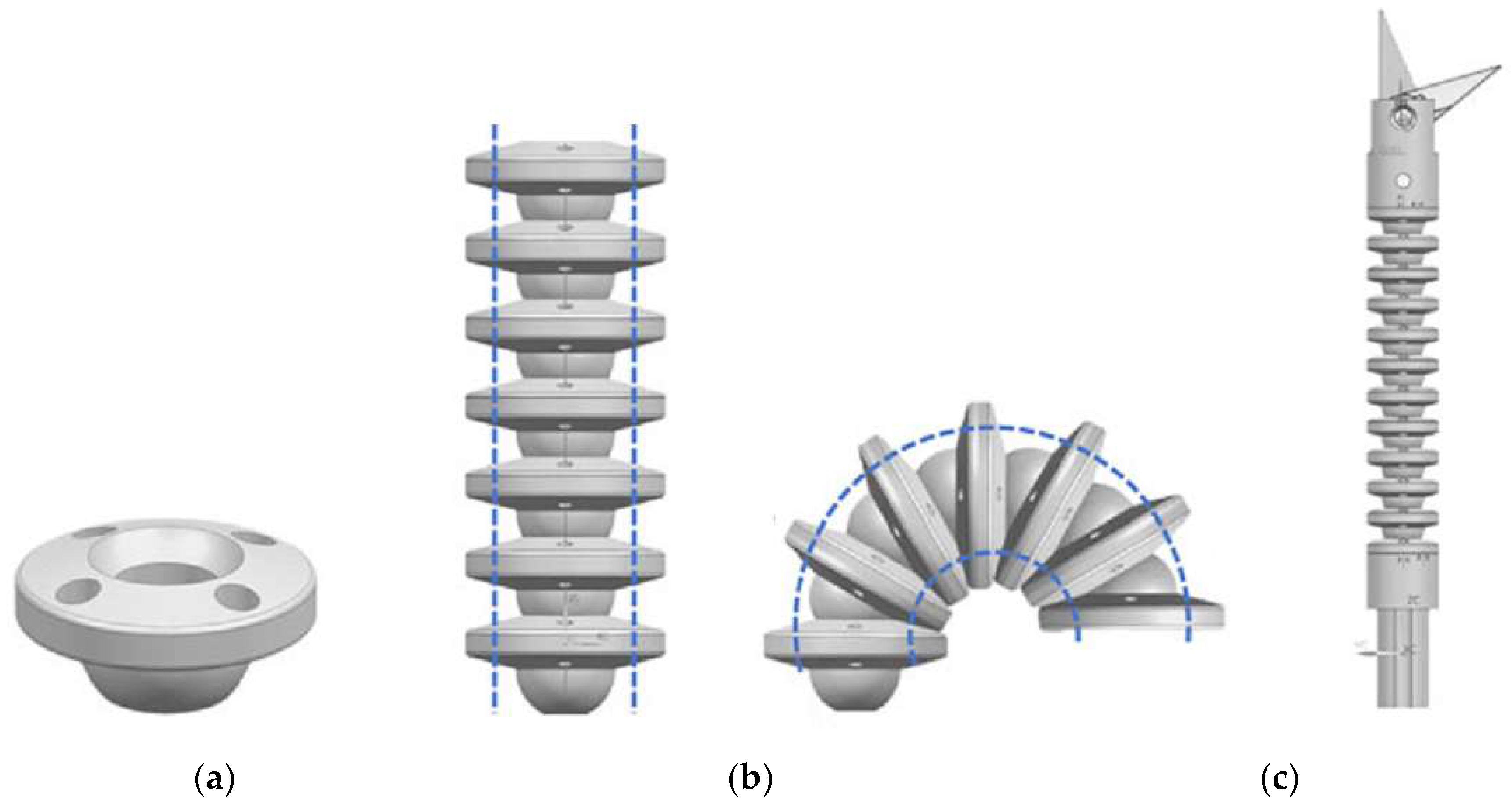
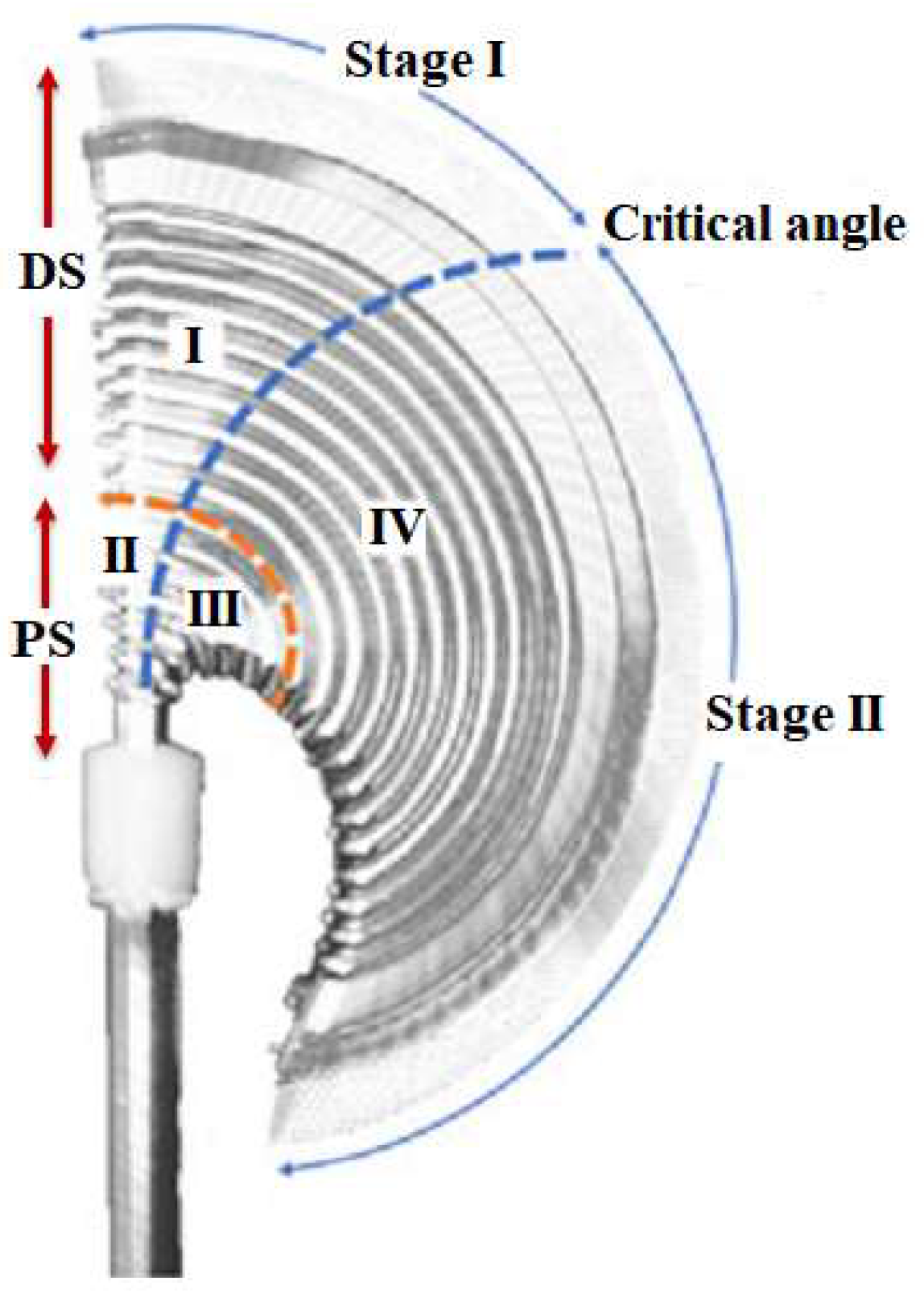
2. Surgical Robot Modeling
2.1. Surgical Robot Kinematics and Dynamics
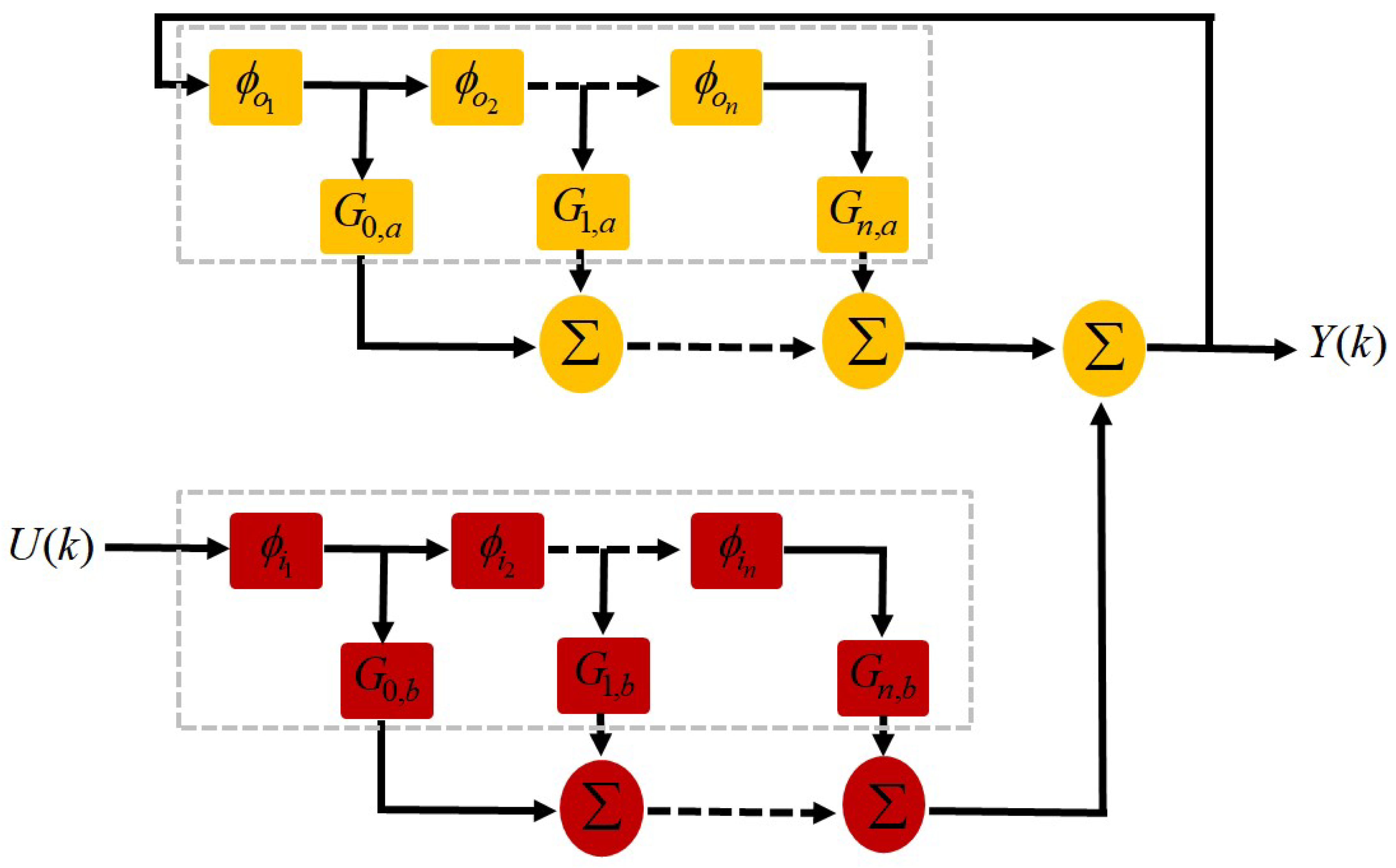
2.2. Fuzzy Auto Regressive with Exogenous Input (ARX) Laguerre System Modeling
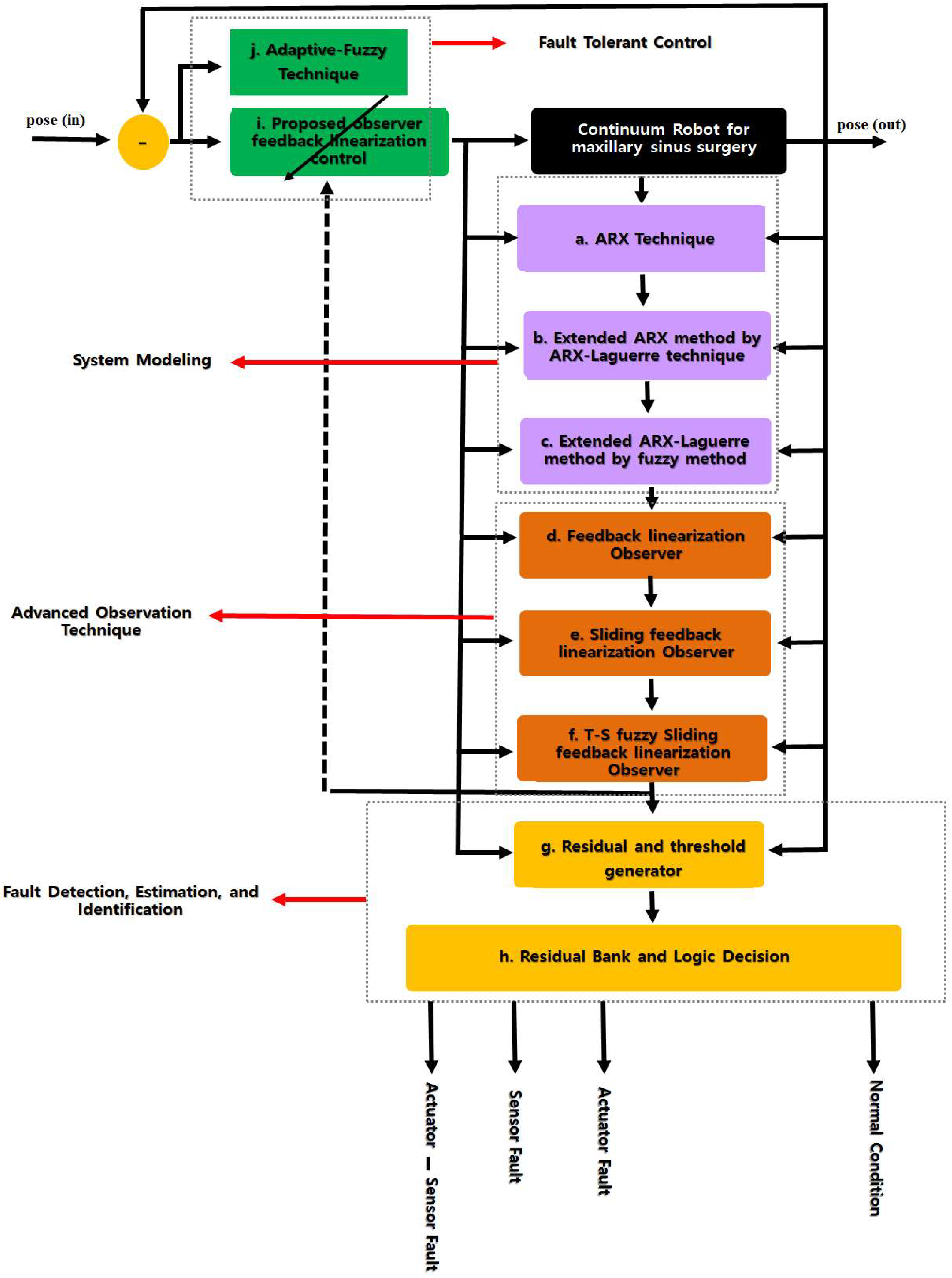
3. Proposed Method for Fault Estimation, Detection, Identification and Tolerant Control
3.1. Takagi–Sugeno (T–S) Fuzzy Advanced Observer
3.2. Fault Detection, Estimation, and Identification Technique
3.3. Fault-Tolerant Control
| Algorithm 1 Online tuning of the observation-based fuzzy ARX-Laguerre T–S fuzzy robust feedback linearization observer for fault detection, estimation, identification, and tolerant control of a surgical robot for the sinus. | |
| 1: | Run the ARX technique for system modeling (11) |
| 2: | Run the extended ARX method using the ARX–Laguerre technique for system modeling (13) |
| 3: | Run the extended ARX-Laguerre technique based on fuzzy ARX-Laguerre system modeling (16) |
| 4: | Run the fuzzy ARX-Laguerre feedback linearization observer (17), (18) |
| 5: | Run the fuzzy ARX-Laguerre robust feedback linearization observer based on the variable structure technique (21), (22) |
| 6: | Run the fuzzy ARX-Laguerre T–S fuzzy robust feedback linearization observer (26), (27) |
| 7: | Run the residual signal generation (29) |
| 8: | Run the threshold generation based on the variable structure technique (30) |
| 9: | Run the proposed fault detection algorithm (31) |
| 10: | Run the proposed fault estimation technique (27) |
| 11: | Run the proposed fault identification method (32) |
| 12: | Run the feedback linearization technique (33) |
| 13: | Run the extended feedback linearization method based on the observation technique for fault tolerance (34) |
| 14: | Run the extended observation-based feedback linearization technique and the adaptive fuzzy observation-based feedback linearization technique for fault tolerance (35), (36) |
4. Results and Analysis
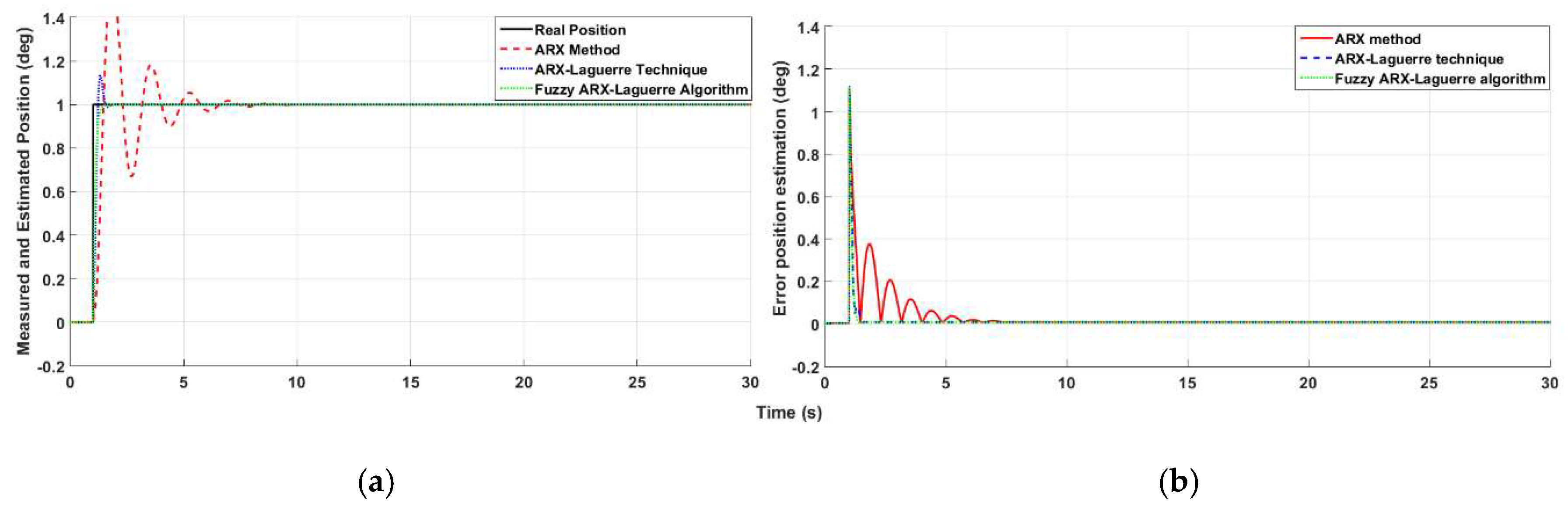
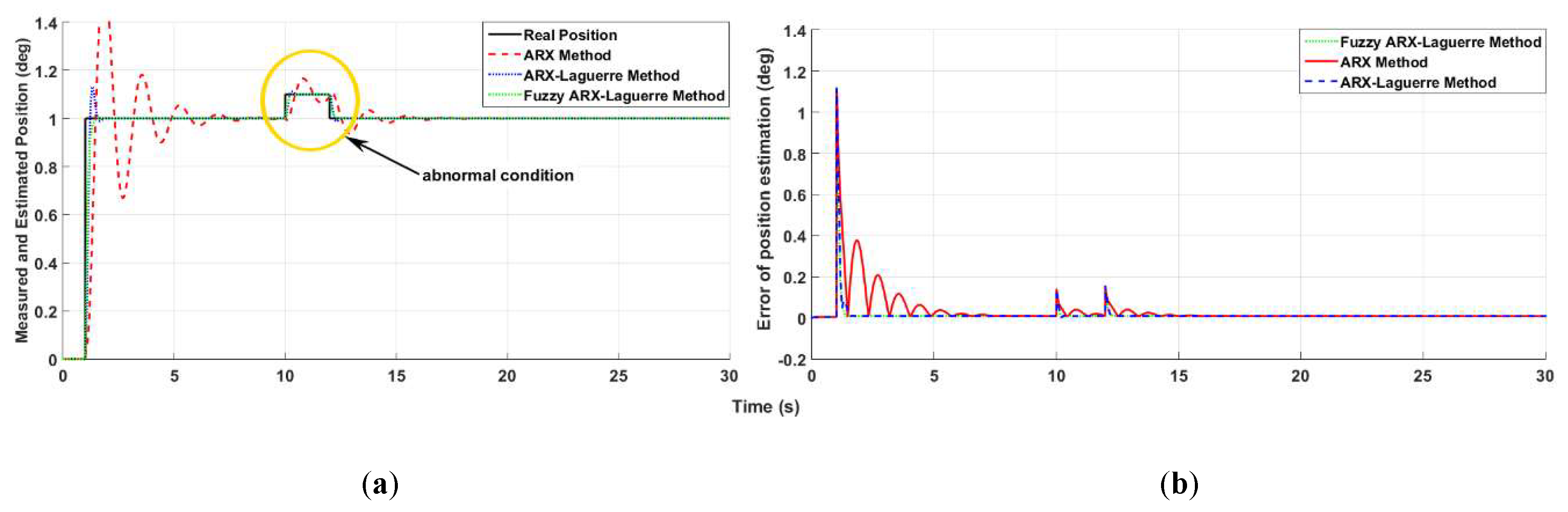
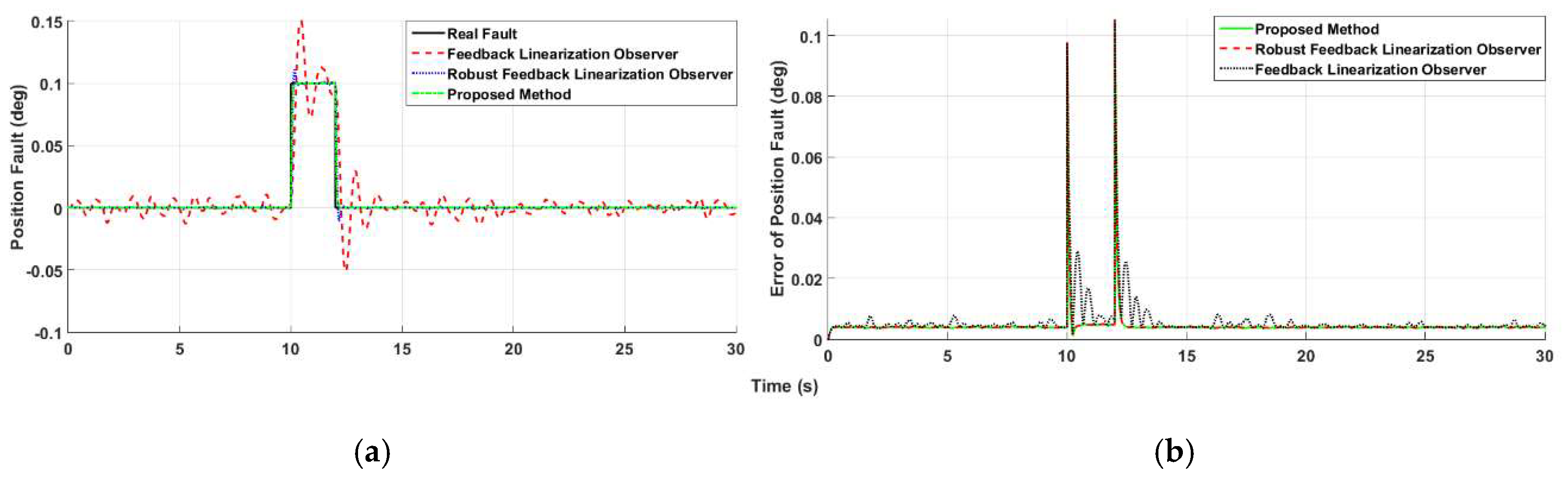
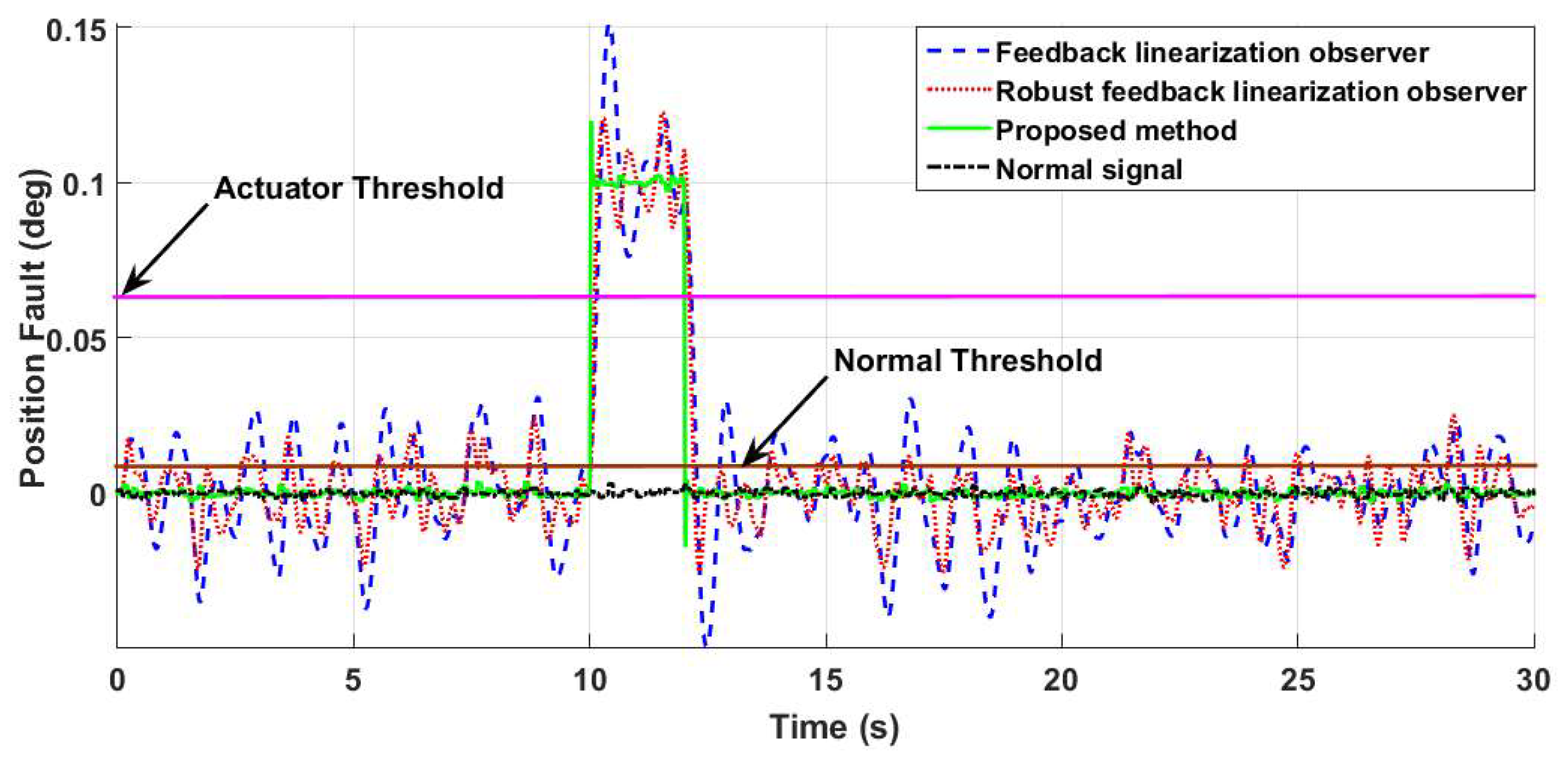
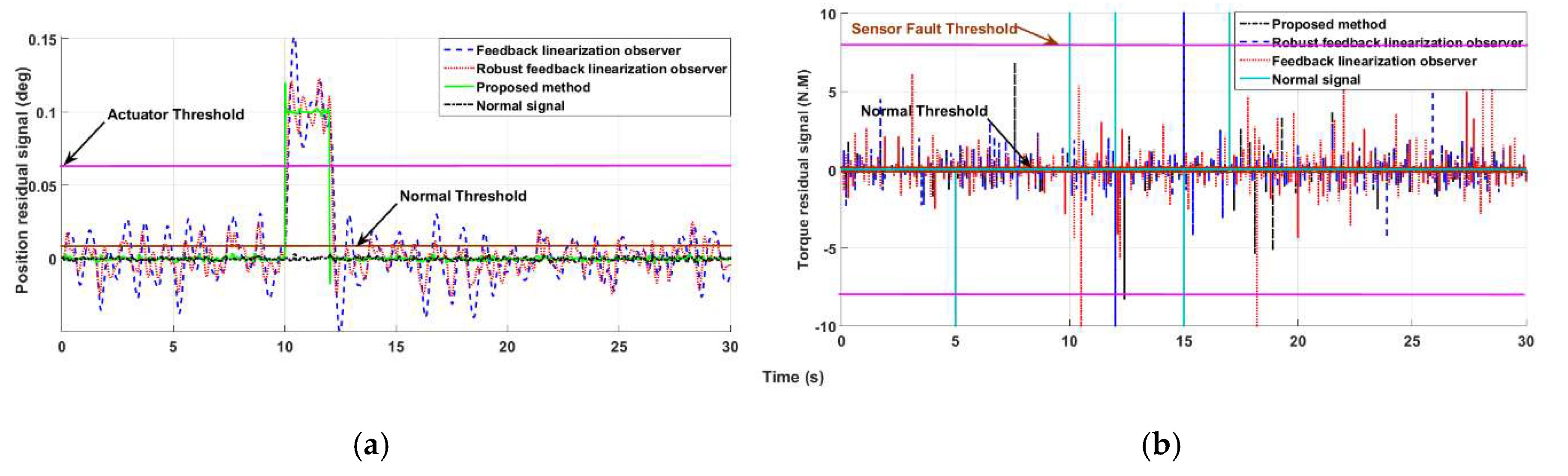
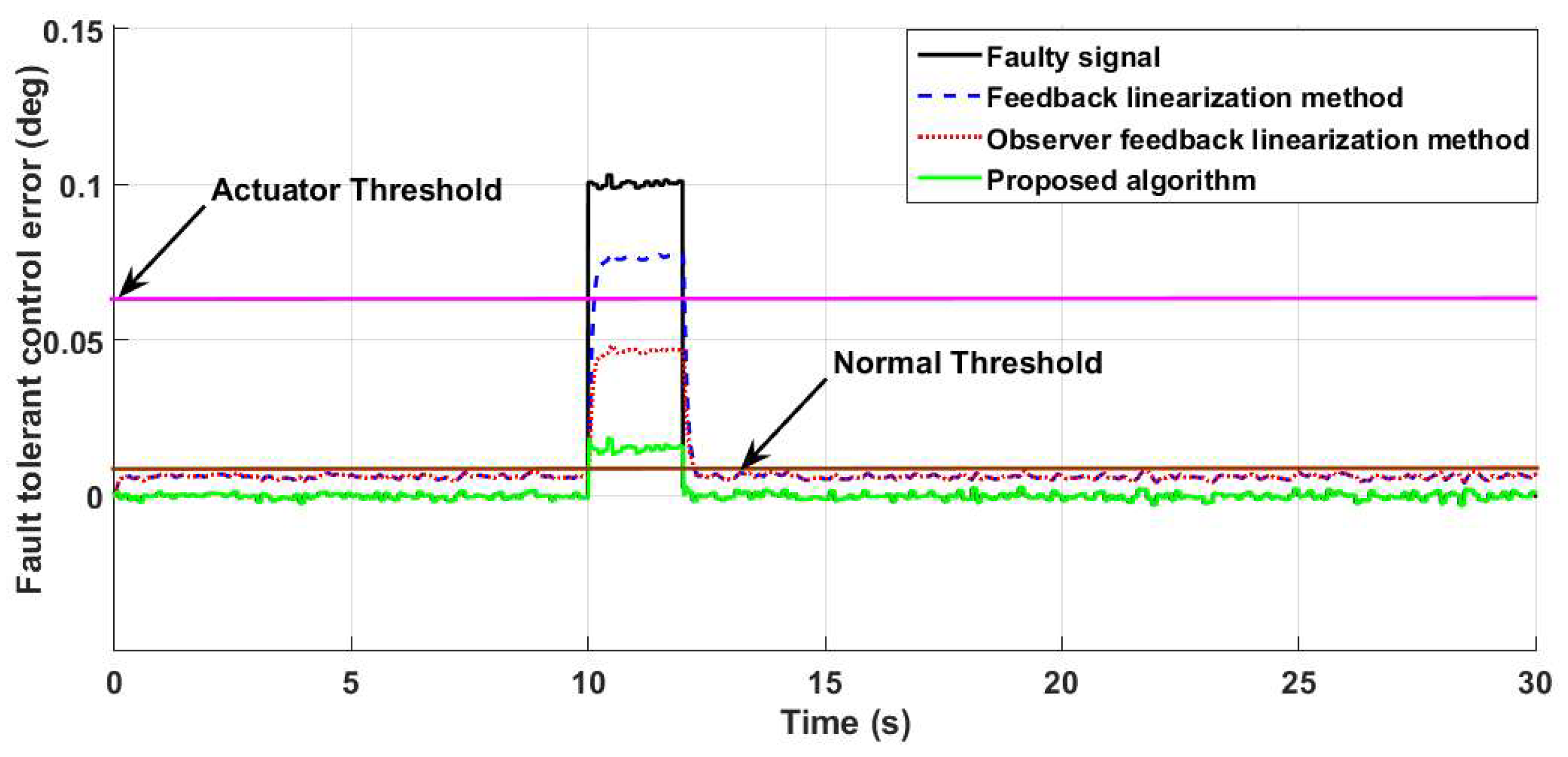
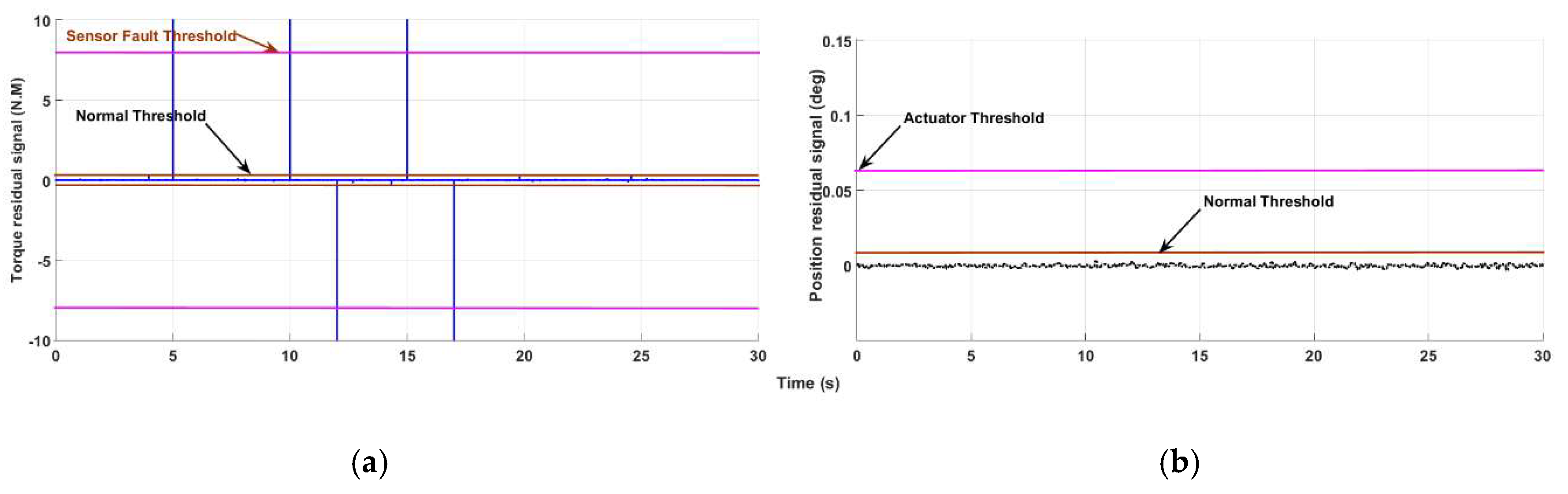
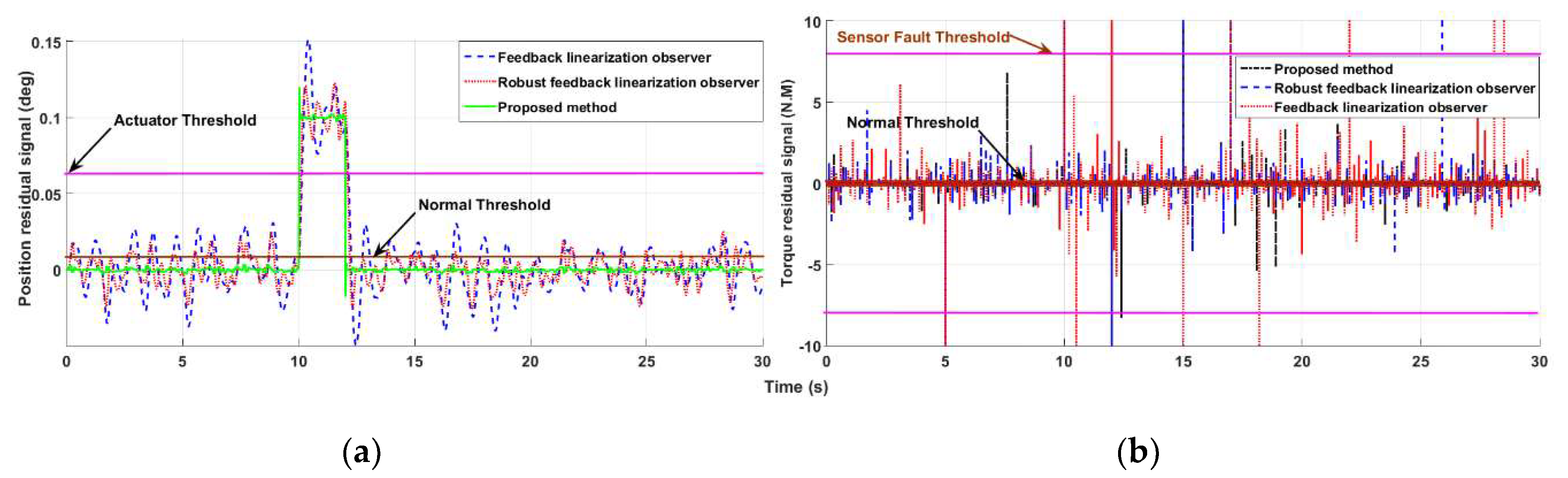
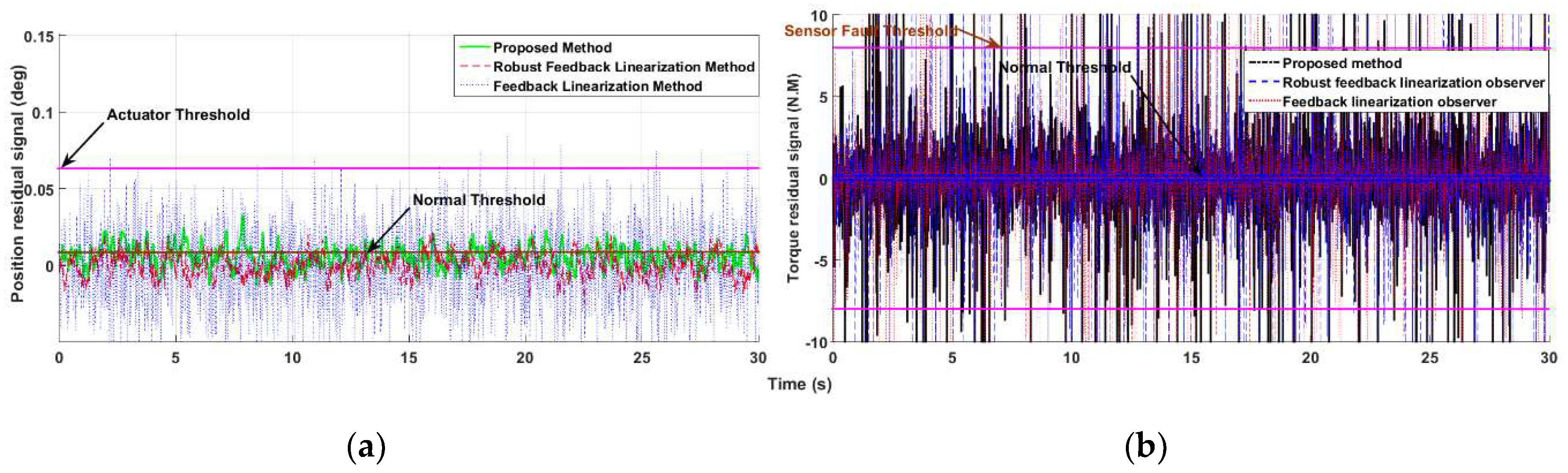
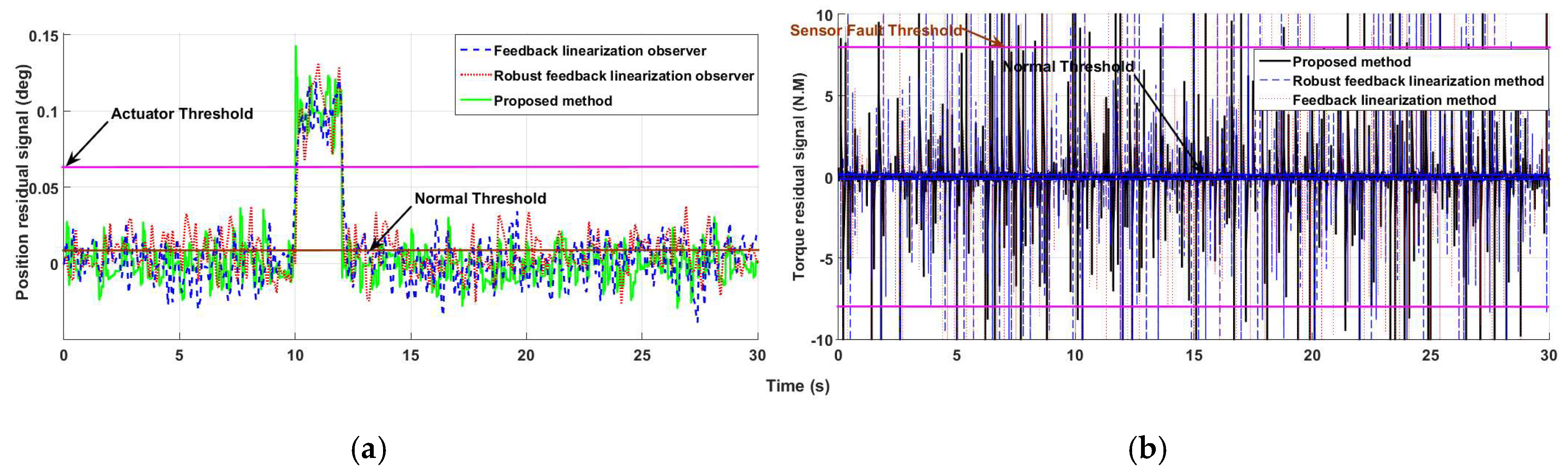
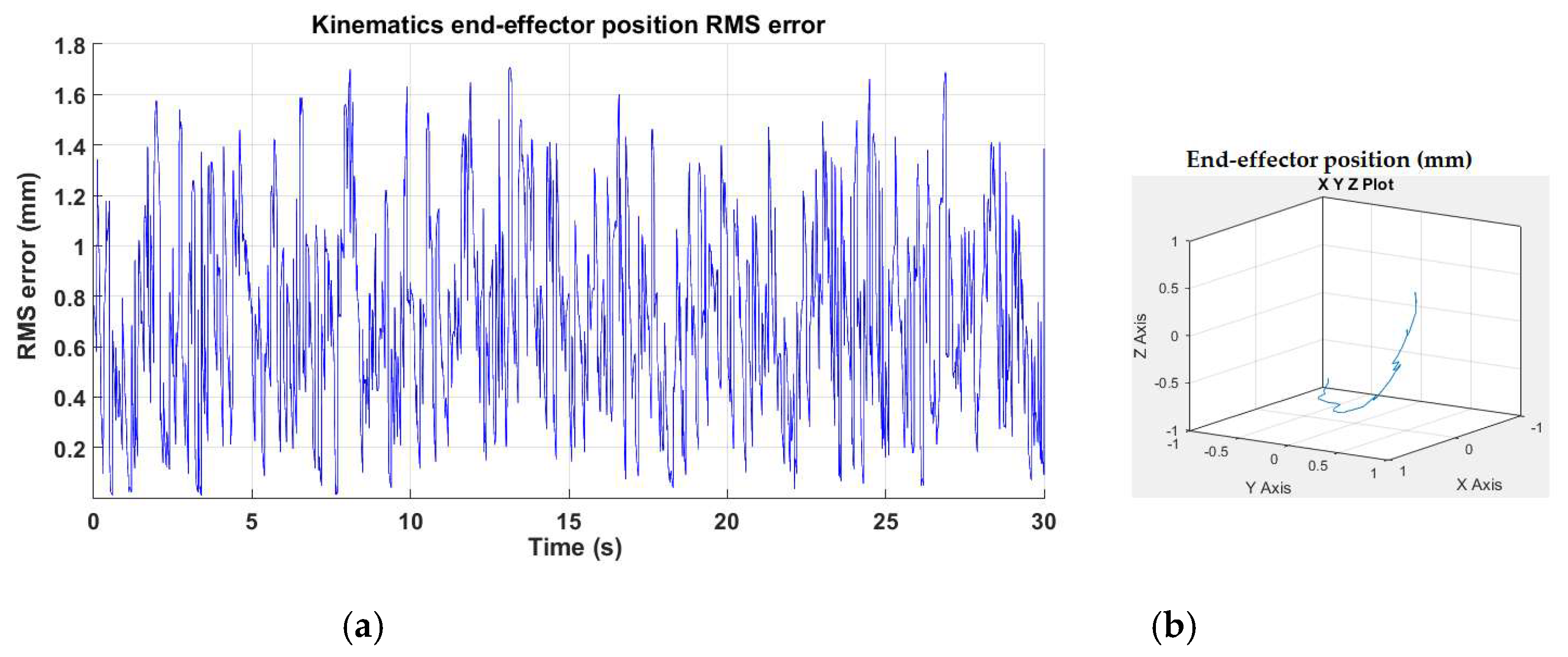
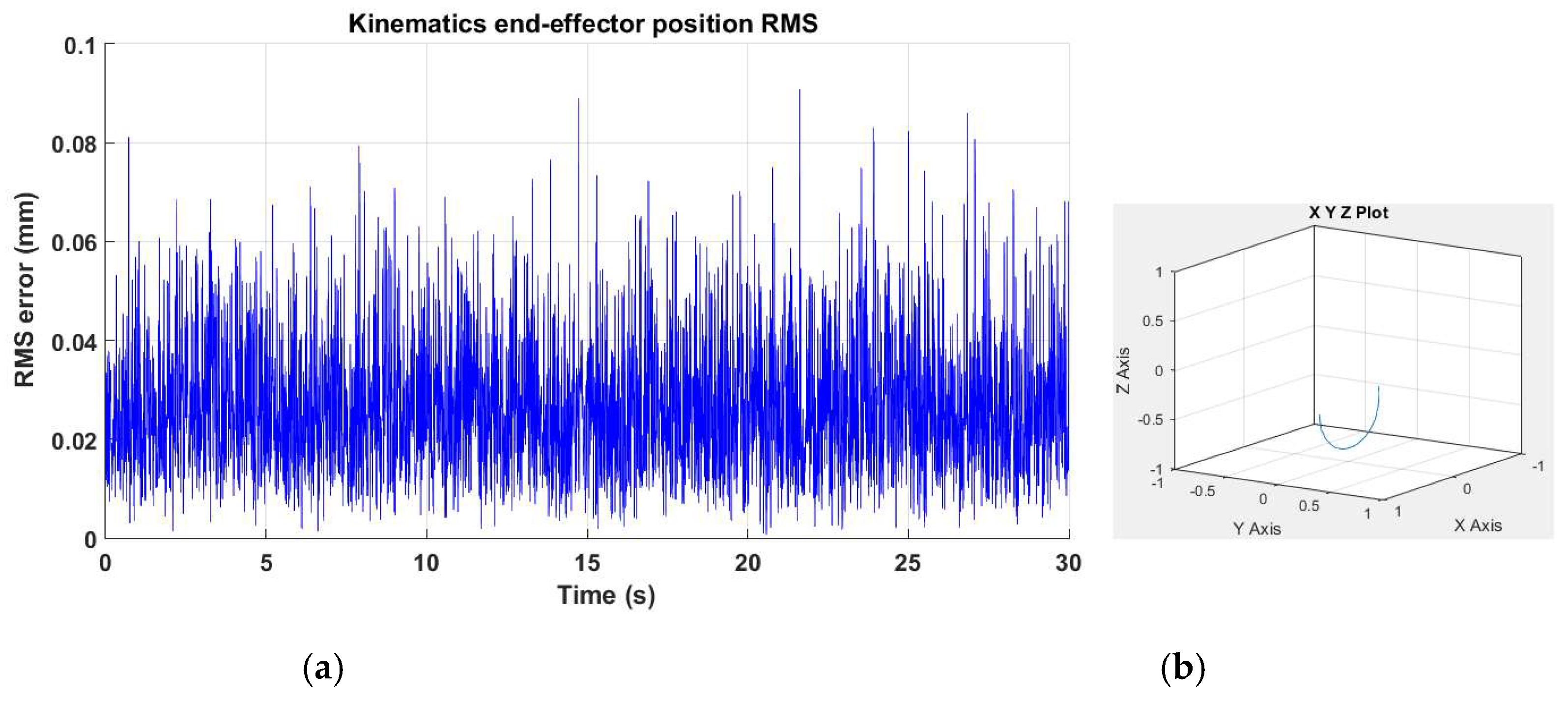
4.1. Fault Detection, Estimation and Identification
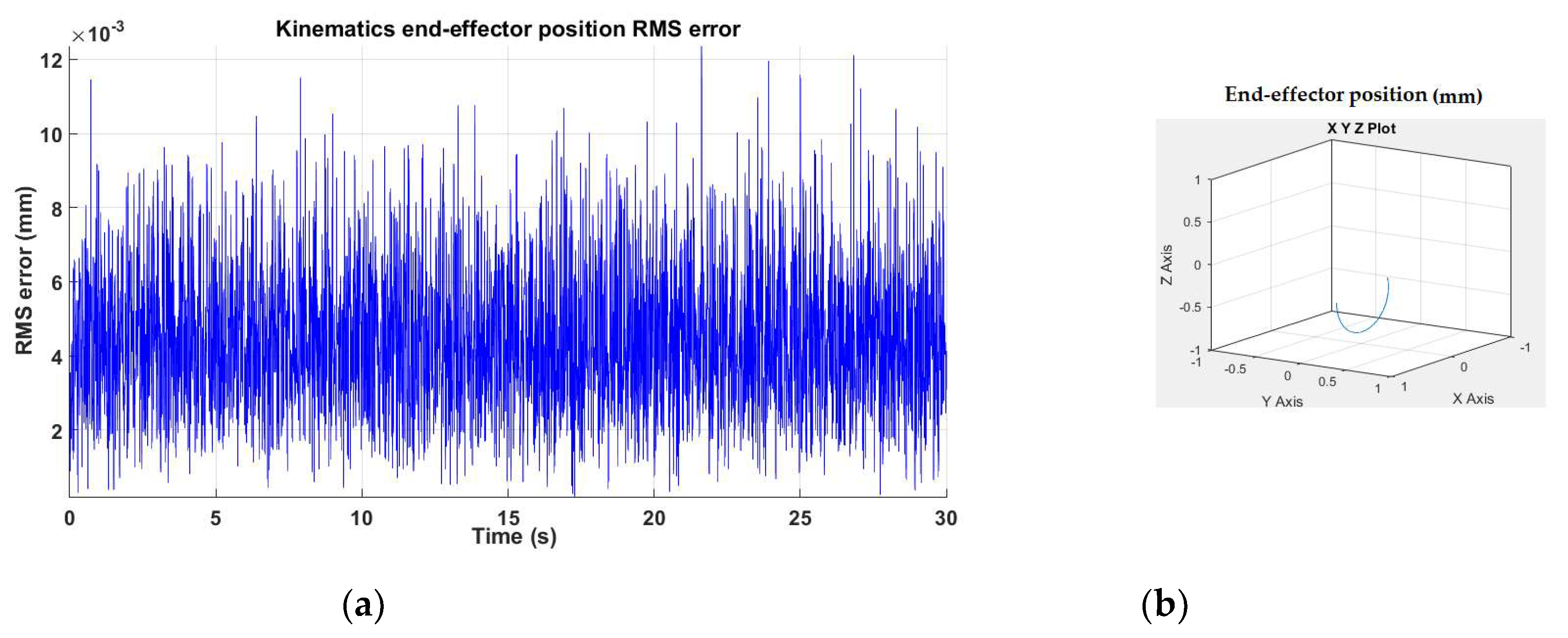
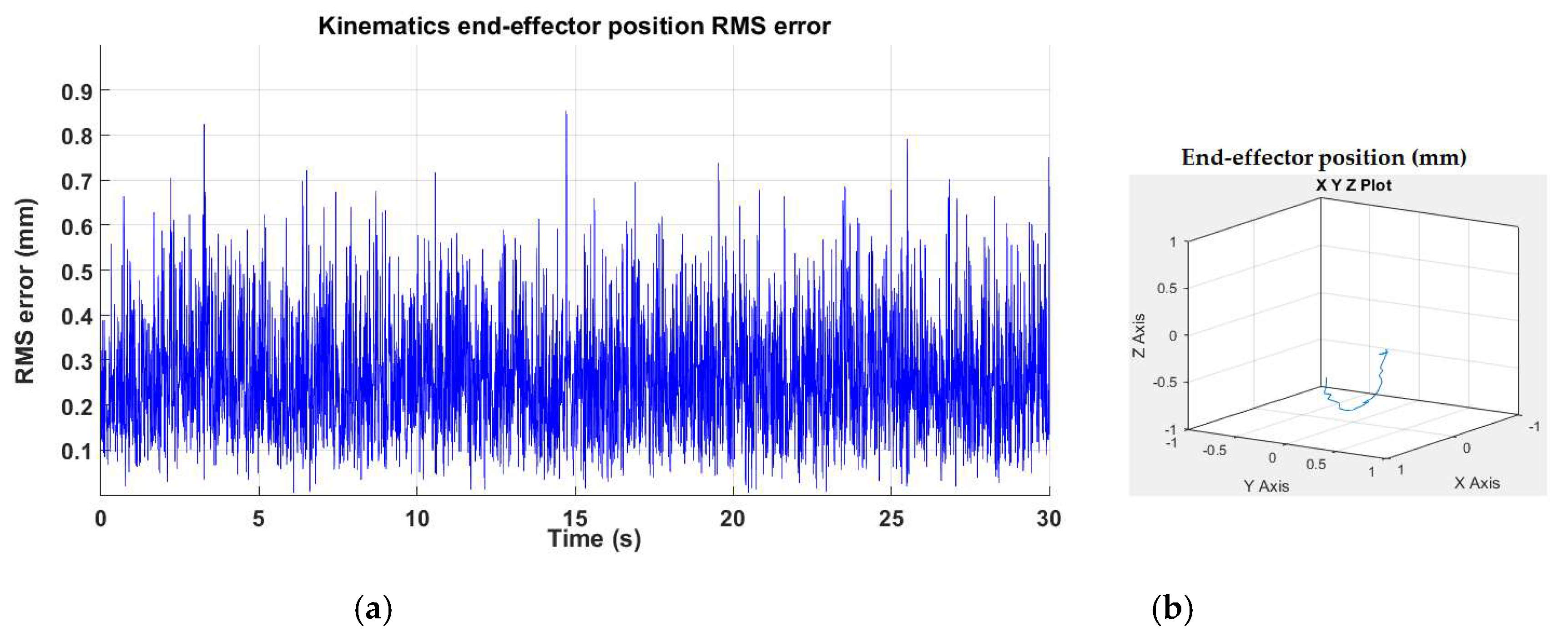
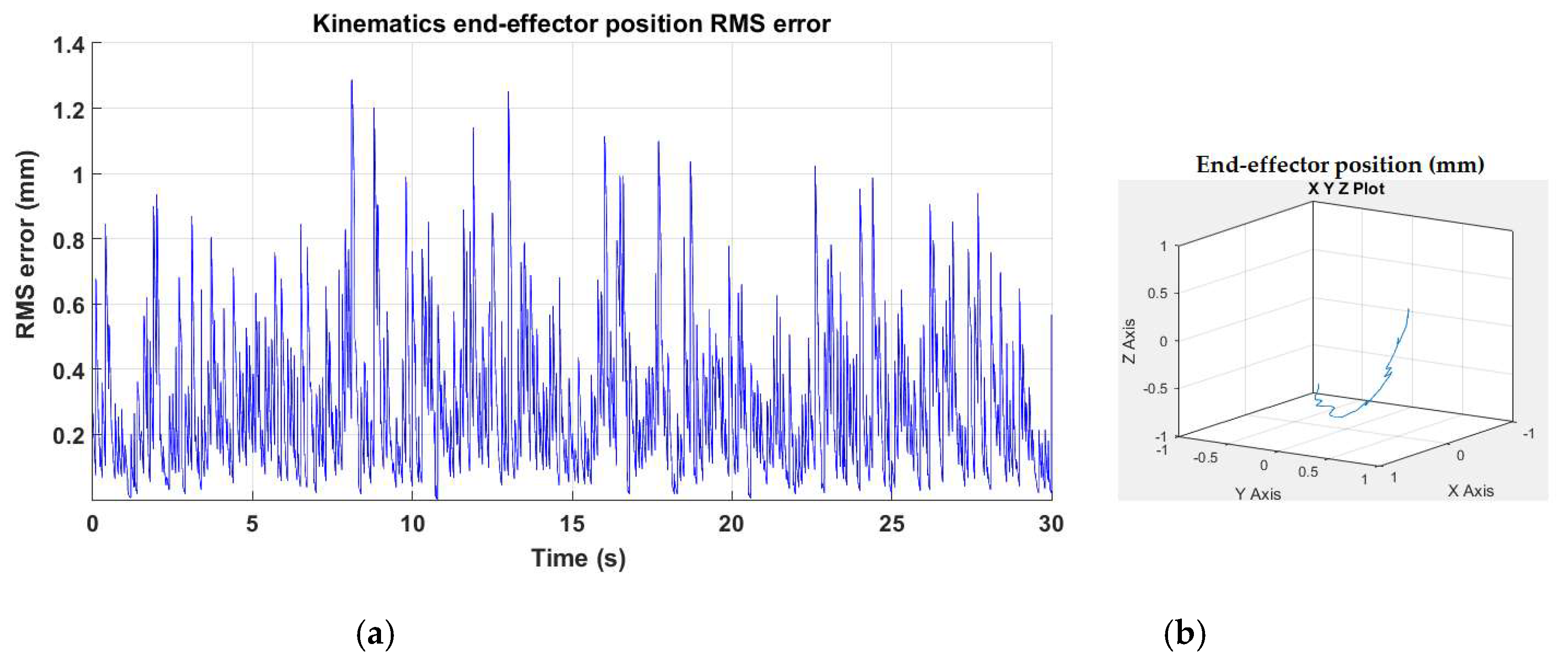
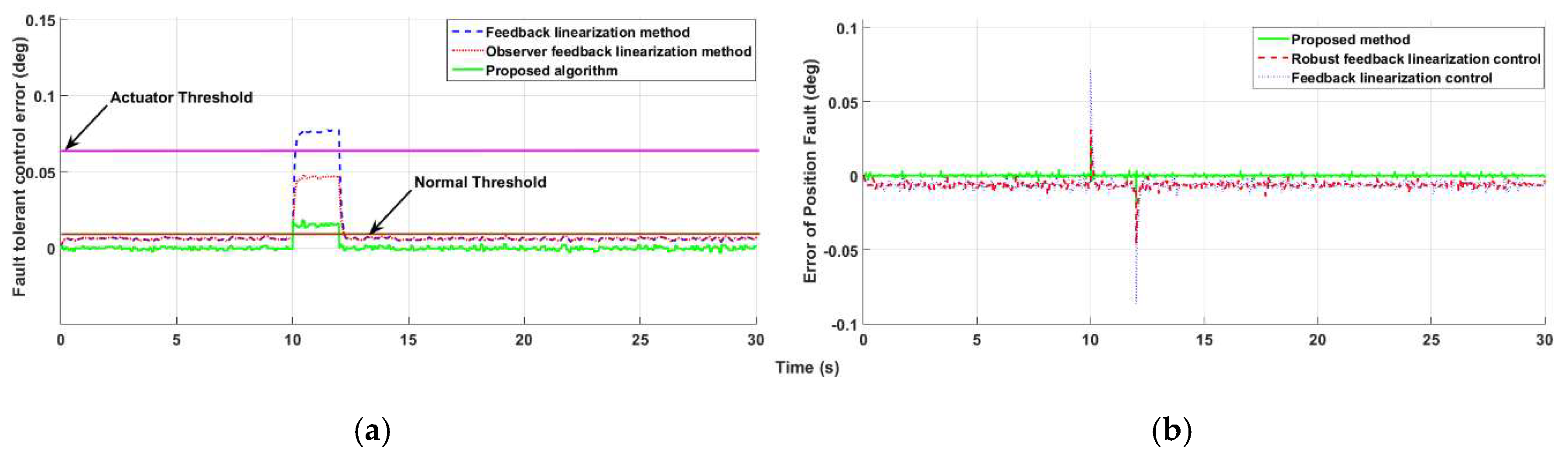
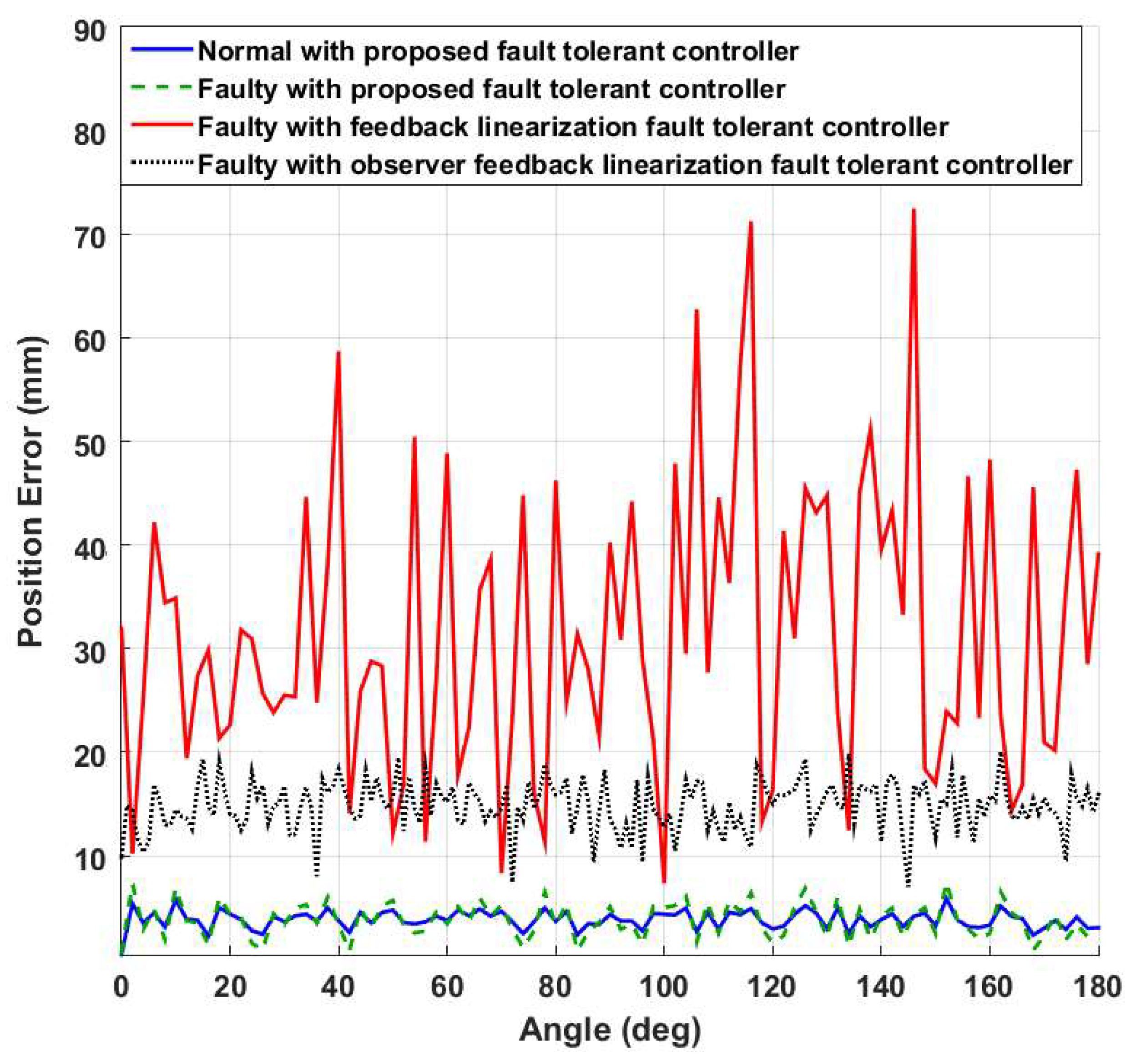
4.2. Fault-Tolerant Control
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Transformation matrix | distance from to | ||
| Angle from to | distance from to | ||
| Angle from to | force coefficient matrix | ||
| Torque | inertial matrix | ||
| Coefficients of the first-order generalized coordinate matrix | gravity | ||
| Faults and uncertainties | state function | ||
| State input | state output | ||
| Fourier function | system lag | ||
| Output | input | ||
| Coefficients | zero mean noise | ||
| Regressor variables | coefficient matrix | ||
| Coefficients | Fourier coefficients | ||
| Robot manipulator order | function of the Laguerre orthonormal | ||
| Product of the convolution | filter system output | ||
| Filter system input | orthonormal basis | ||
| Fuzzy function for system estimation | estimation error | ||
| Fuzzy sets | estimation change of error | ||
| Coefficients | state estimation | ||
| Output estimation | fuzzy estimation function | ||
| Fault estimation | αp | coefficient | |
| State estimation error | fault estimation error | ||
| State estimation | fuzzy ARX-Laguerre robust feedback linearization output estimation | ||
| Fault estimation | observer coefficient | ||
| State estimation error | fault estimation error | ||
| Residual signal for the actuator fault | residual signal for the sensor fault | ||
| Threshold values for the actuator and sensor faults | faulty signal estimator based on the T–S fuzzy algorithm | ||
| Fuzzy coefficient | estimator coefficients for actuator fault, sensor fault, and actuator-sensor fault | ||
| Proposed observer for state estimation | proposed observers for output estimation | ||
| Proposed fault estimation | proposed state estimation error | ||
| Proposed fault estimation error | threshold value for normal condition | ||
| Coefficients of the sliding mode algorithm in different states | residual signal for normal condition | ||
| Change of residual signal for normal condition | integral of residual signal for normal condition | ||
| Residual signal for actuator fault | change of residual signal for actuator fault | ||
| Integral of residual signal for actuator fault | residual signal for sensor fault | ||
| Change of residual signal for sensor fault | integral of residual signal for sensor fault | ||
| Controller’s torque based on the conventional feedback linearization control | controller coefficients | ||
| Controller output based on the proposed observation-based feedback linearization controller | proposed method for fault-tolerant control | ||
| Online tuning part of the feedback linearization controller | online tuning part of the proposed method | ||
| Online tuning coefficients | fuzzy output for tuning the proportional, derivative, and integral coefficients |
References
- Bell, G.W.; Joshi, B.B.; Macleod, R.I. Maxillary sinus disease: Diagnosis and treatment. Br. Dent. J. 2011, 210, 113. [Google Scholar] [CrossRef] [PubMed]
- Minovi, A.; Kollert, M.; Draf, W.; Bockmühl, U. Inverted papilloma: Feasibility of endonasal surgery and long-term results of 87 cases. Rhinology 2006, 44, 205–210. [Google Scholar] [PubMed]
- Hong, W.; Xie, L.; Liu, J.; Sun, Y.; Li, K.; Wang, H. Development of a novel continuum robotic system for maxillary sinus surgery. IEEE/ASME Trans. Mechatron. 2018, 23, 1226–1237. [Google Scholar] [CrossRef]
- Xie, L.; Kemp, C.D.; Yang, S.C. The simulator development of cardiovascular interventional virtual surgery with force feedback. J. Jiangxi Norm. Univ. 2017, 4, 331–337. [Google Scholar]
- Wu, L.; Song, S.; Wu, K.; Lim, C.M.; Ren, H. Development of a compact continuum tubular robotic system for nasopharyngeal biopsy. Med. Biol. Eng. Comput. 2017, 55, 403–417. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L. Design of a novel flexible endoscope–cardioscope. J. Mech. Robot. 2016, 8, 051014. [Google Scholar]
- Wang, H.; Wang, C.; Chen, W.; Liang, X.; Liu, Y. Three-dimensional dynamics for cable-driven soft manipulator. IEEE/ASME Trans. Mechatron. 2017, 22, 18–28. [Google Scholar] [CrossRef]
- Ma, H.-J.; Yang, G.-H. Simultaneous fault diagnosis for robot manipulators with actuator and sensor faults. Inf. Sci. 2016, 366, 12–30. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S.; Ren, H. Finite time fault-tolerant control for robot manipulators using time delay estimation and continuous nonsingular fast terminal sliding mode control. IEEE Trans. Cybern. 2017, 47, 1681–1693. [Google Scholar] [CrossRef]
- Xiao, B.; Shen, Y. An intelligent actuator fault reconstruction scheme for robotic manipulators. IEEE Trans. Cybern. 2018, 48, 639–647. [Google Scholar] [CrossRef]
- Van, M.; Pasquale, F.; Dariusz, C. Fault diagnosis and fault-tolerant control of uncertain robot manipulators using high-order sliding mode. Math. Probl. Eng. 2016, 2016, 7926280. [Google Scholar] [CrossRef]
- Kamel, M.A.; Yu, X.; Zhang, Y. Fault-tolerant cooperative control design of multiple wheeled mobile robots. IEEE Trans. Control Syst. Technol. 2018, 26, 756–764. [Google Scholar] [CrossRef]
- Li, S.; Song, Y.; Zhou, G. Leak detection of water distribution pipeline subject to failure of socket joint based on acoustic emission and pattern recognition. Measurement 2018, 115, 39–44. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, Y.; Ma, Y.; Cheng, X.; Yang, J. Application of the differentiation process into the correlation-based leak detection in urban pipeline networks. Mech. Syst. Signal Process. 2018, 112, 251–264. [Google Scholar] [CrossRef]
- Xu, L.; Cao, M.; Song, B.; Zhang, J.; Liu, Y.; Alsaadi, F.E. Open-circuit fault diagnosis of power rectifier using sparse autoencoder based deep neural network. Neurocomputing 2018, 311, 1–10. [Google Scholar] [CrossRef]
- Cecati, C. A survey of fault diagnosis and fault-tolerant techniques—Part II: Fault diagnosis with knowledge-based and hybrid/active approaches. IEEE Trans. Ind. Electron. 2015, 62, 3752–3756. [Google Scholar]
- Hoang, D.-T.; Kang, H.-J. A survey on Deep Learning based bearing fault diagnosis. Neurocomputing 2019, 335, 327–335. [Google Scholar] [CrossRef]
- Piltan, F.; Kim, C.-H.; Kim, J.-M. Advanced Adaptive Fault Diagnosis and Tolerant Control for Robot Manipulators. Energies 2019, 12, 1281. [Google Scholar] [CrossRef]
- Ravandi, A.K.; Khanmirza, E.; Daneshjou, K. Hybrid force/position control of robotic arms manipulating in uncertain environment based on adaptive fuzzy sliding mode control. Appl. Soft Comput. 2018, 70, 864–874. [Google Scholar] [CrossRef]
- Zhang, T.; Tan, Y.; Zhang, X.; Zhao, J. A novel hybrid technique for leak detection and location in straight pipelines. J. Loss Prev. Process Ind. 2015, 35, 157–168. [Google Scholar] [CrossRef]
- Najeh, T.; Njima, C.B.; Garna, T.; Ragot, J. Input fault detection and estimation using PI observer based on the ARX-Laguerre model. Int. J. Adv. Manuf. Technol. 2017, 90, 1317–1336. [Google Scholar] [CrossRef]
- Bouzrara, K.; Garna, T.; Ragot, J.; Messaoud, H. Decomposition of an ARX model on Laguerre orthonormal bases. ISA Trans. 2012, 51, 848–860. [Google Scholar] [CrossRef] [PubMed]
- Piltan, F.; Kim, J.-M. Bearing fault diagnosis by a robust higher-order super-twisting sliding mode observer. Sensors 2018, 18, 1128. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Mba, D.; Diallo, D.; Delpha, C. Canonical Variate Residuals-Based Fault Diagnosis for Slowly Evolving Faults. Energies 2019, 12, 726. [Google Scholar] [CrossRef]
- Fuentes-García, M.; Maciá-Fernández, G.; Camacho, J. Evaluation of diagnosis methods in PCA-based Multivariate Statistical Process Control. Chemom. Intell. Lab. Syst. 2018, 172, 194–210. [Google Scholar] [CrossRef]
- Piltan, F.; Kim, J.-M. Bearing Fault Diagnosis Using an Extended Variable Structure Feedback Linearization Observer. Sensors 2018, 18, 4359. [Google Scholar] [CrossRef] [PubMed]
- Piltan, F.; Kim, J.-M. Nonlinear Extended-state ARX-Laguerre PI Observer Fault Diagnosis of Bearings. Appl. Sci. 2019, 9, 888. [Google Scholar] [CrossRef]
- Li, L.; Ding, S.X.; Qiu, J.; Yang, Y. Real-time fault detection approach for nonlinear systems and its asynchronous T–S fuzzy observer-based implementation. IEEE Trans. Cybern. 2017, 47, 283–294. [Google Scholar] [CrossRef]
- Li, L.; Chadli, M.; Ding, S.X.; Qiu, J.; Yang, Y. Diagnostic observer design for t–s fuzzy systems: Application to real-time-weighted fault-detection approach. IEEE Trans. Fuzzy Syst. 2018, 26, 805–816. [Google Scholar] [CrossRef]
- Li, L.; Ding, S.X.; Qiu, J.; Yang, Y.; Xu, D. Fuzzy observer-based fault detection design approach for nonlinear processes. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1941–1952. [Google Scholar] [CrossRef]
- Abbaspour, A.; Aboutalebi, P.; Yen, K.K.; Sargolzaei, A. Neural adaptive observer-based sensor and actuator fault detection in nonlinear systems: Application in UAV. ISA Trans. 2017, 67, 317–329. [Google Scholar] [CrossRef]
- Tayebi-Haghighi, S.; Piltan, F.; Kim, J.-M. Robust Composite High-Order Super-Twisting Sliding Mode Control of Robot Manipulators. Robotics 2018, 7, 13. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Salmasi, F.R. Fault-tolerant supervisory controller for a hybrid AC/DC micro-grid. IEEE Trans. Smart Grid 2018, 9, 2809–2823. [Google Scholar] [CrossRef]
- Tan, N.; Gu, X.; Ren, H. Pose Characterization and Analysis of Soft Continuum Robots with Modeling Uncertainties Based on Interval Arithmetic. IEEE Trans. Autom. Sci. Eng. 2018, 99, 1–15. [Google Scholar] [CrossRef]
- Tatlicioglu, E.; Walker, I.D.; Dawson, D.M. Dynamic modelling for planar extensible continuum robot manipulators. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 1357–1362. [Google Scholar]
- Piltan, F.; Eram, M.; Taghavi, M.; Sadrnia, O.R.; Jafari, M. Nonlinear Fuzzy Model-base Technique to Compensate Highly Nonlinear Continuum Robot Manipulator. Int. J. Intell. Syst. Appl. 2013, 5, 135–148. [Google Scholar] [CrossRef][Green Version]
- Piltan, F.; TayebiHaghighi, S.; Jowkar, S.; Bod, H.R.; Sahamijoo, A.; Heo, J.-S. A Novel Intelligent ARX-Laguerre Distillation Column Estimation Technique. Int. J. Intell. Syst. Appl. 2019, 11, 52–60. [Google Scholar] [CrossRef]
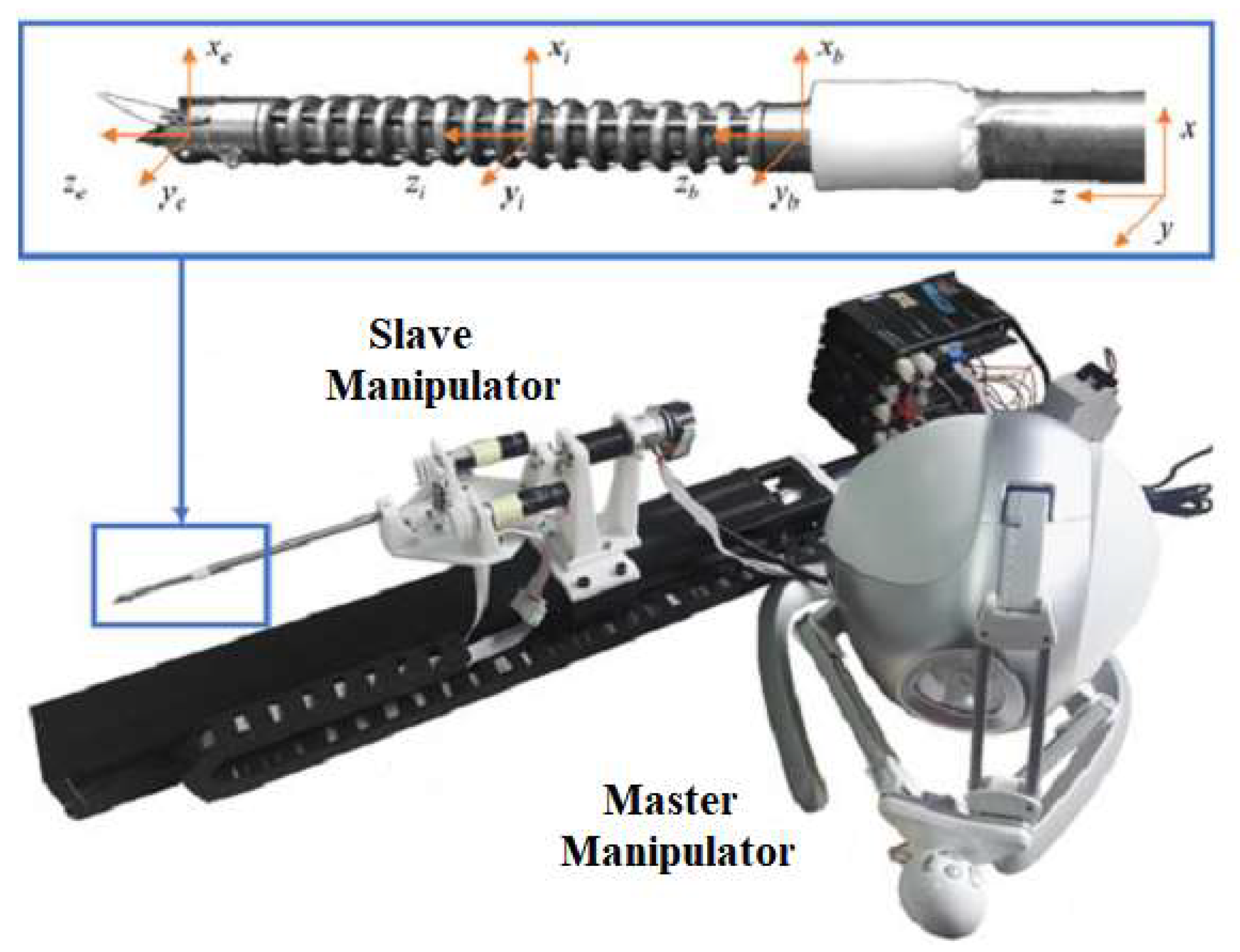
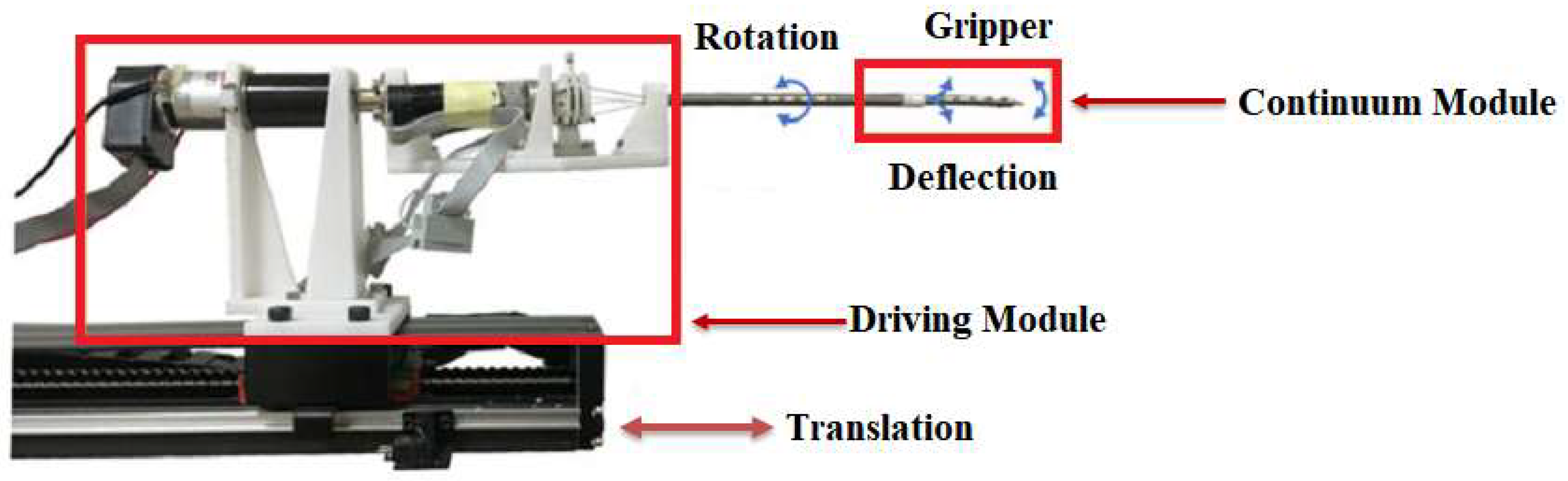
| Part | Quantity | Description |
|---|---|---|
| Manipulator | Degrees of freedom | 4 |
| Continuum module | Diameter | 4 [mm] |
| Number of joints | 17 | |
| Maximum bending angle | 270° | |
| Length of continuum module | 30 [mm] | |
| Diameter of holes | 0.6 [mm] | |
| Minimum radius of curvature | 5.8 [mm] | |
| Radius of curvature at 180° | 10 [mm] | |
| Grippers | Length | 10 [mm] |
| Cables (gripper) | Diameter | 0.2 [mm] |
| Material | Stainless Steel | |
| Cables (deflection) | Diameter | 0.36 [mm] |
| Material | Stainless Steel | |
| NiTiNo1 tube | Outer diameter | 0.508 [mm] |
| Inner diameter | 0.305 [mm] |
| Link | α | a | d | θ | State |
|---|---|---|---|---|---|
| 1 | 0 | 0 | |||
| 2 | −90° | 0 | |||
| 3 | 90° | 0 | 0 | ||
| 4 | −90° | 0 | 0 | ||
| 5 | 90° | 0 | 0 | ||
| 6 | 0 | 0 | 0 | ||
| 7 | 0 | 0 | 0 | ||
| 8 | 0 | 0 | |||
| 9 | −90° | 0 | −90° | ||
| 10 | 90° | 0 | 0 | 90° | |
| 11 | −90° | 0 | −90° | ||
| 12 | 90° | 0 | 0 | 90° | |
| 13 | −90° | 0 | 0 | −90° | |
| 14 | 90° | 0 | 0 | 90° | |
| 15 | −90° | 0 | −90° | ||
| 16 | 90° | 0 | 0 | 90° | |
| 17 | 0 | 0 | 0 |
| Error (e) | Change of Error (de) | |||||
| NB | NS | Z | PS | PB | ||
| NB | PB | PB | PB | PS | Z | |
| NS | PB | PB | PS | Z | NS | |
| Z | PB | PS | Z | NS | NB | |
| PS | PS | Z | NS | NB | NB | |
| PB | Z | NS | NB | NB | NB | |
| Error (e) | Change of Error (de) | |||||||
| NB | NM | NS | Z | PS | PM | PB | ||
| NB | PB | PB | PB | PB | PM | PS | PS | |
| NM | PB | PB | PB | PM | PS | PS | PS | |
| NS | PB | PB | PM | PS | PS | PS | PS | |
| Z | PB | PM | PS | PS | PS | PS | PS | |
| PS | PB | PB | PB | PB | PM | PS | PS | |
| PM | PB | PB | PB | PM | PS | PS | PS | |
| PB | PB | PB | PM | PS | PS | PS | PS | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piltan, F.; Kim, C.-H.; Kim, J.-M. Adaptive Fuzzy-Based Fault-Tolerant Control of a Continuum Robotic System for Maxillary Sinus Surgery. Appl. Sci. 2019, 9, 2490. https://doi.org/10.3390/app9122490
Piltan F, Kim C-H, Kim J-M. Adaptive Fuzzy-Based Fault-Tolerant Control of a Continuum Robotic System for Maxillary Sinus Surgery. Applied Sciences. 2019; 9(12):2490. https://doi.org/10.3390/app9122490
Chicago/Turabian StylePiltan, Farzin, Cheol-Hong Kim, and Jong-Myon Kim. 2019. "Adaptive Fuzzy-Based Fault-Tolerant Control of a Continuum Robotic System for Maxillary Sinus Surgery" Applied Sciences 9, no. 12: 2490. https://doi.org/10.3390/app9122490
APA StylePiltan, F., Kim, C.-H., & Kim, J.-M. (2019). Adaptive Fuzzy-Based Fault-Tolerant Control of a Continuum Robotic System for Maxillary Sinus Surgery. Applied Sciences, 9(12), 2490. https://doi.org/10.3390/app9122490







