Skew Quadrupole Effect of Laser Plasma Electron Beam Transport
Abstract
:1. Introduction
2. Emittance Growth Issues on LPA
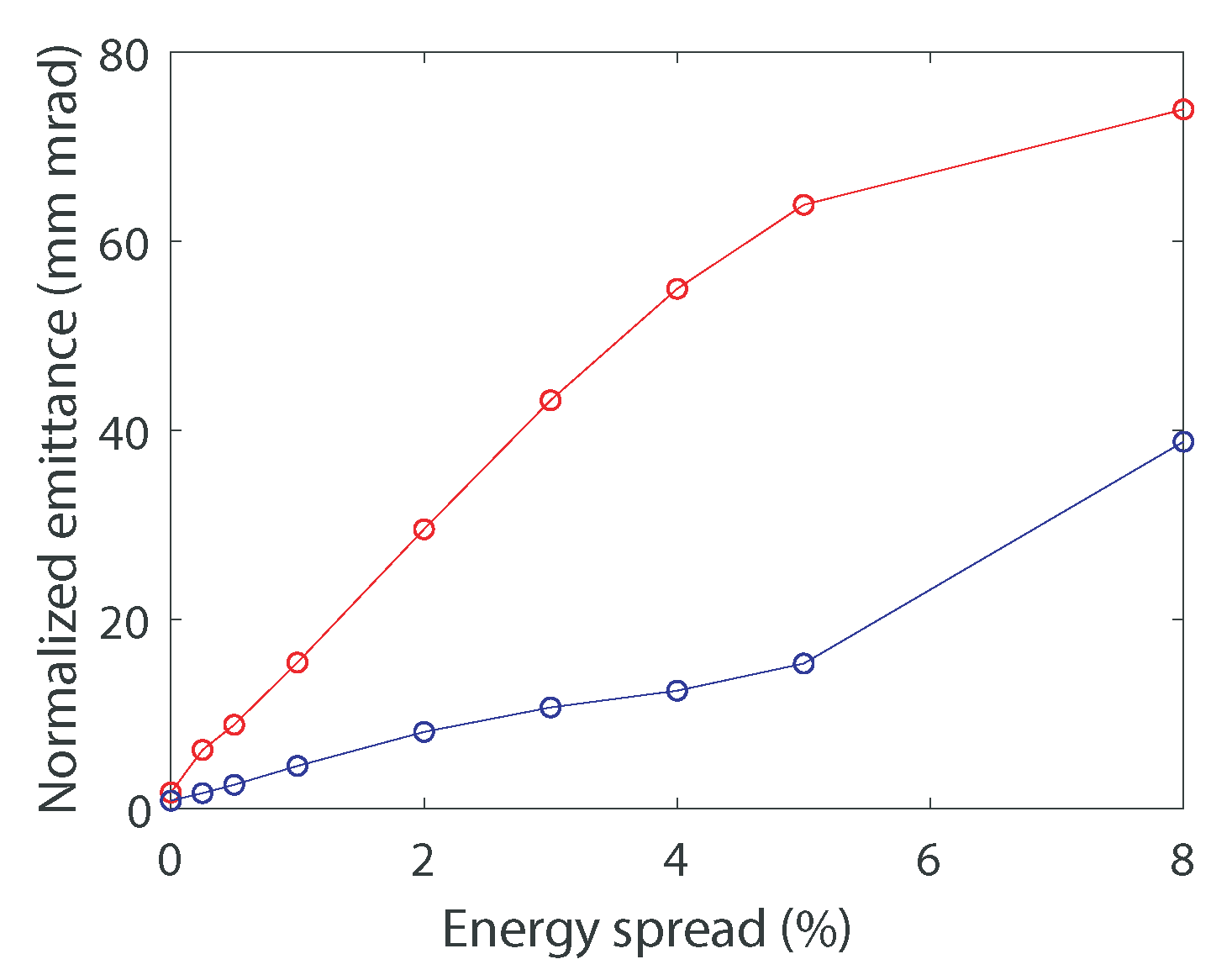
2.1. Theoretical Approach
2.2. Experimental Test Bench: The COXINEL Line
2.3. The Two Electron Beam Initial Conditions
2.4. QUAPEVA: The Two Skew Quadrupolar Components Configurations of the First Strong Focusing Quadrupoles
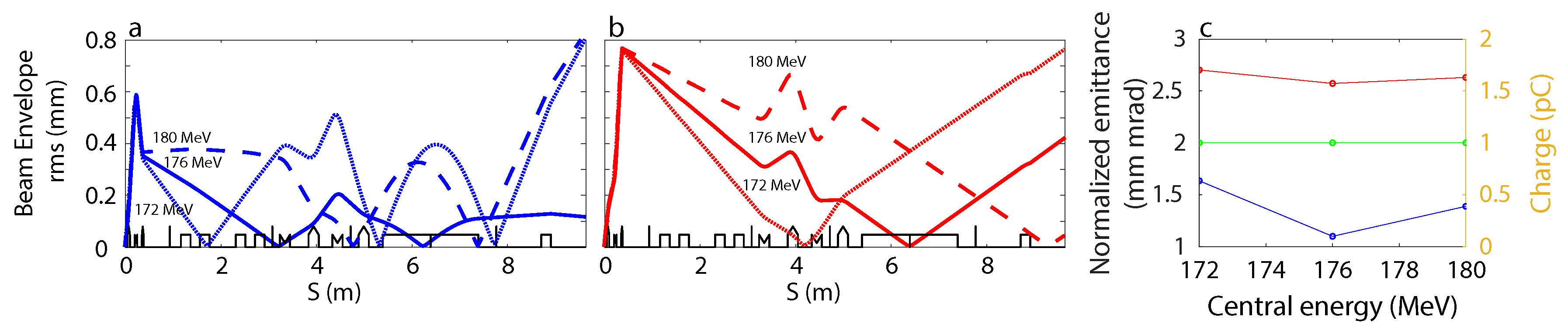
3. Electron Beam Transport for Ideal Magnetic Elements
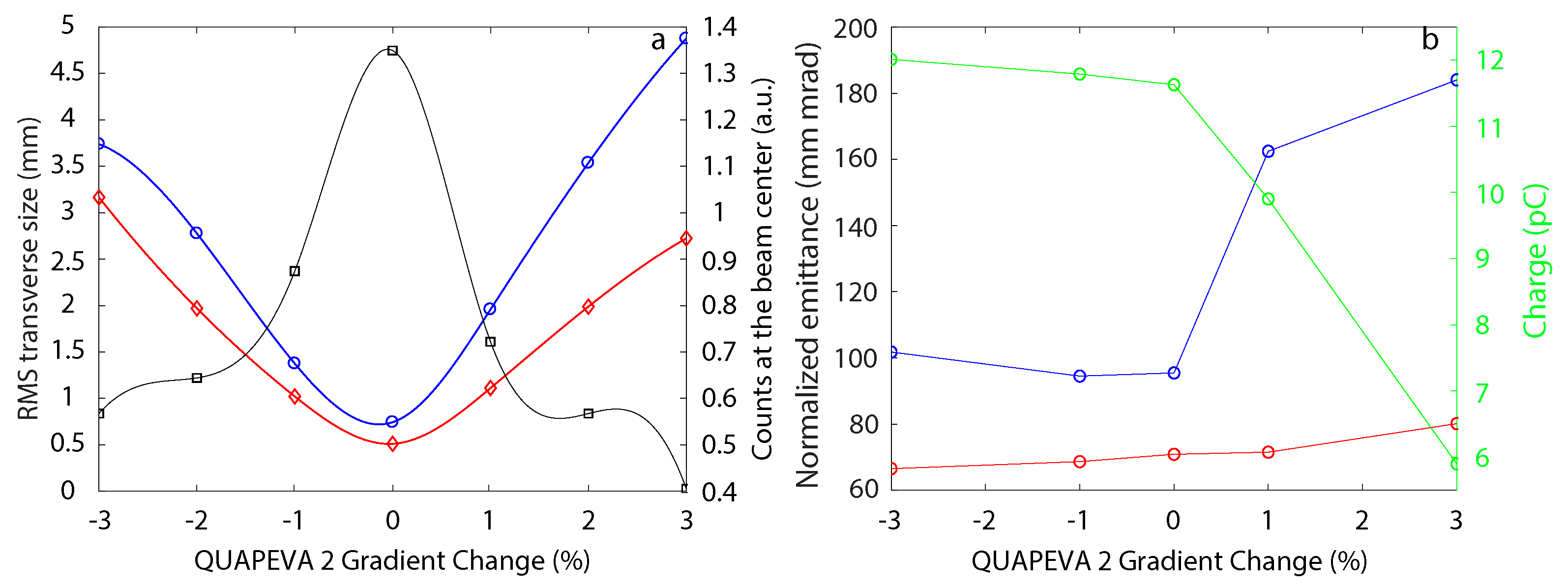
Beam Shape Dependence on QUAPEVA 2 Gradient
4. Effect of the QUAPEVA Skew and Initial Beam Conditions on the Electron Beam Transport
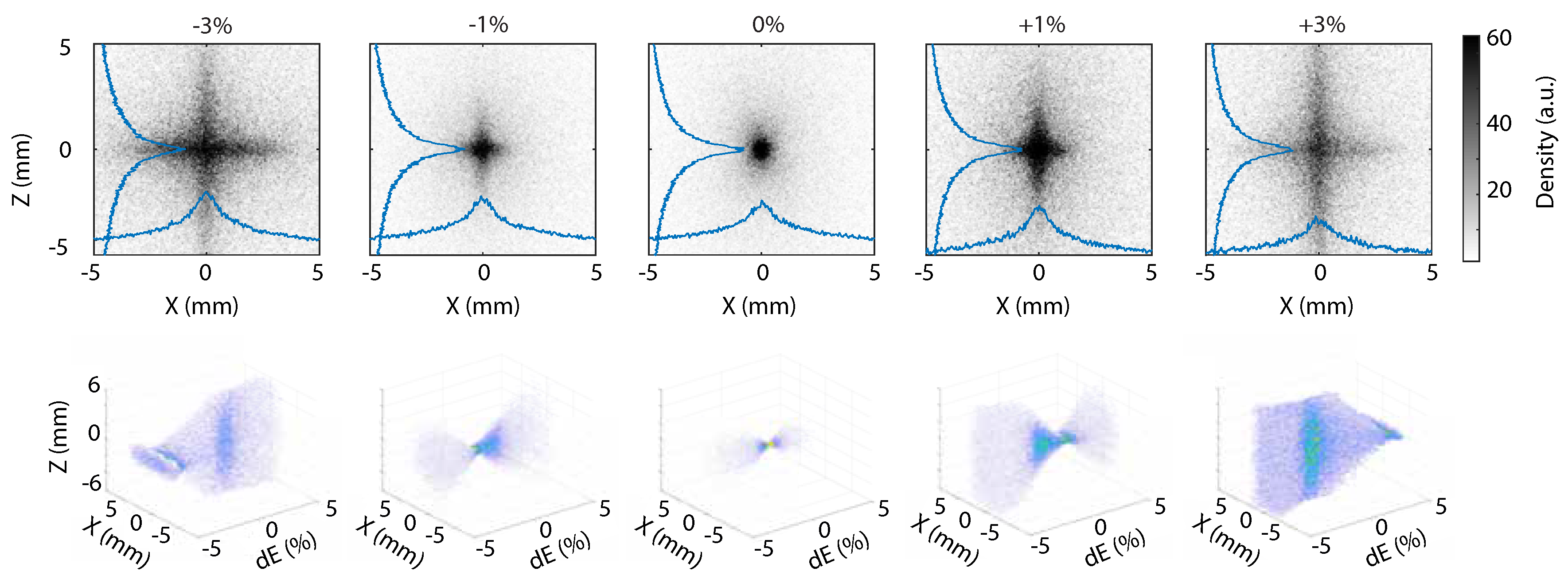
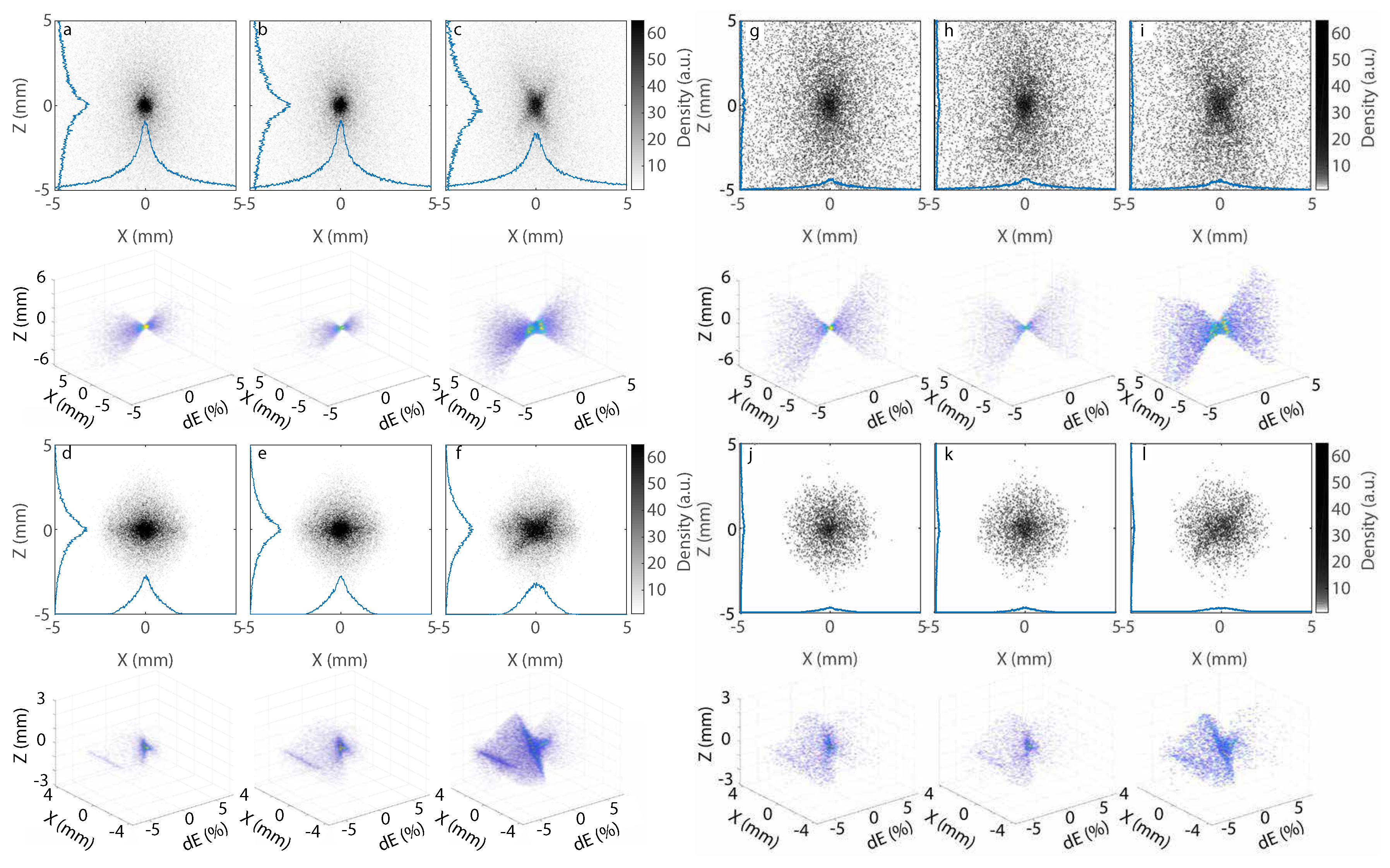
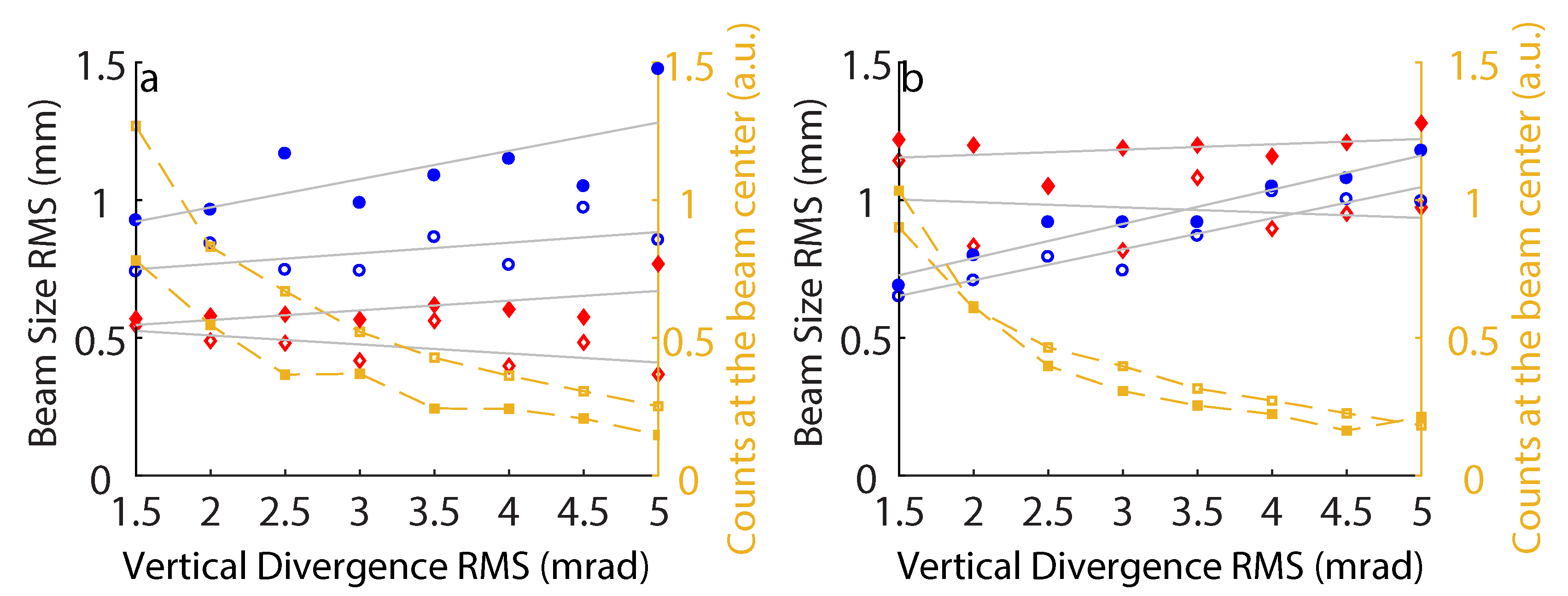
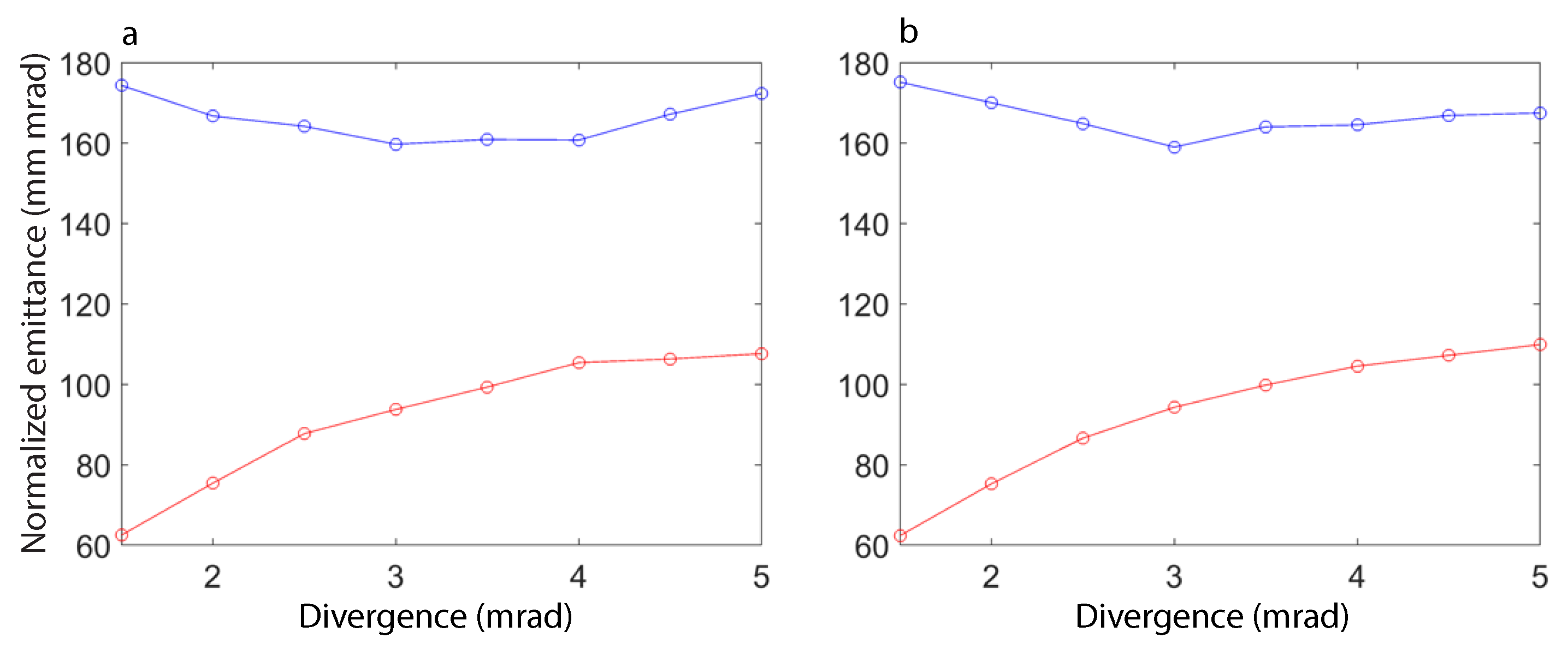
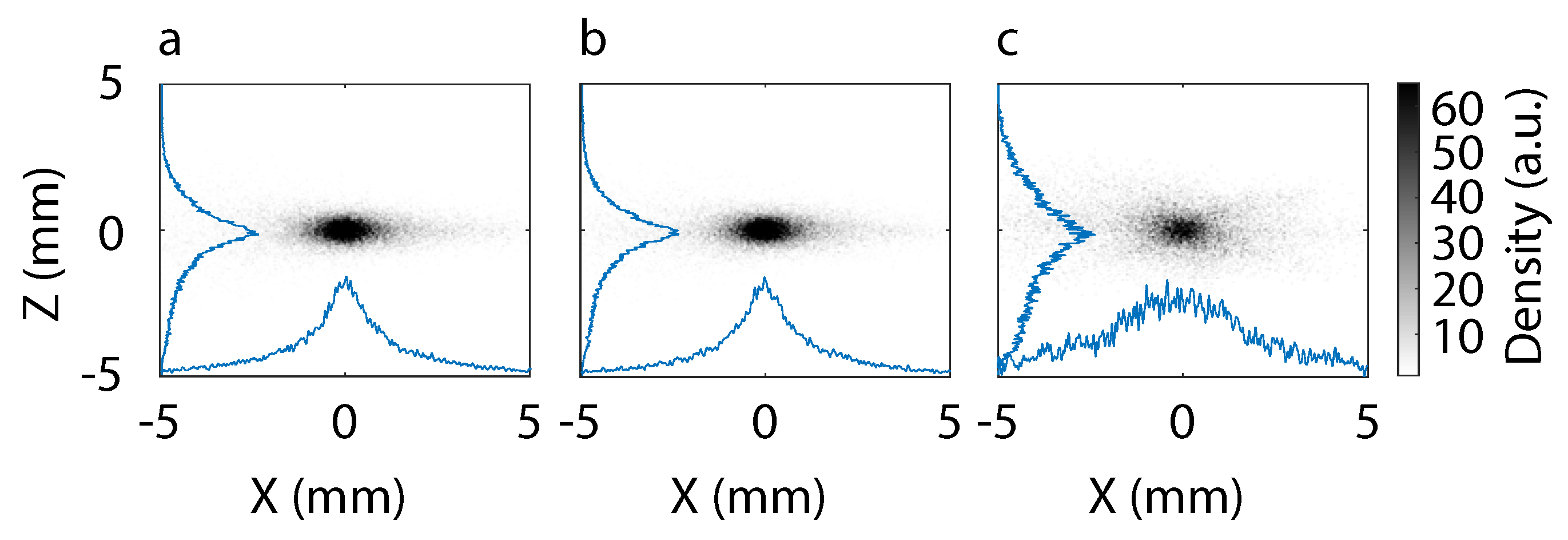
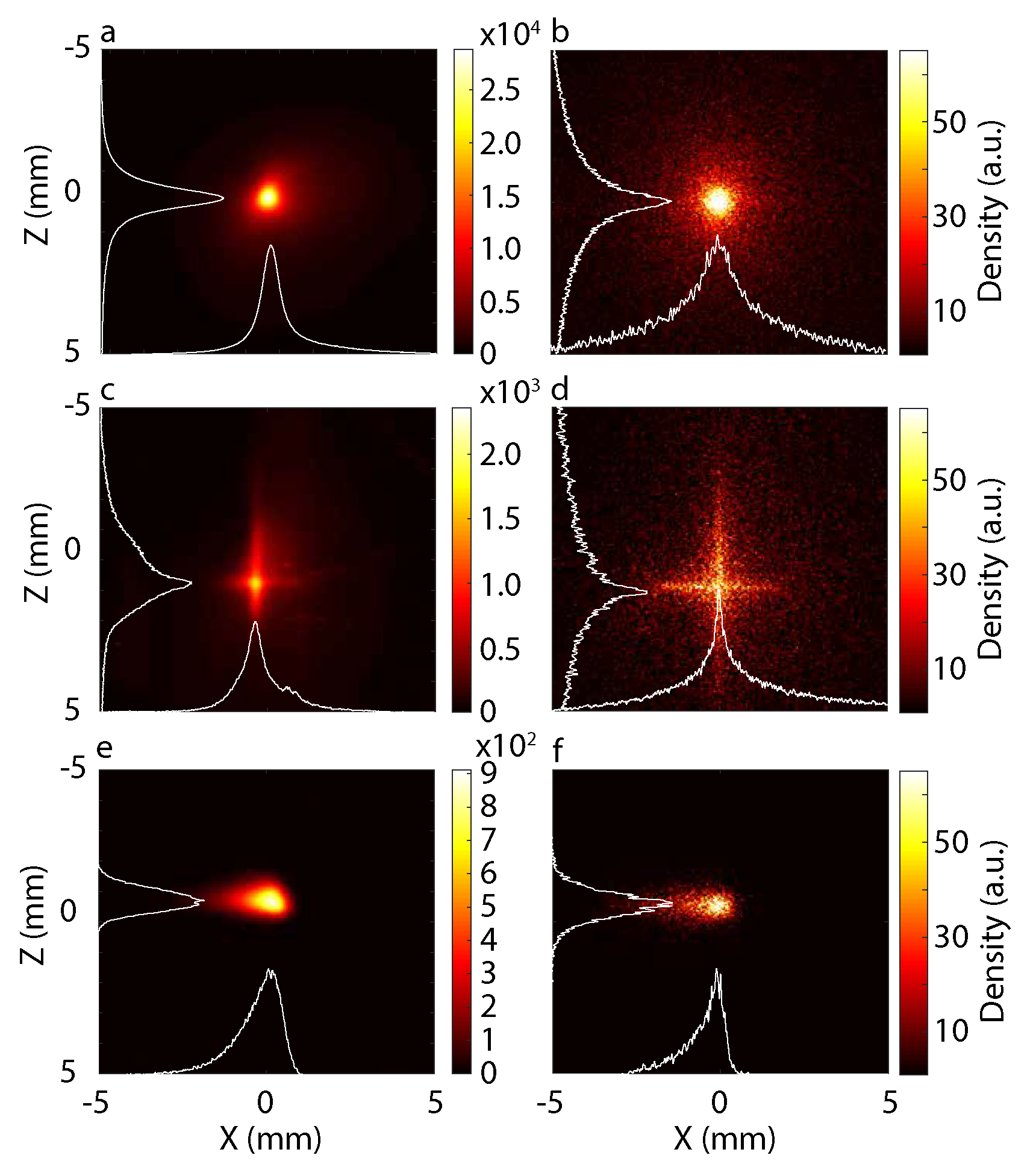
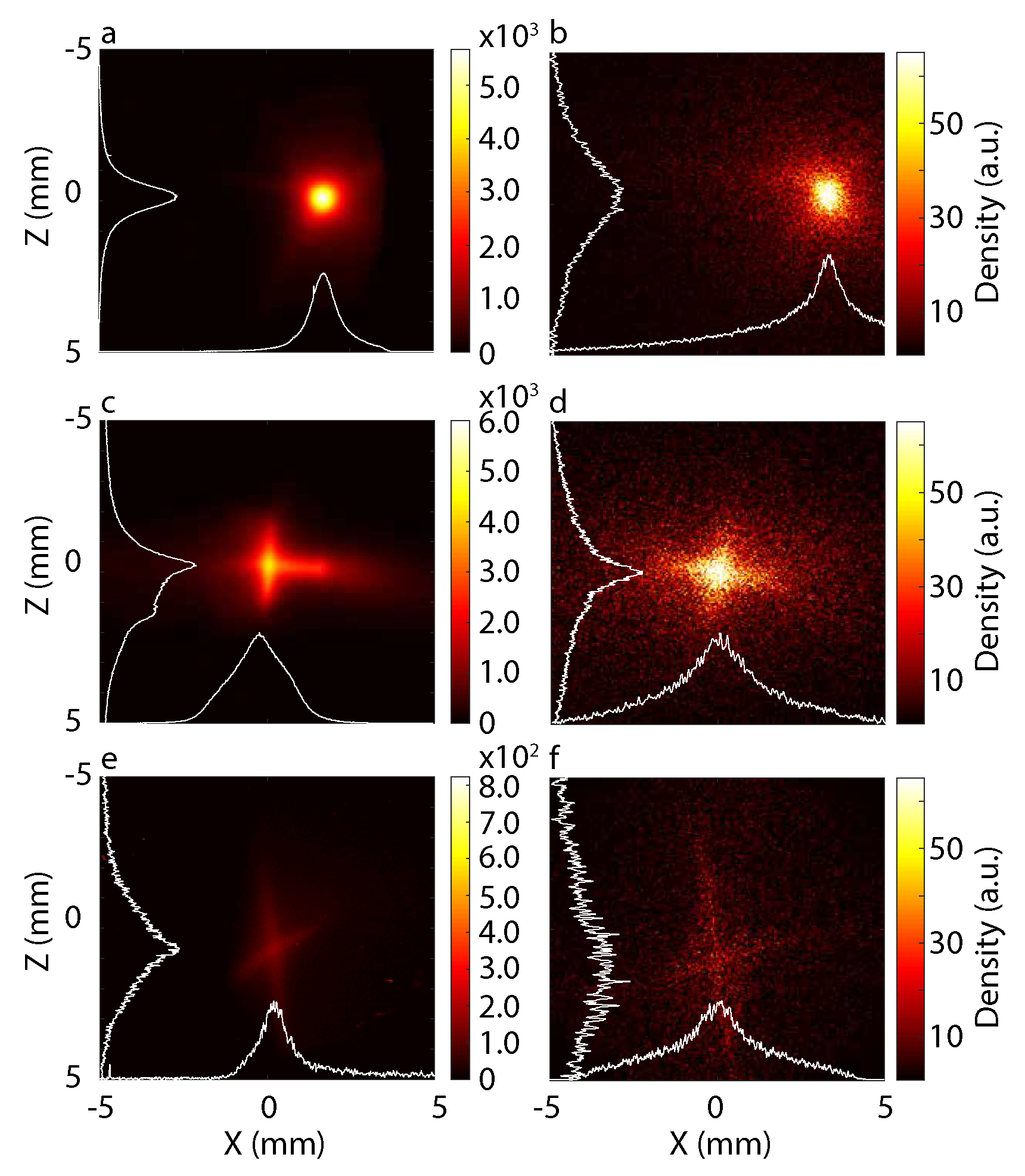
4.1. Variation of Skew Quadrupole Component
4.2. Variation of Initial Divergence
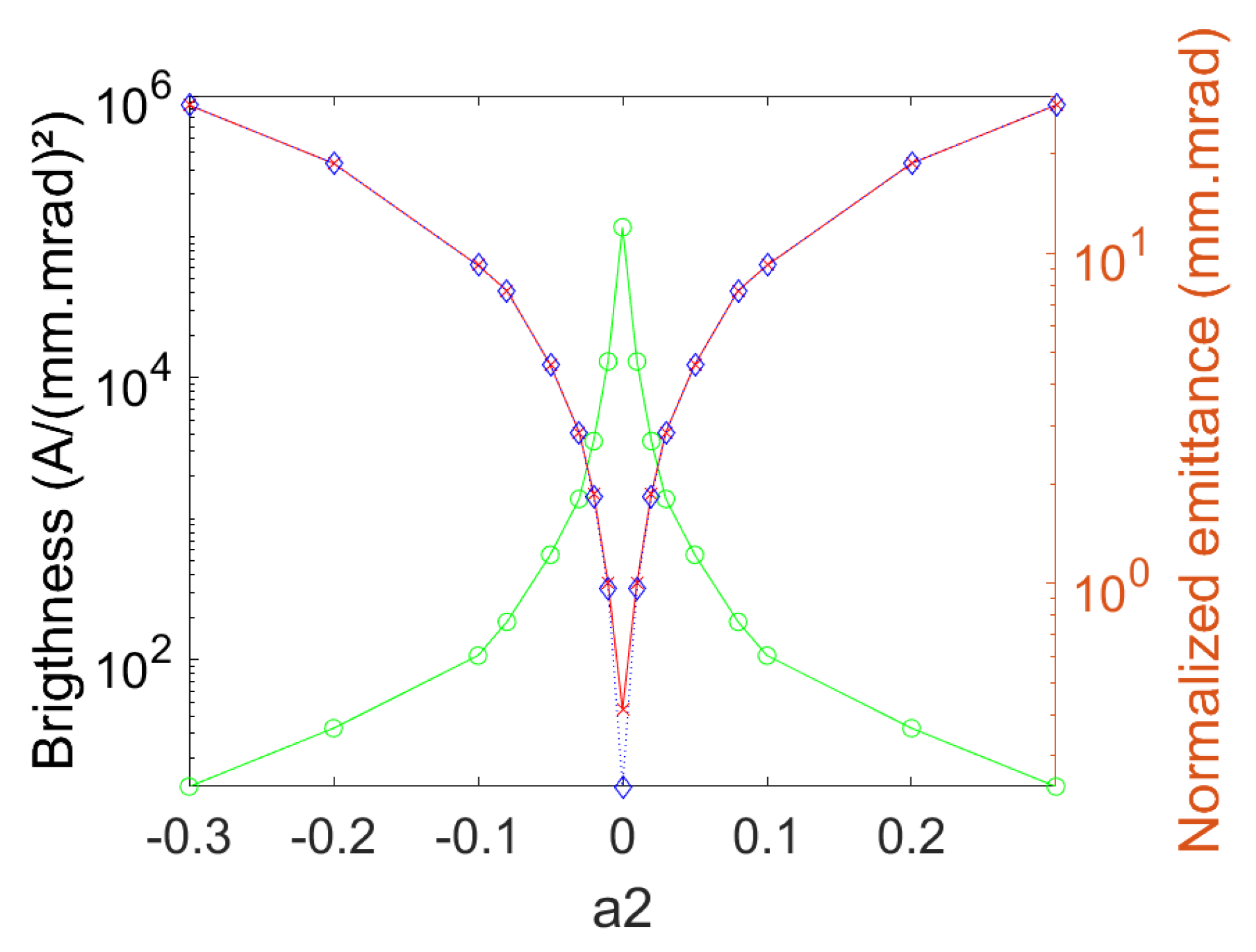
4.3. Brightness
5. Measured Electron Beam Transport in Presence of Skew Quadrupolar Components of the First Triplet
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tajima, T.; Dawson, J.M. Laser electron accelerator. Phys. Rev. Lett. 1979, 43, 267. [Google Scholar] [CrossRef]
- Esarey, E.; Schroeder, C.; Leemans, W. Physics of laser-driven plasma-based electron accelerators. Rev. Mod. Phys. 2009, 81, 1229–1285. [Google Scholar] [CrossRef]
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Opt. Commun. 1985, 55, 447–449. [Google Scholar] [CrossRef]
- Geddes, C.; Toth, C.; Van Tilborg, J.; Esarey, E.; Schroeder, C.; Bruhwiler, D.; Nieter, C.; Cary, J.; Leemans, W. High-quality electron beams from a laser wakefield accelerator using plasma-channel guiding. Nature 2004, 431, 538–541. [Google Scholar] [CrossRef] [PubMed]
- Faure, J.; Glinec, Y.; Pukhov, A.; Kiselev, S.; Gordienko, S.; Lefebvre, E.; Rousseau, J.-P.; Burgy, F.; Malka, V. A laser-plasma accelerator producing monoenergetic electron beams. Nature 2004, 431, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Mangles, S.; Murphy, C.D.; Najmudin, Z.; Thomas, A.G.R.; Collier, J.L.; Dangor, A.E.; Divall, E.J.; Foster, P.S.; Gallacher, J.G.; Hooker, C.J.; et al. Monoenergetic beams of relativistic electrons from intense laser-plasma interactions. Nature 2004, 431, 538–541. [Google Scholar] [CrossRef]
- Malka, V.; Faure, J.; Glinec, Y.; Pukhov, A.; Rousseau, J.P. Monoenergetic electron beam optimization in the bubble regime. Phys. Plasmas 2005, 12, 56702–56709. [Google Scholar] [CrossRef]
- Leemans, W.; Nagler, B.; Gonsalves, A.; Toth, C.; Nakamura, K.; Geddes, C.; Esarey, E.; Schroeder, C.; Hooker, S. GeV electron beams from a centimetre-scale accelerator. Nat. Phys. 2006, 2, 696–699. [Google Scholar] [CrossRef]
- Faure, J.; Rechatin, C.; Norlin, A.; Lifschitz, A.; Glinec, Y.; Malka, V. Controlled injection and acceleration of electrons in plasma wakefields by colliding laser pulses. Nature 2006, 444, 737–739. [Google Scholar] [CrossRef]
- Lu, W.; Tzoufras, M.; Joshi, C.; Tsung, F.S.; Mori, W.B.; Vieira, J.; Fonseca, R.A.; Silva, L.O. Generating multi-GeV electron bunches using single stage laser wakefield acceleration in a 3D nonlinear regime. Phys. Rev. Spec. Top. Accel. Beams 2007, 10, 061301–061312. [Google Scholar] [CrossRef]
- Cipiccia, S.; Islam, M.R.; Ersfeld, B.; Shanks, R.P.; Brunetti, E.; Vieux, G.; Yang, X.; Issac, R.C.; Wiggins, S.M. Gamma-rays from harmonically resonant betatron oscillations in a plasma wake. Nat. Phys. 2011, 7, 867–871. [Google Scholar] [CrossRef]
- Lundh, O.; Lim, J.; Rechatin, C.; Ammoura, L.; Ben-Ismail, A.; Davoine, X.; Gallot, G.; Goddet, J.-P.; Lefebvre, E.; Malka, V.; et al. Few femtosecond, few kiloampere electron bunch produced by a laser–plasma accelerator. Nat. Phys. 2011, 7, 219–222. [Google Scholar] [CrossRef]
- Rechatin, C.; Faure, J.; Ben-Ismail, A.; Lim, J.; Fitour, R.; Specka, A.; Videau, H.; Tafzi, A.; Burgy, F.; Malka, V. Controlling the phase-space volume of injected electrons in a laser-plasma accelerator. Phys. Rev. Lett. 2009, 102, 164801. [Google Scholar] [CrossRef] [PubMed]
- Geddes, C.G.R.; Nakamura, K.; Plateau, G.R.; Toth, C.; Cormier-Michel, E.; Esarey, E.; Schroeder, C.B.; Cary, J.R.; Leemans, W.P. Plasma-density-gradient injection of low absolute-momentum-spread electron bunches. Phys. Rev. Lett. 2008, 100, 215004. [Google Scholar] [CrossRef] [PubMed]
- Kalmykov, S.; Yi, S.; Khudik, V.; Shvets, G. Electron self-injection and trapping into an evolving plasma bubble. Phys. Rev. Lett. 2009, 103, 135004. [Google Scholar] [CrossRef]
- Faure, J.; Rechatin, C.; Lundh, O.; Ammoura, L.; Malka, V. Injection and acceleration of quasimonoenergetic relativistic electron beams using density gradients at the edges of a plasma channel. Phys. Plasmas 2010, 17, 083107. [Google Scholar] [CrossRef] [Green Version]
- Pollock, B.; Clayton, C.; Ralph, J.; Albert, F.; Davidson, A.; Divol, L.; Filip, C.; Glenzer, S.; Herpoldt, K.; Lu, W.; et al. Demonstration of a narrow energy spread, 0.5 GeV electron beam from a two-stage laser wakefield accelerator. Phys. Rev. Lett. 2011, 107, 045001. [Google Scholar] [CrossRef]
- Corde, S.; Thaury, C.; Lifschitz, A.; Lambert, G.; Phuoc, K.T.; Davoine, X.; Lehe, R.; Douillet, D.; Rousse, A.; Malka, V. Observation of longitudinal and transverse self-injections in laser-plasma accelerators. Nat. Commun. 2013, 4, 1501. [Google Scholar] [CrossRef] [Green Version]
- Leemans, W.; Gonsalves, A.; Mao, H.S.; Nakamura, K.; Benedetti, C.; Schroeder, C.; Tóth, C.; Daniels, J.; Mittelberger, D.; Bulanov, S.; et al. Multi-GeV electron beams from capillary-discharge-guided subpetawatt laser pulses in the self-trapping regime. Phys. Rev. Lett. 2014, 113, 245002. [Google Scholar] [CrossRef]
- Weingartner, R.; Raith, S.; Popp, A.; Chou, S.; Wenz, J.; Khrennikov, K.; Heigoldt, M.; Maier, A.R.; Kajumba, N.; Fuchs, M.; et al. Ultralow emittance electron beams from a laser-wakefield accelerator. Phys. Rev. Spec. Top. Accel. Beams 2012, 15, 111302. [Google Scholar] [CrossRef]
- Thaury, C.; Guillaume, E.; Lifschitz, A.; Phuoc, K.T.; Hansson, M.; Grittani, G.; Gautier, J.; Goddet, J.P.; Tafzi, A.; Lundh, O.; et al. Shock assisted ionization injection in laser-plasma accelerators. Sci. Rep. 2015, 5, 16310. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Esarey, E.; Hubbard, R.; Leemans, W.; Ting, A.; Sprangle, P. Electron injection into plasma wakefields by colliding laser pulses. Phys. Rev. Lett. 1997, 79, 2682–2685. [Google Scholar] [CrossRef]
- Bulanov, S.; Naumova, N.; Pegoraro, F.; Sakai, J. Particle injection into the wave acceleration phase due to nonlinear wake wave breaking. Phys. Rev. E 1998, 58, R5257. [Google Scholar] [CrossRef]
- Audet, T.; Hansson, M.; Lee, P.; Desforges, F.; Maynard, G.; Dobosz Dufrénoy, S.; Lehe, R.; Vay, J.L.; Aurand, B.; Persson, A.; et al. Investigation of ionization-induced electron injection in a wakefield driven by laser inside a gas cell. Phys. Plasmas 2016, 23, 023110. [Google Scholar] [CrossRef] [Green Version]
- Osterhoff, J.; Popp, A.; Major, Z.; Marx, B.; Rowlands-Rees, T.; Fuchs, M.; Geissler, M.; Hörlein, R.; Hidding, B.; Becker, S.; et al. Generation of stable, low-divergence electron beams by laser-wakefield acceleration in a steady-state-flow gas cell. Phys. Rev. Lett. 2008, 101, 085002. [Google Scholar] [CrossRef] [PubMed]
- McGuffey, C.; Thomas, A.; Schumaker, W.; Matsuoka, T.; Chvykov, V.; Dollar, F.; Kalintchenko, G.; Yanovsky, V.; Maksimchuk, A.; Krushelnick, K.; et al. Ionization induced trapping in a laser wakefield accelerator. Phys. Rev. Lett. 2010, 104, 025004. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zgadzaj, R.; Fazel, N.; Li, Z.; Yi, S.; Zhang, X.; Henderson, W.; Chang, Y.-Y.; Korzekwa, R.; Tsai, H.-E.; et al. Quasi-monoenergetic laser-plasma acceleration of electrons to 2 GeV. Nat. Commun. 2013, 4, 1988. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schroeder, C.; Esarey, E.; Geddes, C.; Benedetti, C.; Leemans, W. Physics considerations for laser-plasma linear colliders. Phys. Rev. Spec. Top. Accel. Beams 2010, 13, 101301. [Google Scholar] [CrossRef] [Green Version]
- Molodozhentsev, A.; Pribyl, L. ELI Eectron Beam Line for Laser-plasma-driven Undulator X-ray Source. In Proceedings of the IPAC2016, Busan, Korea, 8–13 May 2016. [Google Scholar]
- Madey, J.M. Stimulated emission of bremsstrahlung in a periodic magnetic field. J. Appl. Phys. 1971, 42, 1906–1913. [Google Scholar] [CrossRef]
- Kondratenko, A.; Saldin, E. Generating of coherent radiation by a relativistic electron beam in an ondulator. Part. Accel. 1980, 10, 207–216. [Google Scholar]
- Huang, Z.; Kim, K.J. Review of X-ray free-electron laser theory. Phys. Rev. Spec. Top. Accel. Beams 2007, 10, 034801. [Google Scholar] [CrossRef]
- Couprie, M.E. New generation of light sources: Present and future. J. Electron Spectrosc. Relat. Phenom. 2014, 196, 3–13. [Google Scholar] [CrossRef] [Green Version]
- Grüner, F.; Becker, S.; Schramm, U.; Eichner, T.; Fuchs, M.; Weingartner, R.; Habs, D.; Meyer-ter-Vehn, J.; Geissler, M.; Ferrario, M.; et al. Design considerations for table-top, laser-based VUV and X-ray free electron lasers. Appl. Phys. B 2007, 86, 431–435. [Google Scholar] [CrossRef] [Green Version]
- Nakajima, K. Compact X-ray sources: Towards a table-top free-electron laser. Nat. Phys. 2008, 4, 92–93. [Google Scholar] [CrossRef]
- Steinke, S.; Van Tilborg, J.; Benedetti, C.; Geddes, C.G.R.; Schroeder, C.B.; Daniels, J.; Swanson, K.K.; Gonsalves, A.J.; Nakamura, K.; Matlis, N.H.; et al. Multistage coupling of independent laser-plasma accelerators. Nature 2016, 530, 190–193. [Google Scholar] [CrossRef]
- Hosokai, T.; Zhidkov, A.; Yamazaki, A.; Mizuta, Y.; Uesaka, M.; Kodama, R. Electron energy boosting in laser-wake-field acceleration with external magnetic field B 1 T and laser prepulses. Appl. Phys. Lett. 2010, 96, 121501. [Google Scholar] [CrossRef]
- Fuchs, M.; Weingartner, R.; Popp, A.; Major, Z.; Becker, S.; Osterhoff, J.; Cortrie, I.; Zeitler, B.; Hörlein, R.; Tsakiris, G.D.; et al. Laser-driven soft-X-ray undulator source. Nat. Phys. 2009, 5, 826–829. [Google Scholar] [CrossRef] [Green Version]
- Anania, M.P.; Clark, D.; van der Geer, S.B.; de Loos, M.J.; Isaac, R.; Reitsma, A.J.W.; Welsh, G.H.; Wiggins, S.M.; Jaroszynski, D.A. Transport of ultra-short electron bunches in a free-electron laser driven by a laser-plasma wakefield accelerator. In Conference on Harnessing Relativistic Plasma Waves as Novel Radiation Sources from Terahertz to X-rays and Beyond; International Society for Optics and Photonics: Bellingham, WA, USA, 2009; p. 735916. [Google Scholar]
- Lambert, G.; Corde, S.; Phuoc, K.T.; Malka, V.; Ismail, A.B.; Benveniste, E.; Specka, A.; Labat, M.; Loulergue, A.; Bachelard, R.; et al. Progress on the generation of undulator radiation in the UV from a plasma-based electron beam. In Proceedings of the 34th International Free-Electron Laser Conference, Nara, Japan, 16–31 August 2012; p. 2. [Google Scholar]
- André, T.; Andriyash, I.A.; Loulergue, A.; Labat, M.; Roussel, E.; Ghaith, A.; Khojoyan, M.; Thaury, C.; Valléau, M.; Briquez, F.; et al. Control of laser plasma accelerated electrons for light sources. Nat. Commun. 2018, 9, 1334. [Google Scholar] [CrossRef]
- Floettmann, K. Some basic features of the beam emittance. Phys. Rev. Spec. Top. Accel. Beams 2003, 6, 034202. [Google Scholar] [CrossRef] [Green Version]
- Floettmann, K. Erratum: Some basic features of the beam emittance. Phys. Rev. Spec. Top. Accel. Beams 2003, 6, 079901. [Google Scholar] [CrossRef]
- Antici, P.; Bacci, A.; Benedetti, C.; Chiadroni, E.; Ferrario, M.; Rossi, A.R.; Lancia, L.; Migliorati, M.; Mostacci, A.; Palumbo, L.; et al. Laser-driven electron beamlines generated by coupling laser-plasma sources with conventional transport systems. J. Appl. Phys. 2012, 112, 044902. [Google Scholar] [CrossRef]
- Migliorati, M.; Bacci, A.; Benedetti, C.; Chiadroni, E.; Ferrario, M.; Mostacci, A.; Palumbo, L.; Rossi, A.R.; Serafini, L.; Antici, P.; et al. Intrinsic normalized emittance growth in laser-driven electron accelerators. Phys. Rev. Spec. Top. Accel. Beams 2013, 16, 011302. [Google Scholar] [CrossRef]
- Floettmann, K.; Paramonov, V.V. Beam dynamics in transverse deflecting rf structures. Phys. Rev. Spec. Top. Accel. Beams 2014, 17, 024001. [Google Scholar] [CrossRef]
- Dornmair, I.I.; Dornmair, K. Floettmann, and AR Maier. Phys. Rev. Spec. Top. Accel. Beams 2015, 18, 041302. [Google Scholar] [CrossRef]
- Li, X.; Chancé, A.; Nghiem, P.A.P. Preserving emittance by matching out and matching in plasma wakefield acceleration stage. Phys. Rev. Accel. Beams 2019, 22, 021304. [Google Scholar] [CrossRef] [Green Version]
- Mihara, T. A Super Strong Permanent Magnet Quadrupole for the Final Focus in a Linear Collider; Technical Report; SLAC National Accelerator Lab.: Menlo Park, CA, USA, 2018. [Google Scholar]
- Ghaith, A.; Kitegi, C.; André, T.; Valléau, M.; Marteau, F.; Vétéran, J.; Blache, F.; Benabderrahmane, C.; Cosson, O.; Forest, F.; et al. Tunable high gradient quadrupoles for a laser plasma acceleration based FEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2018, 909, 290–293. [Google Scholar] [CrossRef]
- Hosokai, T.; Kando, M.; Dewa, H.; Kotaki, H.; Kondo, S.; Hasegawa, N.; Nakajima, K.; Horioka, K. Optical guidance of terrawatt laser pulses by the implosion phase of a fast Z-pinch discharge in a gas-filled capillary. Opt. Lett. 2000, 25, 10–12. [Google Scholar] [CrossRef]
- Thaury, C.; Guillaume, E.; Döpp, A.; Lehe, R.; Lifschitz, A.; Phuoc, K.T.; Gautier, J.; Goddet, J.-P.; Tafzi, A.; Flacco, A.; et al. Demonstration of relativistic electron beam focusing by a laser-plasma lens. Nat. Commun. 2015, 6, 6860. [Google Scholar] [CrossRef]
- Van Tilborg, J.; Steinke, S.; Geddes, C.; Matlis, N.; Shaw, B.; Gonsalves, A.; Huijts, J.; Nakamura, K.; Daniels, J.; Schroeder, C.; et al. Active plasma lensing for relativistic laser-plasma-accelerated electron beams. Phys. Rev. Lett. 2015, 115, 184802. [Google Scholar] [CrossRef]
- Pompili, R.; Anania, M.; Bellaveglia, M.; Biagioni, A.; Bini, S.; Bisesto, F.; Brentegani, E.; Castorina, G.; Chiadroni, E.; Cianchi, A.; et al. Experimental characterization of active plasma lensing for electron beams. Appl. Phys. Lett. 2017, 110, 104101. [Google Scholar] [CrossRef]
- Van Tilborg, J.; Barber, S.; Benedetti, C.; Schroeder, C.; Isono, F.; Tsai, H.E.; Geddes, C.; Leemans, W. Comparative study of active plasma lenses in high-quality electron accelerator transport lines. Phys. Plasmas 2018, 25, 056702. [Google Scholar] [CrossRef] [Green Version]
- Lim, J.; Frigola, P.; Travish, G.; Rosenzweig, J.; Anderson, S.; Brown, W.; Jacob, J.; Robbins, C.; Tremaine, A. Adjustable, short focal length permanent-magnet quadrupole based electron beam final focus system. Phys. Rev. Spec. Top. Accel. Beams 2005, 8, 072401. [Google Scholar] [CrossRef] [Green Version]
- Marteau, F.; Ghaith, A.; N’Gotta, P.; Benabderrahmane, C.; Valléau, M.; Kitegi, C.; Loulergue, A.; Vétéran, J.; Sebdaoui, M.; André, T.; et al. Variable high gradient permanent magnet quadrupole (QUAPEVA). Appl. Phys. Lett. 2017, 111, 253503. [Google Scholar] [CrossRef]
- Ghaith, A.; Kitegi, C.; Andre, T.; Valleau, M.; Marteau, F.; Veteran, J.; Blache, F.; Benabderrahmane, C.; Cosson, O.; Forest, F.; et al. Tunable High Gradient Quadrupoles For A Laser Plasma Acceleration Based FEL. arXiv 2017, arXiv:1712.03857. [Google Scholar] [CrossRef]
- Mihara, T.; Iwashita, Y.; Kumada, M.; Evgeny, A.; Spencer, C.M. Super strong permanent magnet quadrupole for a linear collider. IEEE Trans. Appl. Supercond. 2004, 14, 469–472. [Google Scholar] [CrossRef]
- Iwashita, Y.; Mihara, T.; Antokhin, E.; Kumada, M.; Aoki, M. Permanent magnet quadrupole for final focus for linear collider. In Proceedings of the IEEE 2003 Particle Accelerator Conference, Portland, OR, USA, 12–16 May 2003; Volume 4, pp. 2198–2200. [Google Scholar]
- Cesar, D.; Maxson, J.; Musumeci, P.; Sun, Y.; Harrison, J.; Frigola, P.; O’Shea, F.; To, H.; Alesini, D.; Li, R. Demonstration of single-shot picosecond time-resolved MeV electron imaging using a compact permanent magnet quadrupole based lens. Phys. Rev. Lett. 2016, 117, 024801. [Google Scholar] [CrossRef]
- Zhou, Z.; Tang, C.; Rui, T.; Du, Y.C.; Li, F.; Gai, W.; Huang, W. Compact High Energy Electron Radiography System Based on Permanent Magnet Quadrupole. In Proceedings of the 8th International Particle Accelerator Conference (IPAC’17), Copenhagen, Denmark, 14–19 May 2017. [Google Scholar]
- Eichner, T.; Grüner, F.; Becker, S.; Fuchs, M.; Habs, D.; Weingartner, R.; Schramm, U.; Backe, H.; Kunz, P.; Lauth, W. Miniature magnetic devices for laser-based, table-top free-electron lasers. Phys. Rev. Spec. Top. Accel. Beams 2007, 10, 082401. [Google Scholar] [CrossRef] [Green Version]
- Mihara, T.; Iwashita, Y.; Kumada, M.; Spencer, C.M. Variable permanent magnet quadrupole. IEEE Trans. Appl. Supercond. 2006, 16, 224–227. [Google Scholar] [CrossRef]
- Iwashita, Y.; Mihara, T.; Kyoto, U.; Uji, K.; Kumada, J.M.; NIRS, C.; Spencer, J.C. Super strong adjustable permanent magnet quadrupole for the final focus in a linear collider. In Proceedings of the 10th European Particle Accelerator Conference (EPAC), Edinburgh, UK, 26–30 Junuary 2006; Volume 6, pp. 2550–2552. [Google Scholar]
- Gottschalk, S.C.; Taylor, D.J. Magnetic and engineering analysis of an adjustable strength permanent magnet quadrupole. In Proceedings of the 2005 IEEE Particle Accelerator Conference, Knoxville, TN, USA, 16–20 May 2005; pp. 2122–2124. [Google Scholar]
- Couprie, M.; Labat, M.; Evain, C.; Marteau, F.; Briquez, F.; Khojoyan, M.; Benabderrahmane, C.; Chapuis, L.; Hubert, N.; Bourassin-Bouchet, C.; et al. An application of laser–plasma acceleration: Towards a free-electron laser amplification. Plasma Phys. Control. Fusion 2016, 58, 034020. [Google Scholar] [CrossRef]
- Easton, M.J.; Li, H.; Lu, Y.; Zhu, J.; Pfister, P.D. Permanent-magnet quadrupoles for an interdigital H-mode drift tube linear accelerator: Optimization code and adjustable magnet design. Phys. Rev. Accel. Beams 2018, 21, 122401. [Google Scholar] [CrossRef]
- Rosenzweig, J.; Chen, P. Beam optics of a self-focusing plasma lens. Phys. Rev. D 1989, 39, 2039–2045. [Google Scholar] [CrossRef] [Green Version]
- Lejeune, C.; Aubert, J. Emittance and brightness: Definitions and measurements. Appl. Charged Part. Opt. 1980, 1, 159–259. [Google Scholar]
- Mostacci, A.; Bellaveglia, M.; Chiadroni, E.; Cianchi, A.; Ferrario, M.; Filippetto, D.; Gatti, G.; Ronsivalle, C. Chromatic effects in quadrupole scan emittance measurements. Phys. Rev. Spec. Top. Accel. Beams 2012, 15, 082802. [Google Scholar] [CrossRef]
- Labat, M.; Loulergue, L.; André, T.; Andriyash, I.; Ghaith, A.; Khojoyan, M.; Marteau, F.; Valleau, M.; Briquez, F.; Benabderrahmane, C. Robustness of a plasma acceleration based Free Electron Laser. arXiv 2018, arXiv:1806.10848. [Google Scholar] [CrossRef]
- Khojoyan, M.; Briquez, F.; Labat, M.; Loulergue, A.; Marcouillé, O.; Marteau, F.; Sharma, G.; Couprie, M.E. Transport studies of LPA electron beam towards the FEL amplification at COXINEL. Nucl. Instrum. Methods Phys. Res. Sect. A 2016, 829, 260–264. [Google Scholar] [CrossRef] [Green Version]
- André, T.; Andriyash, I.; Basset, C.; Benabderrahmane, C.; Berteaud, P.; Bielawski, S.; Bonnin, S.; Bouvet, F.; Briquez, F.; Cassinari, L.; et al. First electron beam measurements on coxinel. In Proceedings of the 7th International Particle Accelerator Conference (IPAC’16), Busan, Korea, 8–13 May 2016; pp. 712–715. [Google Scholar]
- Bonifacio, R.; Pellegrini, C.; Narducci, L.M. Collective instabilities and high-gain regime in a free electron laser. Opt. Commun. 1984, 50, 373–378. [Google Scholar] [CrossRef] [Green Version]
- Maier, A.; Meseck, A.; Reiche, S.; Schroeder, C.; Seggebrock, T.; Gruener, F. Demonstration scheme for a laser-plasma-driven free-electron laser. Phys. Rev. X 2012, 2, 031019. [Google Scholar] [CrossRef]
- Couprie, M.E.; Loulergue, A.; Labat, M.; Lehe, R.; Malka, V. Towards a free electron laser based on laser plasma accelerators. J. Phys. B 2014, 47, 234001. [Google Scholar] [CrossRef]
- Loulergue, A.; Labat, M.; Evain, C.; Benabderrahmane, C.; Malka, V.; Couprie, M.E. Beam manipulation for compact laser wakefield accelerator based free-electron lasers. New J. Phys. 2015, 17, 023028. [Google Scholar] [CrossRef]
- Huang, Z.; Ding, Y.; Schroeder, C.B. Compact X-ray free-electron laser from a laser-plasma accelerator using a transverse-gradient undulator. Phys. Rev. Lett. 2012, 109, 204801. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, T.; Wang, D.; Huang, Z. Compact beam transport system for free-electron lasers driven by a laser plasma accelerator. Phys. Rev. Accel. Beams 2017, 20, 020701. [Google Scholar] [CrossRef]
- Dattoli, G.; Renieri, A.; Torre, A. Lectures on the Free Electron Laser Theory and Related Topics; World Scientific: Singapore, 1993. [Google Scholar]
- Madur, A. Contribution à la Métrologie Magnétique des Multipôles D’accélérateurs: Les Quadrupôles du Synchroton SOLEIL; Vandoeuvre-les-Nancy, Institut National Polytechnique de Lorraine: Nancy, France, 2006. [Google Scholar]
- Lebec, G.; Chavanne, J.; Penel, C. Stretched-wire Measurements of Small Bore Multipole Magnets. Phys. Rev. Spec. Top. Accel. Beams 2012, 15. [Google Scholar] [CrossRef]
- Payet, J.; Chance, A.; Loulergue, A.; Ropert, A.; Meot, F.; Filhol, J.M.; Laclare, J.-L.; Farvacque, L.; Aniel, T. BETA Code; CEA: Saclay, France, 2001. [Google Scholar]
- Flöttmann, K.; Astra, A. A Space Charge Tracking Algorithm. ASTRA, 2007. Available online: http://www.desy.de/~mpyflo/ (accessed on 1 February 2019).
- Borland, M. Elegant: A Flexible SDDS-Compliant Code for Accelerator Simulation; Technical Report; Argonne National Lab.: Lemont, IL, USA, 2000.
- Agapov, I.; Geloni, G.; Tomin, S.; Zagorodnov, I. OCELOT: A software framework for synchrotron light source and FEL studies. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2014, 768, 151–156. [Google Scholar] [CrossRef]

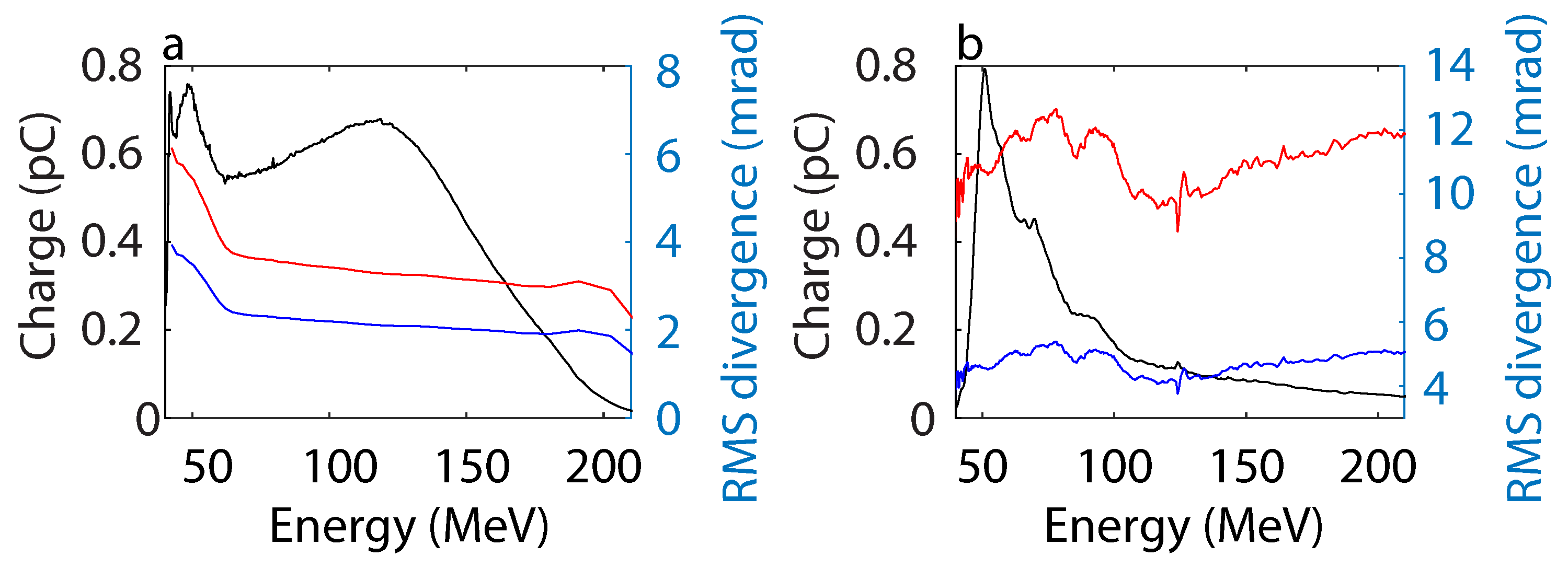
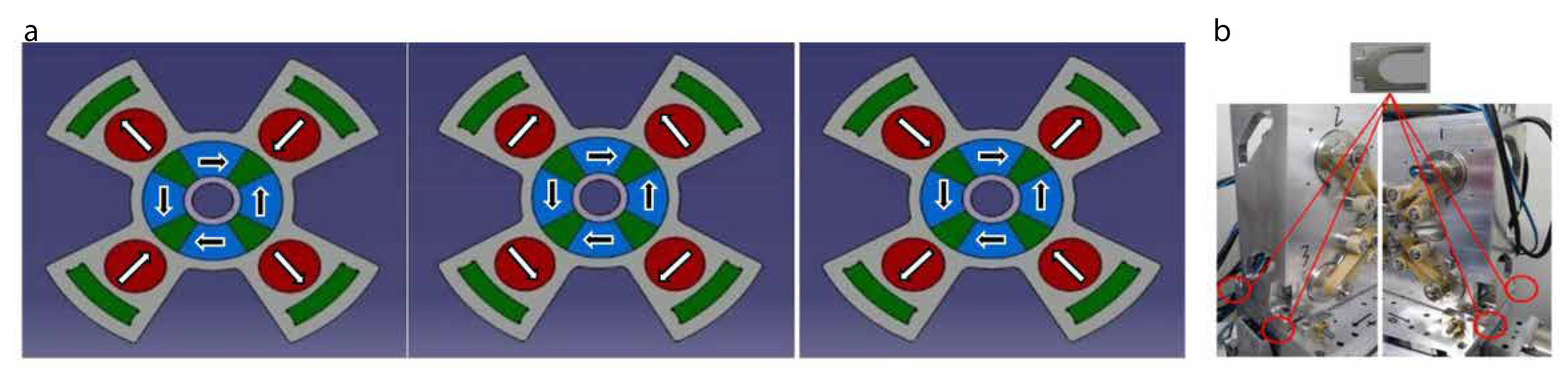
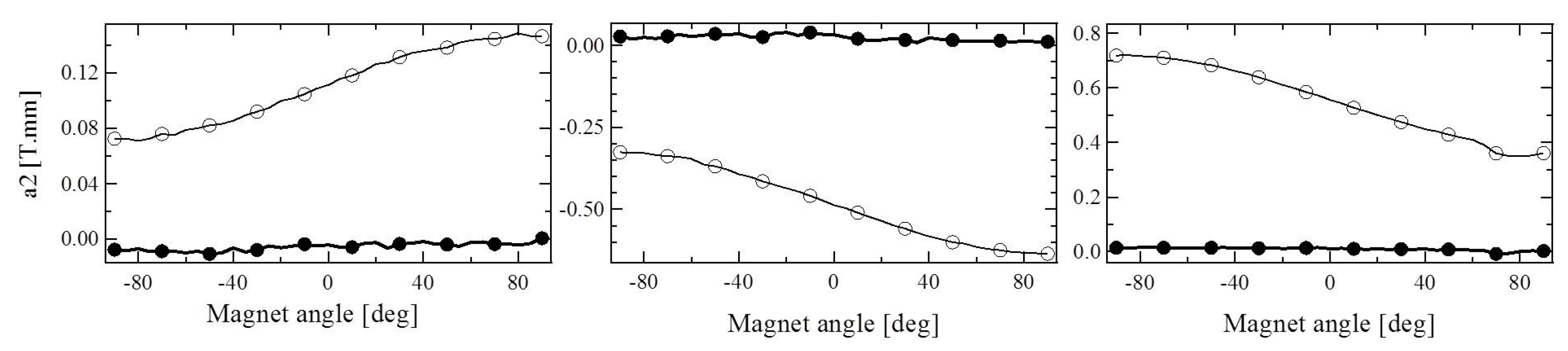
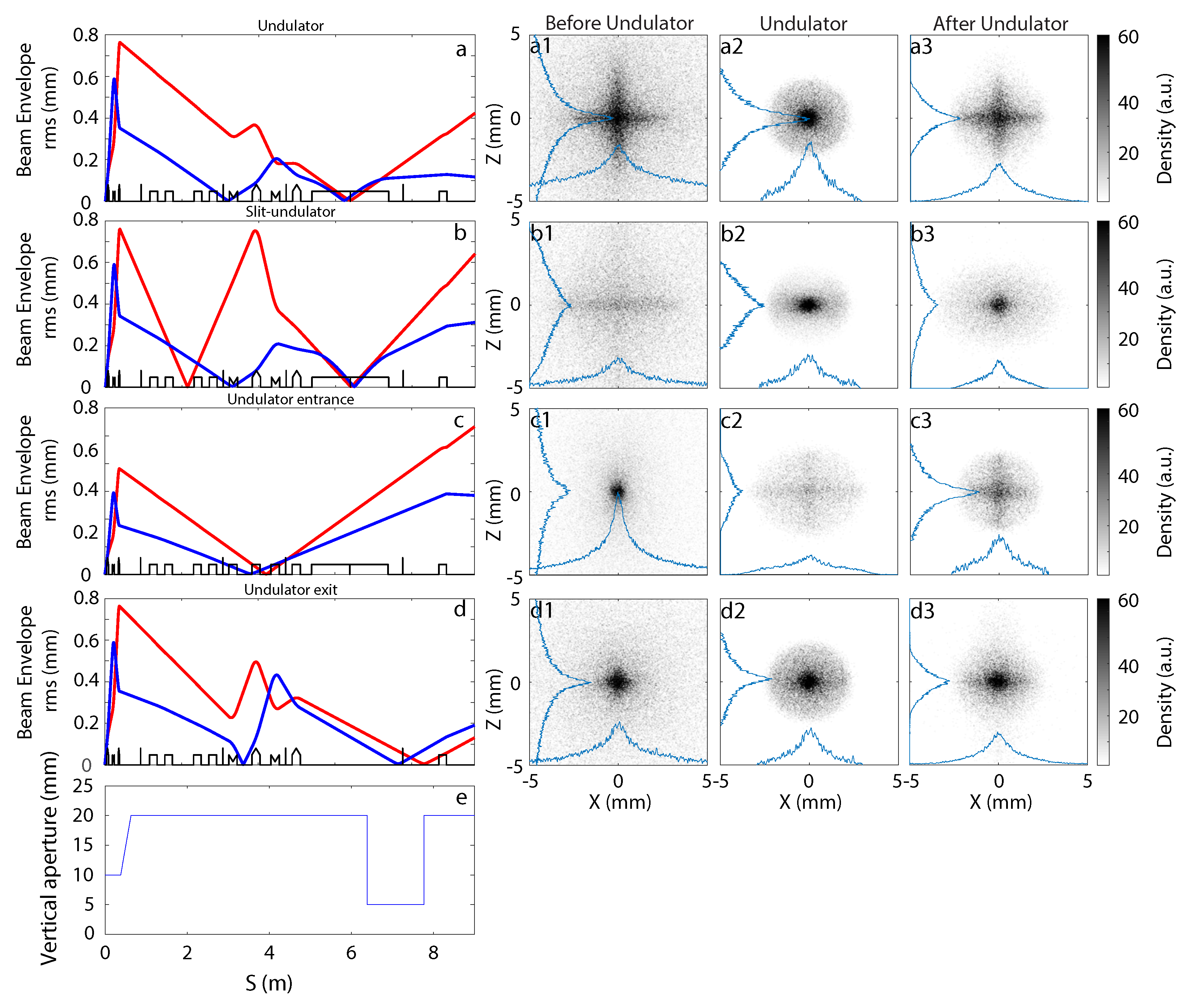
| Initial Parameter | Symbol | Value | Unit | |
|---|---|---|---|---|
| Case | Low Divergence Case | High Divergence Case | ||
| Emittance | 0.2 | 0.2 | mm.mrad | |
| Ratio | 1.56 | 2.35 | ||
| Vertical divergence at 176 MeV | 2.0 | 5 | mrad (RMS) | |
| Horizontal divergence at 176 MeV | 3.12 | 11.75 | mrad (RMS) | |
| Bunch longitudinal length | m (RMS) | |||
| Charge | Q | 100 | 100 | pC |
| Number of macro particles | N | |||
| High Skew Term Case | Low Skew Term Case | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Magnetic Length | a2 | a6 | b2 | b6 | Angle (mrad) | a2 | a6 | b2 | b6 | Angle (mrad) |
| 26 mm | 0.073 | −0.003 | 10.951 | 0.192 | 3.3 | −0.007 | −0.01 | 10.947 | 0.186 | −0.3 |
| 40.7 mm | −0.325 | −0.017 | 17.475 | 0.326 | −9 | 0.027 | −0 | 17.448 | 0.329 | 0.7 |
| 44.7 mm | 0.362 | 0.012 | −19.181 | −0.363 | −9.4 | 0.003 | −0.004 | −19.148 | −0.357 | 0.05 |
| Optics | QUAPEVAs (QAP) | Chicane Dipoles | Electro-Magnetic Quadrupoles (QEM) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Unit Component | Gradient T/m | B Field T | Gap mm | Current A | r56 mm | Gradient T/m | |||||
| QAP1 | QAP2 | QAP3 | QEM1 | QEM2 | QEM3 | QEM4 | |||||
| “Undulator” | +102.68 | −101.14 | +89.10 | 0.24 | 25 | 46.5 | 4.3 | −0.52 | 0.85 | −1.23 | 0.46 |
| “Slit-undulator” | +104.1 | −103 | +96.43 | 0.24 | 25 | 46.5 | 4.3 | −0.01 | 4.70 | −4.40 | 0.29 |
| “Undulator entrance” | +102.8 | −101.2 | +90.26 | 0.24 | 25 | 46.5 | 4.3 | 0 | 0 | 0 | 0 |
| “Undulator exit” | +102.41 | −100.74 | +89.78 | 0.24 | 25 | 46.5 | 4.3 | −1.74 | 1.26 | −1.36 | 0.41 |
| Skew Term | Low Divergence Beam | High Divergence Beam | ||||
|---|---|---|---|---|---|---|
| (mm) | (mm) | Beam Center Counts (a.u.) | (mm) | (mm) | Beam Center Counts (a.u.) | |
| Undulator entrance (“undulator-entrance” optics) | ||||||
| = 0 | 0.52 | 0.80 | 1.00 | 0.63 | 1.08 | 0.20 |
| Low | 0.51 | 0.72 | 1.16 | 0.60 | 1.20 | 0.20 |
| High | 0.63 | 1.01 | 0.78 | 0.98 | 1.98 | 0.14 |
| Undulator exit (“undulator-exit” optics) | ||||||
| = 0 | 0.95 | 0.73 | 0.76 | 0.92 | 0.99 | 0.17 |
| Low | 0.95 | 0.76 | 0.75 | 0.85 | 1.01 | 0.14 |
| High | 1.22 | 0.83 | 0.50 | 1.31 | 0.97 | 0.11 |
| Total Beam | 176 MeV “Monochromatic” Beam | |||||||
|---|---|---|---|---|---|---|---|---|
| Skew Term | (mm.mrad) | (mm.mrad) | Charge % | Brightness (A/(mm.mrad))2 | (mm.mrad) | (mm.mrad) | Charge % | Brightness (A/(mm.mrad))2 |
| = 0 | 103 | 30 | 2.82 | 6.20 | 0.48 | 0.24 | 0.3 | 3.6 |
| Low case | 119 | 35 | 2.79 | 4.56 | 4.83 | 1.14 | 0.3 | 7.0 |
| High case | 328 | 234 | 1.37 | 0.14 | 8.29 | 6.56 | 0.3 | 7.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oumbarek Espinos, D.; Ghaith, A.; André, T.; Kitégi, C.; Sebdaoui, M.; Loulergue, A.; Marteau, F.; Blache, F.; Valléau, M.; Labat, M.; et al. Skew Quadrupole Effect of Laser Plasma Electron Beam Transport. Appl. Sci. 2019, 9, 2447. https://doi.org/10.3390/app9122447
Oumbarek Espinos D, Ghaith A, André T, Kitégi C, Sebdaoui M, Loulergue A, Marteau F, Blache F, Valléau M, Labat M, et al. Skew Quadrupole Effect of Laser Plasma Electron Beam Transport. Applied Sciences. 2019; 9(12):2447. https://doi.org/10.3390/app9122447
Chicago/Turabian StyleOumbarek Espinos, Driss, Amin Ghaith, Thomas André, Charles Kitégi, Mourad Sebdaoui, Alexandre Loulergue, Fabrice Marteau, Frédéric Blache, Mathieu Valléau, Marie Labat, and et al. 2019. "Skew Quadrupole Effect of Laser Plasma Electron Beam Transport" Applied Sciences 9, no. 12: 2447. https://doi.org/10.3390/app9122447
APA StyleOumbarek Espinos, D., Ghaith, A., André, T., Kitégi, C., Sebdaoui, M., Loulergue, A., Marteau, F., Blache, F., Valléau, M., Labat, M., Lestrade, A., Roussel, E., Thaury, C., Corde, S., Lambert, G., Kononenko, O., Goddet, J.-P., Tafzi, A., Malka, V., & Couprie, M.-E. (2019). Skew Quadrupole Effect of Laser Plasma Electron Beam Transport. Applied Sciences, 9(12), 2447. https://doi.org/10.3390/app9122447





