Fatigue Assessment of Prestressed Concrete Slab-Between-Girder Bridges
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
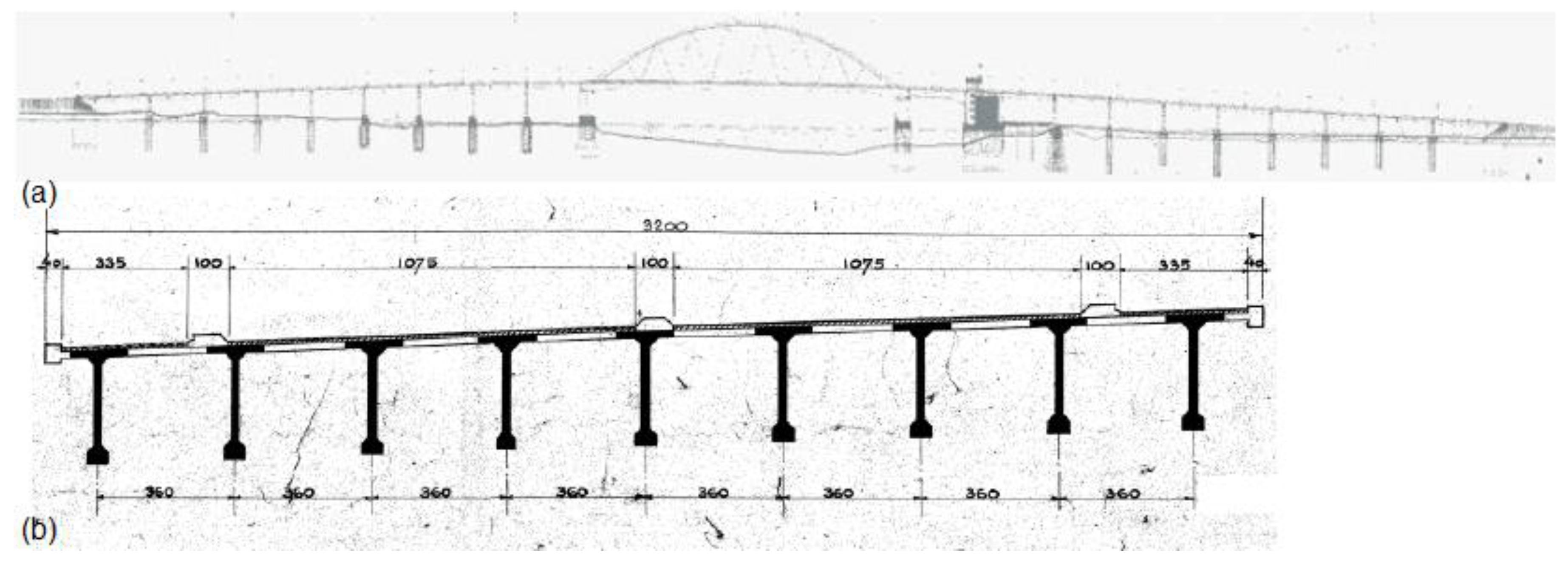
2.1. Description of Case Study Bridge
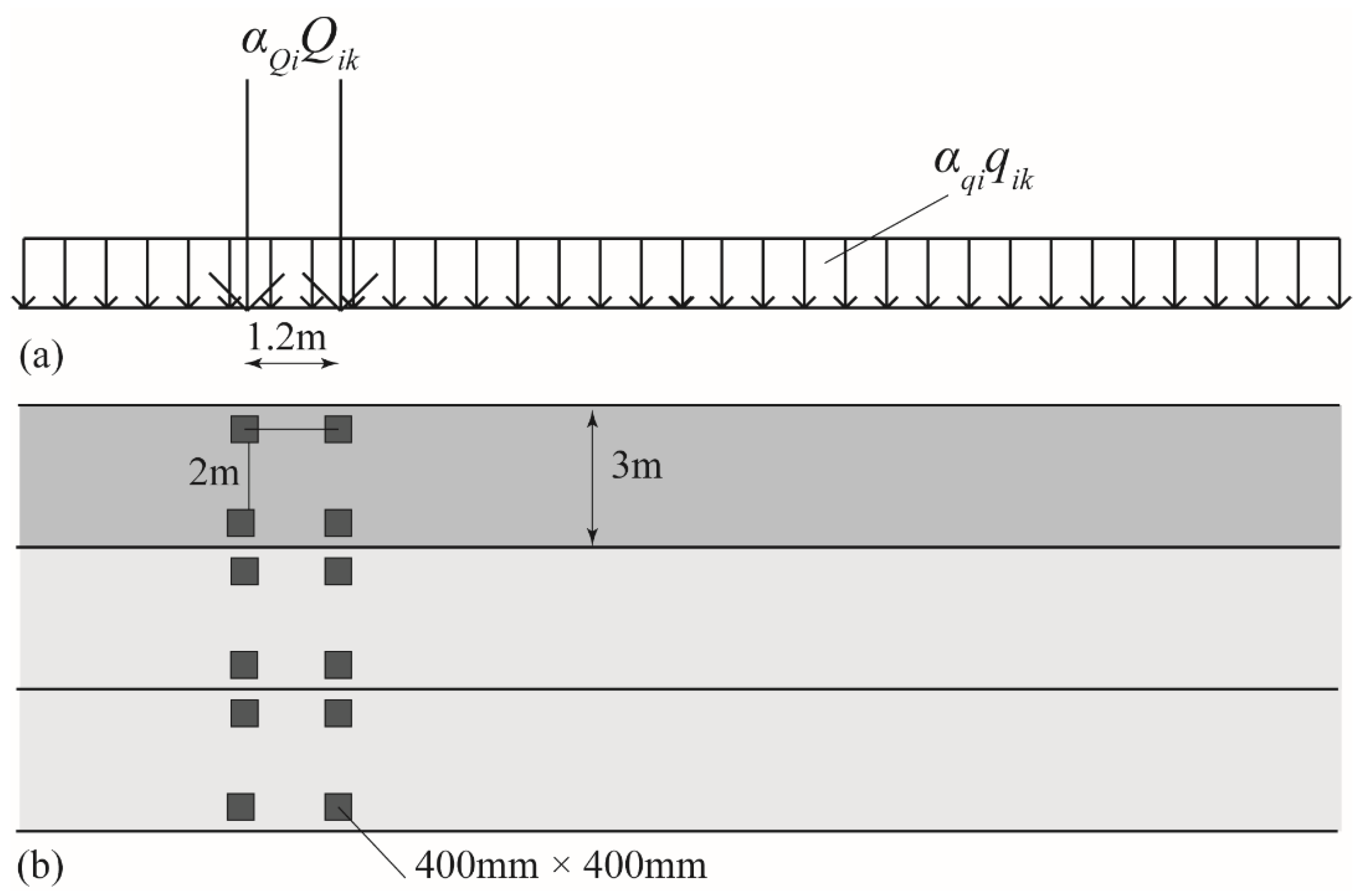
2.2. Live Load Models
2.3. Description of Experiments
3. Results
3.1. Results of the Experiments
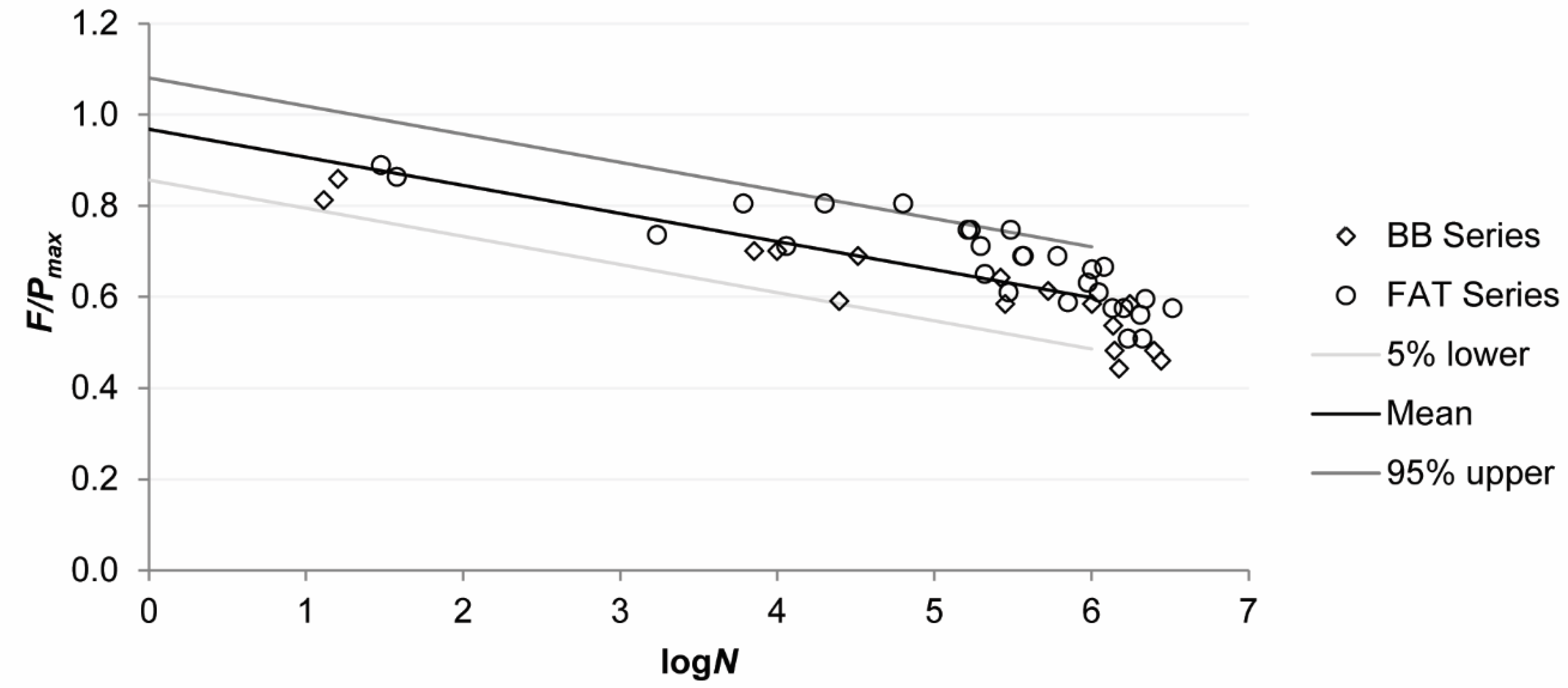
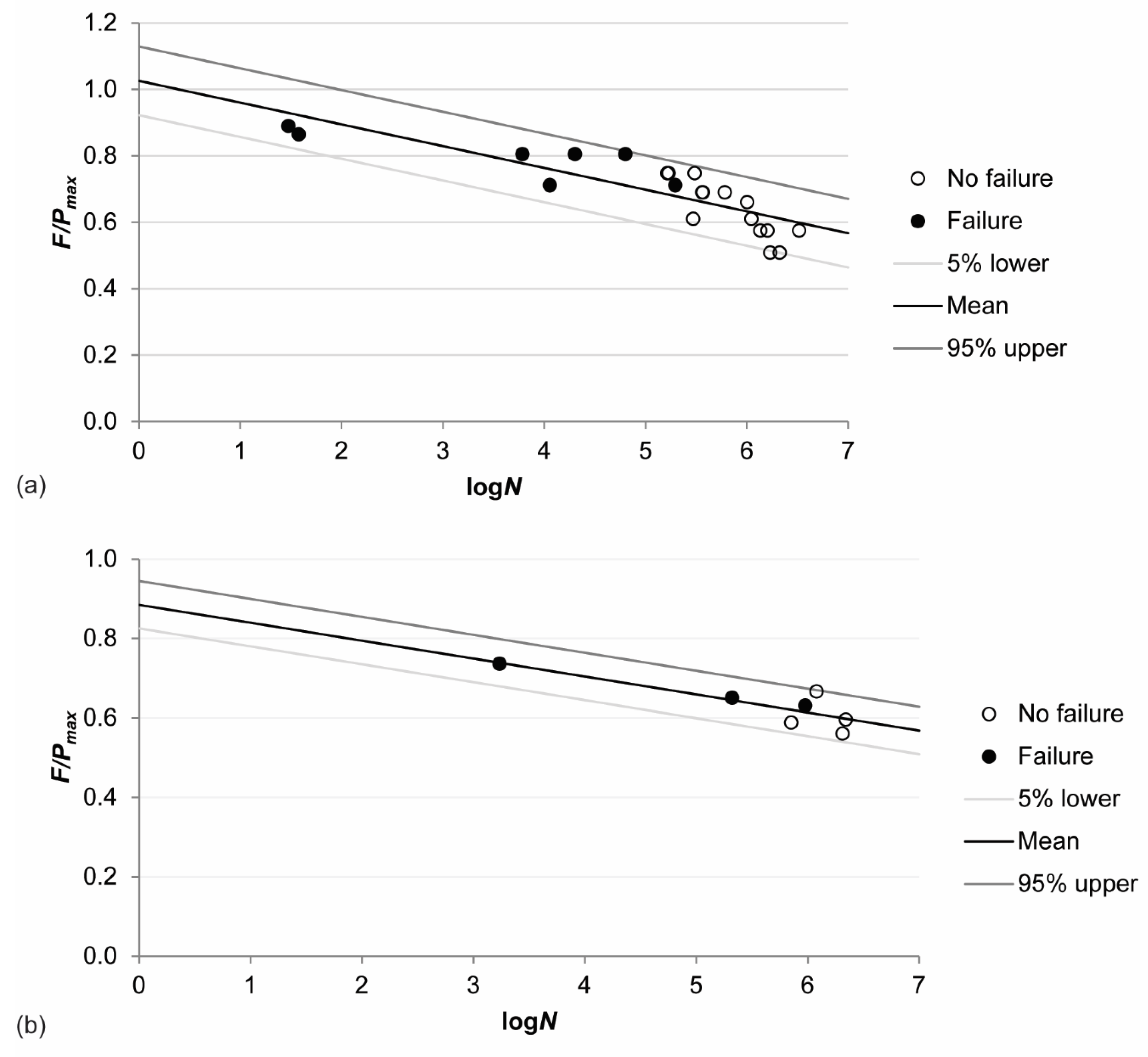
3.2. Resulting Wöhler Curve
3.3. Assessment of the Case Study Bridge for Punching
- The laboratory setup was a 1:2 scale of the case study bridge, resulting in a factor 22;
- Considering scaling laws, a scale factor of 1.2 [13] had to be included in the capacity;
- The partial factor derived from the experiments γT had to be included.
3.4. Assessment of Case Study Bridge for Fatigue
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
List of Notations
| b | width |
| c | concrete cover |
| d | average effective depth |
| dl | effective depth to the longitudinal reinforcement |
| dt | effective depth to the transverse reinforcement |
| fck,cube | characteristic cube concrete compressive strength |
| fcm,cube | average cube concrete compressive strength |
| fck | characteristic cylinder concrete compressive strength |
| fcm | average cylinder concrete compressive strength |
| h | height |
| k | size effect factor |
| k1 | factor on effect of axial stresses |
| l | length |
| lspan | span length |
| qik | distributed lane load |
| u | punching perimeter length |
| vmin | lower bound of shear capacity |
| vR,c | mean capacity for punching shear |
| vRd,c | design capacity for punching shear |
| As,l | longitudinal reinforcement area |
| Asp | area of prestressing steel |
| As,t | transverse reinforcement area |
| Au | area within punching perimeter |
| BRd | design capacity derived from statistical results of experiments |
| COV | coefficient of variation |
| CRd,c | constant in punching capacity equation |
| DL | dead load |
| DW | superimposed dead load |
| F | applied load |
| Feq | equivalent load |
| Fmin | lower limit of the load as used in the fatigue tests |
| LL | live load |
| Mdist,1wheel | bending moment caused by distributed lane load for influence area of one wheel load |
| Mdist,2wheel | bending moment caused by distributed lane load for influence area of two wheel loads |
| N | number of cycles |
| Pmax | load at failure |
| Qik | axle load of design tandem |
| S | load ratio |
| Schar | characteristic value of load ratio (5% lower bound Wöhler curve) |
| U | load combination |
| UC | Unity Check |
| VBB | average capacity of deck of Van Brienenoord Bridge based on experiments |
| VBB,d | design capacity of deck of Van Brienenoord Bridge based on experiments |
| VR,c | mean value of the punching shear capacity |
| VRd,c | design value of the punching shear capacity |
| VEd | design value of punching shear demand |
| Vexp | experimental punching capacity |
| α | factor that considered effect of experiments |
| αqi | factor on distributed lane loads |
| αQi | factor on design tandem |
| β | reliability index |
| γT | partial factor derived from experiments |
| μ | mean value of experimental results |
| ρavg | average reinforcement ratio |
| ρl | longitudinal reinforcement ratio |
| ρt | transverse reinforcement ratio |
| σcp | average axial stress |
| σcx | longitudinal axial stress |
| σcy | transverse axial stress |
References
- CEN. Eurocode 1: Actions on Structures—Part 2: Traffic Loads on Bridges; Nen-en 1991-2:2003; Comité Européen de Normalisation: Brussels, Belgium, 2003; p. 168. [Google Scholar]
- Code Committee 351001. NEN 6720 Technical Foundations for Building Codes, Concrete Provisions Tgb 1990—Structural Requirements and Calculation Methods (VBC 1995); Civil Engineering Center for Research and Regulation, Dutch Normalization Institute: Delft, The Netherlands, 1995; p. 245. (In Dutch) [Google Scholar]
- CEN. Eurocode 2: Design of Concrete Structures—Part 1-1 General Rules and Rules for Buildings; NEN-EN 1992-1-1:2005; Comité Européen de Normalisation: Brussels, Belgium, 2005; p. 229. [Google Scholar]
- Lantsoght, E.O.L.; van der Veen, C.; de Boer, A.; Walraven, J.C. Recommendations for the shear assessment of reinforced concrete slab bridges from experiments. Struct. Eng. Int. 2013, 23, 418–426. [Google Scholar] [CrossRef]
- Amir, S.; Van der Veen, C.; Walraven, J.C.; de Boer, A. Experiments on punching shear behavior of prestressed concrete bridge decks. ACI Struct. J. 2016, 113, 627–636. [Google Scholar] [CrossRef]
- Teworte, F.; Herbrand, M.; Hegger, J. Structural assessment of concrete bridges in germany—Shear resistance under static and fatigue loading. Struct. Eng. Int. 2015, 25, 266–274. [Google Scholar] [CrossRef]
- Bagge, N.; Nilimaa, J.; Puurula, A.; Täljsten, B.; Blanksvärd, T.; Sas, G.; Elfgren, L.; Carolin, A. Full-scale tests to failure compared to assessments—Three concrete bridges. In High Tech Concrete: Where Technology and Engineering Meet; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Brühwiler, E.; Vogel, T.; Lang, T.; Luechinger, P. Swiss standards for existing structures. Struct. Eng. Int. 2012, 22, 275–280. [Google Scholar] [CrossRef]
- Kong, J.S.; Frangopol, D.M. Probabilistic optimization of aging structures considering maintenance and failure costs. J. Struct. Eng. ASCE 2005, 131, 600–616. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Sabatino, S.; Dong, Y. Bridge life-cycle performance and cost: Analysis, prediction, optimization and decision making. In Maintenance, Monitoring, Safety, Risk and Resilience of Bridges and Bridge Networks; Bittencourt, T.N., Frangopol, D.M., Beck, A., Eds.; CRC Press: Foz do Iguacu, Brazil, 2016; pp. 2–20. [Google Scholar]
- Vergoossen, R.; Naaktgeboren, M.; Hart, M.; De Boer, A.; Van Vugt, E. Quick scan on shear in existing slab type viaducts. In Proceedings of the International IABSE Conference, Assessment, Upgrading and Refurbishment of Infrastructures, Rotterdam, The Netherlands, 6–8 May 2013; p. 8. [Google Scholar]
- Lantsoght, E.O.L.; van der Veen, C.; de Boer, A.; Walraven, J. Using eurocodes and aashto for assessing shear in slab bridges. Proc. Inst. Civ. Eng. Bridge Eng. 2016, 169, 285–297. [Google Scholar] [CrossRef]
- Amir, S. Compressive Membrane Action in Prestressed Concrete Deck Slabs. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2014. [Google Scholar]
- Collings, D.; Sagaseta, J. A review of arching and compressive membrane action in concrete bridges. Inst. Civ. Eng. Bridge Eng. 2015, 169, 271–284. [Google Scholar] [CrossRef]
- Eyre, J.R. Direct assessment of safe strengths of rc slabs under membrane action. J. Struct. Eng. ASCE 1997, 123, 1331–1338. [Google Scholar] [CrossRef]
- Highways Agency. Corrections within Design Manual for Roads and Bridges, Use of Compressive Membrane Action in Bridge Decks; Highways Agency: London, UK, 2007; pp. 35–51.
- Kirkpatrick, J.; Rankin, G.I.B.; Long, A.E. The influence of compressive membrane action on the serviceability of beam and slab bridge decks. Struct. Eng. 1986, 64B, 6–9. [Google Scholar]
- Kuang, J.S.; Morley, C.T. A plasticity model for punching shear of laterally restrained slabs with compressive membrane action. Int. J. Mech. Sci. 1993, 35, 371–385. [Google Scholar] [CrossRef]
- Tong, P.Y.; Batchelor, B.V. Compressive membrane enhancement in two-way bridge slabs. SP 30-12 1972, 30, 271–286. [Google Scholar]
- Hewitt, B.E.; de Batchelor, B.V. Punching shear strenght of restrained slabs. J. Struct. Div. 1975, 101, 1837–1853. [Google Scholar]
- Lantsoght, E.O.L.; Van der Veen, C.; Koekkoek, R.T.; Sliedrecht, H. Capacity of prestressed concrete bridge decks under fatigue loading. In Proceedings of the FIB Symposium, Cracow, Poland, 27–29 May 2019. [Google Scholar]
- Bennett, E.W.; Muir, S.E.S.J. Some fatigue tests of high-strength concrete in axial compression. Mag. Concr. Res. 1967, 19, 113–117. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L.; van der Veen, C.; de Boer, A. Proposal for the fatigue strength of concrete under cycles of compression. Constr. Build. Mater. 2016, 107, 138–156. [Google Scholar] [CrossRef]
- Isojeh, B.; El-Zeghayar, M.; Vecchio, F.J. Fatigue resistance of steel fiber-reinforced concrete deep beams. ACI Struct. J. 2017, 114, 1215–1226. [Google Scholar] [CrossRef]
- Teng, S.; Ma, W.; Tan, K.H.; Kong, F.K. Fatigue tests of reinforced concrete deep beams. Struct. Eng. 1998, 76, 347–352. [Google Scholar]
- Teworte, F.; Hegger, J. Shear fatigue of prestressed concrete beams. In Proceedings of the IABSE 2011, London, UK, 23 September 2011; p. 8. [Google Scholar]
- Muller, J.F.; Dux, P.F. Fatigue of prestressed concrete beams with inclined strands. J. Struct. Eng. 1994, 120, 1122–1139. [Google Scholar] [CrossRef]
- Yuan, M.; Yan, D.; Zhong, H.; Liu, Y. Experimental investigation of high-cycle fatigue behavior for prestressed concrete box-girders. Constr. Build. Mater. 2017, 157, 424–437. [Google Scholar] [CrossRef]
- Fujiyama, C.; Gebreyouhannes, E.; Maekawa, K. Present achievement and future possibility of fatigue life simulation technology for rc bridge deck slabs. Soc. Soc. Manag. Syst. Internet J. 2008, 4. [Google Scholar]
- Harajli, M.H.; Naaman, A.E. Static and fatigue tests on partially prestressed beams. J. Struct. Eng. 1985, 111, 1602–1618. [Google Scholar] [CrossRef]
- Xin, Q.; Dou, Y.; Chen, W. Load spectrum and fatigue life computer analysis of prestressed concrete bridges. Int. J. Secur. Appl. 2015, 9, 247–266. [Google Scholar] [CrossRef]
- Rijkswaterstaat. Guidelines Assessment Bridges—Assessment of Structural Safety of an Existing Bridge at Reconstruction, Usage and Disapproval; RTD 1006:2013 1.1; Rijkswaterstaat: Utrecht, The Netherlands, 2013; p. 117. (In Dutch) [Google Scholar]
- Van der Veen, C.; Bosman, A. Vermoeiingssterkte Voorgespannen Tussenstort; Stevin Report nr. 25.5-14-06; Delft University of Technology: Delft, The Netherlands, 2014; p. 65. [Google Scholar]
- Lantsoght, E.O.L.; Van der Veen, C.; Koekkoek, R.T.; Sliedrecht, H. Fatigue testing of transversely prestressed concrete decks. ACI Struct. J. 2019, in press. [Google Scholar] [CrossRef]
- Koekkoek, R.T.; van der Veen, C.; de Boer, A. Fatigue Tests on Post-Tensioned Bridge Decks; Springer International Publishing: Cham, Switzerland, 2018; pp. 912–920. [Google Scholar]
- Koekkoek, R.T.; van der Veen, C. Measurement Report Fatigue Tests on Slabs Cast in-between Prestressed Concrete Beams; Stevin Report 25.5-17-14; Delft University of Technology: Delft, the Netherlands, 2017; p. 196. [Google Scholar]
- Lantsoght, E.O.L.; Van der Veen, C.; Koekkoek, R.T.; Sliedrecht, H. Punching capacity of prestressed concrete bridge decks under fatigue. ACI Struct. J. 2019, in press. [Google Scholar] [CrossRef]
- Castillo, E.; Fernandez-Canteli, A. A Unified Statistical Methodology for Modeling Fatigue Damage; Springer: Dordrecht, The Netherlands, 2009; p. 189. [Google Scholar]
- Hanif, A.; Usman, M.; Lu, Z.; Cheng, Y.; Li, Z. Flexural fatigue behavior of thin laminated cementitious composites incorporating cenosphere fillers. Mater. Des. 2018, 140, 267–277. [Google Scholar] [CrossRef]
- Hanif, A.; Kim, Y.; Park, C. Numerical validation of two-parameter weibull model for assessing failure fatigue lives of laminated cementitious composites—Comparative assessment of modeling approaches. Materials 2018, 12, 110. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Dong, B.; Pan, J.; Shan, Q.; Hanif, A.; Yin, W. An investigation on the behavior of a new connection for precast structures under reverse cyclic loading. Eng. Struct. 2018, 169, 131–140. [Google Scholar] [CrossRef]
- Code Committee 351001. Assessement of Structural Safety of an Existing Structure at Repair or Unfit for Use—Basic Requirements; NEN 8700:2011; Civil Center for the Execution of Research and Standard, Dutch Normalisation Institute: Delft, The Netherlands, 2011; p. 56. (In Dutch) [Google Scholar]
- CEN. Eurocode—Basis of Structural Design; NEN-EN 1990:2002; Comité Européen de Normalisation: Brussels, Belgium, 2002; p. 103. [Google Scholar]
- Walraven, J.C. Background Document for EC-2, Chapter 6.4 Punching Shear; Delft University of Technology: Delft, The Netherlands, 2002; pp. 1–16. [Google Scholar]
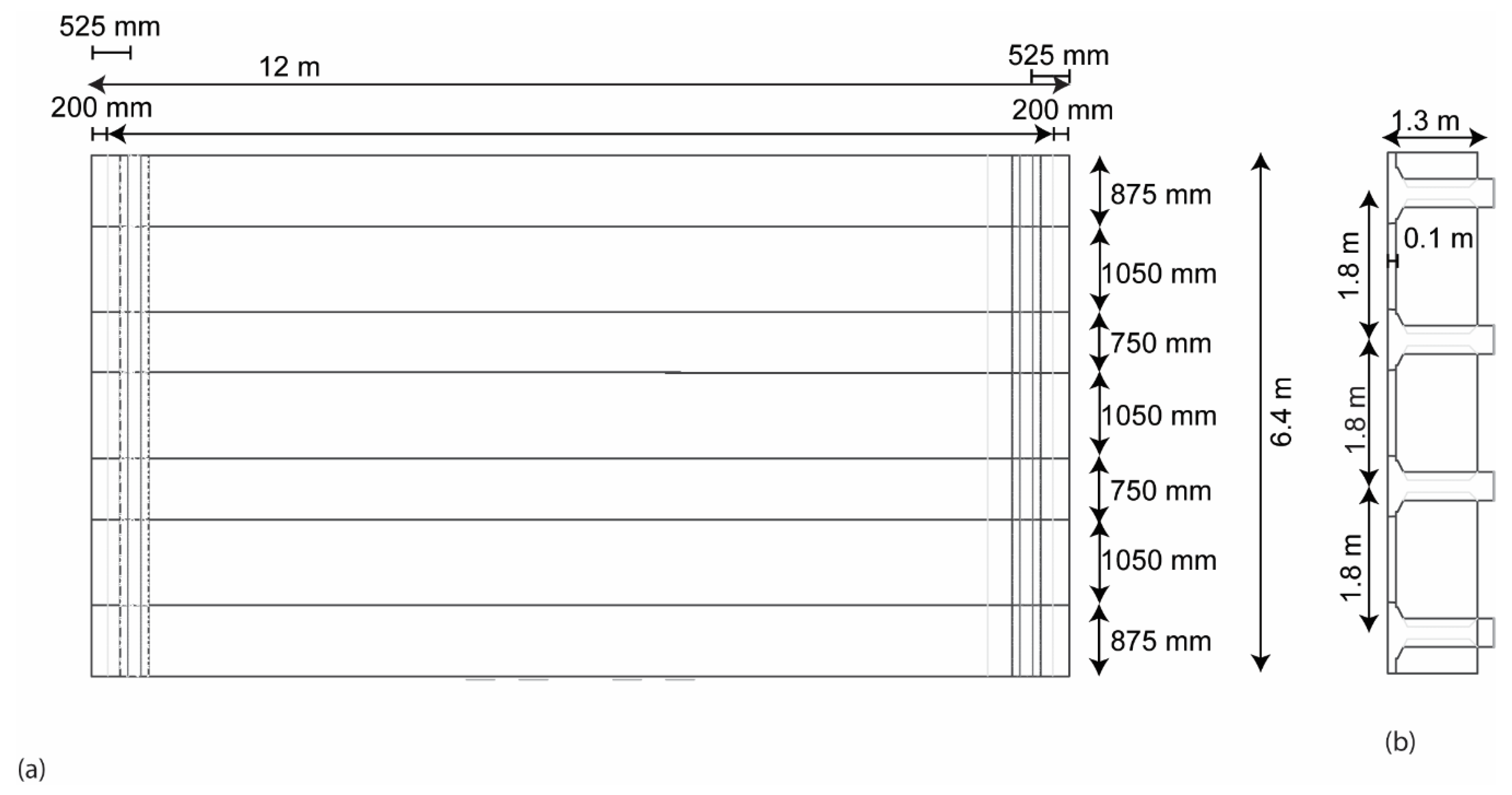
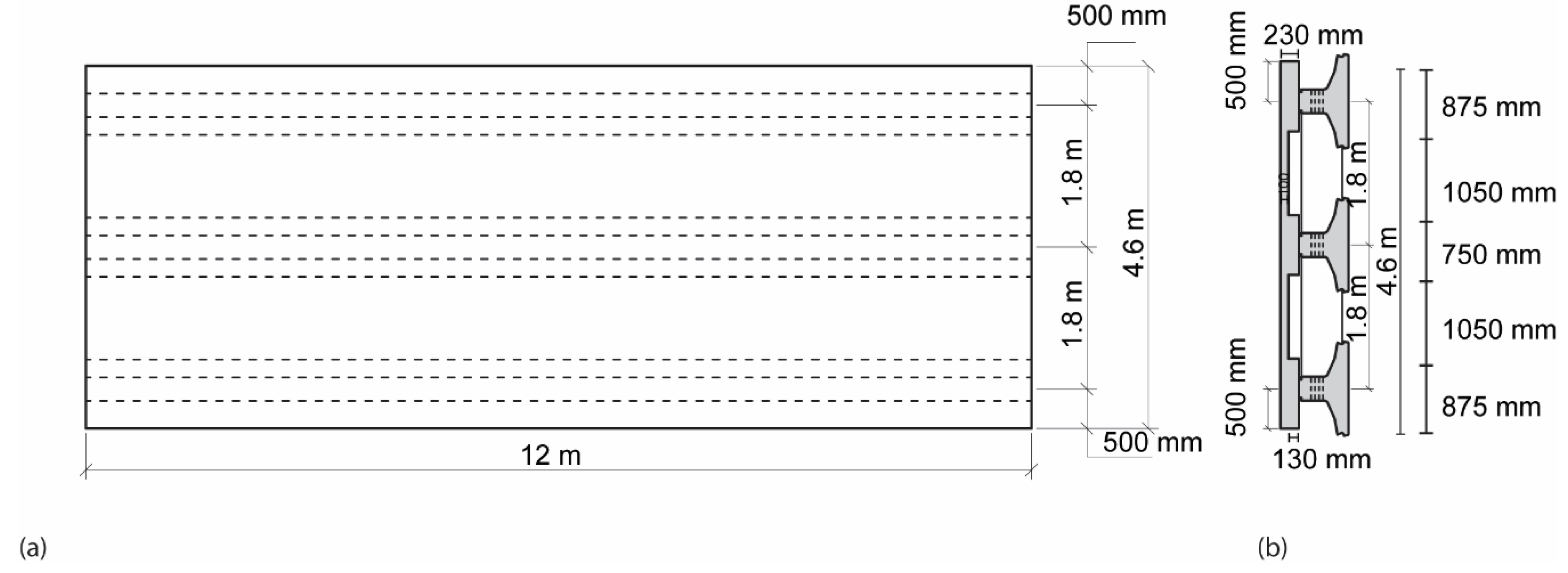

| Dimension | Value |
|---|---|
| Thickness h | 200 mm |
| Concrete cover c | 30 mm |
| Longitudinal reinforcement | ϕ8 mm–250 mm |
| Effective depth longitudinal dl | 166 mm |
| Area of longitudinal reinforcement As,l | 201.1 mm2/m |
| Longitudinal reinforcement ratio ρl | 0.12% |
| Transverse reinforcement | ϕ8 mm–200 mm |
| Effective depth transverse dt | 158 mm |
| Area of transverse reinforcement As,t | 251.3 mm2/m |
| Transverse reinforcement ratio ρt | 0.16% |
| Average effective depth d | 162 mm |
| Average reinforcement ratio ρavg | 0.14% |
| Prestressing reinforcement | 462 mm2–800 mm |
| Area of prestressing steel Asp | 0.5775 mm2/mm |
| Test Number | Size Load (mm × mm) | Pmax (kN) | Age (days) | fcm,cube (MPa) |
|---|---|---|---|---|
| BB1 | 200 × 200 | 348.7 | 96 | 80.0 |
| BB2 | 200 × 200 | 321.4 | 99 | 79.7 |
| BB7 | 200 × 200 | 345.9 | 127 | 80.8 |
| BB19 | 200 × 200 | 317.8 | 223 | 79.9 |
| FAT1S1 | 150 × 115 | 347.8 | 94 | 82.2 |
| FAT7S1 | 150 × 115 | 393.7 | 240 | 88.8 |
| FAT8S2 | 2 of 150 × 115 | 646.1 | 245 | 88.6 |
| Test Number | Setup | Size Load (mm × mm) | Wheel | F/Pmax | N | Age (days) | fcm,cube (MPa) |
|---|---|---|---|---|---|---|---|
| BB17 | 1 | 200 × 200 | S | 0.80 | 13 | 147 | 82.6 |
| BB18 | 1 | 200 × 200 | S | 0.85 | 16 | 56 | 82.6 |
| BB23 | 1 | 200 × 200 | S | 0.60 | 24,800 | 301 | 79.9 |
| BB24 | 1 | 200 × 200 | S | 0.45 | 1,500,000 | 307–326 | 79.9 |
| BB26 | 1, new | 150 × 115 | S | 0.48 | 1,405,337 | 35–59 | 70.5–76.7 |
| BB28 | 1, new | 150 × 115 | S | 0.48 | 1,500,000 | 68–97 | 76.8–77.1 |
| 0.58 | 1,000,000 | 97–113 | 77.1–77.3 | ||||
| 0.70 | 7144 | 113 | 77.3 | ||||
| BB29 | 1, new | 150 × 115 | S | 0.58 | 1,500,000 | 117–136 | 77.3–77.5 |
| 0.64 | 264,840 | 136–139 | 77.5–77.6 | ||||
| BB30 | 1, new | 150 × 115 | D | 0.58 | 100,000 | 143–144 | 77.6 |
| 0.50 | 1,400,000 | 144–162 | 77.6–77.8 | ||||
| 0.58 | 750,000 | 162–171 | 77.8–77.9 | ||||
| 0.67 | 500,000 | 171–177 | 77.9–78.0 | ||||
| 0.75 | 32,643 | 177 | 78.0 | ||||
| BB32 | 1, new | 150 × 115 | S | 0.70 | 10,000 | 184 | 78.1 |
| 0.58 | 272,548 | 185–187 | 78.1 | ||||
| FAT2D1 | 2 | 150 × 115 | S | 0.69 | 100,000 | 102–144 | 82.6–84.6 |
| 0.58 | 2,915,123 | ||||||
| 0.69 | 100,000 | ||||||
| 0.75 | 150,000 | ||||||
| 0.81 | 20,094 | ||||||
| FAT3D1 | 2 | 150 × 115 | S | 0.69 | 200,000 | 149–168 | 84.9–85.8 |
| 0.58 | 1,000,000 | ||||||
| 0.69 | 100,000 | ||||||
| 0.75 | 300,000 | ||||||
| 0.81 | 6114 | ||||||
| FAT4D1 | 2 | 150 × 115 | S | 0.58 | 1,000,000 | 169–190 | 85.8–86.8 |
| 0.69 | 200,000 | ||||||
| 0.75 | 100,000 | ||||||
| 0.81 | 63,473 | ||||||
| FAT5D1 | 2 | 150 × 115 | S | 0.71 | 10,000 | 192–217 | 91.6–89.6 |
| 0.51 | 1,000,000 | ||||||
| 0.61 | 100,000 | ||||||
| 0.66 | 1,000,000 | ||||||
| 0.71 | 1424 | ||||||
| FAT6D1 | 2 | 150 × 115 | S | 0.71 | 10,000 | 219–239 | 89.6–88.8 |
| 0.51 | 1,000,000 | ||||||
| 0.61 | 100,000 | ||||||
| 0.71 | 160,000 | ||||||
| 0.51 | 410,000 | ||||||
| 0.71 | 26,865 | ||||||
| FAT9D2 | 2 | 150 × 115 | D | 0.59 | 500,000 | 246–255 | 88.5–88.2 |
| 0.65 | 209,800 | ||||||
| FAT10D2 | 2 | 150 × 115 | D | 0.63 | 100,000 | 260–284 | 90.2–91.3 |
| 0.56 | 1,000,000 | ||||||
| 0.63 | 950,928 | ||||||
| FAT11D2 | 2 | 150 × 115 | D | 0.67 | 100,000 | 288–315 | 91.5–92.8 |
| 0.60 | 1,000,000 | ||||||
| 0.67 | 1,100,000 | ||||||
| 0.75 | 1720 | ||||||
| FAT12D1 | 2 | 150 × 115 | S | 0.89 | 30 | 318 | 85.9 |
| FAT13D1 | 2 | 150 × 115 | S | 0.86 | 38 | 319 | 85.8 |
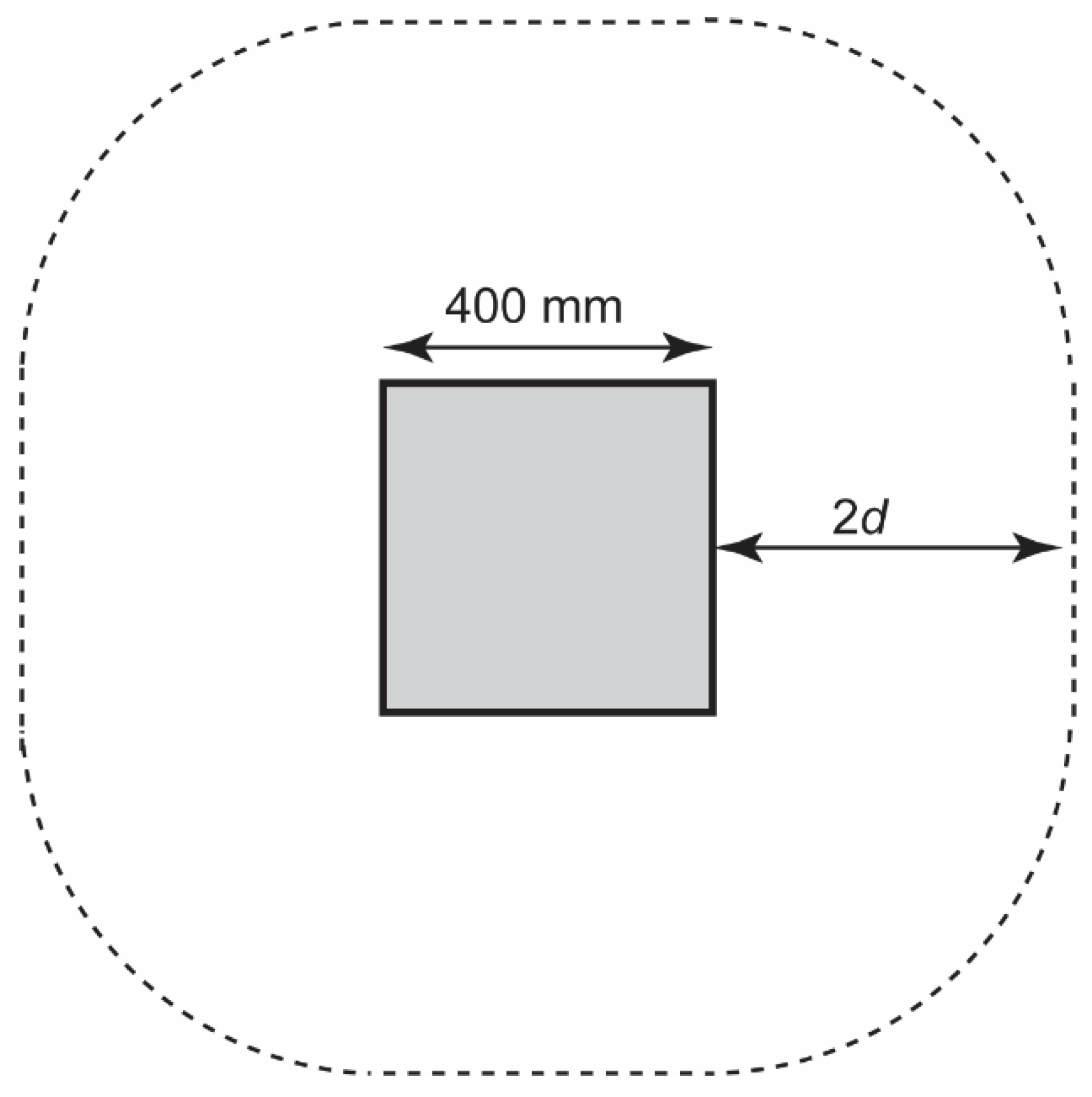
| Wheel Print | VEd (kN) | VRd,c (kN) | Unity Check |
|---|---|---|---|
| 400 mm × 400 mm | 236 | 337 | 0.70 |
| 230 mm × 300 mm | 232 | 287 | 0.81 |
| Test Number | Wheel Print (mm × mm) | Vexp (kN) | VR,c (kN) | Vexp/VR,c |
|---|---|---|---|---|
| BB1 | 200 × 200 | 348.7 | 141.9 | 2.458 |
| BB2 | 200 × 200 | 321.4 | 141.9 | 2.266 |
| BB7 | 200 × 200 | 345.9 | 141.9 | 2.438 |
| BB19 | 115 × 150 | 317.8 | 121.6 | 2.613 |
| FAT1S1 | 115 × 150 | 347.8 | 124.4 | 2.795 |
| FAT7S1 | 115 × 150 | 393.7 | 127.4 | 3.091 |
| Test Number | Vexp (kN) | VBB (kN) | VBB,d (kN) | VEd (kN) | VBB,d/VEd |
|---|---|---|---|---|---|
| BB1 | 348.7 | 1162.3 | 721.9 | 236.0 | 3.06 |
| BB2 | 321.4 | 1071.3 | 665.4 | 236.0 | 2.82 |
| BB7 | 345.9 | 1153.0 | 716.1 | 236.0 | 3.03 |
| BB19 | 317.8 | 1059.3 | 658.0 | 232.0 | 2.84 |
| FAT1S1 | 347.8 | 1159.3 | 720.1 | 232.0 | 3.10 |
| FAT7S1 | 393.7 | 1312.3 | 815.1 | 232.0 | 3.51 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lantsoght, E.O.L.; Koekkoek, R.; van der Veen, C.; Sliedrecht, H. Fatigue Assessment of Prestressed Concrete Slab-Between-Girder Bridges. Appl. Sci. 2019, 9, 2312. https://doi.org/10.3390/app9112312
Lantsoght EOL, Koekkoek R, van der Veen C, Sliedrecht H. Fatigue Assessment of Prestressed Concrete Slab-Between-Girder Bridges. Applied Sciences. 2019; 9(11):2312. https://doi.org/10.3390/app9112312
Chicago/Turabian StyleLantsoght, Eva O.L., Rutger Koekkoek, Cor van der Veen, and Henk Sliedrecht. 2019. "Fatigue Assessment of Prestressed Concrete Slab-Between-Girder Bridges" Applied Sciences 9, no. 11: 2312. https://doi.org/10.3390/app9112312
APA StyleLantsoght, E. O. L., Koekkoek, R., van der Veen, C., & Sliedrecht, H. (2019). Fatigue Assessment of Prestressed Concrete Slab-Between-Girder Bridges. Applied Sciences, 9(11), 2312. https://doi.org/10.3390/app9112312





