Refined Study on Free Vibration of a Cable with an Inertial Mass Damper
Abstract
1. Introduction
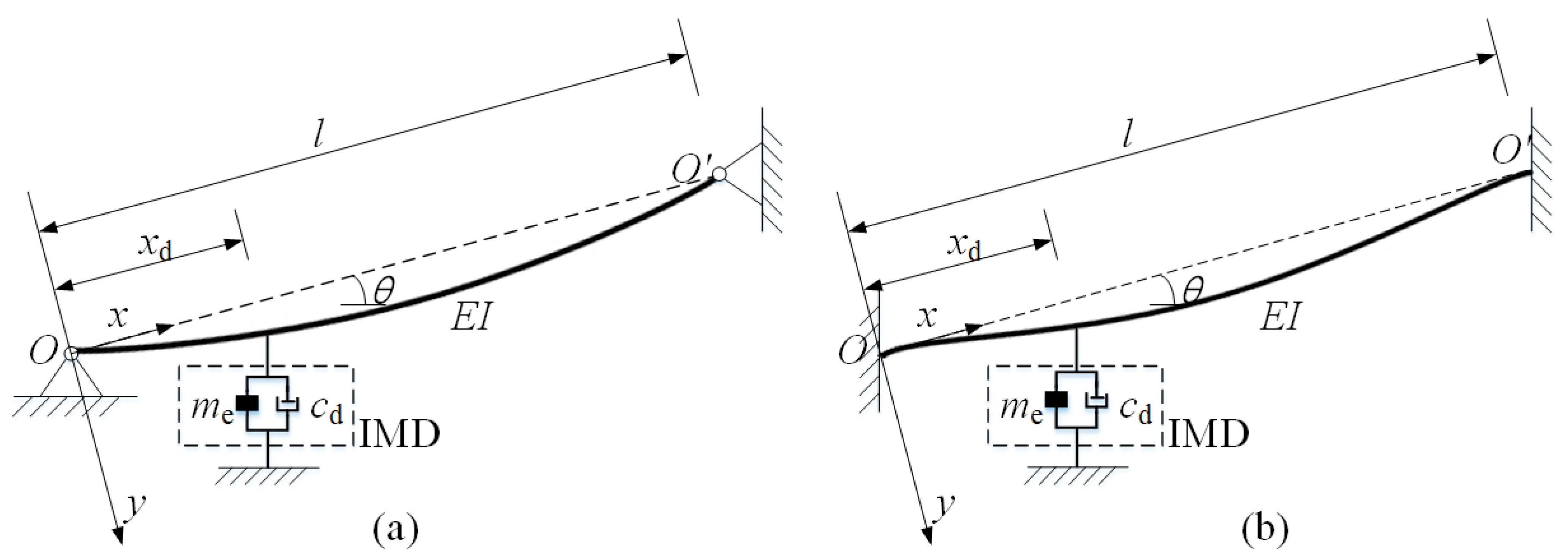
2. Formulation of the Cable-IMD System
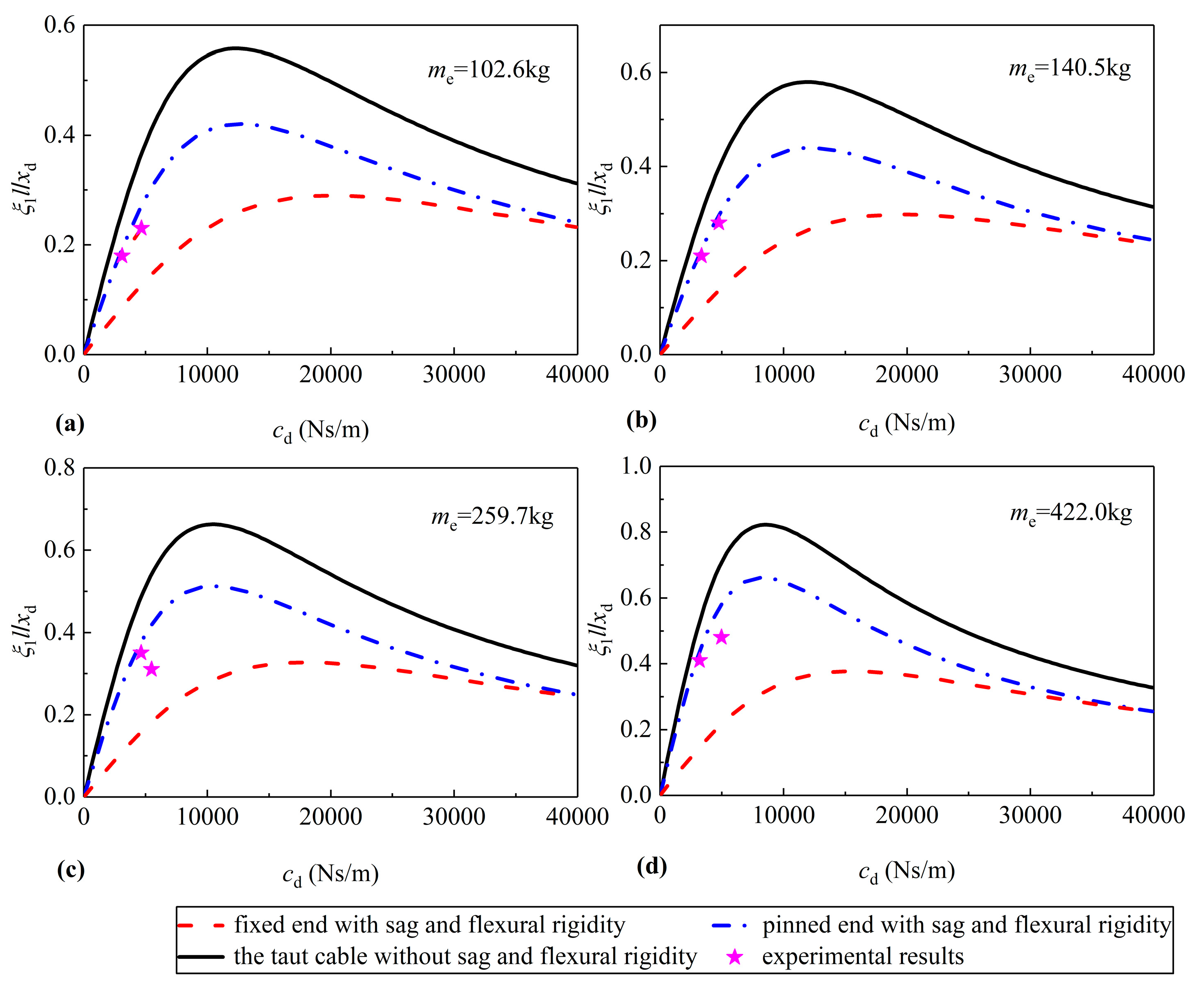
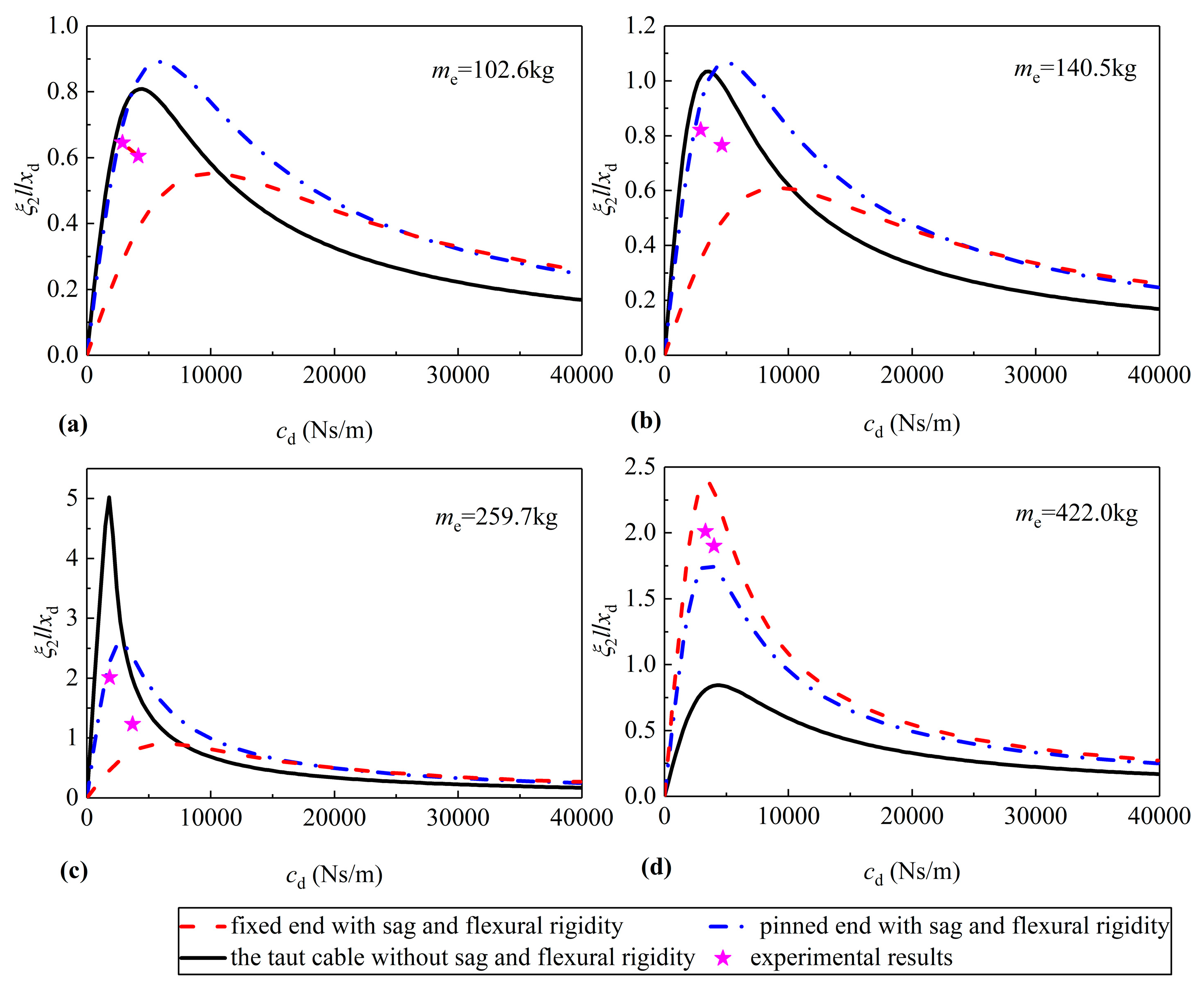
3. Verification of Theoretical Results
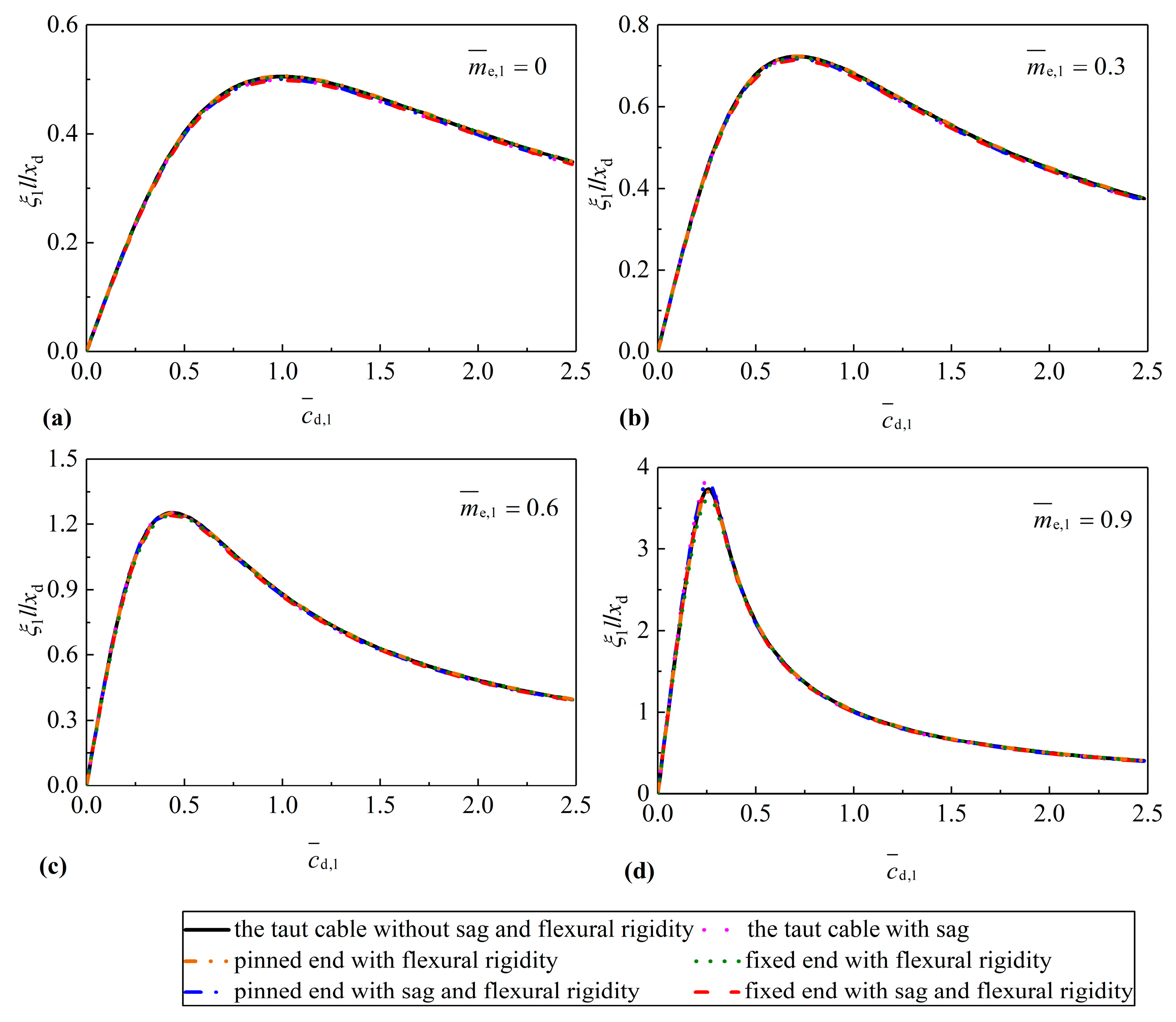
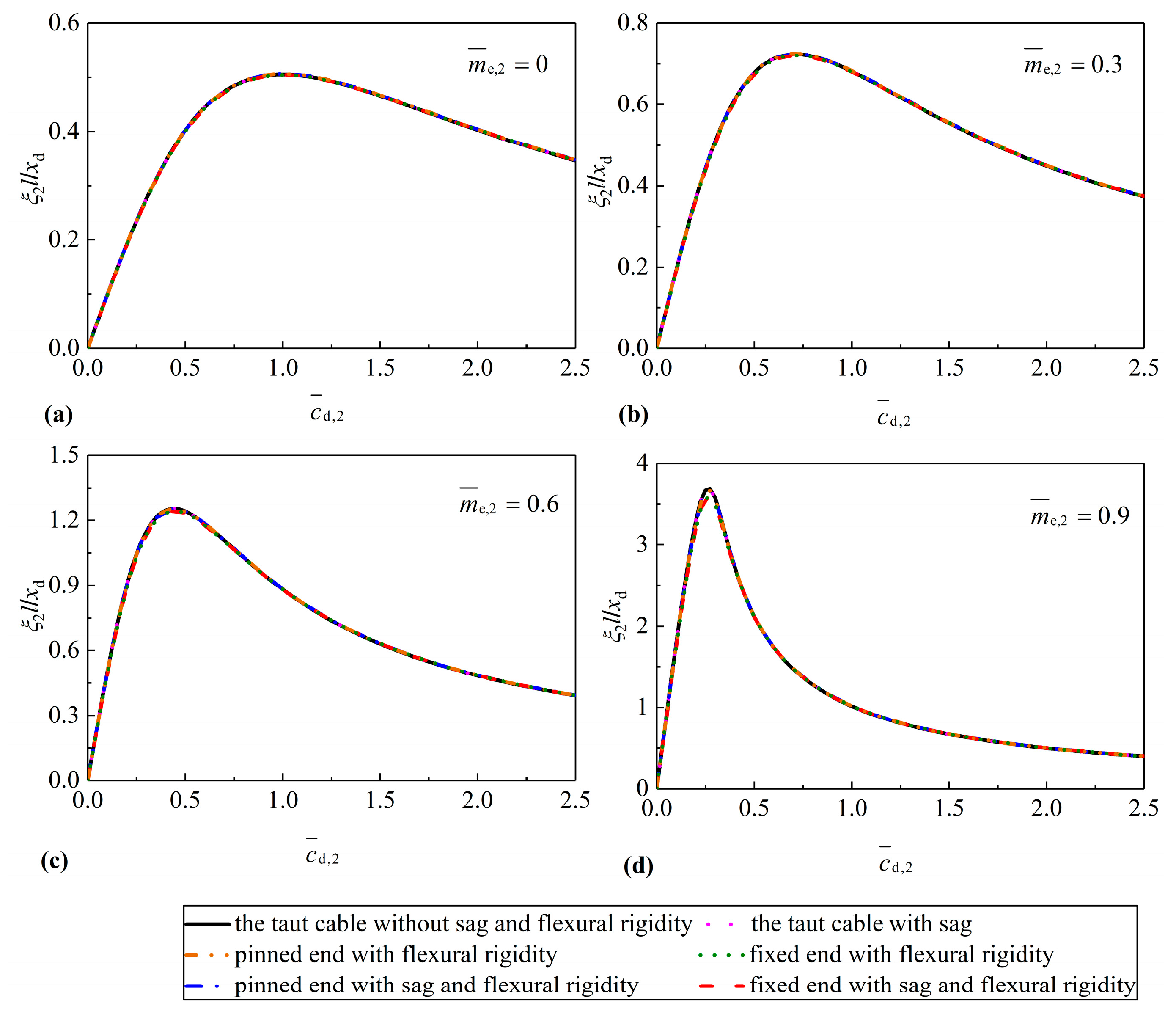
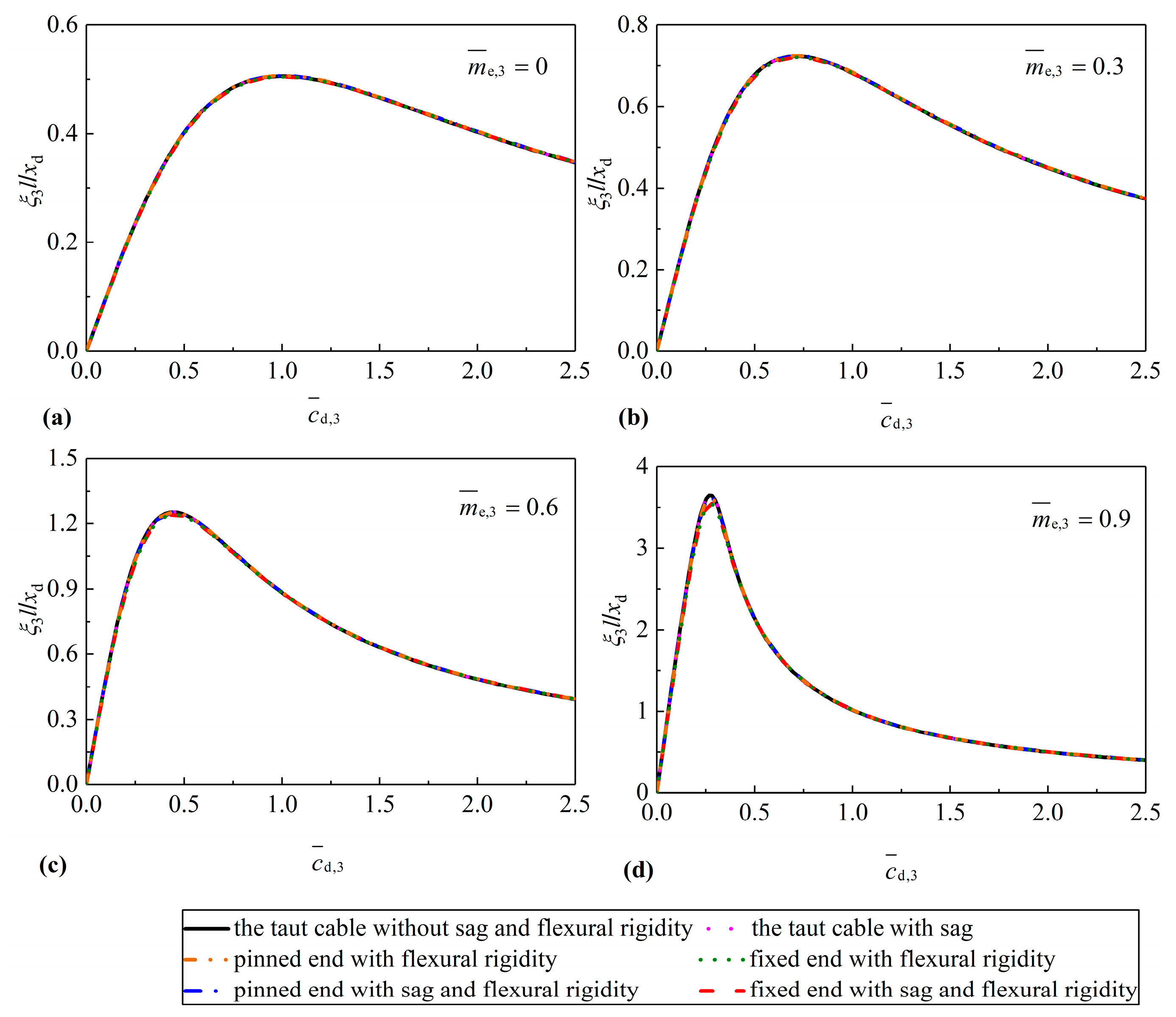
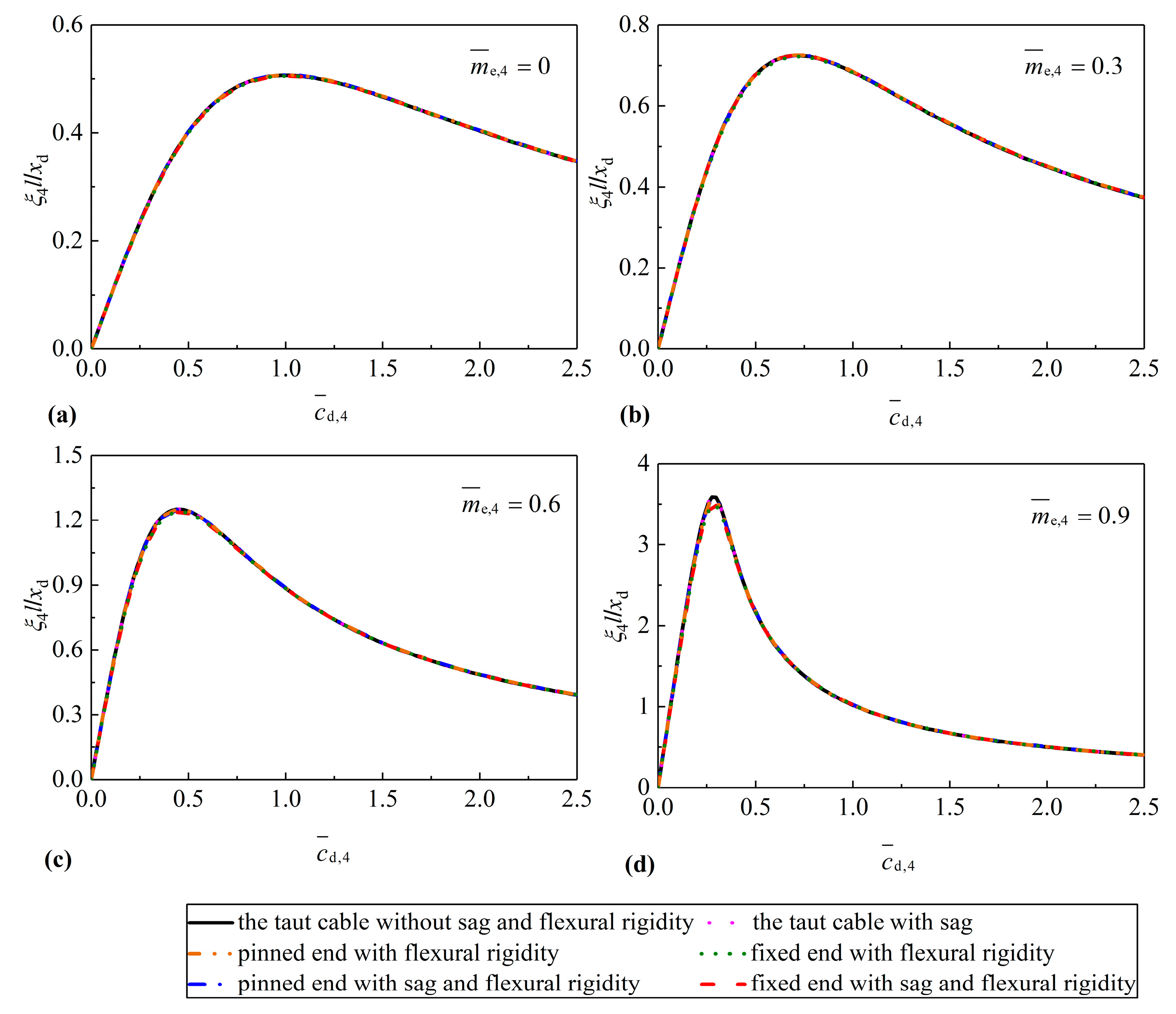
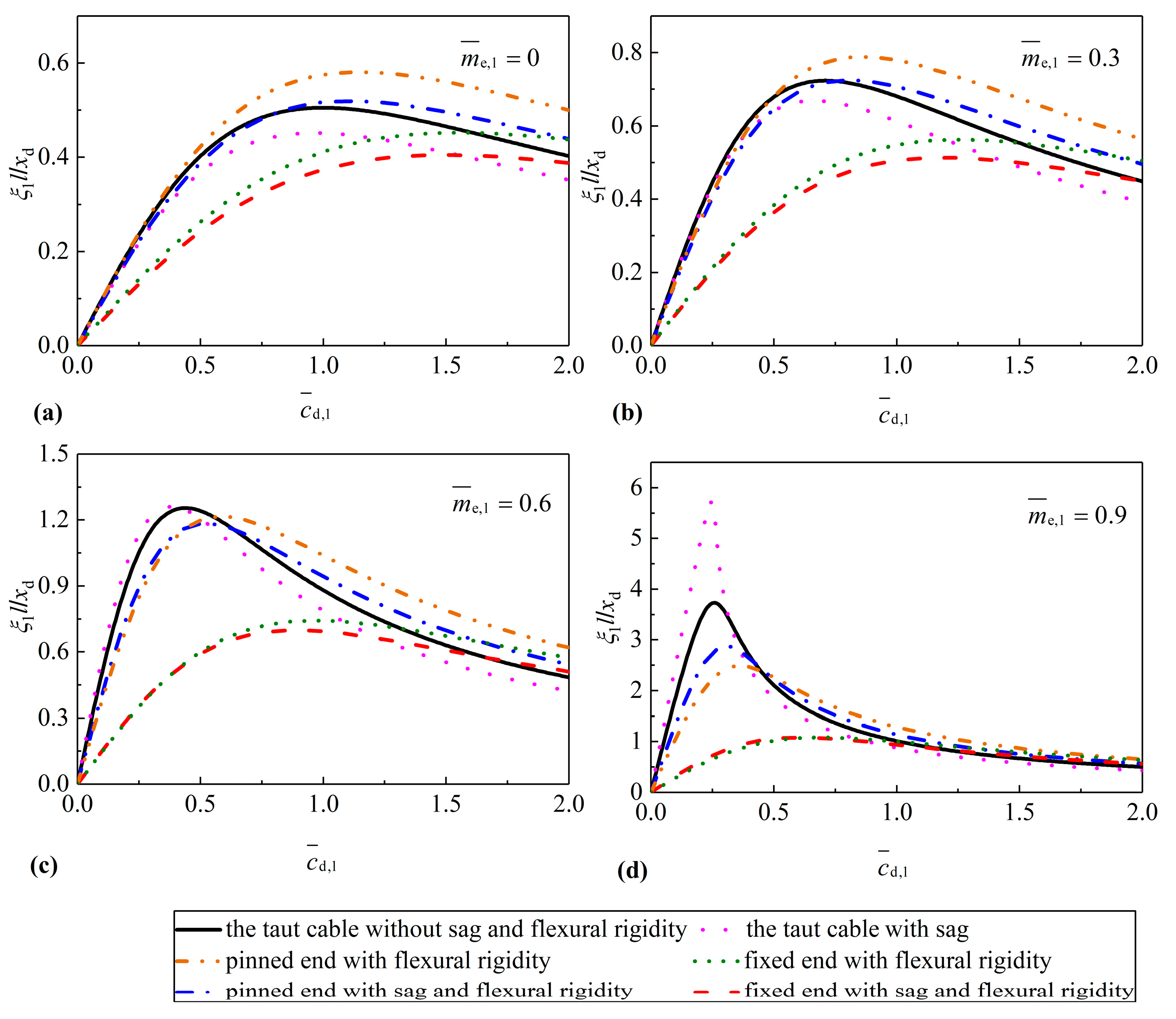
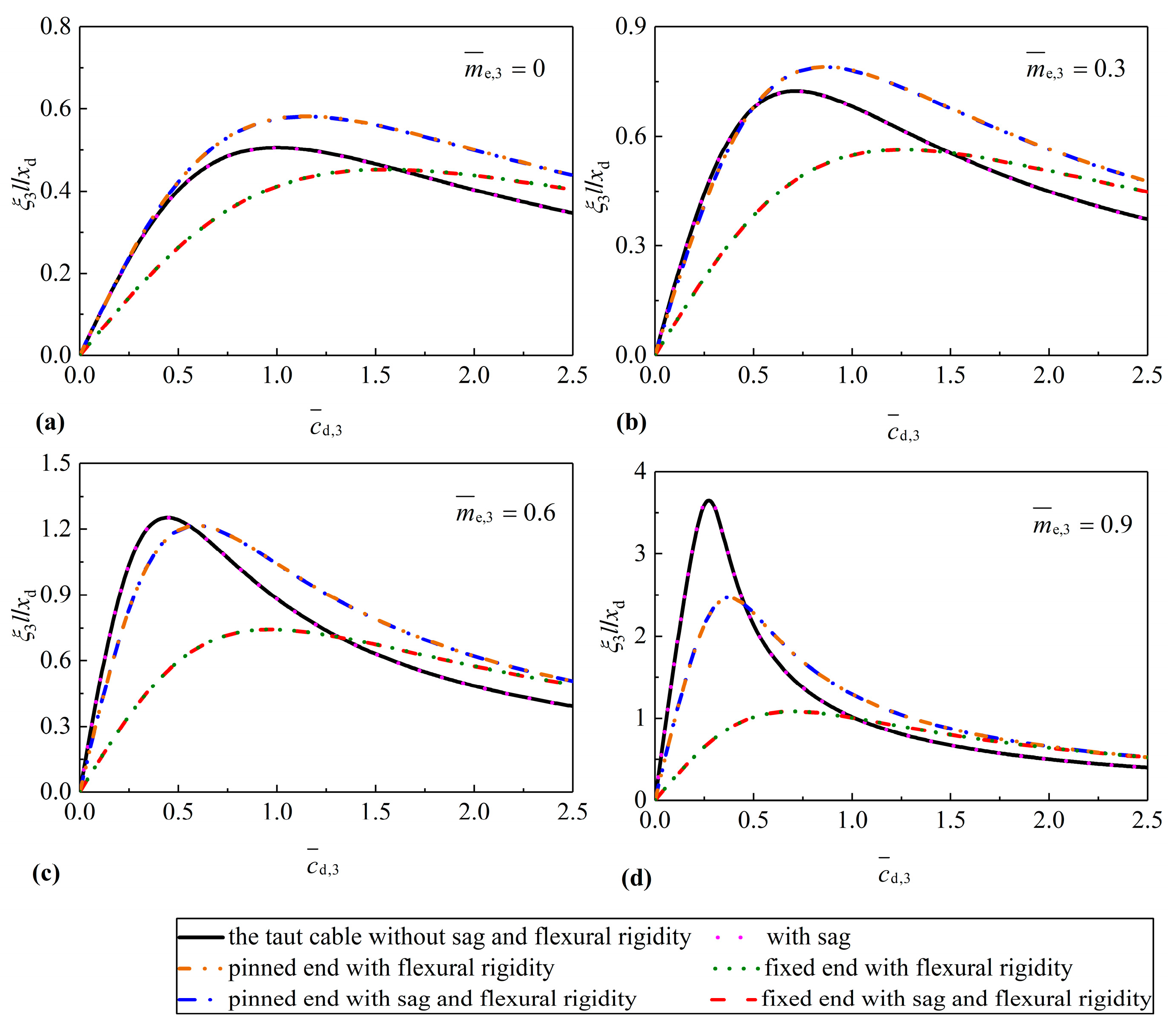
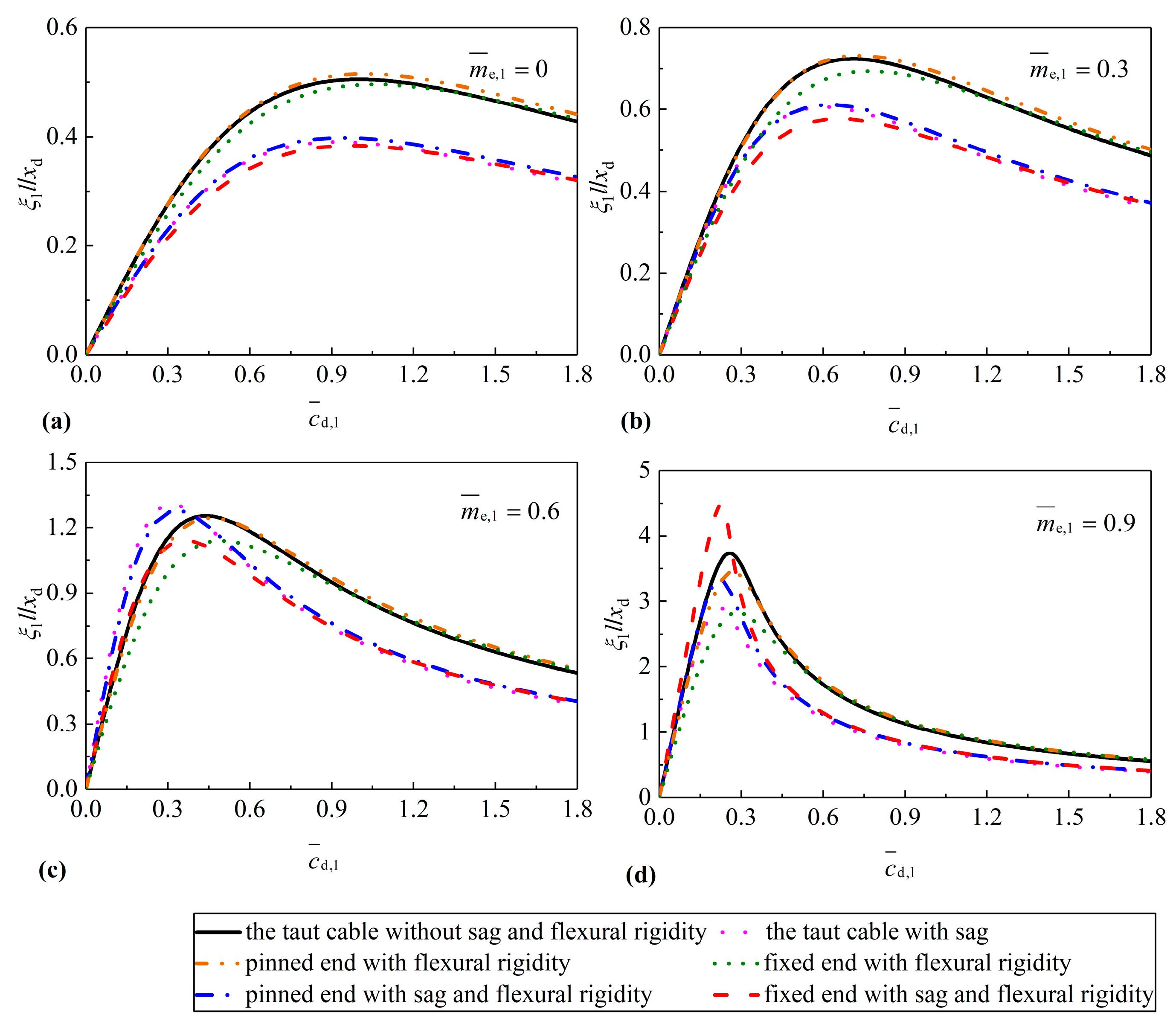
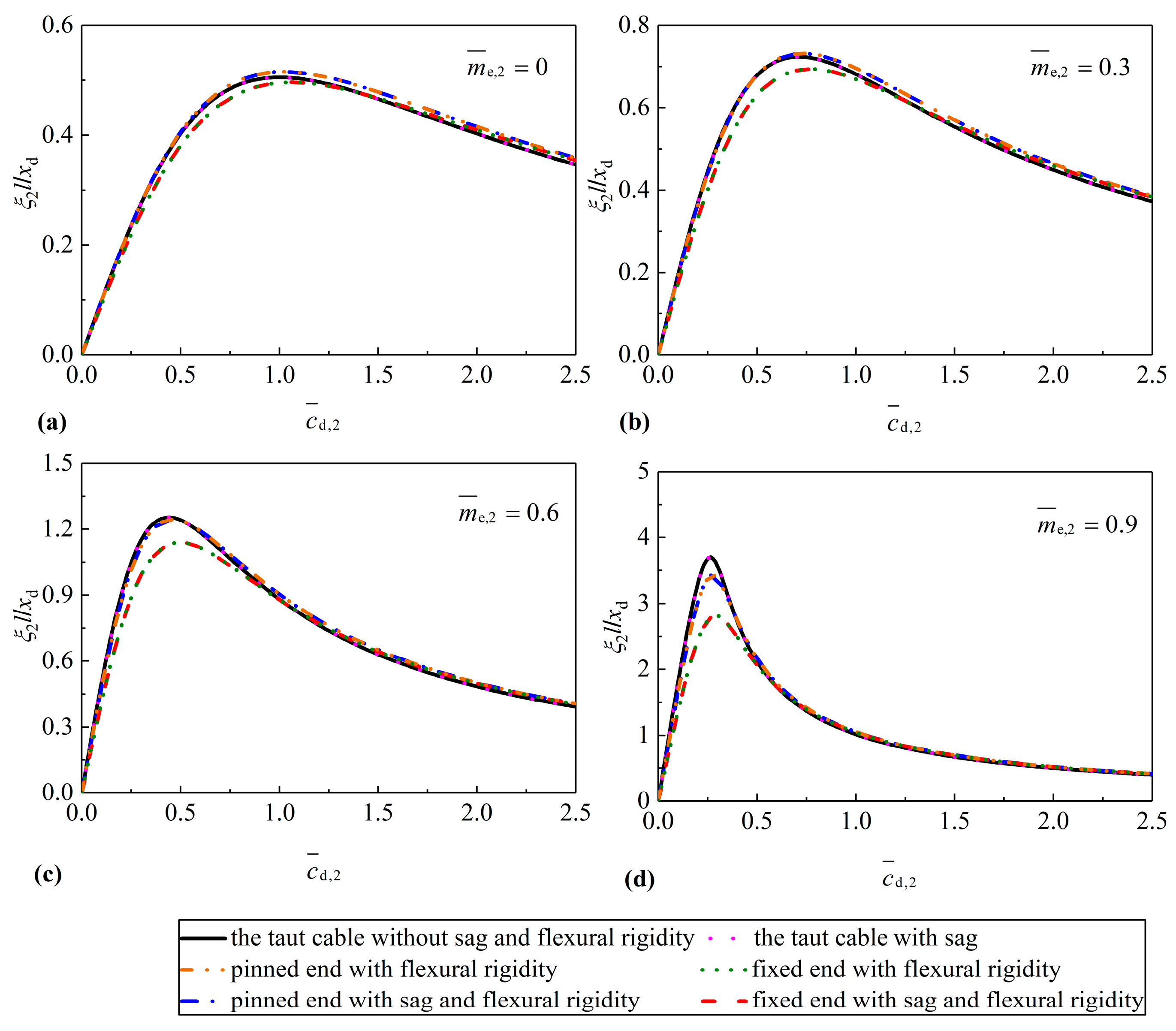
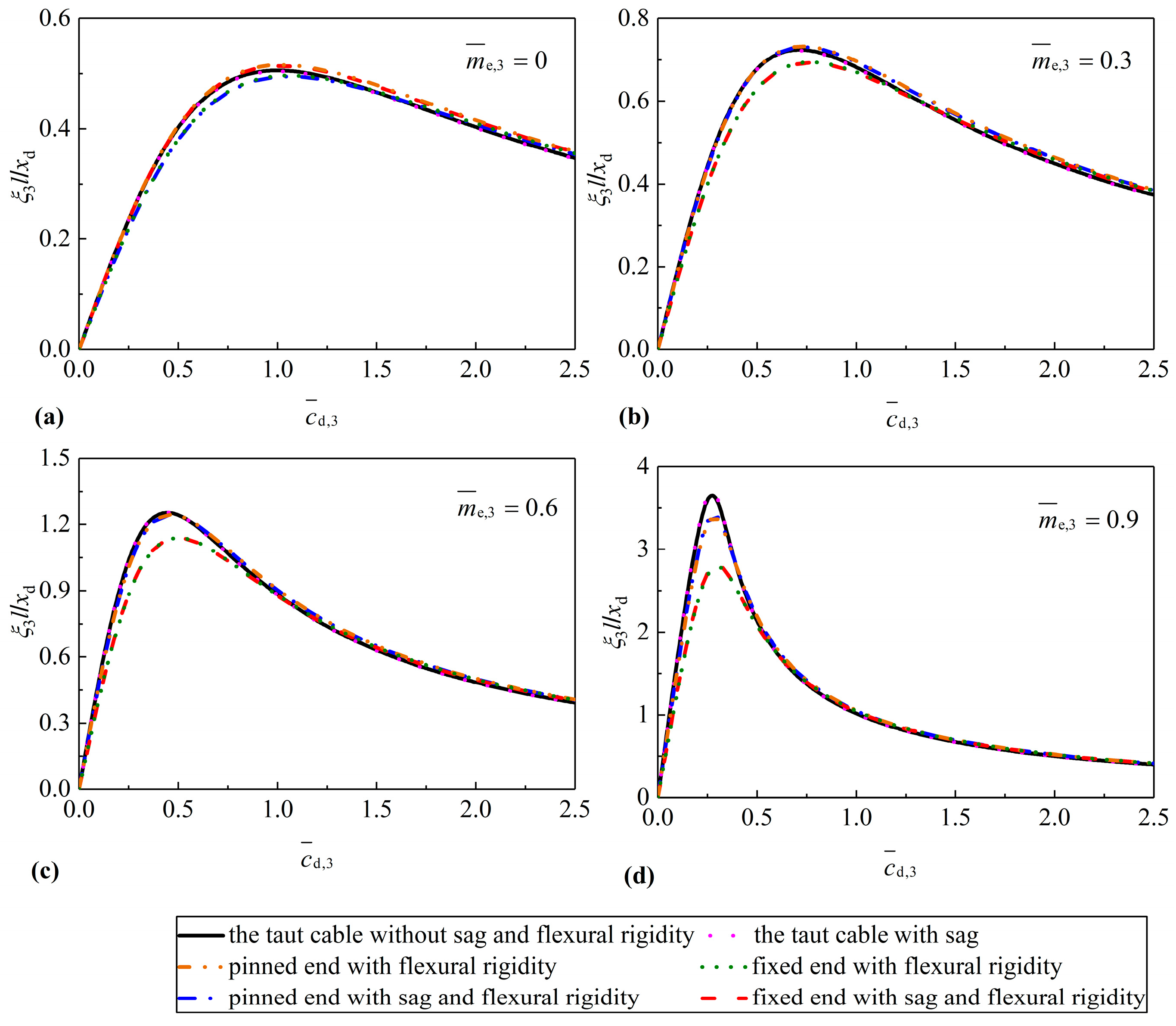
4. Case Studies
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, Z.Q.; Wang, X.Y.; Ko, J.M.; Ni, Y.Q.; Spencer, B.F.; Yang, G. MR damping system for mitigating wind-rain induced vibration on Dongting Lake Cable-Stayed Bridge. Wind Struct. 2004, 7, 293–304. [Google Scholar] [CrossRef]
- Jakobsen, J.B.; Andersen, T.L.; Macdonald, J.H.G.; Nikitas, N.; Larose, G.L.; Savage, M.G.; McAuliffe, B.R. Wind-induced response and excitation characteristics of an inclined cable model in the critical Reynolds number range. J. Wind Eng. Ind. Aerod. 2012, 110, 100–112. [Google Scholar] [CrossRef]
- Nikitas, N.; Macdonald, J.H.G.; Jakobsen, J.B.; Andersen, T.L. Critical Reynolds number and galloping instabilities: Experiments on circular cylinders. Exp. Fluids 2012, 52, 1295–1306. [Google Scholar] [CrossRef]
- Mao, J.X.; Wang, H.; Feng, D.M.; Tao, T.Y.; Zheng, W.Z. Investigation of dynamic properties of long-span cable-stayed bridges based on one-year monitoring data under normal operating condition. Struct. Control Health Monit. 2018, e2146, 1–19. [Google Scholar] [CrossRef]
- Wang, H.; Mao, J.X.; Spencer, B.F. A monitoring-based approach for evaluating dynamic responses of riding vehicle on long-span bridge under strong winds. Eng. Struct. 2019, 189, 35–47. [Google Scholar] [CrossRef]
- Acampora, A.; Macdonald, J.H.G.; Georgakis, C.T.; Nikitas, N. Identification of aeroelastic forces and static drag coefficients of a twin cable bridge stay from full-scale ambient vibration measurements. J. Wind Eng. Ind. Aerod. 2014, 124, 90–98. [Google Scholar] [CrossRef]
- Nikitas, N.; Macdonald, J.H.G. Aerodynamic forcing characteristics of dry cable galloping at critical Reynolds numbers. Eur. J. Mech. B Fluid 2015, 49, 243–249. [Google Scholar] [CrossRef]
- Rezaei Rad, A.; Banazadeh, M. Probabilistic risk-based performance evaluation of seismically base-isolated steel structures subjected to far-field earthquakes. Buildings 2018, 8, 128. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Chen, Y.; Ko, J.M.; Cao, D.Q. Neuro-control of cable vibration using semi-active magnetorheological dampers. Eng. Struct. 2002, 24, 295–307. [Google Scholar] [CrossRef]
- Duan, Y.F.; Ni, Y.Q.; Ko, J.M. State-derivative feedback control of cable vibration using semi-active MR dampers. Comput. Aided Civ. Inf. 2005, 20, 431–449. [Google Scholar] [CrossRef]
- Pakos, W.; Grosel, J. Reduction of cable vibrations in a cable stayed bridge under bi-harmonic excitation. Eng. Struct. 2019, 189, 1–10. [Google Scholar] [CrossRef]
- Kleissl, K.; Georgakis, C.T. Comparison of the aerodynamics of bridge cables with helical fillets and a pattern-indented surface. J. Wind Eng. Ind. Aerod. 2012, 104, 166–175. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Nagahawatta, H.D. Damping effects of cable cross ties in cable-stayed bridge. J. Wind Eng. Ind. Aerod. 1995, 54, 35–43. [Google Scholar] [CrossRef]
- Pacheco, B.M.; Fujino, Y.; Sulekh, A. Estimation curve for modal damping in stay cables with viscous damper. J. Struct. Eng. 1993, 119, 1961–1979. [Google Scholar] [CrossRef]
- Wang, Z.H.; Chen, Z.Q.; Gao, H.; Wang, H. Development of a self-powered magnetorheological damper system for cable vibration control. Appl. Sci. 2018, 8, 1–17. [Google Scholar] [CrossRef]
- Zhou, H.J.; Yang, X.; Sun, L.M.; Xing, F. Free vibrations of a two-cable network with near-support dampers and a cross-link. Struct. Control Health Monit. 2015, 22, 1173–1192. [Google Scholar] [CrossRef]
- Ahmad, J.; Cheng, S.H.; Ghrib, F. Combined effect of external damper and cross-tie on the modal response of hybrid two-cable networks. J. Sound Vib. 2018, 417, 132–148. [Google Scholar] [CrossRef]
- Main, J.A.; Jones, N.P. Evaluation of viscous dampers for stay-cable vibration mitigation. J. Bridge Eng. 2001, 6, 385–397. [Google Scholar] [CrossRef]
- Zhou, H.J.; Sun, L.M.; Xing, F. Damping of full-scale stay cable with viscous damper: Experiment and analysis. Adv. Struct. Eng. 2014, 17, 265–274. [Google Scholar] [CrossRef]
- Krenk, S. Vibration of a taut cable with an external damper. J. Appl. Mech. 2000, 67, 772–776. [Google Scholar] [CrossRef]
- Fournier, J.A.; Cheng, S.H. Impact of damper stiffness and damper support stiffness on the efficiency of a linear viscous damper in controlling stay cable vibrations. J. Bridge Eng. 2013, 19, 04013022. [Google Scholar] [CrossRef]
- Christenson, R.E.; Spencer, B.F.; Johnson, E.A. Experimental verification of smart cable damping. J. Eng. Mech. 2006, 132, 268–278. [Google Scholar] [CrossRef]
- Duan, Y.F.; Ni, Y.Q.; Ko, J.M. Cable vibration control using magnetorheological dampers. J. Intell. Mater. Syst. Struct. 2006, 17, 321–325. [Google Scholar] [CrossRef]
- Li, H.; Liu, M.; Ou, J.P. Negative stiffness characteristics of active and semi-active control systems for stay cables. Struct. Control Health Monit. 2008, 15, 120–142. [Google Scholar] [CrossRef]
- Høgsberg, J. The role of negative stiffness in semi-active control of magneto-rheological dampers. Struct. Control Health Monit. 2011, 18, 289–304. [Google Scholar] [CrossRef]
- Weber, F.; Boston, C. Clipped viscous damping with negative stiffness for semi-active cable damping. Smart Mater. Struct. 2011, 20, 045007. [Google Scholar] [CrossRef]
- Weber, F.; Distl, H. Semi-active damping with negative stiffness for multi-mode cable vibration mitigation: Approximate collocated control solution. Smart Mater. Struct. 2015, 24, 115015. [Google Scholar] [CrossRef]
- Salari, S.; Hormozabad, S.J.; Ghorbani-Tanha, A.K.; Rahimian, M. Innovative Mobile TMD System for Semi-active Vibration Control of Inclined Sagged Cables. KSCE J. Civ. Eng. 2019, 23, 641–653. [Google Scholar] [CrossRef]
- Cai, C.S.; Wu, W.J.; Araujo, M. Cable vibration control with a TMD-MR damper system: Experimental exploration. J. Struct. Eng. 2007, 133, 629–637. [Google Scholar] [CrossRef]
- Liu, M.; Song, G.B.; Li, H. Non-model-based semi-active vibration suppression of stay cables using magneto-rheological fluid dampers. Smart Mater. Struct. 2007, 16, 1447–1452. [Google Scholar] [CrossRef]
- Li, H.; Liu, M.; Li, J.H.; Guan, X.C.; Ou, J.P. Vibration control of stay cables of Shandong Binzhou Yellow River Highway Bridge by using magnetorheological fluid dampers. J. Bridge Eng. 2007, 12, 401–409. [Google Scholar] [CrossRef]
- Weber, F.; Distl, H. Amplitude and frequencyindependent cable damping of Sutong Bridge and Russky Bridge by magnetorheological dampers. Struct. Control Health Monit. 2015, 22, 237–254. [Google Scholar] [CrossRef]
- Chen, L.; Sun, L.M.; Nagarajaiah, S. Cable with discrete negative stiffness device and viscous damper: Passive realization and general characteristics. Smart Struct. Syst. 2015, 15, 627–643. [Google Scholar] [CrossRef]
- Zhou, P.; Li, H. Modeling and control performance of a negative stiffness damper for suppressing stay cable vibrations. Struct. Control Health Monit. 2016, 23, 764–782. [Google Scholar] [CrossRef]
- Shi, X.; Zhu, S.Y.; Spencer, B.F. Experimental study on passive negative stiffness damper for cable vibration mitigation. J. Eng. Mech. 2017, 143, 04017070. [Google Scholar] [CrossRef]
- Javanbakht, M.; Cheng, S.H.; Ghrib, F. Refined damper design formula for a cable equipped with a positive or negative stiffness damper. Struct. Control Health Monit. 2018, e2236, 1–23. [Google Scholar] [CrossRef]
- Li, H.N.; Sun, T.; Lai, Z.L.; Nagarajaiah, S. Effectiveness of negative stiffness system in the benchmark structural-control problem for seismically excited highway bridges. J. Bridge Eng. 2018, 23, 04018001. [Google Scholar] [CrossRef]
- Zhou, P.; Liu, M.; Xiao, H.G.; Li, H. Feasibility of using a negative stiffness damper to two interconnected Stay Cables for damping enhancement. Int. J. Struct. Stab. Dyn. 2019, 1950058. [Google Scholar] [CrossRef]
- Zhou, H.J.; Huang, X.G.; Xiang, N.; He, J.W.; Sun, L.M.; Xing, F. Free vibration of a taut cable with a damper and a concentrated mass. Struct. Control Health Monit. 2018, e2251, 1–21. [Google Scholar] [CrossRef]
- Ikago, K.; Saito, K.; Inoue, N. Seismic control of single-degree-of-freedom structure using tuned viscous mass damper. Earthq. Eng. Struct. D 2012, 41, 453–474. [Google Scholar] [CrossRef]
- Lazar, I.F.; Neild, S.A.; Wagg, D.J. Using an inerter-based device for structural vibration suppression. Earthq. Eng. Strut. D 2014, 43, 1129–1147. [Google Scholar] [CrossRef]
- Nakamura, Y.; Fukukita, A.; Tamura, K.; Matsuoka, T.; Hiramoto, K.; Sunakoda, K. Seismic response control using electro-magnetic inertial mass damper. Earthq. Eng. Struct. D 2014, 43, 507–527. [Google Scholar] [CrossRef]
- Wen, Y.K.; Chen, Z.Q.; Hua, X.G. Design and evaluation of tuned inerter-based dampers for the seismic control of MDOF structures. J. Struct. Eng. 2016, 143, 04016207. [Google Scholar] [CrossRef]
- Pan, C.; Zhang, R.F. Design of structure with inerter system based on stochastic response mitigation ratio. Struct. Control Health Monit. 2018, e2169, 1–21. [Google Scholar] [CrossRef]
- Luo, J.N.; Jiang, J.Z.; Macdonald, J.H.G. Cable vibration suppression with inerter-based absorbers. J. Eng. Mech. 2019, 145, 04018134. [Google Scholar] [CrossRef]
- Wang, Z.H.; Gao, H.; Wang, H.; Chen, Z.Q. Development of stiffness-adjustable tuned mass dampers for frequency retuning. Adv. Struct. Eng. 2019, 22, 473–485. [Google Scholar] [CrossRef]
- Sun, H.X.; Zuo, L.; Wang, X.Y.; Peng, J.; Wang, W.X. Exact H2 optimal solutions to inerter-based isolation systems for building structures. Struct. Control Health Monit. 2019, e2357, 1–21. [Google Scholar]
- Zhu, H.P.; Li, Y.M.; Shen, W.A.; Zhu, S.Y. Mechanical and energy-harvesting model for electro-magnetic inertial mass dampers. Mech. Syst. Signal Pr. 2019, 120, 203–220. [Google Scholar] [CrossRef]
- Lu, L.; Duan, Y.F.; Spencer, B.F.; Lu, X.L.; Zhou, Y. Inertial mass damper for mitigating cable vibration. Struct. Control Health Monit. 2017, 24, 1–12. [Google Scholar] [CrossRef]
- Cu, V.H.; Han, B.; Pham, D.H.; Yan, W.T. Free vibration and damping of a taut cable with an attached viscous mass damper. KSCE J. Civ. Eng. 2018, 22, 1792–1802. [Google Scholar] [CrossRef]
- Shi, X.; Zhu, S.Y. Dynamic characteristics of stay cables with inerter dampers. J. Sound Vib. 2018, 423, 287–305. [Google Scholar] [CrossRef]
- Lazar, I.F.; Neild, S.A.; Wagg, D.J. Vibration suppression of cables using tuned inerter dampers. Eng. Struct. 2016, 122, 62–71. [Google Scholar] [CrossRef]
- Sun, L.M.; Hong, D.X.; Chen, L. Cables interconnected with tuned inerter damper for vibration mitigation. Eng. Struct. 2017, 151, 57–67. [Google Scholar] [CrossRef]
- Xu, Y.L.; Yu, Z. Vibration of inclined sag cables with oil dampers in cable stayed bridges. J. Bridge Eng. 1998, 3, 194–203. [Google Scholar] [CrossRef]
- Krenk, S.; Nielsen, S.R.K. Vibrations of a shallow cable with a viscous damper. Proc. R. Soc. Lond. A 2002, 458, 339–357. [Google Scholar] [CrossRef]
- Johnson, E.A.; Christenson, R.E.; Spencer, B.F. Semiactive damping of cables with sag. Comput. Aided Civ. Inf. 2003, 18, 132–146. [Google Scholar] [CrossRef]
- Hoang, N.; Fujino, Y. Analytical study on bending effects in a stay cable with a damper. J. Eng. Mech. 2007, 133, 1241–1246. [Google Scholar] [CrossRef]
- Fujino, Y.; Hoang, N. Design formulas for damping of a stay cable with a damper. J. Struct. Eng. 2008, 134, 269–278. [Google Scholar] [CrossRef]
- Tabatabai, H.; Mehrabi, A.B. Design of mechanical viscous dampers for stay cables. J. Bridge Eng. 2000, 5, 114–123. [Google Scholar] [CrossRef]
- Cheng, S.H.; Darivandi, N.; Ghrib, F. The design of an optimal viscous damper for a bridge stay cable using energy-based approach. J. Sound Vib. 2010, 329, 4689–4704. [Google Scholar] [CrossRef]
- Main, J.A.; Jones, N.P. Vibration of tensioned beams with intermediate damper. II: Damper near a support. J. Eng. Mech. 2007, 133, 379–388. [Google Scholar] [CrossRef]
- Javanbakht, M.; Cheng, S.H.; Ghrib, F. Control-oriented model for the dynamic response of a damped cable. J. Sound Vib. 2019, 442, 249–267. [Google Scholar] [CrossRef]
- Wang, Z.H.; Gao, H.; Fan, B.Q.; Chen, Z.Q. Inertial mass damper for vibration control of cable with sag. J. Low Freq. Noise Vib. Act. Control 2018. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, J. Practical formula for cable tension estimation by vibration method. J. Struct. Eng. 2010, 17, 161–164. [Google Scholar] [CrossRef]
- Wang, Z.H.; Xu, Y.W.; Gao, H.; Chen, Z.Q.; Xu, K.; Zhao, S.B. Vibration control of a stay cable with a rotary electromagnetic inertial mass damper. Smart Struct. Syst. 2019, 23. in press. [Google Scholar]



| Parameter | Value |
|---|---|
| Cable length l (m) | 11.4 |
| Cable cross-section area A (cm2) | 1.374 |
| Mass per unit length m (kg/m) | 9.5 |
| Elastic modulus E (GPa) | 200 |
| Flexural rigidity EI (N/m2) | 42.95 |
| Static tension T (kN) | 19.2 |
| Inclination angle θ (°) | 0 |
| Sag parameter λ2 | 4.513 |
| Case | Inertialmass (kg) | Damping Coefficient (Ns/m) | Source | |||
|---|---|---|---|---|---|---|
| Experiment (%) | Theory (%) | |||||
| EI = 0, λ2 = 0 | With EI and λ2 | |||||
| Pinned end | Fixed end | |||||
| 1 | 102.6 | 4659 | 0.23 | 0.37 | 0.27 | 0.13 |
| 3117 | 0.18 | 0.26 | 0.19 | 0.09 | ||
| 2 | 140.5 | 4778 | 0.28 | 0.40 | 0.30 | 0.14 |
| 3356 | 0.21 | 0.30 | 0.22 | 0.10 | ||
| 3 | 259.7 | 5488 | 0.31 | 0.54 | 0.42 | 0.18 |
| 4636 | 0.35 | 0.49 | 0.38 | 0.16 | ||
| 4 | 422.0 | 4968 | 0.48 | 0.71 | 0.58 | 0.22 |
| 3197 | 0.41 | 0.53 | 0.44 | 0.15 | ||
| Case | Inertial Mass (kg) | Damping Coefficient (Ns/m) | Source | |||
|---|---|---|---|---|---|---|
| Experiment (%) | Theory (%) | |||||
| EI = 0, λ2 = 0 | With EI and λ2 | |||||
| Pinned end | Fixed end | |||||
| 1 | 102.6 | 2884 | 0.65 | 0.74 | 0.70 | 0.29 |
| 4160 | 0.61 | 0.81 | 0.84 | 0.39 | ||
| 2 | 140.5 | 2921 | 0.82 | 1.02 | 0.92 | 0.35 |
| 4536 | 0.77 | 1.00 | 1.06 | 0.48 | ||
| 3 | 259.7 | 1847 | 2.01 | 5.02 | 2.28 | 0.46 |
| 3704 | 1.23 | 1.98 | 2.35 | 0.77 | ||
| 4 | 422.0 | 3298 | 2.01 | 0.81 | 1.76 | 2.40 |
| 4015 | 1.90 | 0.84 | 1.74 | 2.31 | ||
| Parameters | Short Cable (Dongting Lake Bridge) | Medium Cable (Stonecutters Bridge) | Long Cable (Sutong Bridge) |
|---|---|---|---|
| Cable length l (m) | 114.7 | 306.7 | 576.8 |
| Mass per unit length m (kg/m) | 51.8 | 98.6 | 100.8 |
| Flexural rigidity EI (N/m2) | 3.842 × 103 | 5.525 × 106 | 2.309 × 106 |
| Axial stiffness EA(N) | 1.255 × 109 | 2.429 × 109 | 2.409 × 109 |
| Inclination angle θ (°) | 37.0 | 30.5 | 22.5 |
| Sag parameter λ2 | 0.0915 | 0.9365 | 2.2101 |
| Tension force T (kN) | 3095 | 5530 | 6708 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Yue, F.; Wang, H.; Gao, H.; Fan, B. Refined Study on Free Vibration of a Cable with an Inertial Mass Damper. Appl. Sci. 2019, 9, 2271. https://doi.org/10.3390/app9112271
Wang Z, Yue F, Wang H, Gao H, Fan B. Refined Study on Free Vibration of a Cable with an Inertial Mass Damper. Applied Sciences. 2019; 9(11):2271. https://doi.org/10.3390/app9112271
Chicago/Turabian StyleWang, Zhihao, Fangfang Yue, Hao Wang, Hui Gao, and Buqiao Fan. 2019. "Refined Study on Free Vibration of a Cable with an Inertial Mass Damper" Applied Sciences 9, no. 11: 2271. https://doi.org/10.3390/app9112271
APA StyleWang, Z., Yue, F., Wang, H., Gao, H., & Fan, B. (2019). Refined Study on Free Vibration of a Cable with an Inertial Mass Damper. Applied Sciences, 9(11), 2271. https://doi.org/10.3390/app9112271






